Mechanical Model and Damping Effect of a Particle-Inertial Damper
Abstract
:1. Introduction
2. Mechanical Model of the PID
2.1. Without Particle Collision
2.2. With Particle Collision
2.3. Displacement Response Characteristic of SDOF-PID
3. Damping Effect of PID
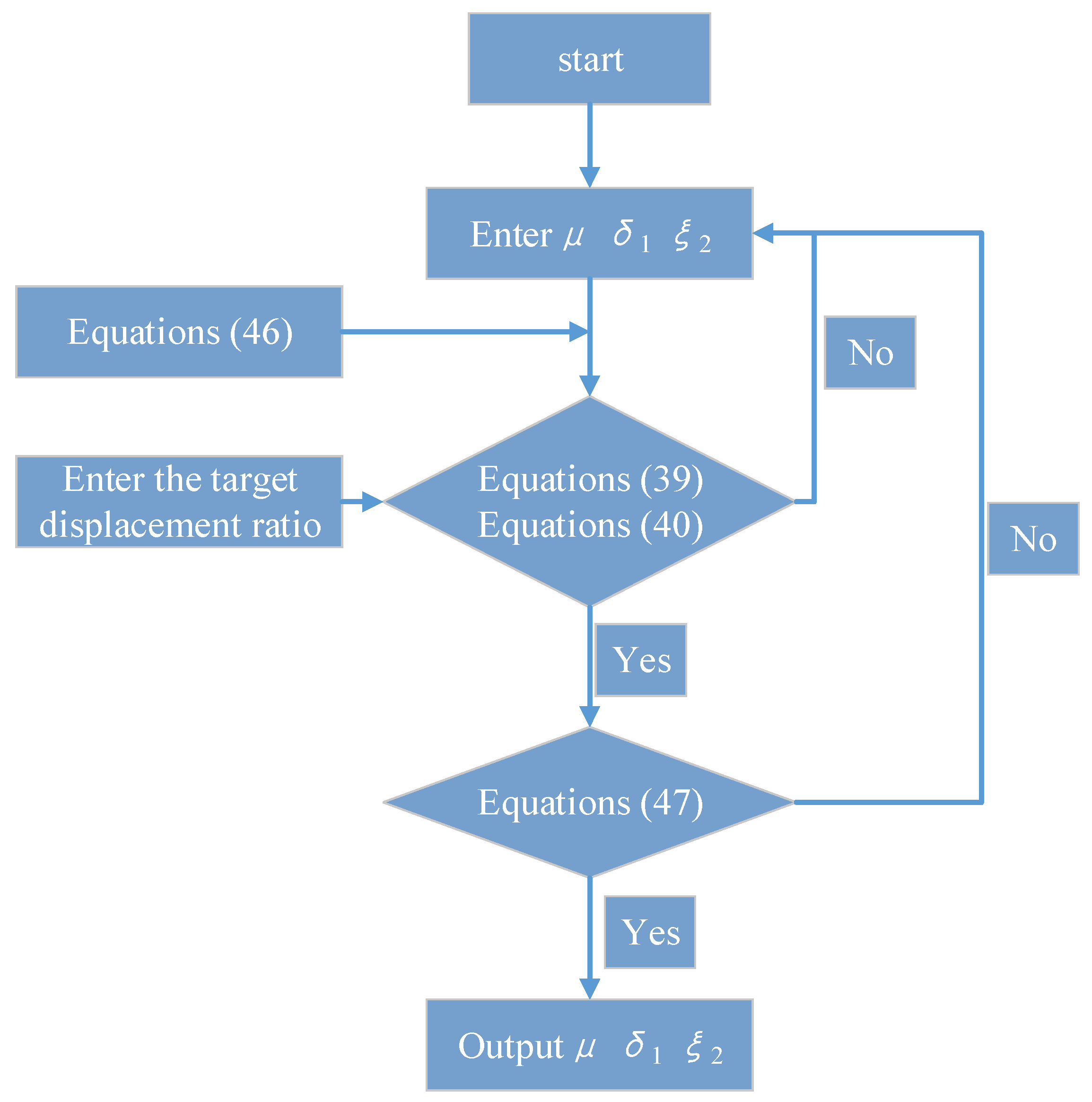
3.1. Parameter Optimization
3.1.1. Fixed Point Theory
3.1.2. Performance–Cost Theory
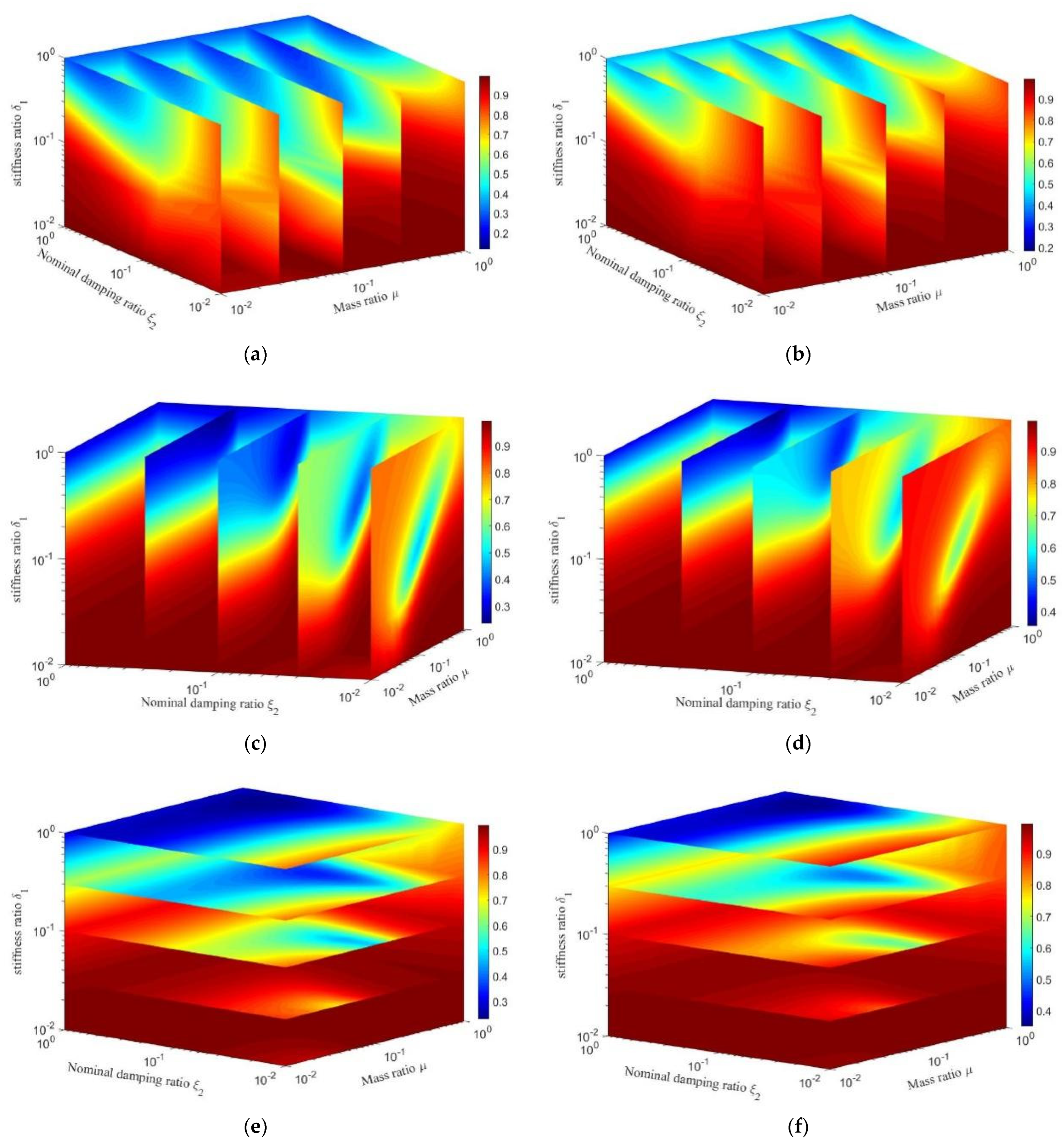
3.2. Parameter Optimization of the SDOF with Different Dampers
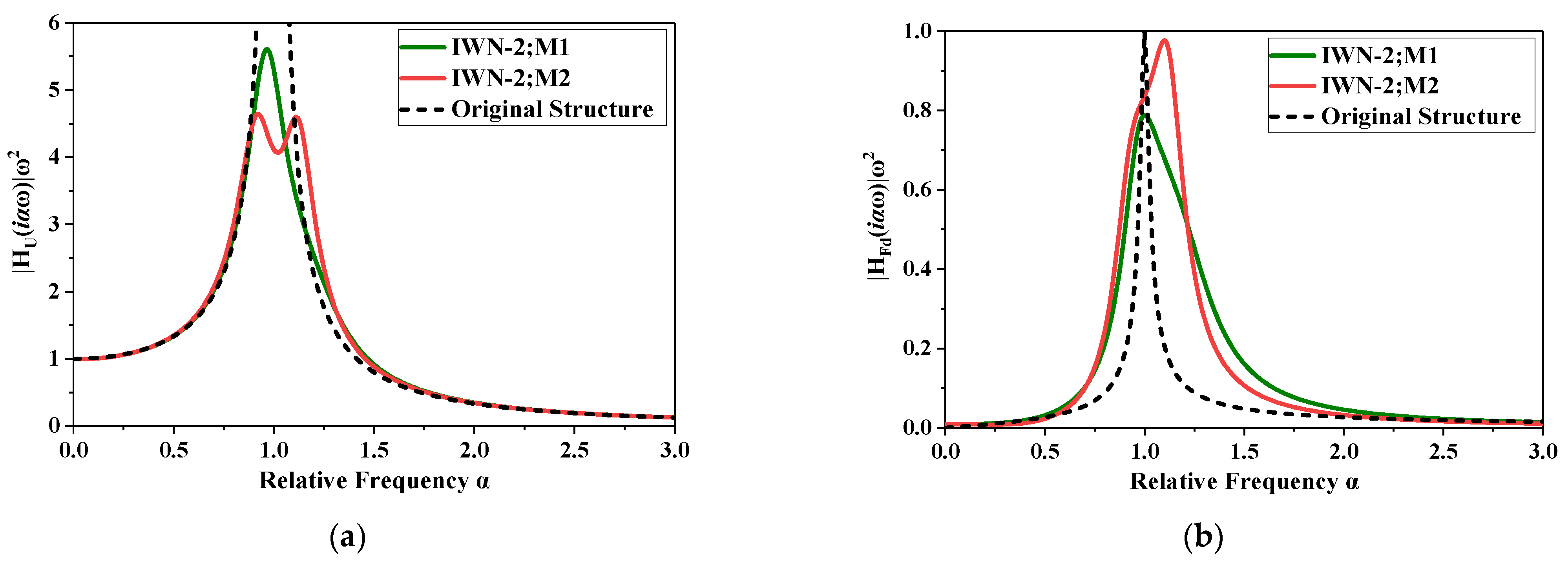
3.3. Damping Effect Analysis
4. Conclusions
- (1)
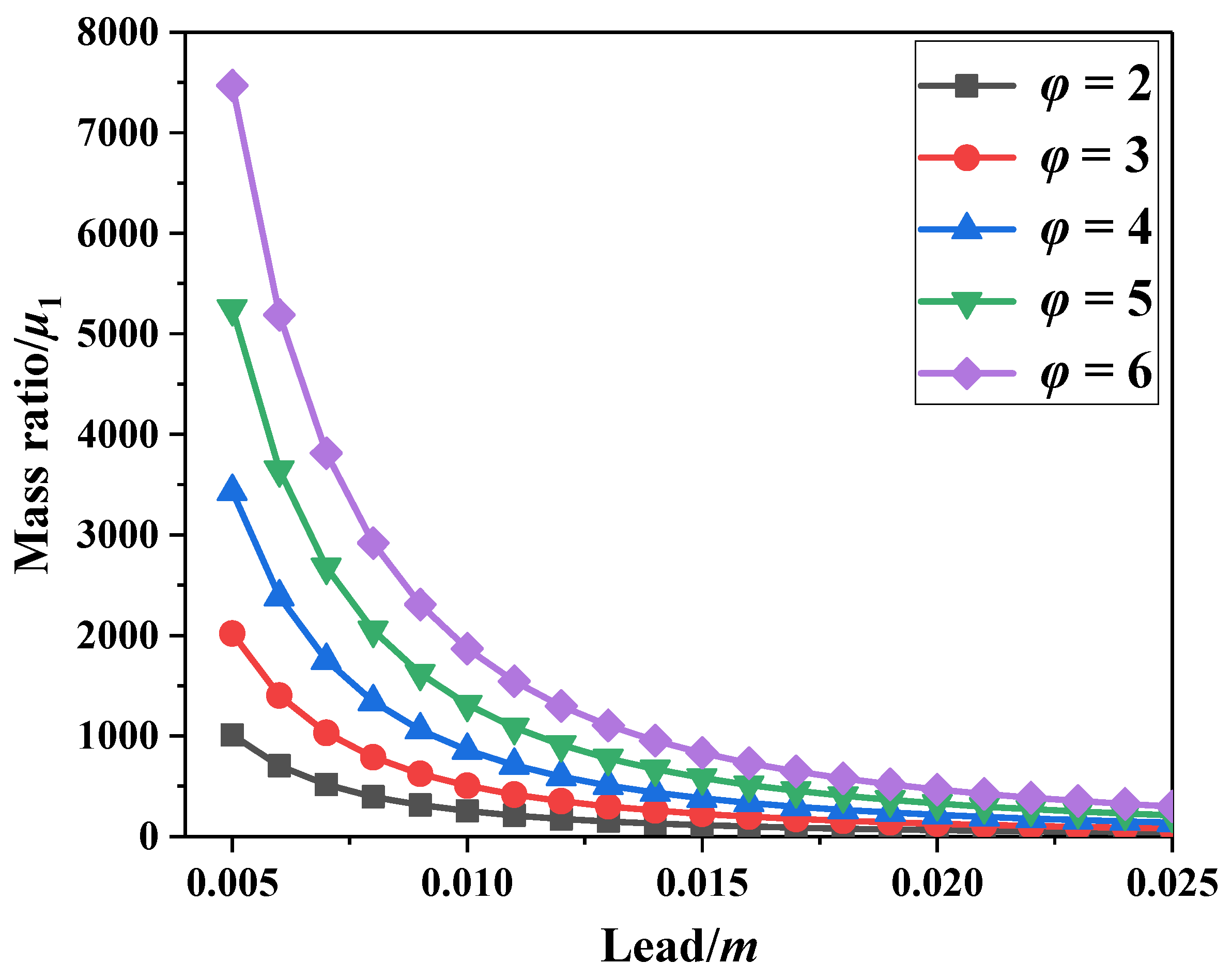
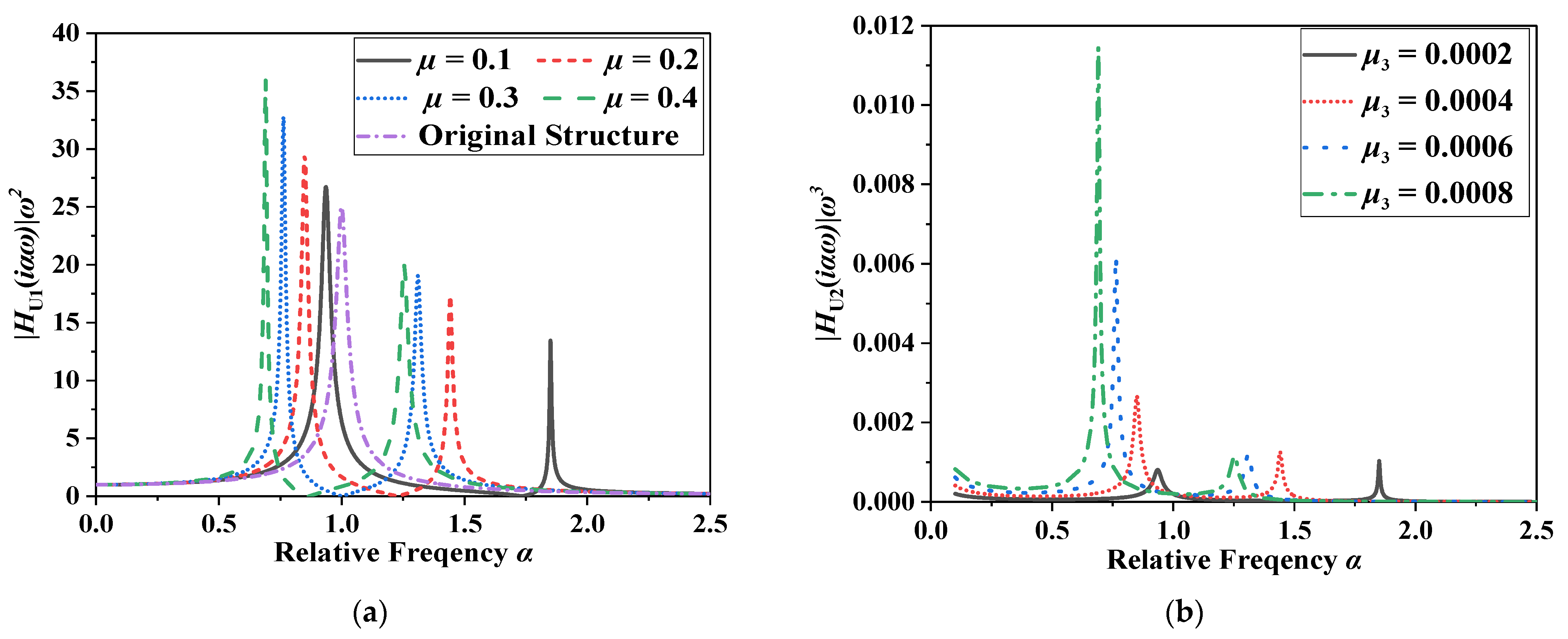
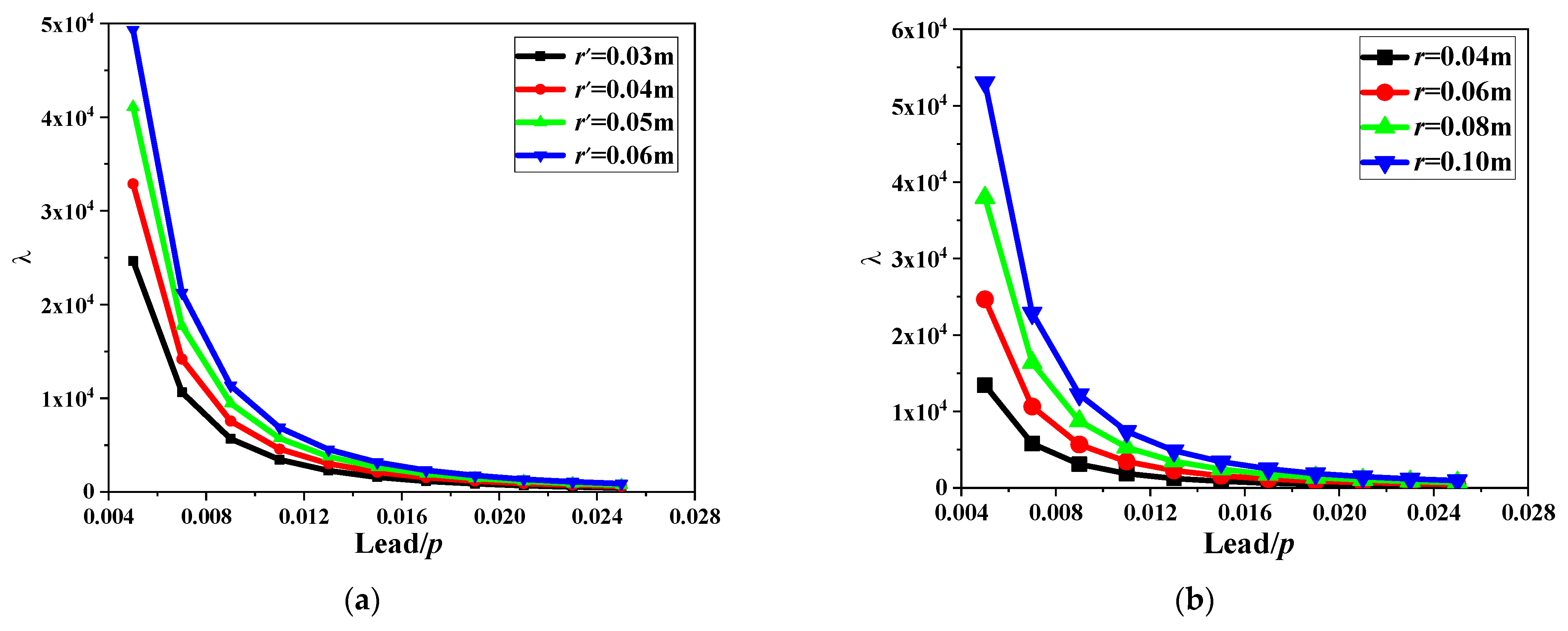
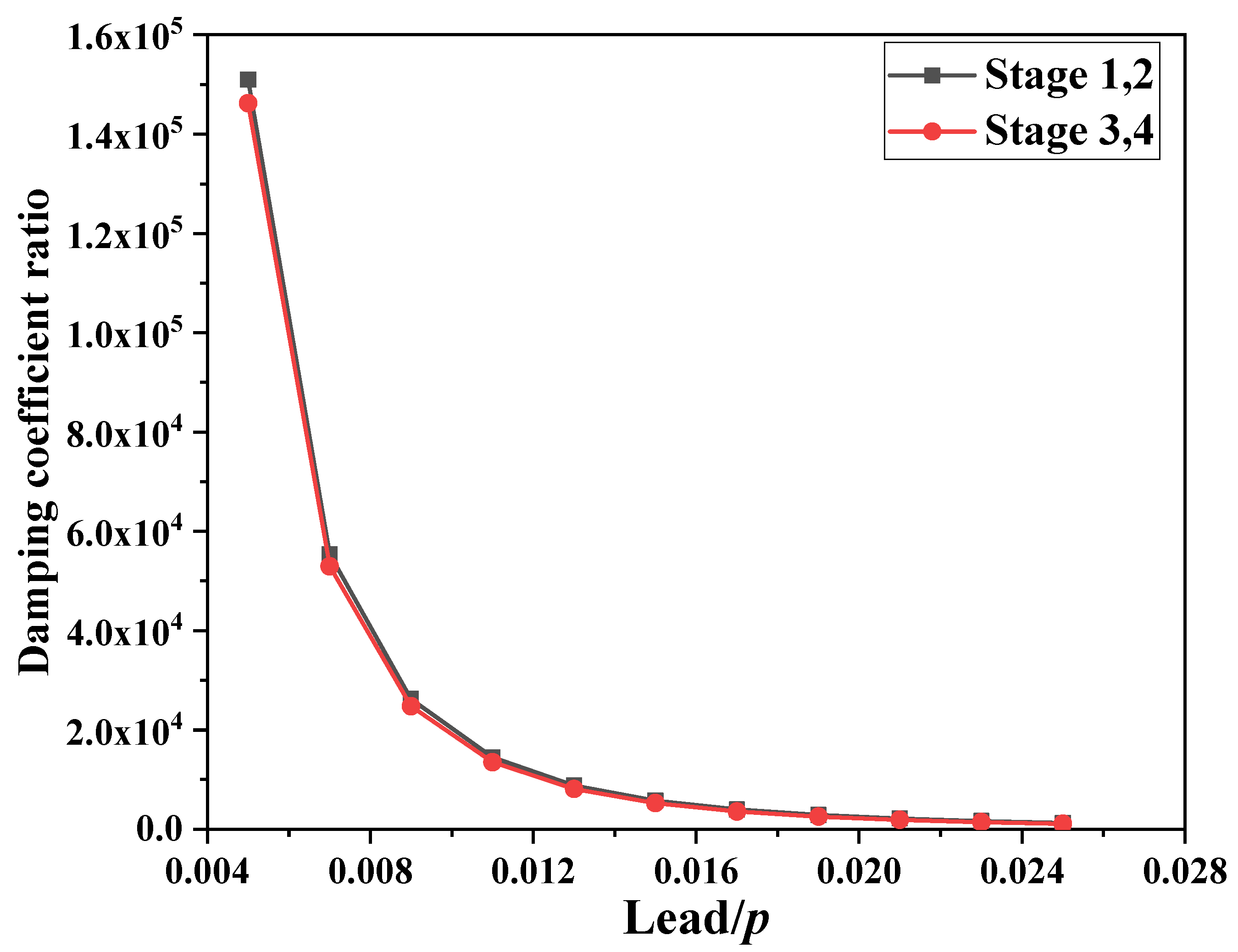
- The mechanical model of the SDOF-PID considering particle rolling friction and particle collision can be used for analysing the damping effect and damping mechanism of the PID and for the relevant dynamic response of the SDOF. Without particle collision, the particle rolling friction has little influence on the inertia amplification effect of the PID and displacement response of the SDOF-PID. Under harmonic excitation, the damping mechanism of the PID is affected significantly by its equivalent inertia coefficient, equivalent damping coefficient, and equivalent stiffness coefficient considering particle collision. These equivalent parameters are significantly influenced by the lead of the ball screw. Theoretically, the damping coefficient and stiffness of the proposed PID can be amplified thousands of times with certain optimized parameters;
- (2)
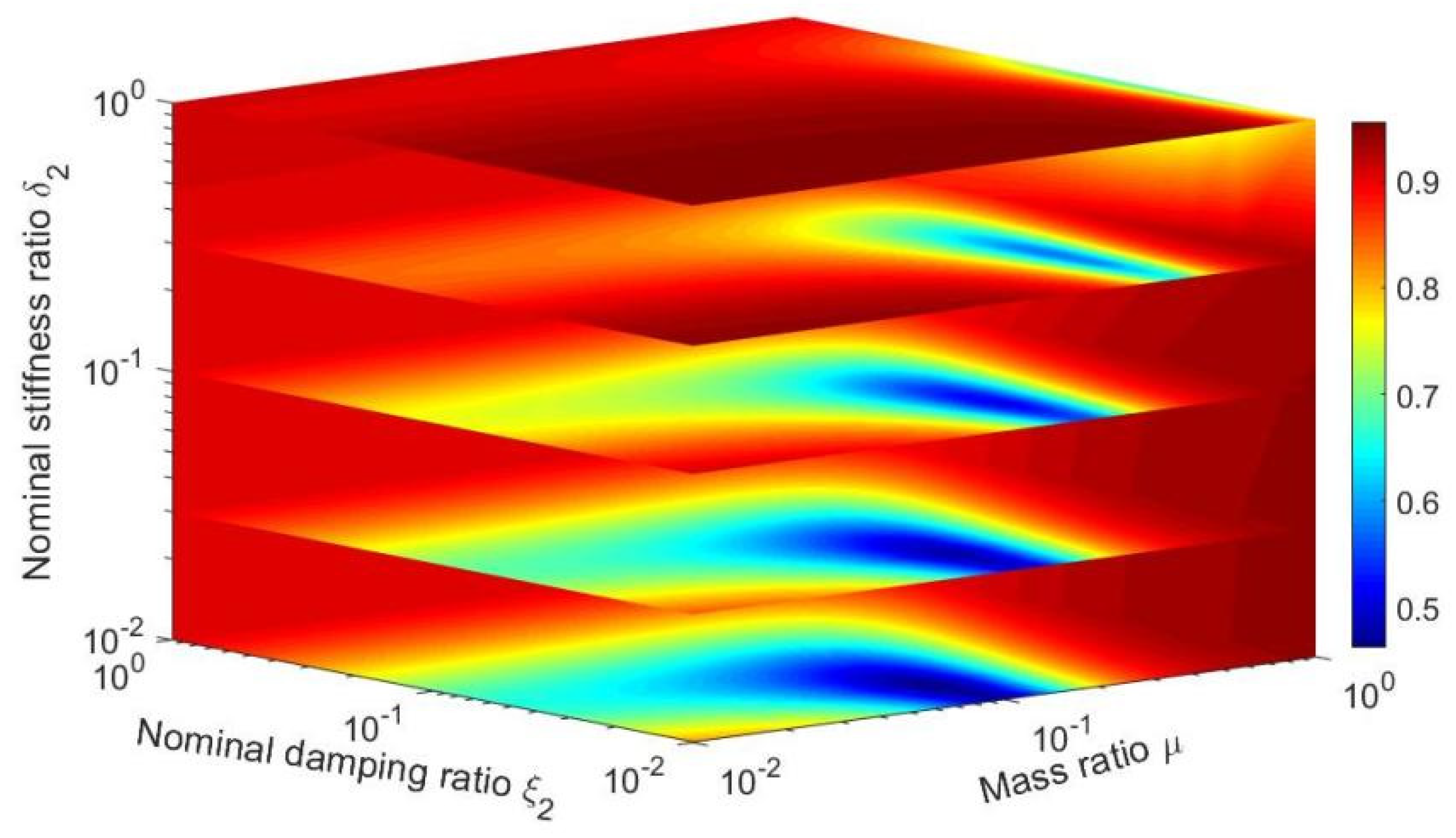
- The PID optimised based on fixed-point theory has a wide damping band for the SDOF. However, the fixed-point theory can result in a higher damping force (control cost) for the PID. The PID optimised by the ‘performance–cost’ theory can effectively reduce the output of the damping force (control cost) without affecting the rate of a decrease in displacement. However, the ‘performance–cost’ theory may induce poor robustness and a narrower damping band in the PID;
- (3)
- The damping effect of the PID on the SDOF under the most severe seismic excitation is better than that of the PID under white noise excitation. The damping effect of the PID under broadband excitation (actual ground motion) needs further exploration. Under the same damping capacity demand, the additional mass ratio of the PID is only one thousandth that of the TMD;
- (4)
- An equivalent linearization model of the PID can be used to optimize its design parameters without considering the high nonlinear characteristic. Therefore, the model of the PID needs to be verified through subsequent experiments. Moreover, the effective analysis methods of the PID or PID-controlled structure system need to be proposed and verified with considering the high nonlinear characteristic in future.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

- (1)
- Stage 1
- (2)
- Stage 2
- (3)
- Stage 3
- (4)
- Stage 4
References
- Fricke, J.R. Lodengraf damping: An advanced vibration damping technology. SV Sound Vib. 2000, 34, 22–27. [Google Scholar]
- Panossian, H.V. Structural damping enhancement via Non-obstructive particle damping technique. J. Vib. Acoust. 1992, 114, 101–105. [Google Scholar] [CrossRef]
- Mao, K.; Wang, M.Y.; Xu, Z.; Chen, T. Simulation and characterization of particle damping in transient vibrations. J. Vib. Acoust. 2004, 126, 202–211. [Google Scholar] [CrossRef]
- Lieber, P.; Jensen, D.P. An acceleration damper: Development, design and some application. Trans. Am. Soc. Mech. Eng. 1945, 67, 523–530. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, T.; Wang, X.; Fang, J. Rheology behavior and optimal damping effect of granular particles in a Non-obstructive particle damper. J. Sound Vib. 2015, 364, 30–43. [Google Scholar] [CrossRef]
- Paget, A.L. Vibration in steam turbine buckets and damping by impacts. Engineering 1937, 143, 305–307. [Google Scholar]
- Grubin, C. On the theory of the acceleration damper. J. Appl. Mech. 1956, 23, 373–378. [Google Scholar] [CrossRef]
- Masri, S.F.; Caughey, T.K. On the stability of the impact damper. J. Appl. Mech. 1966, 33, 586–592. [Google Scholar] [CrossRef]
- Masri, S.F. Analytical and experimental studies of multiple-unit impact dampers. J. Acoust. Soc. Am. 1969, 45, 1111–1117. [Google Scholar] [CrossRef]
- Saeki, M. Analytical study of multi-particle damping. J. Sound Vib. 2005, 281, 1133–1144. [Google Scholar] [CrossRef]
- Yan, W.; Wang, B.; He, H. Research of mechanical model of particle damper with friction effect and its experimental verification. J. Sound Vib. 2019, 460, 114898. [Google Scholar]
- He, H.; Wang, B.; Yan, W. Mechanical model and optimization analysis of multiple unidirectional single particle damper. J. Eng. Mech. 2021, 147, 1–19. [Google Scholar] [CrossRef]
- Lu, Z.; Ma, N.; Zhou, C. Multi-objective optimization design of multiple tuned impact dampers. J. Vib. Shock 2022, 41, 33–41. [Google Scholar]
- Akbar, M.A.; Wong, W.O.; Rustighi, E. A Hybrid Damper with Tunable Particle Impact Damping and Coulomb Friction. Machines 2023, 11, 545. [Google Scholar] [CrossRef]
- Papalou, A.; Masri, S.F. An experimental investigation of particle dampers under harmonic excitation. J. Vib. Acoust. 1998, 4, 361–379. [Google Scholar] [CrossRef]
- Friend, R.D.; Kinra, V.K. Particle impact damping. J. Sound Vib. 2000, 233, 93–118. [Google Scholar] [CrossRef]
- Saeki, M. Impact damping with granular materials in a horizontally vibrating system. J. Sound Vib. 2002, 251, 153–161. [Google Scholar] [CrossRef]
- Pendleton, S.; Basile, J.; Guerra, J.; Tran, B.; Ogomori, H.; Lee, S. Particle damping for launch vibration mitigation: Design and test validatio. In Proceedings of the 4th AIAA Multidisciplinary Design Optimization Specialists Conference, Schaumburg, IL, USA, 7–10 August 2008; pp. 7–10. [Google Scholar]
- Wang, X.; Liu, X.; Shan, Y.; He, T. Design, simulation and experiment of particle dampers attached to a precision instrument in spacecraft. J. Vibroeng. 2015, 17, 1605–1614. [Google Scholar]
- Lu, Z.; Lu, X.; Lu, W.; Masri, S.F. Experimental studies of the effects of buffered particle dampers attached to a multi-degree-of-freedom system under dynamic loads. J. Sound Vib. 2012, 331, 2007–2022. [Google Scholar] [CrossRef]
- Lu, Z.; Huang, B.; Zhou, Y. Theoretical study and experimental validation on the energy dissipation mechanism of particle dampers. Struct. Control Health Monit. 2018, 25, e2125. [Google Scholar] [CrossRef]
- Yan, W.; Xu, W.; Wang, J.; Chen, Y. Experimental Research on the Effects of a Tuned Particle Damper on a Viaduct System under Seismic Loads. J. Bridge Eng. 2014, 19, 04013004. [Google Scholar] [CrossRef]
- Luo, Z.; Yan, W.; Xu, W.; Zheng, Q.; Wang, B. Experimental research on the multilayer compartmental particle damper and its application methods on long-period bridge structures. Front. Struct. Civ. Eng. 2019, 13, 751–766. [Google Scholar] [CrossRef]
- Lu, Z.; Huang, Z.K. Analytical and experimental studies on particle damper used for tremor suppression. J. Vib. Control 2021, 27, 2887–2897. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, Q.Q.; Fan, Q.Q.; Li, Q. Studies on dissipative characteristics and equivalent model of particle damper in railway application. J. Sound Vib. 2023, 560, 117788. [Google Scholar] [CrossRef]
- Papalou, A.; Masri, S.F. Performance of particle dampers under random excitation. J. Vib. Acoust. 1996, 118, 614–621. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, X.; Zhou, Y. An equivalent method for optimization of particle tuned mass damper based on experimental parametric study. J. Sound Vib. 2018, 419, 571–584. [Google Scholar] [CrossRef]
- Huang, X.H.; Xu, W.B.; Yan, W.M. Equivalent model of a multiparticle damper considering the mass coupling coefficient. Struct. Control Health Monit. 2020, 27, e2580. [Google Scholar] [CrossRef]
- Shen, B.; Xu, W.; Wang, J.; Chen, Y.; Yan, W.; Huang, J.; Tang, Z. Seismic control of super high-rise structures with double-layer tuned particle damper. Earthq. Eng. Struct. Dyn. 2021, 50, 791–810. [Google Scholar] [CrossRef]
- Huang, X.H.; Xu, W.B.; Wang, J.; Yan, W.M.; Chen, Y.J. Equivalent model of a multi-particle damper considering particle rolling and its analytical solution. Struct. Control Health Monit. 2021, 28, e2718. [Google Scholar] [CrossRef]
- Huang, X.H.; Xu, W.B.; Yan, W.M.; Wang, J. Equivalent model and parameter analysis of non-packed particle damper. J. Sound Vib. 2021, 491, 115775. [Google Scholar] [CrossRef]
- Cao, X.-Y.; Shen, D.; Feng, D.-C.; Wang, C.-L.; Qu, Z.; Wu, G. Seismic retrofitting of existing frame buildings through externally attached sub-structures: State of the art review and future perspectives. J. Build. Eng. 2022, 57, 104904. [Google Scholar] [CrossRef]
- Liao, C.C.; Chung, Y.C.; Weng, C.H. A study on the energy dissipation mechanism of dynamic mechanical systems with particle dampers by using the novel energy method. Nonlinear Dyn. 2023, 111, 15955–15980. [Google Scholar] [CrossRef]
- Cao, X.-Y.; Feng, D.-C. Michael Consistent seismic hazard and fragility analysis considering combined capacity-demand uncertainties via probability density evolution method. Struct. Saf. 2023, 103, 102330. [Google Scholar] [CrossRef]
- Crandall, S.H.; Mark, W.D. Random Vibration in Mechanical Systems; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Using an inerter-based device for structural vibration suppression. Earthq. Eng. Struct. Dyn. 2014, 43, 1129–1147. [Google Scholar] [CrossRef]
- Zhang, R.F.; Zhao, Z.P.; Pan, C.; Ikago, K.; Xue, S. Damping enhancement principle of inerter system. Struct. Control Health Monit. 2020, 27, e2523. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations, 4th ed.; Dover: New York, NY, USA, 1985. [Google Scholar]
- Pan, C.; Zhang, R.; Luo, H.; Li, C.; Shen, H. Demand-based optimal design of oscillator with parallel-layout viscous inerter damper. Struct. Control Health Monit. 2018, 25, e2051. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R.F. Design of structure with inerter system based on stochastic response mitigation ratio. Struct. Control Health Monit. 2018, 25, e2169. [Google Scholar] [CrossRef]
- Ikago, K.; Saito, K.; Inoue, N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq. Eng. Struct. Dyn. 2012, 41, 453–474. [Google Scholar] [CrossRef]
- Kanai, K. Semi-empirical formula for the seismic characteristics of the ground. Bull. Earthq. Res. Inst. Univ. Tokyo 1957, 35, 309–325. [Google Scholar]



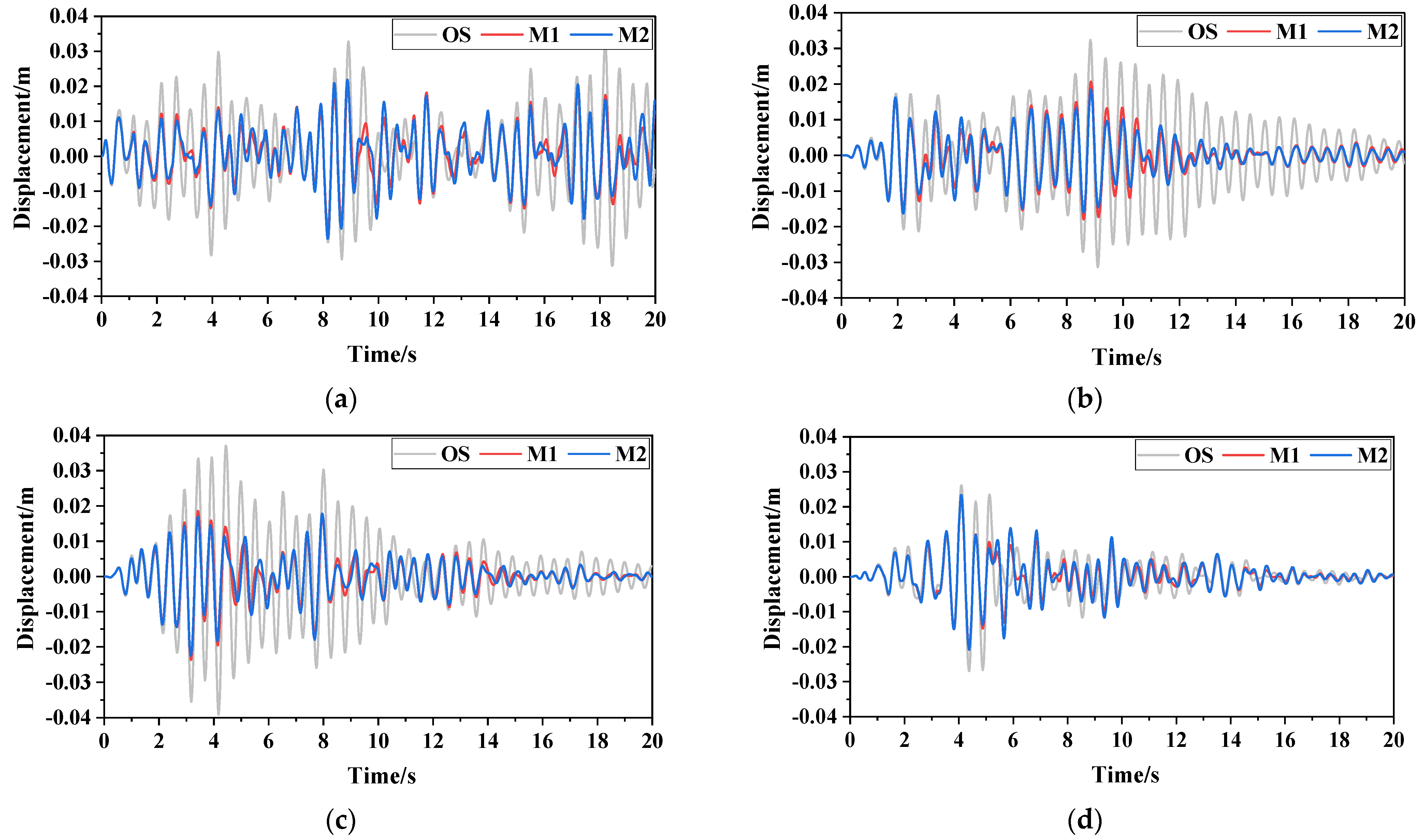
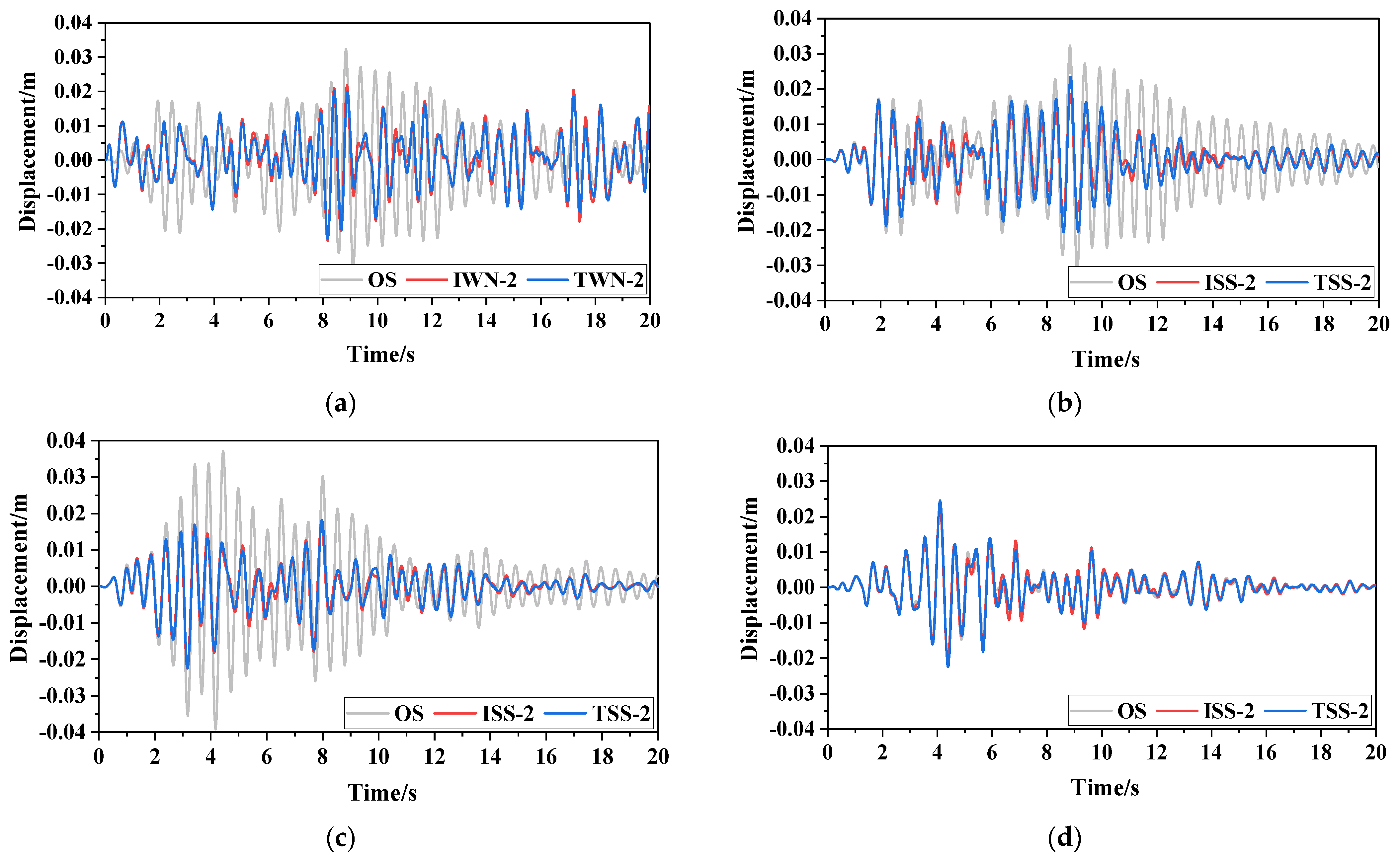

| Excitation Type | Damper Type | Condition | Displacement Decreasing Ratio (%) |
|---|---|---|---|
| White noise excitation | PID | IWN-1 | 40 |
| IWN-2 | 50 | ||
| TMD | TWN-1 | 40 | |
| TWN-2 | 50 | ||
| most severe seismic excitation αpeak = 1.0 | PID | ISS-1 | 40 |
| ISS-2 | 50 | ||
| TMD | TSS-1 | 40 | |
| TSS-2 | 50 |
| Optimization Method | Condition | Design Parameter | |||||
|---|---|---|---|---|---|---|---|
| μ | μ0 | ξ2 | δ1 | ||||
| M1 | IWN-1 | 0.048 | 0.00002 | 0.015 | 0.062 | 0.60 | 1.17 |
| IWN-2 | 0.076 | 0.00003 | 0.020 | 0.093 | 0.50 | 1.75 | |
| ISS-1 | 0.046 | 0.00002 | 0.014 | 0.060 | 0.60 | 1.07 | |
| ISS-2 | 0.069 | 0.00003 | 0.019 | 0.086 | 0.50 | 1.54 | |
| M2 | IWN-1 | 0.041 | 0.00002 | 0.004 | 0.032 | 0.60 | 1.45 |
| IWN-2 | 0.076 | 0.00003 | 0.012 | 0.071 | 0.50 | 2.02 | |
| ISS-1 | 0.038 | 0.00002 | 0.003 | 0.029 | 0.60 | 1.48 | |
| ISS-2 | 0.065 | 0.00003 | 0.009 | 0.059 | 0.50 | 1.84 | |
| TWN-1 | 0.026 | 0.026 | 0.003 | 0.025 | 0.60 | 1.43 | |
| TWN-2 | 0.068 | 0.068 | 0.010 | 0.060 | 0.50 | 1.94 | |
| TSS-1 | 0.023 | 0.023 | 0.002 | 0.022 | 0.60 | 1.39 | |
| TSS-2 | 0.057 | 0.057 | 0.008 | 0.051 | 0.50 | 1.84 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, M.; Xu, W.; Wang, J.; Chen, Y.; Zhou, D.; Hou, L.; Sun, Y.; Li, Y. Mechanical Model and Damping Effect of a Particle-Inertial Damper. Buildings 2023, 13, 2264. https://doi.org/10.3390/buildings13092264
Xie M, Xu W, Wang J, Chen Y, Zhou D, Hou L, Sun Y, Li Y. Mechanical Model and Damping Effect of a Particle-Inertial Damper. Buildings. 2023; 13(9):2264. https://doi.org/10.3390/buildings13092264
Chicago/Turabian StyleXie, Mengfei, Weibing Xu, Jin Wang, Yanjiang Chen, Daxing Zhou, Liqun Hou, Yulong Sun, and Yong Li. 2023. "Mechanical Model and Damping Effect of a Particle-Inertial Damper" Buildings 13, no. 9: 2264. https://doi.org/10.3390/buildings13092264
APA StyleXie, M., Xu, W., Wang, J., Chen, Y., Zhou, D., Hou, L., Sun, Y., & Li, Y. (2023). Mechanical Model and Damping Effect of a Particle-Inertial Damper. Buildings, 13(9), 2264. https://doi.org/10.3390/buildings13092264






