A Constitutive Model for Stud Connection in Composite Structures
Abstract
:1. Introduction
2. Outline of the Model
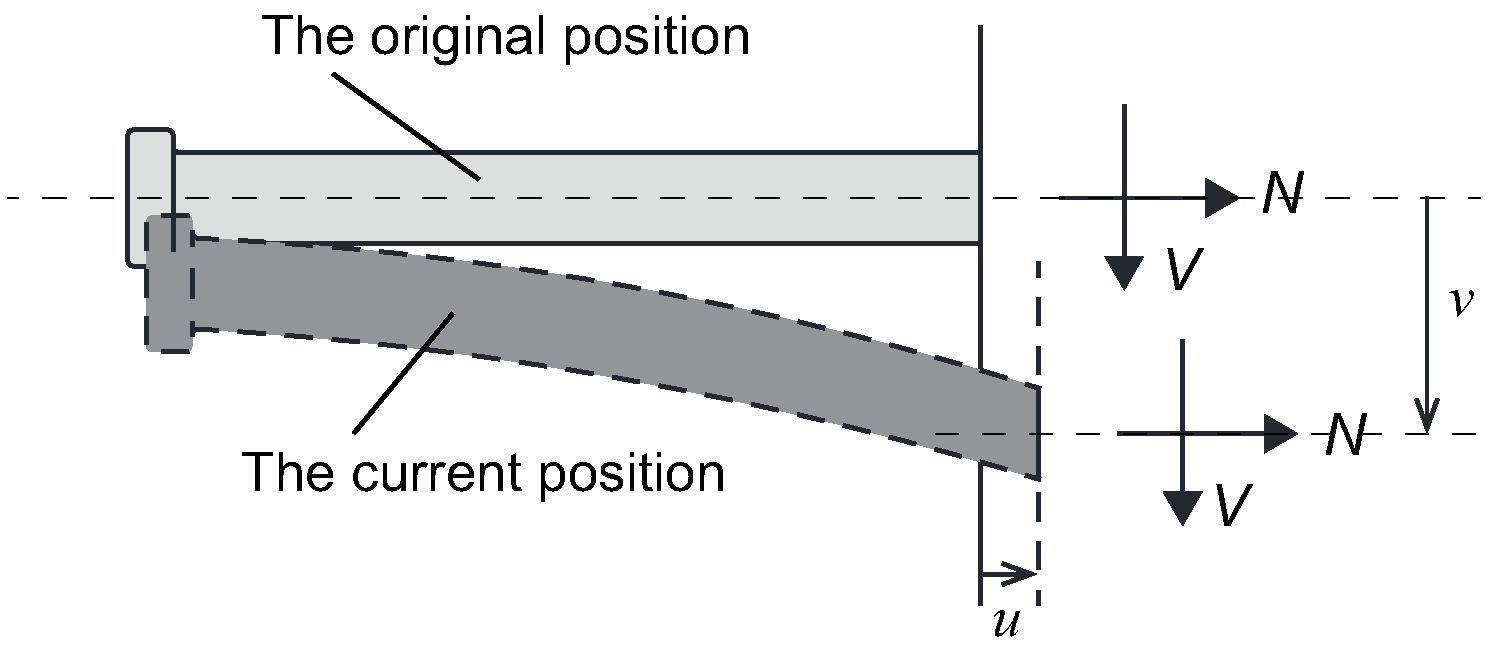
- (1)
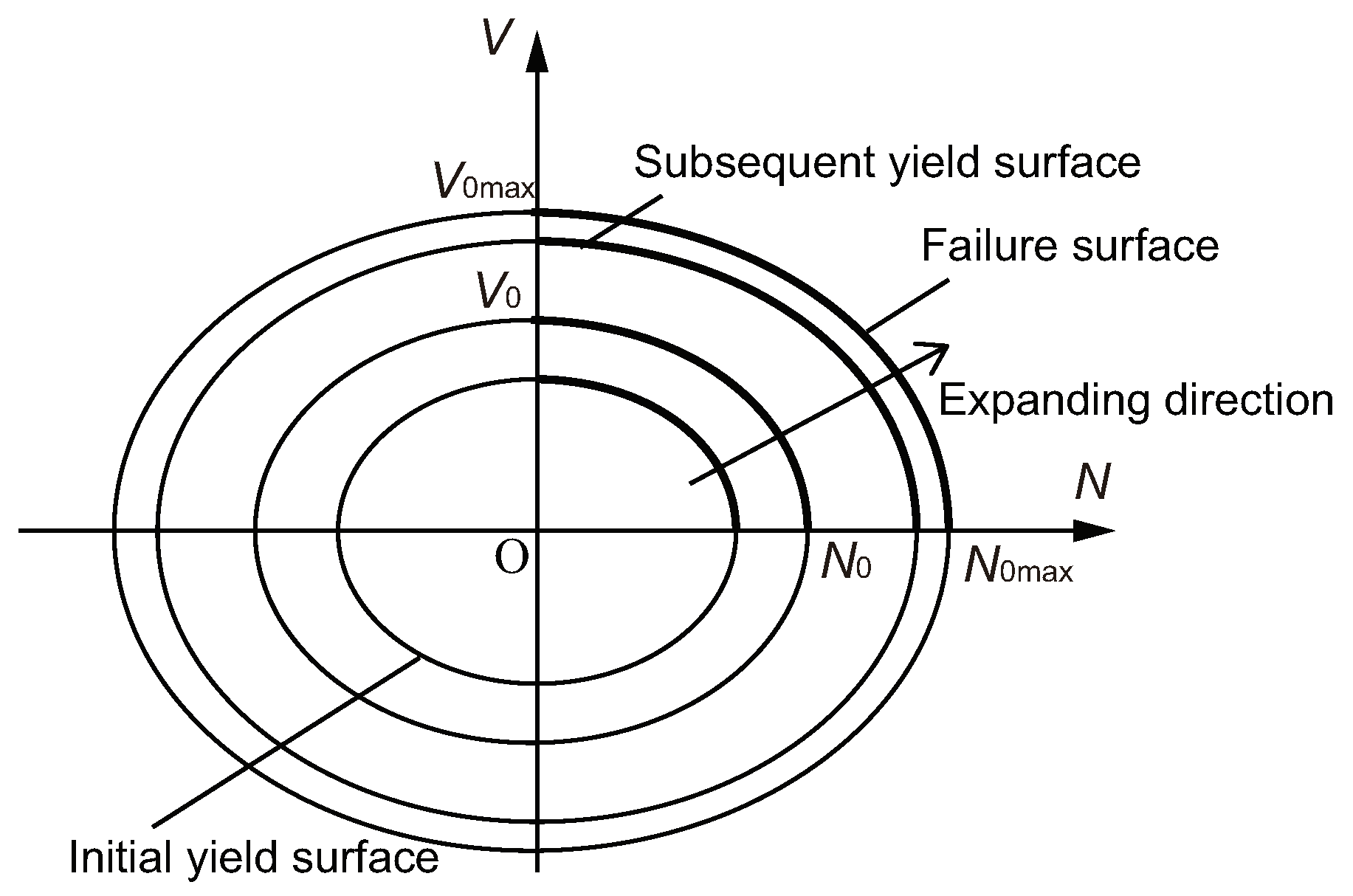
- An empirical formulation of the yield surface within the force plane, labeled as . This is achieved by delineating the contour of the yield surface, which is informed by the shape of the failure envelope;
- (2)
- A strain hardening scheme that elucidates the functional interrelation between the magnitude of the yield surface and the plastic deformation. The expansion of the yield surface is a function of the evolution of plastic displacement (where ). The extent to which the yield surface expands is quantified by the shear force that corresponds to a given plastic displacement;
- (3)
- An aptly chosen flow rule that enables the prediction of increments in plastic displacement, denoted as , which results from the yield surface’s dilation or constriction.
- (4)
- An elastic load–displacement relationship is employed to delineate the load–displacement behavior that occurs within the confines of the yield surface.
- (1)
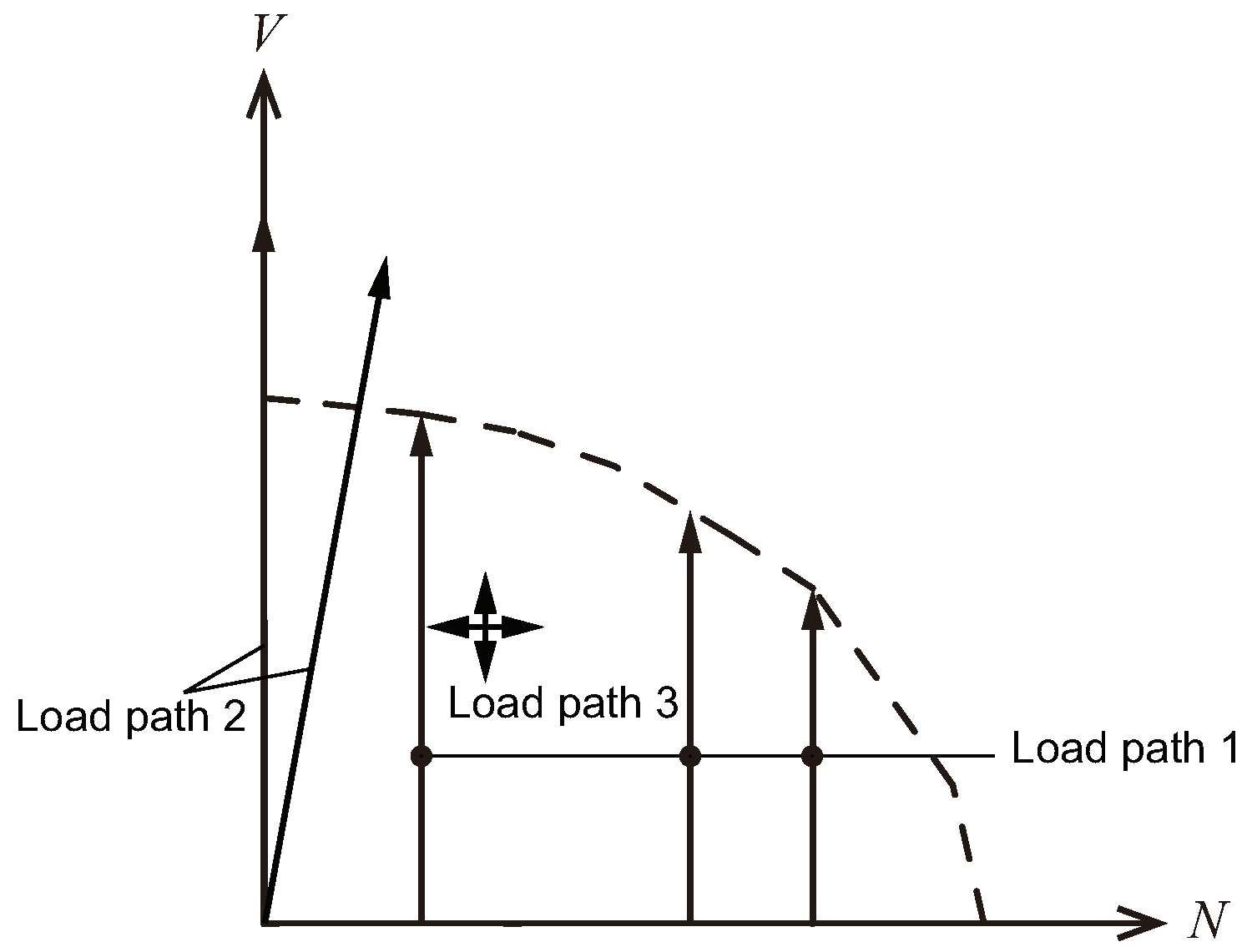
- Load path 1: shear direction loading under different drawing force levels. The shape enclosed by the extremities of the load path may be posited as depicting the trajectory of the yield surface which is apt for the elastoplastic model. This load path is instrumental in deducing both the hardening rule and the flow principle inherent to the elastoplastic material model;
- (2)
- Load path 2: radial loading. These loading trajectories inform the hardening principle as well as the flow rule characteristic of the elastoplastic model. The instance of pure shear loading does indeed represent a specific case within this load path, from which the shear–slip hardening principle applicable to the stud connection can be extrapolated;
- (3)
- Load path 3: elastic stiffness test. By introducing minimal displacements in both planar directions while concurrently unloading the stud connection, it is feasible to establish an estimation of the elastic stiffness coefficient.
3. Details of the Model
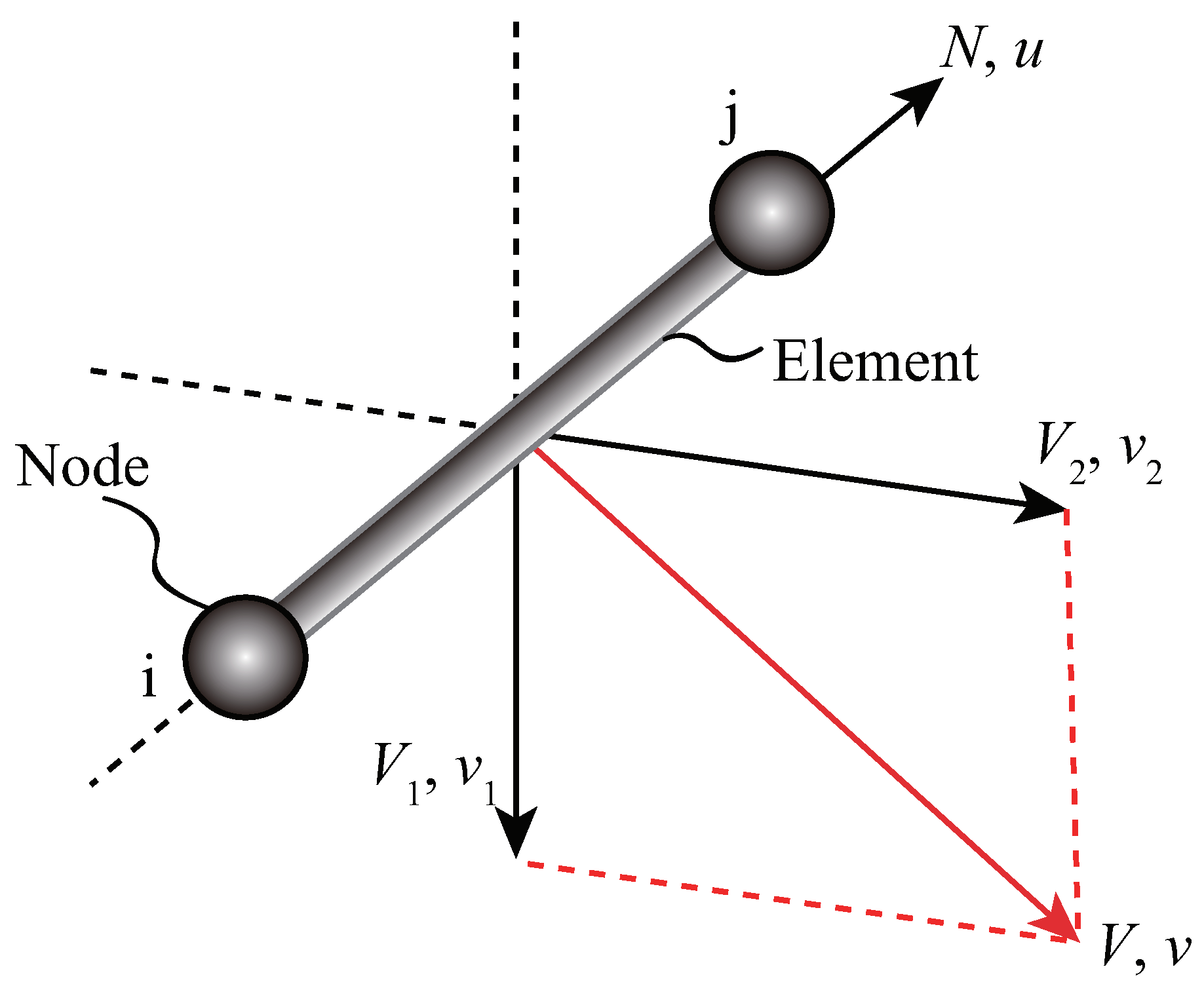
3.1. Elastic Behavior
3.2. Yield Surface
3.3. Hardening Law
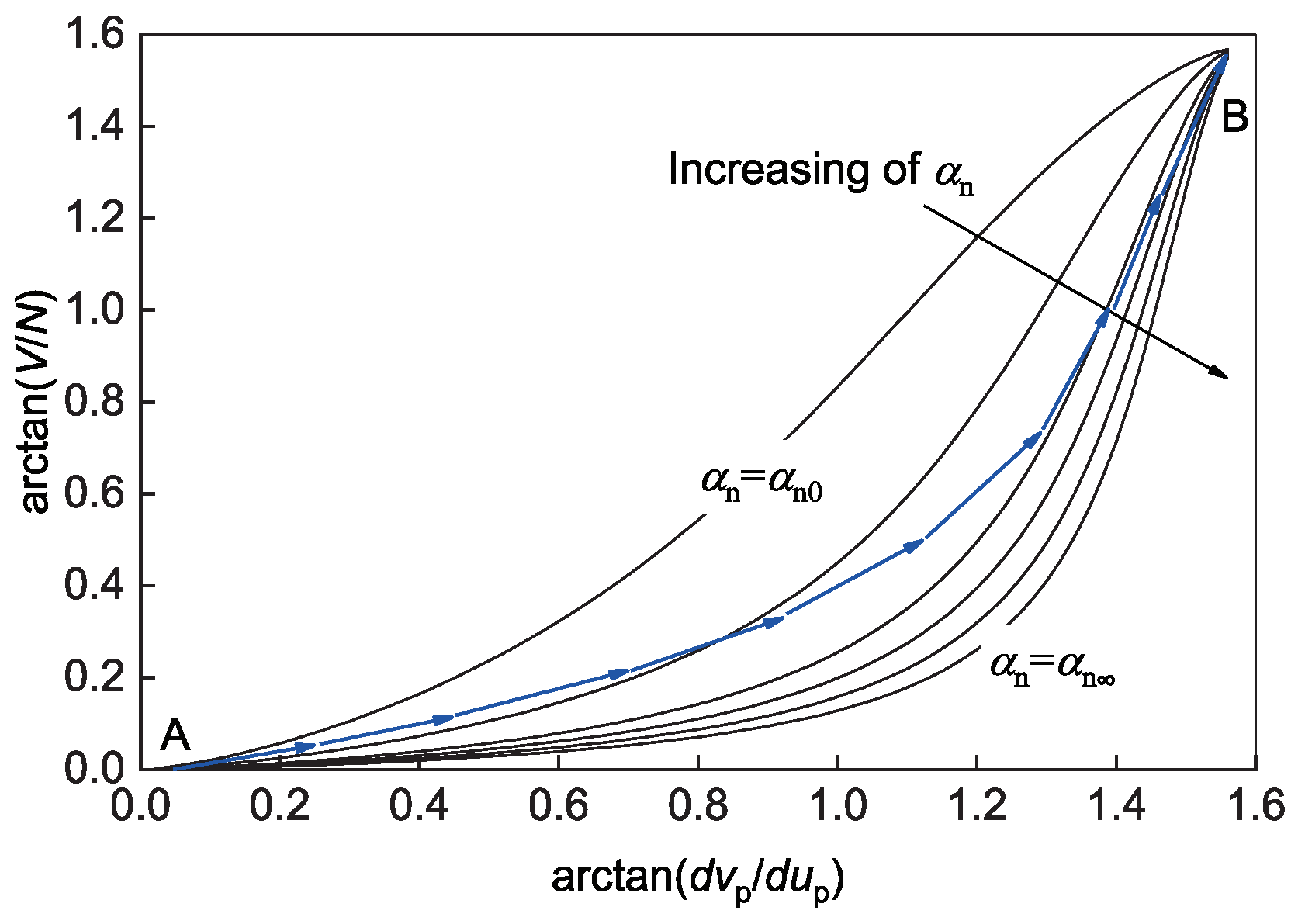
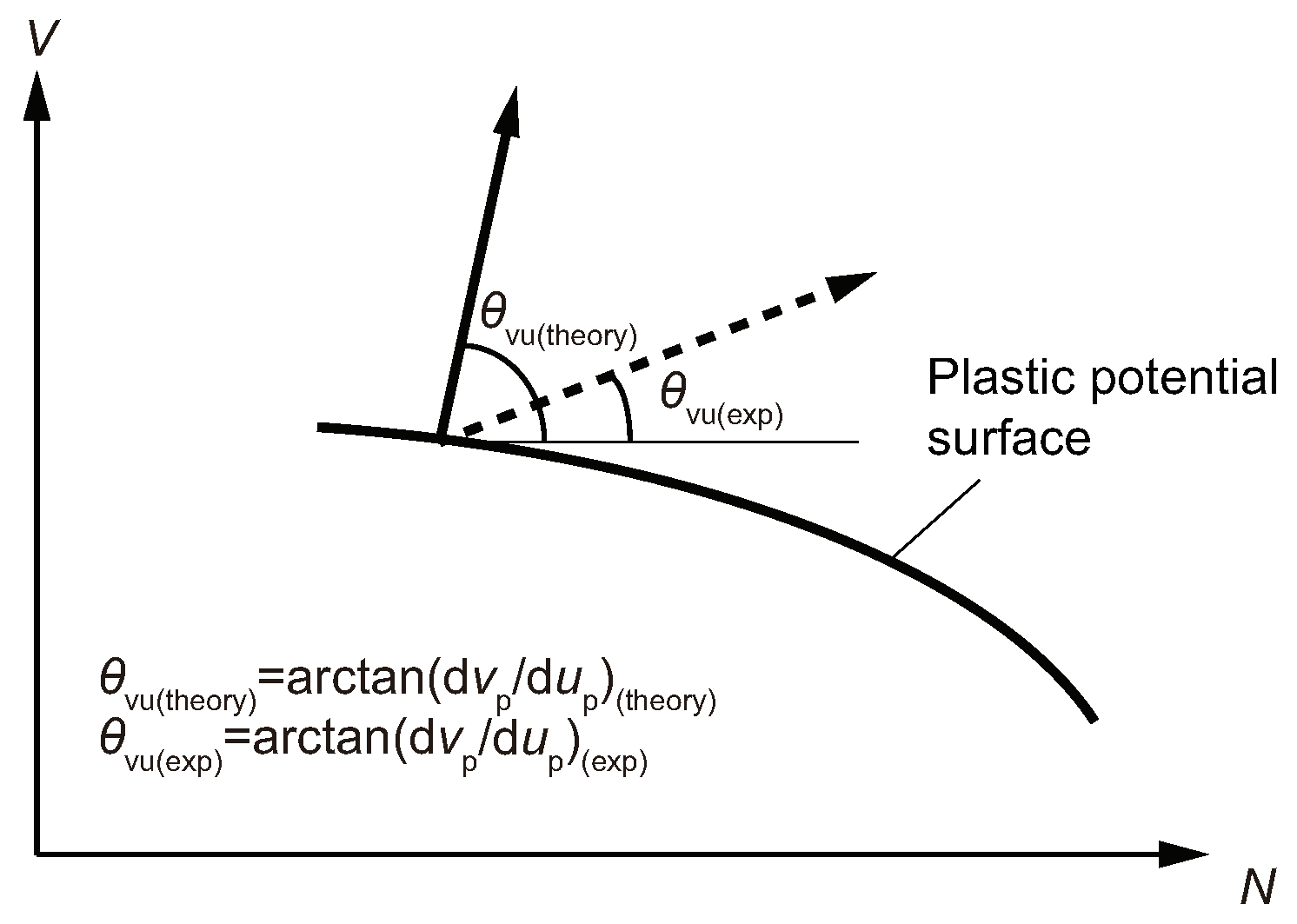
3.4. Flow Rule
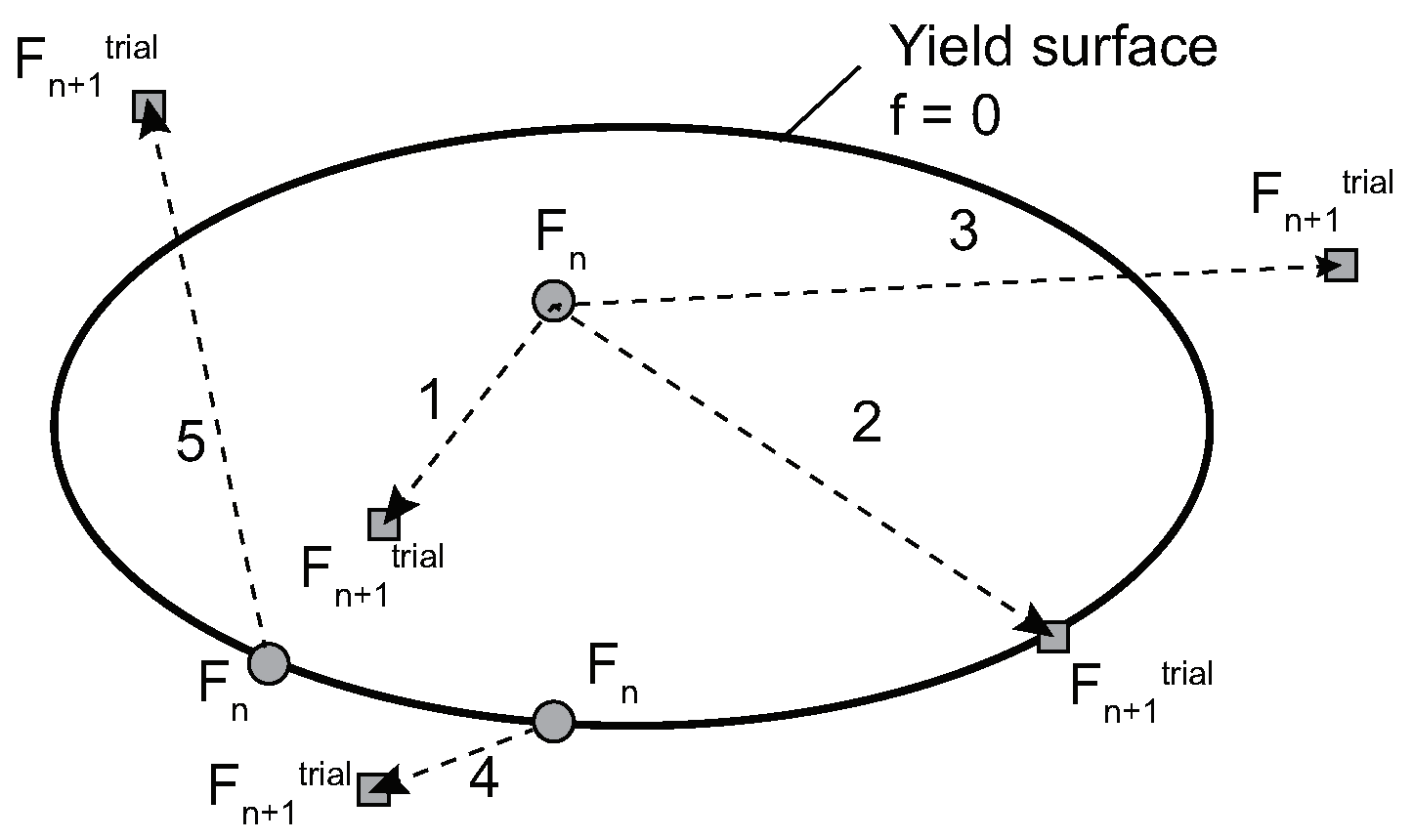
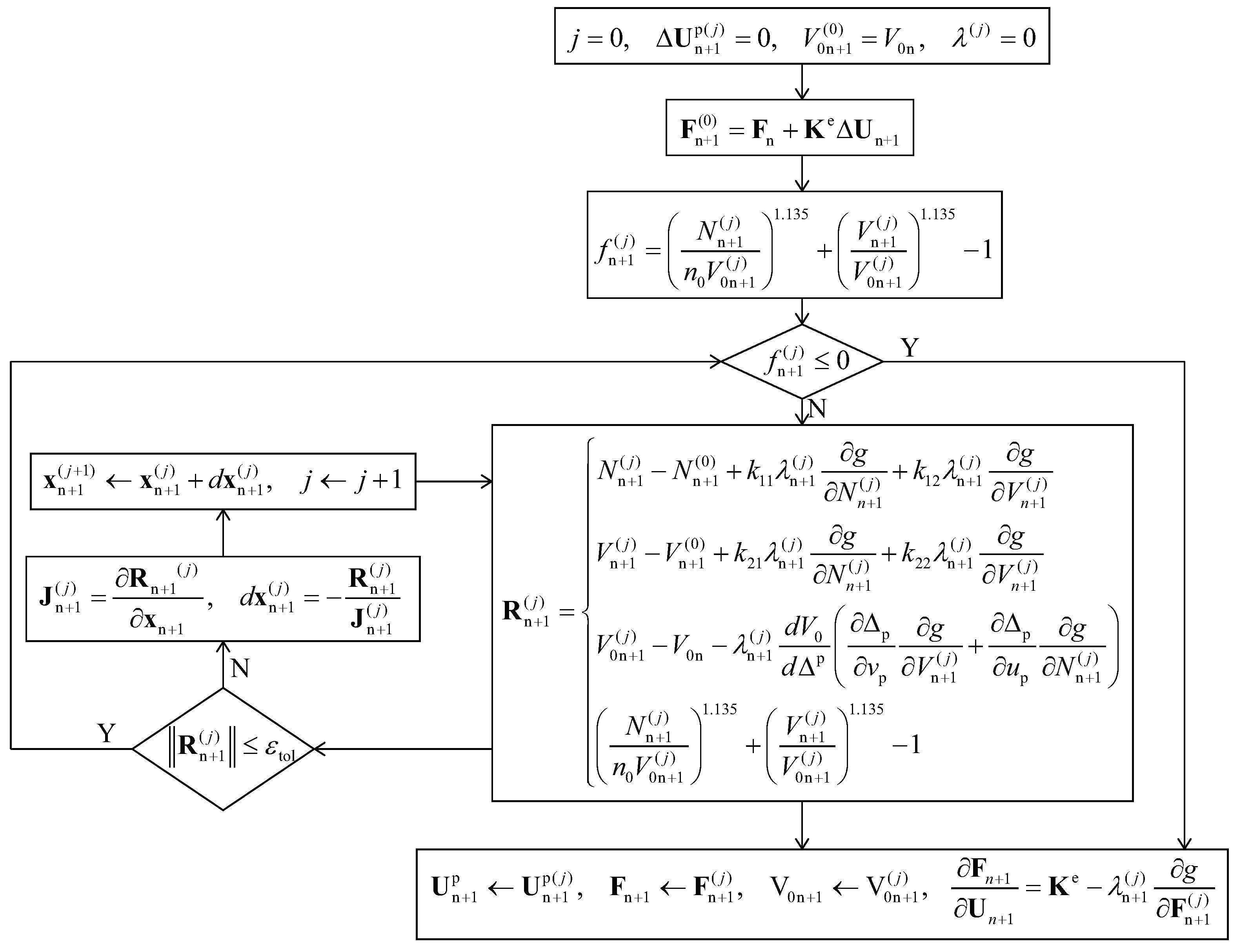
4. Constitutive Integration Algorithm
5. Continuum and Consistent Tangent Stiffness
5.1. Continuum Tangent Stiffness
5.2. Consistent Tangent Stiffness
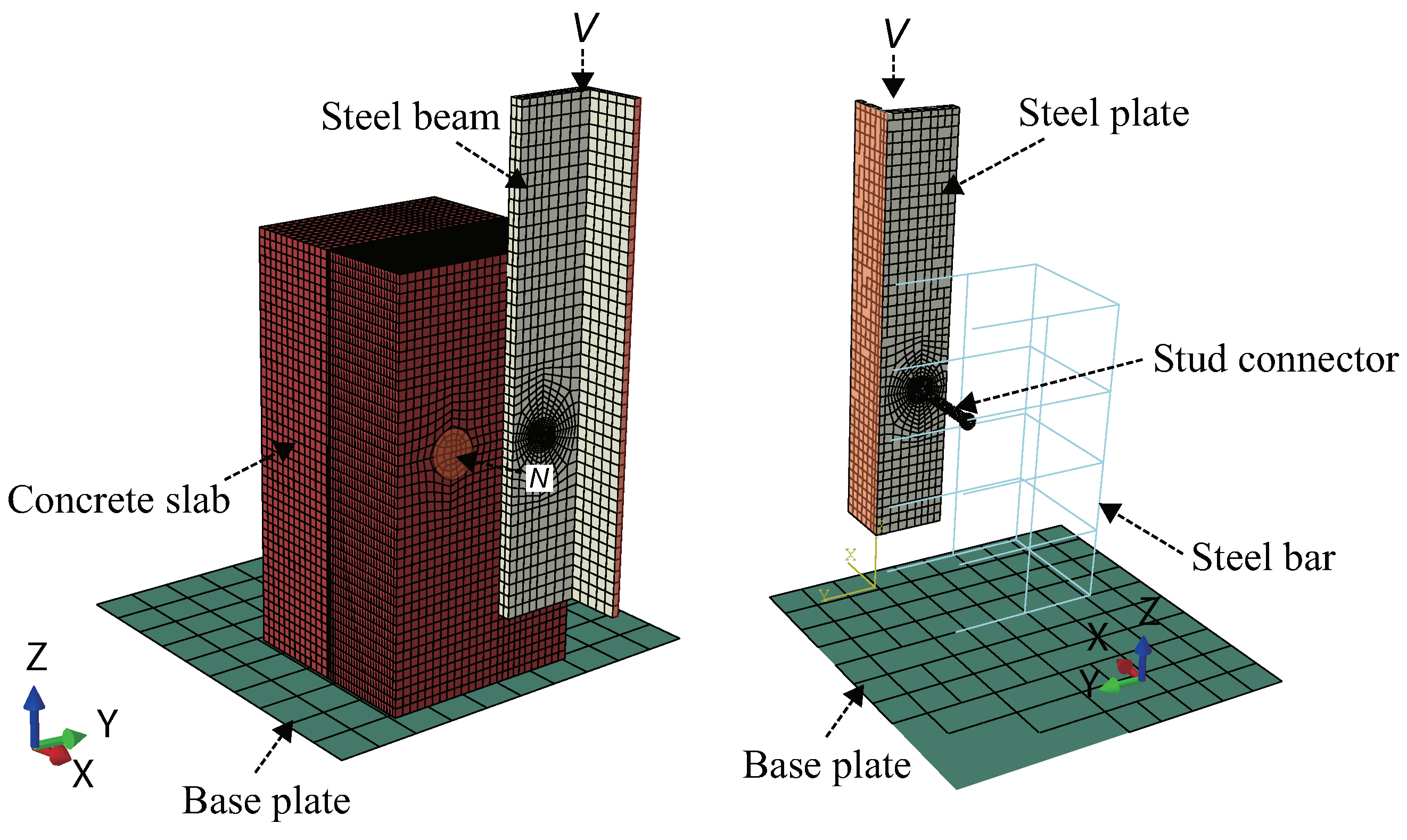
6. Finite Element Formulation
7. Application and Validation
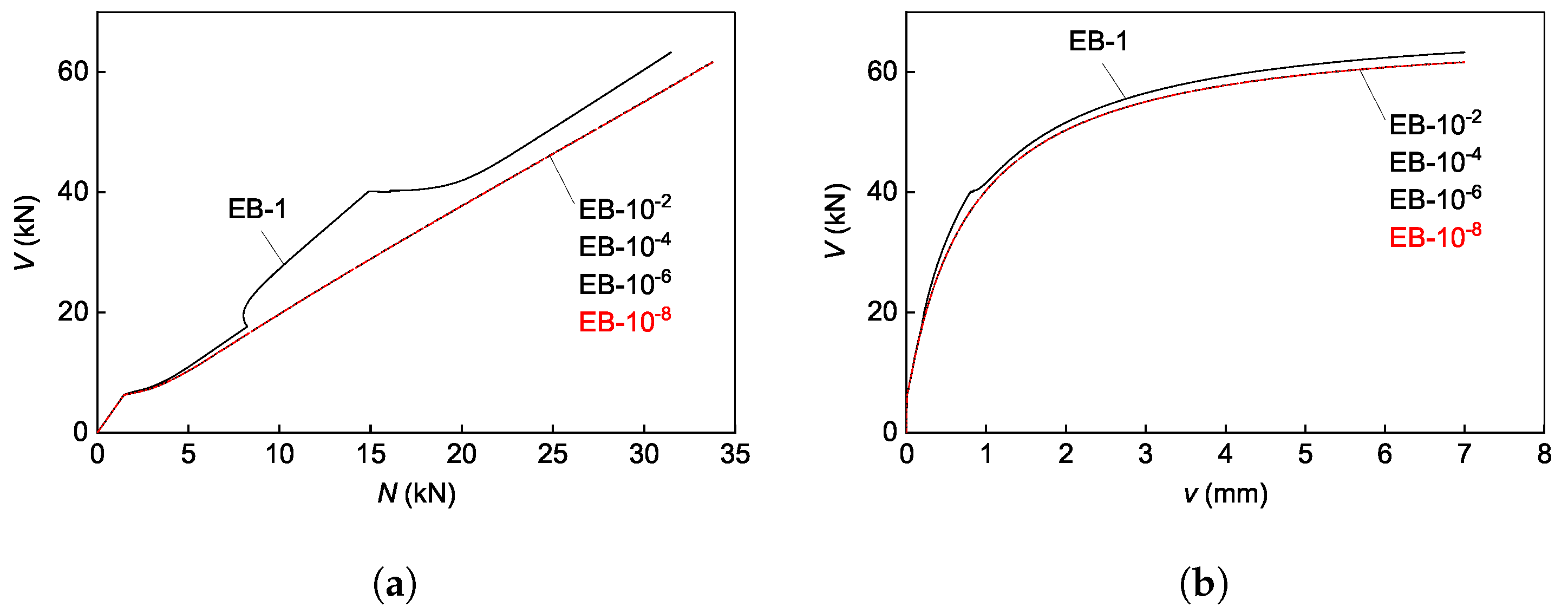
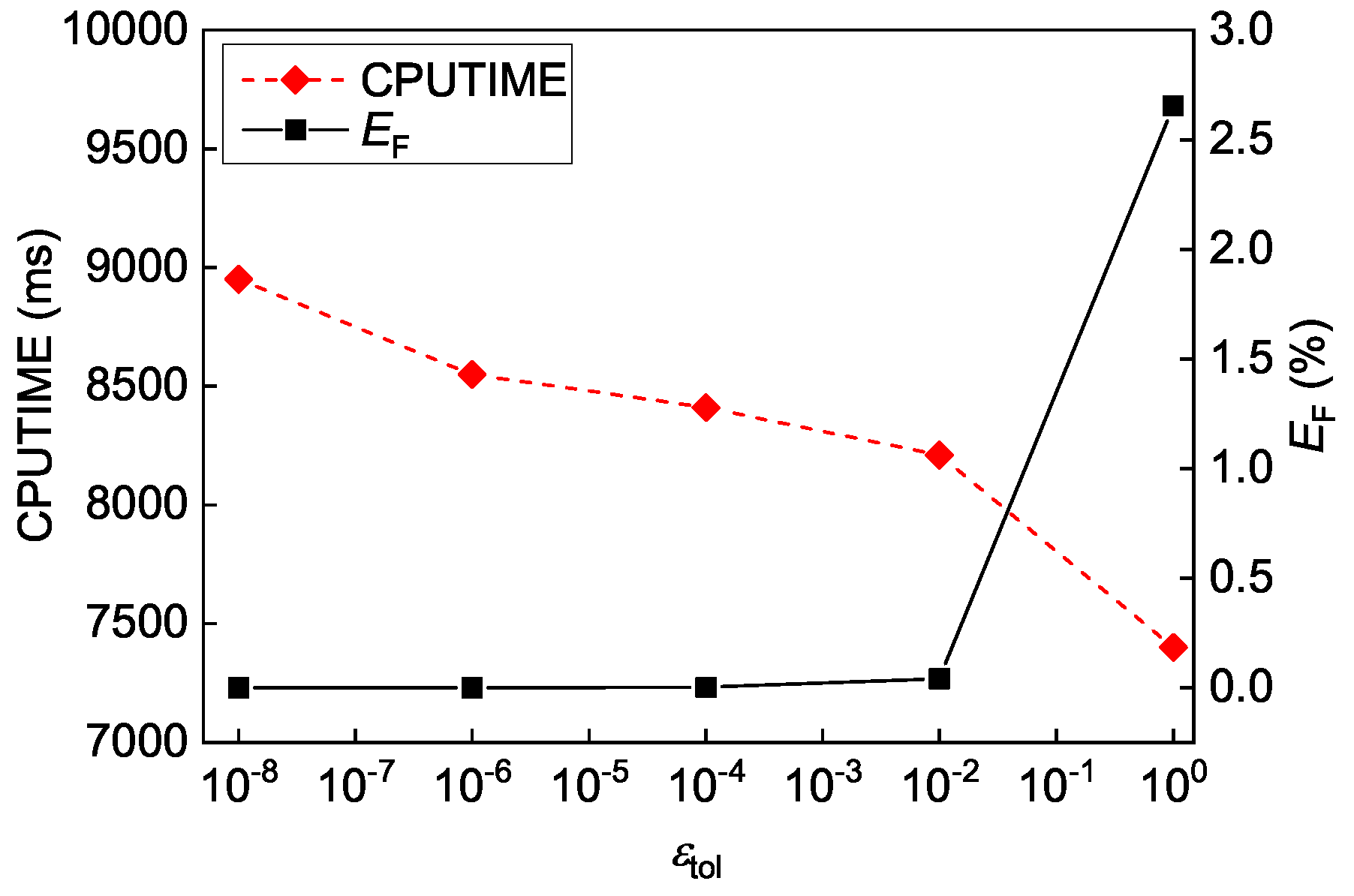
7.1. Application of Integration Algorithm
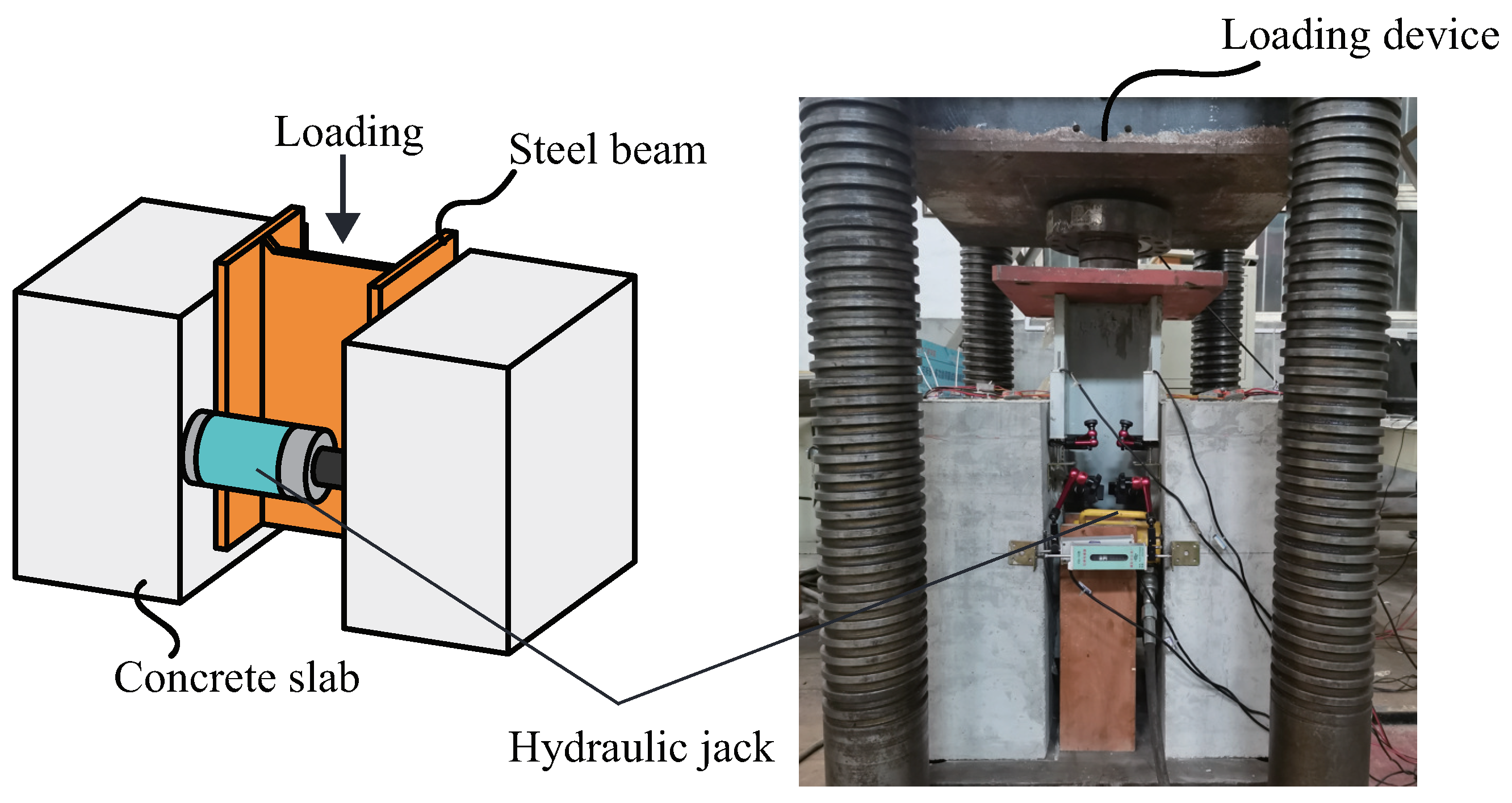
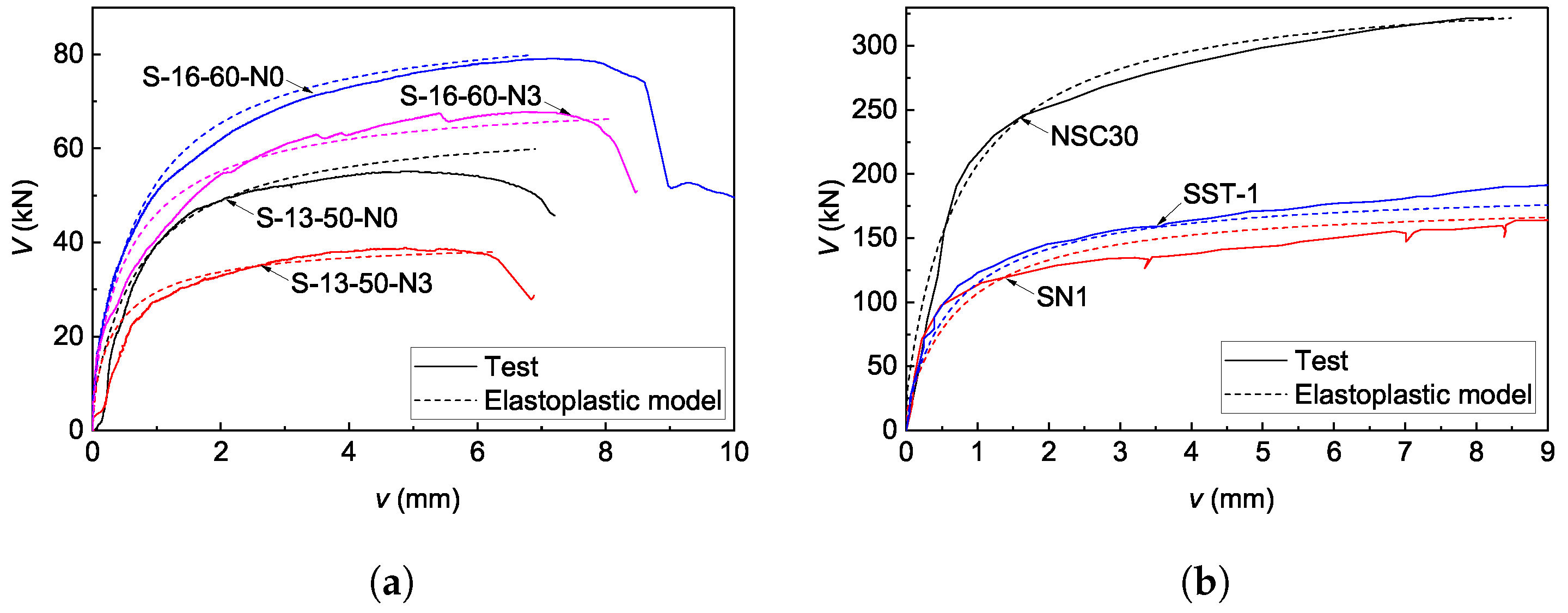
7.2. Validation by Experimental Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akbas, S.D. Nonlinear behavior of fiber reinforced cracked composite beams. Steel Compos. Struct. 2019, 30, 327–336. [Google Scholar]
- Aklilu, G.; Adali, S.; Bright, G. Failure analysis of rotating hybrid laminated composite beams. Eng. Fail. Anal. 2019, 101, 274–282. [Google Scholar] [CrossRef]
- Lu, B.; Zhai, C.; Li, S.; Ji, D.; Lu, X. Influence of Brittle Fracture of Shear Connectors on Flexural Behavior of Steel–Plate Concrete Composite Beams Under Cyclic Loading. Int. J. Steel Struct. 2020, 20, 1703–1719. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, A.; Chen, B.; Zhang, J.; Pi, Y.L.; Bradford, M.A. Experimental and numerical study of shear connection in composite beams of steel and steel-fibre reinforced concrete. Eng. Struct. 2020, 215, 110707. [Google Scholar] [CrossRef]
- Lima, J.M.; Bezerra, L.M.; Bonilla, J.; Barbosa, W.C. Study of the behavior and resistance of right-angle truss shear connector for composite steel concrete beams. Eng. Struct. 2022, 253, 113778. [Google Scholar] [CrossRef]
- Lawson, R.M.; Taufiq, H. Partial shear connection in light steel composite beams. J. Constr. Steel Res. 2019, 154, 55–66. [Google Scholar] [CrossRef]
- Jiang, H.; Fang, H.; Liu, J.; Fang, Z.; Zhang, J. Experimental investigation on shear performance of transverse angle shear connectors. In Proceedings of the Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 33, pp. 2050–2060. [Google Scholar]
- Wang, Y.H.; Yu, J.; Liu, J.P.; Chen, Y.F. Shear behavior of shear stud groups in precast concrete decks. Eng. Struct. 2019, 187, 73–84. [Google Scholar] [CrossRef]
- Kim, S.E.; Papazafeiropoulos, G.; Truong, V.H.; Nguyen, P.C.; Kong, Z.; Duong, N.T.; Pham, V.T.; Vu, Q.V. Finite element simulation of normal–Strength CFDST members with shear connectors under bending loading. Eng. Struct. 2021, 238, 112011. [Google Scholar] [CrossRef]
- Wei, X.; Xiao, L.; Pei, S.L. Shear behavior of multi-hole perfobond connectors in steel-concrete structure. Struct. Eng. Mech. 2015, 56, 983–1001. [Google Scholar]
- Zheng, S.J.; Liu, Y.Q.; Yoda, T.; Lin, W.W. Shear behavior and analytical model of perfobond connectors. Steel Compos. Struct. 2016, 20, 71–89. [Google Scholar] [CrossRef]
- Ataei, A.; Zeynalian, M.; Yazdi, Y. Cyclic behaviour of bolted shear connectors in steel-concrete composite beams. Eng. Struct. 2019, 198, 109455. [Google Scholar] [CrossRef]
- Zhai, C.; Lu, B.; Wen, W.; Ji, D.; Xie, L. Experimental study on shear behavior of studs under monotonic and cyclic loadings. J. Constr. Steel Res. 2018, 151, 1–11. [Google Scholar] [CrossRef]
- Chiniforush, A.A.; Ataei, A.; Bradford, M.A. Experimental study of deconstructable bolt shear connectors subjected to cyclic loading. J. Constr. Steel Res. 2021, 183, 106741. [Google Scholar] [CrossRef]
- Nie, J.; Tang, L.; Cai, C. Performance of steel-concrete composite beams under combined bending and torsion. J. Struct. Eng. 2009, 135, 1048–1057. [Google Scholar] [CrossRef]
- Lin, W. Study on steel-concrete composite beams under pure negative bending and combined negative bending and torsion. In Proceedings of the IABSE Conference, Kuala Lumpur 2018: Engineering the DevelopingWorld. International Association for Bridge and Structural Engineering (IABSE), Kuala Lumpur, Malaysia, 25–27 April 2018; pp. 103–110. [Google Scholar]
- Rehman, N.; Lam, D.; Dai, X.; Ashour, A. Testing of composite beam with demountable shear connectors. Proc. Inst. Civ. Eng. Struct. Build. 2018, 171, 3–16. [Google Scholar] [CrossRef]
- Tan, E.L.; Uy, B. Experimental study on curved composite beams subjected to combined flexure and torsion. J. Constr. Steel Res. 2009, 65, 1855–1863. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, Y.; He, J. Behavior of stud connectors under combined shear and tension loads. Eng. Struct. 2014, 81, 362–376. [Google Scholar] [CrossRef]
- Tan, E.L.; Varsani, H.; Liao, F. Experimental study on demountable steel-concrete connectors subjected to combined shear and tension. Eng. Struct. 2019, 183, 110–123. [Google Scholar] [CrossRef]
- Shen, M.; Chung, K.F. Structural behaviour of stud shear connections with solid and composite slabs under co-existing shear and tension forces. Structures 2017, 9, 79–90. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, Q.; Zhou, Y.; Cheng, Z.; Li, M.; Cui, C. Static and fatigue behaviors of short stud connectors embedded in ultra-high performance concrete. Eng. Struct. 2022, 273, 114888. [Google Scholar] [CrossRef]
- Meng, H.; Wang, W.; Xu, R. Analytical model for the Load-Slip behavior of headed stud shear connectors. Eng. Struct. 2022, 252, 113631. [Google Scholar] [CrossRef]
- Song, L.; Fang, S.; Cui, C.; Yu, Z.; Wang, Z. A load-slip model for stud connector in steel-concrete composite structures. Adv. Struct. Eng. 2023, 26, 489–504. [Google Scholar] [CrossRef]
- Gao, Y.; Li, C.; Wang, X.; Zhou, Z.; Fan, L.; Heng, J. Shear-slip behaviour of prefabricated composite shear stud connectors in composite bridges. Eng. Struct. 2021, 240, 112148. [Google Scholar] [CrossRef]
- Wu, F.; Tang, W.; Xue, C.; Sun, G.; Feng, Y.; Zhang, H. Experimental investigation on the static performance of stud connectors in steel-HSFRC composite beams. Materials 2021, 14, 2744. [Google Scholar] [CrossRef] [PubMed]
- Uddin, A.; Sheikh, A.H.; Brown, D.; Bennett, T.; Uy, B. A higher order model for inelastic response of composite beams with interfacial slip using a dissipation based arc-length method. Eng. Struct. 2017, 139, 120–134. [Google Scholar] [CrossRef]
- Zhou, W.B.; Jiang, L.Z.; Huang, Z.; Li, S.J. Flexural natural vibration characteristics of composite beam considering shear deformation and interface slip. Steel Compos. Struct. 2016, 20, 1023–1042. [Google Scholar] [CrossRef]
- Massonnet, C.; Olszak, W.; Phillips, A. Plasticity in Structural Engineering, Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2014; Volume 241. [Google Scholar]
- Chakrabarty, J. Theory of Plasticity; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hartmaier, A. Data-oriented constitutive modeling of plasticity in metals. Materials 2020, 13, 1600. [Google Scholar] [CrossRef] [PubMed]
- Kocks, U. Realistic constitutive relations for metal plasticity. Mater. Sci. Eng. A 2001, 317, 181–187. [Google Scholar] [CrossRef]
- Tasiopoulou, P.; Gerolymos, N. Constitutive modeling of sand: Formulation of a new plasticity approach. Soil Dyn. Earthq. Eng. 2016, 82, 205–221. [Google Scholar] [CrossRef]
- Cassidy, M.; Cassidy, M. Non-Linear Analysis of Jack-Up Structures Subjected to Random Waves. Ph.D. Thesis, University of Oxford, Oxford, UK, 1999. [Google Scholar]
- Houlsby, G.T.; Cassidy, M.J. A plasticity model for the behaviour of footings on sand under combined loading. Géotechnique 2002, 52, 117–129. [Google Scholar] [CrossRef]
- Martin, C.; Houlsby, G. Combined loading of spudcan foundations on clay: Numerical modelling. Géotechnique 2001, 51, 687–699. [Google Scholar] [CrossRef]
- Zhang, Y. A Force Resultant Model for Spudcan Foundations in Soft Clay. Ph.D. Thesis, University of Western Australia, Perth, Australia, 2013. [Google Scholar]
- Tian, Y.; Cassidy, M.J. Modeling of pipe–soil interaction and its application in numerical simulation. Int. J. Geomech. 2008, 8, 213–229. [Google Scholar] [CrossRef]
- Vaiana, N.; Rosati, L. Classification and unified phenomenological modeling of complex uniaxial rate-independent hysteretic responses. Mech. Syst. Signal Process. 2023, 182, 109539. [Google Scholar] [CrossRef]
- Vaiana, N.; Rosati, L. Analytical and differential reformulations of the Vaiana–Rosati model for complex rate-independent mechanical hysteresis phenomena. Mech. Syst. Signal Process. 2023, 199, 110448. [Google Scholar] [CrossRef]
- Qin, X. Constitutive Models for Stud Connection in Steel and Concrete Composite Structures. Ph.D. Thesis, Qingdao University of Technology, Qingdao, China, 2023. [Google Scholar]
- Bode, H.; Roik, K. Headed studs-embedded in concrete and loaded in tension. Anchorage Concr. 1987, 103, 61–88. [Google Scholar]
- McMackin, P.J.; Slutter, R.G.; Fisher, J.W. Headed steel anchor under combined loading. Eng. J. 1973, 10, 43–52. [Google Scholar]
- Takami, K.; Nishi, K.; Hamada, S. Shear strength of headed stud shear connector subjected to tensile load. J. Constr. Steel 2000, 7, 233–240. [Google Scholar]
- Wang, Q. Experimental Research on Mechanical Behavior and Design Method of Stud Connectors. Ph.D. Thesis, Department of Bridge Engineering, College of Civil Engineering, Tongji University, Shanghai, China, 2013. [Google Scholar]
- Dassault Systèmes. Abaqus User Subroutines Reference Guide; Dassault Systèmes: Providence, RI, USA, 2016. [Google Scholar]
- Lubliner, J. Plasticity Theory; Courier Corporation: North Chelmsford, MA, USA, 2008. [Google Scholar]
- Simo, J.C.; Taylor, R.L. Consistent tangent operators for rate-independent elastoplasticity. Comput. Methods Appl. Mech. Eng. 1985, 48, 101–118. [Google Scholar] [CrossRef]
- Simo, J.; Taylor, R. A return mapping algorithm for plane stress elastoplasticity. Int. J. Numer. Methods Eng. 1986, 22, 649–670. [Google Scholar] [CrossRef]
- Borja, R.I. Cam-Clay plasticity, Part II: Implicit integration of constitutive equation based on a nonlinear elastic stress predictor. Comput. Methods Appl. Mech. Eng. 1991, 88, 225–240. [Google Scholar] [CrossRef]
- Wang, J.; Qi, J.; Tong, T.; Xu, Q.; Xiu, H. Static behavior of large stud shear connectors in steel-UHPC composite structures. Eng. Struct. 2019, 178, 534–542. [Google Scholar] [CrossRef]
- Xu, C.; Su, Q.; Masuya, H. Static and fatigue behavior of the stud shear connector in lightweight concrete. Int. J. Steel Struct. 2018, 18, 569–581. [Google Scholar] [CrossRef]

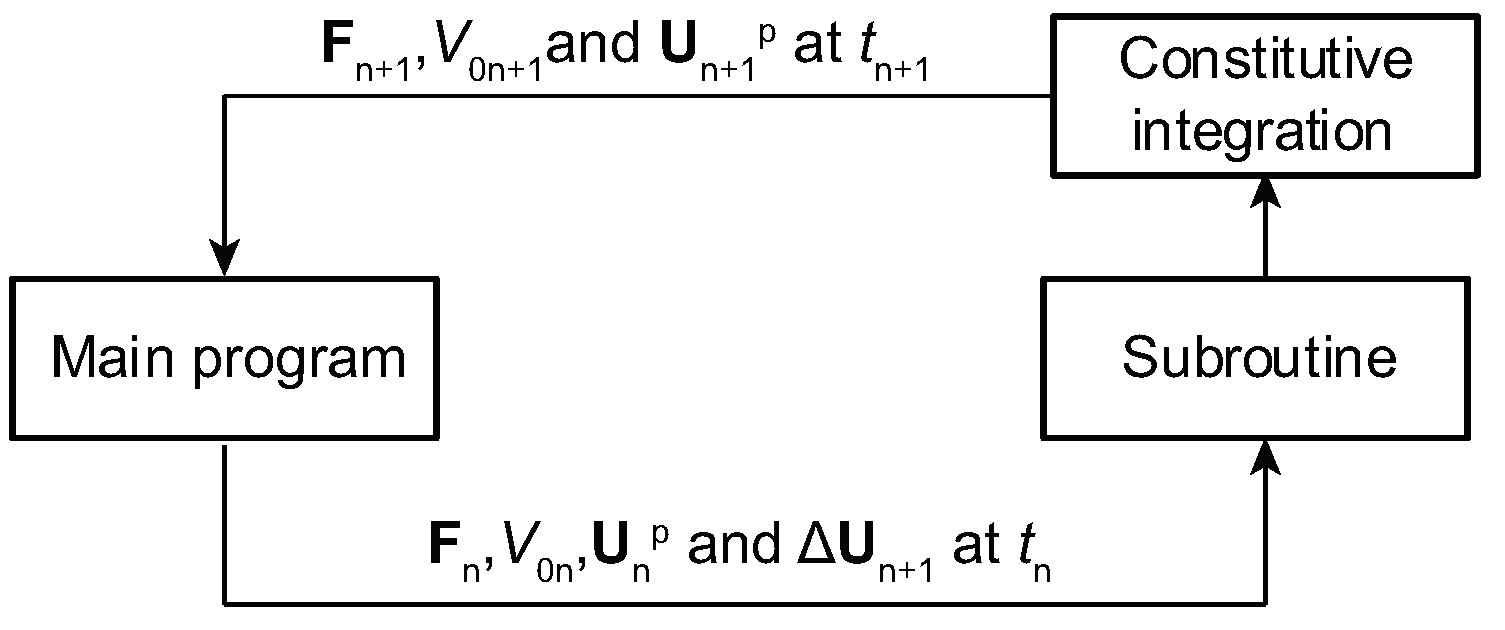
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Zhao, W. A Constitutive Model for Stud Connection in Composite Structures. Buildings 2024, 14, 1018. https://doi.org/10.3390/buildings14041018
Qin X, Zhao W. A Constitutive Model for Stud Connection in Composite Structures. Buildings. 2024; 14(4):1018. https://doi.org/10.3390/buildings14041018
Chicago/Turabian StyleQin, Xi, and Wei Zhao. 2024. "A Constitutive Model for Stud Connection in Composite Structures" Buildings 14, no. 4: 1018. https://doi.org/10.3390/buildings14041018




