Rotational Stiffening Performance of Roof Folded Plates in Torsion Tests and the Stiffening Effect of Roof Folded Plates on the Lateral Buckling of H Beams in Steel Structures
Abstract
1. Introduction
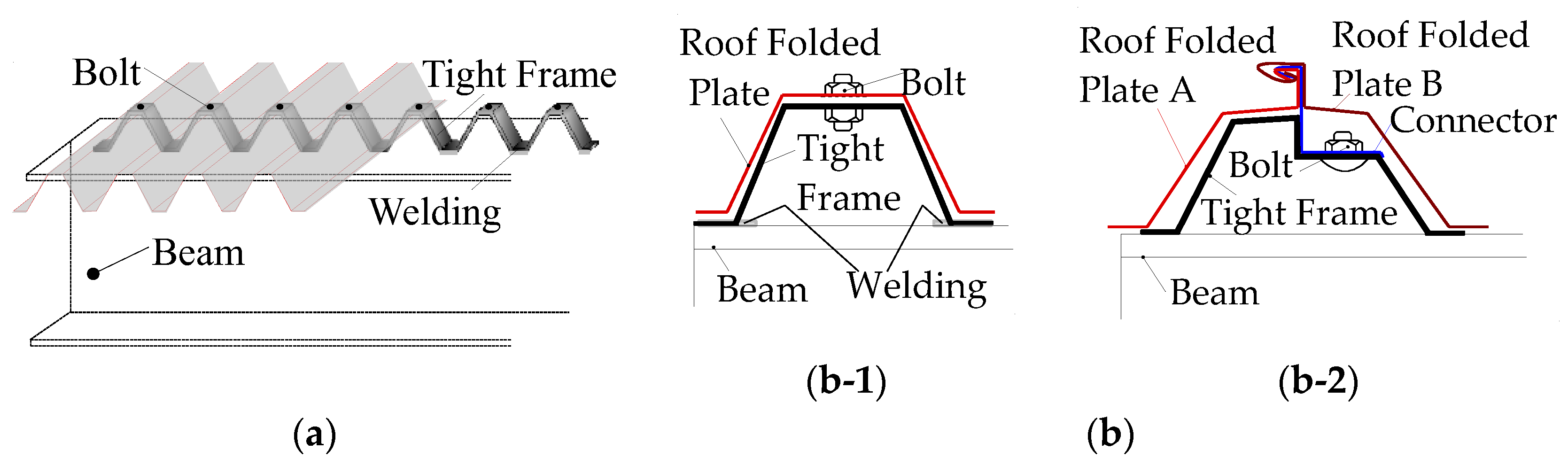
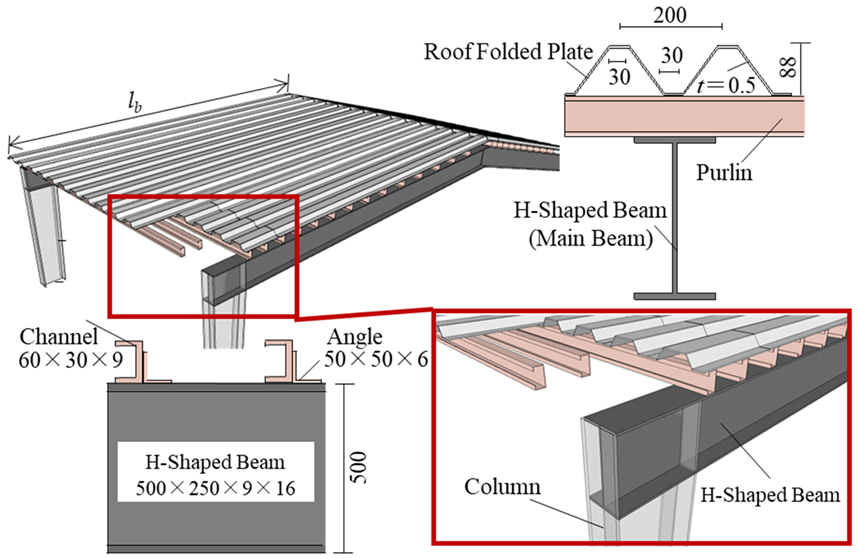
2. Outline of Torsional Experiment on Roof Folded Plates
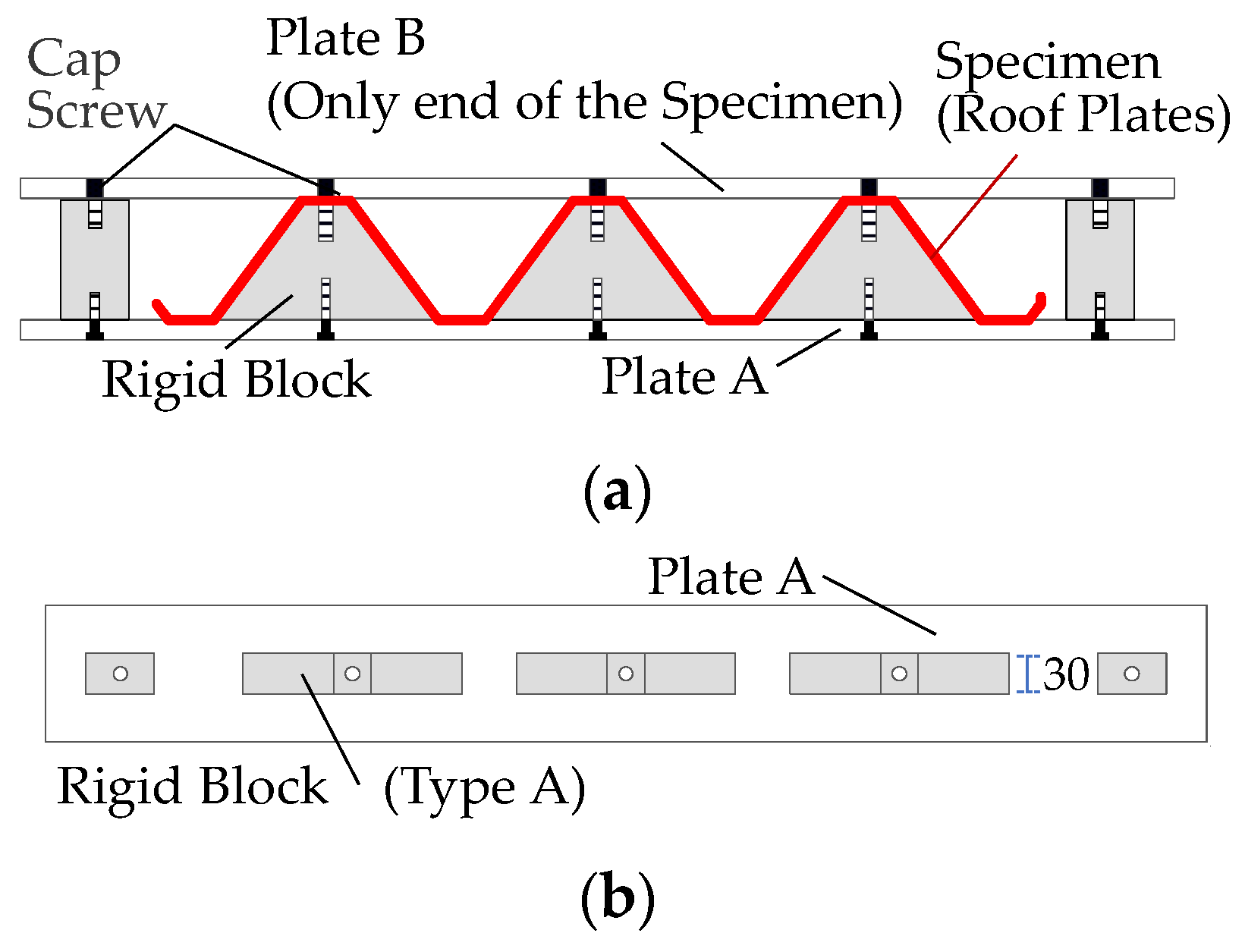
2.1. Outline of Torsional Experiment Apparatus
2.2. Loading Protocols
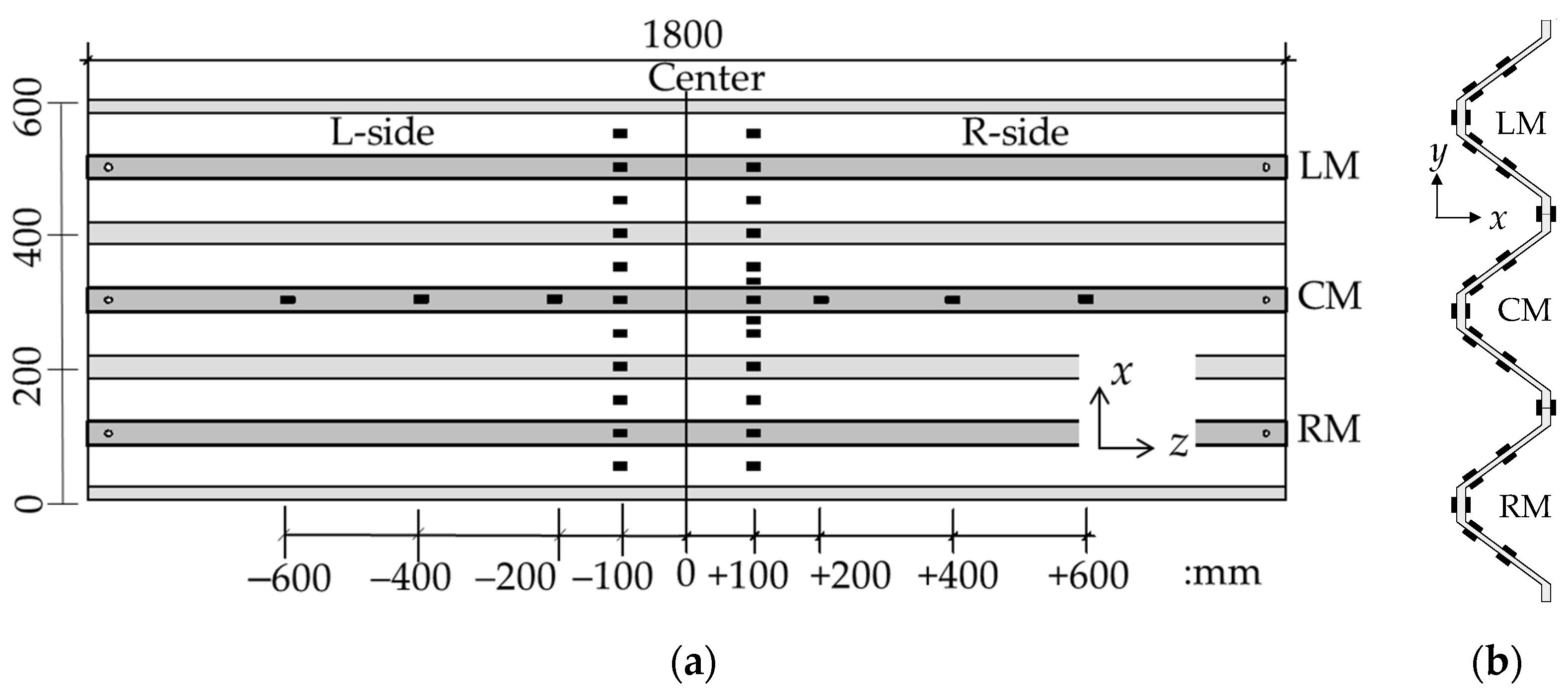
2.3. Specimen Configuration
2.4. Material Properties
2.5. Measurement Methods
3. Results of Torsional Experiment on Roof Folded Plate
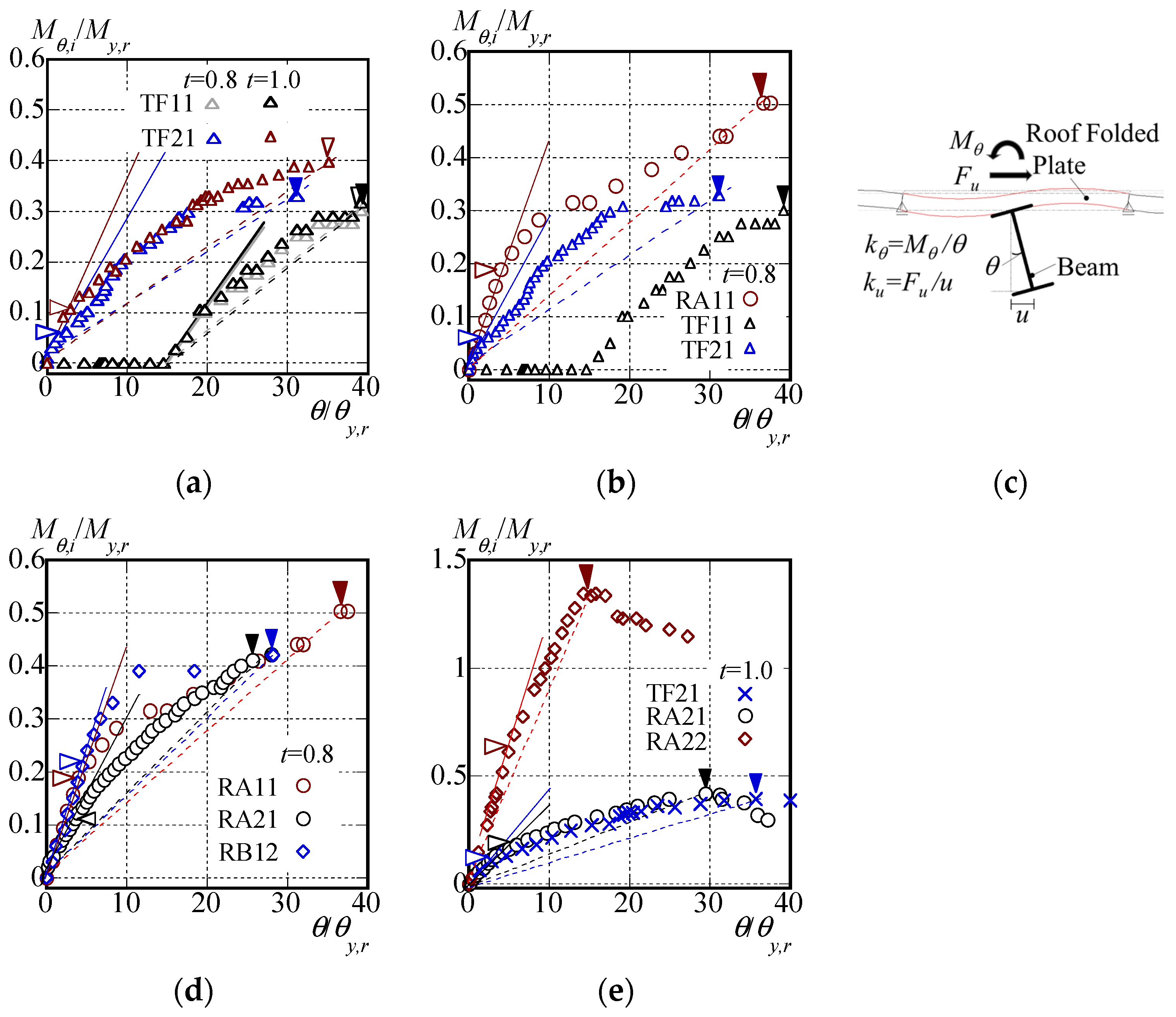
3.1. Rotational Stiffness and Torsional Moment of Roof Folded Plate
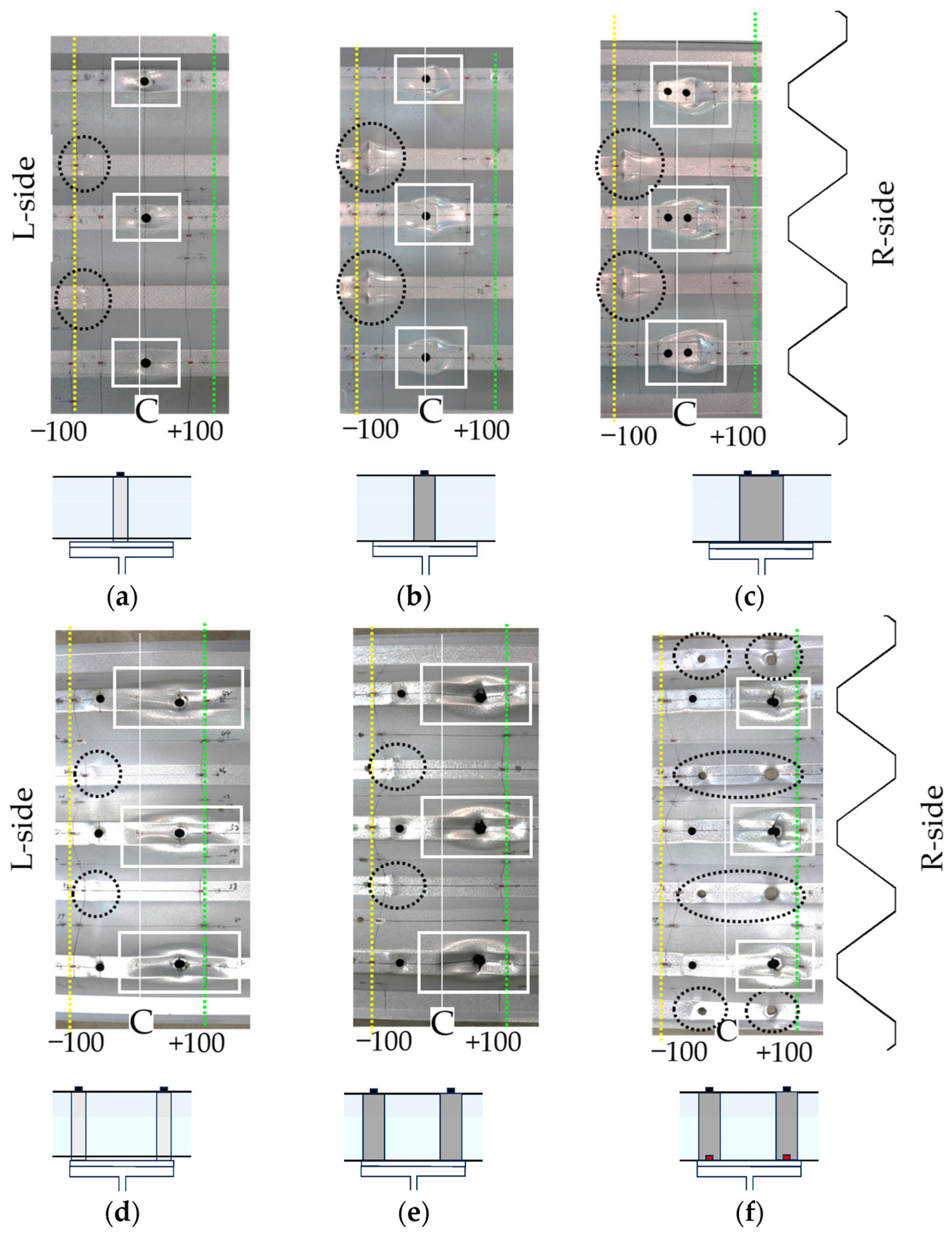
3.2. Deformation Mechanism of Roof folded Plate
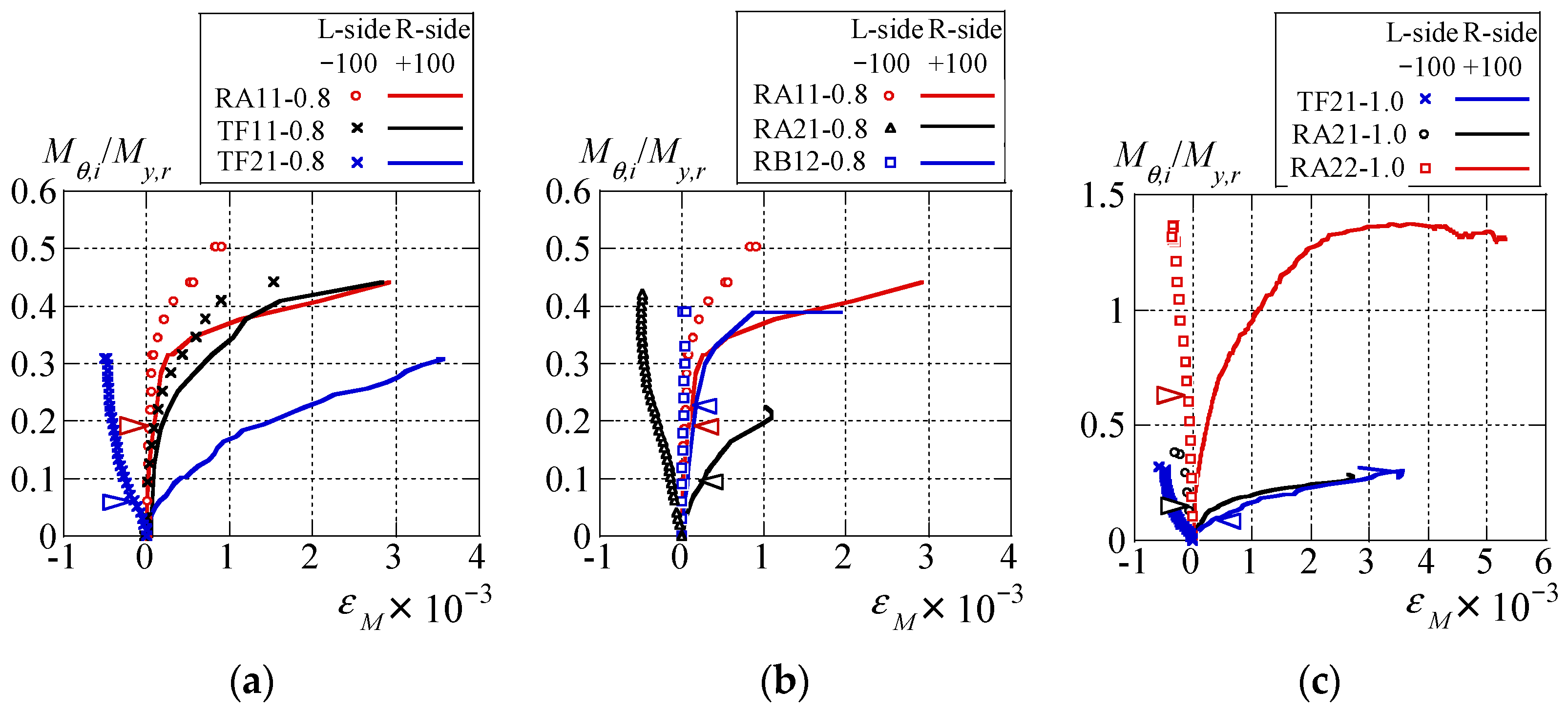
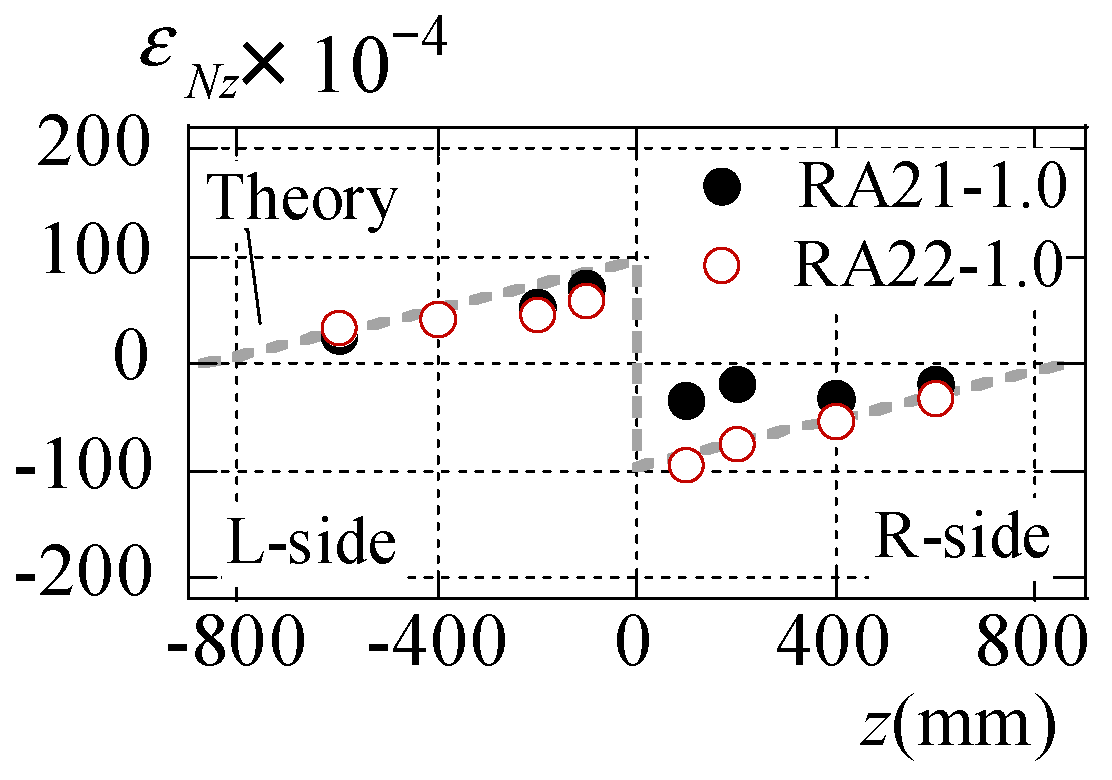
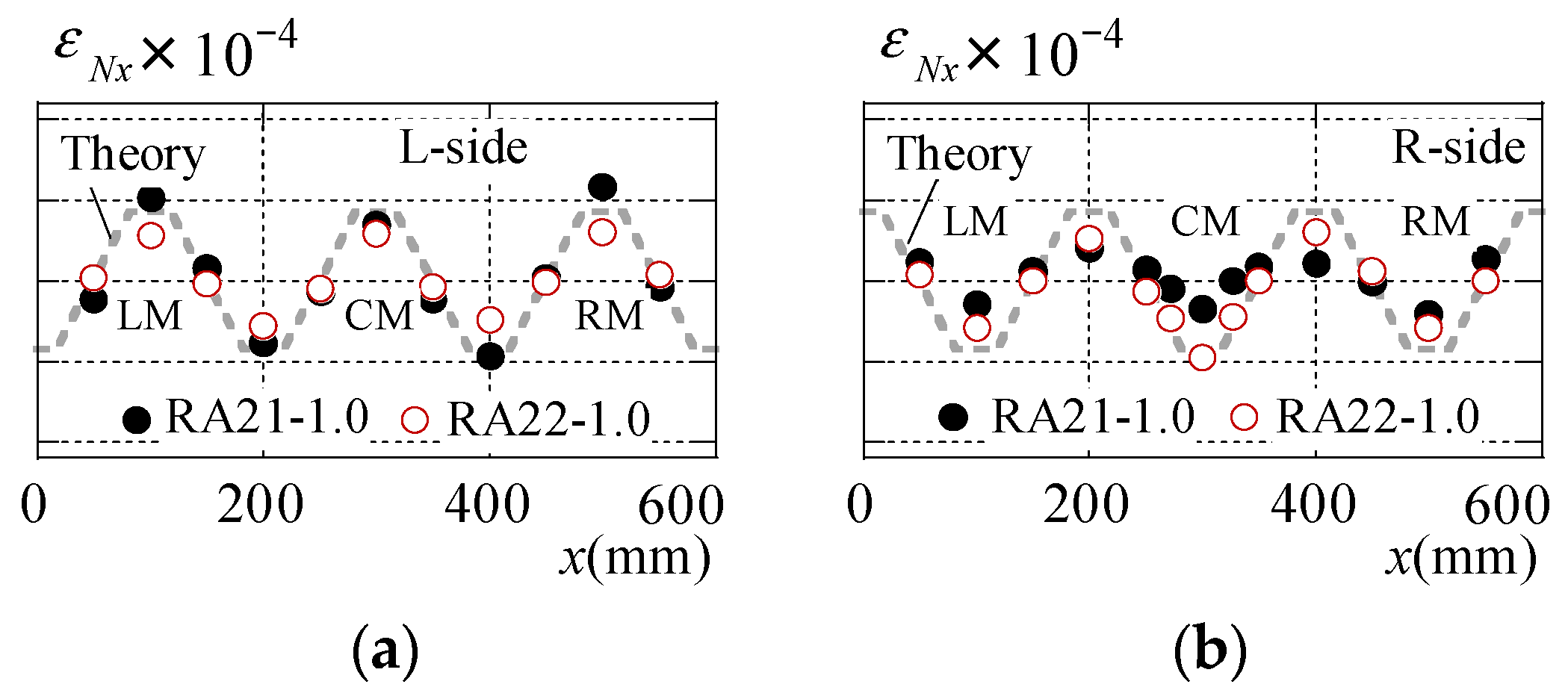
3.3. Stress State of Roof Folded Plate
3.4. Summary of Torsion Experiment Results
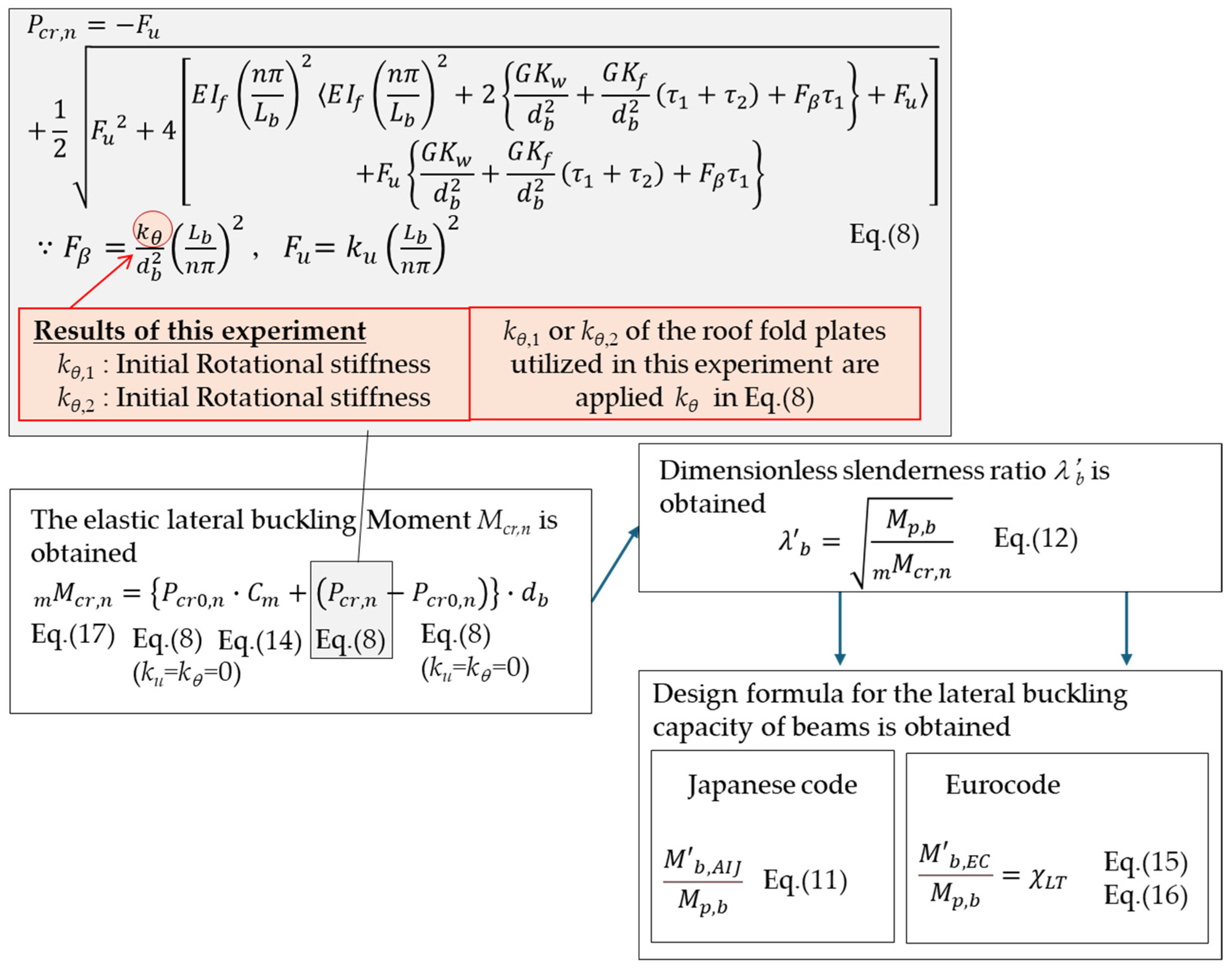
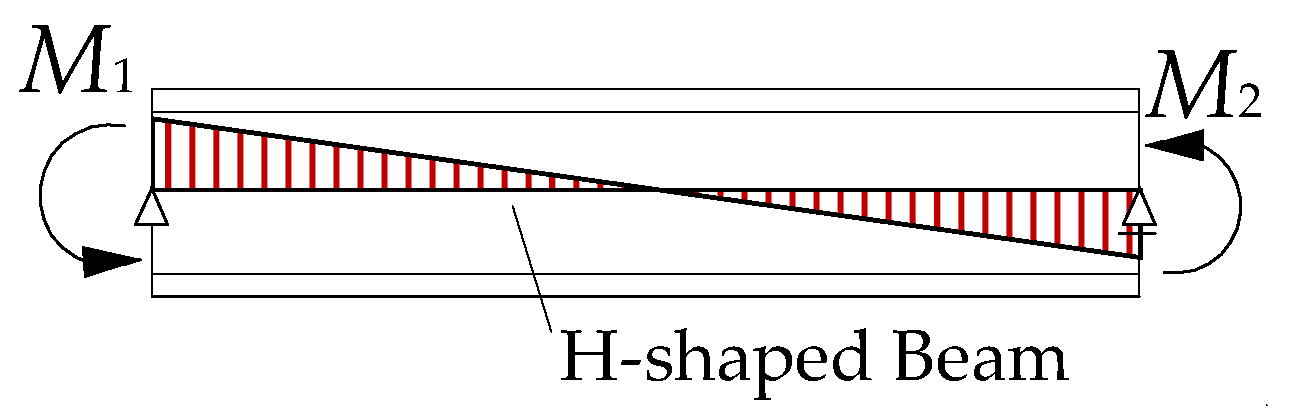
4. Effect of Roof Folded Plates on Lateral Buckling of H Beams in Steel Structures
5. Conclusions
- (1)
- When the top flange of the beam is pressed against the bottom flange of the roof folded plate during torsional deformation of the H beam, the small thickness of the roof folded plate causes bending deformation of the plate where it contacts the top flange of the H beam. Consequently, the rotational stiffness of the roof folded plate falls notably short of the theoretical stiffness posited for a rigid connection between the beam and the roof folded plate.
- (2)
- In the actual structural connection method (where tight frames are welded in a row along the length direction of the beam at the center of the top flange), the gap between the roof folded plate and the tight frame welded to the beam prevents torsional moments in the roof folded plate until the bottom flange of the roof folded plate contacts the top flange of the H steel beam, resulting in the non-exhibition of initial rotational stiffness kθ,1.
- (3)
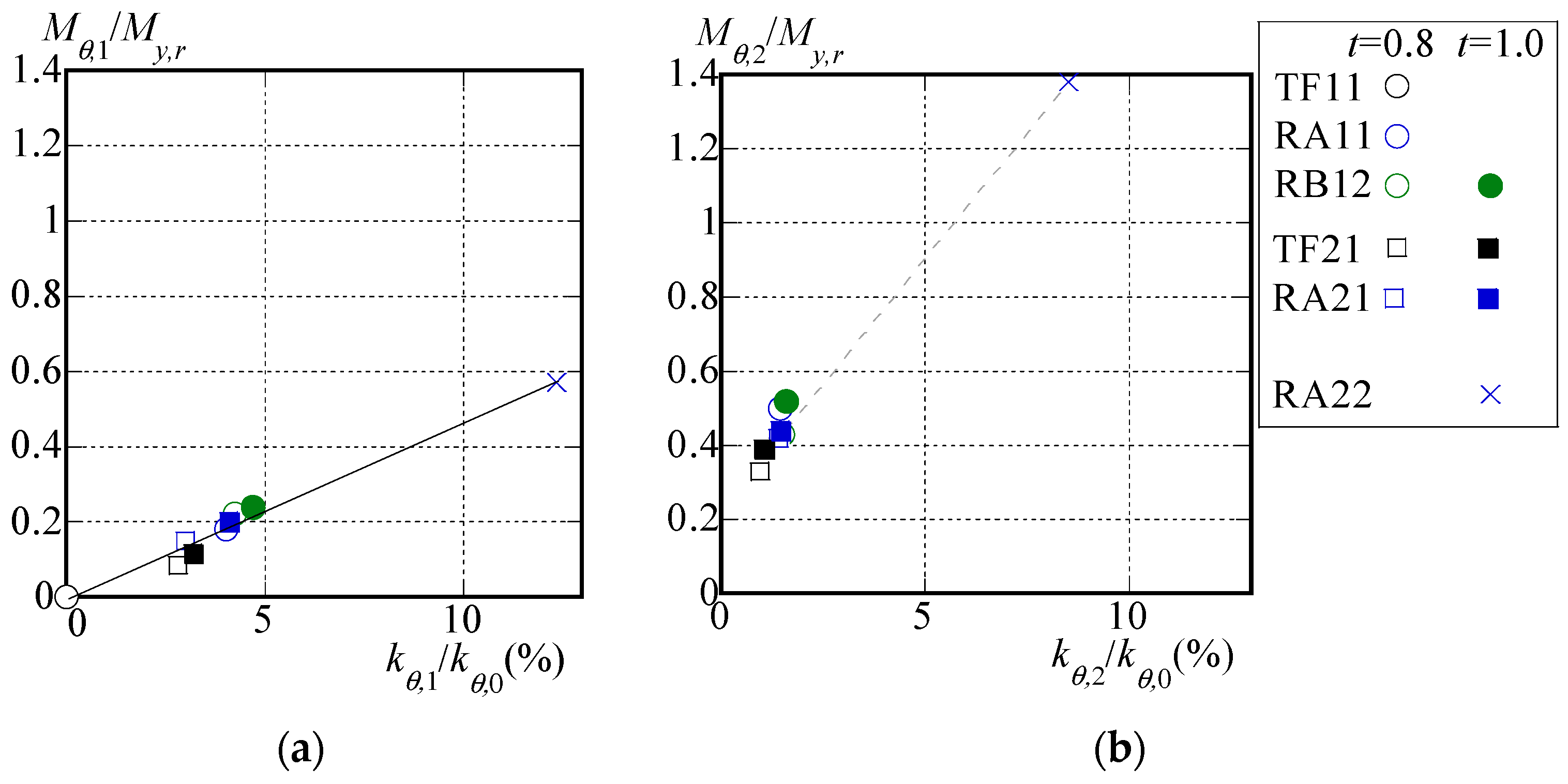
- For specimens in which the tight frames are welded in two rows along the length direction at the top flange of the beam, a torsional moment is induced in the roof folded plate from the onset of loading, resulting in the initial rotational stiffness kθ,1 of the roof folded plate, being 2–3% of the theoretical rotational stiffness kθ,0.
- (4)
- For specimens in which connectors with stiffened blocks are utilized and both the top and bottom flanges of the roof folded plate are constrained, the initial rotational stiffness surpasses that of the other specimens. Specifically, the initial rotational stiffness kθ,1 of the roof folded plate amounts to approximately 12% of the theoretical rotational stiffness kθ,0.
- (5)
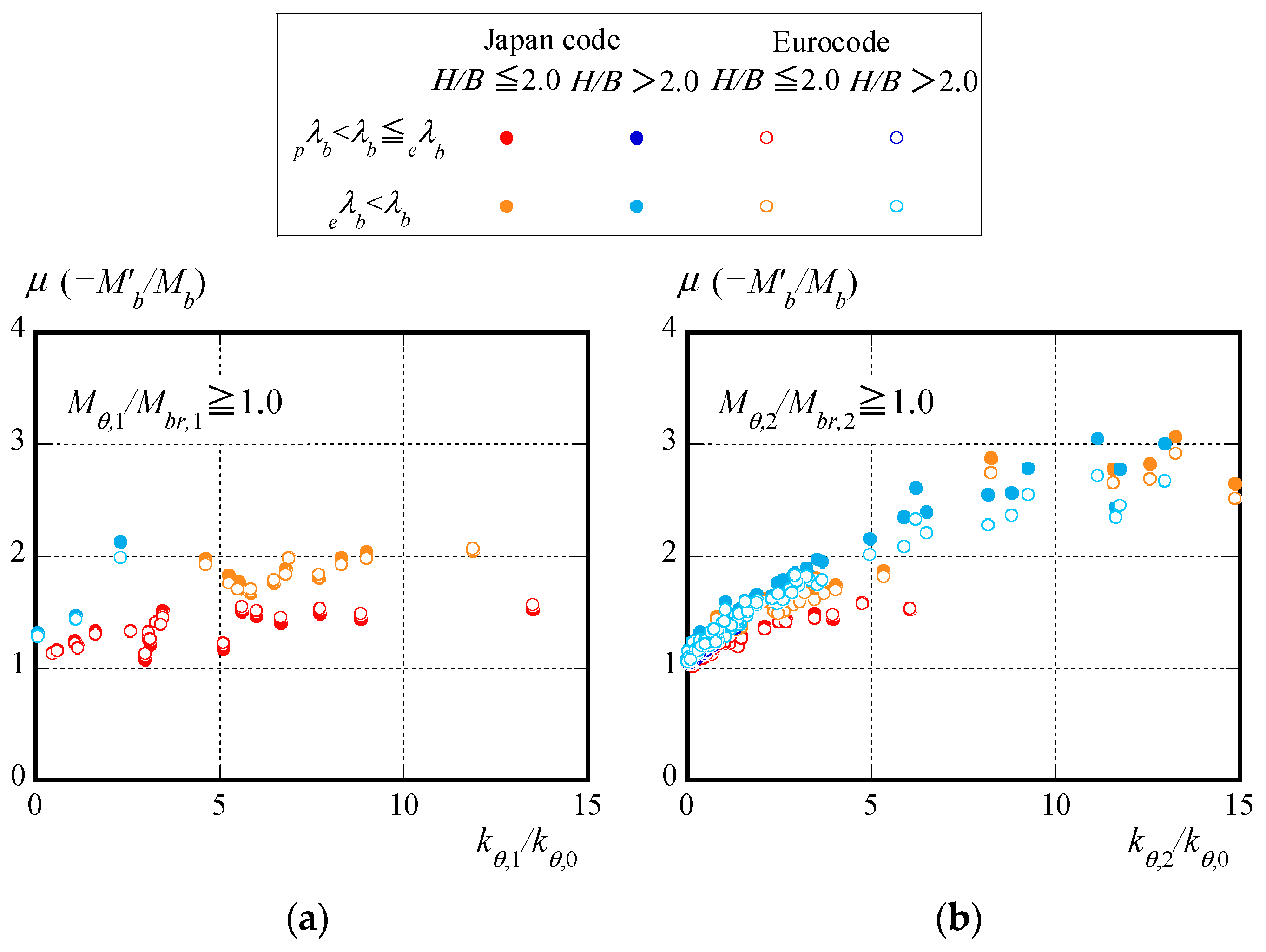
- When evaluating the lateral buckling capacity of continuously stiffened H beams using the buckling design capacities specified by the Japan code [46] and the Eurocode [47], it was observed that the design capacity outlined by the Japan code exceeded that of the Eurocode, even when the dimensionless slenderness ratio was equivalent.
- (6)
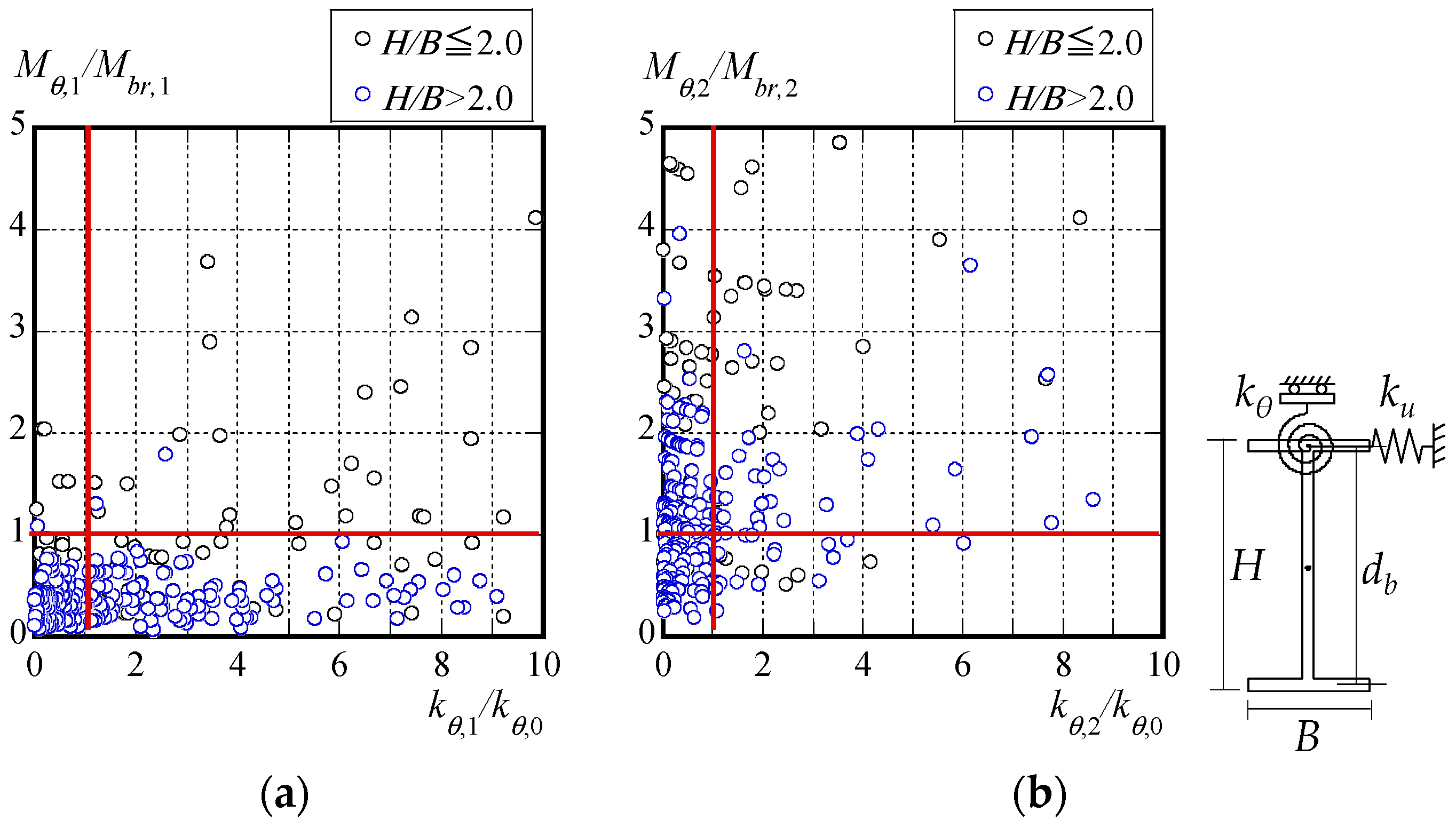
- Upon attaching the roof folded plates used in the experiments to the surveyed structures, it was observed that, in 16% of all of the structures, the torsional moment Mbr,1 occurring in the roof folded plates during the lateral buckling of the main beams was smaller than the torsional moment Mθ,1 at the onset of stiffness reduction, at which the initial rotational stiffness kθ,1 of the roof folded plates used in this study can be achieved. In contrast, in 62% of all structures, the maximum torsional moment Mθ,2, for which the secant rotational stiffness kθ,2 of the roof folded plates used in this study can be demonstrated, exceeds the torsional moment Mbr,2 occurring in the roof folded plates during the lateral buckling of the main beams. Thus, it can be inferred that the number of structures in which the roof folded plate exhibits the required performance against lateral buckling of the beams can be increased by utilizing the maximum torsional moment and the secant stiffness, rather than by relying on the initial stiffness and the bearing capacity at the onset of stiffness reduction, as the metrics for the holding performance of a roof folded plate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ishida, T.; Iyama, J.; Kishiki, S.; Shimada, Y.; Yamada, S.; Seike, T. Structural Damage to School Gymnasiums due to the 2016 Kumamoto Earthquake. J. Technol. Des. (Trans. AIJ) 2018, 58, 1313–1318. (In Japanese) [Google Scholar] [CrossRef]
- Suzuki, A.; Fujita, T.; Kimura, Y. Identifying damage mechanisms of gymnasium structure damaged by the 2011 Tohoku earthquake based on biaxial excitation. Structures 2022, 35, 1321–1338. [Google Scholar] [CrossRef]
- Kobayashi, F.; Sato, E.; Tomokiyo, E.; Noda, M.; Gavanski, E.; Takadate, Y.; Takamori, K.; Kimura, K.; Nakato, S.; Moriyama, H.; et al. Immediate Report on Wind Disasters Occurred by Typhoon 1915. J. Wind Eng. (JAWE) 2020, 45, 30–39. (In Japanese) [Google Scholar] [CrossRef]
- Akatsuka, T.; Tomokiyo, E. Investigation of Damage to Houses Caused by Typhoon JEBI and the Influence of Surrounding Environments on Its Occurrence. J. Wind Eng. (JAWE) 2020, 26, 96–101. (In Japanese) [Google Scholar] [CrossRef]
- Timoshenko, S.P. Beam without Lateral Support; American Society of Civil Engineers (ASCE): Reston, VA, USA, 1924; Volume 87. [Google Scholar]
- Bleich, F. Buckling Strength of Metal Structures; McGraw-Hill: New York, NY, USA, 1952; p. 405. [Google Scholar]
- Nethercot, D.A.; Rockey, K.C. A Unified Approach to the Elastic Lateral Buckling of Beams. Struct. Eng. 1971, 49, 96–107. [Google Scholar] [CrossRef]
- Suzuki, T. Lateral Buckling of Open Web. Trans. Archit. Inst. Jpn. (Trans. AIJ) 1960, 166, 537–540. (In Japanese) [Google Scholar]
- Wakabayashi, M.; Nakamura, T. Numerical Analysis of Lateral Buckling Strength of H-Shaped Steel Beams Subjected to End Moments and Uniformly Distributed Load. Trans. Archit. Inst. Jpn. (Trans. AIJ) 1973, 208, 7–13. (In Japanese) [Google Scholar] [CrossRef]
- Narayanan, R. Beam and Beam Columns-Stability and Strength; Applied Science Publisher: Boca Raton, FL, USA, 1983. [Google Scholar]
- Salvador, T.G. Lateral Buckling of Eccentrically Loaded I–Columns. Am. Soc. Civ. Eng. (ASCE) 1956, 121, 1163–1178. [Google Scholar] [CrossRef]
- Trahair, N.S. Laterally unsupported beams. Eng. Struct. 1996, 18, 759–768. [Google Scholar] [CrossRef]
- Lebastard, M.; Couchaux, M.; Bureau, A.; Hjiaj, M. Lateral-torsional buckling of uniform and tapered welded I-section beams. Eng. Struct. 2024, 303, 117301. [Google Scholar] [CrossRef]
- Yura, J.A. Fundamentals of beam bracing. Eng. J.-Am. Inst. Steel Constr. 2001, 38, 11–26. [Google Scholar] [CrossRef]
- Gengshu, T.; Shaofan, C. The elastic buckling of interbraced girders. J. Constr. Steel Res. 1989, 14, 87–105. [Google Scholar] [CrossRef]
- Kimura, Y.; Sugita, Y.; Yoshino, Y. Effect of lateral-rotational restraint of continuous braces on lateral buckling strength for H-shaped steel beams with compressive axial force and flexural moment. J. Struct. Constr. Eng. (Trans. AIJ) 2016, 81, 1321–1331. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Kimura, Y.; Sato, Y. Effect of warping restraint of beams to column joint on lateral buckling behavior for H-shaped beams with continuous braces under gradient flexural moment. J. Struct. Constr. Eng. (Trans. AIJ) 2021, 86, 145–155. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Yoshino, Y. Required Bracing Capacity on Lateral Buckling Strength for H-Shaped Beams with Bracings. J. Struct. Constr. Eng. (Trans. AIJ) 2011, 76, 2143–2152. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Kimura, Y.; Matsuo, T.; Yoshino, Y. Estimation of Elasto-Plastic Lateral Buckling Stress for H-Shaped Beams with Lateral-Rotational Braces on Subjected to Axial Force and Flexural Moment. J. Struct. Constr. Eng. (Trans. AIJ) 2014, 79, 1299–1308. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Kawai, R.; Kanao, I. Numerical Studies on Lateral Bracing Method with Effective Restraint on Out-of-Plane Deformation of Wide Flange Beam. J. Struct. Constr. Eng. (Trans. AIJ) 2014, 79, 323–329. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Igawa, N.; Ikarashi, K.; Mitsui, K. Buckling Behavior of H-shaped Beam with Continuous Restraint Installed Transverse Stiffeners and Method for Deciding Stiffening Position. J. Struct. Constr. Eng. (Trans. AIJ) 2020, 85, 1491–1501. (In Japanese) [Google Scholar] [CrossRef]
- Nguyen, C.T.; Moon, J.; Lee, H.E. Lateral–torsional buckling of I-girders with discrete torsional bracings. J. Constr. Steel Res. 2010, 66, 170–177. [Google Scholar] [CrossRef]
- Ji, X.L.D.; Twizell, S.C.; Driver, R.G.; Imanpour, A. Lateral Torsional Buckling Response of Compact I-Shaped Welded Steel Girders. J. Struct. Eng. 2022, 148, 04022149. [Google Scholar] [CrossRef]
- Mohammadi, E.; Hosseini, S.S.; Rohanimanesh, M.S. Elastic lateral-torsional buckling strength and torsional bracing stiffness requirement for monosymmetric I-beams. Eng. Struct. 2016, 104, 116–125. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Joo, H.S.; Moon, J.; Lee, H.E. Flexural-torsional buckling strength of I-girders with discrete torsional braces under various loading conditions. Eng. Struct. 2022, 36, 337–350. [Google Scholar] [CrossRef]
- Fukunaga, I.; Todaka, T.; Zhang, Z.; Kanao, I. Deformation Capacity of Wide Flange Beam with Lateral Bracings. J. Struct. Constr. Eng. (Trans. AIJ) 2022, 87, 372–380. (In Japanese) [Google Scholar] [CrossRef]
- Matsui, R.; Yamaura, Y.; Takeuchi, T. Lateral Bracing Requirements for H-Section Beams with Supports Attached to Top Flange Subjected to Cyclic Antisymmetric Moment. J. Struct. Constr. Eng. (Trans. AIJ) 2013, 78, 1485–1492. (In Japanese) [Google Scholar] [CrossRef]
- Idota, H.; Kato, Y.; Ono, T. Lateral Bracing Spacing and Strength of H- Shaped Steel Beams under Cyclic Loading. J. Struct. Constr. Eng. (Trans. AIJ) 2013, 78, 1989–1998. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Ikarashi, K.; Ohnishi, Y.; Sano, T. Collapse Mode and Plastic Deformation Capacity of H-Shaped Beams with Continuous Restraint on Upper Flange. J. Struct. Constr. Eng. (Trans. AIJ) 2018, 83, 491–501. (In Japanese) [Google Scholar] [CrossRef]
- Kanao, I.; Nakashima, M.; Liu, D. Lateral Buckling Behavior and Lateral Bracing of Wide-Flange Beams Subjected Cyclic Loading. J. Struct. Constr. Eng. (Trans. AIJ) 2001, 66, 147–154. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Bradford, M.A.; Gao, Z. Distortional buckling solutions for continuous composite beams. J. Struct. Eng. 1992, 118, 73–89. [Google Scholar] [CrossRef]
- Rossi, A.; Nicoletti, R.S.; de Souza, A.S.C.; Martins, C.H. Lateral distortional buckling in steel-concrete composite beams: A review. Structures 2020, 27, 1299–1312. [Google Scholar] [CrossRef]
- Egilmez, O.O.; Herman, R.S.; Helwig, T.A. Lateral stiffness of steel bridge I-girders braced by metal deck forms. J. Bridge Eng. 2009, 14, 17–25. [Google Scholar] [CrossRef]
- Suzuki, A.; Kimura, Y. Rotation capacity of I-shaped beam failed by local buckling in buckling-restrained braced frames with rigid beam-column connections. J. Struct. Eng. 2023, 149, 04022243. [Google Scholar] [CrossRef]
- Suzuki, A.; Suzuki, K.; Kimura, Y. Ultimate shear strength of perfobond shear connectors subjected to fully reversed cyclic loading. Eng. Struct. 2021, 248, 113240. [Google Scholar] [CrossRef]
- Tsuda, K.; Kido, M. Buckling Strength of Columns Braced Continuously with Varying Axial Force -Flexural Buckling of Compressive Flange of H-shaped Steel Restrained by Web or Slab-. J. Struct. Constr. Eng. (Trans. AIJ) 2013, 78, 1513–1521. (In Japanese) [Google Scholar] [CrossRef]
- Ikarashi, K.; Sano, T. Influence of Upper Flange Restraint Condition on Lateral Buckling Behavior of H-Shaped Beam. J. Struct. Constr. Eng. (Trans. AIJ) 2018, 83, 1063–1073. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Yoshino, Y.; Ogawa, J. Effect of Lateral-Rotational Restraint and Strength of Continuously Braces on Lateral Buckling Load for H-Shaped Beams. J. Struct. Constr. Eng. (Trans. AIJ) 2013, 78, 193–201. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Sugita, Y. Effect of Lateral-Rotational Restraint by Continuous Braces on Lateral Buckling Strength for H-Shaped Beams with Gradient Flexural Moment and Compressive Axial Force. J. Struct. Constr. Eng. (Trans. AIJ) 2017, 82, 1799–1809. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Yoshino, Y. Effect of Lateral and Rotational Restraint for Bracings on Lateral Buckling Load for H-Shaped Beams under Moment Gradient. J. Struct. Constr. Eng. (Trans. AIJ) 2014, 79, 761–770. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Kimura, Y.; Yoshino, Y. Effect of Lateral-Rotational Restraint of Continuous Braces on Lateral Buckling Strength for H-Shaped Beams with Flexural Moment Gradient. J. Struct. Constr. Eng. (Trans. AIJ) 2016, 81, 1309–1319. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Kimura, Y.; Miya, M.; Liao, W. Effect of Restraint for Continuous Braces on Lateral Buckling Load for H-Shaped Beams with Warping Restraint of Beams to Column Joint. J. Struct. Constr. Eng. (Trans. AIJ) 2018, 83, 1355–1363. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Miya, M. Effect of Warping Restraint of Beams to Column Joint on Lateral Buckling Behavior for H-Shaped Beams with Continuous Braces under Gradient Flexural Moment. J. Struct. Constr. Eng. (Trans. AIJ) 2019, 84, 1601–1611. (In Japanese) [Google Scholar] [CrossRef]
- Architectural Institute of Japan (AIJ). Recommendations for Stability Design of Steel Structures; Maruzen Publishing Co., Ltd.: Tokyo, Japan, 2012. [Google Scholar]
- Architectural Institute of Japan (AIJ). Design Standard for Structures–Based on Allowable Stress Concept; Maruzen Publishing Co., Ltd.: Tokyo, Japan, 2012. [Google Scholar]
- Architectural Institute of Japan (AIJ). Recommendation for Limit State Design of Steel Structures; Maruzen Publishing Co., Ltd.: Tokyo, Japan, 2011. [Google Scholar]
- Eurocode-3: Design of Steel Structures Part 1–1,1-3,1-5: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005.
- Japan Metal Roofing Association. Standard of Steel Roofing (SSR); Japan Metal Roofing Association: Tokyo, Japan, 2007. [Google Scholar]
- JIS-A6514; Component for Metal Roof-Decks. Japanese Industrial Standards Committee: Tokyo, Japan, 2019. (In Japanese)
- Suzuki, A.; Abe, K.; Suzuki, K.; Kimura, Y. Cyclic behavior of perfobond-shear connectors subjected to fully reversed cyclic loading. J. Struct. Eng. 2021, 147, 04020355. [Google Scholar] [CrossRef]
- Yoshino, Y.; Liao, W.; Kimura, Y. Restraint effect on lateral buckling load of continuous braced H-shaped beams based on partial frame loading tests. J. Struct. Constr. Eng. (Trans. AIJ) 2022, 87, 634–645. (In Japanese) [Google Scholar] [CrossRef]
- Ikarashi, K.; Fujisawa, M.; Shimizu, N. Evaluation of Elastic Buckling Strength of Rectangular Corrugate Plate under Shear Loading. J. Struct. Constr. Eng. (Trans. AIJ) 2008, 73, 1883–1890. (In Japanese) [Google Scholar] [CrossRef]
- Ikarashi, K.; Nakano, S.; Shimizu, N. Evaluation of Shear Stiffness of Rectangular Corrugate Plate under Shear Loading. J. Struct. Constr. Eng. (Trans. AIJ) 2009, 74, 2327–2334. (In Japanese) [Google Scholar] [CrossRef]
- Shimizu, N.; Okada, T.; Ikarashi, K. A Study on Post Shear Buckling Behavior in Corrugated Steel Plate. J. Struct. Constr. Eng. (Trans. AIJ) 2010, 75, 1013–1020. (In Japanese) [Google Scholar] [CrossRef]
- Wei, X.; Li, G.; Xiao, L.; Zhou, L.; He, K.; Han, B. Shear strength reduction of trapezoidal corrugated steel plates with artificial corrosion pits. J. Constr. Steel Res. 2021, 180, 106583. [Google Scholar] [CrossRef]
- Wen, C.-B.; Guo, Y.-L.; Zuo, J.-Q.; Zhao, X.-Y. Strength design of prefabricated corrugated steel plate shear walls under combined compression and shear loads. J. Build. Eng. 2023, 65, 105790. [Google Scholar] [CrossRef]
- Elamary, A.S.; Saddek, A.B.; Alwetaishi, M. Effect of corrugated web on flexural capacity of steel beams. Int. J. Appl. Eng. Res 2017, 12, 470–481. [Google Scholar]
- Kubo, M.; Watanabe, K. Lateral-Torstional Buckling Capacity of Steel Girders with Corrugated Web Plates. Doboku Gakkai Ronbunshu A 2007, 63, 179–193. (In Japanese) [Google Scholar] [CrossRef]
- Watanabe, K.; Uchida, S.; Kubo, M. Shear buckling capacity of steel girders with corrugated webs. J. Struct. Eng. A 2007, 53A, 13–24. (In Japanese) [Google Scholar]
- Elkawas, A.A.; Hassanein, M.F.; Elchalakani, M. Lateral-torsional buckling strength and behaviour of high-strength steel corrugated web girders for bridge construction. Thin-Walled Struct. 2018, 122, 112–123. [Google Scholar] [CrossRef]
- Yi, J.; Gil, H.; Youm, K.; Lee, H. Interactive shear buckling behavior of trapezoidally corrugated steel webs. Eng. Struct. 2008, 30, 1659–1666. [Google Scholar] [CrossRef]
- Suzuki, A.; Liao, W.; Shibata, D.; Yoshino, Y.; Kimura, Y.; Shimoi, N. Structural damage detection technique of secondary building components using piezoelectric sensors. Build. 2023, 13, 2368. [Google Scholar] [CrossRef]
- Degtyarev, V.V. Flexural strength of steel decks with square and rectangular holes: Numerical studies. J. Constr. Steel Res. 2020, 172, 106241. [Google Scholar] [CrossRef]
- Degtyarev, V.V. Concentrated load distribution in corrugated steel decks: A parametric finite element study. Eng. Struct. 2020, 206, 110158. [Google Scholar] [CrossRef]
- Cho, H.; Ozaki, F.; Sato, Y.; Miyabayashi, K. Collapse Temperature of a Simple Supported Roof Member Using a Corrugated Steel Thin Plate. Steel Constr. Eng. 2024, 30, 63–74. (In Japanese) [Google Scholar] [CrossRef]
- Steel Deck Institute. Standard for Steel Roof Deck; Steel Deck Institute: Allison Park, PA, USA, 2017. [Google Scholar]
- Steel Deck Institute. Roof Deck Design Manual; Steel Deck Institute: Allison Park, PA, USA, 2012. [Google Scholar]
- Steel Deck Institute. Manual of Construction with Steel Deck; Steel Deck Institute: Allison Park, PA, USA, 2016. [Google Scholar]
- Otsu, T.; Takagi, J.; Okada, T.; Sato, Y.; Shoji, Y. In-Plane Shear Performance Evaluation of Roof Deck Plates Connected with Puddle Welding. J. Technol. Des. (Trans. AIJ) 2019, 60, 691–696. (In Japanese) [Google Scholar] [CrossRef]
- Takagi, J.; Shoji, Y.; Okada, T.; Sato, Y.; Otsu, T. Material Property of Roof Deck Steel Plates and Shear Behavior of Connections with Puddle Welding. J. Technol. Des. (Trans. AIJ) 2019, 59, 177–182. (In Japanese) [Google Scholar] [CrossRef]
- Kikitsu, H.; Ohkuma, T.; Okuda, Y.; Nishimura, H. Vulnerability of V-beam Steel Roofing Subjected to High Wind Hazard. J. Wind Eng. (JAWE) 2008, 20, 223–228. (In Japanese) [Google Scholar] [CrossRef]
- Coni, N.; Gipiela, M.L.; D’Oliveira, A.S.C.M.; Marcondes, P.V.P. Study of the mechanical properties of the hot dip galvanized steel and galvalume. J. Braz. Soc. Mech. Sci. Eng. 2009, 32, 319–326. [Google Scholar] [CrossRef]
- JIS Z 2241; Metallic Materials—Tensile Testing Method of Test at Room Temperature. Japan Industrial Standards (JIS): Tokyo, Japan, 2011.




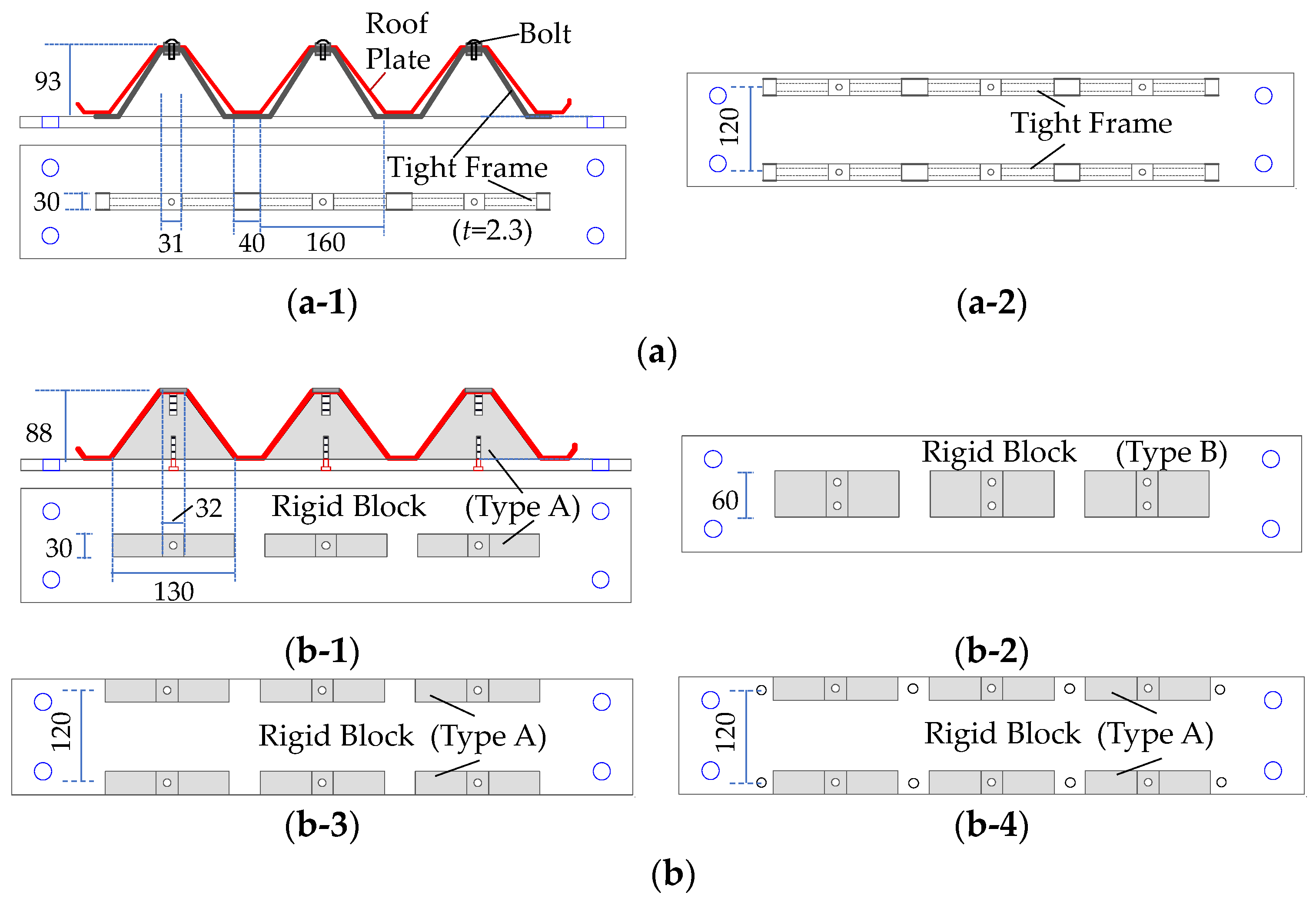



| Specimen | Roof Folded Plate’s Thickness | Roof Folded Plate—Joint | ||
|---|---|---|---|---|
| Material | Position | Bolt | ||
| (mm) | − | − | − | |
| TF11-0.8 | 0.8 | Tight frame | One line | One bolt/top flange |
| TF11-1.0 | 1.0 | |||
| TF21-0.8 | 0.8 | Two line | ||
| TF21-1.0 | 1.0 | |||
| RA11-0.8 | 0.8 | Rigid block (Type A) | One line | |
| RB12-0.8 | 0.8 | Rigid block (Type B) | One line | Two bolt/top flange |
| RB12-1.0 | 1.0 | |||
| RA21-0.8 | 0.8 | Rigid block (Type A) | Two line | One bolt/top flange |
| RA21-1.0 | 1.0 | |||
| RA22-1.0 | 1.0 | Two bolt/top and bottom flange | ||
| Example of specimen name | ||||
 | ||||
| Thickness (mm) | Young’s Modulus (×103 N/mm2) | Yield Strength (N/mm2) | Ultimate Strength (N/mm2) |
|---|---|---|---|
| 0.8 | 185 | 322 | 380 |
| 1.0 | 178 | 309 | 383 |
| Specimen | Rotational Stiffness | Bracing Moment | ||||||
|---|---|---|---|---|---|---|---|---|
| Theory | Initial | Secant | Initial | Secant | Yield | Initial | Maximum | |
| Equation (5) | Equation (4) | Equation (4)/Equation (5) | Equation (2) | Equation (1)/Equation (2) | ||||
| kθ,0 | kθ,1 | kθ,2 | kθ,1/kθ,0 | kθ,2/kθ,0 | My,r | Mθ,1/My,r | Mθ,2/My,r | |
| ×102 kN/rad | % | % | ×102 kN/rad | |||||
| TF11-0.8 | 37.75 | 0 | 0 | − | − | 1271 | − | − |
| TF11-1.0 | 45.3 | 0 | 0 | − | − | 1528 | − | − |
| TF21-0.8 | 37.75 | 1.08 | 0.36 | 2.85 | 0.95 | 1271 | 0.07 | 0.33 |
| TF21-1.0 | 45.3 | 1.47 | 0.47 | 3.25 | 1.04 | 1528 | 0.11 | 0.39 |
| RA11-0.8 | 37.75 | 1.51 | 0.54 | 4.01 | 1.42 | 1271 | 0.18 | 0.5 |
| RB12-0.8 | 37.75 | 1.60 | 0.57 | 4.24 | 1.5 | 1528 | 0.22 | 0.43 |
| RB12-1.0 | 45.3 | 2.14 | 0.72 | 4.72 | 1.6 | 1271 | 0.24 | 0.52 |
| RA21-0.8 | 37.75 | 1.15 | 0.53 | 3.04 | 1.4 | 1528 | 0.11 | 0.42 |
| RA21-1.0 | 45.3 | 1.85 | 0.66 | 4.09 | 1.45 | 1271 | 0.2 | 0.44 |
| RA22-1.0 | 45.3 | 5.60 | 3.85 | 12.36 | 8.5 | 1528 | 0.57 | 1.38 |
| Slenderness Ratio of Main Beams | Percentage of Total (%) | Number of Buildings |
| 67 ≤ λb ≤ 200 | 34.0 | 206 |
| 200 < λb ≤ 300 | 45.9 | 278 |
| 300 <λb | 20.1 | 122 |
| Types of Small Beams | Percentage of Total (%) | Number of Buildings |
| H | 94.4 | 572 |
| Angle and channel | 5.0 | 30 |
| Not listed | 0.6 | 4 |
| Types of Purlin Members | Percentage of Total (%) | Number of Buildings |
| Channel (C,2C) | 89.3 | 541 |
| Angle (L,2L) | 1.0 | 6 |
| T | 0.5 | 3 |
| Not listed | 9.2 | 56 |
| Types of Roofing Members | Percentage of Total (%) | Number of Buildings |
| Roof folded plate | 2.8 | 17 |
| Colored steel plate | 78.4 | 476 |
| Not listed | 18.8 | 113 |
 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshino, Y.; Kimura, Y. Rotational Stiffening Performance of Roof Folded Plates in Torsion Tests and the Stiffening Effect of Roof Folded Plates on the Lateral Buckling of H Beams in Steel Structures. Buildings 2024, 14, 1158. https://doi.org/10.3390/buildings14041158
Yoshino Y, Kimura Y. Rotational Stiffening Performance of Roof Folded Plates in Torsion Tests and the Stiffening Effect of Roof Folded Plates on the Lateral Buckling of H Beams in Steel Structures. Buildings. 2024; 14(4):1158. https://doi.org/10.3390/buildings14041158
Chicago/Turabian StyleYoshino, Yuki, and Yoshihiro Kimura. 2024. "Rotational Stiffening Performance of Roof Folded Plates in Torsion Tests and the Stiffening Effect of Roof Folded Plates on the Lateral Buckling of H Beams in Steel Structures" Buildings 14, no. 4: 1158. https://doi.org/10.3390/buildings14041158
APA StyleYoshino, Y., & Kimura, Y. (2024). Rotational Stiffening Performance of Roof Folded Plates in Torsion Tests and the Stiffening Effect of Roof Folded Plates on the Lateral Buckling of H Beams in Steel Structures. Buildings, 14(4), 1158. https://doi.org/10.3390/buildings14041158