Shear Performance and Damage Characterization of Prefabricated Basalt Fiber Reactive Powder Concrete Capping Beam Formwork Structure
Abstract
1. Introduction
2. Materials and Experimental Program
2.1. Design of Test Formwork Dimensions
2.2. Materials
2.3. Structural Test
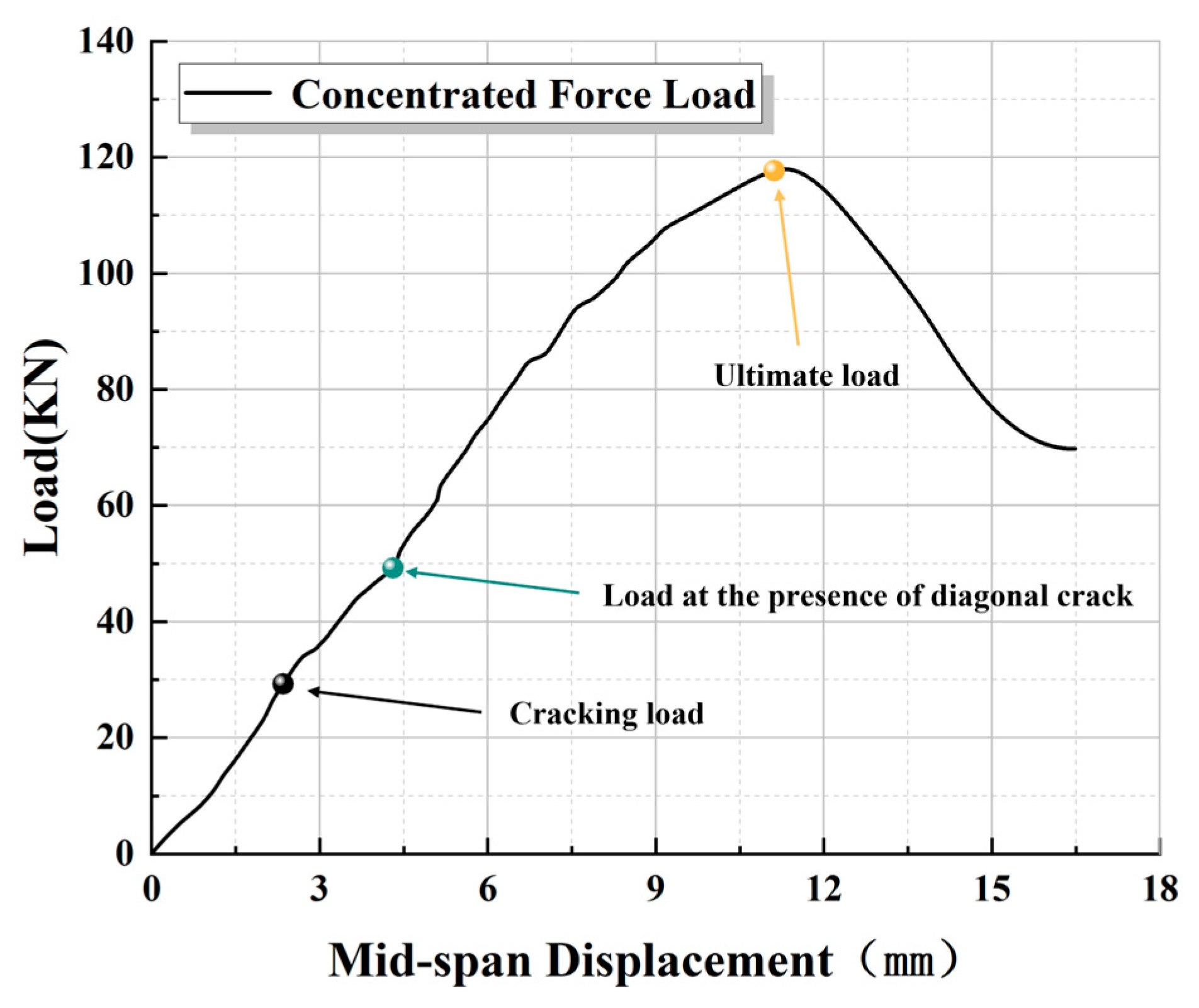
3. Results
3.1. Shear Failure Mode of Prefabricated BFRPC Capping Beam Formwork
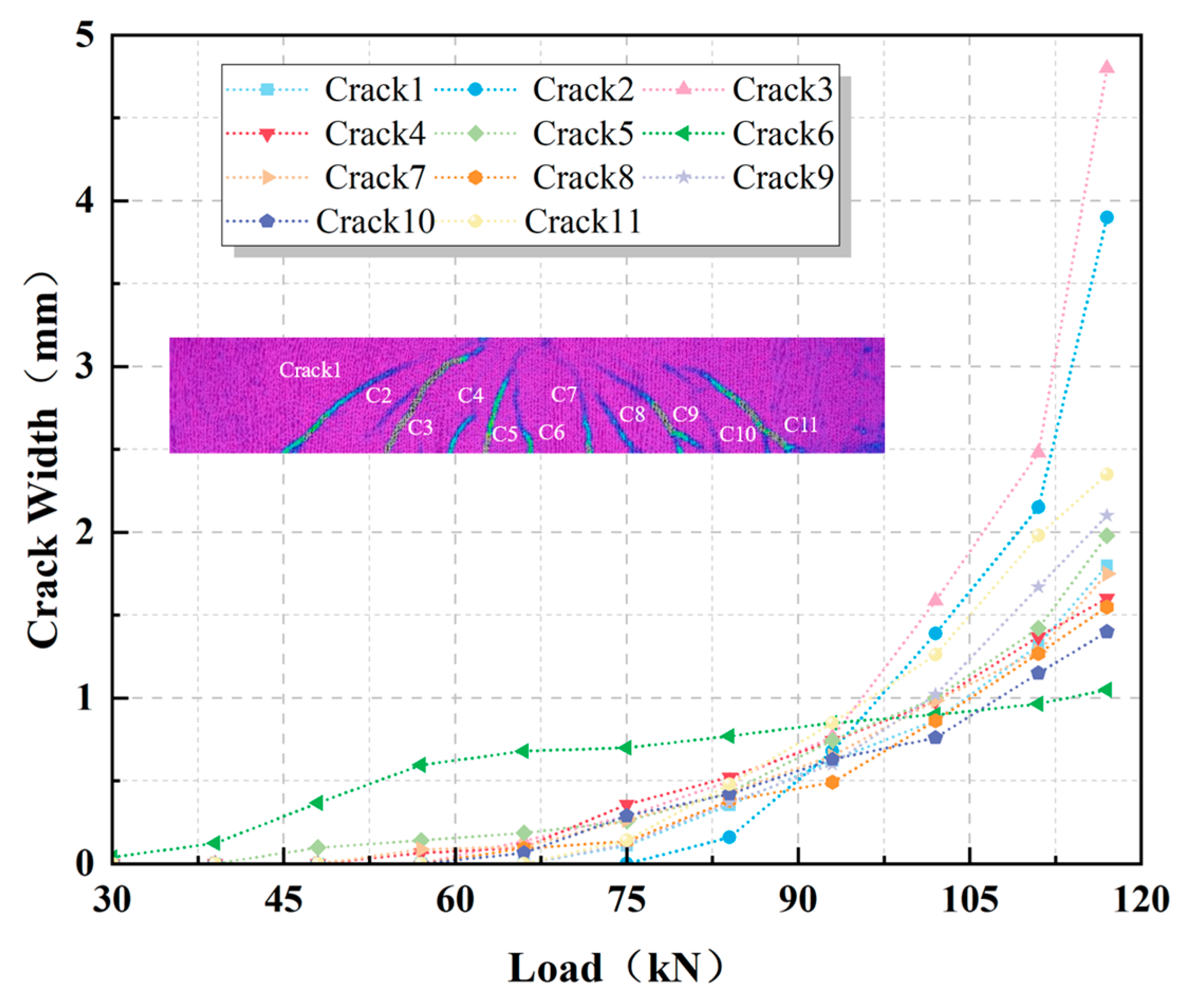
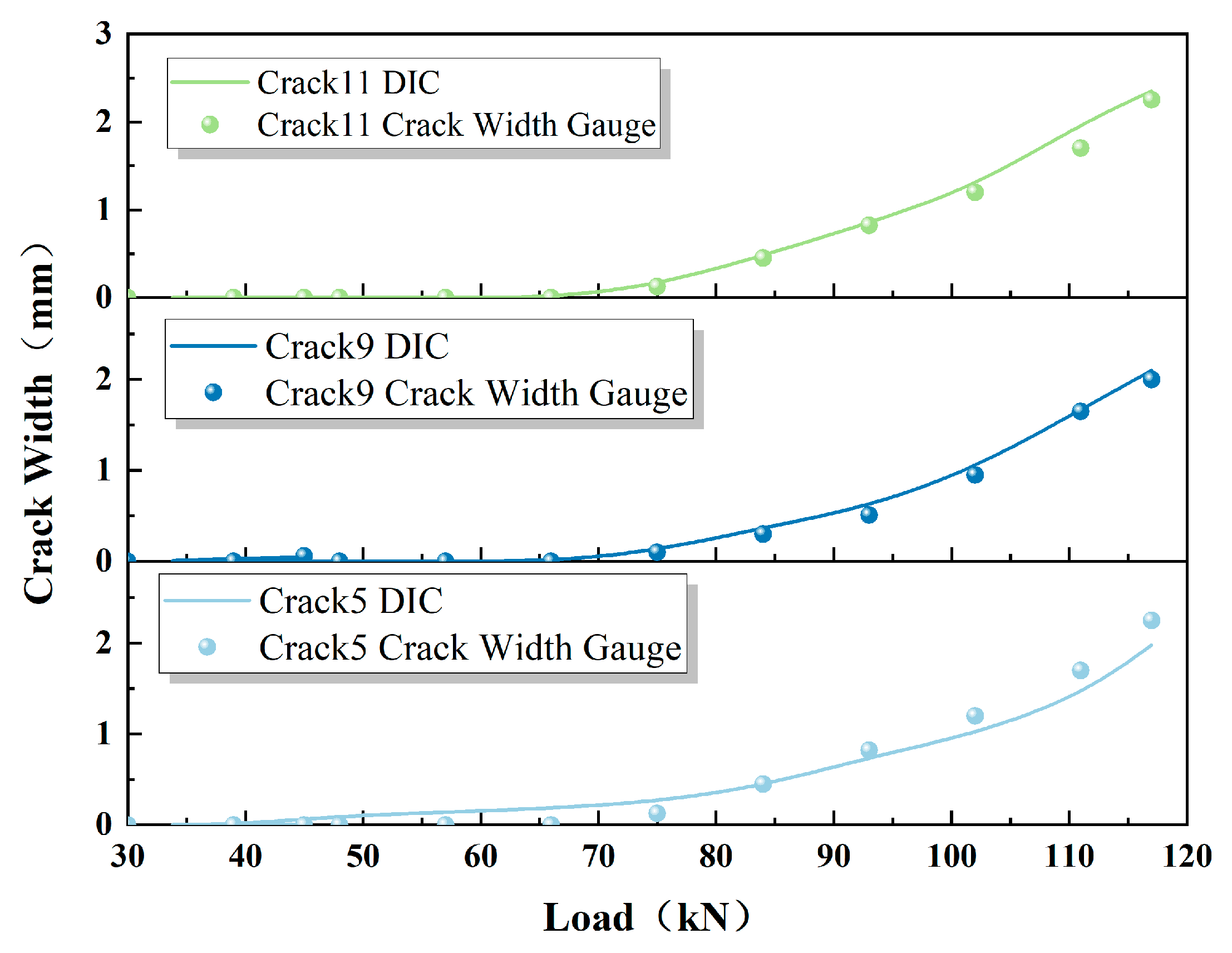
3.2. Evolution of Cracks during Shear Damage
3.3. Acoustic Characterization of Shear Damage in BFRPC Capping Beam Formwork
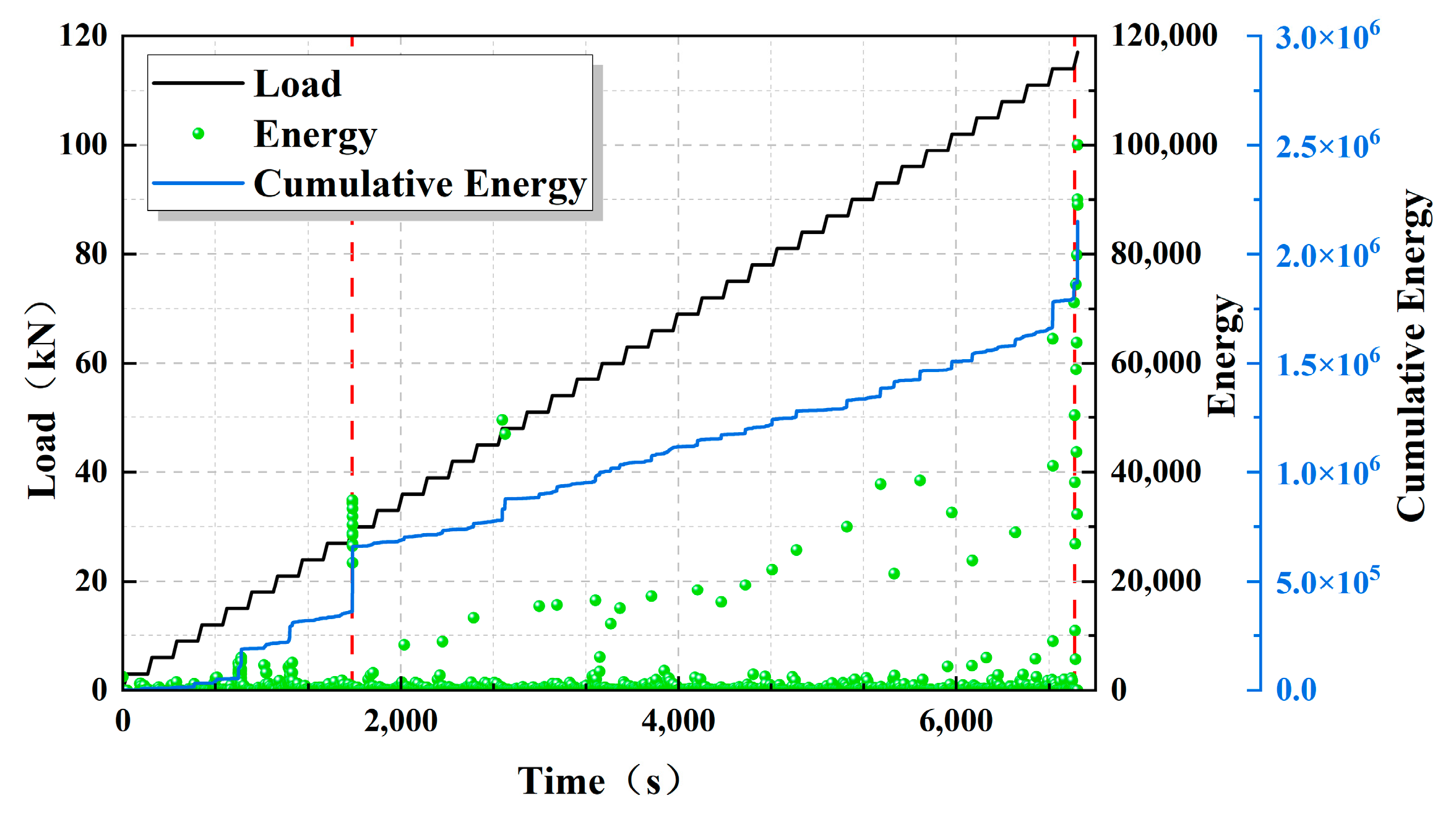
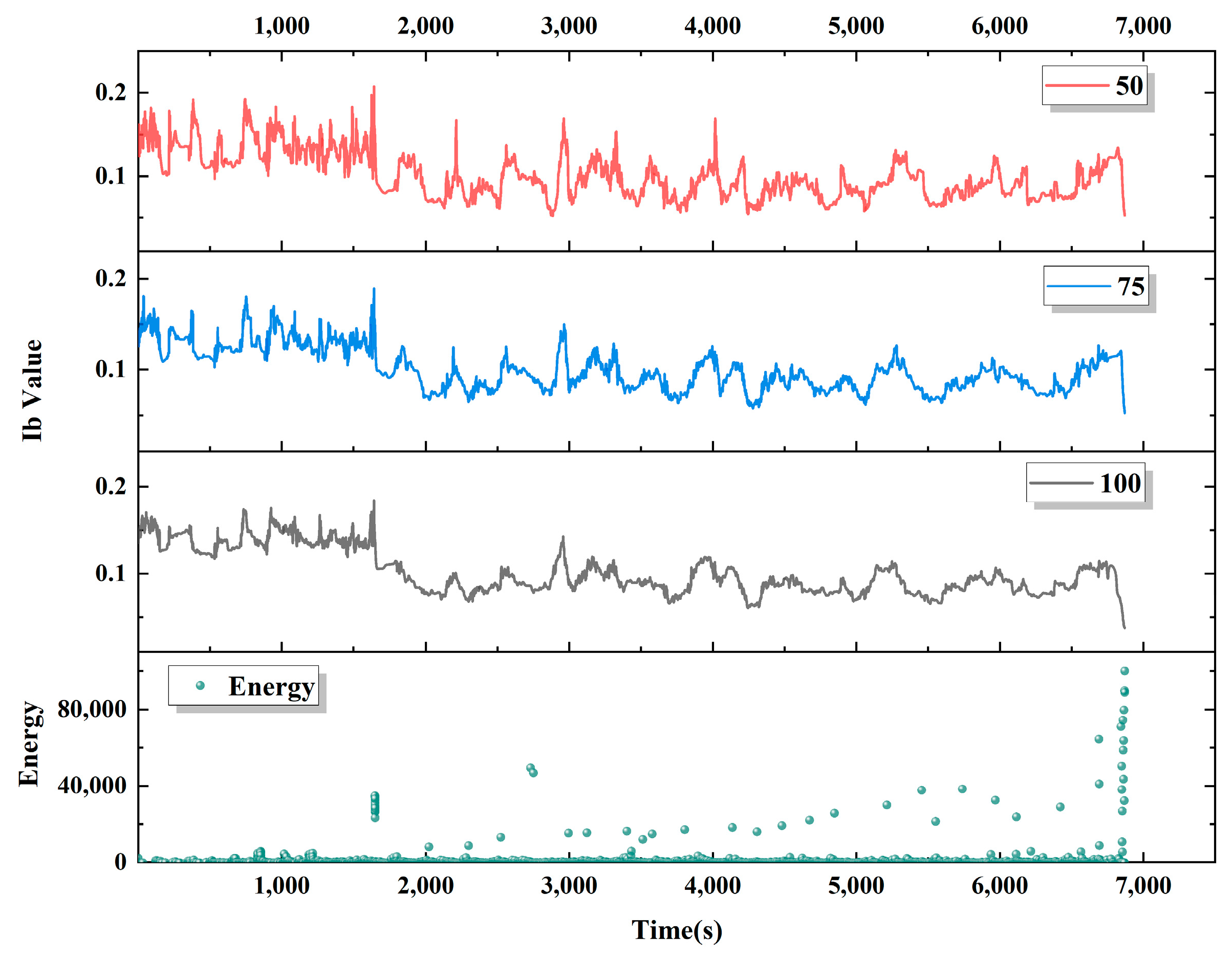
3.3.1. Energy Analysis
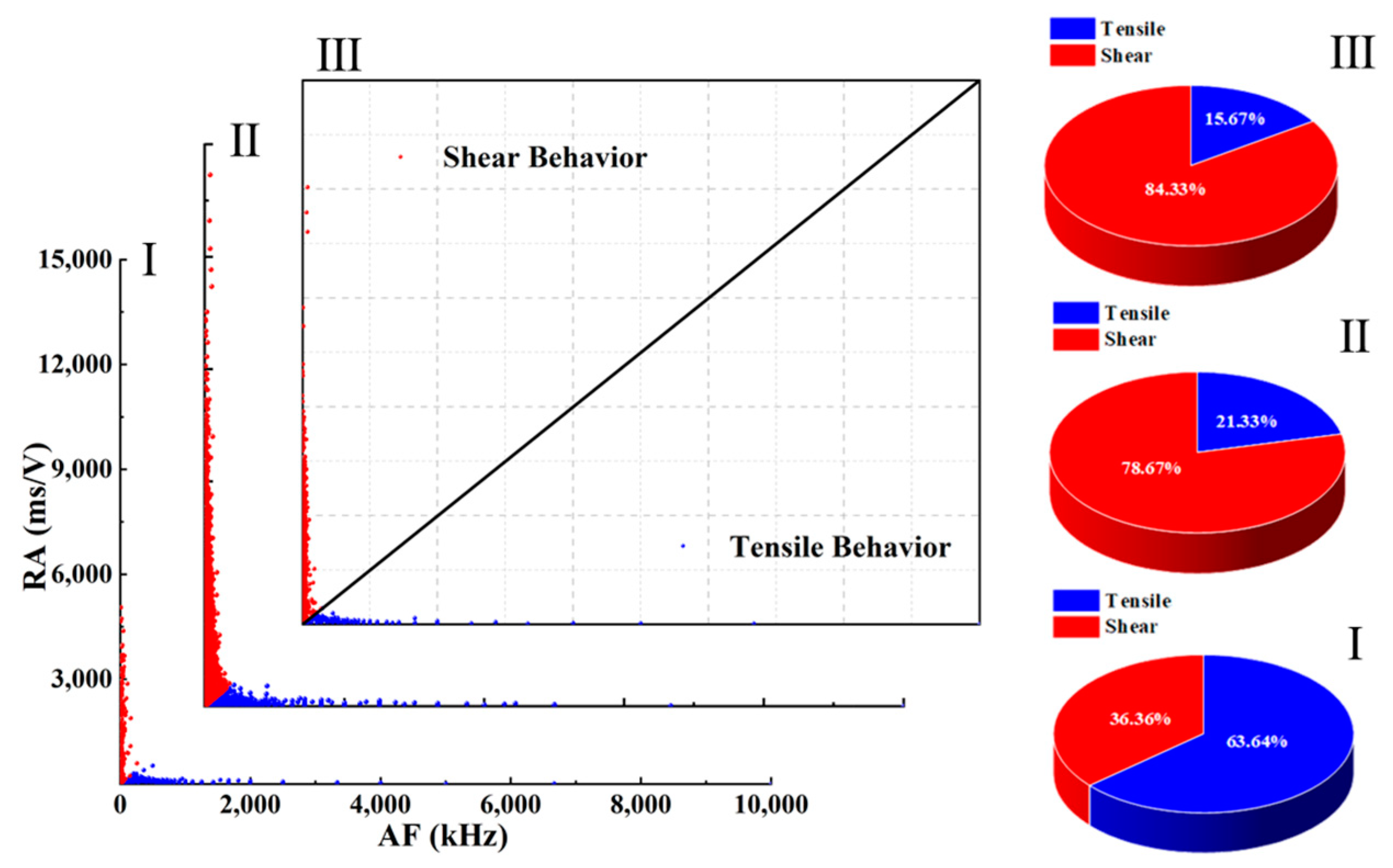
3.3.2. RA-AF Correlation Analysis
3.3.3. Ib Value Analysis
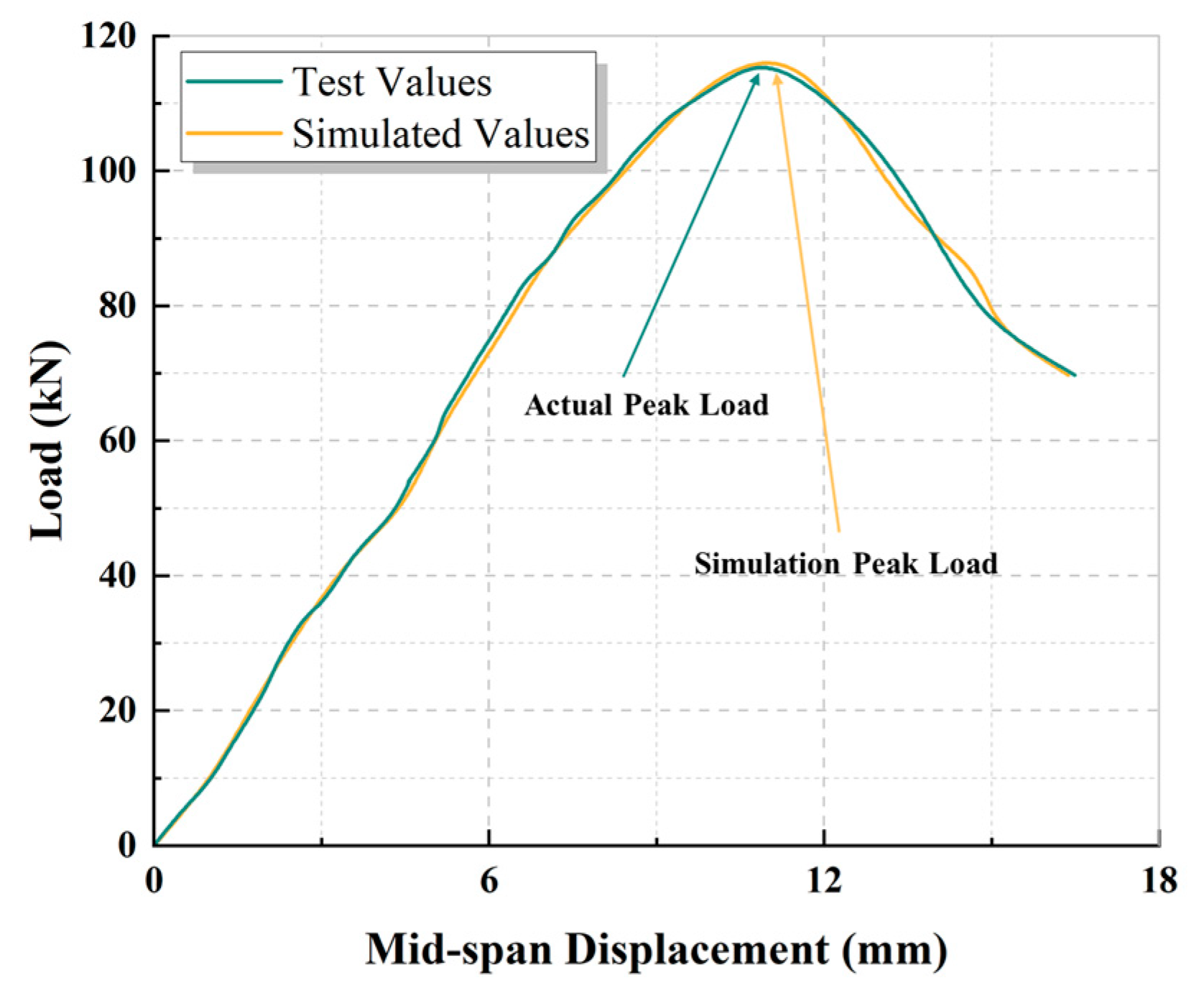
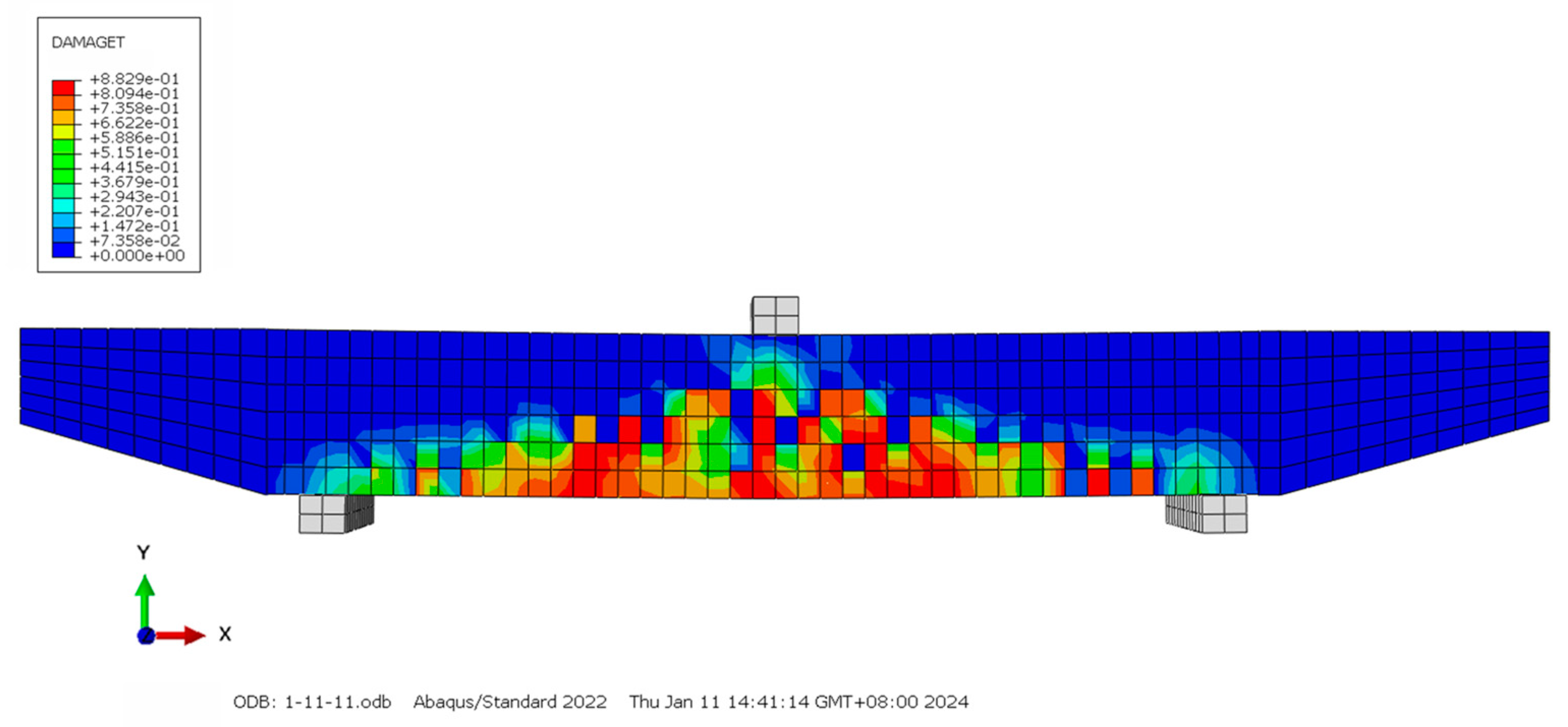
3.4. Numerical Simulation Analysis of BFRPC Capping Beam Formwork
3.5. Theoretical Model of BFRPC Capping Beam Formwork Shear Capacity Based on Subdivision Superposition Theory
3.5.1. Shear Contribution of Concrete in Shear Compression Zone
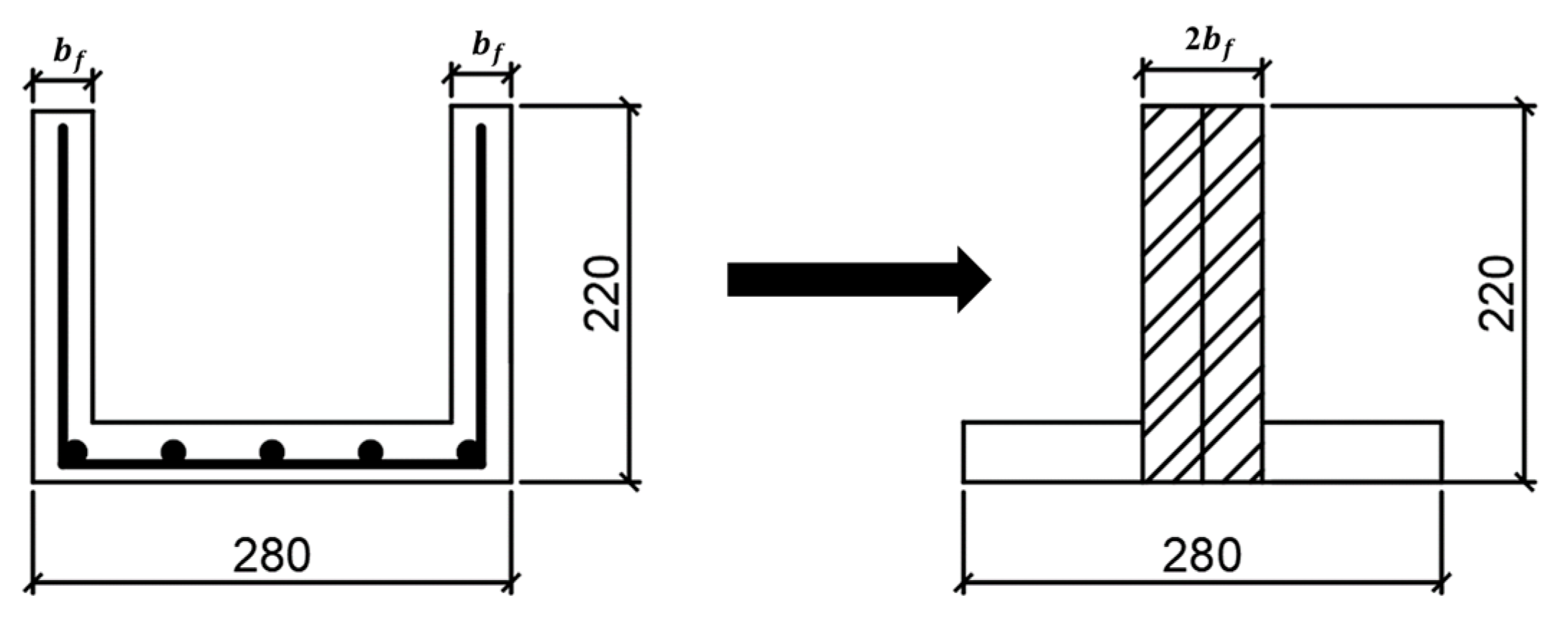
3.5.2. Shear Contribution of Fiber
3.5.3. Shear Contribution of Stirrup
3.5.4. Prediction of Shear Capacity of BFRPC Capping Beam Formwork
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| the tensile strength of concrete | |
| the compressive strength of concrete | |
| the normal stress of concrete | |
| the shear stress of concrete | |
| the height of the ultimate pressure zone | |
| the cross-sectional area of the longitudinal reinforcement | |
| the stress in the longitudinal bar at the limit state | |
| the area of the fiber involved in shear resistance | |
| the inclination angle of the inclined pressure bar | |
| an itemized safety factor | |
| the residual tensile strength | |
| the fiber orientation coefficient | |
| the maximum width of the crack | |
| the residual tensile stress at crack width | |
| the yield stress of the stirrup | |
| the sum of the cross-sectional areas of the stirrups | |
| the spacing of the stirrups | |
| the effective height of the section | |
| the half-open stirrup strength discount factor |
References
- Li, C.; Zhuo, W.; Lin, K.; Sun, Y.; Chen, M. Experimental study on flexural behavior of segmental precast large-cantilevered prestressed concrete cap beam. Structures 2023, 57, 105166. [Google Scholar] [CrossRef]
- Liu, S.; Shao, Y. Discussion on design ideas of new precast pier cap beam. Highway 2023, 68, 217–222. [Google Scholar]
- Chen, A.; Li, H. Stress analysis of post-inserted steel bar of formwork support for non-floor cover beam. Highw. Traffic Technol. 2020, 38, 70–77. [Google Scholar]
- Wang, D.; Ju, Y. Mechanical properties of high performance concrete reinforced with basalt fiber and polypropylene fiber. Constr. Build. Mater. 2019, 197, 464–473. [Google Scholar] [CrossRef]
- Ge, L.; Zhang, Y.; Usama, S.; Li, H. Study on properties of basalt fiber reinforcing reactive powder concrete under different curing conditions. J. Mater. Res. Technol. 2023, 27, 5739–5751. [Google Scholar] [CrossRef]
- Lin, C.; Wang, Q. Mechanical behavior and constitutive relation of basalt fiber reactive powder concrete under impact load. Mater. Guide 2022, 36, 103–109. [Google Scholar]
- Ge, J.; Mei, D.; Yan, X.; Wang, Z. Comparative analysis of construction methods of precast assembled capping beam. J. Appl. Technol. 2018, 18, 56–62. [Google Scholar]
- Orcutt, C.; Cook, W.D.; Mitchell, D. Response of Variable-Depth Reinforced Concrete Pier Cap Beam. J. Bridge Eng. 2020, 25, 04020024. [Google Scholar] [CrossRef]
- Li, J.; Xia, Z.; Sun, M.; Xia, J. Experimental study on mechanical performance of UHPC shell-RC composite cap beam. China J. Highw. Transp. 2021, 34, 157–167. [Google Scholar] [CrossRef]
- Chung, C.H.; Lee, J.H.; Kwon, S.H. Proposal of a New Partially Precast Pier Cap System and Experimental Verification of its Structural Performance. KSCE J. Civ. Eng. 2018, 22, 2362–2370. [Google Scholar] [CrossRef]
- Zhi, Z.; Zhang, D.; Lu, Z.; Liu, Y. The Making Methods of U–Shaped Shell of RC beams in fabricated integral structure with precast shell and CAST-IN-PLACE core concrete. J. Yancheng Inst. Technol. 2011, 24, 66–70. [Google Scholar] [CrossRef]
- Zhi, Z.; Zhang, D.; Xun, Y.; Lu, Z. Experimental studies on shearing behavior of integral assembly RC beams with precast external shell and cast-in. place core concrete. Eng. Mech. 2012, 29, 342–348. [Google Scholar] [CrossRef]
- Zhang, D.; Zhi, Z.; Lu, Z.; Jin, R.; Liu, Y. Experimental studies of bending capacities of RC beams with precast external shell and cast-in-place core concrete. Eng. Mech. 2009, 26, 164–170. [Google Scholar]
- Zhi, Z.; Zhang, D.; Lu, Z. Test study on bending-resistance of precast shell for RC beam in fabricated integral structure with precast shell and cast in-place core concrete. Sichuan Build. Sci. 2010, 36, 1–4. [Google Scholar]
- Lin, Y. Flexural and Shear Behavior of UHPCC Composite Beams. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- WU, C.; Lin, Y.; Zhang, X.; Tian, Y.; Jiang, H.; Wang, Z. Study on short-term performance of interface bonding between precast ultra-high performance concrete repair layer and existing concrete. J. Build. Struct. 2018, 39, 156–163. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X. Seismic performance analysis of existing masonry structure strengthened with ultra-high performance concrete. Build. Struct. 2022, 52, 77–81. [Google Scholar] [CrossRef]
- Guo, M. Experimental and Theoretical Study on Static Mechanical Performance of RPC-NC Composite Beam. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Mohammed, T.J.; Abu Bakar, B.H.; Bunnori, N.M. Torsional improvement of reinforced concrete beams using ultra high-performance fiber reinforced concrete (UHPFC) jackets Experimental study. Constr. Build. Mater. 2016, 106, 533–542. [Google Scholar] [CrossRef]
- Mohammed, T.J.; Abu Bakar, B.H.; Bunnori, N.M.; Ibraheem, F. Finite element analysis of longitudinal reinforcement beams with UHPFC under torsion. Comput. Concr. 2015, 16, 1–16. [Google Scholar] [CrossRef]
- Mohammed, T.J.; Abu Bakar, B.H.; Bunnori, N.M. Strengthening of reinforced concrete beams subjected to torsion with UHPFC composites. Struct. Eng. Mech. 2015, 56, 123–136. [Google Scholar] [CrossRef]
- Zhang, R.; Hu, P.; Zheng, X.; Cai, L.; Guo, R.; Wei, D. Shear behavior of RC slender beams without stirrups by using precast U-shaped ECC permanent formwork. Constr. Build. Mater. 2020, 163, 120430. [Google Scholar] [CrossRef]
- Wang, X. Research on Static Performance of Precast U-Shaped RPC Permanent Beam Formwork and Its Composite Beam. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Xie, H.; Wei, P.; Liu, N.; Gao, J.; Yang, Y.; Li, J.; Chen, S. Study on failure characteristics of basalt fiber reactive powder concrete under uniaxial loading. Constr. Build. Mater. 2023, 404, 133246. [Google Scholar] [CrossRef]
- Yun, H.; Lim, S.; Choi, W. Effects of Reinforcing Fiber Strength on Mechanical Properties of High-Strength Concrete. Fibers 2019, 7, 93. [Google Scholar] [CrossRef]
- Yang, X.; Liang, N.; Hu, Y.; Feng, R. An Experimental Study of Shear Resistance for Multisize Polypropylene Fiber Concrete Beams. Int. J. Concr. Struct. Mater. 2021, 15, 1–11. [Google Scholar] [CrossRef]
- Dong, H. Preparation and performance analysis of polypropylene fiber-reinforced concrete composite. Asia-Pac. J. Chem. Eng. 2020, 15, 1–9. [Google Scholar] [CrossRef]
- Yu, R.; Liu, K.; Yin, T.; Tang, L.; Ding, M.; Shui, Z. Comparative study on the effect of steel and polyoxymethylene fibers on the characteristics of Ultra-High Performance Concrete (UHPC). Cem. Concr. Comp. 2022, 127, 104418. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, R.; Liu, J.; Yang, L. Comparative study on the effect of steel and plastic synthetic fibers on the dynamic compression properties and microstructure of ultra-high-performance concrete (UHPC). Compos. Struct. 2023, 324, 117570. [Google Scholar] [CrossRef]
- Zhou, S. Multi-Scale Study on the Properties of Basalt Fiber Reactive Powder Concrete. Master’s Thesis, Jilin University, Changchun, China, 2023. [Google Scholar]
- Gong, Y.; Wu, S.; Bi, H.; Zhou, D.; Tan, G.; Huang, X. Acoustic characteristics characterization of bond-slip process between basalt fiber reactive powder concrete and steel strand. J. Jilin Univ. 2023, 53, 1819–1832. [Google Scholar] [CrossRef]
- Wu, S. Study on Bond-Slip Performance and Damage Behavior of BFRPC and Steel Strand Anchorage System. Master’s Thesis, Jilin University, Changchun, China, 2023. [Google Scholar]
- Zou, X.; Lin, H.; Feng, P.; Bao, Y.; Wang, J. A review on FRP-concrete hybrid sections for bridge applications. Compos. Struct. 2021, 262, 113336. [Google Scholar] [CrossRef]
- GB/T 50080-2016; Standard for Test Method of Performance on Ordinary Fresh Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- T/CCPA 7-2018; Fundamental Characteristics and Test Methods of Ultra-High Performance Concrete. China Building Materials Federation: Beijing, China, 2019.
- GB/T 50152-2012; Standard for Test Methods for Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.
- Hossein, N.; Pooya, R. Static capacity of tubular X-joints reinforced with fiber reinforced polymer subjected to compressive load. Eng. Struct. 2021, 236, 112041. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, X.; Chen, F.; Zhang, H.; Xiao, X. Numerical Simulation on Crack–Inclusion Interaction for Rib-to-Deck Welded Joints in Orthotropic Steel Deck. Metals 2023, 13, 1402. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.; Li, Z.; Luo, Y.; Xiao, X.; Liu, Y. Residual stresses effects on fatigue crack growth behavior of rib-to-deck double-sided welded joints in orthotropic steel decks. Adv. Struct. Eng. 2023, 27, 35–50. [Google Scholar] [CrossRef]
- American Concrete Institute. ACI318R-2019 Building Code Requirements for Structural Concrete and Commentary; ACI Committee 318; American Concrete Institute: Potomac, MD, USA, 2019. [Google Scholar]
- Federal Highway Administration. AASHTO LRFD Bridge Design Specifications and Commentary; Federal Highway Administration: Washington, DC, USA, 2012.
- Wang, J.; Qi, J. Unified shear strength computation model for reinforced concrete beams with and without stirrups. China Civ. Eng. J. 2013, 46, 47–57. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Huang, Y.; Tong, M.-N. Reliability-based analysis of the flexural strength of concrete beams reinforced with hybrid BFRP and steel rebars. Arch. Civ. Mech. Eng. 2022, 22, 171. [Google Scholar] [CrossRef]
- Qi, J.; Wang, J.; Lyv, Z. Calculation method of shear strength of externally prestressed concrete beams. J. Build. Struct. 2015, 36, 92–97. [Google Scholar] [CrossRef]
- Qi, J.; Wang, J.; Zhou, K.; Liu, J.; Li, W. Experimental and Theoretical Investigations on Shear Strength of UHPC Beams. China J. Highw. Transp. 2020, 33, 95–103. [Google Scholar] [CrossRef]
- AFGC-SÉTRA. Ultra High Performance Fibre-Reinforced Concretes; AFGC-SETRA Working Group: Paris, France, 2013. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
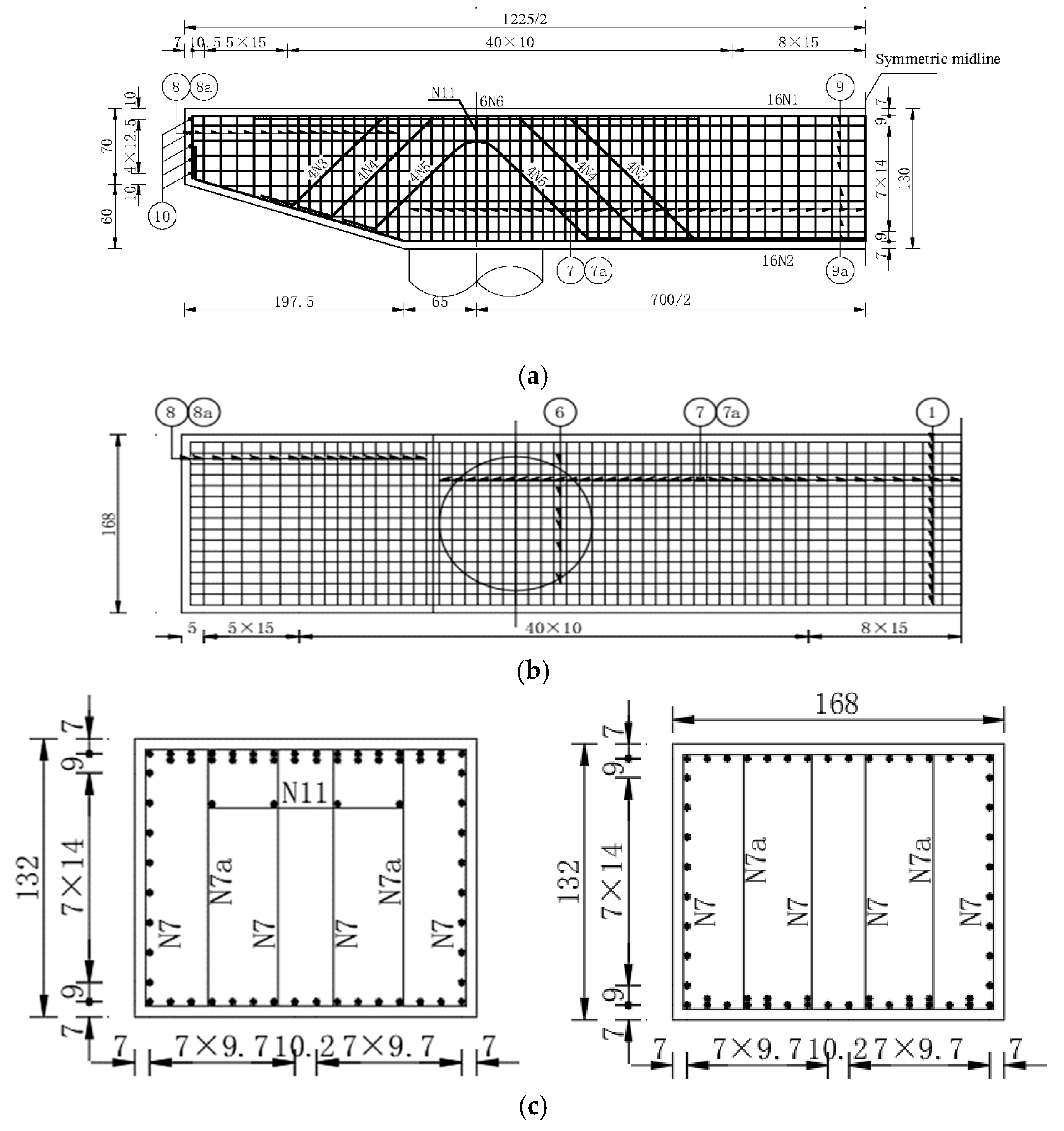

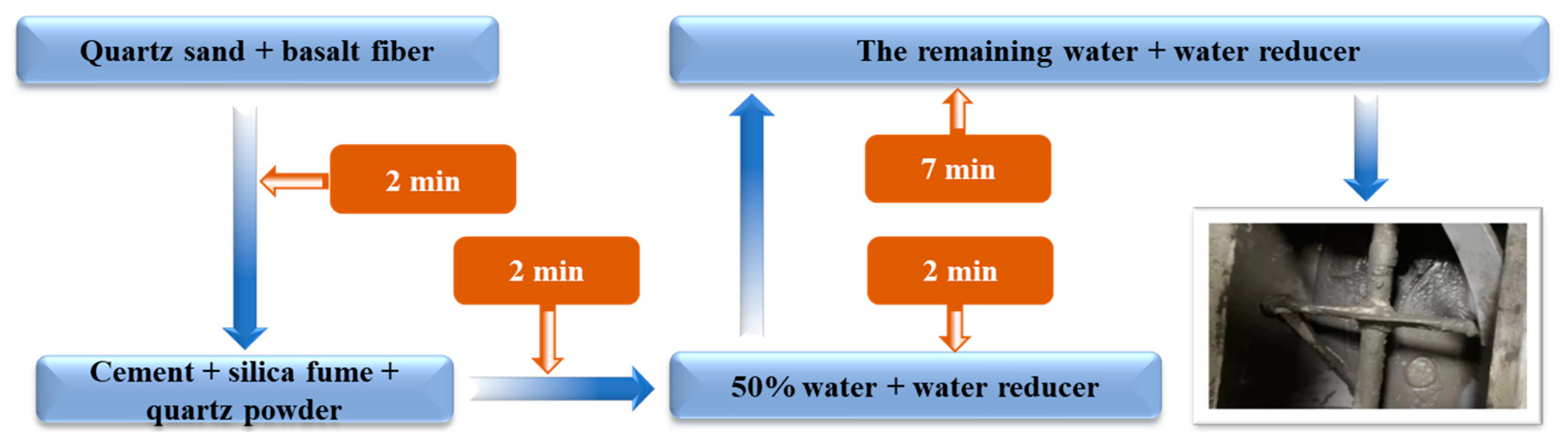







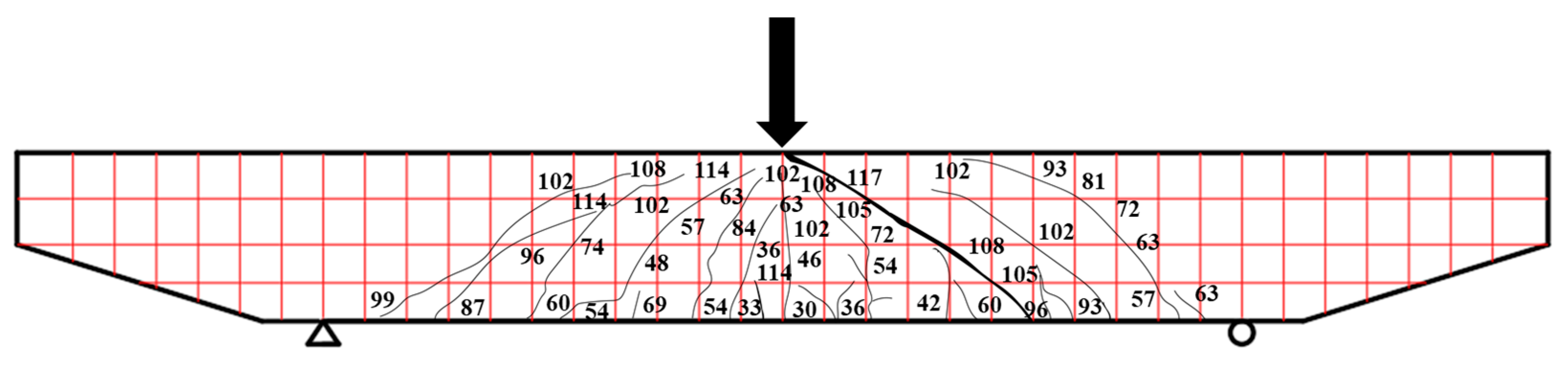





| Capping Beam Parameter | Similarity Ratio | Dimensional Parameter of BFRPC Capping Beam Formwork | T-1 |
|---|---|---|---|
| Material stress | 1:1 | Length | 2000 mm |
| Elastic modulus | 1:1 | Base plate width | 280 mm |
| Poisson ratio | 1:1 | Base plate thickness | 34 mm |
| Density | 1:1 | Sidewall height | 220 mm |
| Dimension | 1:6 | Sidewall thickness | 34 mm |
| Moment of inertia | 1:64 | Longitudinal bar diameter | 5φ8 |
| Bending moment | 1:63 | Riser bar diameter | 4φ8 |
| Load | 1:62 | Stirrup diameter | φ6@200 |
| Cement | Quartz Sand | Quartz Powder | Silica Fume | Water | Superplasticizer | Basalt Fiber | |
|---|---|---|---|---|---|---|---|
| 0.15–0.3 mm | 0.3–0.6 mm | ||||||
| 841.8 | 582.8 | 364.2 | 311.4 | 210.4 | 151.4 | 69.1 | 8 |
| Load (kN) | Strain (mm) | Load (kN) | Strain (mm) |
|---|---|---|---|
| 0 | 0 | 70 | 5.65 |
| 10 | 1.08 | 80 | 6.37 |
| 20 | 1.81 | 90 | 7.31 |
| 30 | 2.37 | 100 | 8.34 |
| 40 | 3.37 | 110 | 9.68 |
| 50 | 4.35 | 117 | 11.13 |
| 60 | 5.08 | 93 | 13.79 |
| Number | Reinforcement Rate (%) | Stirrup Spacing (mm) | Cracking Load (kN) | Ultimate Load (kN) |
|---|---|---|---|---|
| T-1 | 1.28 | 200 | 30 | 117 |
| M-1 | 1.28 | 200 | 31.62 | 118.2 |
| M-2 | 1.54 | 200 | 33.27 | 122.8 |
| M-3 | 1.93 | 200 | 35.16 | 128.2 |
| M-4 | 1.28 | 250 | 30.85 | 101.1 |
| M-5 | 1.28 | 300 | 29.86 | 90 |
| Number | Without Discount Factor | Consideration of Discount Factor | ||||
|---|---|---|---|---|---|---|
| Test | Calculated | Test | Calculate | |||
| T-1 | 117 | 130.082 | 0.898 | 117 | 116.673 | 1.003 |
| M-1 | 118.202 | 130.082 | 0.909 | 118.202 | 116.673 | 1.013 |
| M-2 | 122.812 | 135.401 | 0.907 | 122.812 | 121.992 | 1.007 |
| M-3 | 128.208 | 141.335 | 0.907 | 128.208 | 127.920 | 1.002 |
| M-4 | 101.115 | 110.010 | 0.919 | 101.115 | 100.811 | 1.003 |
| M-5 | 90.035 | 96.623 | 0.930 | 90.035 | 90.242 | 0.997 |
| Average | - | - | 0.912 | - | - | 1.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Wu, S.; Ning, C.; Hu, X.; Yi, Z.; Du, H. Shear Performance and Damage Characterization of Prefabricated Basalt Fiber Reactive Powder Concrete Capping Beam Formwork Structure. Buildings 2024, 14, 1701. https://doi.org/10.3390/buildings14061701
Gong Y, Wu S, Ning C, Hu X, Yi Z, Du H. Shear Performance and Damage Characterization of Prefabricated Basalt Fiber Reactive Powder Concrete Capping Beam Formwork Structure. Buildings. 2024; 14(6):1701. https://doi.org/10.3390/buildings14061701
Chicago/Turabian StyleGong, Yafeng, Shuzheng Wu, Changyuan Ning, Xinpeng Hu, Zhongqiang Yi, and Hongchi Du. 2024. "Shear Performance and Damage Characterization of Prefabricated Basalt Fiber Reactive Powder Concrete Capping Beam Formwork Structure" Buildings 14, no. 6: 1701. https://doi.org/10.3390/buildings14061701
APA StyleGong, Y., Wu, S., Ning, C., Hu, X., Yi, Z., & Du, H. (2024). Shear Performance and Damage Characterization of Prefabricated Basalt Fiber Reactive Powder Concrete Capping Beam Formwork Structure. Buildings, 14(6), 1701. https://doi.org/10.3390/buildings14061701






