Next Article in Journal
Sustainable Construction with Cattail Fibers in Imbabura, Ecuador: Physical and Mechanical Properties, Research, and Applications
Next Article in Special Issue
Derivation and Application of Analytical Coupling Loss Coefficient by Transfer Function in Soil–Building Vibration
Previous Article in Journal
Shear Performance and Damage Characterization of Prefabricated Basalt Fiber Reactive Powder Concrete Capping Beam Formwork Structure
Previous Article in Special Issue
Seismic Assessment of Large-Span Spatial Structures Considering Soil–Structure Interaction (SSI): A State-of-the-Art Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 14
Issue 6
10.3390/buildings14061702
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of Train-Induced Vibration Transmission and Distribution Characteristics in Double-Layer Metro Depot

by
Xinwei Luo
1,
Xuan Jiang
2,
Qingsong Feng
2,*,
Wenlin Hu
3,
Qinming Tu
1 and
Yanming Chen
2
1
Guangzhou Metro Design & Research Institute Co., Ltd., Guangzhou 510010, China
2
State Key Laboratory of Performance Monitoring Protecting of Rail Transit Infrastructure, East China Jiaotong University, Nanchang 330013, China
3
National Engineering Center for Digital Construction and Evaluation Technology of Urban Rail Transit, China Railway Design Corporation, Tianjin 300308, China
*
Author to whom correspondence should be addressed.
Buildings 2024, 14(6), 1702; https://doi.org/10.3390/buildings14061702
Submission received: 26 April 2024 / Revised: 31 May 2024 / Accepted: 3 June 2024 / Published: 7 June 2024
(This article belongs to the Special Issue Building Vibration and Soil Dynamics)
Browse Figures
Versions Notes

Abstract

:
When urban subway trains run in the depot, they can cause vibration and noise, which affects the safety and reliability of the structure under the track, and these transmits to the over-track buildings and often trouble passengers and staff. This paper established a coupling model of a track–metro depot–over-track building based on the structural finite element method and analyzed vibration response and then summarized the vibration transmission and distribution characteristics as the speed changes. The results show that, at train speeds of 20 km/h and 5 km/h, the Z-vibration level difference between the two at the rail is nearly 20 dB, and the vibration can be reduced by 17.9% at most. The difference between the two on the 9 m platform is 6–8 dB and 5–14 dB on the 16 m platform, and the vibration can be reduced by 17.7% at most. The difference between the two in the over-track building is 3–11 dB, and the vibration can be reduced by 13.0% at most. The vibration has the highest energy within a range of 2 m radiating from the center of the line, reaching a maximum of 118.5 dB. The vibration shows a ring-shaped distribution, and the ring-shaped distribution is more pronounced as the train speed increases. In the horizontal direction of the track line, the vibration energy distribution is within a range of −4 m to 11.5 m from the track line. In the longitudinal direction of the track line, the ring-shaped distribution of vibration energy exhibits a periodic pattern. The results provide a reference for the vibration control of the over-track buildings.

1. Introduction

With the rapid development of urbanization brought about by population gathering in cities, major cities have begun to operate urban rail transit to alleviate the increasing traffic pressure. The top 10 cities with the highest subway mileage in the world are shown in Table 1. As of the end of 2022, a total of 55 cities in mainland China have invested in and operated urban rail transit, with a total length of 10,287.45 km, of which the subway operation line is 8008.17 km, accounting for 77.84%. A total of 489 metro depots and parking lots have been put into operation. The metro depot is the largest area used by the subway system, responsible for the parking and maintenance of subway trains. It can be divided into throat areas, testing lines, parking and inspection garages, and entrance and exit section lines according to the operating area. Developing over-track properties of the metro depots can not only improve land use efficiency and alleviate urban land scarcity but also generate huge commercial value and raise funds for subway operation and maintenance as well as the construction of new lines. Nowadays, the development of over-track properties for metro depots has become a popular trend for major cities to develop real estate and comprehensive commercial districts.
However, the operation of subway trains can cause environmental vibration, which will transmit to nearby buildings and over-track buildings through the foundation, soil layer, and columns under the track. Not only does it affect the staff in the metro depot, but it also affects the sleep, study, work, and daily life of residents of the building and even affects the safety of the building and the normal use of precision instruments. Zou et al. [1] conducted field measurements of vibration during subway operations at Shenzhen and found that vibration amplification around the natural frequency in the vertical direction of over-track building made the peak values of indoor floor vibration about 16 dB greater than outdoor platform vibration. Then, it is recommended to carefully examine the design of new over-track buildings within 40 m on the platform over the throat area to avoid excessive vertical vibrations and noise. Xia et al. [2] conducted field measurements on the over-track buildings in a certain city and found that, when the train speed was 15–20 km/h, the vibration level was as high as 85 dB. Therefore, the rationality of the design of vibration reduction measures for metro depots is crucial, and the issue of train-induced vibration of the buildings above the depots cannot be ignored.
Many international scholars have conducted extensive research on the train-induced vibration characteristics [3,4,5,6,7,8,9,10,11]. The research methods for environmental vibration caused by urban rail transit mainly include field measurement and numerical simulation. Chen et al. [12,13] conducted field measurements on the largest underground metro depot in Asia and found that the vibration acceleration level of the top platform in the throat area was about 78 dB, which was 6 dB higher than the nighttime threshold, and the intermediate frequency vibration had a higher vibration level and a smaller attenuation rate. Feng et al. [14,15,16] conducted field measurements and numerical simulations on different areas and over-track buildings in metro depots, analyzing the differences in vibration attenuation patterns among various areas. However, it must be acknowledged that field measurement methods have certain limitations for vibration prediction. Sanayei et al. [17,18], Zou et al. [19,20,21,22], and Tao et al. [23,24,25,26] presented impedance-based (wave propagation) model for predicting train-induced floor vibrations in buildings and conducted field measurement to compare the test results with the predicted results of the impedance-based model. These studies indicate that using the impedance-based model to predict train-induced vibration is feasible and has high computational efficiency. Liu et al. [27], Liang et al. [28,29,30], Zhou et al. [31], and He et al. [32] proposed a deep learning-based approach to identify train-induced vibration segments efficiently for subsequent vibration evaluations. He et al. [33] presented a three-dimensional analytical model that regarded tunnels as cylindrical shells of infinite length, to predict ground vibrations from two parallel tunnels embedded in a full space. He et al. [34] used the potential decomposition, multiple scattering theory and combined it with the transfer matrix method to derive the fundamental solution for the soil-inclusion dynamic interaction in a layered half-space and then used periodic barriers in a layered half space to mitigate railway-induced vibrations. Li et al. [35] proposed a deep learning-based approach to learn the generation, distribution, and dissipation mechanisms of indoor structure-borne noise while also enabling the convenient acquisition of indoor structure-borne noise. Qiu et al. [36] developed a numerical model based on train track coupled dynamic theory and the finite element method to investigate the effectiveness of two mitigation measures implemented in the elevated metro depot. Hu et al. [37] simplified the building floor into a rectangular plate composed of multiple orthogonal structural girders and structural columns in vertical contact with the floor, to obtain the vertical vibrations of the building floor in the time domain.
Existing research is mostly based on conducting field measurements on the metro depot and carrying out numerical simulation for specific buildings or areas and analyzes the vibration transmission and distribution characteristics based on the measurements and simulation results and then takes targeted vibration reduction measures. But there is little research on the impact of different train speeds on the vibration transmission and distribution characteristics of the vibration sources inside the double-layer metro depot and the over-track buildings. The train speed not only affects the vibration characteristics of the vibration source and the over-track building but also has a certain effect on the vibration reduction and noise reduction of the over-track building by controlling the train speed. Based on this, this paper combines the operation zone of a certain metro depot in Guangzhou and then establishes a coupling model of a track–metro depot–over-track building based on the structural finite element method to calculate the vibration response. It further analyzes the vibration response characteristics of the vibration source and over-track building under different train speeds and then summarizes the transmission and distribution characteristics of vibration in a double-layer prefabricated assembly metro depot and provides an useful reference for metro depots to take vibration reduction measures at vibration sources, propagation paths, or sensitive targets during the vibration reduction design stage.

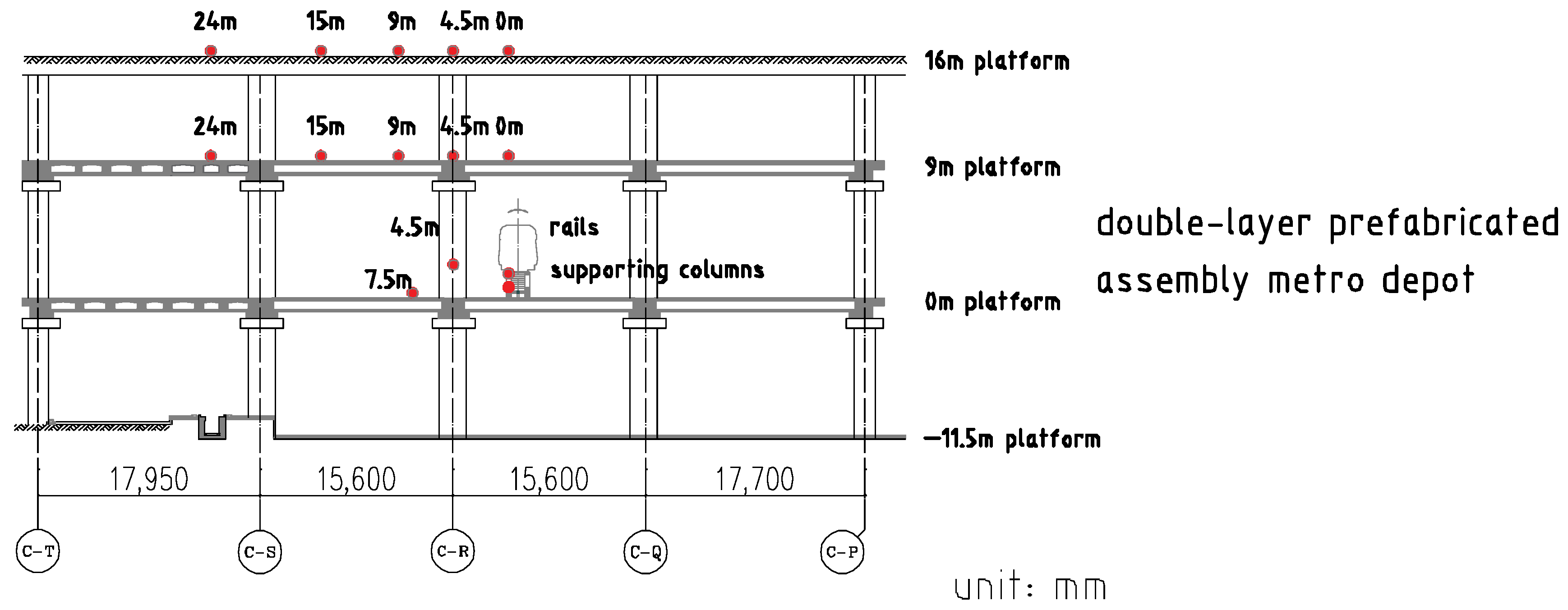
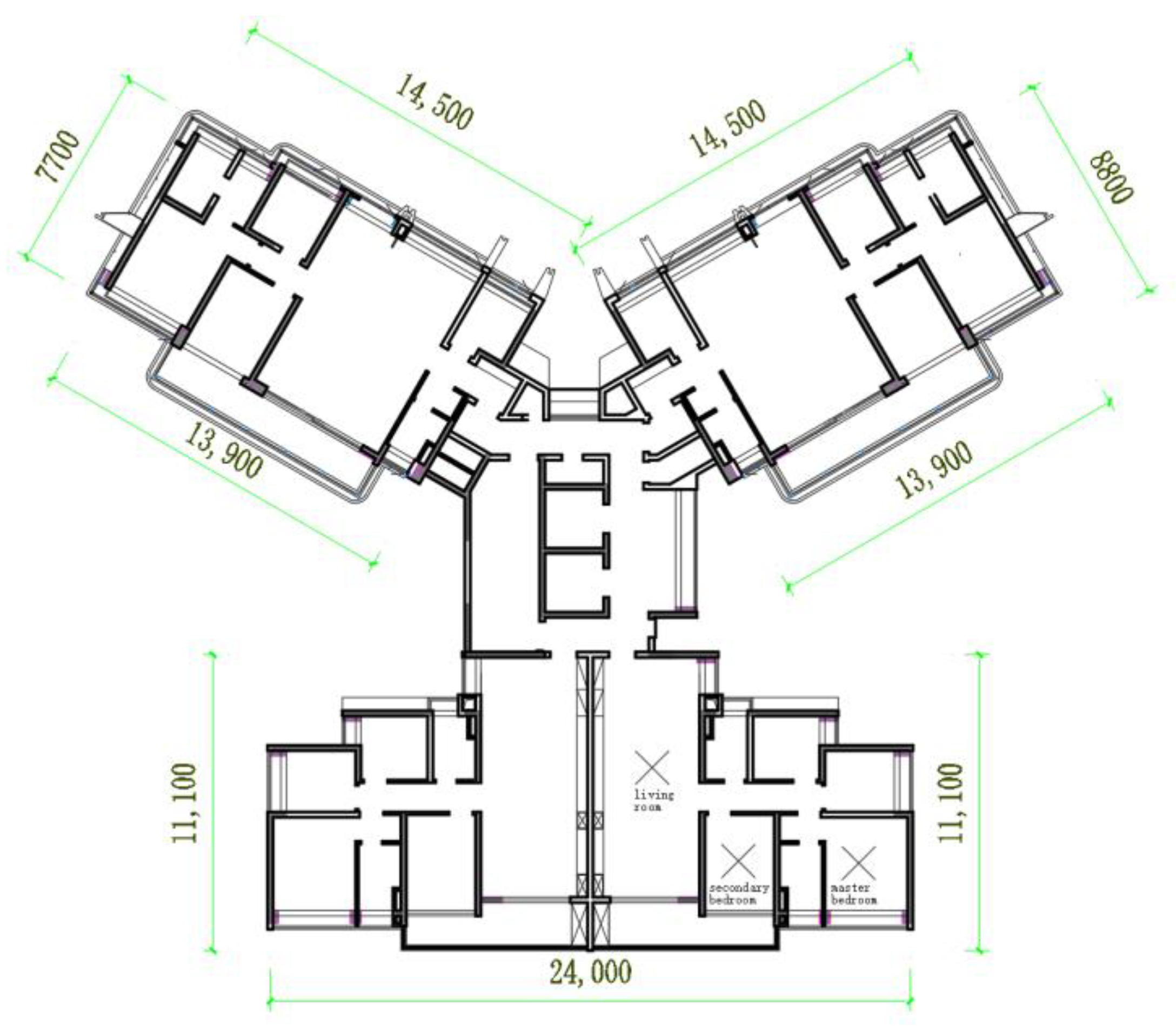
2. Project Profile

This metro depot is a double-layer prefabricated assembly metro depot. It is planned to carry out property development on the cover and adjacent plots. The main structure of the metro depot adopts a double-layer reinforced concrete frame structure. The building plan of the over-track buildings is shown in Figure 1. The main cover platforms of the metro depot include −11.5 m bottom platform, 0 m platform, 9 m platform, and 16 m platform. The project covers an area of 179,500 square meters. Among them, the −11.5 m bottom platform is the negative driving layer of the metro depot, the 0 m platform is the first driving layer of the metro depot, the 9 m platform is the car parking garage and equipment layer, and the 16 m platform is the ground layer of the community.
When the train is running on the first floor (the 0 m platform) of the operation zone, vertical vibration analysis is conducted at points such as rails, supporting columns, columns (1.8 m above the 0 m platform), and the ground at a distance of 7.5 m from the rails at the vibration source. Points on the platform such as 0 m, 4.5 m, 9 m, 15 m, and 24 m to the left above the rails are selected to analyze vertical vibration. The layout of analysis points on vibration source and platform is shown in Figure 2. The over-track building has a total of 41 floors, with four households on each floor. The total height of the over-track building is 134 m, with a first-floor height of 6 m, and a standard height of 3.2 m for floors above two. The center of the living room floor, the center of the master bedroom floor, and the center of the secondary bedroom floor are selected to analyze vertical vibration. The layout of analysis points in the over-track building is shown in Figure 3.

3. Modeling

3.1. The Vehicle–Track Coupling Model

The coupling model of a track–metro depot–over-track building was established for structural dynamic analysis. The coupling model includes two sub-models. Firstly, the “vehicle–track” coupling model, based on the running train and the track structure in the metro depot, and the multi-body system dynamics simulation software UM 9 is used to calculate the vertical force between wheels and rails. The depot adopts subway 6A model, which is mainly composed of car body, bogie, and wheel pair. The sample of track irregularity is obtained from the short-band processing of the superposition of Sato spectrum in the depot. The “vehicle–track” coupling model is shown in Figure 4.
Based on the actual line conditions on site, this article adopts field measured track irregularities of lines with similar working conditions. Due to the fact that the track inspection vehicles (GJ-4 and GJ-5) on the existing lines in China are still unable to accurately detect short-wave irregularities with wavelengths below 1 m, this article uses measured track irregularities in the metro depot in the long-wavelength range (1.5–42 m) and adds Sato spectrum processing in the short-wavelength range to obtain a sample of track irregularity as shown in Figure 5. Using the sample of track irregularity and train motion speed as the input excitation for the “vehicle–track” coupling model, the vertical force between wheels and rails can be calculated.

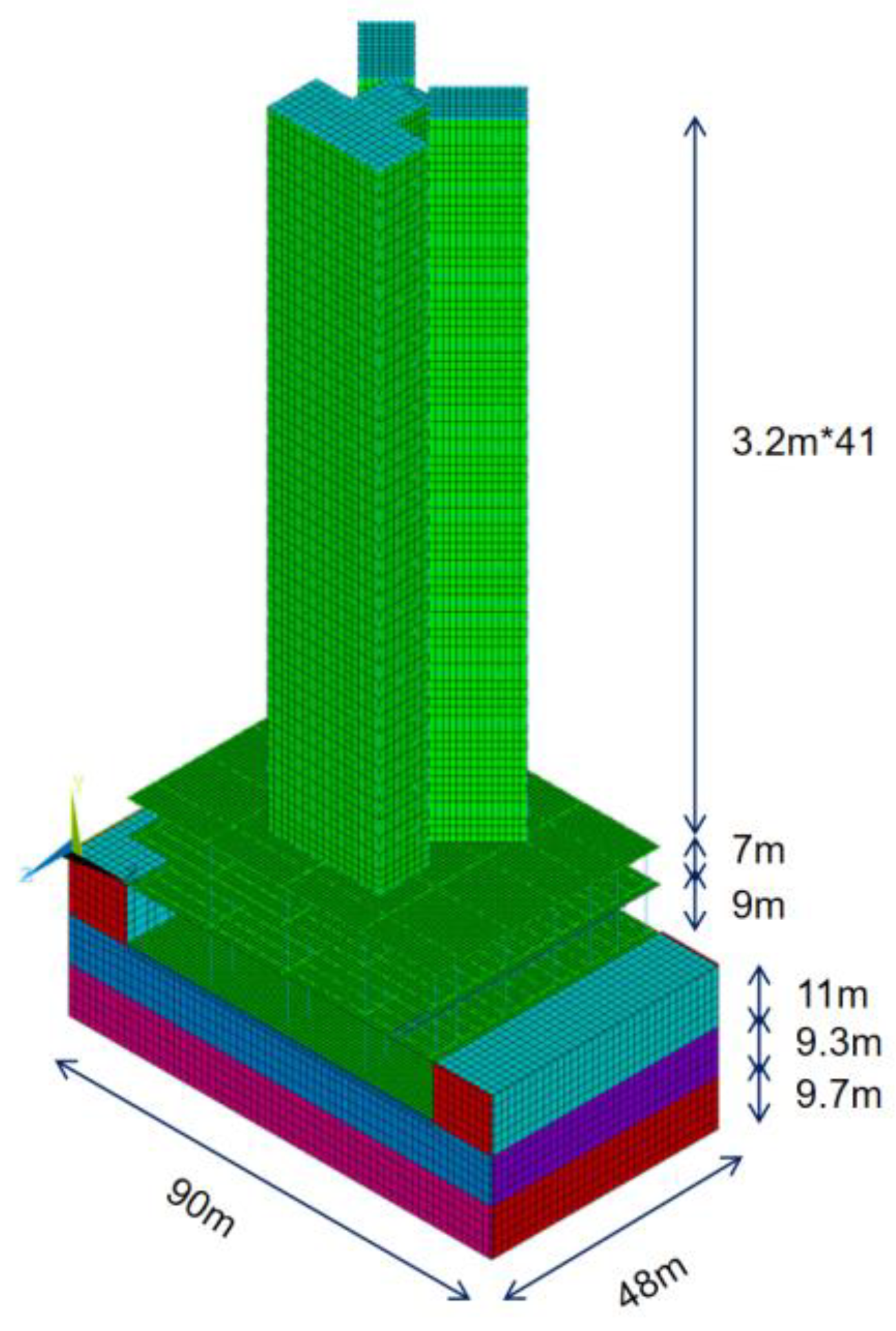
3.2. The FEM Model of “Track–Metro Depot–Over-Track Building”

This article considers the actual parameters of the track structure, soil layer, and building and establishes a coupling finite element analysis model of a “track–metro depot–over-track building” using the finite element software, ANSYS 19.0. Using the vertical force between wheels and rails as the input excitation for the “track–metro depot–over-track building” model, the vibration response can be calculated. Among them, solid elements are used for the simulation of soil, and the Mohr–Coulomb (MC) model is chosen as the constitutive model of soil. Beam elements are used for the simulation of beams, columns, and pile foundations, and shell elements are used for the simulation of shear walls and floor slabs. The element size is controlled at around 1.5 m, and a three-dimensional viscoelastic artificial boundary is used to simulate the boundary of the computational domain [38]. The size of the soil is 90 m*30 m*48 m. The building has a total of 41 floors, with a total structural height of 134 m. The first floor of the building is 6 m high, and the standard height for floors above two is 3.2 m. The selection and material parameters of each structural element in the model are shown in Table 2, where the material parameters are set based on the information provided by the design company. The coupling model of “track–metro depot–over-track building” is shown in Figure 6.

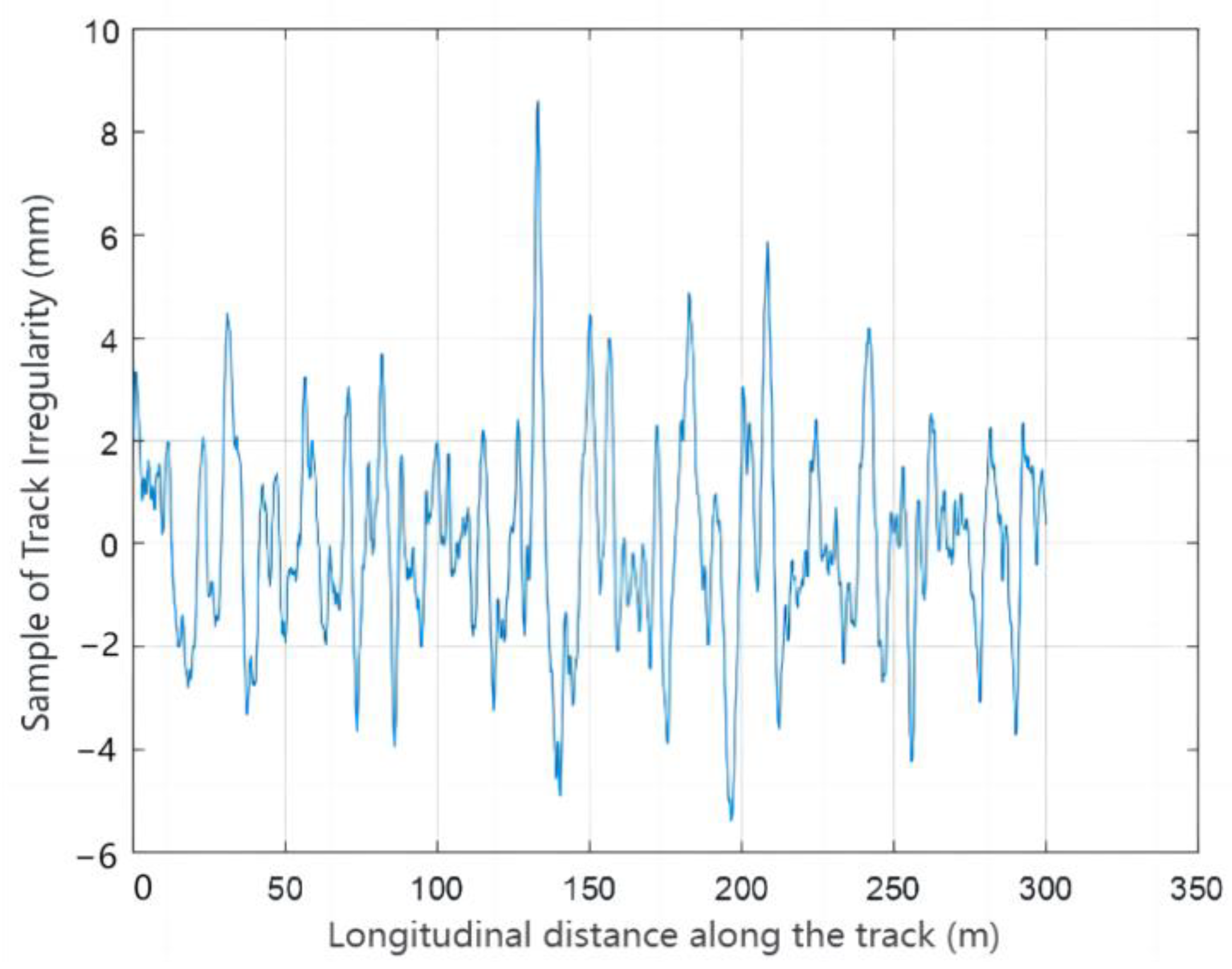
3.3. Model Validation

Due to the incomplete construction of the over-track building of this double-layer prefabricated assembly metro depot, in order to verify the rationality and feasibility of the method for establishing the “track–metro depot–over-track building” coupling model, this paper takes a single-layer ground metro depot in Guangzhou as an example to compare the simulation results with the measurement results. The platform above the operation zone is a complete cast-in-place concrete slab that is separated from the throat area and maintenance zone through expansion joints. The pillars in this area are evenly distributed in a chessboard pattern, and the entire platform is divided into small areas. The parameters of the model constructed in this article are basically consistent with the geological exploration soil layer data and building structural parameters provided by the design institute for the metro depot. Therefore, when using ANSYS to establish the single-layer ground metro depot, it is considered that the selection of each structural element and material parameters are consistent with the double-layer prefabricated assembly metro depot model established in this paper, as shown in Table 1. The sample of track irregularity used to calculate the wheel–rail force is the measured sample of track irregularity of the rails in the depot, and the train speed is 2.5 m/s.
The team responsible for measurement uses the SQuadriga III data acquisition instrument for vibration source testing and platform vibration testing and uses trigger sampling for monitoring. PCB-352 vibration accelerometer and PCB-393 vibration accelerometer are used to collect vibration signals. The instrument and accelerometers are shown in Figure 7. Through field measurement, the vibration response of the vibration source in the operation zone was obtained. Measuring points 1 and 2 were placed in the center of the two areas on the platform, with the direction of the measuring line perpendicular to the track line. Measuring point 1 is located directly above the track, and measuring point 2 is located 9 m to the right above the track. The layout of the measuring points is shown in Figure 8. The spectrum analysis of the measured and the simulated vibration frequency at the two measuring points is shown in Figure 9. It can be seen from the figure that the measured and the simulated vibration frequency at the two measuring points is in the range of 20–60 Hz, and the waveforms are similar. The simulation results are in good agreement with the measurement results, indicating that the method for establishing “track–metro depot–over-track building” coupling model is reasonable and feasible.

4. Analysis of Vibration Transmission and Distribution Characteristics

As the speed of the train running in the metro depot is 5–25 km/h, this simulation considers three working conditions: the standard working condition is the train running at the first layer of the operation zone at the speed of 10 km/h (hereinafter referred to as working condition 2), and it sets the comparative working condition of the train running at the speed of 5 km/h (hereinafter referred to as working condition 3) and 20 km/h (hereinafter referred to as working condition 1) in the first layer of the operation zone.

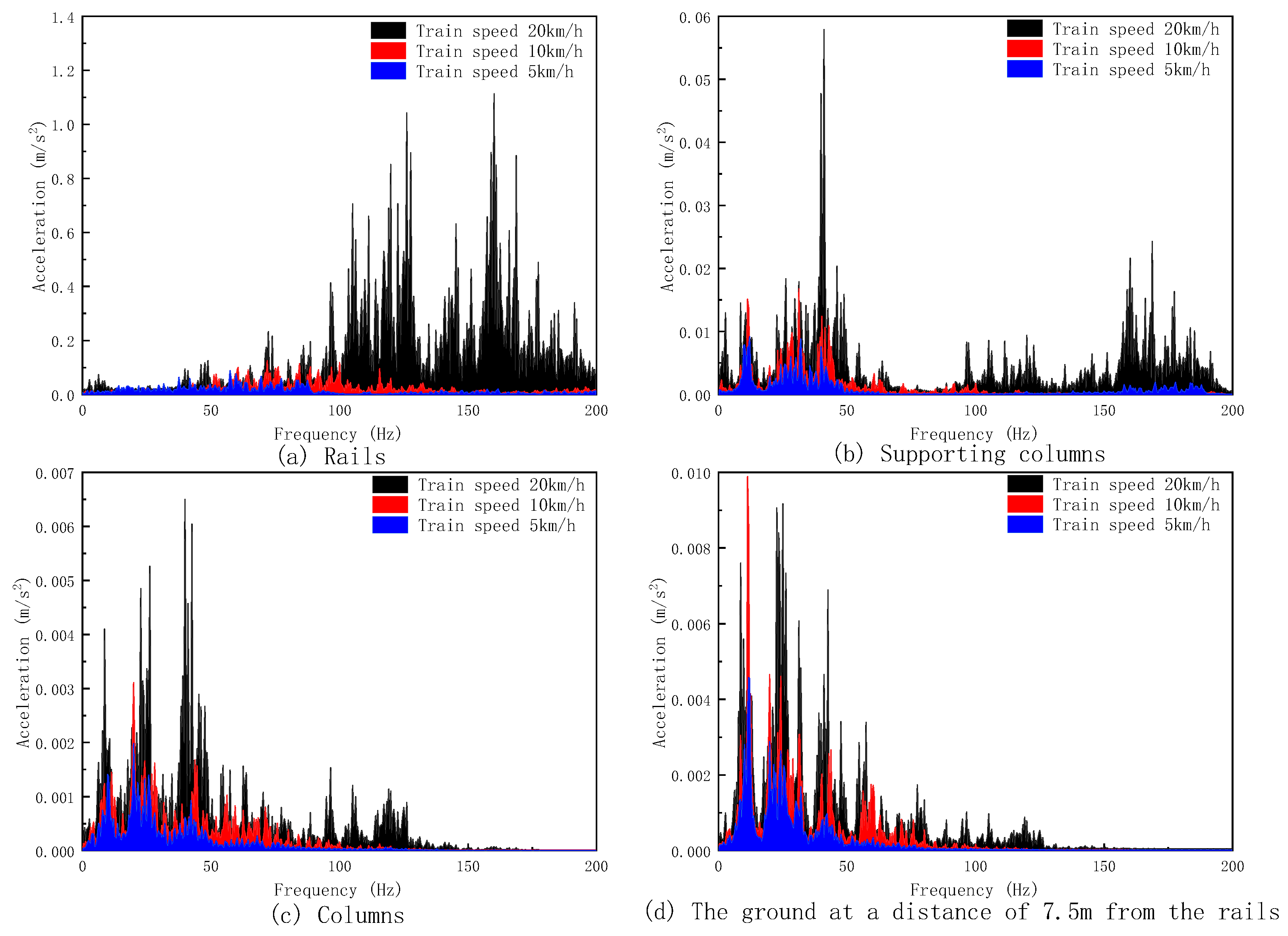
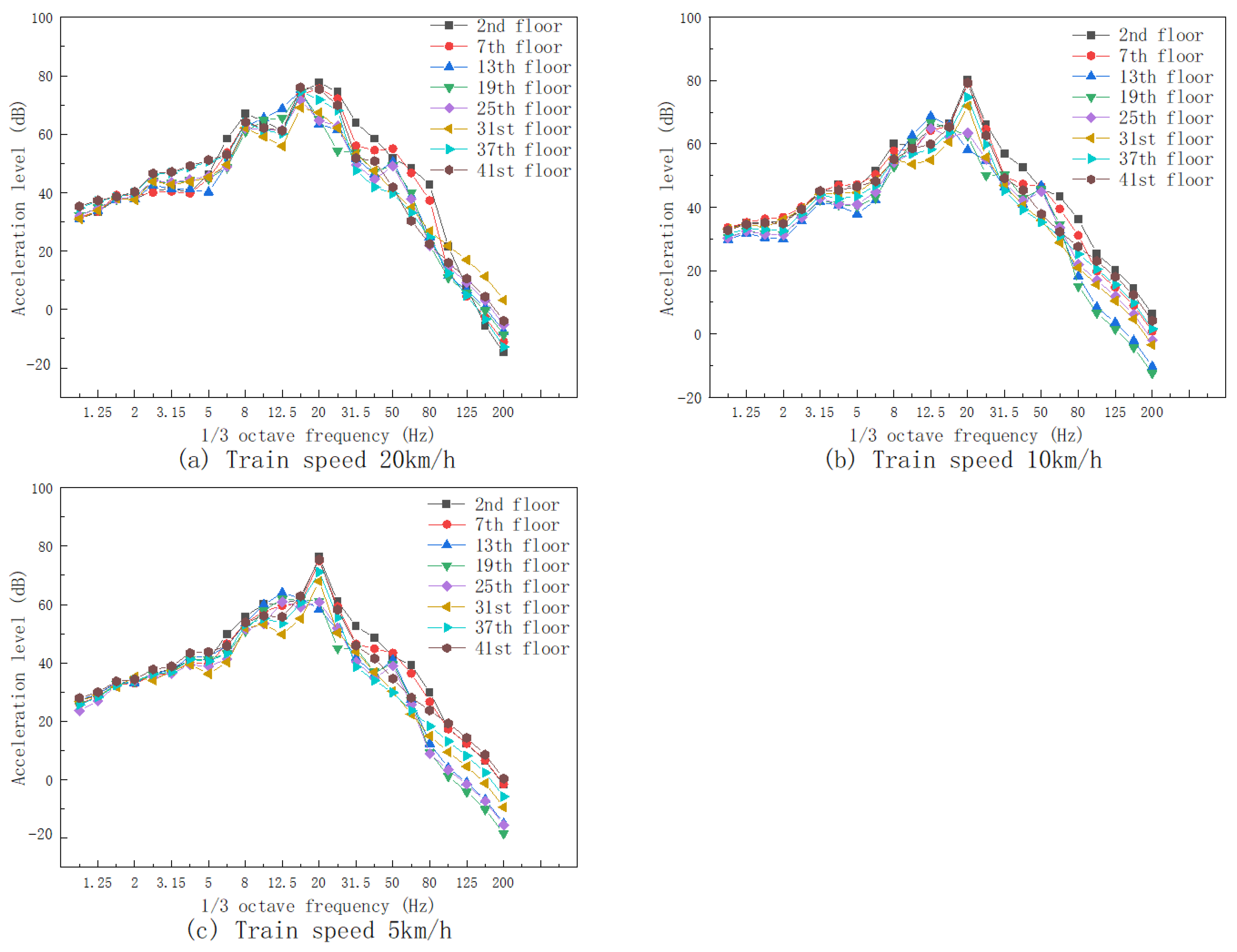
4.1. Analysis of Vibration Response at Vibration Source

The vibration response of each analysis point at the vibration source of the depot under various working conditions is shown in Table 3, and the analysis of vibration frequency domain is shown in Figure 10. It can be seen that, with the decrease in the speed, the vibration response of the vibration source analysis point decreases significantly, and the difference at the rail is the most significant. When the train speeds are 20 km/h and 5 km/h, the difference in Z-vibration level is nearly 20 dB, and the difference in other analysis points is about 7 dB. As the train speed decreases, the peak frequency of vibration decreases significantly. When the train speed is 10 km/h and 5 km/h, the peak frequency of vibration at each analysis point of the vibration source is similar, and the peak frequency of vibration is lower than that of the train speed of 20 km/h. The difference at the rail is the most significant, with a peak vibration frequency of around 160 Hz at a speed of 20 km/h, and around 70 Hz at a speed of 10 km/h and 5 km/h. The higher the train speed, the greater the vibration response of each analysis point. Therefore, the scheme of the trains running at low speeds in the operation zone can be adopted to reduce the vibration response at vibration source, and the vibration at the rail can be reduced by 17.9% at most.

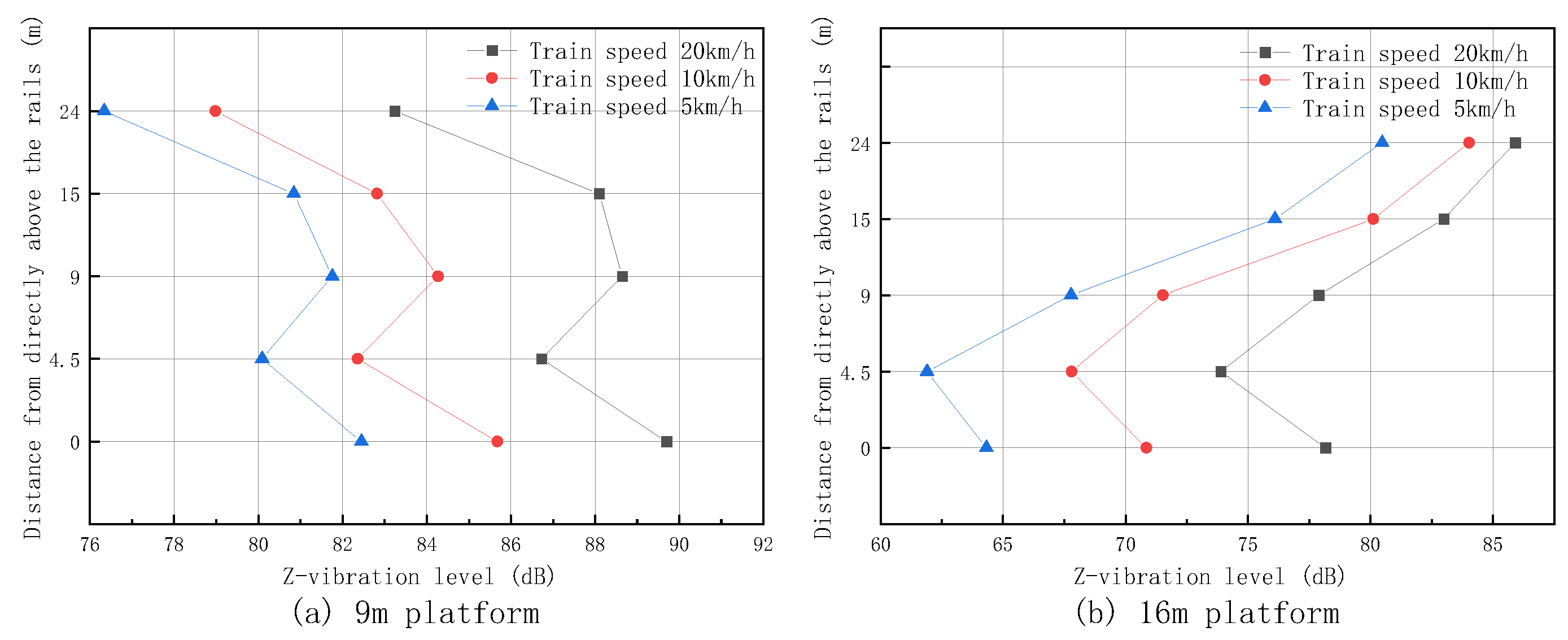
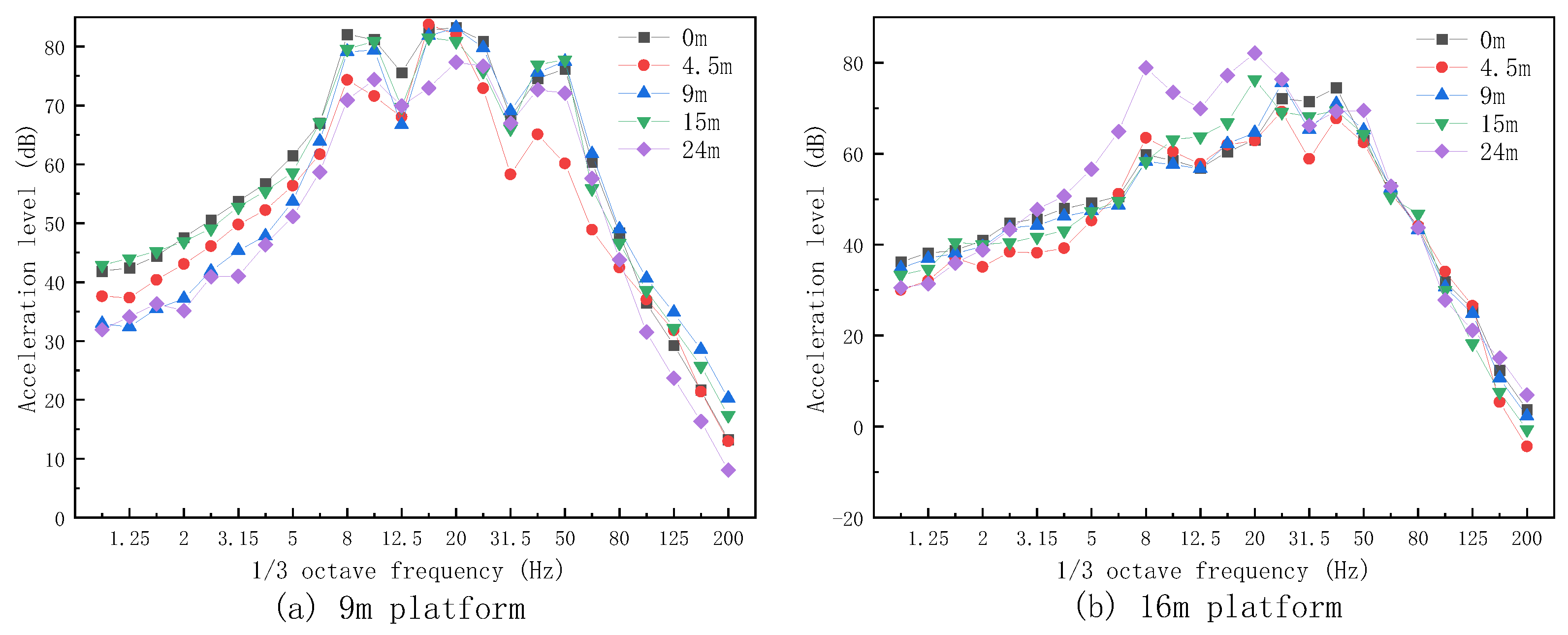
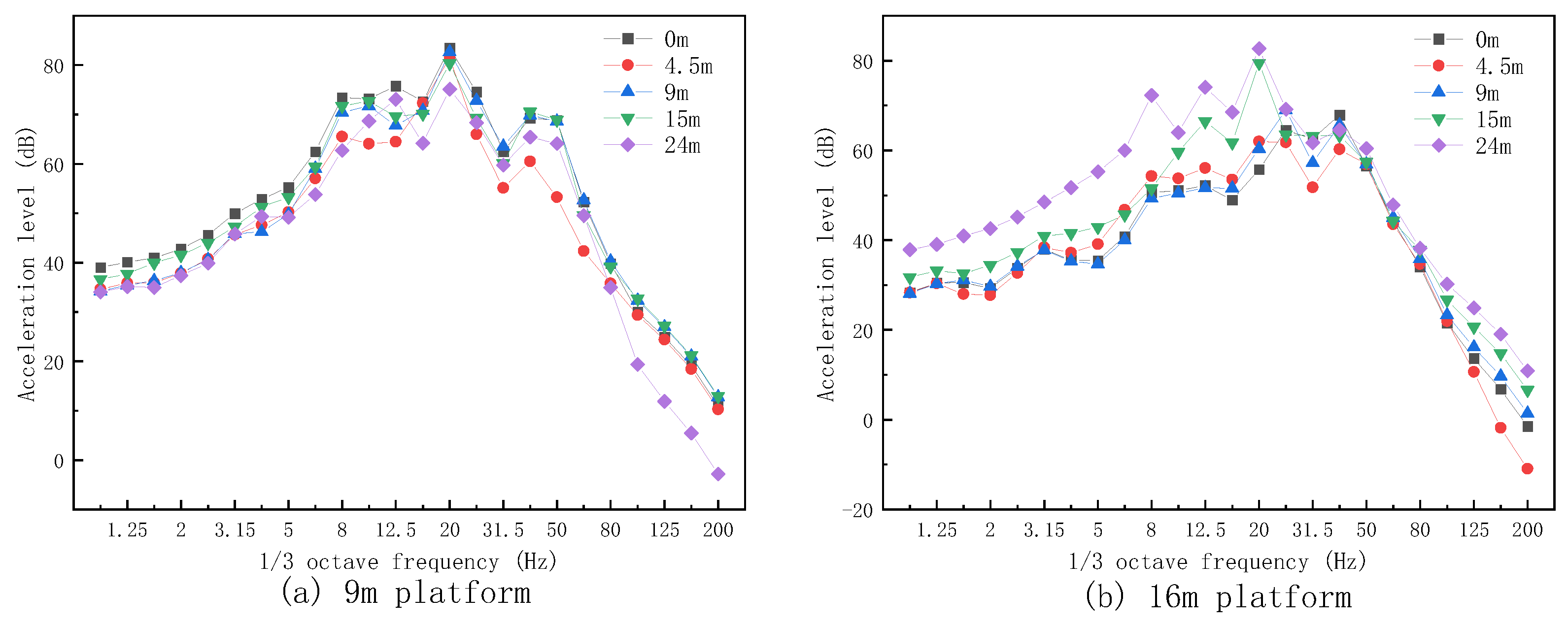
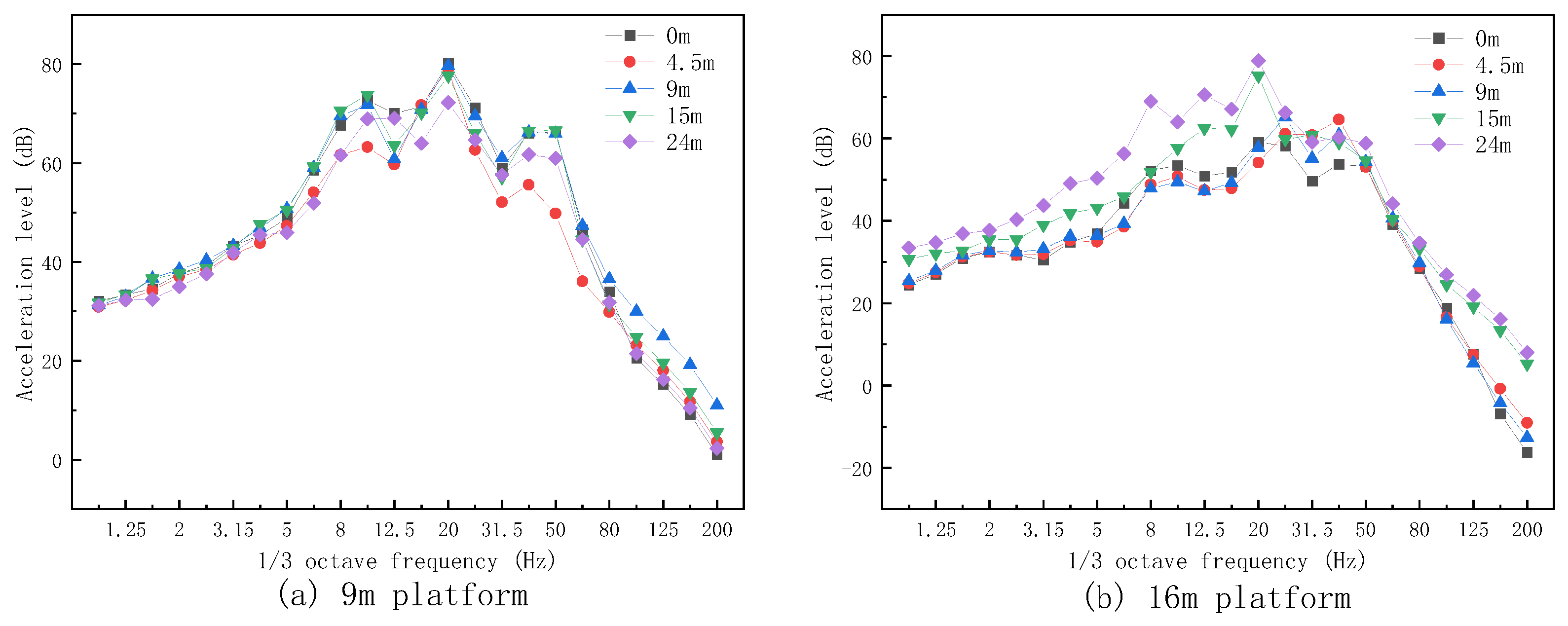
4.2. Analysis of Vibration Transmission on the Platforms

The plane view of the platform of the operation zone is shown in Figure 11, and the vibration response of each analysis point on the 9 m and 16 m platforms of the operation zone under various working conditions is shown in Figure 12. It can be seen that, with the decrease in the speed, the vibration response of the analysis points on the platforms decreases significantly. Compared with the speed of 20 km/h, the Z-vibration level of each analysis point at the speed of 5 km/h is different by 6–8 dB on the 9 m platform, and the Z-vibration level of each analysis point at the speed of 5 km/h is different by 5–14 dB on the 16 m platform. It can achieve the effect of reducing the vibration response at the platform by running at low speeds in the operation zone, with a maximum reduction of 17.7% at the platform. When the vibration is transmitted laterally from 0 m to the left above the rails on the platform to 24 m above it, the vibration response generally decreases with increasing distance. The reason for the amplification of vibration at a distance of 9 m and 15 m directly above the rails is that the 9 m and 15 m points are located in the middle of plate 2, while the 4.5 m and 24 m points are located at the edges of plate 1 and plate 3, respectively. The vibration in the middle of plate is generally greater than that at the edge of plate, resulting in the amplification phenomenon.
During the vertical transmission of vibration response from the 9 m platform to the 16 m platform, there is a trend of an initial decrease and then an increase. At the speed of 10 km/h, within a range of 0–15 m to the left above the rails, the Z-vibration level of the analysis point on the 9 m platform are significantly higher than that on the 16 m platform, with a difference of 2–15 dB between the two. Within a range of 15–24 m to the left above the rails, the Z-vibration level of the analysis points on the 9 m platform is smaller than that of the 16 m platform, with a difference of about 5 dB between the two.
The 1/3 octave frequency of each analysis point on the 9 m and 16 m platforms in the operation zone under various working conditions is shown in Figure 13, Figure 14 and Figure 15. It can be seen that the vibration energy of each analysis point on the platforms attenuates the vast majority in the frequency band above 50 Hz. During the vertical transmission of vibration response from 9 m platform to 16 m platform, the analysis points within the range of 0–15 m to the left above the rails exhibit a certain range of attenuation in the entire frequency band. The analysis points within the range of 15–24 m to the left above the rails have a certain amplification in the frequency bands of 0–20 Hz and 100–200 Hz, and the difference is not significant in the frequency band of 20–100 Hz.

4.3. Analysis of Vibration Response in the Over-Track Building

The vibration response of each analysis point in the over-track building under various working conditions is shown in Figure 16. It can be seen that, with the decrease in the speed, the vibration response of the over-track building decreases significantly. Compared with the speed of 5 km/h, the vibration response of each analysis point at the speed of 20 km/h is different by 3–11 dB. According to the standard for limits and measurement methods of vibration in the room of residential building [39], it is found that the Z-vibration level of individual floors at speeds of 10 km/h and 20 km/h exceeds the second-level limit. After reducing the speed, there is no overrun. Therefore, the scheme of the trains running at low speeds in the operation zone can be adopted to reduce the vibration response in the over-track buildings, and the vibration in the over-track buildings can be reduced by 13.0% at most. During the transmission of vibration response from the 2nd floor to the 41st floor, there is a trend of an initial decrease and then an increase.
Taking the living room of the over-track buildings as an example, the 1/3 octave frequency of each floor under various working conditions is shown in Figure 17. It can be seen that the vibration energy of each analysis point in the over-track building attenuates the vast majority in the frequency band above 20 Hz. During the transmission of vibration response from the 2nd floor to the 41st floor, there is a trend of an initial decrease and then an increase. Compared with the speed of 5 km/h, each analysis point has a certain range of attenuation in the full frequency band.

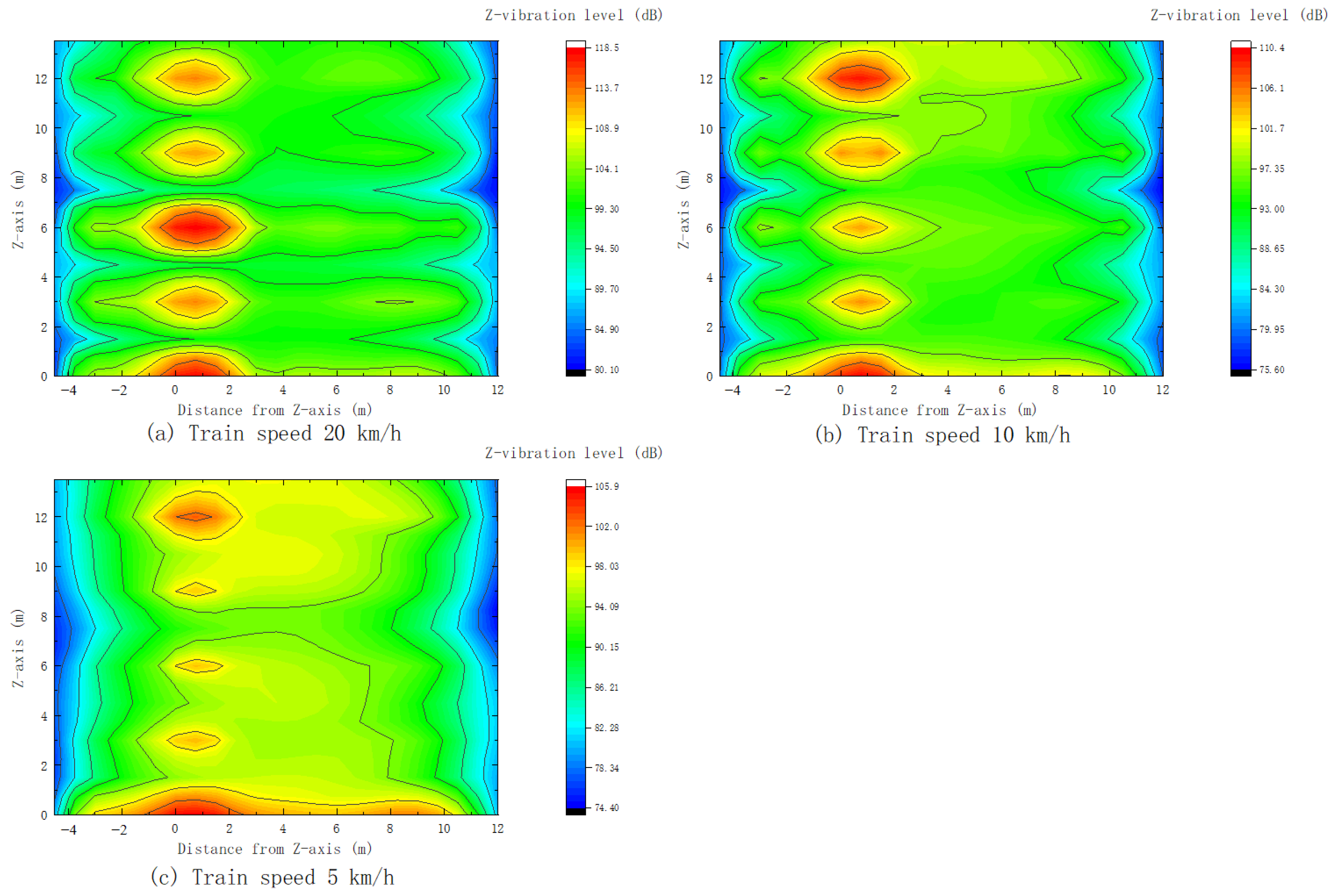
4.4. Spatial Distribution of Vibration Energy

To study the distribution law of vibration energy at the vibration source in the operation zone, the plate 1 area on the 0 m platform is selected for analysis. Using the track line as the Z-axis, the distribution of vibration energy at the vibration source under various working conditions is shown in Figure 18. It can be seen that the maximum energy of vibration is within a radius of 2 m centered on the line, showing a ring-shaped distribution, and the ring-shaped distribution is more pronounced as the train speed increases. In the horizontal direction of the track line, the vibration energy distribution is within a range of −4 m to 11.5 m from the track line. The distribution of vibration energy is significantly affected by the boundary effect of the edges, and the vibration at the edge of plate is significantly smaller than that in the middle of the plate. In the longitudinal direction of the track line, the ring-shaped distribution of vibration energy exhibits a periodic pattern and is not affected by the boundary effect of the edges.

5. Conclusions

This paper established a coupling model of a track–metro depot–over-track building based on the structural finite element method to calculate the vibration response, and it further analyzed the vibration response characteristics of the vibration source and over-track building under different train speeds and then summarized the transmission and distribution characteristics of vibration. It yields the following conclusions:
(1)
With the decrease in the speed, the vibration response of the vibration source, platforms, and the over-track building decreases significantly. The Z-vibration level difference at the rail is the most significant. At train speeds of 20 km/h and 5 km/h, the difference between the two is nearly 20 dB, and the vibration at the rail can be reduced by 17.9% at most. The peak frequency of vibration decreases significantly. The difference between the two on the 9 m platform is 6–8 dB, and the difference between the two on the 16 m platform is 5–14 dB. The vibration on the platforms can be reduced by 17.7% at most. The difference between the two in the over-track building is 3–11 dB, and the vibration can be reduced by 13.0% at most. Therefore, the scheme of the trains running at low speeds in the operation zone can be adopted to reduce the vibration response.
(2)
When the vibration is transmitted laterally from 0 m to the left above the rails on the platform to 24 m above it, the vibration response generally decreases with the increasing distance. During the vertical transmission of vibration response from the 9 m platform to the 16 m platform, there is a trend of an initial decrease and then an increase.
(3)
The vibration energy of each analysis point on the platforms attenuates the vast majority in the frequency band above 50 Hz. Therefore, when conducting vibration reduction design, engineers should focus on vibrations in the frequency band below 50 Hz. During the vertical transmission of vibration response from the 9 m platform to the 16 m platform, the analysis points within the range of 0–15 m to the left above the rails exhibit a certain range of attenuation in the entire frequency band. The analysis points within the range of 15–24 m to the left above the rails have a certain amplification in the frequency band of 0–20 Hz and 100–200 Hz.
(4)
The maximum vibration energy of vibration source in the operation zone is within a radius of 2 m centered on the line, showing a ring-shaped distribution, and the ring-shaped distribution is more pronounced as the train speed increases. In the horizontal direction of the track line, the vibration energy distribution is within a range of −4 m to 11.5 m from the track line. The vibration at the edge of plate is significantly smaller than that in the middle of the plate. In the longitudinal direction of the track line, the ring-shaped distribution of vibration energy exhibits a periodic pattern.
This study explored the structural dynamic response of a double-layer metro depot and an over-track building. An increase in the number of metro depots and over-track buildings makes the vibration reduction design more important. This research provides design references for future double-layer prefabricated assembly metro depot and data for vibration reduction design. In this paper, we found that the vibration energy of each analysis point on the platforms attenuates the vast majority in the frequency band above 50 Hz. And the maximum vibration energy of vibration source in the operation zone is within a radius of 2 m centered on the line. Moreover, this study focused only on the vibration transmission and distribution characteristics, without studying the transmission and distribution characteristics of noise. Future research should extend to include the transmission and distribution characteristics of noise.

Author Contributions

Conceptualization, Q.F.; methodology, X.L.; software, X.J.; validation, X.J. and Y.C.; formal analysis, X.J. and Q.T.; investigation, X.J., Y.C. and W.H.; resources, X.L.; data curation, X.L. and Q.T.; writing—original draft preparation, X.J.; writing—review and editing, X.L. and Q.F.; visualization, W.H.; supervision, Q.F. and W.H.; project administration, X.L.; funding acquisition, Q.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (grant number: 52068029).

Data Availability Statement

Data are available upon reasonable request.

Conflicts of Interest

Authors Xinwei Luo and Qinming Tu were employed by the company Guangzhou Metro Design & Research Institute Co., Ltd., Author Wenlin Hu was employed by the company China Railway Design Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Zou, C.; Wang, Y.M.; Moore, J.A.; Sanayei, M. Train-induced field vibration measurements of ground and over-track buildings. Sci. Total Environ. 2017, 575, 1339–1351. [Google Scholar] [CrossRef] [PubMed]
  2. Xia, H.; Wu, X.; Yu, D.M. Environmental vibration induced by urban rail transit system. J. Beijing Jiaotong Univ. 1999, 23, 7–13. [Google Scholar]
  3. Triepaischajonsak, N.; Thompson, D.J. A hybrid modelling approach for predicting ground vibration from trains. J. Sound. Vib. 2015, 335, 147–173. [Google Scholar] [CrossRef]
  4. Gupta, S.; Liu, W.F.; Degrande, G.; Lombaert, G.; Liu, W.N. Prediction of vibrations induced by underground railway traffic in Beijing. J. Sound. Vib. 2008, 310, 608–630. [Google Scholar] [CrossRef]
  5. Lombaert, G.; Degrande, G.; Vanhauwere, B.; Vandeborght, B.; François, S. The control of ground-borne vibrations from railway traffic by means of continuous floating slabs. J. Sound. Vib. 2006, 297, 946–961. [Google Scholar] [CrossRef]
  6. Sanayei, M.; Maurya, P.; Moore, J.A. Measurement of building foundation and ground-borne vibrations due to surface trains and subways. Eng. Struct. 2013, 53, 102–111. [Google Scholar] [CrossRef]
  7. Yang, J.J.; Zhu, S.Y.; Zhai, W.M.; Kouroussis, G.; Wang, Y.; Wang, K.Y.; Lan, K.; Xu, F.Z. Prediction and mitigation of train-induced vibrations of large-scale building constructed on subway tunnel. Sci. Total Environ. 2019, 668, 485–499. [Google Scholar] [CrossRef] [PubMed]
  8. Feng, Q.S.; Liao, C.M.; Zhang, L. Evaluation of subway vibration influence on human exposure comfort of whole-body vibration. Noise Vib. Control. 2021, 41, 237–243. [Google Scholar]
  9. Qiu, Y.T.; Zou, C.; Wu, J.H.; Shen, Z.X.; Zhong, Z.X. Building vibration measurements induced by train operation on concrete floor. Constr. Build. Mater. 2023, 394, 132283. [Google Scholar] [CrossRef]
  10. Kouroussis, G.; Conti, C.; Verlinden, O. Experimental study of ground vibrations induced by Brussels IC/IR trains in their neighborhood. Mech. Ind. 2013, 14, 99–105. [Google Scholar] [CrossRef]
  11. Liang, R.H.; Ding, D.Y.; Liu, W.F.; Sun, F.Q.; Cheng, Y.L. Experimental study of the source and transmission characteristics of train-induced vibration in the over-track building in a metro depot. J. Sound. Vib. 2023, 29, 1738–1751. [Google Scholar] [CrossRef]
  12. Chen, Y.M.; Feng, Q.S.; Liu, Q.J.; Jiang, J. Experimental study on the characteristics of train-induced vibration in a new structure of metro depot. Environ. Sci. Pollut. Res. 2021, 28, 41407–41422. [Google Scholar] [CrossRef] [PubMed]
  13. Chen, Y.M.; Feng, Q.S.; Liu, Q.J.; Liu, W.W.; Luo, X.W. Test and Analysis of Vibration Induced by Train Operation in Sinking Metro Depot Service Shop. J. Vib. Meas. Diagn. 2021, 41, 532–538+623. [Google Scholar]
  14. Feng, Q.S.; Zhang, Y.L.; Jiang, J.; Wang, Z.Y.; Lei, X.Y.; Zhang, L. Field measurement and evaluation of vibration in different areas of a metro depot. Earthq. Eng. Eng. Vibr. 2022, 21, 529–542. [Google Scholar]
  15. Feng, Q.S.; Wang, Z.Y.; Liu, Q.M.; Luo, X.W.; Li, J.Y. Vibration characteristics of metro depot upper building under double vibration source excitation. J. Traffic Transp. Eng. 2019, 19, 59–69. [Google Scholar]
  16. Feng, Q.S.; Wang, Z.Y.; Liu, Q.M.; Luo, X.W.; Luo, K.; Li, J.Y. Comparative analysis of environmental vibration characteristics in different regions of a metro depot. J. Vib. Shock. 2020, 39, 179–185+200. [Google Scholar]
  17. Sanayei, M.; Kayiparambil, P.A.; Moore, J.A.; Brett, C.R. Measurement and prediction of train-induced vibrations in a full-scale building. Eng. Struct. 2014, 77, 119–128. [Google Scholar] [CrossRef]
  18. Sanayei, M.; Zhao, N.Y.; Maurya, P.; Moore, J.A.; Zapfe, J.A.; Hines, E.M. Prediction and mitigation of building floor vibrations using a blocking floor. J. Struct. 2012, 138, 1181–1192. [Google Scholar] [CrossRef]
  19. Zou, C.; Wang, Y.M.; Wang, P.; Guo, J.X. Measurement of ground and nearby building vibration and noise induced by trains in a metro depot. Sci. Total Environ. 2015, 536, 761–773. [Google Scholar] [CrossRef] [PubMed]
  20. Zou, C.; Wang, Y.M.; Zhang, X.; Tao, Z.Y. Vibration isolation of over-track buildings in a metro depot by using trackside wave barriers. J. Build. 2020, 30, 101270. [Google Scholar] [CrossRef]
  21. Zou, C.; Moore, J.A.; Sanayei, M.; Wang, Y.M. Impedance model for estimating train-induced building vibrations. Eng. Struct. 2018, 172, 739–750. [Google Scholar] [CrossRef]
  22. Zou, C.; Moore, J.A.; Sanayei, M.; Wang, Y.M.; Tao, Z.Y. Efficient impedance model for the estimation of train-induced vibrations in over-track buildings. J. Vib. Control. 2020, 27, 924–942. [Google Scholar] [CrossRef]
  23. Tao, Z.Y.; Wang, Y.M.; Zou, C. Prediction model of vehicle-induced vibration of metro depot superstructure based on impedance and power conservation method. Zhendong Yu Chongji 2022, 41, 62–67+73. [Google Scholar]
  24. Tao, Z.Y.; Zou, C.; Yang, G.R.; Wang, Y.M. A semi-analytical method for predicting train-induced vibrations considering train-track-soil and soil-pile-building dynamic interactions. Soil. Dyn. Earthq. Eng. 2023, 167, 107822. [Google Scholar] [CrossRef]
  25. Tao, Z.Y.; Wang, Y.M.; Sanayei, M.; Moore, J.A.; Zou, C. Experimental study of train-induced vibration in over-track buildings in a metro depot. Eng. Struct. 2019, 198, 109473. [Google Scholar] [CrossRef]
  26. Tao, Z.Y.; Wang, Y.M.; Zou, C.; Li, Q.; Luo, Y. Assessment of ventilation noise impact from metro depot with over-track platform structure on workers and nearby inhabitants. Environ. Sci. Pollut. Res. 2019, 26, 9203–9218. [Google Scholar] [CrossRef]
  27. Liu, W.F.; Liang, R.H.; Zhang, H.G.; Wu, Z.Z.; Jiang, B.L. Deep learning based identification and uncertainty analysis of metro train induced ground-borne vibration. Mech. Syst. Signal. Process. 2023, 189, 110062. [Google Scholar] [CrossRef]
  28. Liang, R.H.; Liu, W.F.; Ma, M.; Liu, W.N. An efficient model for predicting the train-induced ground-borne vibration and uncertainty quantification based on Bayesian neural network. J. Sound. Vib. 2021, 495, 115908. [Google Scholar] [CrossRef]
  29. Liang, R.H.; Liu, W.F.; Li, C.Y.; Li, W.B.; Wu, Z.Z. A novel efficient probabilistic prediction approach for train-induced ground vibrations based on transfer learning. J. Vib. Control. 2024, 30, 576–587. [Google Scholar] [CrossRef]
  30. Liang, R.H.; Liu, W.F.; Kaewunruen, S.; Zhang, H.G.; Wu, Z.Z. Classification of External Vibration Sources through Data-Driven Models Using Hybrid CNNs and LSTMs. Struct. Control. Health Monit. 2023, 2023, 1900447. [Google Scholar] [CrossRef]
  31. Zhou, Y.; Pei, Y.L.; Zhou, S.; Zhao, Y.; Hu, J.X.; Yi, W.J. Novel methodology for identifying the weight of moving vehicles on bridges using structural response pattern extraction and deep learning algorithms. Measurement 2021, 168, 108384. [Google Scholar] [CrossRef]
  32. He, Y.P.; Zhang, Y.; Yao, Y.Y.; He, Y.L.; Sheng, X.Z. Review on the Prediction and Control of Structural Vibration and Noise in Buildings Caused by Rail Transit. Buildings 2023, 13, 2310. [Google Scholar] [CrossRef]
  33. He, C.; Zhou, S.H.; Guo, P.J.; Di, H.G.; Zhang, X.H. Analytical model for vibration prediction of two parallel tunnels in a full-space. J. Sound. Vib. 2018, 423, 306–321. [Google Scholar] [CrossRef]
  34. He, C.; Zhou, S.H.; Guo, P.J. Mitigation of railway-induced vibrations by using periodic wave impeding barriers. Appl. Acoust. 2022, 105, 496–514. [Google Scholar] [CrossRef]
  35. Li, X.M.; Chen, Y.K.; Zou, C.; Wang, H.; Zheng, B.K.; Chen, J.L. Building structure-borne noise measurements and estimation due to train operations in tunnel. Sci. Total Environ. 2024, 926, 172080. [Google Scholar] [CrossRef]
  36. Qiu, Y.T.; Zou, C.; Hu, J.H.; Chen, J.L. Prediction and mitigation of building vibrations caused by train operations on concrete floors. Appl. Acoust. 2024, 219, 109941. [Google Scholar] [CrossRef]
  37. Hu, J.H.; Zou, C.; Liu, Q.M.; Li, X.M.; Tao, Z.Y. Floor vibration predictions based on train-track-building coupling model. J. Build. Eng. 2024, 89, 109340. [Google Scholar] [CrossRef]
  38. Gu, Y.; Liu, J.B.; Du, Y.X. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element. Eng. Mech. 2007, 12, 31–37. [Google Scholar]
  39. GB/T 50355-2018; Standard for Limits and Measurement Methods of Vibration in the Room of Residential Building. Architecture & Building Press: Beijing, China, 2018.
Buildings 14 01702 g001
Figure 1. Building plan of the over-track buildings.
Figure 1. Building plan of the over-track buildings.
Buildings 14 01702 g001
Buildings 14 01702 g002
Figure 2. Layout of analysis points on vibration source and platform.
Figure 2. Layout of analysis points on vibration source and platform.
Buildings 14 01702 g002
Buildings 14 01702 g003
Figure 3. Layout of analysis points in the over-track building.
Figure 3. Layout of analysis points in the over-track building.
Buildings 14 01702 g003
Buildings 14 01702 g004
Figure 4. The “vehicle–track” coupling model.
Figure 4. The “vehicle–track” coupling model.
Buildings 14 01702 g004
Buildings 14 01702 g005
Figure 5. Sample of track irregularity.
Figure 5. Sample of track irregularity.
Buildings 14 01702 g005
Buildings 14 01702 g006
Figure 6. The “track–metro depot–over-track building” coupling model.
Figure 6. The “track–metro depot–over-track building” coupling model.
Buildings 14 01702 g006
Buildings 14 01702 g007
Figure 7. The instrument and accelerometers. (a) SQuadriga III data acquisition instrument; (b) PCB-352 vibration accelerometer; (c) PCB-393 vibration accelerometer.
Figure 7. The instrument and accelerometers. (a) SQuadriga III data acquisition instrument; (b) PCB-352 vibration accelerometer; (c) PCB-393 vibration accelerometer.
Buildings 14 01702 g007
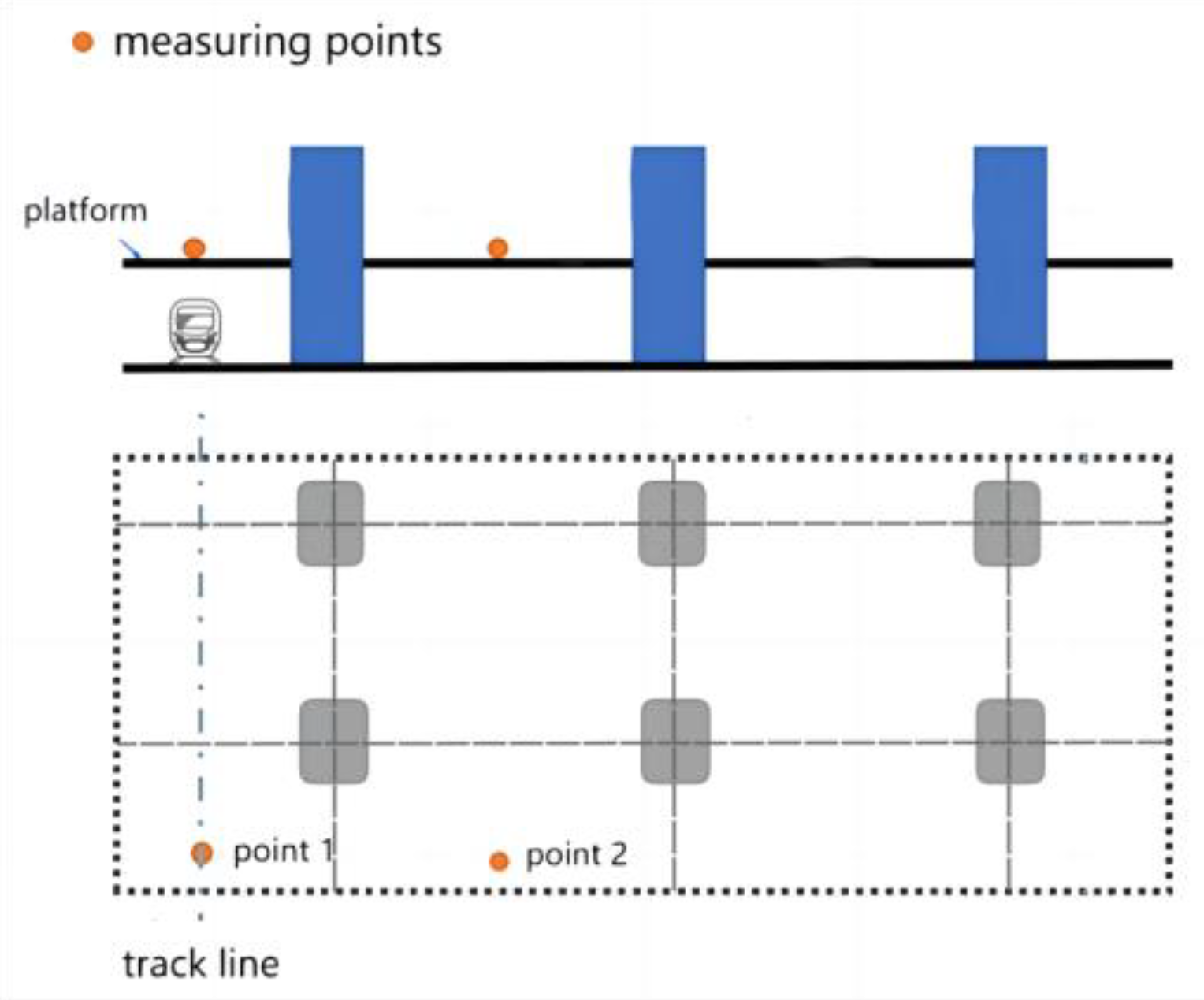
Buildings 14 01702 g008
Figure 8. Layout of the measuring points.
Figure 8. Layout of the measuring points.
Buildings 14 01702 g008
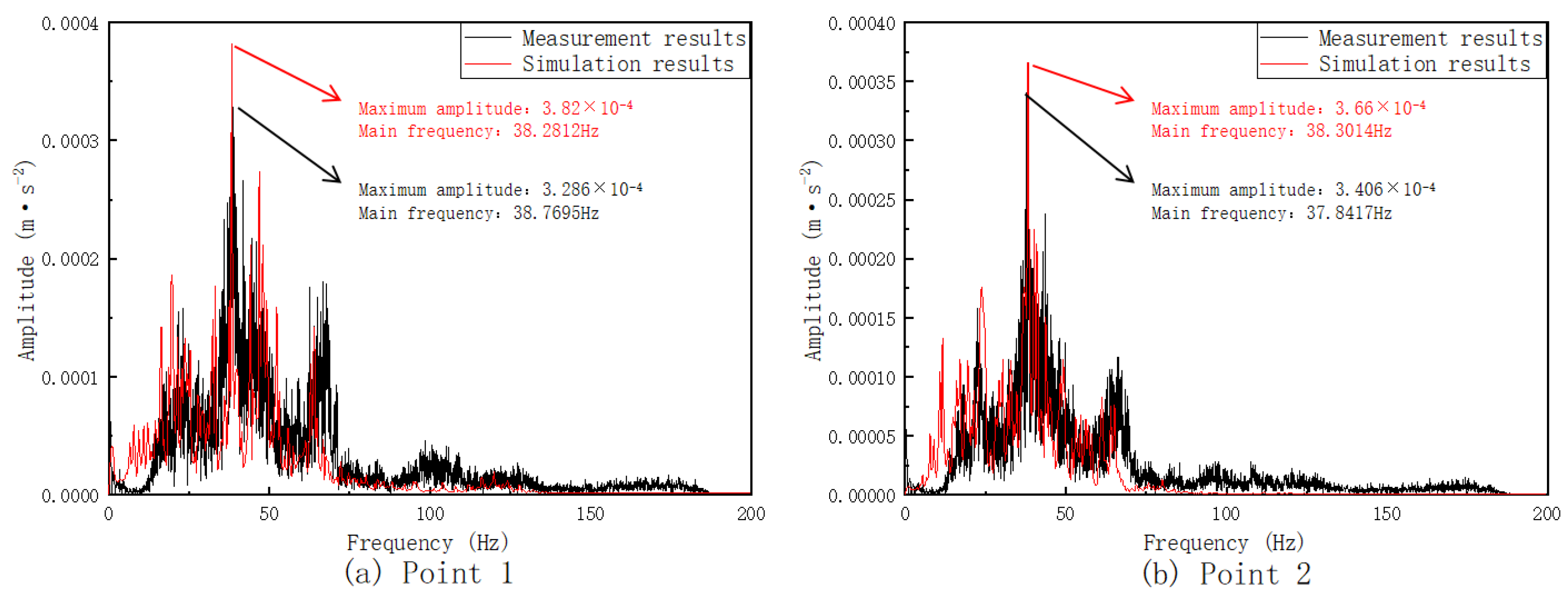
Buildings 14 01702 g009
Figure 9. Comparison of measured and simulation calculations.
Figure 9. Comparison of measured and simulation calculations.
Buildings 14 01702 g009
Buildings 14 01702 g010
Figure 10. Spectrum of vibration sources at different running speeds.
Figure 10. Spectrum of vibration sources at different running speeds.
Buildings 14 01702 g010
Buildings 14 01702 g011
Figure 11. The plane view of the platform of the operation zone.
Figure 11. The plane view of the platform of the operation zone.
Buildings 14 01702 g011
Buildings 14 01702 g012
Figure 12. Z-vibration level of platforms at different running speeds.
Figure 12. Z-vibration level of platforms at different running speeds.
Buildings 14 01702 g012
Buildings 14 01702 g013
Figure 13. The 1/3 octave frequency of each analysis point on the platforms at a speed of 20 km/h.
Figure 13. The 1/3 octave frequency of each analysis point on the platforms at a speed of 20 km/h.
Buildings 14 01702 g013
Buildings 14 01702 g014
Figure 14. The 1/3 octave frequency of each analysis point on the platforms at a speed of 10 km/h.
Figure 14. The 1/3 octave frequency of each analysis point on the platforms at a speed of 10 km/h.
Buildings 14 01702 g014
Buildings 14 01702 g015
Figure 15. The 1/3 octave frequency of each analysis point on the platforms at a speed of 5 km/h.
Figure 15. The 1/3 octave frequency of each analysis point on the platforms at a speed of 5 km/h.
Buildings 14 01702 g015
Buildings 14 01702 g016
Figure 16. The vibration response in the over-track building at different running speeds.
Figure 16. The vibration response in the over-track building at different running speeds.
Buildings 14 01702 g016
Buildings 14 01702 g017
Figure 17. The 1/3 octave frequency of the living room at different running speeds.
Figure 17. The 1/3 octave frequency of the living room at different running speeds.
Buildings 14 01702 g017
Buildings 14 01702 g018
Figure 18. The distribution of vibration energy at the vibration source under various working conditions.
Figure 18. The distribution of vibration energy at the vibration source under various working conditions.
Buildings 14 01702 g018
Table 1. The top 10 cities with the highest subway mileage in the world.
Table 1. The top 10 cities with the highest subway mileage in the world.
CityMileage (km)
Shanghai831
Beijing783
Guangzhou621.05
Chengdu518
Moscow466.8
Hangzhou450
Wuhan435
Chongqing432.8
Nanjing427
Shenzhen419
Table 2. Selection of structural elements and material parameters.
Table 2. Selection of structural elements and material parameters.
NamePoisson’s RatioElastic Modulus (MPa)Density
(kg/m3)		Element Selection
Plain fill
(the first layer)		0.470206.631760solid 45
Mucky soil
(the second layer)		0.48385.41700solid 45
Fine sand
(the third layer)		0.471206.41950solid 45
Bearing platform0.233002500solid 45
Pile foundation0.234502400beam 188
Rails0.3210,0007830beam 188
Supporting columns0.234,5002400beam 188
Concrete masonry0.234,5002400beam 188
Exterior wall0.233,0002500shell 63
Table 3. The vibration response at the vibration source under various working conditions.
Table 3. The vibration response at the vibration source under various working conditions.
Working ConditionAnalysis PointPeak Acceleration (m/s2)Z-Vibration Level (dB)
Train speed of 20 km/h
(working condition 1)		Rails4.01107.57
Supporting columns0.5491.63
Columns0.0877.82
The ground at a distance of 7.5 m from the rails0.1283.63
Train speed of 10 km/h
(working condition 2)		Rails1.9997.51
Supporting columns0.1686.51
Columns0.0371.84
The ground at a distance of 7.5 m from the rails0.0781.08
Train speed of 5 km/h
(working condition 3)		Rails2.1188.36
Supporting columns0.1484.37
Columns0.0469.78
The ground at a distance of 7.5 m from the rails0.0577.31
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Luo, X.; Jiang, X.; Feng, Q.; Hu, W.; Tu, Q.; Chen, Y. Analysis of Train-Induced Vibration Transmission and Distribution Characteristics in Double-Layer Metro Depot. Buildings 2024, 14, 1702. https://doi.org/10.3390/buildings14061702

AMA Style

Luo X, Jiang X, Feng Q, Hu W, Tu Q, Chen Y. Analysis of Train-Induced Vibration Transmission and Distribution Characteristics in Double-Layer Metro Depot. Buildings. 2024; 14(6):1702. https://doi.org/10.3390/buildings14061702

Chicago/Turabian Style

Luo, Xinwei, Xuan Jiang, Qingsong Feng, Wenlin Hu, Qinming Tu, and Yanming Chen. 2024. "Analysis of Train-Induced Vibration Transmission and Distribution Characteristics in Double-Layer Metro Depot" Buildings 14, no. 6: 1702. https://doi.org/10.3390/buildings14061702

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop