Indoor Air Temperature Distribution and Heat Transfer Coefficient for Evaluating Cold Storage of Phase-Change Materials during Night Ventilation
Abstract
:1. Introduction
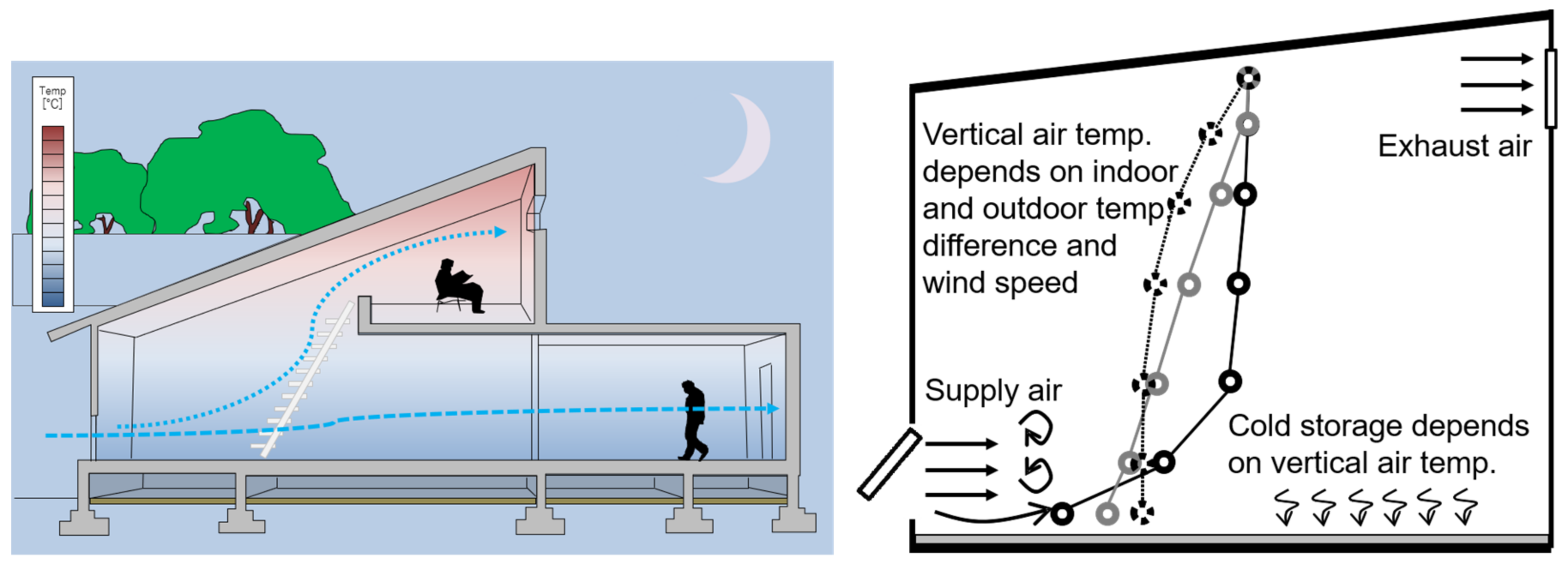
1.1. Background
1.2. Previous Research on Indoor Air Temperature Distribution
1.3. Purpose and Methodology
2. Measurement
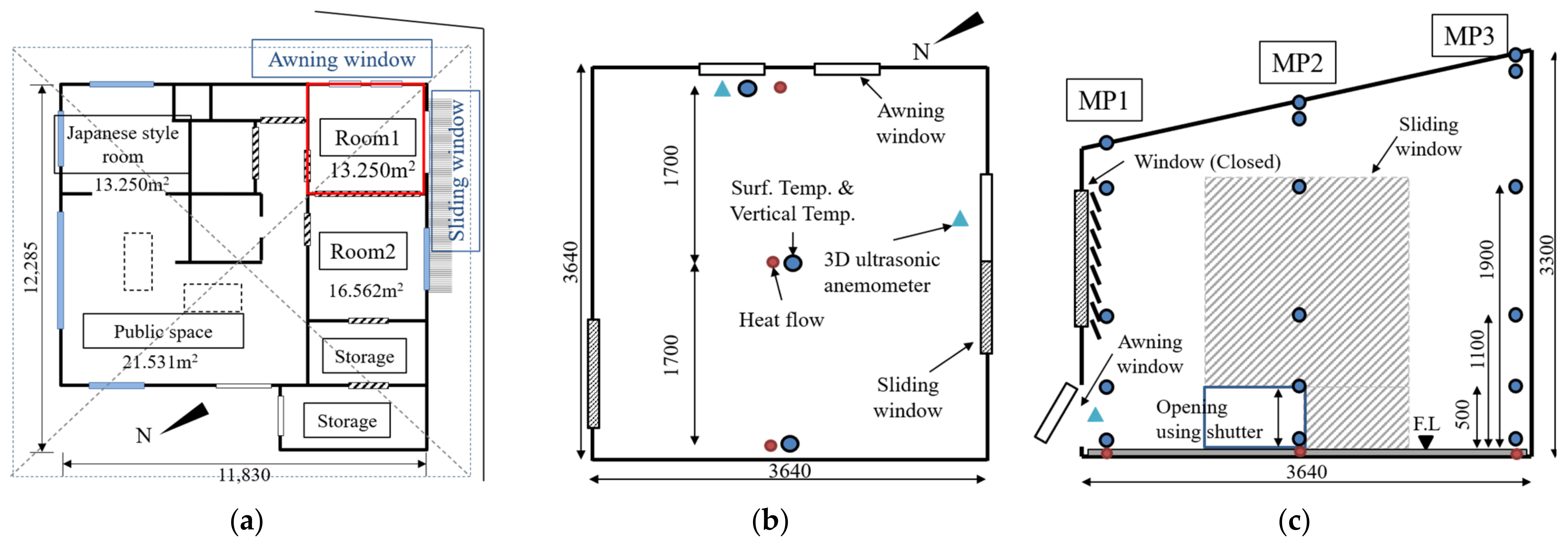
2.1. Overview
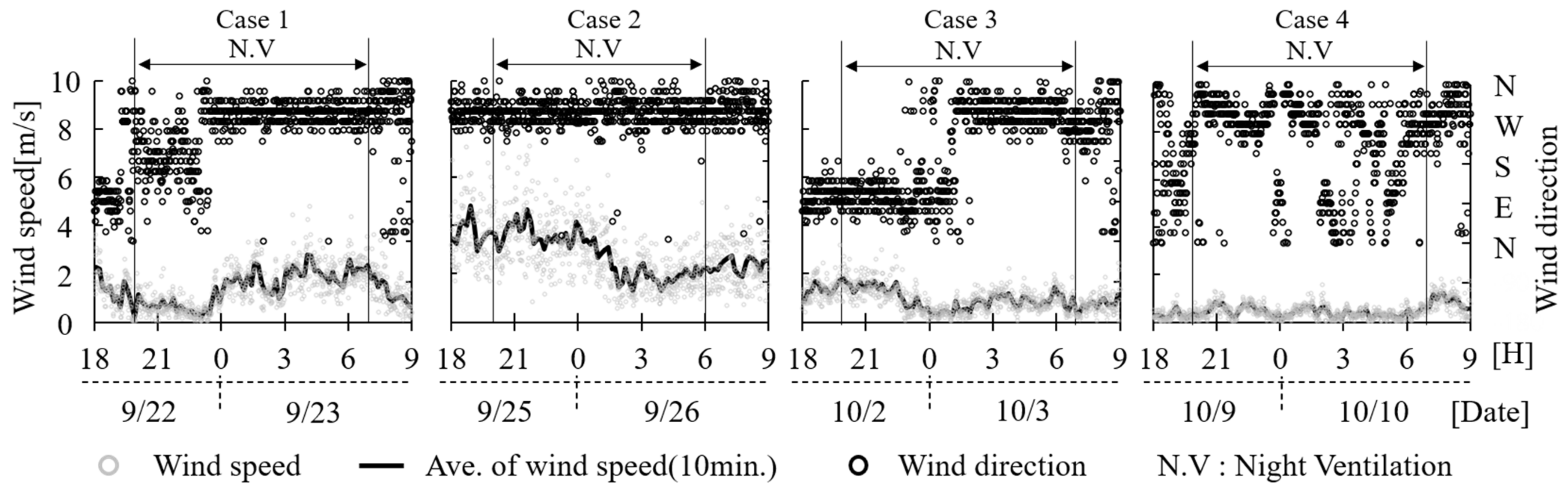
2.2. Weather Conditions
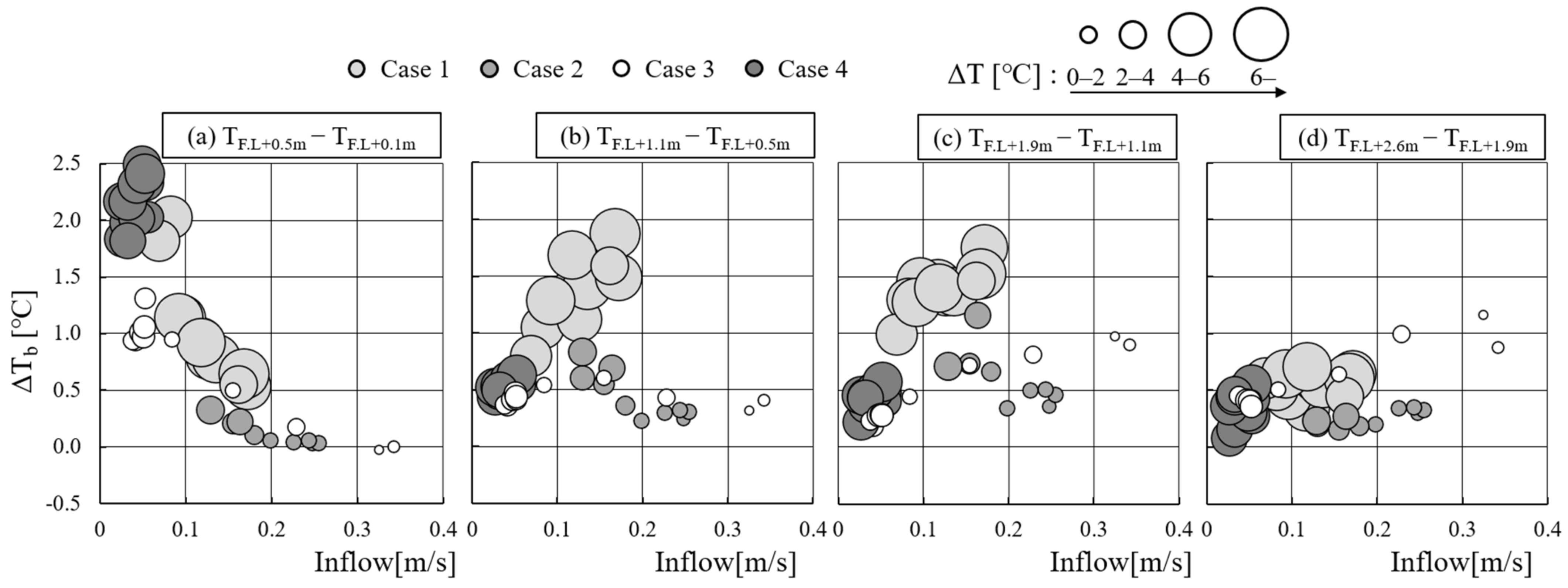
2.3. Parameters Affecting the Vertical Indoor Temperature Distribution
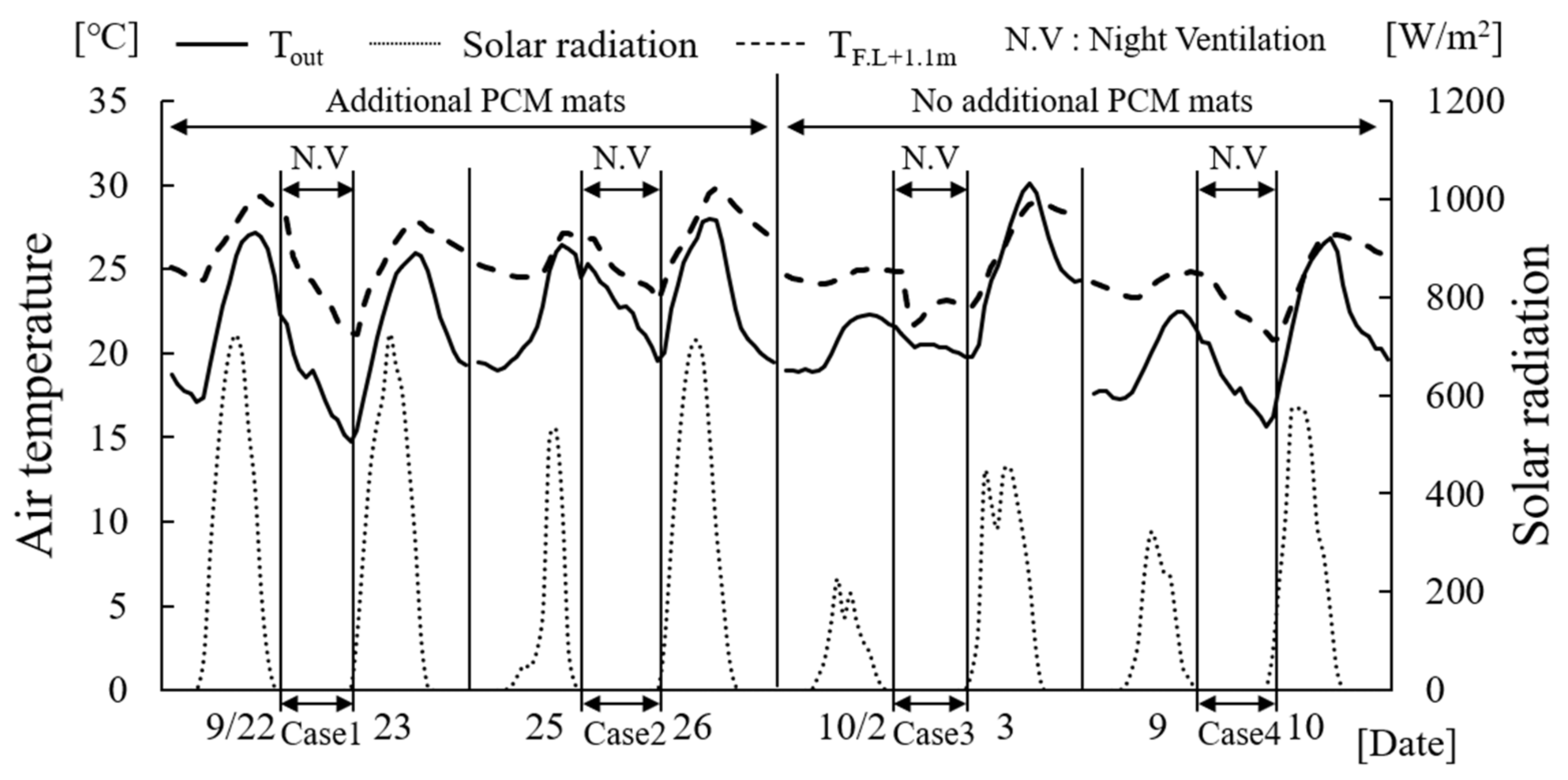
2.4. Thermal Characteristics of the Space with Night Ventilation
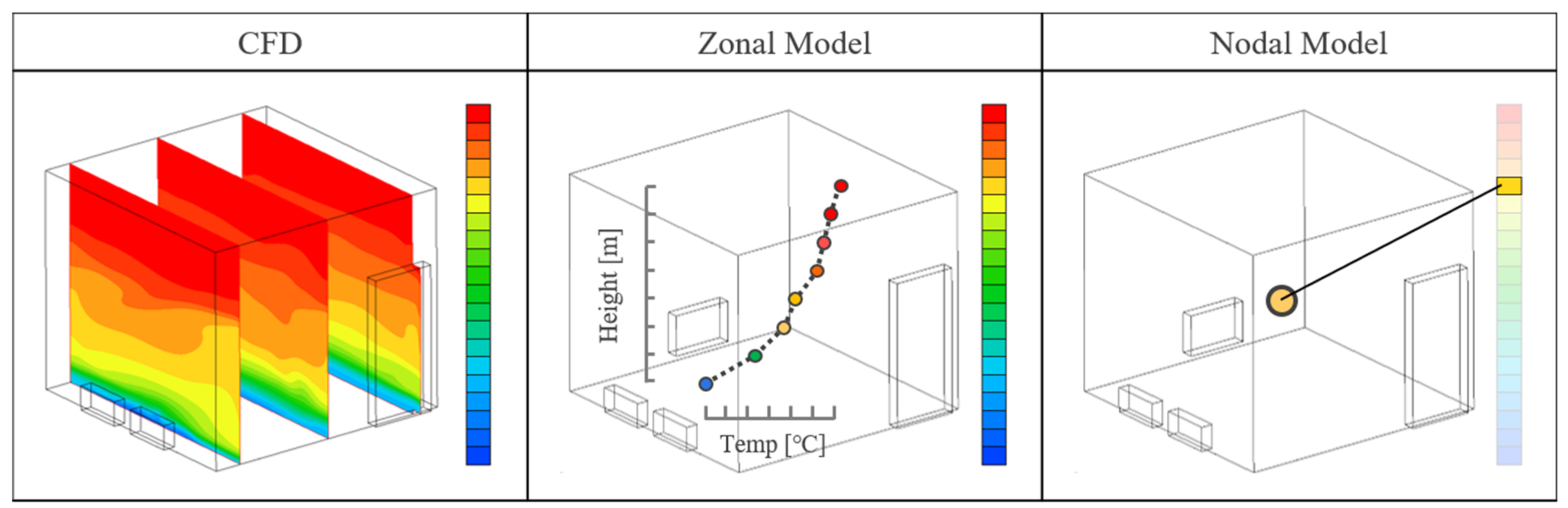
3. Block Model (Zonal Simulation or Numerical Analysis)
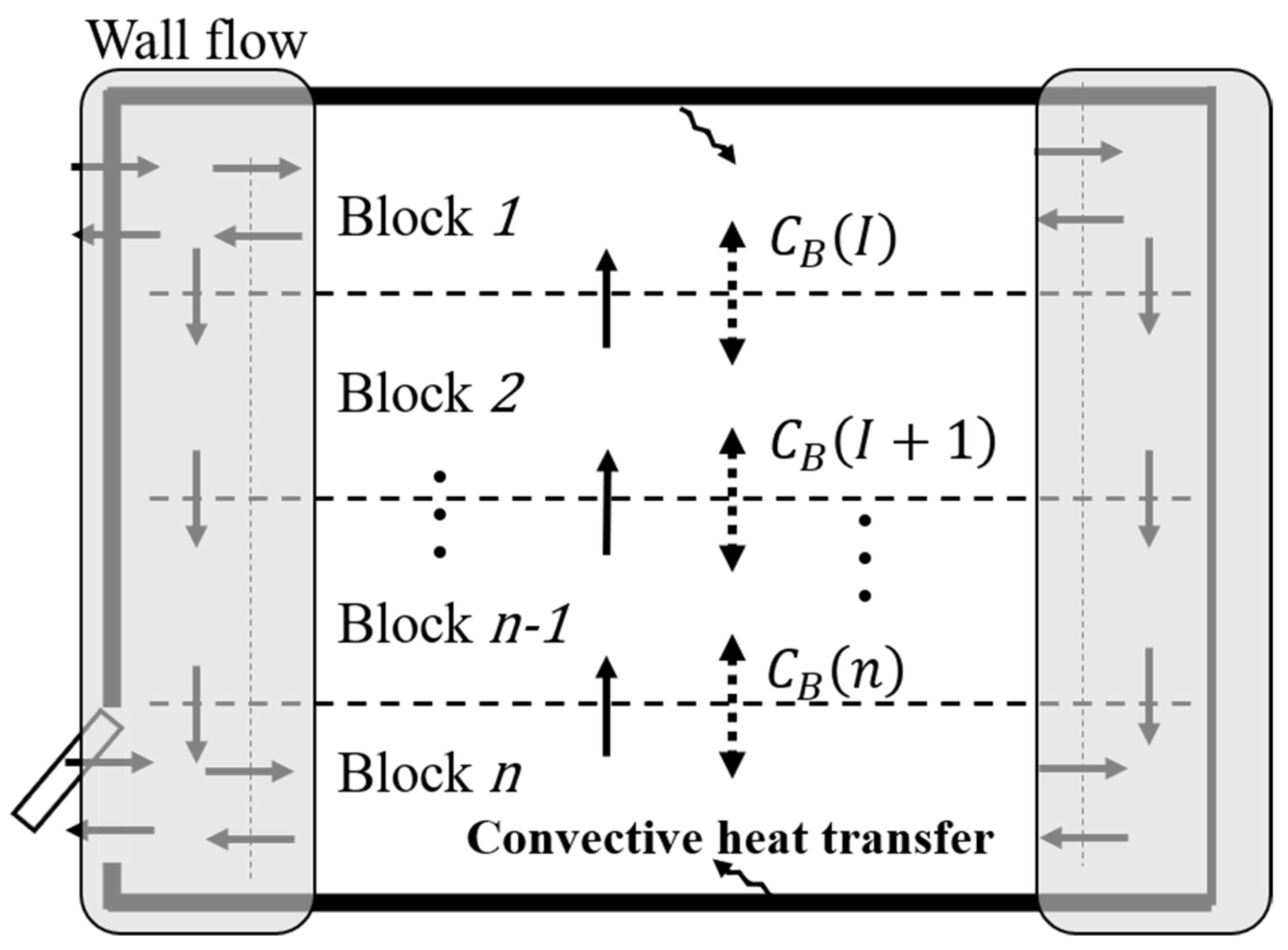
3.1. Model Description
- Wall surface current model: This model evaluates the ascending and descending air currents along vertical surfaces due to convective heat transfer. It employs boundary layer analysis on a flat plate to determine the air currents formed along the wall owing to the temperature difference between the wall and air (Figure 10);
- Primary airstream evaluation model: This model considers the air streams discharged from the outlets as non-isothermal free jets. It assesses the influence of these jets on the vertical temperature distribution by entraining air from different zones, moving upward owing to buoyancy, and affecting the surrounding air temperatures;
- Heat transfer by temperature difference between adjacent zones: This component is used to calculate the heat transfer caused by the temperature difference between vertically adjacent zones. It employs a heat transfer factor to model the conduction and convection processes between zones.
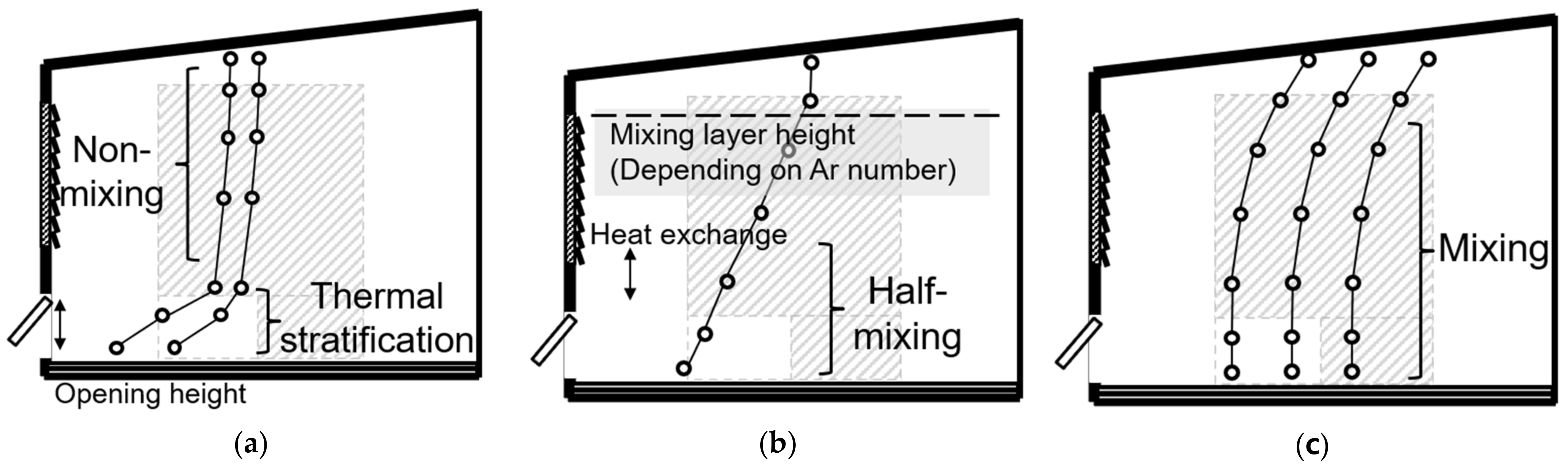
3.2. Indoor Air Temperature Distribution
3.3. Heat Transfer in Each Block
3.4. Verification
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC AR6 SYR, Summary for Policemakers. Available online: https://www.ipcc.ch/report/ar6/syr/ (accessed on 1 April 2023).
- International Energy Agency. World Energy Outlook 2018; International Energy Agency: Paris, France, 2018. [CrossRef]
- Santamouris, M. Cooling the buildings—past, present and future. Energy Build. 2016, 128, 617–638. [Google Scholar] [CrossRef]
- Santamouris, M.; Asimakopoulos, D. Passive Cooling of Buildings; James and James Science Publishers: London, UK, 1996. [Google Scholar]
- Solgi, E.; Hamedani, Z.; Fernando, R.; Skates, H.; Orji, N.E. A literature review of night ventilation strategies in buildings. Energy Build. 2018, 173, 337–352. [Google Scholar] [CrossRef]
- Shaviv, E.; Yezioro, A.; Capeluto, I.G. Thermal mass and night ventilation as passive cooling design strategy. Renew. Energy 2001, 24, 445–452. [Google Scholar] [CrossRef]
- Exizidou, P.; Christoforou, E.; Fokaides, P.A. Numerical assessment of night ventilation impact on the thermal comfort of vernacular buildings. J. Build. Pathol. Rehabil. 2017, 2, 2. [Google Scholar] [CrossRef]
- Blondeau, P.; Spérandio, M.; Allard, F. Night ventilation for building cooling in summer. Sol. Energy 1997, 61, 327–335. [Google Scholar] [CrossRef]
- Borderon, J.; Virgone, J.; Cantin, R.; Kuznik, F. Full-scale study of a building equipped with a multi-layer rack latent heat thermal energy storage system. HVACR Res. 2011, 17, 566–576. [Google Scholar] [CrossRef]
- Ling, H.; Chen, C.; Wei, S.; Guan, Y.; Ma, C.; Xie, G.; Li, N.; Chen, Z. Effect of phase change materials on indoor thermal environment under different weather conditions and over a long time. Appl. Energy 2015, 140, 329–337. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Li, L.; Zhao, M. Experimental assessment on the use of phase change materials (PCMs)-bricks in the exterior wall of a full-scale room. Energy Convers. Manag. 2016, 120, 81–89. [Google Scholar] [CrossRef]
- Wonorahardjo, S.; Sutjahja, I.M.; Tunçbilek, E.; Achsani, R.A.; Arıcı, M.; Rahmah, N. PCM-based passive air conditioner in urban houses for the tropical climates: An experimental analysis on the stratum air circulation. Build. Environ. 2021, 192, 107632. [Google Scholar] [CrossRef]
- Andersen, K.T. Theory for natural ventilation by thermal buoyancy in one zone with uniform temperature. Build. Environ. 2003, 38, 1281–1289. [Google Scholar] [CrossRef]
- Fanger, P.O. Local discomfort to the human body caused by non-uniform thermal environments. Ann. Occup. Hyg. 1977, 20, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Santamouris, M.; Sfakianaki, A.; Pavlou, K. On the efficiency of night ventilation techniques applied to residential buildings. Energy Build. 2010, 42, 1309–1313. [Google Scholar] [CrossRef]
- Ito, H.; Yokoi, M.; Nakahara, N. Simplified calculation model of vertical air temperature distribution during heating in air-conditioned room—Studies on thermal properties in air-conditioned space Part 2. J. Archit. Plann. Environ. Engng AIJ 1989, 398, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Togari, S.; Arai, Y.; Miura, K. Simplified prediction model of vertical air temperature distribution in a large space—Study on a thermal environment design system for large spaces, Part 1. J. Archit. Plan. Environ. Eng. AIJ 1991, 427, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Togari, S.; Arai, Y.; Miura, K. A simplified model for predicting vertical temperature distribution in a large space. ASHRAE Trans. 1993, 99, 84–99. Available online: https://www.scopus.com/inward/record.uri?eid=2-s2.0-0027269039&partnerID=40&md5=8a73bb2ccc4ca8ee55fa2759b0ced9b3 (accessed on 2 April 2024).
- Inard, C.; Bouia, H.; Dalicieux, P. Prediction of air temperature distribution in buildings with a zonal model. Energy Build. 1996, 24, 125–132. [Google Scholar] [CrossRef]
- Wurtz, E.; Nataf, J.M.; Winkelmann, F. Two- and three-dimensional natural and mixed convection simulation using modular zonal models in buildings. Int. J. Heat Mass Transf. 1999, 42, 923–940. [Google Scholar] [CrossRef]
- Haghighat, F.; Li, Y.; Megri, A.C. Development and validation of a zonal model—POMA. Build. Environ. 2001, 36, 1039–1047. [Google Scholar] [CrossRef]
- Musy, M.; Wurtz, E.; Winkelmann, F.; Allard, F. Generation of a zonal model to simulate natural convection in a room with a radiative/convective heater. Build. Environ. 2001, 36, 589–596. [Google Scholar] [CrossRef]
- Musy, M.; Winkelmann, F.; Wurtz, E.; Sergent, A. Automatically generated zonal models for building air flow simulation: Principles and applications. Build. Environ. 2002, 37, 873–881. [Google Scholar] [CrossRef]
- Higashimoto, T.; Yamanaka, T.; Kotani, H.; Hanano, H. Temperature and contaminant concentration distribution of displacement ventilated rooms with cooled wall. J. Environ. Eng. AIJ 2003, 68, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Stewart, J. Simulating air flow and temperature distribution inside buildings using a modified version of COMIS with sub-zonal divisions. Energy Build. 2003, 35, 257–271. [Google Scholar] [CrossRef]
- Wurtz, E.; Mora, L.; Inard, C. An equation-based simulation environment to investigate fast building simulation. Build. Environ. 2006, 41, 1571–1583. [Google Scholar] [CrossRef]
- Gao, J.; Zhao, J.; Xiaodong, L.; Gao, F. A Zonal Model for Large Enclosures With Combined Stratification Cooling and Natural Ventilation Part 1—Model Generation and its Procedure. J. Sol. Energy Eng. 2006, 128, 367–375. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, X.; Jiang, Y.; Gopal, V.; Dobbs, G.; Sahm, M. A new approach on zonal modeling of indoor environment with mechanical ventilation. Build. Environ. 2008, 43, 278–286. [Google Scholar] [CrossRef]
- Chen, Q. Ventilation performance prediction for buildings A method overview and recent applications. Build. Environ. 2009, 44, 848–858. [Google Scholar] [CrossRef]
- Megri, A.C.; Yu, Y. New calibrated zonal model (POMA+) for temperature and airflow predictions. Build. Environ. 2015, 94, 109–121. [Google Scholar] [CrossRef]
- Huang, C.; Li, R.; Liu, Y.; Liu, J.; Wang, X. Study of indoor thermal environment and stratified air-conditioning load with low-sidewall air supply for large space based on Block-Gebhart model. Build. Environ. 2019, 147, 495–505. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Xu, Y.; Wang, F.; Zhang, Q.; Huang, C.; Shi, C. Prediction of vertical thermal stratification of large space buildings based on Block-Gebhart model: Case studies of three typical hybrid ventilation scenarios. J. Build. Eng. 2021, 41, 102452. [Google Scholar] [CrossRef]
- Lee, T.; Sato, R.; Asawa, T.; Kawai, H.; Hirayama, Y.; Ohya, I.; Sato, Y.; Hayashi, Y. Study on cold storage of phase change material on the floor of a house with night natural ventilation. J. Environ. Eng. (Trans. AIJ) 2017, 82, 1025–1034. (In Japanese) [Google Scholar] [CrossRef]
- Landsberg, D.R.; Misuriello, H.P.; Moreno, S. Design strategies for energy-efficient atrium spaces. ASHRAE Trans. 1986, 92 Pt 2, 310–328. Available online: https://www.scopus.com/inward/record.uri?eid=2-s2.0-0022940710&partnerID=40&md5=88e2d69119e7811b3c330f27ac78b0d2 (accessed on 15 January 2023).
- Chow, W.K. Assessment of thermal environment in an atrium with air-conditioning. J. Environ. Syst. 1996, 25, 409–420. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, X.; Zhao, J.; Gao, F. A heat transfer parameter at air interfaces in the BLOCK model for building thermal environment. Int. J. Therm. Sci. 2010, 49, 463–470. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, P.; Guo, C.; Tang, X.; Xue, Y.; Huang, C. On the calculation of heat migration in thermally stratified environment of large space building with sidewall nozzle air-supply. Build. Environ. 2019, 147, 221–230. [Google Scholar] [CrossRef]




| Items | Instrument | Accuracy |
|---|---|---|
| Air temperature | 0.1-mmΦ T-type thermocouple | −40 °C to 125 °C: ±0.5 °C |
| Relative humidity | Resistance change type (TDK (Tokyo, Japan), CHS-UPS) | 0 °C to 50 °C: ±3% RH |
| Globe temperature | 0.1-mmΦ T-type thermocouple inside a globe thermometer | −40 °C to 125 °C: ±0.5 °C |
| Surface temperature | 0.3-mmΦ T-type thermocouple | −40 °C to 125 °C: ±0.5 °C |
| Wind speed in indoor spaces | Air velocity probe (KANOMAX (Tokyo, Japan), 0965-09) | ±3% (KANOMAX) |
| Wind direction & speed | 3D ultrasonic anemometers (Young-81000): Outdoor measurement (KAIJO (Tokyo, Japan), DA-600): Indoor measurement | ±1%, ±0.05 m/s (Young-81000) ±2° (Young-81000) ±3% (KAIJO, DA-600) ±3° (KAIJO, DA-600) |
| Weather data | Air temp.: 0.1-mmΦ T-type thermocouple Humidity: Resistance change type (TDK, CHS-UPS) Wind: Wind vane anemometer (EKO (Tokyo, Japan), MA-110) Solar radiation: Thermopile pyranometer | ±5% (EKO, MA-110) ±5° (EKO, MA-110) ±5% (Thermopile pyranometer) |
| Case No. | Date & Time of Natural Ventilation | Additional PCM Mats on the Floor |
|---|---|---|
| Case 1 | 22 September—20 p.m.–23 September—7 a.m. | ○ |
| Case 2 | 25 September—20 p.m.–26 September—6 a.m. | ○ |
| Case 3 | 2 October—20 p.m.–3 October—7 a.m. | × |
| Case 4 | 9 October—20 p.m.–10 October—7 a.m. | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, T.; Sato, R.; Asawa, T.; Yoon, S. Indoor Air Temperature Distribution and Heat Transfer Coefficient for Evaluating Cold Storage of Phase-Change Materials during Night Ventilation. Buildings 2024, 14, 1872. https://doi.org/10.3390/buildings14061872
Lee T, Sato R, Asawa T, Yoon S. Indoor Air Temperature Distribution and Heat Transfer Coefficient for Evaluating Cold Storage of Phase-Change Materials during Night Ventilation. Buildings. 2024; 14(6):1872. https://doi.org/10.3390/buildings14061872
Chicago/Turabian StyleLee, TaeCheol, Rihito Sato, Takashi Asawa, and Seonghwan Yoon. 2024. "Indoor Air Temperature Distribution and Heat Transfer Coefficient for Evaluating Cold Storage of Phase-Change Materials during Night Ventilation" Buildings 14, no. 6: 1872. https://doi.org/10.3390/buildings14061872
APA StyleLee, T., Sato, R., Asawa, T., & Yoon, S. (2024). Indoor Air Temperature Distribution and Heat Transfer Coefficient for Evaluating Cold Storage of Phase-Change Materials during Night Ventilation. Buildings, 14(6), 1872. https://doi.org/10.3390/buildings14061872










