Cyclic Behavior of Concrete-Filled Tube Columns with Bidirectional Moment Connections Considering the Local Slenderness Effect
Abstract
:1. Introduction
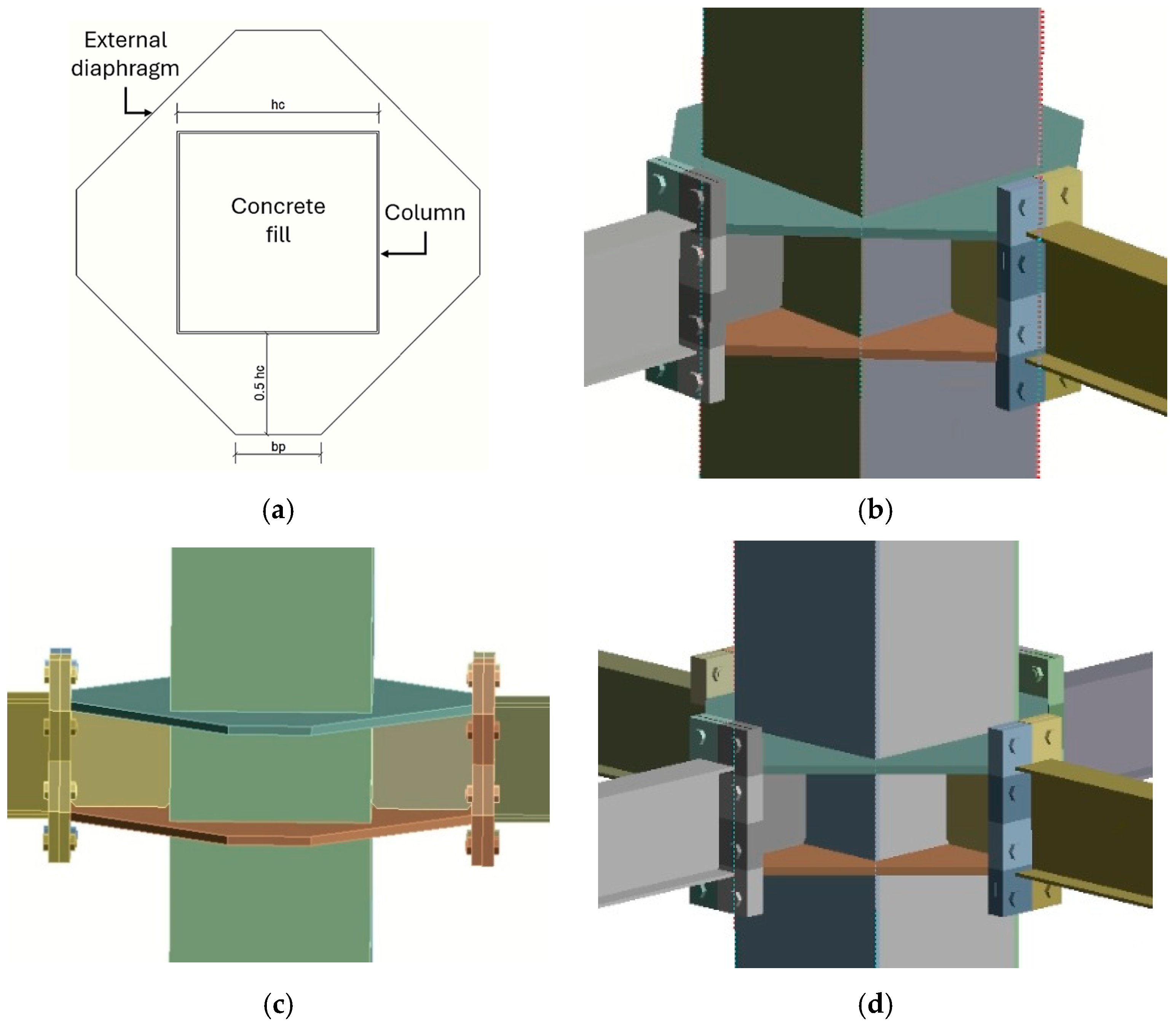
2. Design Considerations of Joint Configurations
3. Numerical Models
3.1. Material Fundamental Law
3.2. Loading and Boundary Conditions
3.3. Finite Element Type, Mesh Size, and Contacts
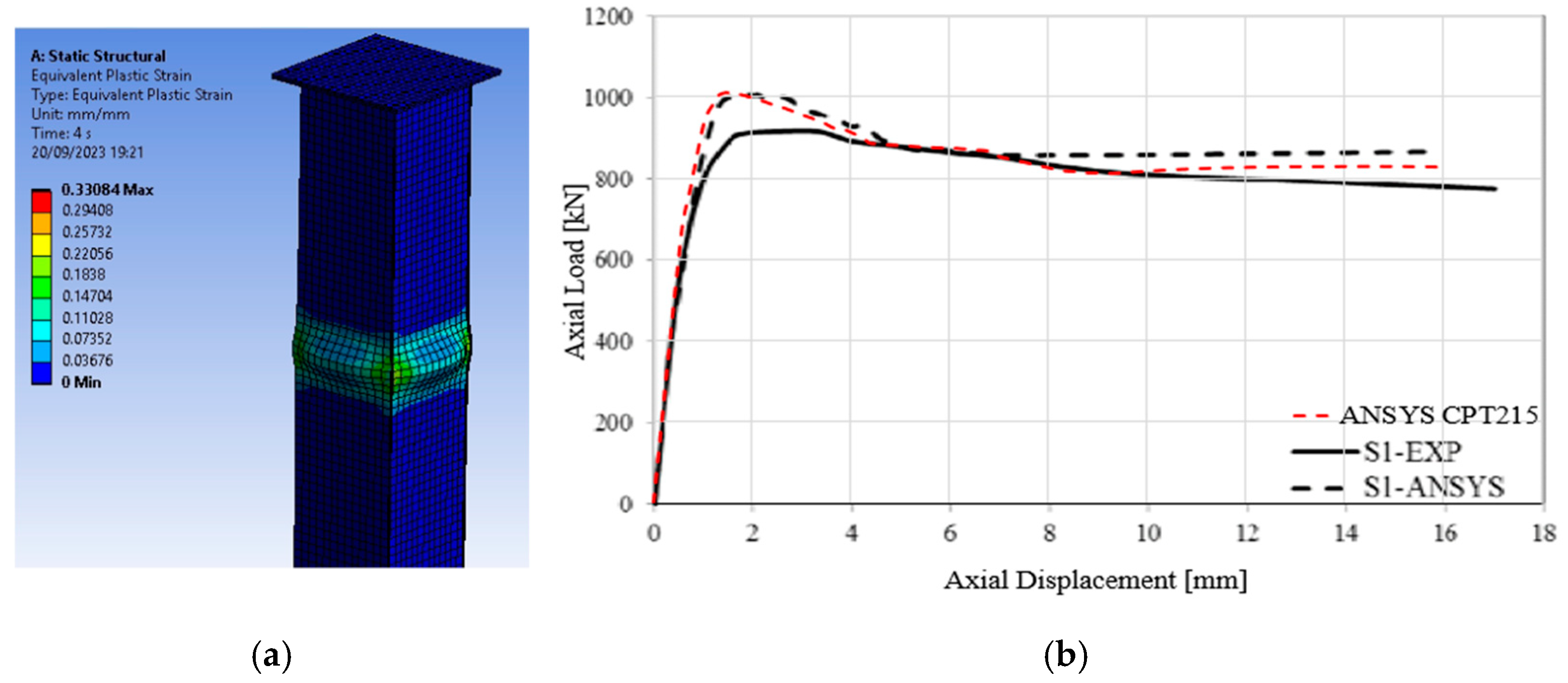
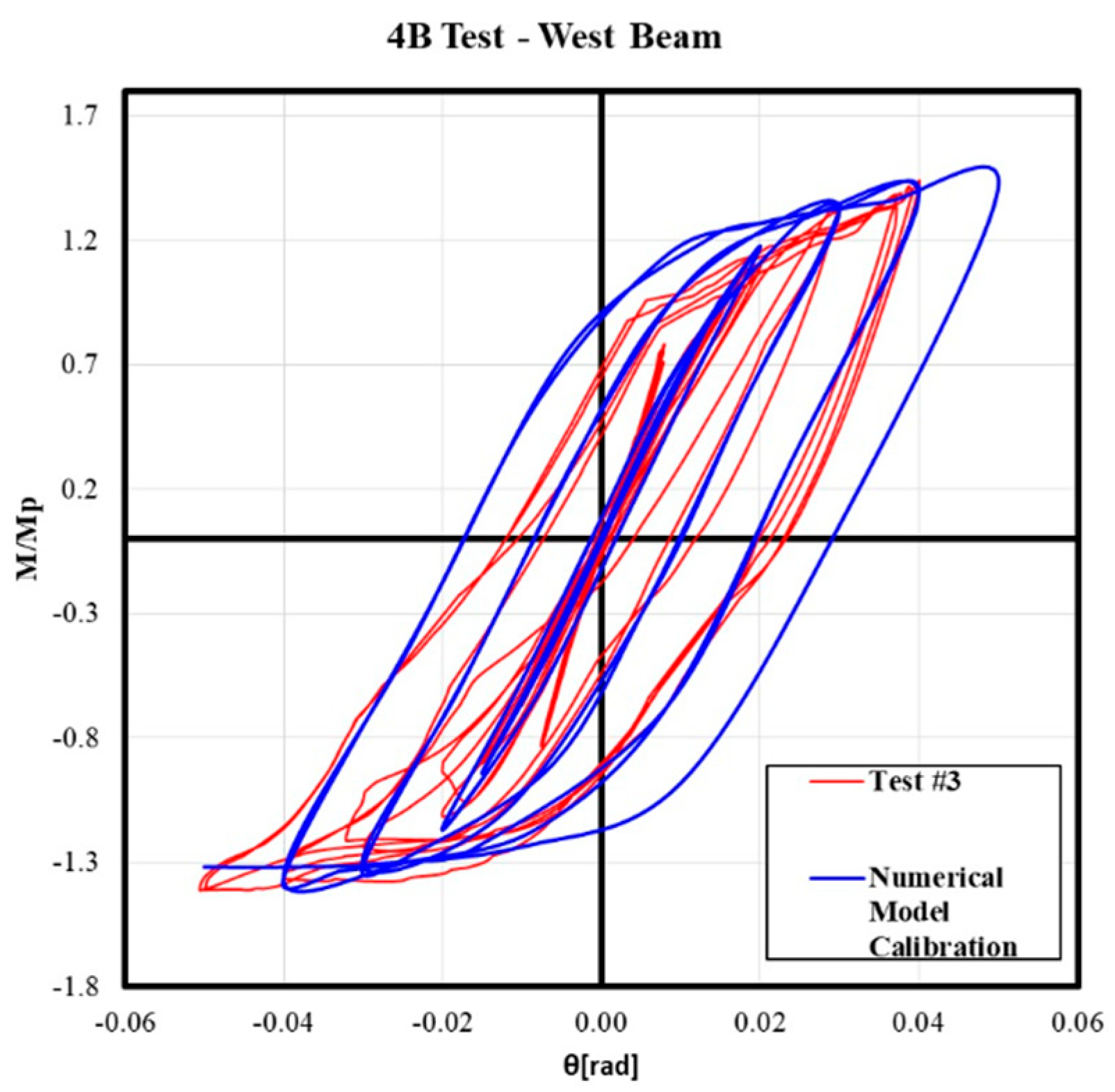
4. Calibration and Validation of the Numerical Model
5. Results of the Parametric Assessment of Cyclic Behavior
5.1. Bidirectional Effect
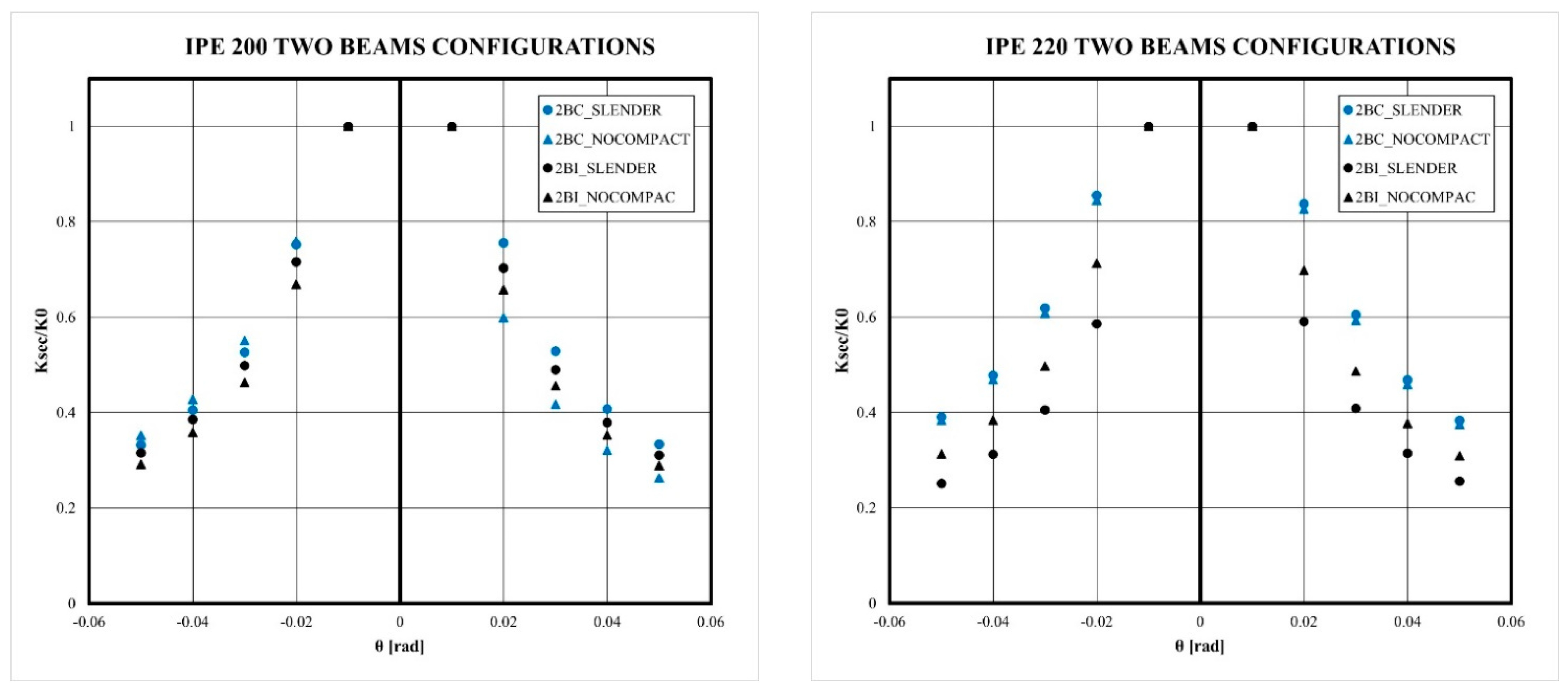
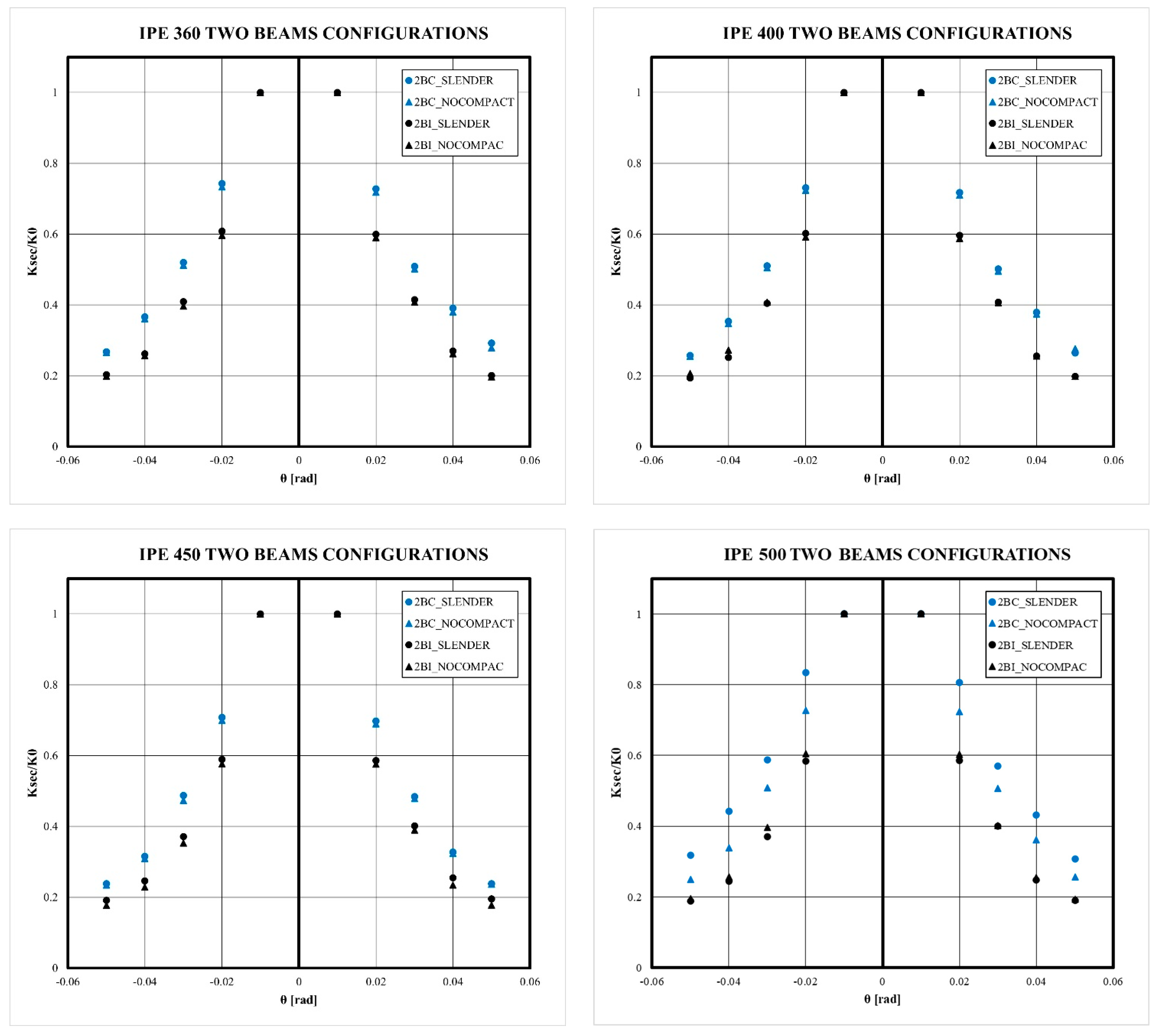
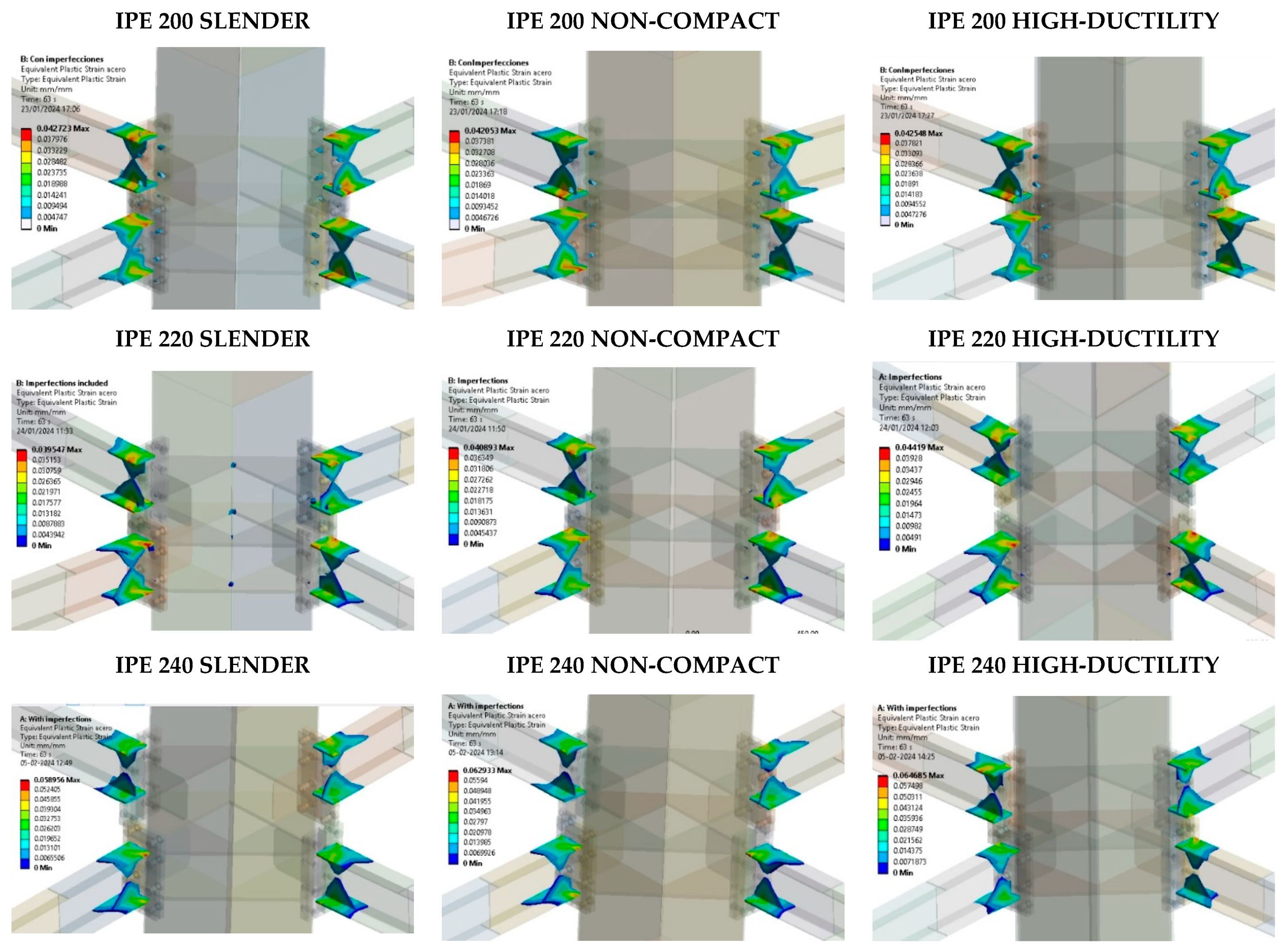
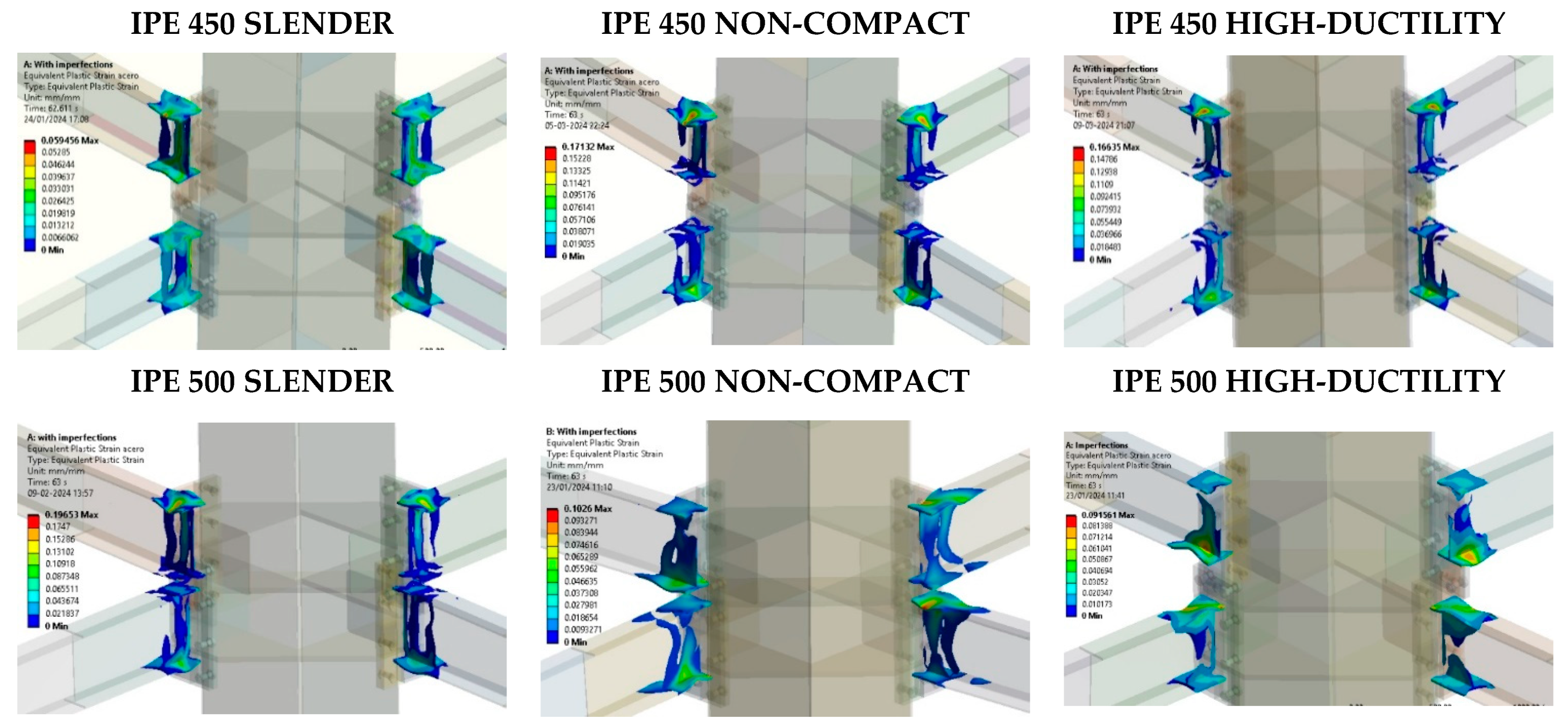
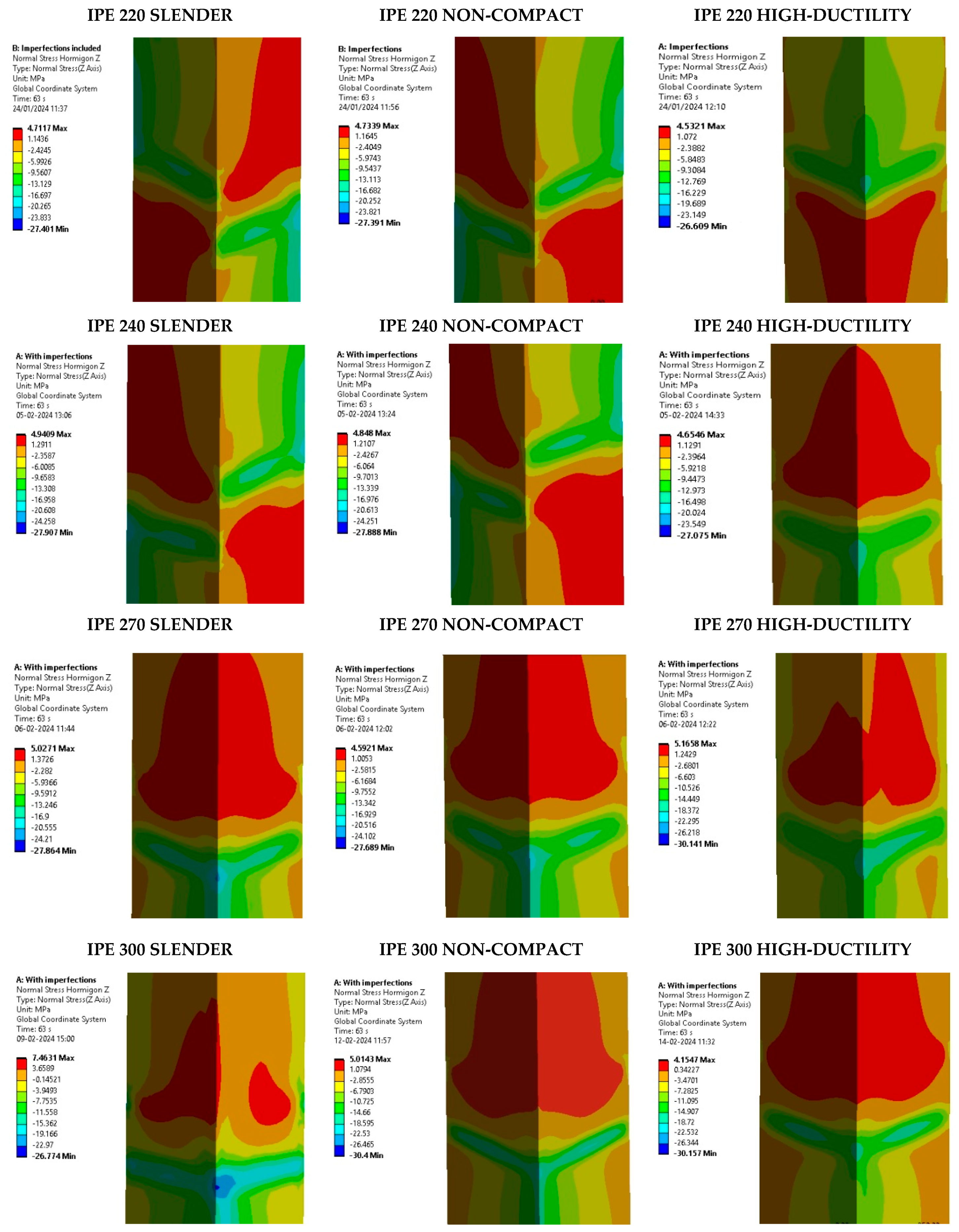
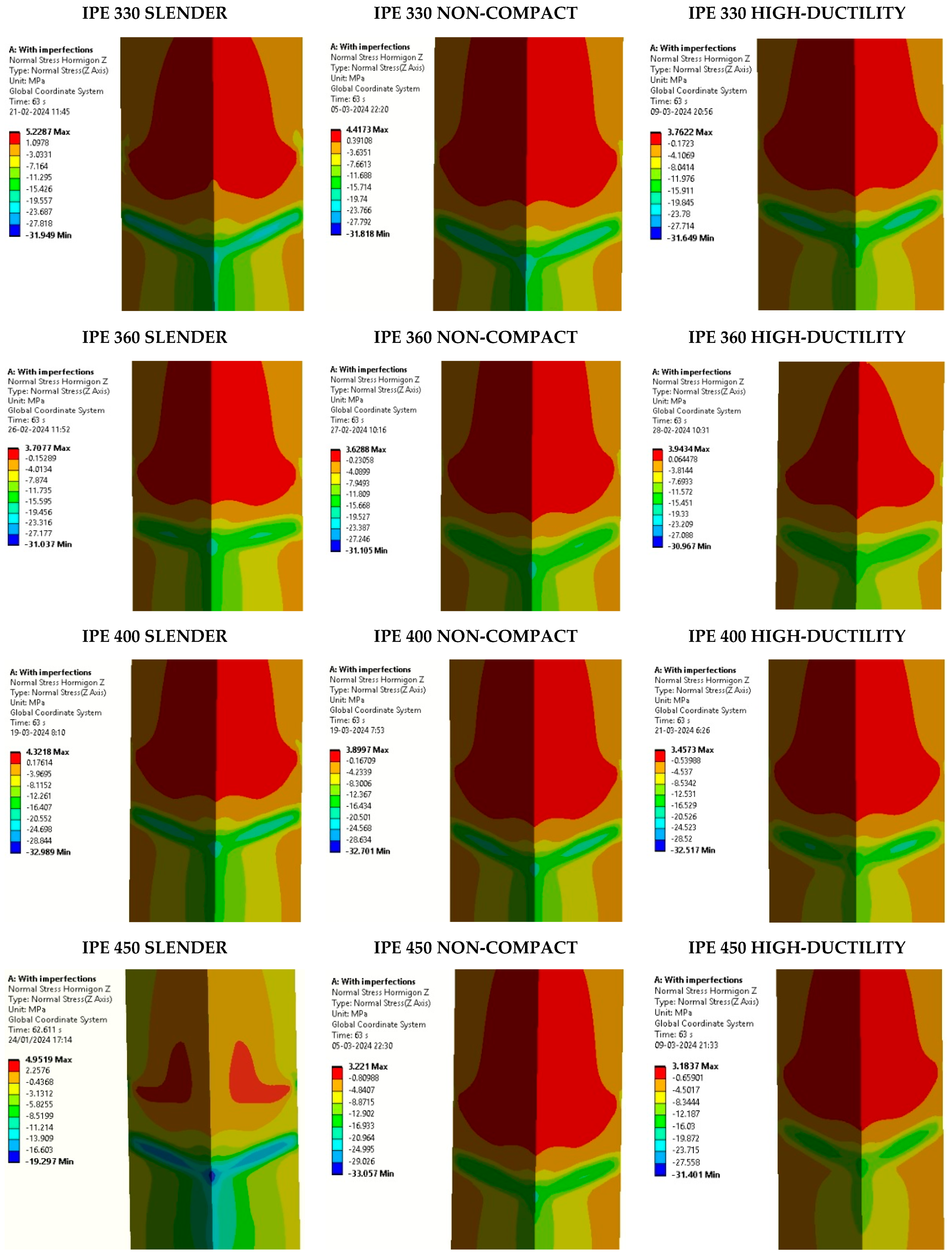
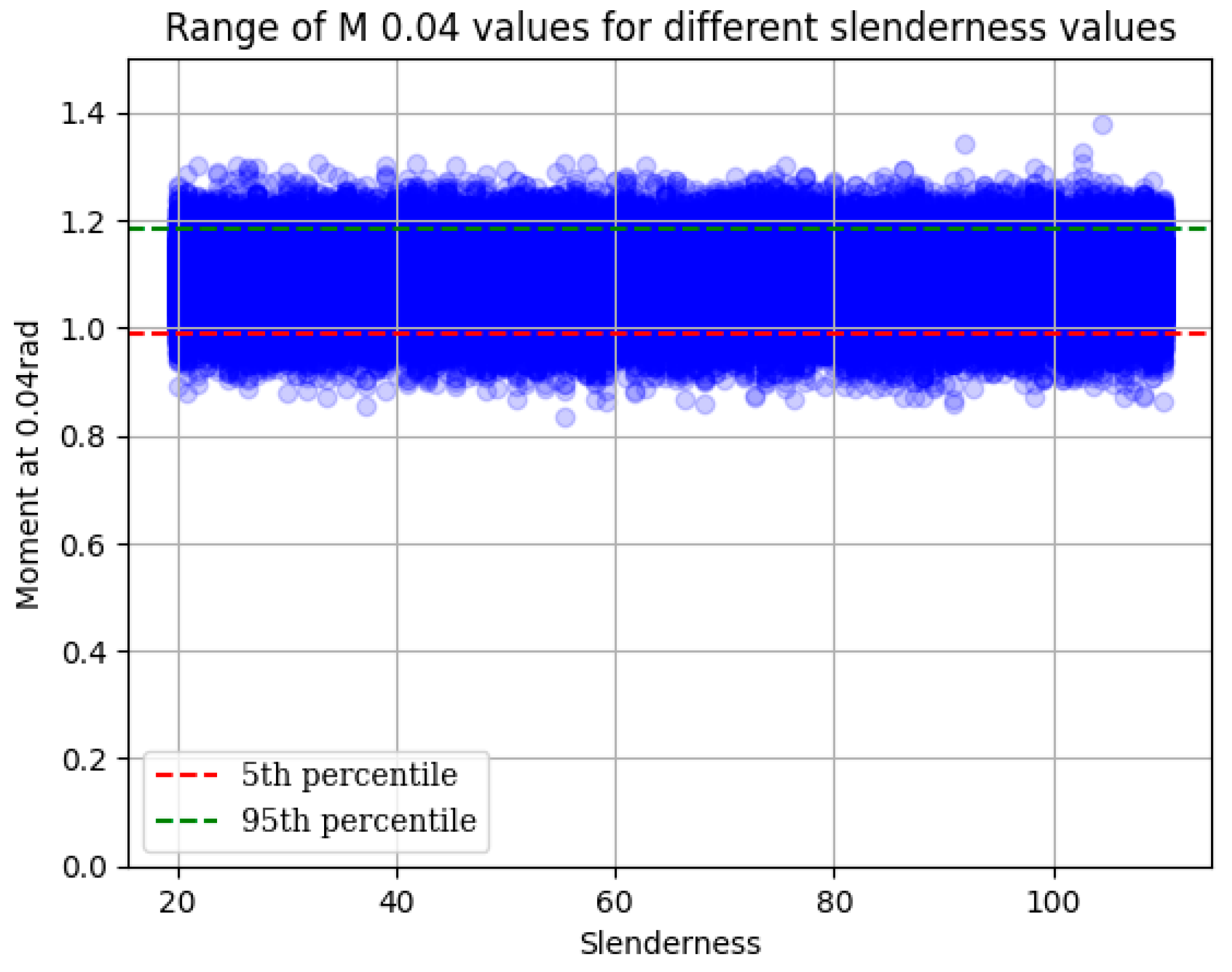
5.2. Effect of the Slenderness of the CFT Column
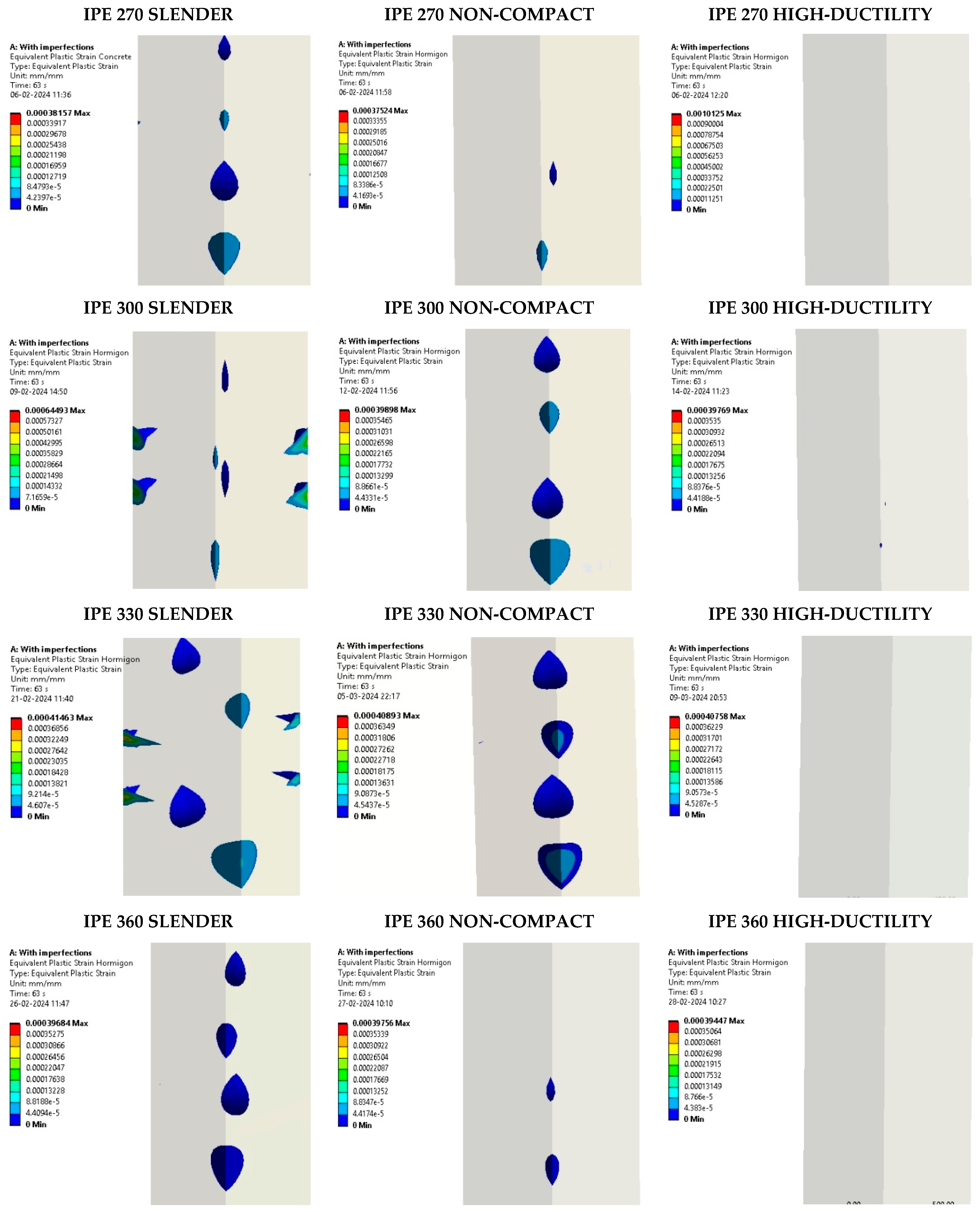
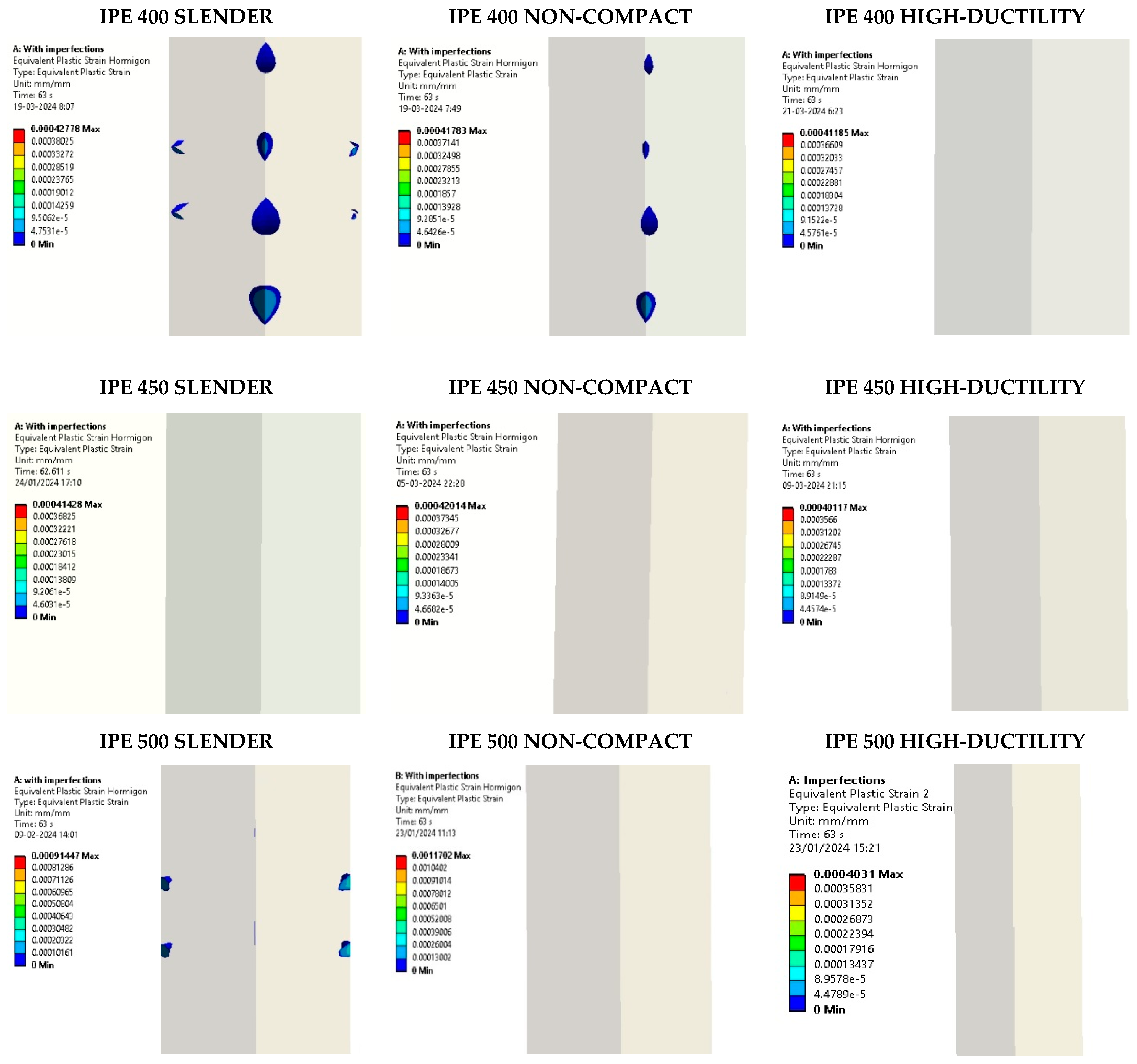
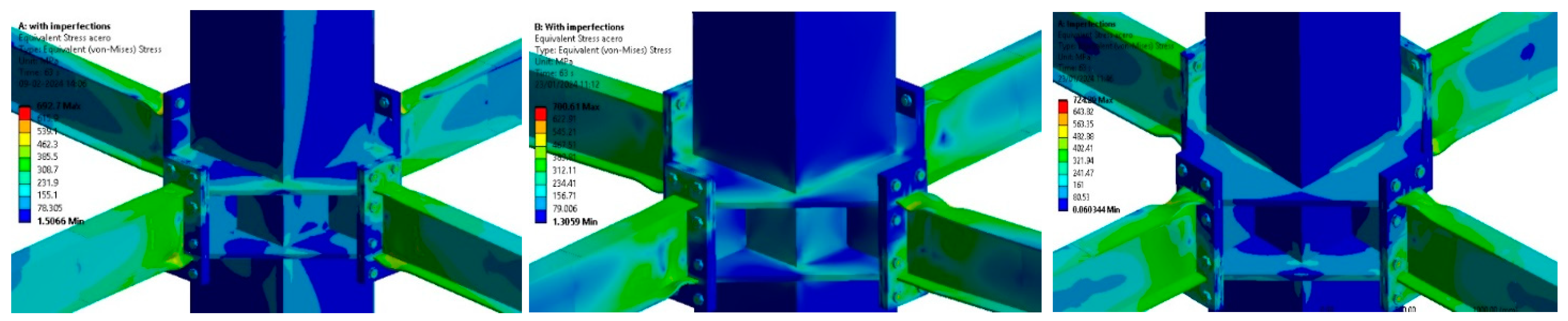
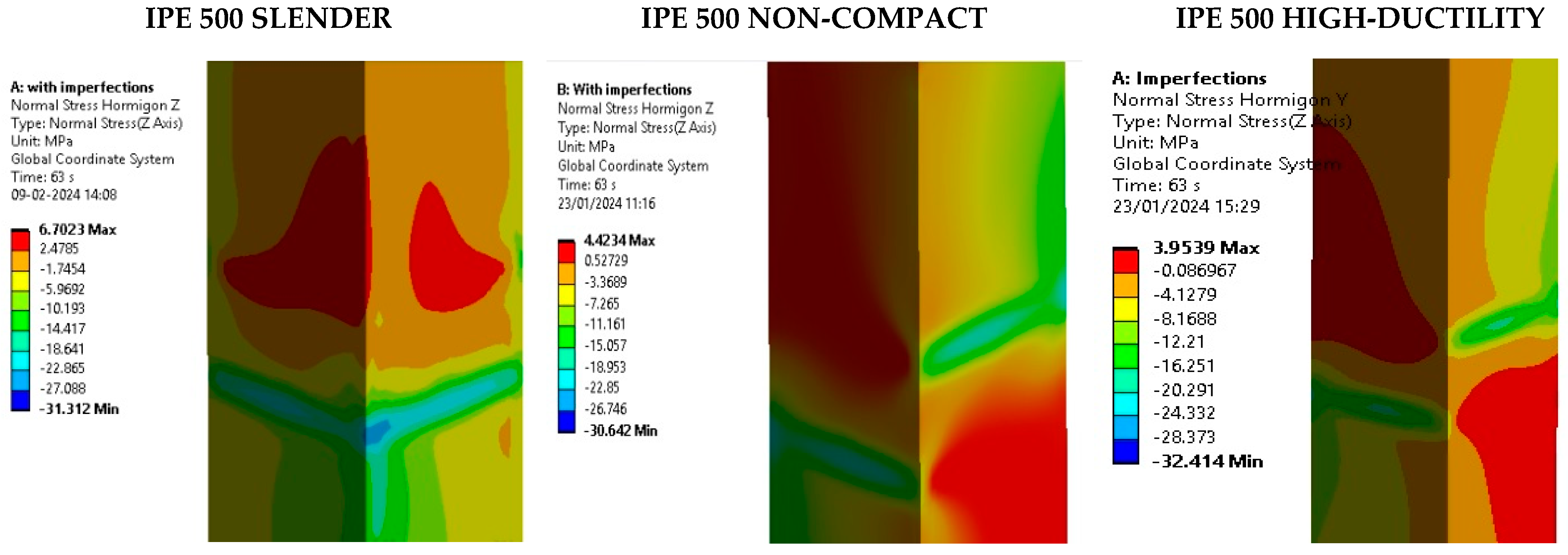
5.3. Assessment of Concrete Core Damage
5.4. Rupture Index Assessment
6. Conclusions
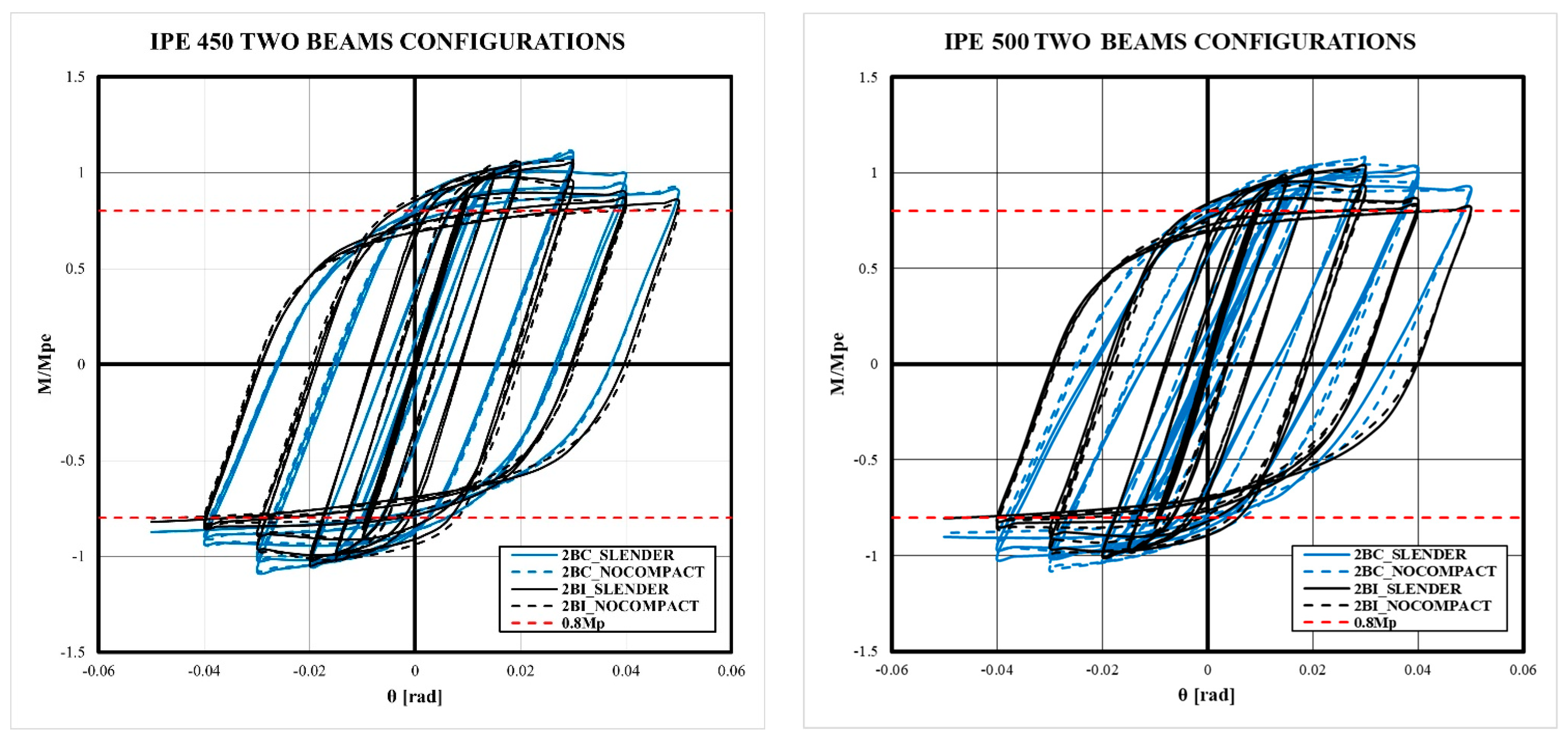
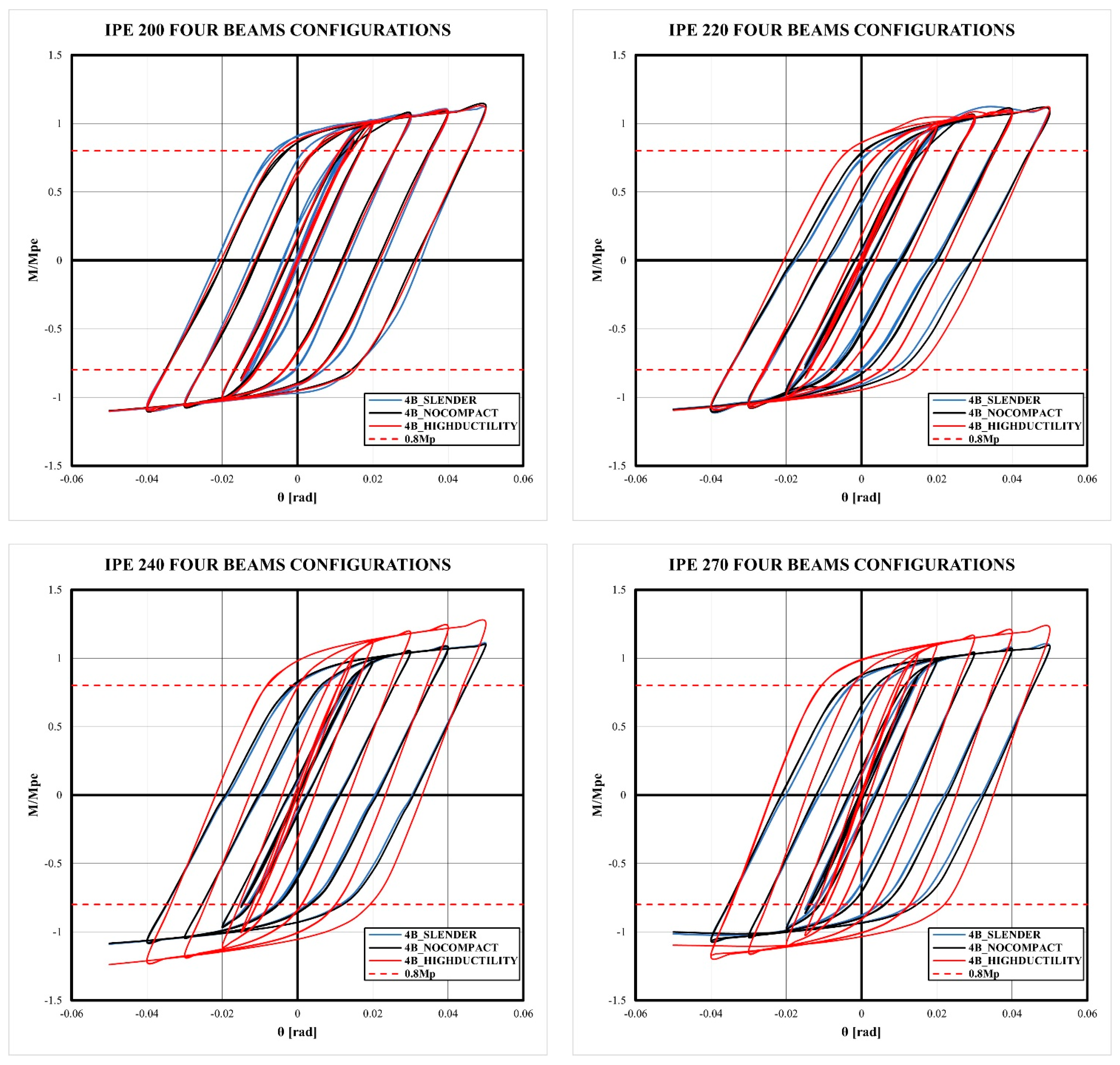
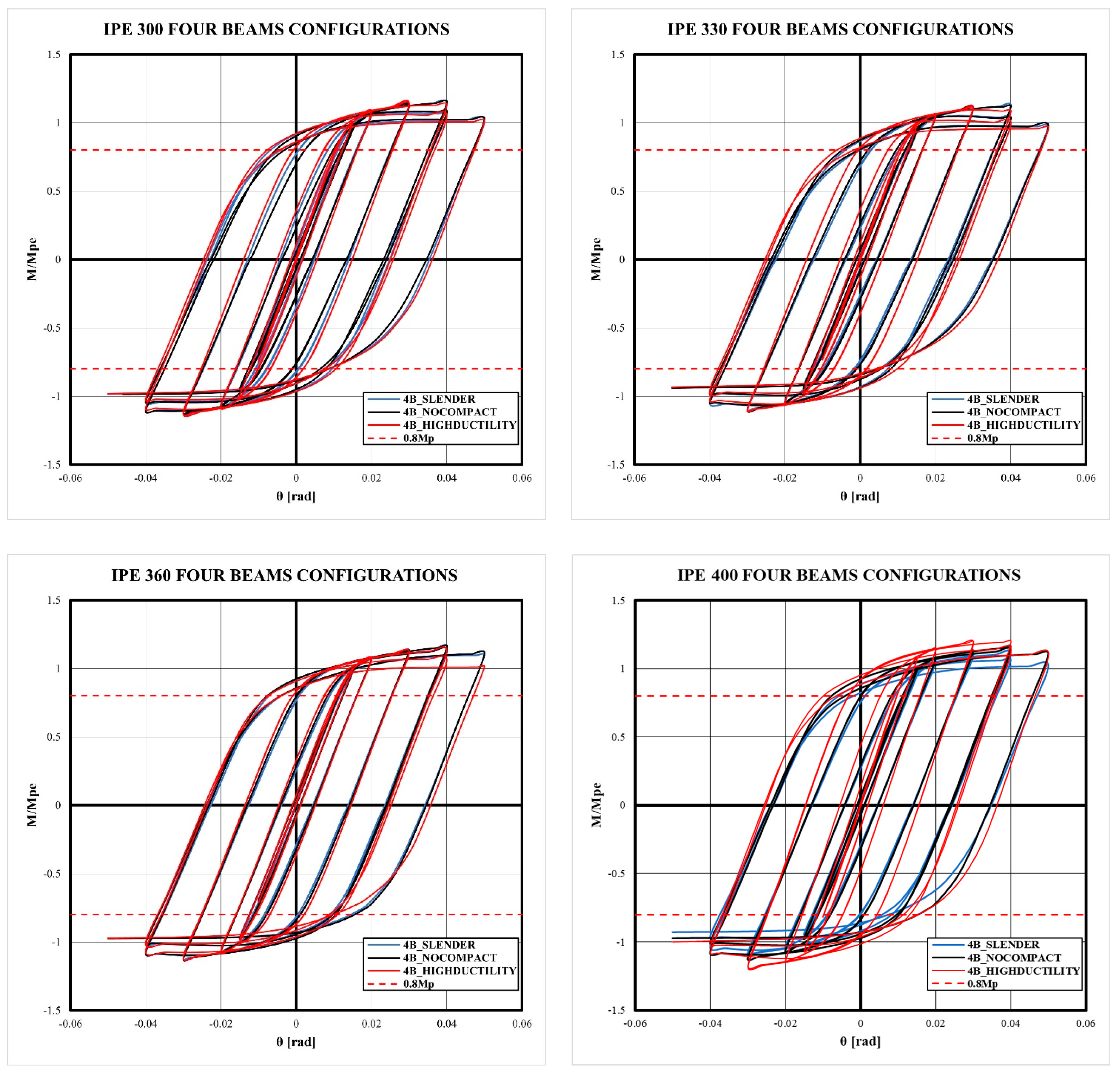
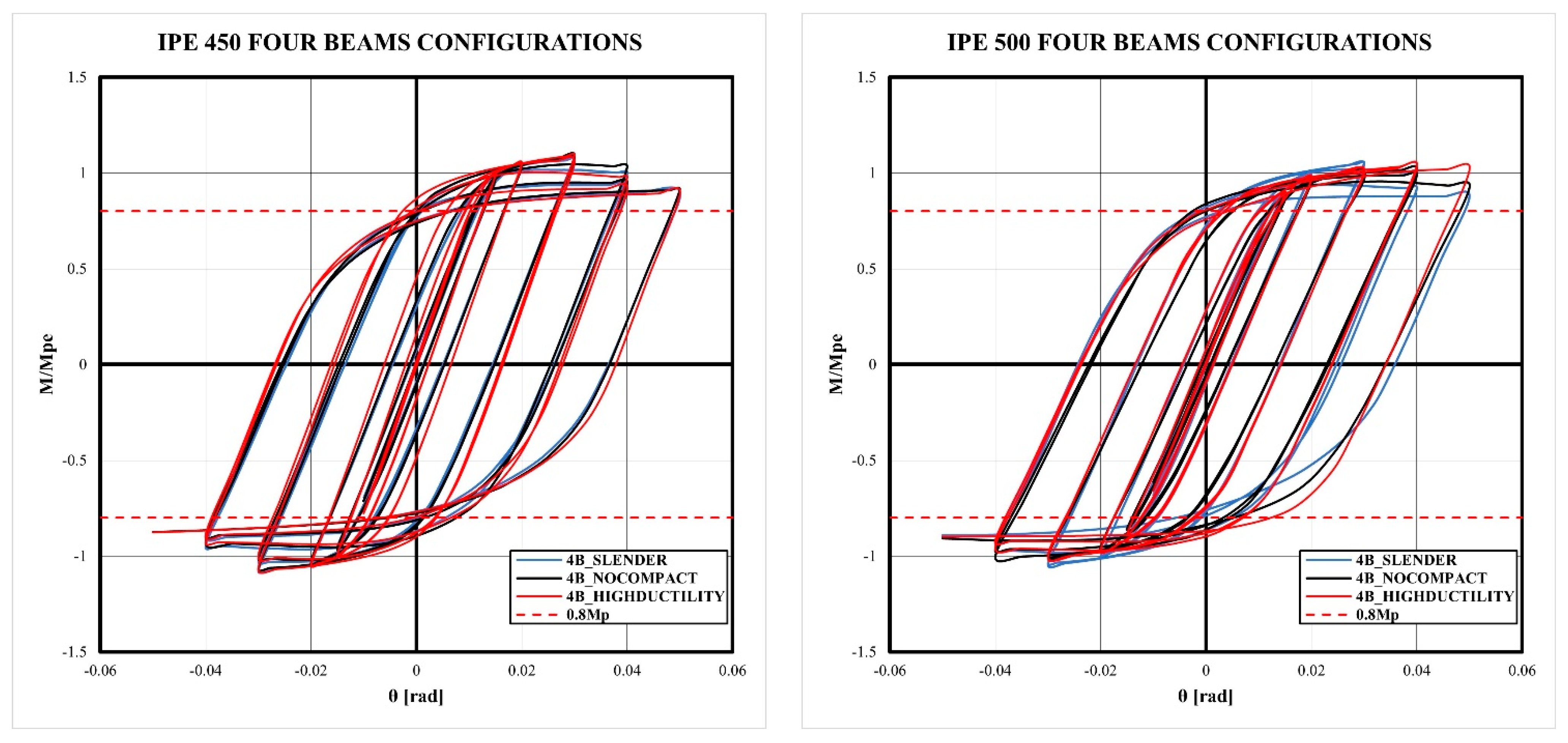
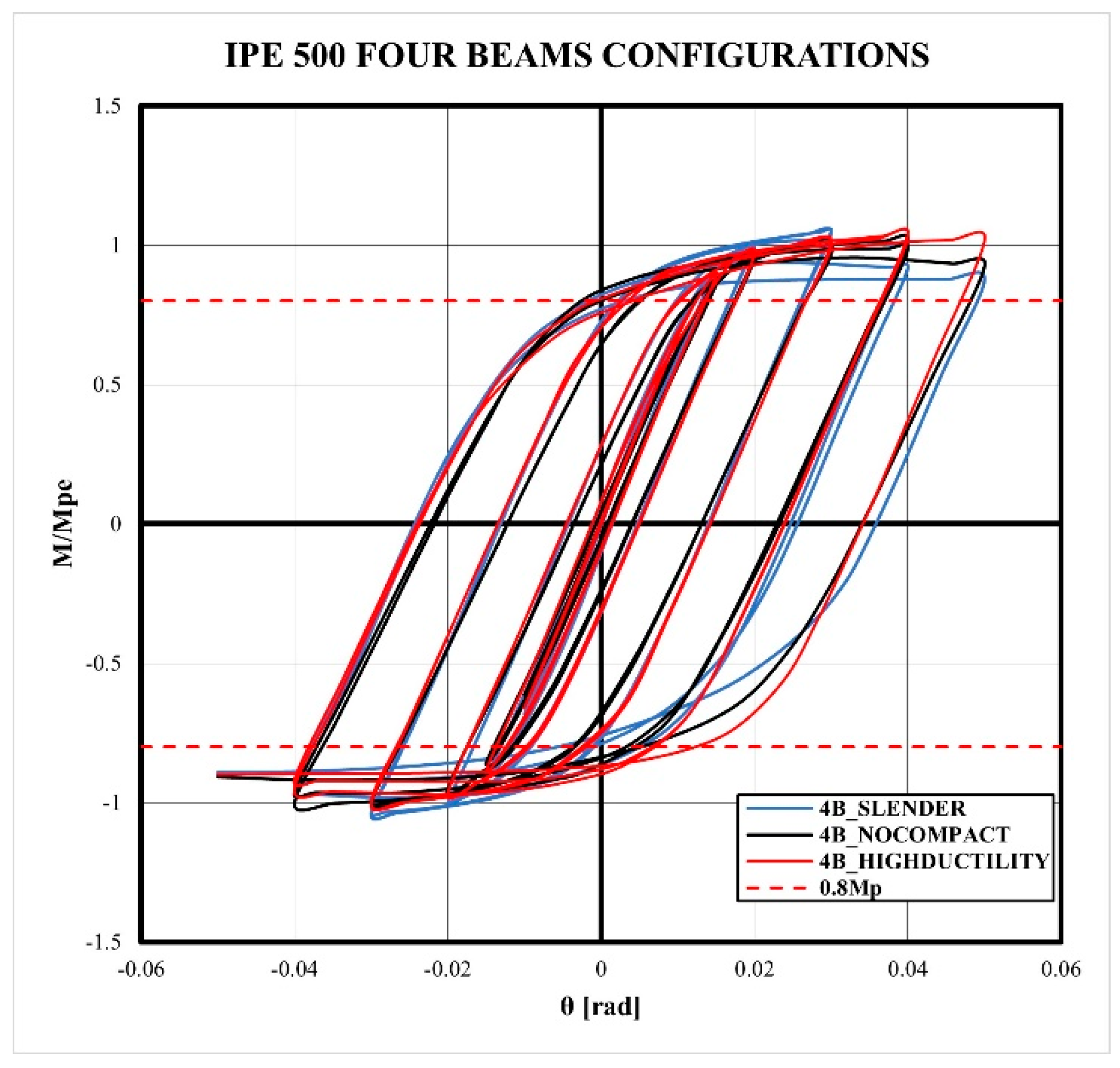
- The models exhibited a stable cyclic behavior until 0.03 rad of drift, without the loss of strength and stiffness. After this limit, the strength decreased a 10% of the maximum strength for 0.04 rad of drift and 20% for 0.05 rad of drift. However, the flexural strength of 0.8 Mp was reached for 4% of the drift ratio according to the Seismic Provisions.
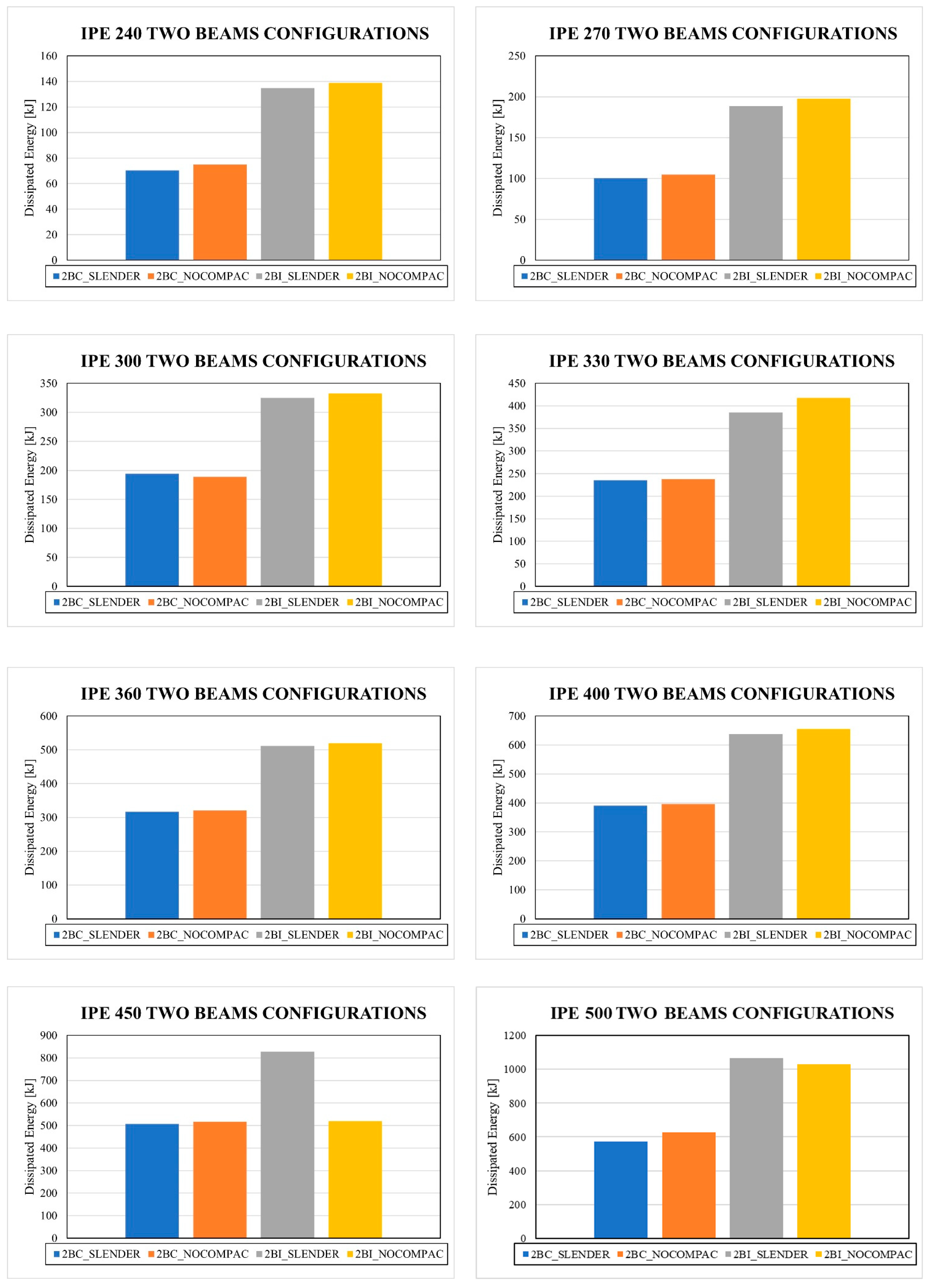
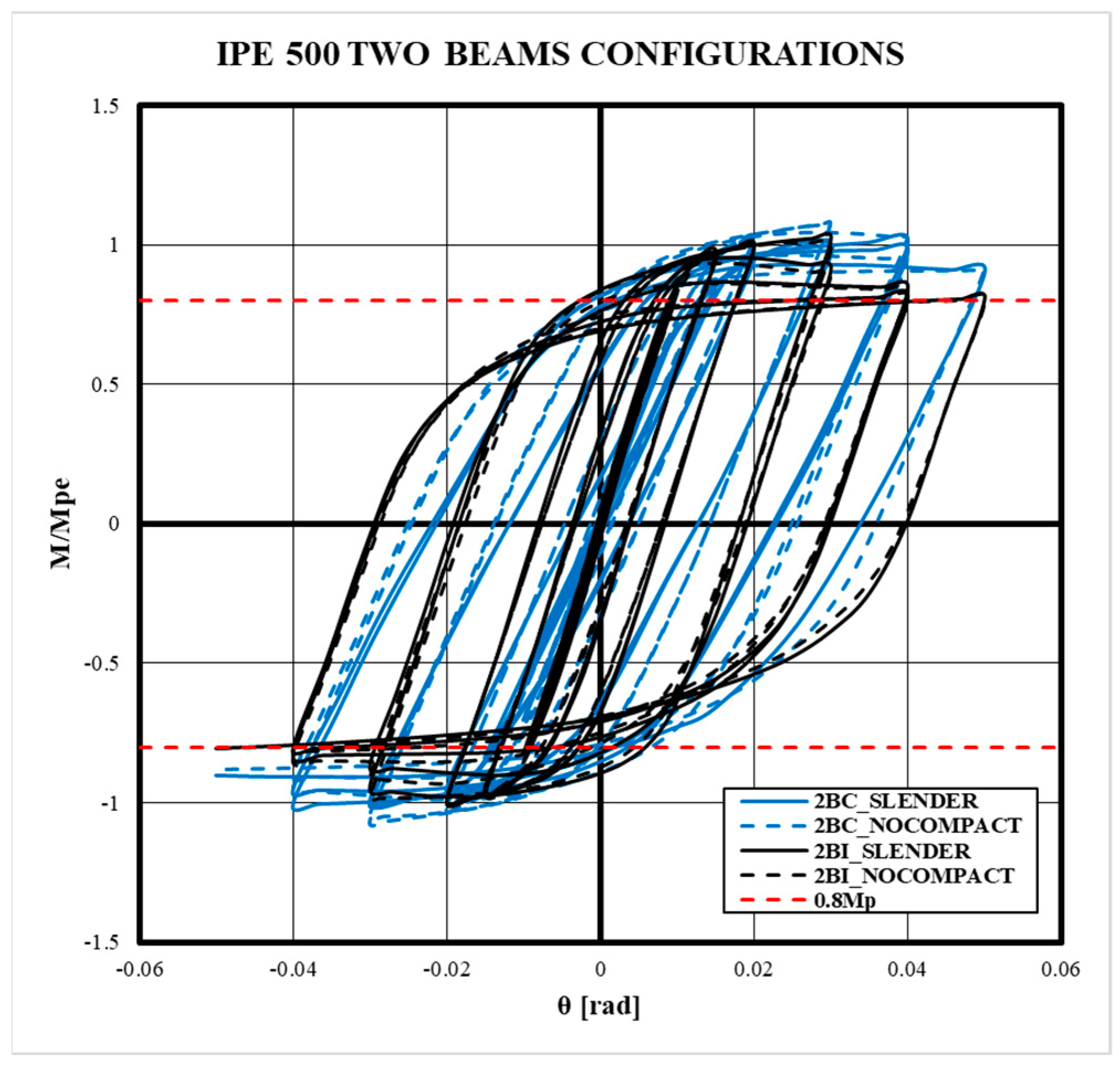
- Although the bidirectional effect reduces the stiffness and the strength of moment connections with CFT columns, this phenomenon makes it possible to maintain the stability of the hysteretic behavior of the connection, reducing pinching in comparison to the 2BI models. Therefore, 2BI models may develop out-of-plane instability.
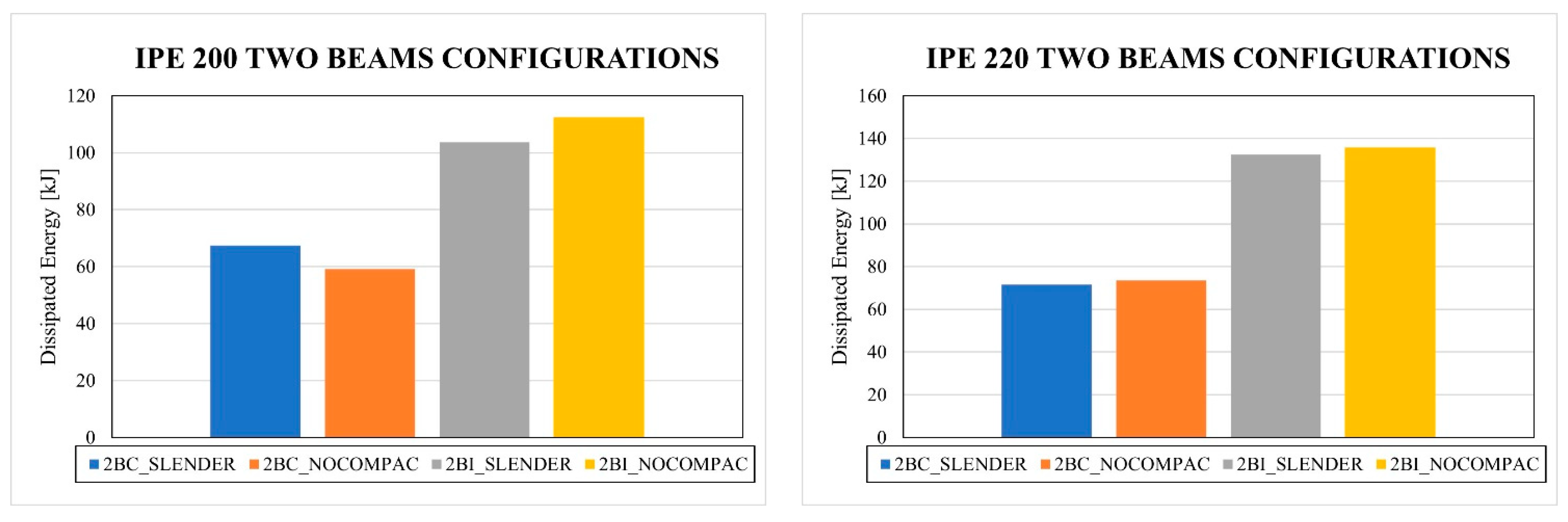
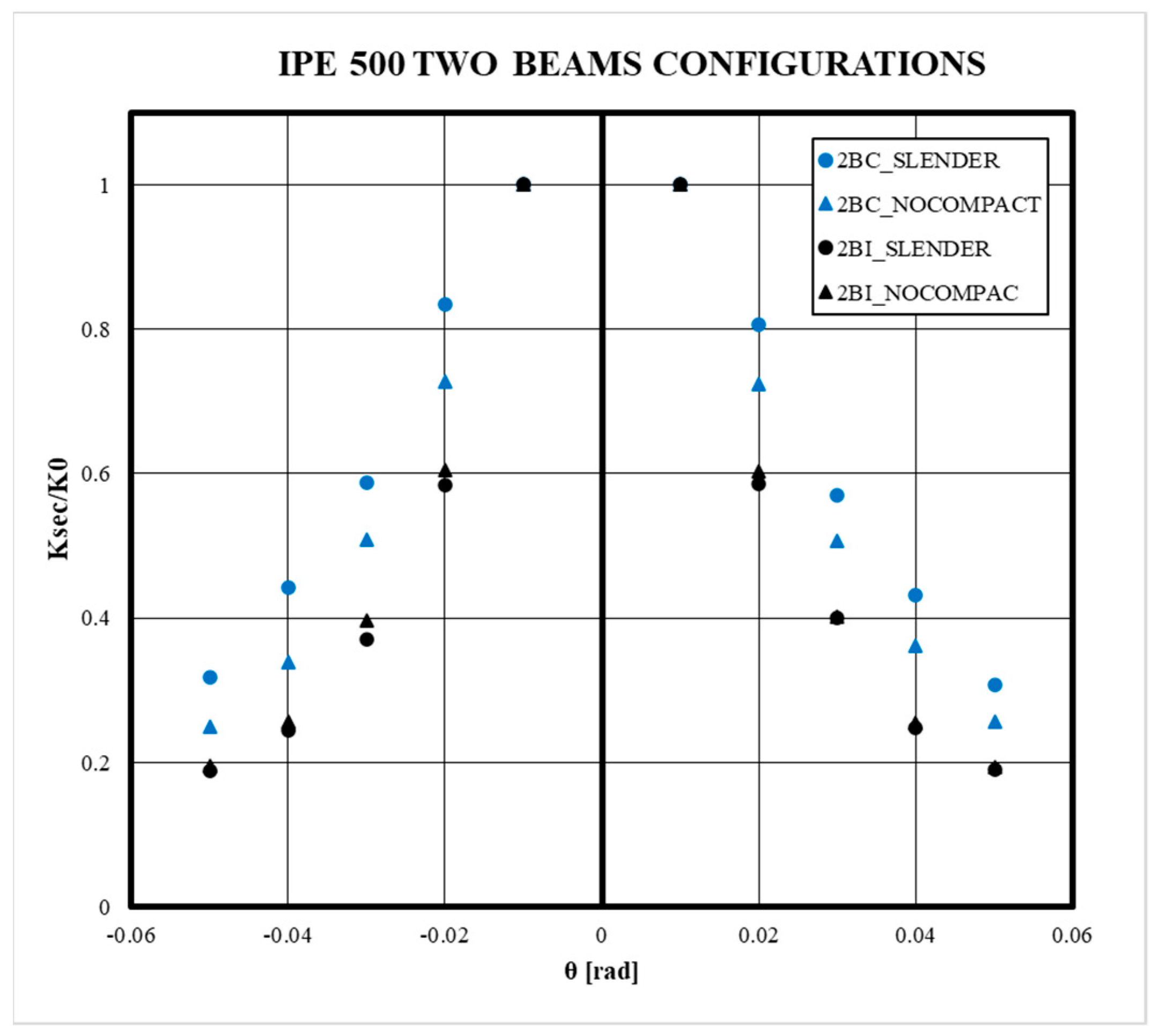
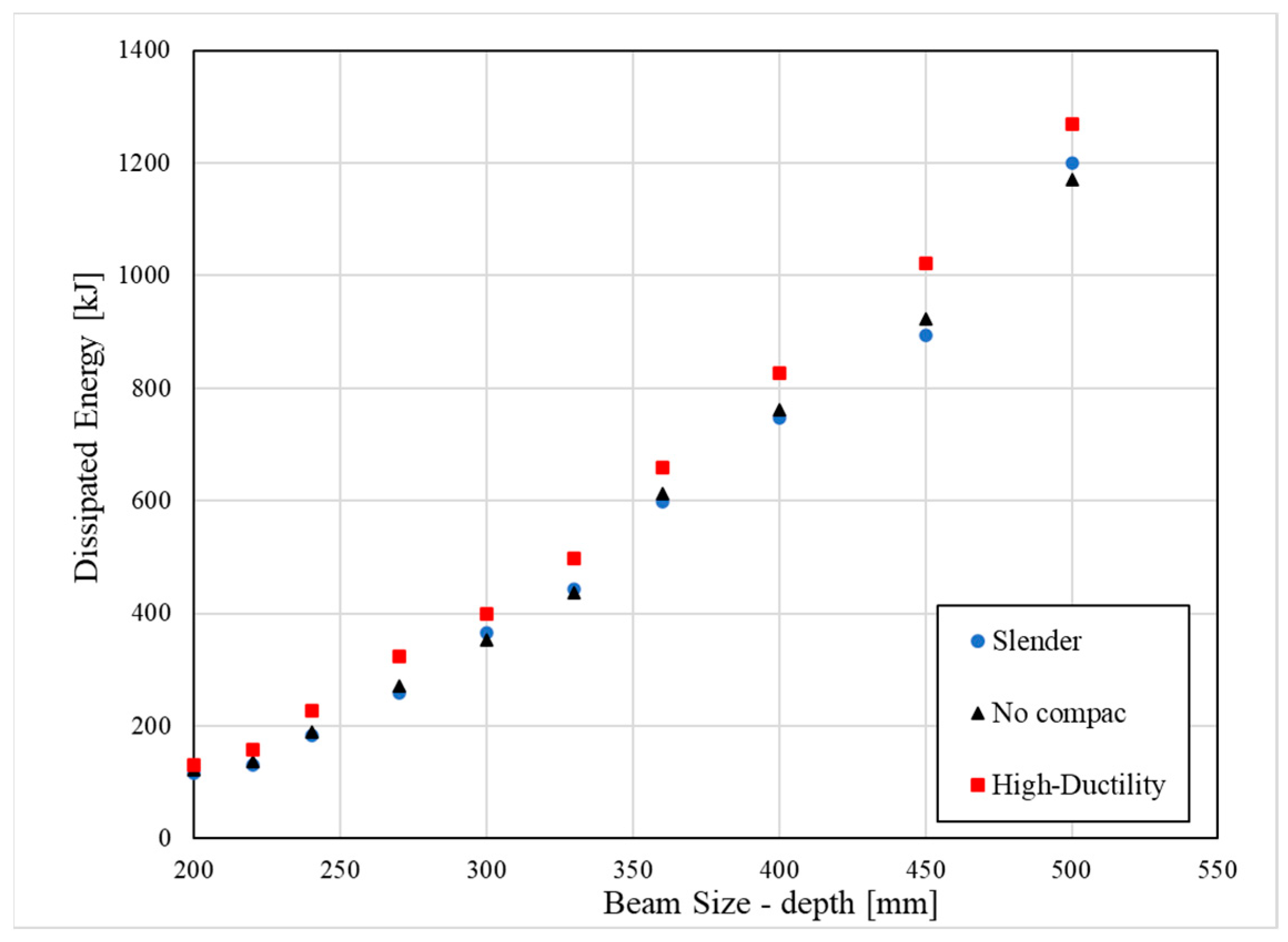
- The slenderness column effect slightly reduces the strength and the dissipated energy of the connection in comparison to columns with a high-ductility ratio. However, the prequalification limitations according to Chapter K-Seismic Provisions are satisfied.
- The concrete damages achieved a fracture in concrete for cyclic loads higher than 3% of the drift. This effect was obtained for all models studied. Furthermore, the maximum compression strength was not reached; therefore, the main use of concrete is to avoid deformation by local buckling.
7. Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A









References
- Okazaki, T.; Lignos, D.G.; Midorikawa, M.; Ricles, J.M.; Love, J. Damage to steel buildings observed after the 2011 Tohoku-oki earthquake. Earthq. Spectra 2013, 29 (Suppl. 1), 219–243. [Google Scholar] [CrossRef]
- Midorikawa, M.; Okazaki, T. Earthquake and tsunami damage to steel structures. In Proceedings of the 2012 Structures Congress, Tokyo, Japan, 1–4 March 2012. [Google Scholar] [CrossRef]
- Nishiyama, I.; Yamanouchi, H.; Aoyama, H. U.S.-Japan cooperative earthquake engineering research on composite and hybrid structures. AIJ J. Technol. Des. 1999, 5, 107–110. [Google Scholar] [CrossRef] [PubMed]
- Longo, A.; Montuori, R.; Nastri, E.; Piluso, V. On the use of HSS in seismic-resistant structures. J. Constr. Steel Res. 2014, 103, 1–12. [Google Scholar] [CrossRef]
- Horikawa, K.; Sakino, Y. Damages to steel structures caused by the 1995 Kobe earthquake. Struct. Eng. Int. J. Int. Assoc. Bridge Struct. Eng. (IABSE) 1996, 6, 181–182. [Google Scholar] [CrossRef]
- Xiao, Y.; He, W.; Choi, K. Confined Concrete-Filled Tubular Columns. J. Struct. Eng. 2005, 131, 488–497. [Google Scholar] [CrossRef]
- Mao, X.Y.; Xiao, Y. Seismic behavior of confined square CFT columns. Eng. Struct. 2006, 28, 1378–1386. [Google Scholar] [CrossRef]
- Goto, Y.; Kumar, G.P.; Kawanishi, N. Nonlinear Finite-Element Analysis for Hysteretic Behavior of Thin-Walled Circular Steel Columns with In-Filled Concrete. J. Struct. Eng. 2010, 136, 1413–1422. [Google Scholar] [CrossRef]
- Gajalakshmi, P.; Helena, H.J. Behaviour of concrete-filled steel columns subjected to lateral cyclic loading. J. Constr. Steel Res. 2012, 75, 55–63. [Google Scholar] [CrossRef]
- Aydin, F.; Saribiyik, M. Investigation of flexural behaviors of hybrid beams formed with GFRP box section and concrete. Constr. Build. Mater. 2013, 41, 563–569. [Google Scholar] [CrossRef]
- Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Parameter identification of three hysteretic models for the simulation of the response of CFT columns to cyclic loading. Eng. Struct. 2014, 61, 44–60. [Google Scholar] [CrossRef]
- Skalomenos, K.A.; Hayashi, K.; Nishi, R.; Inamasu, H.; Nakashima, M. Experimental Behavior of Concrete-Filled Steel Tube Columns Using Ultrahigh-Strength Steel. J. Struct. Eng. 2016, 142, 04016057. [Google Scholar] [CrossRef]
- Wang, Y.T.; Cai, J.; Long, Y.L. Hysteretic behavior of square CFT columns with binding bars. J. Constr. Steel Res. 2017, 131, 162–175. [Google Scholar] [CrossRef]
- ANSI/AISC 341-22; Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2022.
- Araújo, M.; Macedo, L.; Castro, J.M. Evaluation of the rotation capacity limits of steel members defined in EC8-3. J. Constr. Steel Res. 2017, 135, 11–29. [Google Scholar] [CrossRef]
- Ning, K.Y.; Yang, L.; Ban, H.Y.; Sun, Y.N. Experimental and numerical studies on hysteretic behaviour of stainless steel welded box-section columns. Thin-Walled Struct. 2019, 136, 280–291. [Google Scholar] [CrossRef]
- Chou, C.C.; Wu, S.C. Cyclic lateral load test and finite element analysis of high-strength concrete-filled steel box columns under high axial compression. Eng. Struct. 2019, 189, 89–99. [Google Scholar] [CrossRef]
- ANSI/AISC 358-22; Prequalified Connections for Special and Intermediate Steel Moment Frames for. American Institute of Steel Construction: Chicago, IL, USA, 2022.
- Simmons, R.J. Quick-Set, Full-Moment-Lock, Column and Beam Building Frame System and Method. US8453414B2, 4 June 2013. [Google Scholar]
- Bock, C.; Bong, W. Moment Resisting Connection Apparatus and Method. 20020124520A1, 12 September 2002. [Google Scholar]
- Kang, C.H.; Shin, K.J.; Oh, Y.S.; Moon, T.S. Hysteresis behavior of CFT column to H-beam connections with external T-stiffeners and penetrated elements. Eng. Struct. 2001, 23, 1194–1201. [Google Scholar] [CrossRef]
- Varma, A.H.; Ricles, J.M.; Sause, R.; Lu, L.W. Seismic behavior and modeling of high-strength composite concrete-filled steel tube (CFT) beam-columns. J. Constr. Steel Res. 2002, 58, 725–758. [Google Scholar] [CrossRef]
- Tizani, W.; Wang, Z.Y.; Hajirasouliha, I. Hysteretic performance of a new blind bolted connection to concrete filled columns under cyclic loading: An experimental investigation. Eng. Struct. 2013, 46, 535–546. [Google Scholar] [CrossRef]
- Sheet, I.S.; Gunasekaran, U.; MacRae, G.A. Experimental investigation of CFT column to steel beam connections under cyclic loading. J. Constr. Steel Res. 2013, 86, 167–182. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, Z.; Wang, X. Experimental investigation of new internal-diaphragm connections to CFT columns under cyclic loading. J. Constr. Steel Res. 2014, 98, 35–44. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, Z.; Bai, J.; Li, Z. Test of extended thick-walled through-diaphragm connection to thick-walled CFT column. Steel Compos. Struct. 2016, 20, 1–12. [Google Scholar] [CrossRef]
- Vulcu, C.; Stratan, A.; Ciutina, A.; Dubina, D. Beam-to-CFT High-Strength Joints with External Diaphragm. I: Design and Experimental Validation. J. Struct. Eng. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Azar, A.S.; Shaghaghi, T.M. Seismic behavior of conxl connections in concrete filled steel Tube Columns (CFT). J. Fundam. Appl. Sci. 2017, 9, 217. [Google Scholar] [CrossRef]
- Koloo, F.A.; Badakhshan, A.; Fallahnejad, H.; Jamkhaneh, M.E.; Ahmadi, M. Investigation of Proposed Concrete Filled Steel Tube Connections under Reversed Cyclic Loading. Int. J. Steel Struct. 2018, 18, 163–177. [Google Scholar] [CrossRef]
- Rezaifar, O.; Younesi, A. Experimental study discussion of the seismic behavior on new types of internal/external stiffeners in rigid beam-to-CFST/HSS column connections. Constr. Build. Mater. 2017, 136, 574–589. [Google Scholar] [CrossRef]
- Lai, Z.; Fischer, E.C.; Varma, A.H. Database and Review of Beam-to-Column Connections for Seismic Design of Composite Special Moment Frames. J. Struct. Eng. 2019, 145, 04019023. [Google Scholar] [CrossRef]
- Fanaie, N.; Moghadam, H.S. Experimental study of rigid connection of drilled beam to CFT column with external stiffeners. J. Constr. Steel Res. 2019, 153, 209–221. [Google Scholar] [CrossRef]
- Parvari, A.; Zahrai, S.M.; Mirhosseini, S.M.; Zeighami, E. Numerical and experimental study on the behavior of drilled flange steel beam to CFT column connections. Structures 2020, 28, 726–740. [Google Scholar] [CrossRef]
- Ahmadi, M.M.; Mirghaderi, S.R. Experimental studies on through-plate moment connection for beam to HSS/CFT column. J. Constr. Steel Res. 2019, 161, 154–170. [Google Scholar] [CrossRef]
- Parvari, A.; Zahrai, S.M.; Mirhosseini, S.M.; Zeighami, E. Comparing cyclic behaviour of RBS, DFC and proposed rigid connections in a steel moment frame with CFT column. Aust. J. Civ. Eng. 2021, 19, 164–183. [Google Scholar] [CrossRef]
- Jeddi, M.Z.; Sulong, N.H.R.; Ghanbari-Ghazijahani, T. Behaviour of double-sleeve TubeBolt moment connections in CFT columns under cyclic loading. J. Constr. Steel Res. 2022, 194, 107302. [Google Scholar] [CrossRef]
- Paul, S.; Deb, S.K. Experimental study on a new V-cut RBS and CFT connections with bidirectional bolts under cyclic loadings. J. Build. Eng. 2022, 46, 103688. [Google Scholar] [CrossRef]
- Du, H.; Zhao, P.; Wang, Y.; Sun, W. Seismic experimental assessment of beam-through beam-column connections for modular prefabricated steel moment frames. J. Constr. Steel Res. 2022, 192, 107208. [Google Scholar] [CrossRef]
- Habibi, A.; Fanaie, N.; Shahbazpanahi, S. Experimental and numerical investigation of I-beam to concrete-filled tube (CFT) column moment connections with pipe-stiffened internal diaphragm. J. Constr. Steel Res. 2023, 200, 107648. [Google Scholar] [CrossRef]
- Razavi, S.A.; Kandi, A.H.; Alimardani, M.; Jovaini, E. Tube-in-tube rigid beam to CFT column connection in moment-resisting frames: An experimental study. Soil Dyn. Earthq. Eng. 2023, 171, 107901. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, S.; Mou, B.; Wang, Y.; Skalomenos, K.A. Bi-directional seismic behavior of steel beam-column connections with outer annular stiffener. Eng. Struct. 2021, 227, 111443. [Google Scholar] [CrossRef]
- Gallegos, M.; Nuñez, E.; Herrera, R. Numerical study on cyclic response of end-plate biaxial moment connection in box columns. Metals 2020, 10, 523. [Google Scholar] [CrossRef]
- Mata, R.; Nuñez, E. Parametric study of 3D steel moment connections with built-up box column subjected to biaxial cyclic loads. J. Constr. Steel Res. 2022, 197, 107453. [Google Scholar] [CrossRef]
- Nuñez, E.; Torres, R.; Herrera, R. Seismic performance of moment connections in steel moment frames with HSS columns. Steel Compos. Struct. 2017, 25, 271–286. [Google Scholar] [CrossRef]
- Mata, R.; Nuñez, E.; Sanhueza, F.; Maureira, N.; Roco, Á. Assessment of Web Panel Zone in Built-up Box Columns Subjected to Bidirectional Cyclic Loads. Buildings 2023, 13, 71. [Google Scholar] [CrossRef]
- Nuñez-Castellanos, E.; Bustos-Figueroa, J.; Mata-Lemus, R.; Sanhueza-Espinoza, F.; Lapeña-Mañero, P. Cyclic behavior of 3D moment connections subjected to bidirectional load: Experimental approach. Eng. Struct. 2023, 291, 116392. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS v2022; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- ANSI/AISC 360-22; Specification for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2022.
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19); American Concrete Institute: Indianapolis, IN, USA, 2019. [Google Scholar]
- Nuñez, E.; Mata, R. Strong column-weak beam relationship of 3D steel joints with tubular columns: Assessment, Validation and Design proposal. J. Build. Eng. 2024, 82, 108399. [Google Scholar] [CrossRef]
- Gerbens-Leenes, P.W.; Hoekstra, A.Y.; Bosman, R. The blue and grey water footprint of construction materials: Steel, cement and glass. Water Resour. Ind. 2018, 19, 1–12. [Google Scholar] [CrossRef]
- Vilela, P.M.L.; Carvalho, H.; Grilo, L.F.; Montenegro, P.A.; Calçada, R.B. Unitary model for the analysis of bolted connections using the finite element method. Eng. Fail Anal. 2019, 104, 308–320. [Google Scholar] [CrossRef]
- Zreid, I.; Kaliske, M. A gradient enhanced plasticity–damage microplane model for concrete. Comput. Mech. 2018, 62, 1239–1257. [Google Scholar] [CrossRef]
- Jiang, J.F.; Wu, Y.F. Identification of material parameters for Drucker-Prager plasticity model for FRP confined circular concrete columns. Int. J. Solids Struct. 2012, 49, 445–456. [Google Scholar] [CrossRef]
- Kedziora, S.; Anwaar, M.O. Concrete-filled steel tubular (CFTS) columns subjected to eccentric compressive load. AIP Conf. Proc. 2019, 2060, 020004. [Google Scholar] [CrossRef]
- Bayraktar, A.; Şahin, A.; Özcan, D.M.; Yildirim, F. Numerical damage assessment of Haghia Sophia bell tower by nonlinear FE modeling. Appl. Math. Model. 2010, 34, 92–121. [Google Scholar] [CrossRef]
- Avci, O.; Bhargava, A. Finite-Element Analysis of Cantilever Slab Deflections with ANSYS SOLID65 3D Reinforced-Concrete Element with Cracking and Crushing Capabilities. Pract. Period. Struct. Des. Constr. 2019, 24, 05018007. [Google Scholar] [CrossRef]
- Schneider, S.P. Axially Loaded Concrete-Filled Steel Tubes. J. Struct. Eng. 1998, 124, 1125–1138. [Google Scholar] [CrossRef]
- Gupta, P.K.; Khaudhair, Z.; Ahuja, A.K. 3D numerical simulation of concrete filled steel tubular columns using ANSYS. In UKIERI Concrete Congress—Innovation in Concrete Construction; Jalandhar, India; 2013; pp. 2262–2271. Available online: https://www.researchgate.net/publication/317380097_3D_NUMERICAL_SIMULATION_OF_CONCRETE_FILLED_STEEL_TUBULAR_COLUMNS_USING_ANSYS (accessed on 25 February 2024).
- Tartaglia, R.; D’Aniello, M.; Rassati, G.A.; Swanson, J.A.; Landolfo, R. Full strength extended stiffened end-plate joints: AISC vs recent European design criteria. Eng. Struct. 2018, 159, 155–171. [Google Scholar] [CrossRef]
- ASTM Committee. Standard Specification for General Requirements for Rolled Structural Steel Bars, Plates, Shapes, and Sheet Piling; American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2001. [Google Scholar]
- A1085/A1085M−15; Standard Specification for Cold-Formed Welded Carbon Steel Hollow Structural Sections (HSS). American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2015.
- Behrooz, S.M.; Erfani, S. Parametric study of Stub-Beam Bolted Extended End-Plate connection to box-columns. J. Constr. Steel Res. 2020, 171, 106155. [Google Scholar] [CrossRef]
- Goudarzi, A.; Erfani, S. Seismic performance of beam to box-column connection by a short stub beam. J. Constr. Steel Res. 2022, 190, 107145. [Google Scholar] [CrossRef]
- Wei, J.P.; Tian, L.M.; Guo, Y.; Qiao, H.Y.; Bao, Y.; Jiao, Z.A.; Shi, X.J. Numerical study of the seismic performance of a double-hinge steel frame joint. J. Constr. Steel Res. 2021, 187, 106963. [Google Scholar] [CrossRef]
- Zhang, A.L.; Qiu, P.; Guo, K.; Jiang, Z.Q.; Wu, L.; Liu, S.C. Experimental study of earthquake-resilient end-plate type prefabricated steel frame beam-column joint. J. Constr. Steel Res. 2020, 166, 105927. [Google Scholar] [CrossRef]
- Torres-Rodas, P.; Medalla, M.; Zareian, F.; Lopez-Garcia, D. Cyclic behavior and design methodology of exposed base plates with extended anchor bolts. Eng. Struct. 2022, 260, 114235. [Google Scholar] [CrossRef]
- Trautner, C.A.; Hutchinson, T.; Grosser, P.R.; Silva, J.F. Effects of Detailing on the Cyclic Behavior of Steel Baseplate Connections Designed to Promote Anchor Yielding. J. Struct. Eng. 2016, 142, 04015117. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamic of Structures; Pearsons: London, UK, 2012. [Google Scholar]
- Wu, L.Y.; Chung, L.L.; Tsai, S.F.; Lu, C.F.; Huang, G.L. Seismic behavior of bidirectional bolted connections for CFT columns and H-beams. Eng. Struct. 2007, 29, 395–407. [Google Scholar] [CrossRef]
- Li, X.; Xiao, Y.; Wu, Y.T. Seismic behavior of exterior connections with steel beams bolted to CFT columns. J. Constr. Steel Res. 2009, 65, 1438–1446. [Google Scholar] [CrossRef]
- Rahnavard, R.; Hassanipour, A.; Siahpolo, N. Analytical study on new types of reduced beam section moment connections affecting cyclic behavior. Case Stud. Struct. Eng. 2015, 3, 33–51. [Google Scholar] [CrossRef]








| Beam | Column | Span between Columns (m) | Bolt Diameter (in) | End Plate Thickness (mm) | Horizontal Stiffener Thickness (mm) | Vertical Stiffener Thickness Vertical (mm) | Ratio WPZS (Panel Zone) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Section | Steel | Section Slender | Section Non-Compact | Section High-Ductility | Steel | ||||||
| IPE-200 | A-36 | 425 × 425 × 4 | 425 × 425 × 6 | 425 × 425 × 14 | A-36 | 2.4 | 3/4″ | 20 | 16 | 6 | 0.93 |
| IPE-220 | A-36 | 450 × 450 × 5 | 450 × 450 × 6 | 450 × 450 × 14 | A-36 | 2.64 | 7/8″ | 22 | 16 | 8 | 0.90 |
| IPE-240 | A-36 | 500 × 500 × 5 | 500 × 500 × 6 | 500 × 500 × 16 | A-36 | 2.88 | 7/8″ | 25 | 18 | 8 | 0.89 |
| IPE-270 | A-36 | 525 × 525 × 6 | 525 × 525 × 8 | 525 × 525 × 16 | A-36 | 3.24 | 1″ | 25 | 20 | 8 | 0.88 |
| IPE-300 | A-36 | 575 × 575 × 6 | 575 × 575 × 8 | 575 × 575 × 18 | A-36 | 3.6 | 1″ | 28 | 22 | 8 | 0.87 |
| IPE-330 | A-36 | 625 × 625 × 6 | 625 × 625 × 8 | 625 × 625 × 18 | A-36 | 3.96 | 1 1/8″ | 28 | 25 | 8 | 0.87 |
| IPE-360 | A-36 | 700 × 700 × 8 | 700 × 700 × 10 | 700 × 700 × 22 | A-36 | 4.32 | 1 1/4″ | 38 | 28 | 10 | 0.74 |
| IPE-400 | A-36 | 750 × 750 × 8 | 750 × 750 × 10 | 750 × 750 × 22 | A-36 | 4.8 | 1 1/4″ | 38 | 30 | 10 | 0.75 |
| IPE-450 | A-36 | 825 × 825 × 8 | 825 × 825 × 10 | 825 × 825 × 25 | A-36 | 5.4 | 1 3/8″ | 40 | 38 | 10 | 0.72 |
| IPE-500 | A-36 | 875 × 875 × 10 | 875 × 875 × 12 | 875 × 875 × 28 | A-36 | 6 | 1 1/2″ | 50 | 38 | 10 | 0.68 |
| Beam/Configuration | Column Slender CFT | Column Non-Compact CFT | Column High-Ductility CFT | |||||
|---|---|---|---|---|---|---|---|---|
| 2BC | 2BI | 4B | 2BC | 2BI | 4B | 4B | Total | |
| IPE-200 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-220 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-240 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-270 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-300 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-330 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-360 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-400 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-450 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| IPE-500 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
| Total | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 70 |
| Material | Fy (MPa) | εy (mm/mm) | Fu (MPa) | εu (mm/mm) |
|---|---|---|---|---|
| ASTM A36 | 320.33 | 0.0014017 | 441.67 | 0.1036 |
| ASTM A-325 | 627.45 | 0.00393 | 934.32 | 0.1601 |
| N° | Interaction Contact Zone | Type of Contact |
|---|---|---|
| 1 | End Plate–End Plate | Frictional μ = 0.3 |
| 2 | Bolt shank–End Plate | Frictional μ = 0.3 |
| 3 | Bolt shank–Bolt head | Bonded |
| 4 | Bolt head–End Plate | Frictional μ = 0.3 |
| 5 | Bolt shank–Nut | Bonded |
| 6 | Nut–End Plate | Frictional μ = 0.3 |
| 7 | End Plate–Horizontal Diaphragm | Bonded |
| 8 | End Plate–Vertical Stiffener | Bonded |
| 9 | Horizontal Diaphragm–Vertical Stiffener | Bonded |
| 10 | Horizontal Diaphragm–Column | Bonded |
| 11 | End Plate–Beam | Bonded |
| 12 | Beam–Beam | Bonded |
| 13 | Column Plates–Column Plates | Bonded |
| 14 | Column Plates–Concrete Core | Frictional μ = 0.6 |
| Beam Size | Joint Configuration | Slenderness Ratio | Max Lateral Load (kN) | M0.04/Mp | M Max/Mp | θmax (rad) | Initial Stiffness West Beam (kN·m/rad) | Dissipated Energy (kJ) |
|---|---|---|---|---|---|---|---|---|
| IPE-200 | 2BC | Slender | 73,150 | 1.084 | 1.109 | 0.050 | 6,489,480 | 67,406 |
| Non-compact | 82,059 | 1.109 | 1.109 | 0.050 | 8,424,600 | 59,053 | ||
| 2BI | Slender | 86,817 | 1.113 | 1.141 | 0.050 | 7,277,120 | 103,647 | |
| Non-compact | 87,396 | 1.117 | 1.143 | 0.050 | 7,980,777 | 112,484 | ||
| 4B | Slender | 127,100 | 1.086 | 1.111 | 0.050 | 6,730,320 | 131,587 | |
| Non-compact | 124,790 | 1.079 | 1.104 | 0.050 | 6,051,840 | 115,365 | ||
| High-ductility | 127,650 | 1.081 | 1.106 | 0.050 | 6,036,240 | 122,743 | ||
| IPE-220 | 2BC | Slender | 69,704 | 1.073 | 1.098 | 0.050 | 7,239,012 | 71,640 |
| Non-compact | 70,156 | 1.075 | 1.100 | 0.050 | 7,401,372 | 73,453 | ||
| 2BI | Slender | 106,770 | 1.118 | 1.133 | 0.050 | 9,213,502 | 132,523 | |
| Non-compact | 103,480 | 1.110 | 1.138 | 0.050 | 9,359,856 | 135,814 | ||
| 4B | Slender | 147,630 | 1.069 | 1.120 | 0.050 | 6,710,939 | 130,802 | |
| Non-compact | 148,110 | 1.072 | 1.096 | 0.050 | 6,943,929 | 136,508 | ||
| High-ductility | 151,270 | 1.078 | 1.102 | 0.050 | 7,785,917 | 157,828 | ||
| IPE-240 | 2BC | Slender | 82,090 | 1.076 | 1.099 | 0.050 | 9,737,136 | 70,330 |
| Non-compact | 86,549 | 1.216 | 1.216 | 0.040 | 11,312,208 | 74,899 | ||
| 2BI | Slender | 120,400 | 1.100 | 1.100 | 0.040 | 12,247,776 | 134,874 | |
| Non-compact | 120,540 | 1.100 | 1.100 | 0.040 | 12,377,664 | 138,819 | ||
| 4B | Slender | 172,430 | 1.072 | 1.097 | 0.050 | 9,213,840 | 183,422 | |
| Non-compact | 172,520 | 1.070 | 1.091 | 0.050 | 9,427,824 | 189,265 | ||
| High-ductility | 185,470 | 1.220 | 1.248 | 0.050 | 11,973,168 | 228,389 | ||
| IPE-270 | 2BC | Slender | 104,360 | 1.062 | 1.062 | 0.050 | 13,470,462 | 106,096 |
| Non-compact | 105,400 | 1.064 | 1.069 | 0.050 | 13,974,120 | 143,525 | ||
| 2BI | Slender | 152,120 | 1.050 | 1.055 | 0.050 | 16,856,100 | 242,183 | |
| Non-compact | 152,620 | 1.037 | 1.057 | 0.050 | 17,507,340 | 251,553 | ||
| 4B | Slender | 217,600 | 1.059 | 1.079 | 0.050 | 12,725,748 | 258,978 | |
| Non-compact | 219,180 | 1.061 | 1.077 | 0.050 | 13,335,516 | 272,294 | ||
| High-ductility | 229,920 | 1.184 | 1.204 | 0.050 | 17,126,640 | 324,394 | ||
| IPE-300 | 2BC | Slender | 132,130 | 1.122 | 1.135 | 0.050 | 19,509,660 | 194,437 |
| Non-compact | 131,730 | 1.134 | 1.134 | 0.050 | 20,172,600 | 188,772 | ||
| 2BI | Slender | 184,550 | 0.939 | 1.062 | 0.050 | 22,271,544 | 324,591 | |
| Non-compact | 183,960 | 0.947 | 1.059 | 0.050 | 22,813,200 | 332,266 | ||
| 4B | Slender | 270,040 | 1.138 | 1.138 | 0.050 | 19,376,010 | 366,289 | |
| Non-compact | 270,490 | 1.148 | 1.148 | 0.050 | 19,405,549 | 353,614 | ||
| High-ductility | 270,160 | 1.126 | 1.135 | 0.050 | 21,826,800 | 398,715 | ||
| IPE-330 | 2BC | Slender | 145,320 | 1.109 | 1.112 | 0.050 | 25,256,880 | 235,315 |
| Non-compact | 145,570 | 1.095 | 1.107 | 0.050 | 25,664,760 | 238,151 | ||
| 2BI | Slender | 206,300 | 0.907 | 1.041 | 0.050 | 28,700,100 | 385,390 | |
| Non-compact | 207,370 | 0.890 | 1.023 | 0.050 | 31,345,380 | 417,632 | ||
| 4B | Slender | 302,440 | 1.121 | 1.121 | 0.050 | 24,550,020 | 444,289 | |
| Non-compact | 303,020 | 1.117 | 1.117 | 0.050 | 24,771,780 | 436,629 | ||
| High-ductility | 305,170 | 1.081 | 1.110 | 0.050 | 27,707,460 | 497,868 | ||
| IPE-360 | 2BC | Slender | 163,260 | 1.157 | 1.157 | 0.050 | 34,097,040 | 316,829 |
| Non-compact | 163,330 | 1.141 | 1.141 | 0.050 | 34,749,360 | 320,434 | ||
| 2BI | Slender | 234,500 | 0.931 | 1.071 | 0.050 | 40,690,080 | 511,352 | |
| Non-compact | 234,540 | 0.920 | 1.072 | 0.050 | 40,992,994 | 519,173 | ||
| 4B | Slender | 343,290 | 1.157 | 1.157 | 0.050 | 31,680,720 | 598,759 | |
| Non-compact | 343,550 | 1.158 | 1.158 | 0.050 | 32,365,440 | 613,515 | ||
| High-ductility | 378,330 | 1.131 | 1.131 | 0.050 | 33,274,800 | 658,428 | ||
| IPE-400 | 2BC | Slender | 191,420 | 1.108 | 1.108 | 0.050 | 43,903,200 | 390,951 |
| Non-compact | 191,700 | 1.107 | 1.107 | 0.050 | 44,624,800 | 396,125 | ||
| 2BI | Slender | 276,380 | 0.871 | 1.040 | 0.050 | 50,081,720 | 638,187 | |
| Non-compact | 277,300 | 0.883 | 1.051 | 0.050 | 52,508,800 | 655,127 | ||
| 4B | Slender | 403,420 | 1.110 | 1.110 | 0.050 | 41,503,200 | 746,655 | |
| Non-compact | 404,010 | 1.111 | 1.111 | 0.050 | 42,305,600 | 761,987 | ||
| High-ductility | 406,390 | 1.194 | 1.194 | 0.050 | 50,238,067 | 826,726 | ||
| IPE-450 | 2BC | Slender | 227,470 | 0.979 | 1.088 | 0.050 | 56,189,700 | 507,024 |
| Non-compact | 218,660 | 0.981 | 1.088 | 0.050 | 56,891,700 | 517,100 | ||
| 2BI | Slender | 327,410 | 0.880 | 1.027 | 0.050 | 64,810,800 | 827,266 | |
| Non-compact | 319,270 | 0.850 | 1.008 | 0.050 | 68,096,100 | 519,173 | ||
| 4B | Slender | 476,000 | 0.997 | 1.083 | 0.050 | 53,592,823 | 898,216 | |
| Non-compact | 462,040 | 1.027 | 1.086 | 0.050 | 55,668,600 | 986,388 | ||
| High-ductility | 480,280 | 0.976 | 1.092 | 0.050 | 61,230,600 | 1,071,928 | ||
| IPE-500 | 2BC | Slender | 257,850 | 1.014 | 1.014 | 0.050 | 57,042,000 | 571,528 |
| Non-compact | 324,950 | 1.023 | 1.078 | 0.050 | 68,831,840 | 627,984 | ||
| 2BI | Slender | 388,800 | 0.847 | 1.040 | 0.050 | 78,791,100 | 1,066,038 | |
| Non-compact | 389,030 | 0.840 | 1.063 | 0.050 | 80,298,000 | 1,030,614 | ||
| 4B | Slender | 560,070 | 0.999 | 1.052 | 0.050 | 57,494,850 | 1,199,222 | |
| Non-compact | 551,830 | 1.019 | 1.019 | 0.050 | 60,936,000 | 1,170,716 | ||
| High-ductility | 556,670 | 1.040 | 1.040 | 0.050 | 65,319,000 | 1,269,456 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mata, R.; Nuñez, E. Cyclic Behavior of Concrete-Filled Tube Columns with Bidirectional Moment Connections Considering the Local Slenderness Effect. Buildings 2024, 14, 2240. https://doi.org/10.3390/buildings14072240
Mata R, Nuñez E. Cyclic Behavior of Concrete-Filled Tube Columns with Bidirectional Moment Connections Considering the Local Slenderness Effect. Buildings. 2024; 14(7):2240. https://doi.org/10.3390/buildings14072240
Chicago/Turabian StyleMata, Ramón, and Eduardo Nuñez. 2024. "Cyclic Behavior of Concrete-Filled Tube Columns with Bidirectional Moment Connections Considering the Local Slenderness Effect" Buildings 14, no. 7: 2240. https://doi.org/10.3390/buildings14072240
APA StyleMata, R., & Nuñez, E. (2024). Cyclic Behavior of Concrete-Filled Tube Columns with Bidirectional Moment Connections Considering the Local Slenderness Effect. Buildings, 14(7), 2240. https://doi.org/10.3390/buildings14072240









