Effect of Diaphragm Above Concrete-Filled Part on Horizontal Load Capacity of Partially Concrete-Filled Circular Piers Subjected to Axial Forces
Abstract
:1. Introduction
2. Numerical Conditions
2.1. Outline of Numerical Model
2.2. Elemental Partition
2.3. Material Properties
2.4. Boundary Conditions
2.5. Contact Conditions
3. Numerical Results
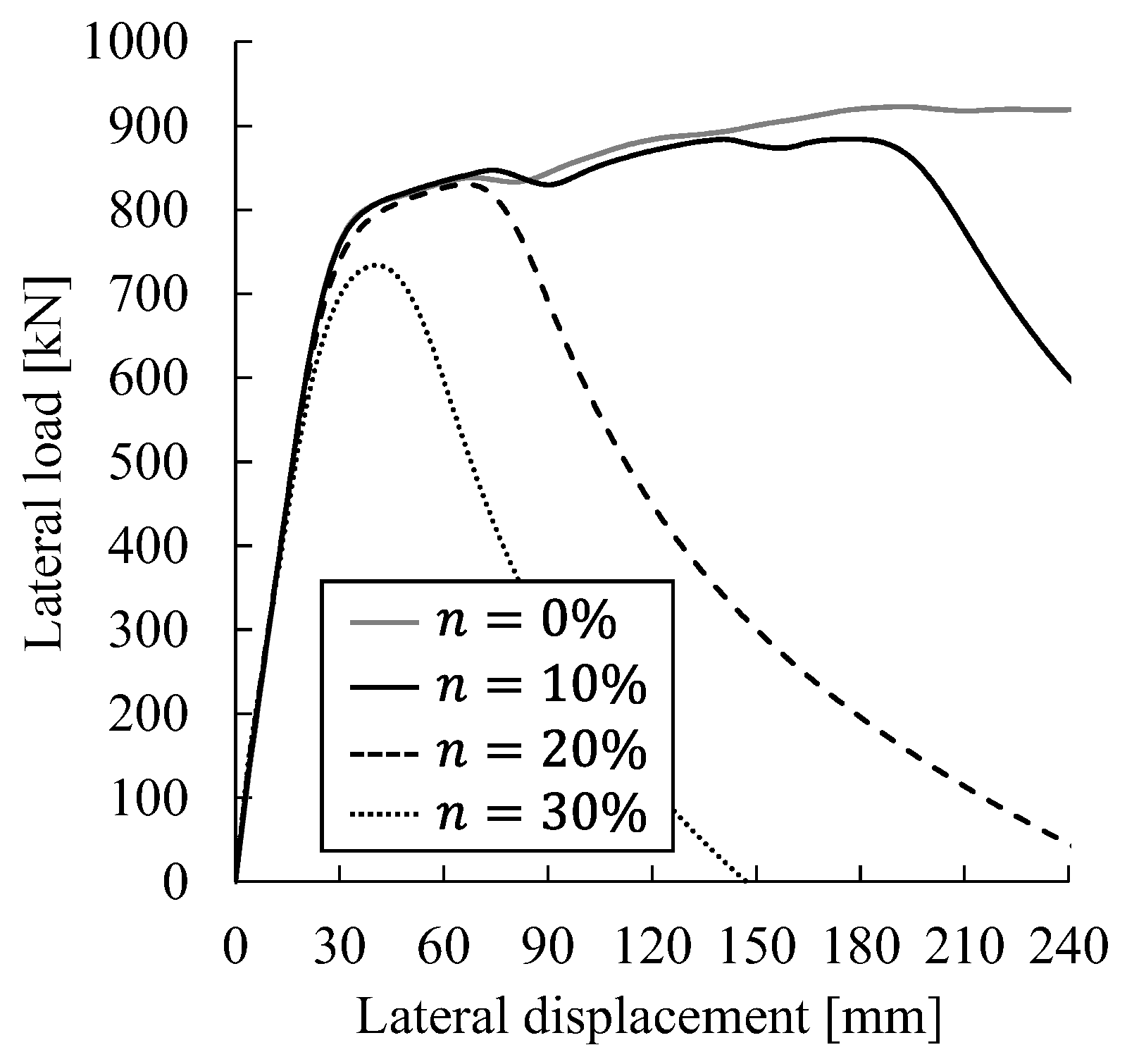
3.1. Relationship Between Horizontal Load and Horizontal Displacement
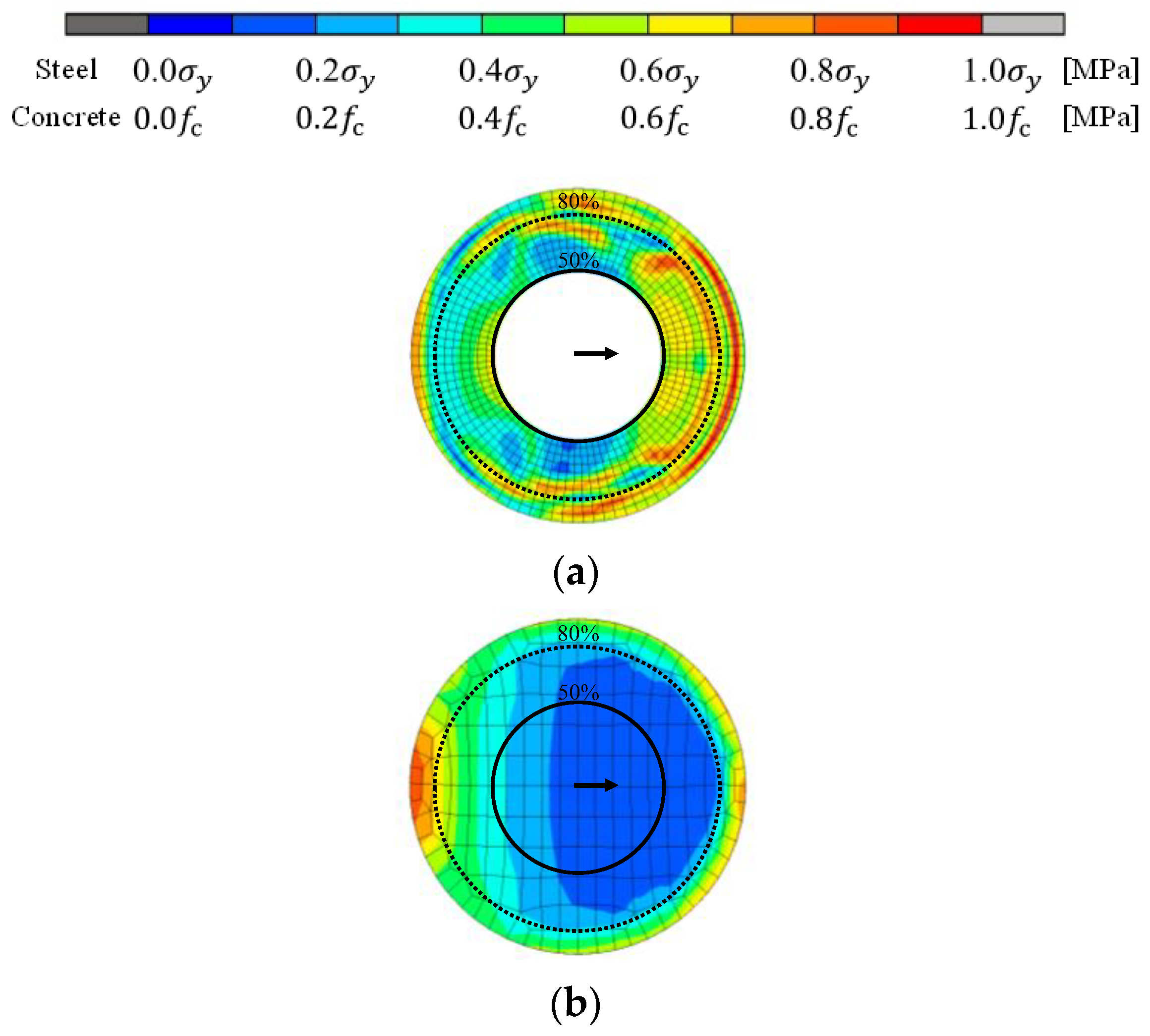
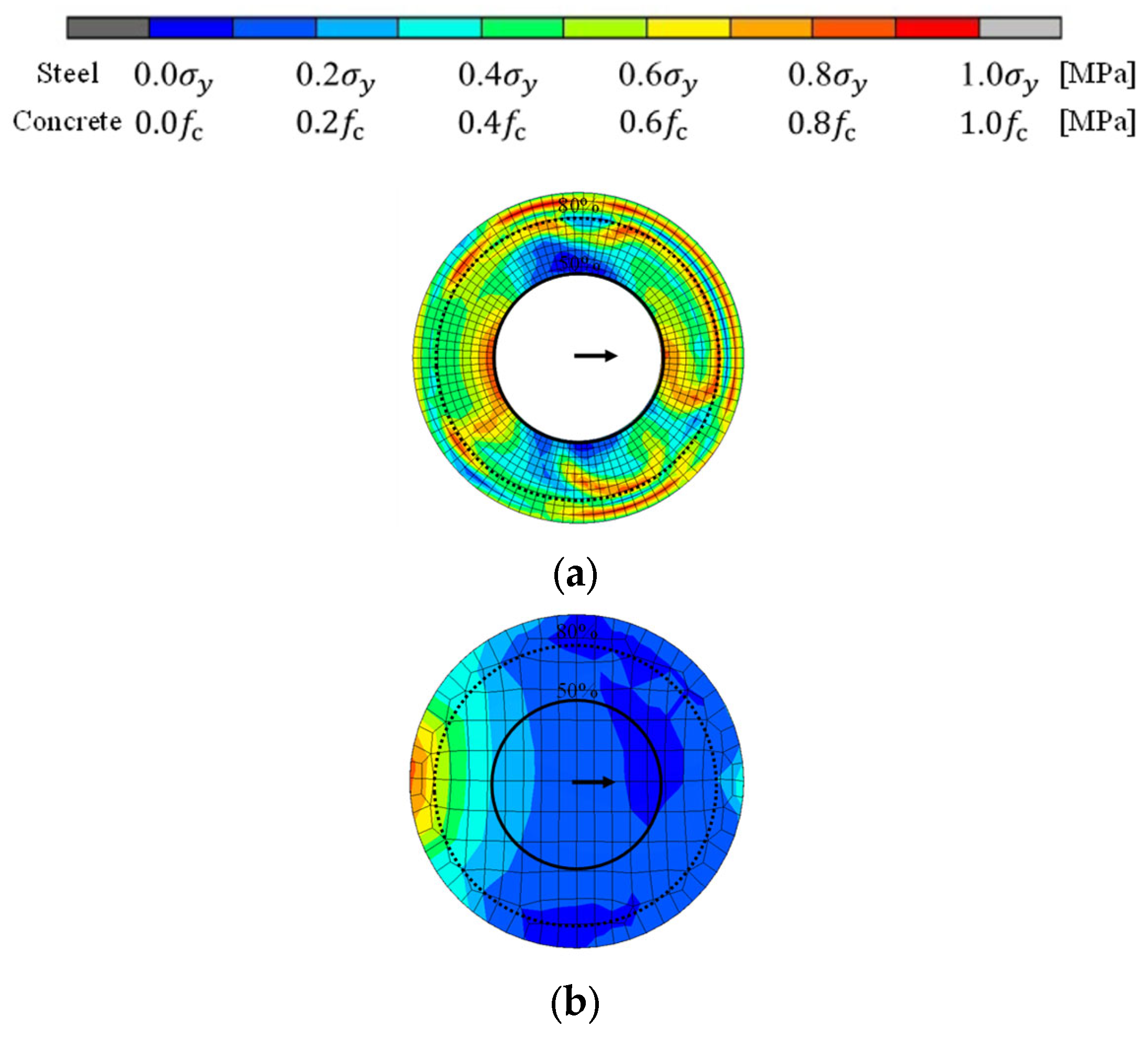
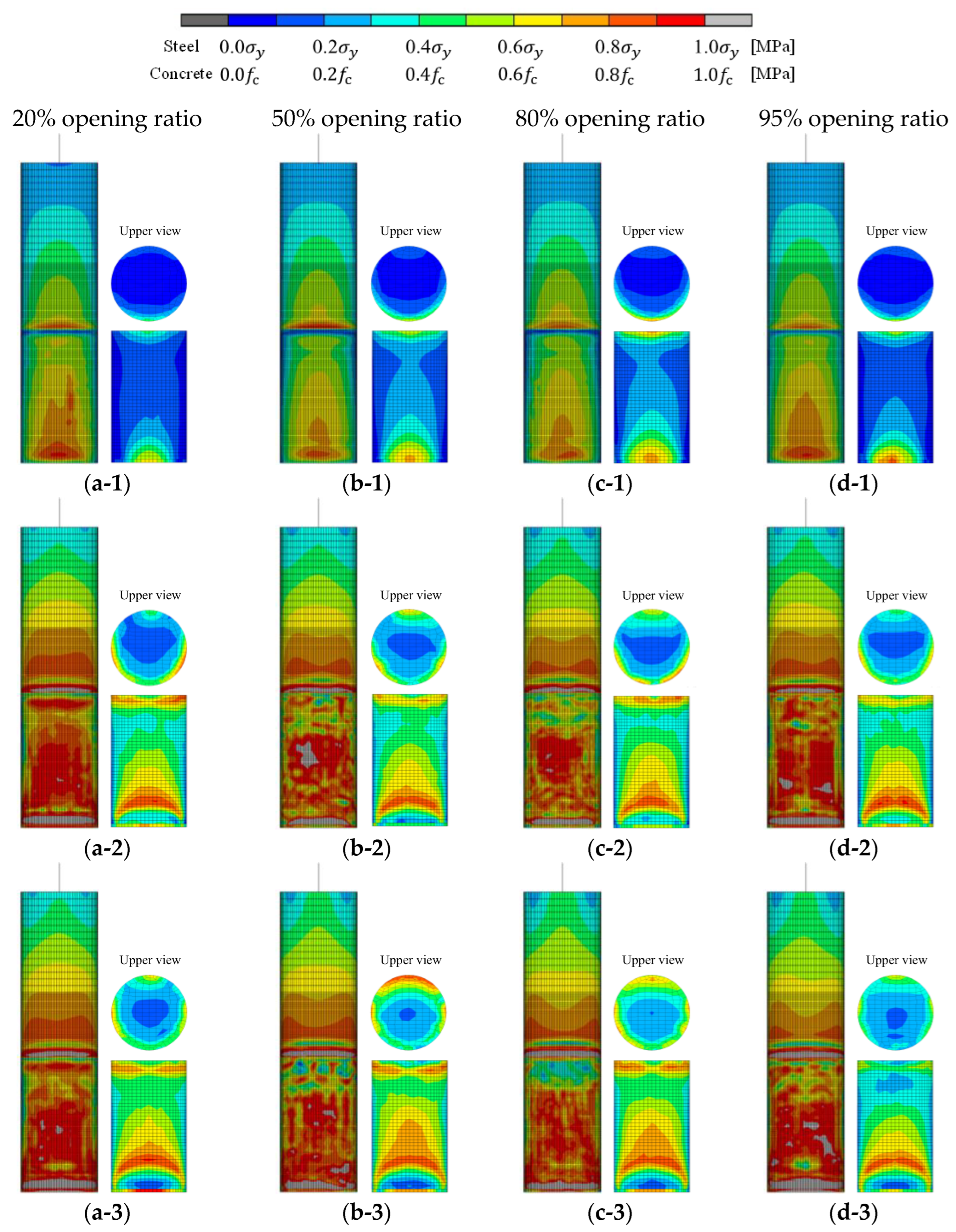
3.2. Shape Deformation and Mises Stress Distribution State
4. Discussion Focusing on the Diaphragm
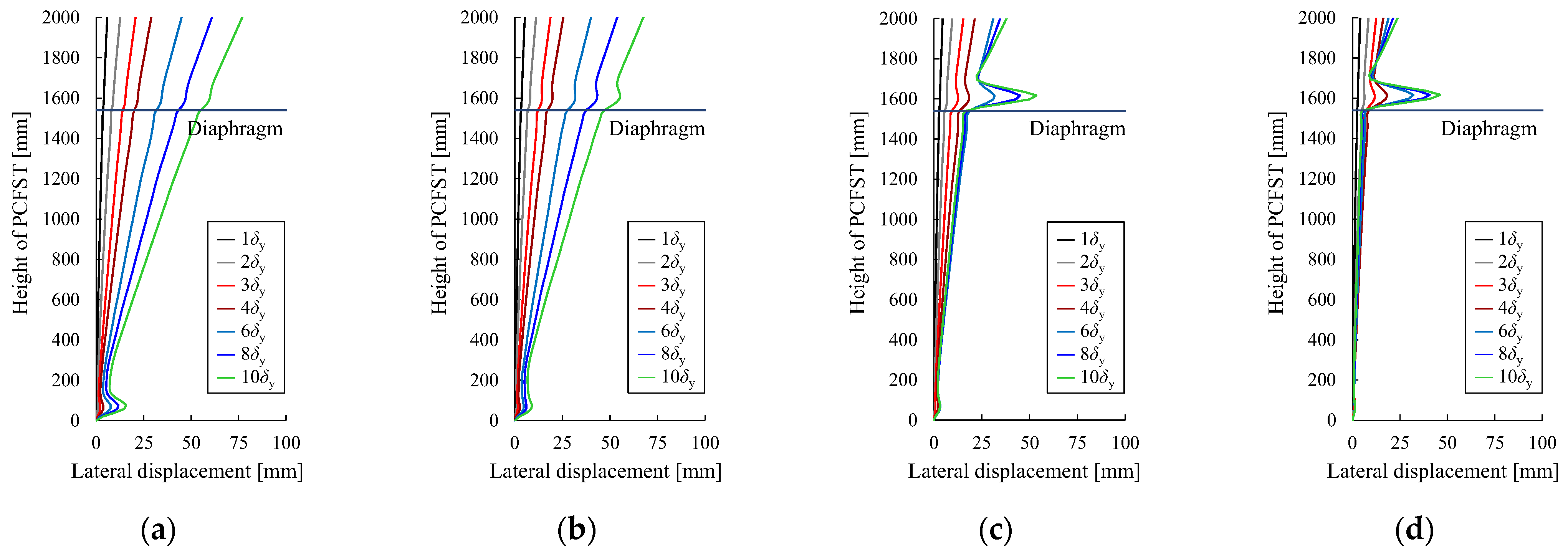
4.1. Location of Local Buckling
4.1.1. Primary Cases
4.1.2. All Cases
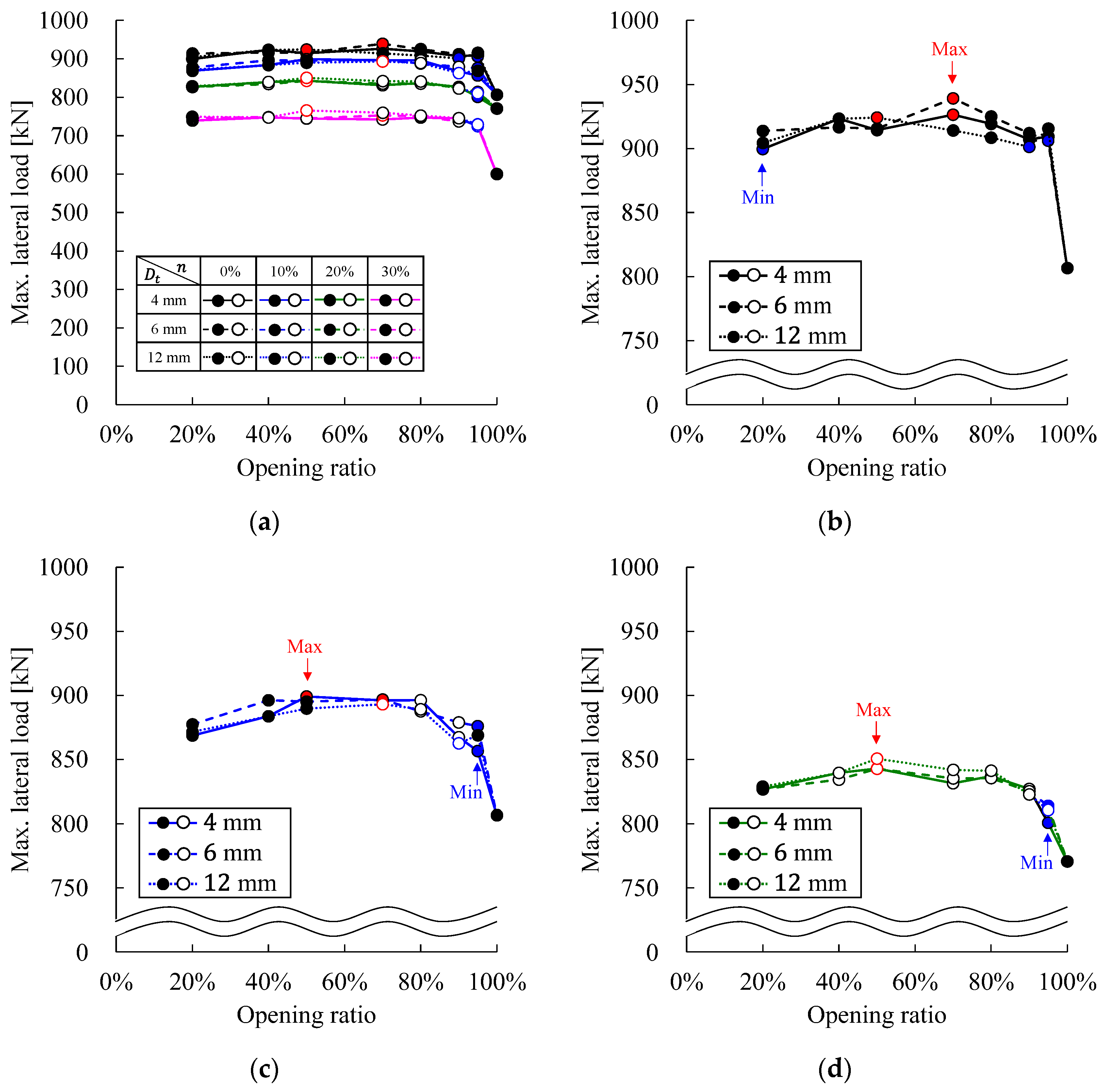
4.2. Horizontal Load Capacity
4.2.1. Primary Cases
4.2.2. All Cases
4.3. Mises Stress Distribution Diagram
5. Conclusions
- >
- The thickness of the diaphragm had little effect on the horizontal load capacity, and the amount of variation in the horizontal load capacity with respect to changes in the axial force ratio was also small.
- >
- The maximum horizontal load capacity was distributed from 40% to 70% opening ratios, and minimum values occurred from 90% to 95%, except for the 100% opening ratio, where no diaphragm was installed.
- >
- When the opening ratio of the diaphragm was as small as 20%, local buckling was likely to occur at the base of the steel tube, and when the opening ratio was as large as 80% or 90%, local buckling was only likely to occur directly above the concrete filling.
- >
- When the opening ratio of the diaphragm was as large as 95%, local buckling was likely to occur at the base of the steel tube due to the smaller contact area between the diaphragm and the concrete filling and the yielding of the diaphragm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, L.H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Zhang, D.Y.; Li, X.; Yan, W.M.; Xie, W.C.; Pandey, M.D. Stochastic seismic analysis of a concrete-filled steel tubular (CFST) arch bridge under tridirectional multiple excitations. Eng. Struct. 2013, 52, 355–371. [Google Scholar] [CrossRef]
- Cho, J.; Moon, J.; Ko, H.J.; Lee, H.E. Flexural strength evaluation of concrete-filled steel tube (CFST) composite girder. J. Constr. Steel Res. 2018, 151, 12–24. [Google Scholar] [CrossRef]
- Chen, B.W.; Han, L.H.; Qin, D.Y.; Li, W. Life-cycle based structural performance of long-span CFST hybrid arch bridge: A study on arch of Pingnan Third Bridge. J. Constr. Steel Res. 2023, 207, 107939. [Google Scholar] [CrossRef]
- Hu, W.; Liu, J.; Liu, Y.; Lyu, Y.; Li, H.; Xian, J.; Ma, Y. Construction alignment and closure control of CFST truss arch bridges based on temperature effect. Structures 2024, 63, 106471. [Google Scholar] [CrossRef]
- JSCE/Committee on Steel Structure. Guidelines for Stability Design of Steel Structures, 2nd ed.; Japan Society of Civil Engineers: Tokyo, Japan, 2005; pp. 428–429. (In Japanese) [Google Scholar]
- Iura, M.; Orino, A.; Ishizawa, T. Elasto-Plastic Behaviour of Concrete-Filled Steel Tubular Columns. J. JSCE 2002, 696, 285–298. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Orino, A.; Iura, M. Tests on concrete-filled steel tubular columns subject to lateral load. In Proceedings of the 3rd Symposium on Nonlinear Numerical Analysis and Application to Seismic Design of Steel Structures, Nagoya, Japan, 7–8 January 2000; pp. 83–88. (In Japanese). [Google Scholar]
- Goto, Y.; Kumar, G.P.; Kawanishi, N. FEM analysis for hysteretic behavior of CFT bridge piers considering interaction between steel tube and infilled concrete. J. JSCE A 2009, 65, 487–504. (In Japanese) [Google Scholar] [CrossRef]
- Goto, Y.; Kumar, G.P.; Kawanishi, N. Nonlinear finite-element analysis for hysteretic behavior of thin-walled circular steel columns with in-filled concrete. J. Struct. Eng. 2010, 136, 1413–1422. [Google Scholar] [CrossRef]
- Goto, Y.; Mizuno, K.; Kumar, G.P. Nonlinear finite element analysis for cyclic behavior of thin-walled stiffened rectangular steel columns with in-filled concrete. J. Struct. Eng. 2012, 138, 571–584. [Google Scholar] [CrossRef]
- Zenzai, S.; Chikahiro, Y.; Shimizu, S. Estimation Equation for Horizontal Load Bearing Capacity of Circular PCFST with Diaphragm. Appl. Sci. 2022, 12, 8739. [Google Scholar] [CrossRef]
- Ota, T.; Suzuki, M.; Shimaguchi, Y. A Study on Seismic Performance of Circular Steel Bridge Piers which have Different Level of Damages and Concrete Filled Repair. J. JSCE A2 (Appl. Mech.) 2013, 69, 381–390. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Shimaguchi, Y.; Suzuki, M. Seismic performance evaluation of circular steel bridge piers which have damage and concrete filled repair. J. Struct. Eng. 2015, 61A, 292–301. (In Japanese) [Google Scholar] [CrossRef]
- Zenzai, S.; Shimizu, S.; Chikahiro, Y.; Ohkami, T. Effect of Diaphragm on Seismic Behaviour of Partially Concrete-Filled Steel Tube. Steel Constr. Eng. 2019, 26, 25–36. (In Japanese) [Google Scholar] [CrossRef]
- Japan Road Association. Specification for Highway Bridges Part V: Seismic Design; Japan Road Association: Tokyo, Japan, 2012; pp. 251–274. [Google Scholar]
- Public Works Research Institute, Ministry of Construction. Cooperative Research on a Limit State Design of Piers of Highway Bridge Under Seismic Loading (Summarized Edition); Public Works Research Institute, Ministry of Construction: Tsukuba, Japan, 1999; p. 51. (In Japanese)
- Goto, Y.; Seki, K.; Ebisawa, T.; Lu, X. Improved seismic performance of CFT piers by a newly discovered mechanism to restrain progress of local buckling deformations. J. JSCE A1 (Struct. Eng. Earthq. Eng.) 2013, 69, 101–120. (In Japanese) [Google Scholar] [CrossRef]
- Yuan, H.; Dang, J.; Aoki, T. Behavior of partially concrete-filled steel tube under bidirectional seismic excitations. J. Constr. Steel Res. 2014, 93, 44–54. [Google Scholar] [CrossRef]
- ACI318-99; Building Code Requirement for Structural Concrete and Commentary. American Concrete Institute: Indianapolis, IN, USA, 1999; p. 83.
- Chen, W.F. Plasticity in Reinforced Concrete; J. Ross Publishing LLC: New York, NY, USA, 2007; pp. 19–48. [Google Scholar]
- Popovics, S. A Numerical Approach to the Complete Stress-Strain Curve of Concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Ngo, D.; Scordelis, A.C. Finite Element Analysis of Reinforced Concrete Beams. J. Proc. 1967, 64, 152–163. [Google Scholar] [CrossRef]
- Johansson, M.; Gylltoft, K. Structural behavior of slender circular steel-concrete composite columns under various means of load application. Steel Compos. Struct. 2001, 1, 393–410. [Google Scholar] [CrossRef]
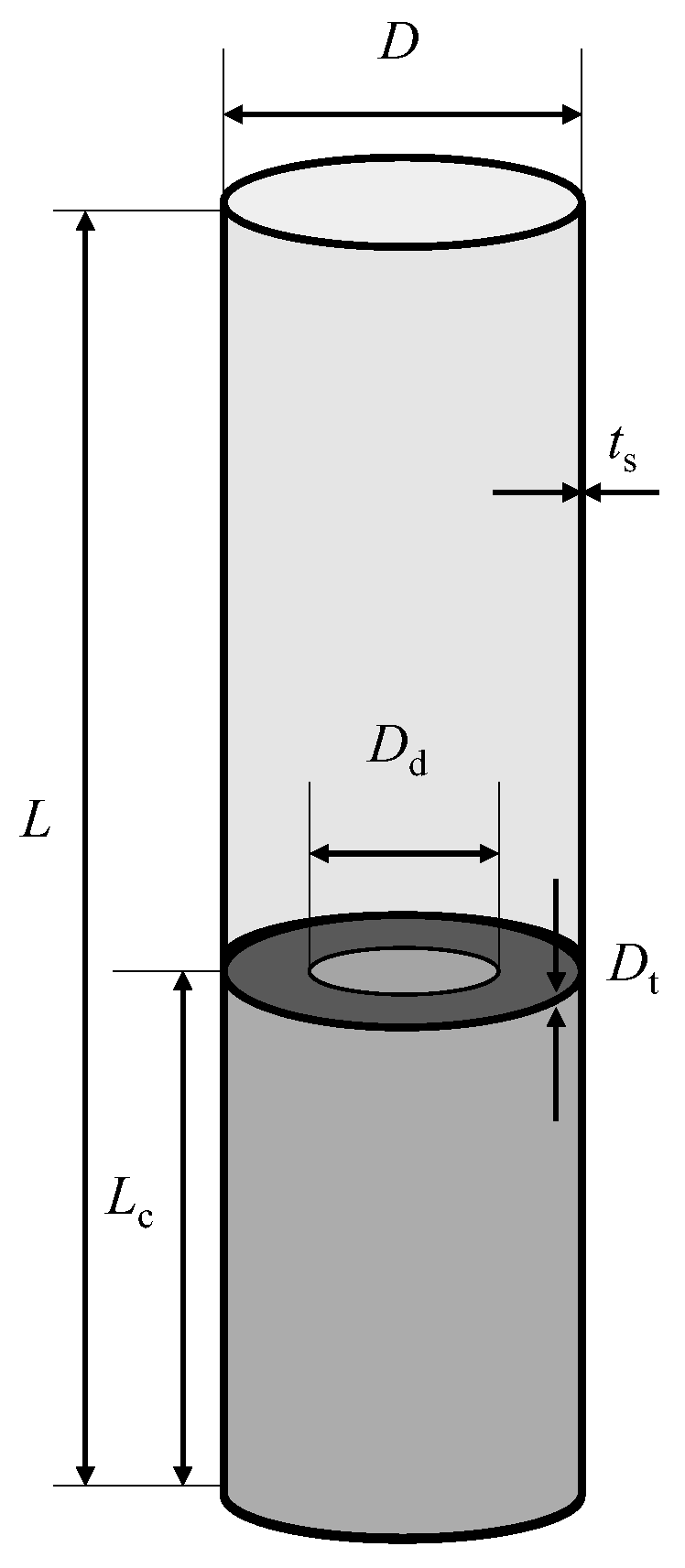

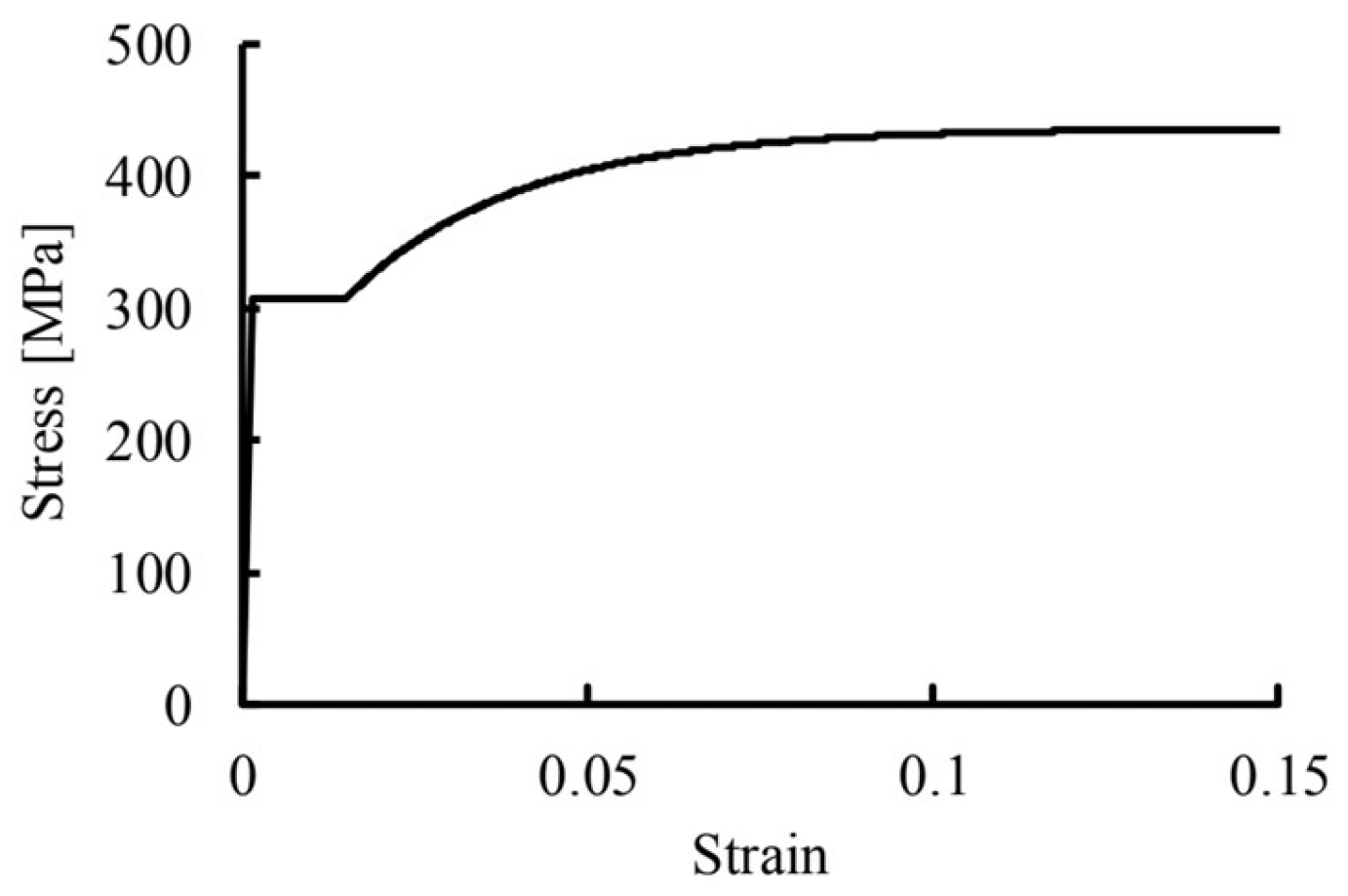
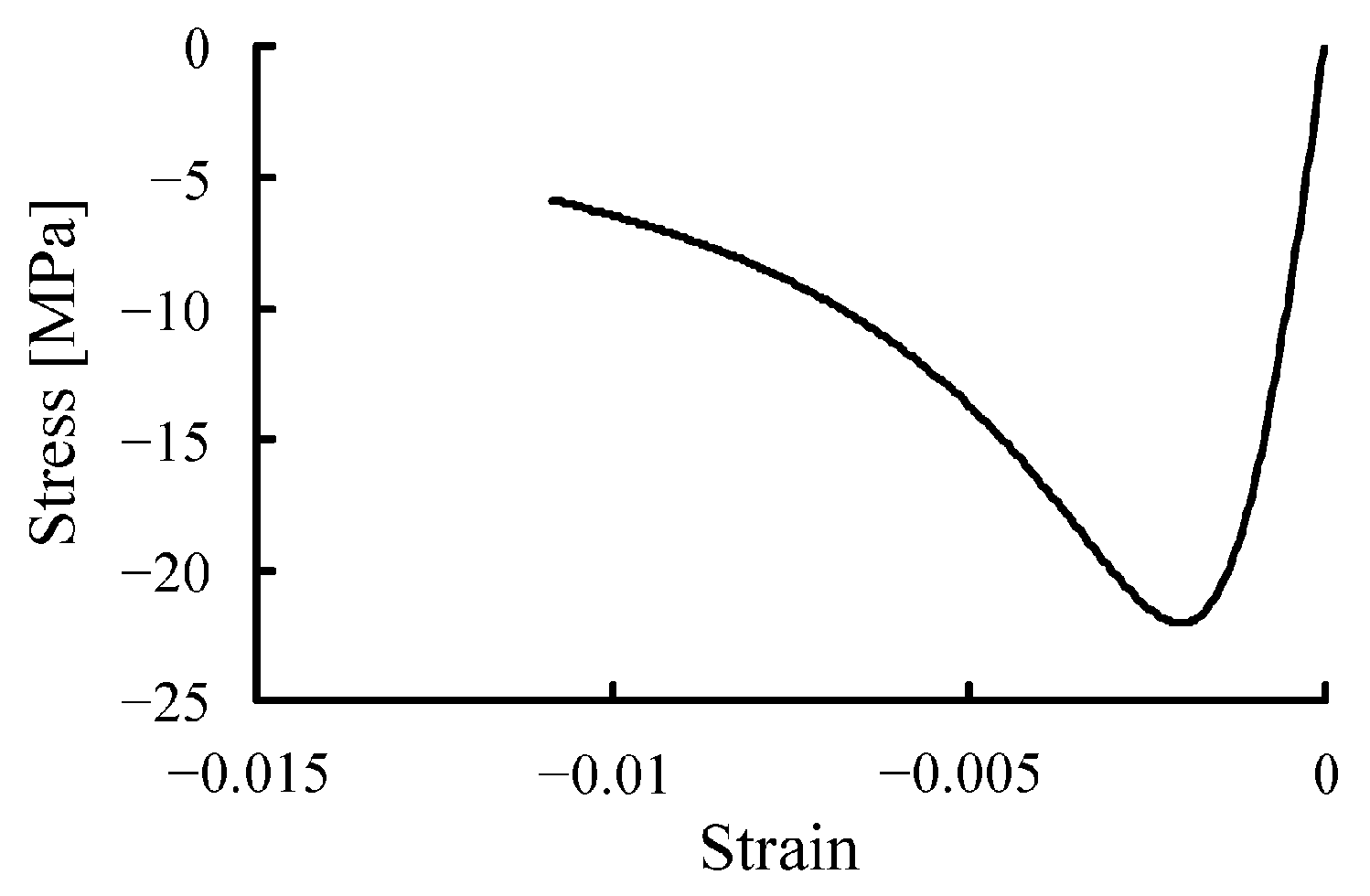

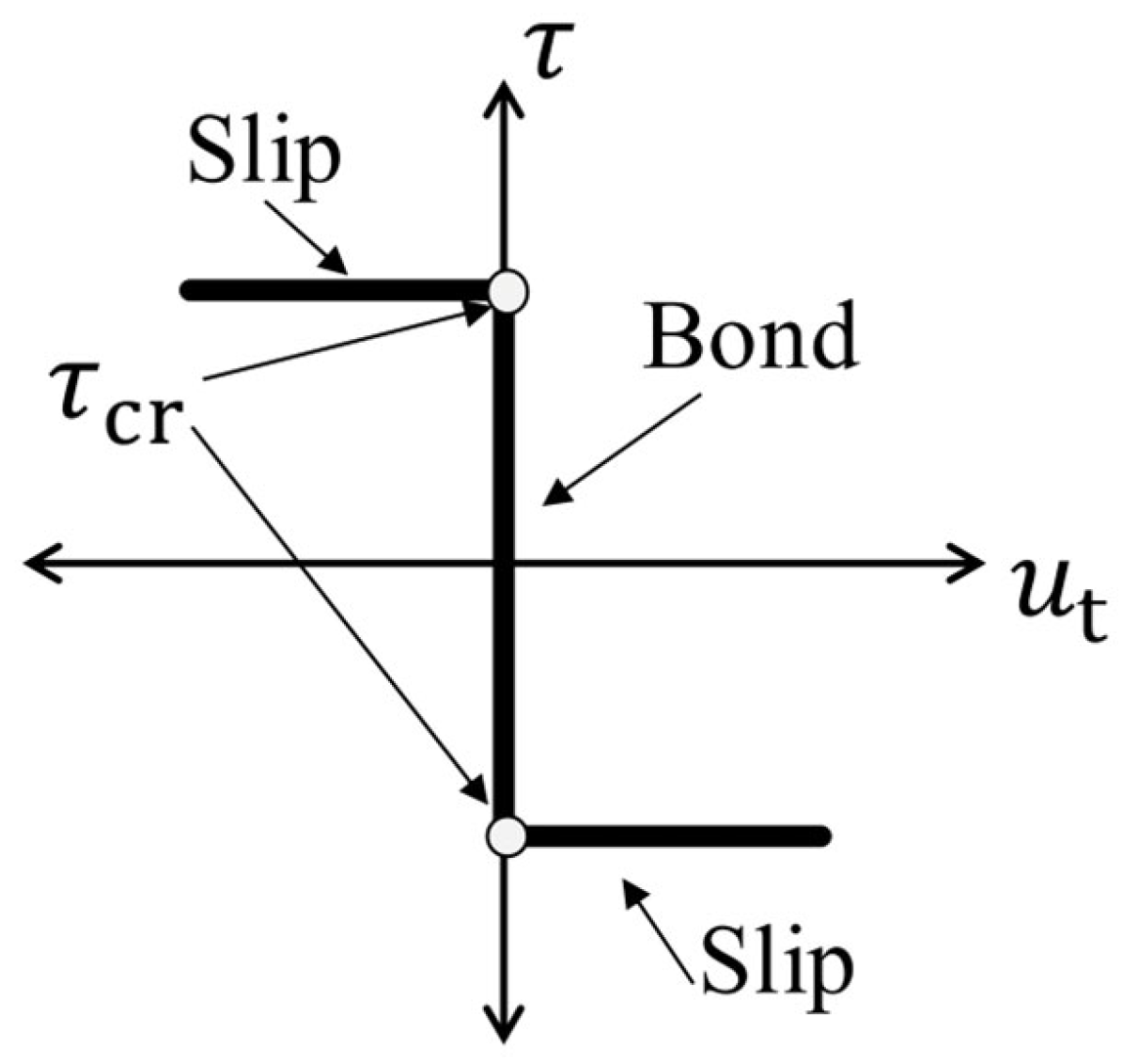






| Parameter | Value |
|---|---|
| Diameter of steel tube [mm] | 900 |
| Thickness of steel tube [mm] | 9.3 |
| Height of steel tube [mm] | 3850 |
| Section of steel tube [mm2] | 26,023.4 |
| Secondary radius of the section of steel tube [mm] | 314.9 |
| Young’s modulus of steel tube [GPa] | 206.0 |
| Poisson’s ratio of steel tube | 0.3 |
| Yielding stress of steel tube [MPa] | 308.0 |
| Concrete filling ratio [%] | 40 |
| Radius thickness ratio parameter | 0.12 |
| Slenderness ratio parameter | 0.3 |
| Opening ratio of diaphragm [%] | 20, 40, 50, 70 80, 90, 95, 100 |
| Thickness of diaphragm [mm] | 4, 6, 12 |
| Axial force ratio [%] | 0, 10, 20, 30 |
| 0% | 10% | 20% | 30% | 0% | 10% | 20% | 30% | 0% | 10% | 20% | 30% | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20% | |||||||||||||
| 40% | |||||||||||||
| 50% | |||||||||||||
| 70% | |||||||||||||
| 80% | |||||||||||||
| 90% | |||||||||||||
| 95% | |||||||||||||
| 100% | |||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chikahiro, Y.; Huong, N.T.H.; Zenzai, S. Effect of Diaphragm Above Concrete-Filled Part on Horizontal Load Capacity of Partially Concrete-Filled Circular Piers Subjected to Axial Forces. Buildings 2025, 15, 863. https://doi.org/10.3390/buildings15060863
Chikahiro Y, Huong NTH, Zenzai S. Effect of Diaphragm Above Concrete-Filled Part on Horizontal Load Capacity of Partially Concrete-Filled Circular Piers Subjected to Axial Forces. Buildings. 2025; 15(6):863. https://doi.org/10.3390/buildings15060863
Chicago/Turabian StyleChikahiro, Yuki, Nguyen Thi Hong Huong, and Seiya Zenzai. 2025. "Effect of Diaphragm Above Concrete-Filled Part on Horizontal Load Capacity of Partially Concrete-Filled Circular Piers Subjected to Axial Forces" Buildings 15, no. 6: 863. https://doi.org/10.3390/buildings15060863
APA StyleChikahiro, Y., Huong, N. T. H., & Zenzai, S. (2025). Effect of Diaphragm Above Concrete-Filled Part on Horizontal Load Capacity of Partially Concrete-Filled Circular Piers Subjected to Axial Forces. Buildings, 15(6), 863. https://doi.org/10.3390/buildings15060863





