Multiperiod Location–Allocation Optimization of Construction Logistics Centers for Large-Scale Projects in Complex Environmental Regions
Abstract
:1. Introduction
2. Literature Review
2.1. Optimization of Construction Logistics
2.2. Multiperiod Facility Location Problems
2.3. Research Gap Analysis
3. Model Establishment
3.1. Problem Definition
3.2. Model Assumptions
- The MDC has a complete range of materials that meet all construction material demands.
- The construction design unit determines the potential location of the CLC through research and survey.
- Logistics land in complex environmental regions is restricted. Thus, the storage capacity of the CLC is known and has an upper limit.
- Because of the different storage requirements of construction materials, the capacity limit of the CLC is different for various engineering materials.
- After the research and demonstration of the construction design unit, construction material demands in different periods of each construction section are known.
- The CLC can only provide construction materials in one MDC.
- The types of materials provided by each CLC are the same as the types of materials required by construction sections. To simplify the model, it is set that only one CLC can provide construction materials for a construction section.
- Transportation risks in the construction logistics network are assessed based on historical meteorological, disaster, and other data.
- CLC safety stock period is based on the stability of the transport network in different seasons.
- The minimum utilization of the capacity of the CLC depends on the minimum number of construction sections to be served when it is opened.
- There is no transportation of construction materials between CLCs.
- If the CLC is closed, there is no inventory remaining at the end of the period.
3.3. Notations
3.4. Objective Function
3.5. Constraints
4. Algorithm Design
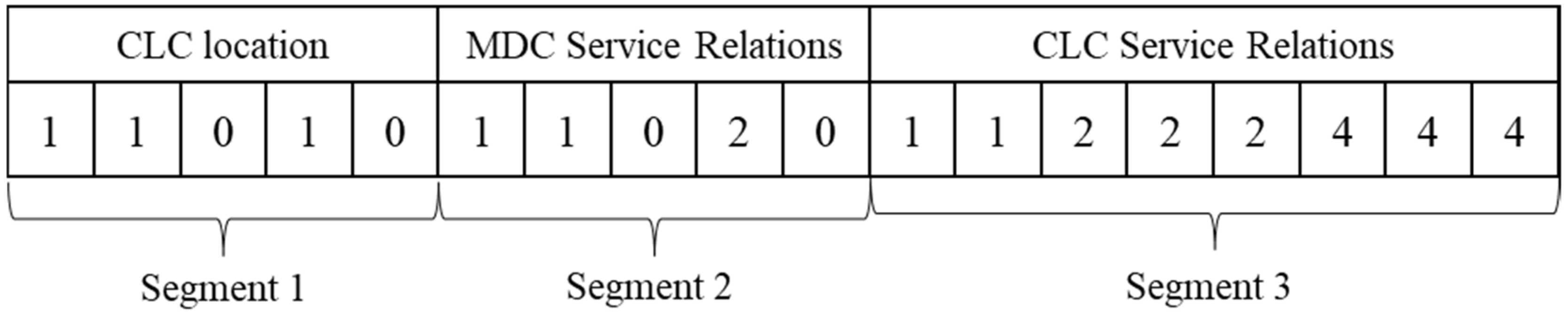
4.1. Chromosome Coding and Initial Population Generation
4.2. Fitness Calculation and Fast Non-Dominated Sorting
4.3. Dynamic Crowding Distance
4.4. Binary Tournament Selection
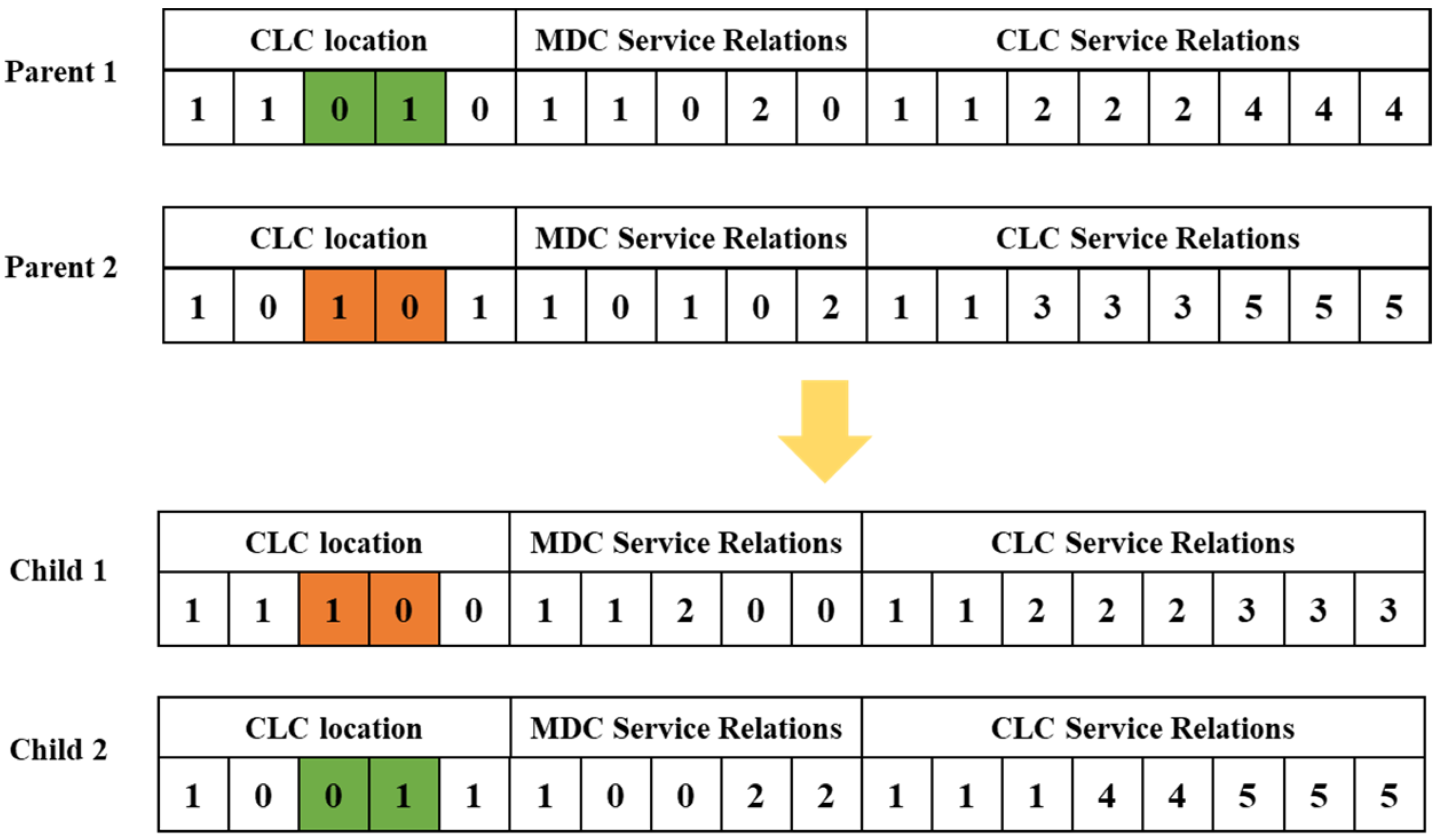
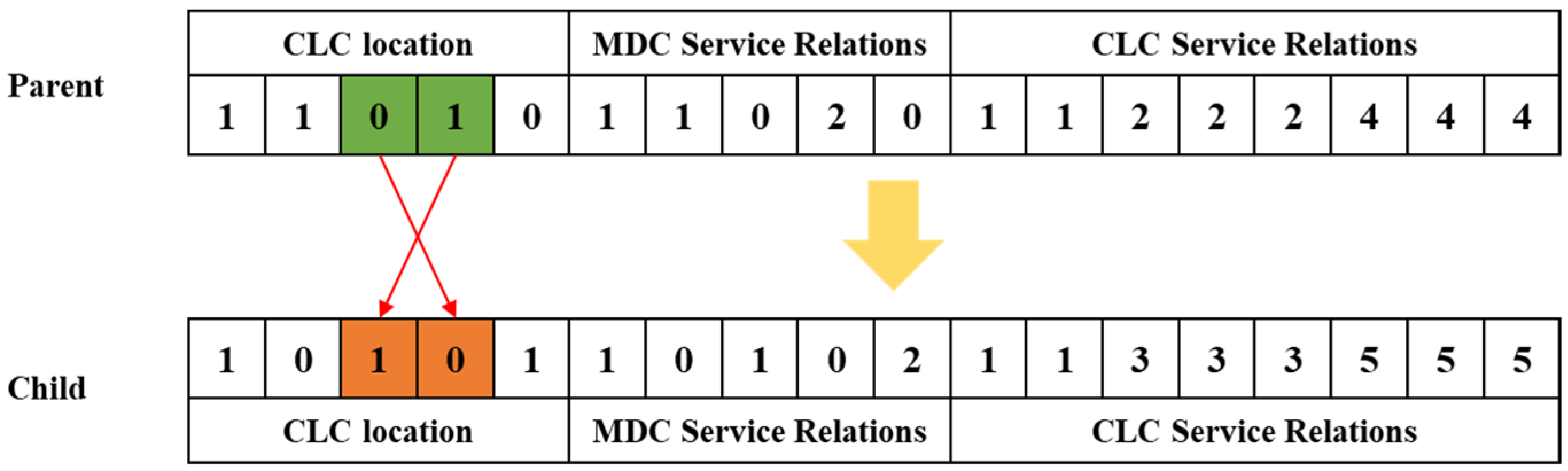
4.5. Crossover, Variational Operator Design
5. Result and Discussion
5.1. Case Data Collection
5.2. Model and Algorithm Performance Analysis
5.2.1. Model Performance Analysis
5.2.2. Algorithm Performance Analysis
5.3. Results Analysis
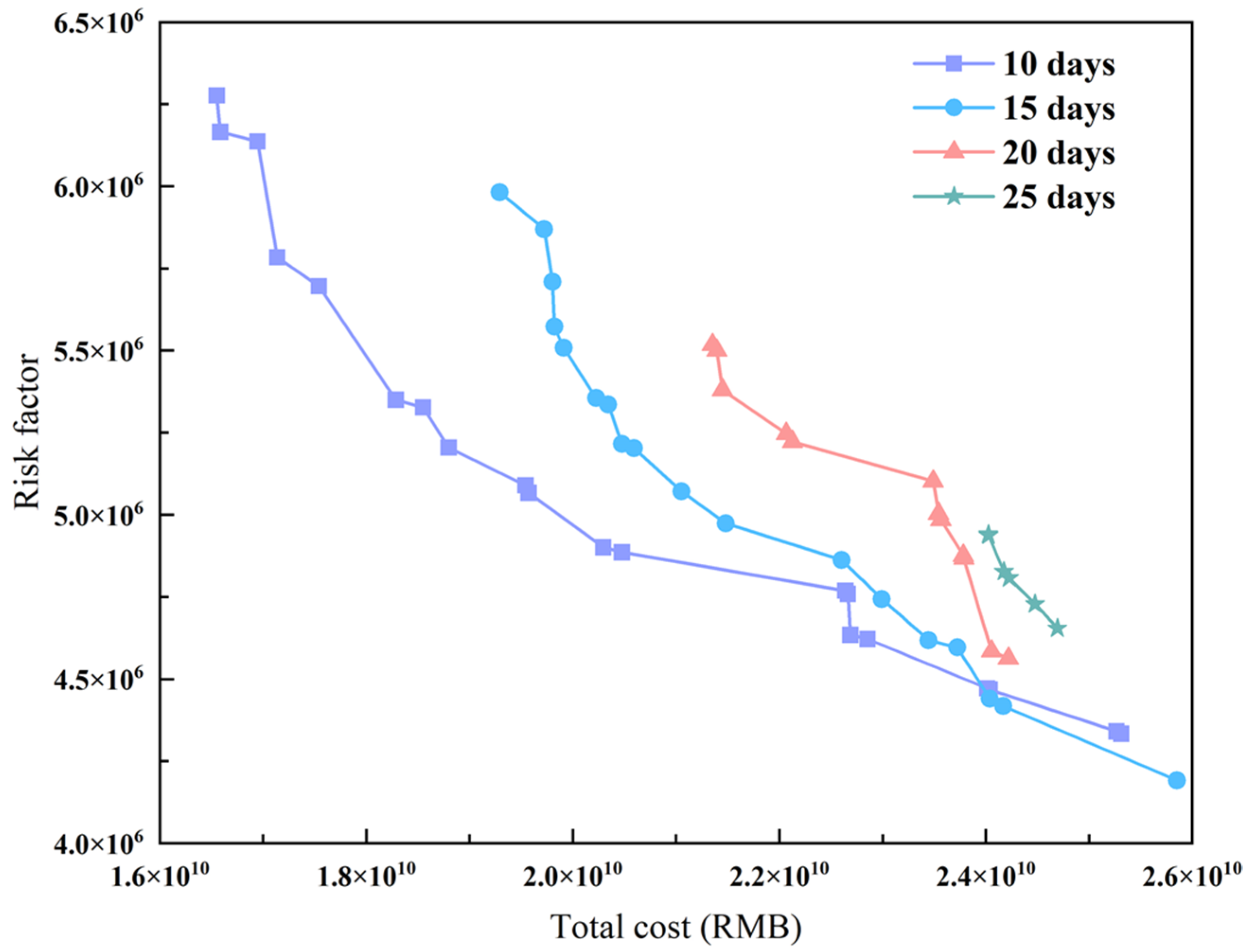
5.4. Sensitivity Analysis
5.4.1. Coverage Sensitivity Analysis
5.4.2. Safety Stock Period Sensitivity Analysis
5.5. Managerial Insights
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fredriksson, A.; Janné, M.; Rudberg, M. Characterizing third-party logistics setups in the context of construction. Int. J. Phys. Distrib. Logist. Manag. 2021, 51, 325–349. [Google Scholar] [CrossRef]
- Ahmadian, F.F.A.; Akbarnezhad, A.; Rashidi, T.H.; Waller, S.T. Accounting for Transport Times in Planning Off-Site Shipment of Construction Materials. J. Constr. Eng. Manag. 2016, 142, 04015050. [Google Scholar] [CrossRef]
- Tetik, M.; Peltokorpi, A.; Seppänen, O.; Leväniemi, M.; Holmström, J. Kitting Logistics Solution for Improving On-Site Work Performance in Construction Projects. J. Constr. Eng. Manag. 2021, 147, 05020020. [Google Scholar] [CrossRef]
- Fallahnejad, M.H. Delay causes in Iran gas pipeline projects. Int. J. Proj. Manag. 2013, 31, 136–146. [Google Scholar] [CrossRef]
- Guerlain, C.; Renault, S.; Ferrero, F. Understanding Construction Logistics in Urban Areas and Lowering Its Environmental Impact: A Focus on Construction Consolidation Centres. Sustainability 2019, 11, 6118. [Google Scholar] [CrossRef]
- Josephson, P.-E.; Saukkoriipi, L. Waste in Construction Projects: Call for a New Approach; 9197618179; Chalmers University of Technology: Gothenburg, Sweden, 2007. [Google Scholar]
- Zeng, L.; Du, Q.; Zhou, L.; Wang, X.; Zhu, H.; Bai, L. Side-payment contracts for prefabricated construction supply chain coordination under just-in-time purchasing. J. Clean. Prod. 2022, 379, 134830. [Google Scholar] [CrossRef]
- Yao, J.; Yi, W.; Wang, H.; Zhen, L.; Liu, Y. Stackelberg game model for construction waste disposal network design. Autom. Constr. 2022, 144, 104573. [Google Scholar] [CrossRef]
- Sundquist, V.; Gadde, L.E.; Hulthén, K. Reorganizing construction logistics for improved performance. Constr. Manag. Econ. 2018, 36, 49–65. [Google Scholar] [CrossRef]
- Hedborg Bengtsson, S. Coordinated construction logistics: An innovation perspective. Constr. Manag. Econ. 2018, 37, 294–307. [Google Scholar] [CrossRef]
- Dubois, A.; Gadde, L.-E. The construction industry as a loosely coupled system: Implications for productivity and innovation. Constr. Manag. Econ. 2002, 20, 621–631. [Google Scholar] [CrossRef]
- Dubois, A.; Hulthén, K.; Sundquist, V. Organising logistics and transport activities in construction. Int. J. Logist. Manag. 2019, 30, 620–640. [Google Scholar] [CrossRef]
- El Moussaoui, S.; Lafhaj, Z.; Leite, F.; Laqdid, Y.; BuHamdan, S.; Brunet, F.; Fléchard, J.; Linéatte, B. The Assessment of Pollutant Emissions from Transportation of Construction Materials and the Impact of Construction Logistics Centers. J. Manag. Eng. 2022, 38, 04022038. [Google Scholar] [CrossRef]
- Dakhli, Z.; Lafhaj, Z. Considering Materials Management in Construction: An Exploratory Study. Logistics 2018, 2, 7. [Google Scholar] [CrossRef]
- Sezer, A.A.; Fredriksson, A. Environmental impact of construction transport and the effects of building certification schemes. Resour. Conserv. Recycl. 2021, 172, 105688. [Google Scholar] [CrossRef]
- Janné, M.; Fredriksson, A. Construction logistics governing guidelines in urban development projects. Constr. Innov. 2019, 19, 89–109. [Google Scholar] [CrossRef]
- El Moussaoui, S.; Lafhaj, Z.; Leite, F.; Fléchard, J.; Linéatte, B. Construction Logistics Centres Proposing Kitting Service: Organization Analysis and Cost Mapping. Buildings 2021, 11, 105. [Google Scholar] [CrossRef]
- Shafiei Kisomi, M.; Solimanpur, M.; Doniavi, A. An integrated supply chain configuration model and procurement management under uncertainty: A set-based robust optimization methodology. Appl. Math. Modell. 2016, 40, 7928–7947. [Google Scholar] [CrossRef]
- Amiri, A. Designing a distribution network in a supply chain system: Formulation and efficient solution procedure. Eur. J. Oper. Res. 2006, 171, 567–576. [Google Scholar] [CrossRef]
- Hsu, P.-Y.; Angeloudis, P.; Aurisicchio, M. Optimal logistics planning for modular construction using two-stage stochastic programming. Autom. Constr. 2018, 94, 47–61. [Google Scholar] [CrossRef]
- Azambuja, M.; O’Brien, W.J. Supply chain modeling: Issues and perspectives. In Construction Supply Chain Management Handbook; CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Lei, L.; Liu, S.; Ruszczynski, A.; Park, S. On the integrated production, inventory, and distribution routing problem. IIE Trans. (Inst. Ind. Eng.) 2006, 38, 955–970. [Google Scholar] [CrossRef]
- Said, H.; El-Rayes, K. Optimizing Material Procurement and Storage on Construction Sites. J. Constr. Eng. Manag. 2011, 137, 421–431. [Google Scholar] [CrossRef]
- Li, J.Q.; Han, Y.Q.; Duan, P.Y.; Han, Y.Y.; Niu, B.; Li, C.D.; Zheng, Z.X.; Liu, Y.P. Meta-heuristic algorithm for solving vehicle routing problems with time windows and synchronized visit constraints in prefabricated systems. J. Clean. Prod. 2020, 250, 119464. [Google Scholar] [CrossRef]
- RezaHoseini, A.; Noori, S.; Ghannadpour, S.F. Integrated scheduling of suppliers and multi-project activities for green construction supply chains under uncertainty. Autom. Constr. 2021, 122, 103485. [Google Scholar] [CrossRef]
- Guerra, B.C.; Shahi, S.; Molleai, A.; Skaf, N.; Weber, O.; Leite, F.; Haas, C. Circular economy applications in the construction industry: A global scan of trends and opportunities. J. Clean. Prod. 2021, 324, 129125. [Google Scholar] [CrossRef]
- Lundesjo, G.T.L. Using Construction Consolidation Centres to Reduce Construction Waste and Carbon Emissions; Waste & Resources Action Programme: Banbury, UK, 2011; pp. 1–19. [Google Scholar]
- Ding, L.; Wang, T.; Chan, P.W. Forward and reverse logistics for circular economy in construction: A systematic literature review. J. Clean. Prod. 2023, 388, 135981. [Google Scholar] [CrossRef]
- Lundesjö, G. Supply Chain Management and Logistics in Construction: Delivering Tomorrow’s Built Environment; Kogan Page Publishers: London, UK, 2015. [Google Scholar]
- El-Anwar, O.; Kim, Y.W. Multi-objective optimization of process design using process-based sustainable impact analysis. In Proceedings of the EG-ICE 2010—17th International Workshop on Intelligent Computing in Engineering, Enschede, The Netherlands, 6–8 July 2011. [Google Scholar]
- Fang, Y.; Ng, S.T. Genetic algorithm for determining the construction logistics of precast components. Eng. Constr. Arch. Manag. 2019, 26, 2289–2306. [Google Scholar] [CrossRef]
- Xu, J.; Gang, J. Multi-objective bilevel construction material transportation scheduling in large-scale construction projects under a fuzzy random environment. Transp. Plan. Technol. 2013, 36, 352–376. [Google Scholar] [CrossRef]
- Hsu, P.-Y.; Aurisicchio, M.; Angeloudis, P. Risk-averse supply chain for modular construction projects. Autom. Constr. 2019, 106, 102898. [Google Scholar] [CrossRef]
- Ebrahimi-Zade, A.; Hosseini-Nasab, H.; Zare-Mehrjerdi, Y.; Zahmatkesh, A. Multi-period hub set covering problems with flexible radius: A modified genetic solution. Appl. Math. Modell. 2016, 40, 2968–2982. [Google Scholar] [CrossRef]
- Canel, C.; Khumawala, B.M.; Law, J.; Loh, A. An algorithm for the capacitated, multi-commodity multi-period facility location problem. Comput. Oper. Res. 2001, 28, 411–427. [Google Scholar] [CrossRef]
- Campbell, J.F. Locating transportation terminals to serve an expanding demand. Transp. Res. Part B Methodol. 1990, 24, 173–192. [Google Scholar] [CrossRef]
- Gelareh, S. Hub Location Models in Public Transport Planning; VDM Verlag: Riga, Latvia, 2008. [Google Scholar]
- Fattahi, P.; Kebria, Z.S. A bi-objective dynamic reliable hub location problem with congestion effects. Int. J. Ind. Eng. Prod. Res. 2020, 31, 63–74. [Google Scholar] [CrossRef]
- Contreras, I.; Cordeau, J.F.; Laporte, G. The Dynamic Uncapacitated Hub Location Problem. Transp. Sci. 2011, 45, 18–32. [Google Scholar] [CrossRef]
- Alumur, S.A.; Nickel, S.; Saldanha-da-Gama, F.; Seçerdin, Y. Multi-period hub network design problems with modular capacities. Ann. Oper. Res. 2016, 246, 289–312. [Google Scholar] [CrossRef]
- Fotuhi, F.; Huynh, N. A reliable multi-period intermodal freight network expansion problem. Comput. Ind. Eng. 2018, 115, 138–150. [Google Scholar] [CrossRef]
- Wang, X.-F.; Sun, X.-M.; Fang, Y. Genetic algorithm solution for multi-period two-echelon integrated competitive/uncompetitive facility location problem. Asia-Pac. J. Oper. Res. 2008, 25, 33–56. [Google Scholar] [CrossRef]
- Khosravian, Y.; Shahandeh Nookabadi, A.; Moslehi, G. Mathematical Model for Bi-objective Maximal Hub Covering Problem with Periodic Variations of Parameters. Int. J. Eng. 2019, 32, 964–975. [Google Scholar] [CrossRef]
- Reddy, K.N.; Kumar, A.; Choudhary, A.; Cheng, T.C.E. Multi-period green reverse logistics network design: An improved Benders-decomposition-based heuristic approach. Eur. J. Oper. Res. 2022, 303, 735–752. [Google Scholar] [CrossRef]
- Bashiri, M.; Rezanezhad, M.; Tavakkoli-Moghaddam, R.; Hasanzadeh, H. Mathematical modeling for a p-mobile hub location problem in a dynamic environment by a genetic algorithm. Appl. Math. Modell. 2018, 54, 151–169. [Google Scholar] [CrossRef]
- Goodarzian, F.; Wamba, S.F.; Mathiyazhagan, K.; Taghipour, A. A new bi-objective green medicine supply chain network design under fuzzy environment: Hybrid metaheuristic algorithms. Comput. Ind. Eng. 2021, 160, 107535. [Google Scholar] [CrossRef]
- Ghaderi, A.; Jabalameli, M.S. Modeling the budget-constrained dynamic uncapacitated facility location–network design problem and solving it via two efficient heuristics: A case study of health care. Math. Comput. Modell. 2013, 57, 382–400. [Google Scholar] [CrossRef]
- Wan, M.; Ye, C.; Peng, D. Multi-period dynamic multi-objective emergency material distribution model under uncertain demand. Eng. Appl. Artif. Intell. 2023, 117, 105530. [Google Scholar] [CrossRef]
- Delfani, F.; Samanipour, H.; Beiki, H.; Yumashev, A.V.; Akhmetshin, E.M. A robust fuzzy optimisation for a multi-objective pharmaceutical supply chain network design problem considering reliability and delivery time. Int. J. Syst. Sci. Oper. Logist. 2022, 9, 155–179. [Google Scholar] [CrossRef]
- Li, K.; Li, D.; Wu, D.Q. Carbon Transaction-Based Location-Routing-Inventory Optimization for Cold Chain Logistics. Alex. Eng. J. 2022, 61, 7979–7986. [Google Scholar] [CrossRef]
- Giusti, R.; Manerba, D.; Tadei, R. Multiperiod transshipment location–allocation problem with flow synchronization under stochastic handling operations. Networks 2021, 78, 88–104. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Huang, X.; Zong, J.; Wang, Q.; Liu, Y.; Wang, J.; Chen, P. Placement Approach for the Data Storage Management Function in a RAN-CN Converged Network. IEEE Access 2023, 11, 94898–94910. [Google Scholar] [CrossRef]
- Almansour, F.M.; Alroobaea, R.; Ghiduk, A.S. An Empirical Comparison of the Efficiency and Effectiveness of Genetic Algorithms and Adaptive Random Techniques in Data-Flow Testing. IEEE Access 2020, 8, 12884–12896. [Google Scholar] [CrossRef]
- Farhy, L.S. Modeling of Oscillations in Endocrine Networks with Feedback. In Methods Enzymology; Academic Press: Cambridge, MA, USA, 2004; Volume 384, pp. 54–81. [Google Scholar]
- Zhang, Q.; Zhou, Q.; Wu, W.; Zhao, J.; Yuan, R. Hengduan Mountain Area Natural Disaster Risk and Comprehensive Risk Assessment Data Set (2020); National Tibetan Plateau/Third Pole Environment Data Center: Tibetan, China, 2021. [Google Scholar] [CrossRef]
- Pan, L.Q.; Xu, W.T.; Li, L.H.; He, C.; Cheng, R. Adaptive simulated binary crossover for rotated multi-objective optimization. Swarm Evol. Comput. 2021, 60, 100759. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Kun, Z.; Zhiwei, L.; Yuguo, W.; Changjian, Z.; Xinyan, G.; Xuan, L. Improved Hormone Algorithm for Solving the Permutation Flow Shop Scheduling Problem. J. Univ. Electron. Sci. Technol. China 2022, 51, 890–903. [Google Scholar]
- Wang, Y.N.; Wu, L.H.; Yuan, X.F. Multi-objective self-adaptive differential evolution with elitist archive and crowding entropy-based diversity measure. soft Comput. 2010, 14, 193–209. [Google Scholar] [CrossRef]
- Wu, J.; Azarm, S. Metrics for Quality Assessment of a Multiobjective Design Optimization Solution Set. J. Mech. Des. 2000, 123, 18–25. [Google Scholar] [CrossRef]





| Article | Objective Function | Strategic Decisions | Product | Model | Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Economic | Environment | Risk | Efficiency | Facility Selection | Supplier Selection | Demand Allocation | Inventory | ||||
| Ebrahimi-Zade et al., 2016 [34] | √ | √ | √ | SP | MINLP | HA | |||||
| Fattahi Canel et al., 2020 [38] | √ | √ | √ | √ | SP | MINLP | EA | ||||
| Contreras et al., 2011 [39] | √ | √ | √ | SP | MINLP | EA | |||||
| Alumur et al., 2016 [40] | √ | √ | √ | SP | MILP | EA | |||||
| Fotuhi et al., 2018 [41] | √ | √ | √ | SP | MILP | HA | |||||
| Gelareh et al., 2015 [37] | √ | √ | √ | SP | MINLP | HA | |||||
| Wang et al., 2008 [42] | √ | √ | √ | √ | SP | MILP | HA | ||||
| Khosravian et al., 2019 [43] | √ | √ | √ | √ | SP | MILP | EA | ||||
| Reddy et al., 2022 [44] | √ | √ | √ | √ | √ | SP | MILP | EA | |||
| Bashiri et al., 2018 [45] | √ | √ | √ | SP | MILP | HA | |||||
| Goodarzian et al., 2021 [46] | √ | √ | √ | √ | √ | √ | MP | MILP | HA | ||
| Ghaderi et al., 2013 [47] | √ | √ | √ | MP | MILP | HA | |||||
| Wan et al., 2023 [48] | √ | √ | √ | √ | MP | MILP | HA | ||||
| Delfani et al., 2022 [49] | √ | √ | √ | √ | √ | √ | MP | MINLP | HA | ||
| This paper | √ | √ | √ | √ | √ | √ | MP | MINLP | HA | ||
| Sets | |
|---|---|
| Set of construction sections, | |
| Set of MDCs, | |
| Set of potential construction logistic centers, | |
| Set of construction periods, | |
| Set of construction materials, | |
| Parameters | |
| Total demand for construction materials of construction section in period | |
| Daily demand for construction materials of construction section in period | |
| Safety stock period (the CLC is required to reserve a safety stock of construction materials for days of continuous construction for the construction sections it serves) | |
| Duration of period | |
| Distance between MDC and construction logistic center | |
| Distance between CLC and construction section | |
| Coverage of CLCs | |
| Unit transportation cost of construction materials from material logistic center to CLC | |
| Unit transportation cost of construction materials from construction logistic center to construction section | |
| Transportation risk factor between MDC and construction logistic center | |
| Transportation risk factor between construction logistic center and construction section | |
| Maximum stockpile capacity for material in construction logistic center | |
| Minimum utilization of construction logistic center opening; | |
| Area of construction logistic center | |
| Unit construction costs for construction logistic center | |
| Unit closing costs for construction logistic center | |
| Unit opening costs for construction logistic center | |
| Unit fixed operating costs for construction logistic center | |
| Unit warehousing costs for material in construction logistic centers | |
| A sufficiently large constant | |
| Variables | |
| 1 if the construction logistic center is open in the period , 0 otherwise | |
| 1 if the material demand at construction logistic center is supplied by material distribution point in period , 0 otherwise | |
| 1 if the material demand for construction sections is supplied by construction logistic center in period , 0 otherwise | |
| The safety stock of construction materials at construction logistic center in period | |
| The total amount of construction materials transported to the construction logistic center by the MDC in period | |
| The total amount of construction materials transported from construction logistic center to construction sections in period |
| Number | Periodic Average Daily Demand (t) | Number | Periodic Average Daily Demand (t) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | I | II | III | IV | V | ||
| 1 | 43.9 | 73.1 | 73.1 | 43.9 | / | 17 | / | 9.9 | 16.5 | 16.5 | 9.9 |
| 2 | 25.2 | 42 | 42 | 25.2 | / | 18 | / | 25.2 | 42.1 | 42.1 | 25.2 |
| 3 | 8.5 | 14.2 | 14.2 | 8.5 | / | 19 | / | 21.8 | 36.3 | 36.3 | 21.8 |
| 4 | 95.3 | 158.8 | 158.8 | 95.3 | / | 20 | / | 11.1 | 18.6 | 18.6 | 11.1 |
| 5 | 43.3 | 72.1 | 72.1 | 43.3 | / | 21 | / | 21.9 | 36.4 | 36.4 | 21.9 |
| 6 | / | 48.6 | 81.0 | 81.0 | 48.6 | 22 | / | 8.5 | 14.1 | 14.1 | 8.5 |
| 7 | / | 17.3 | 28.8 | 28.8 | 17.3 | 23 | / | 21.1 | 35.2 | 35.2 | 21.1 |
| 8 | / | 19.7 | 32.9 | 32.9 | 19.7 | 24 | / | 7.6 | 12.7 | 12.7 | 7.6 |
| 9 | / | 33.5 | 55.8 | 55.8 | 33.5 | 25 | 9 | 15.1 | 15.1 | 9 | / |
| 10 | / | 26 | 43.4 | 43.4 | 26 | 26 | 4.6 | 7.6 | 7.6 | 4.6 | / |
| 11 | / | 20.4 | 33.9 | 33.9 | 20.4 | 27 | 19.1 | 31.8 | 31.8 | 19.1 | / |
| 12 | / | 16 | 26.6 | 26.6 | 16 | 28 | 14.1 | 23.5 | 23.5 | 14.1 | / |
| 13 | / | 14.7 | 24.4 | 24.4 | 14.7 | 29 | 12.7 | 21.2 | 21.2 | 12.7 | / |
| 14 | / | 4 | 6.7 | 6.7 | 4 | 30 | 13.2 | 22 | 22 | 13.2 | / |
| 15 | / | 24.7 | 41.2 | 41.2 | 24.7 | 31 | 10.3 | 17.1 | 17.1 | 10.3 | / |
| 16 | / | 15.4 | 25.7 | 25.7 | 15.4 | 32 | 10.6 | 17.7 | 17.7 | 10.6 | / |
| Potential CLC Number | Area (mu 1) | Potential CLC-Related Unit Costs (RMB/mu) | Capacity Ceiling (t) | |||||
|---|---|---|---|---|---|---|---|---|
| Construction | Opening | Fixed Operating | Closing | Steel | Fly Ash | Cement | ||
| 1 | 50 | 200,000 | 30,000 | 80,000 | 60,000 | 10,000 | 100,000 | 12,000 |
| 2 | 40 | 200,000 | 30,000 | 80,000 | 60,000 | 8000 | 80,000 | 9600 |
| 3 | 30 | 300,000 | 40,000 | 100,000 | 80,000 | 6000 | 60,000 | 7200 |
| 4 | 40 | 300,000 | 50,000 | 100,000 | 80,000 | 8000 | 80,000 | 9600 |
| 5 | 40 | 300,000 | 50,000 | 120,000 | 80,000 | 8000 | 80,000 | 9600 |
| 6 | 35 | 350,000 | 50,000 | 120,000 | 90,000 | 7000 | 70,000 | 8400 |
| 7 | 45 | 500,000 | 60,000 | 150,000 | 90,000 | 9000 | 90,000 | 10,800 |
| 8 | 45 | 500,000 | 60,000 | 150,000 | 100,000 | 9000 | 90,000 | 10,800 |
| 9 | 40 | 500,000 | 60,000 | 160,000 | 120,000 | 8000 | 80,000 | 9600 |
| 10 | 45 | 500,000 | 70,000 | 160,000 | 120,000 | 9000 | 90,000 | 10,800 |
| 11 | 50 | 500,000 | 70,000 | 160,000 | 140,000 | 10,000 | 100,000 | 12,000 |
| 12 | 40 | 300,000 | 60,000 | 140,000 | 90,000 | 8000 | 80,000 | 9600 |
| 13 | 50 | 300,000 | 50,000 | 120,000 | 80,000 | 10,000 | 100,000 | 12,000 |
| Modeling Objective | Single-Period Model | Multiperiod Model |
|---|---|---|
| Transportation costs (RMB) | 2.55 × 1010 | 2.55 × 1010 |
| Construction cost (RMB) | 7.35 × 107 | 9.7 × 107 |
| Opening cost (RMB) | 1.03 × 107 | 1.29 × 107 |
| Closing cost (RMB) | 1.94 × 107 | 2.81 × 107 |
| Operating cost (RMB) | 3.28 × 108 | 1.19 × 108 |
| Warehousing cost (RMB) | 1.58 × 107 | 1.57 × 107 |
| Total cost (RMB) | 2.59 × 1010 | 2.38 × 1010 |
| Risk factor | 5,275,545 | 4,794,092 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 1 | 2 | ||
| 2 | Population size | 50 | |
| Initial crossover probability | 0.6 | Iterations | 500 |
| Initial mutation probability | 0.05 |
| Objective | EHR-NSGA-II | NSGA-II | NSGA-II-ARSBX | NSGA-III |
|---|---|---|---|---|
| Total Cost (RMB) | 1.93 × 1010 | 2.32 × 1010 | 2.25 × 1010 | 2.56 × 1010 |
| Gap | / | 16.8% | 14.2% | 24.6% |
| Risk factor | 4,191,693 | 4,678,358 | 4,220,307 | 4,271,501 |
| Gap | / | 10.4% | 0.7% | 1.9% |
| Evaluation Indicators | EHR-NSGA-II | NSGA-II | NSGA-II-ARSBX | NSGA-III |
|---|---|---|---|---|
| Pareto solution quantity | 18 | 7 | 13 | 10 |
| Gap | / | 157.1% | 38.5% | 80% |
| Spread | 6.56 × 109 | 6.49 × 108 | 3.1 × 109 | 2.25 × 109 |
| Gap | / | 910.8% | 111.6% | 191.6% |
| Spacing | 1.81 × 107 | 2.03 × 107 | 3.96 × 107 | 6.32 × 107 |
| Gap | / | 10.8% | 54.3% | 71.4% |
| No. | Total Cost | Risk Factor | No. | Total Cost | Risk Factor | No. | Total Cost | Risk Factor |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.93 × 1010 | 5,981,568 | 7 | 2.03 × 1010 | 5,335,713 | 13 | 2.30 × 1010 | 4,743,494 |
| 2 | 1.97 × 1010 | 5,869,065 | 8 | 2.05 × 1010 | 5,215,202 | 14 | 2.34 × 1010 | 4,617,659 |
| 3 | 1.98× 1010 | 5,709,204 | 9 | 2.06 × 1010 | 5,202,250 | 15 | 2.37 × 1010 | 4,596,207 |
| 4 | 1.98 × 1010 | 5,572,658 | 10 | 2.1 × 1010 | 5,071,215 | 16 | 2.40 × 1010 | 4,440,042 |
| 5 | 1.99 × 1010 | 5,508,576 | 11 | 2.15 × 1010 | 4,973,909 | 17 | 2.42 × 1010 | 4,417,647 |
| 6 | 2.02 × 1010 | 5,355,170 | 12 | 2.26 × 1010 | 4,862,238 | 18 | 2.59 × 1010 | 4,191,694 |
| Objectives | Scheme I | Scheme II | Scheme III |
|---|---|---|---|
| Transportation costs (RMB) | 1,898,816 | 2,556,901 | 2,120,308 |
| Construction cost (RMB) | 10,450 | 9700 | 9550 |
| Opening cost (RMB) | 1600 | 1585 | 1420 |
| Closing cost (RMB) | 2820 | 2685 | 2505 |
| Operating cost (RMB) | 13,960 | 12,600 | 12,460 |
| Warehousing cost (RMB) | 1576 | 1576 | 1576 |
| Total cost (RMB) | 1,929,222 | 2,585,048 | 2,403,886 |
| Risk factor | 5,981,568 | 4,191,694 | 4,440,042 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, H.; Zhang, J.; Sun, W.; Yang, W.; Li, G. Multiperiod Location–Allocation Optimization of Construction Logistics Centers for Large-Scale Projects in Complex Environmental Regions. Buildings 2025, 15, 1045. https://doi.org/10.3390/buildings15071045
Shen H, Zhang J, Sun W, Yang W, Li G. Multiperiod Location–Allocation Optimization of Construction Logistics Centers for Large-Scale Projects in Complex Environmental Regions. Buildings. 2025; 15(7):1045. https://doi.org/10.3390/buildings15071045
Chicago/Turabian StyleShen, Hao, Jin Zhang, Wenjie Sun, Wenguang Yang, and Guoqi Li. 2025. "Multiperiod Location–Allocation Optimization of Construction Logistics Centers for Large-Scale Projects in Complex Environmental Regions" Buildings 15, no. 7: 1045. https://doi.org/10.3390/buildings15071045
APA StyleShen, H., Zhang, J., Sun, W., Yang, W., & Li, G. (2025). Multiperiod Location–Allocation Optimization of Construction Logistics Centers for Large-Scale Projects in Complex Environmental Regions. Buildings, 15(7), 1045. https://doi.org/10.3390/buildings15071045






