Seismic Response Analysis of Double-Layer Isolation Structures in High-Rise Buildings
Abstract
:1. Introduction
2. Numerical Model
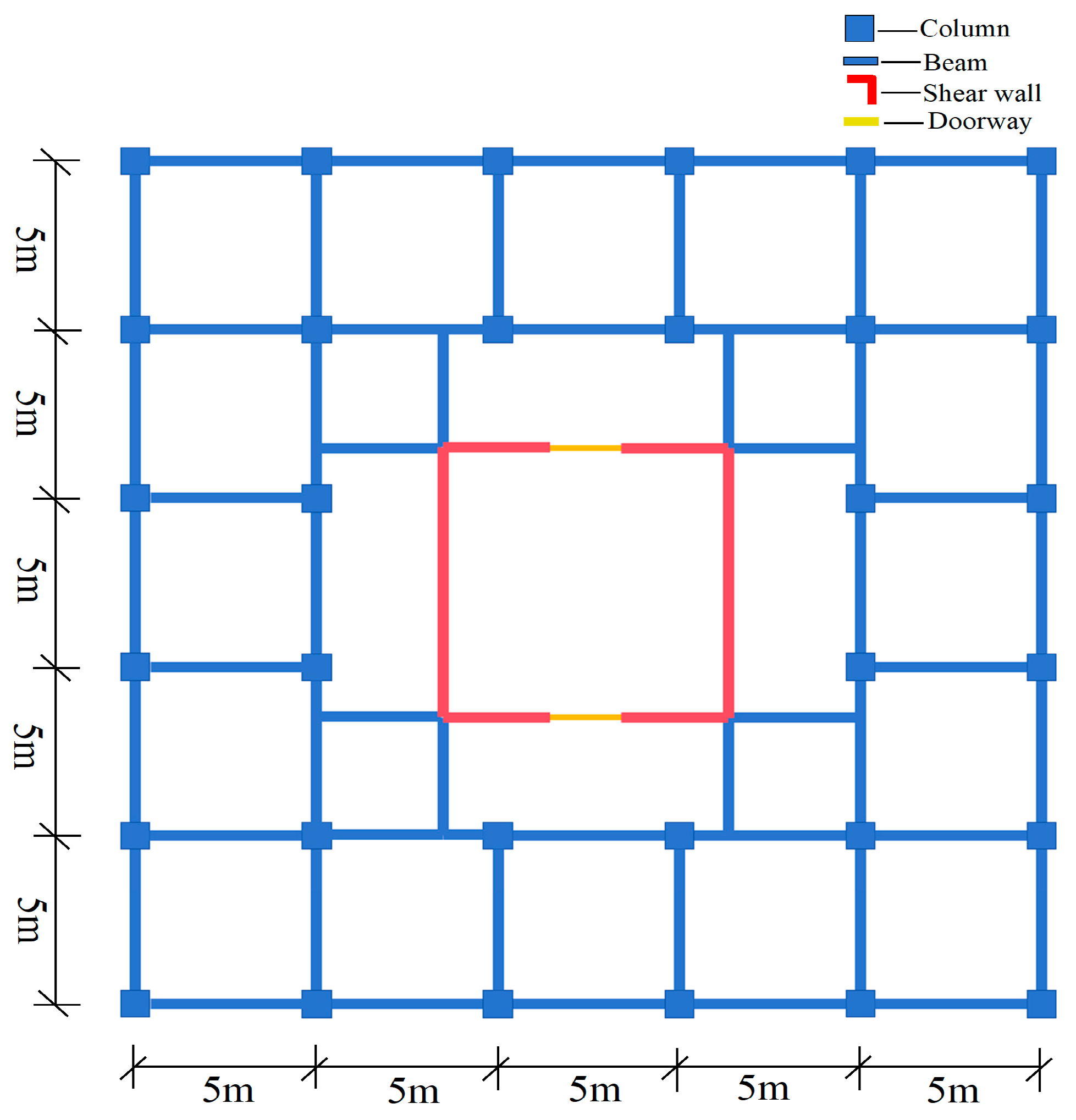
2.1. Engineering Overview
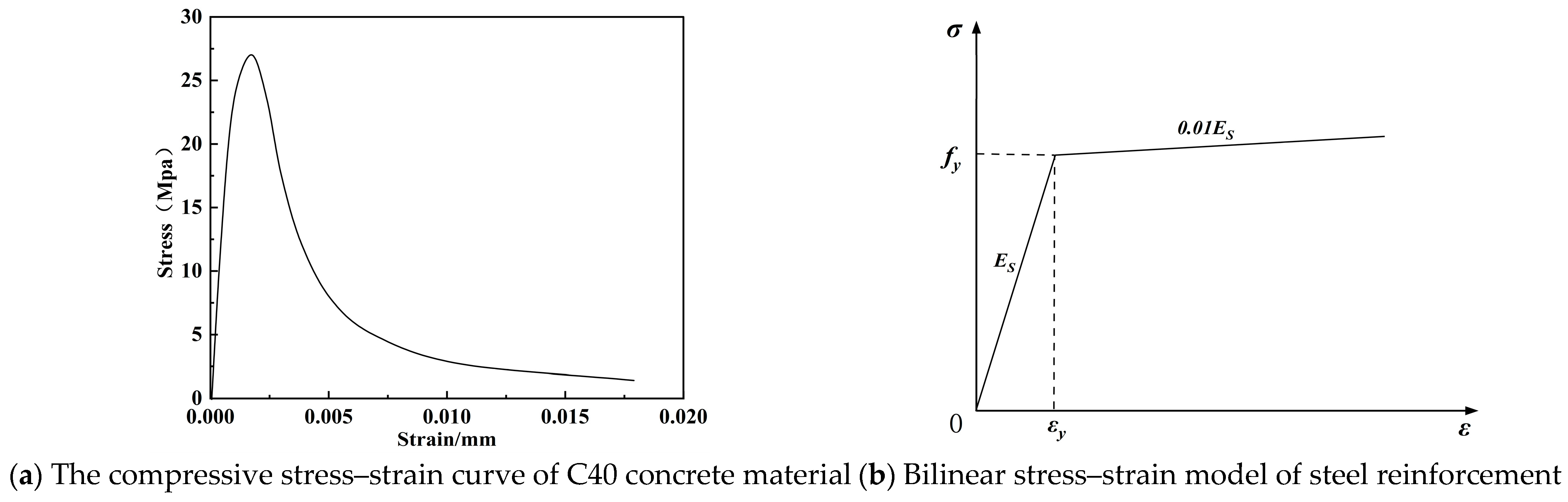
2.2. Numerical Simulation
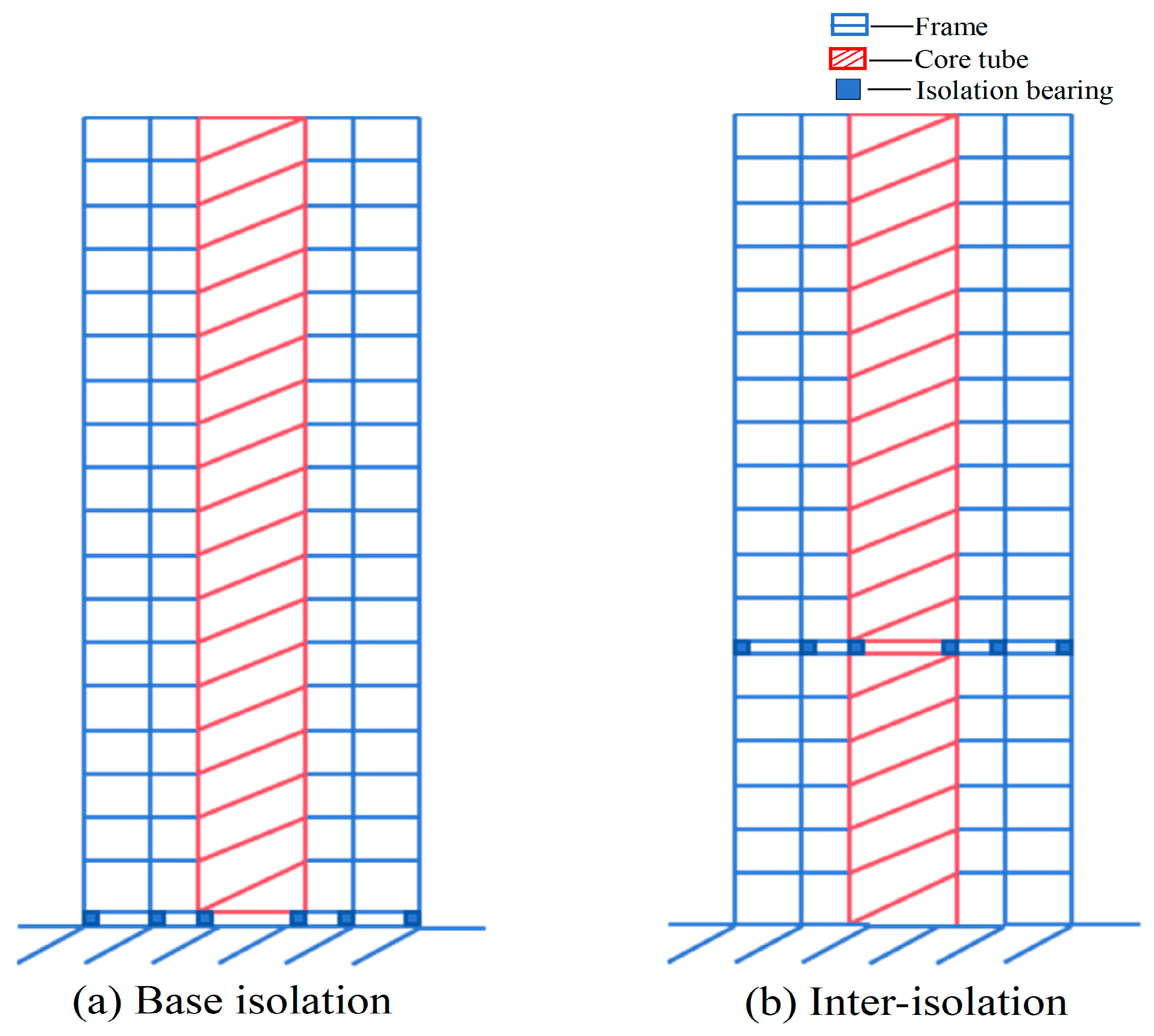
2.3. The Design of the Isolation Layer
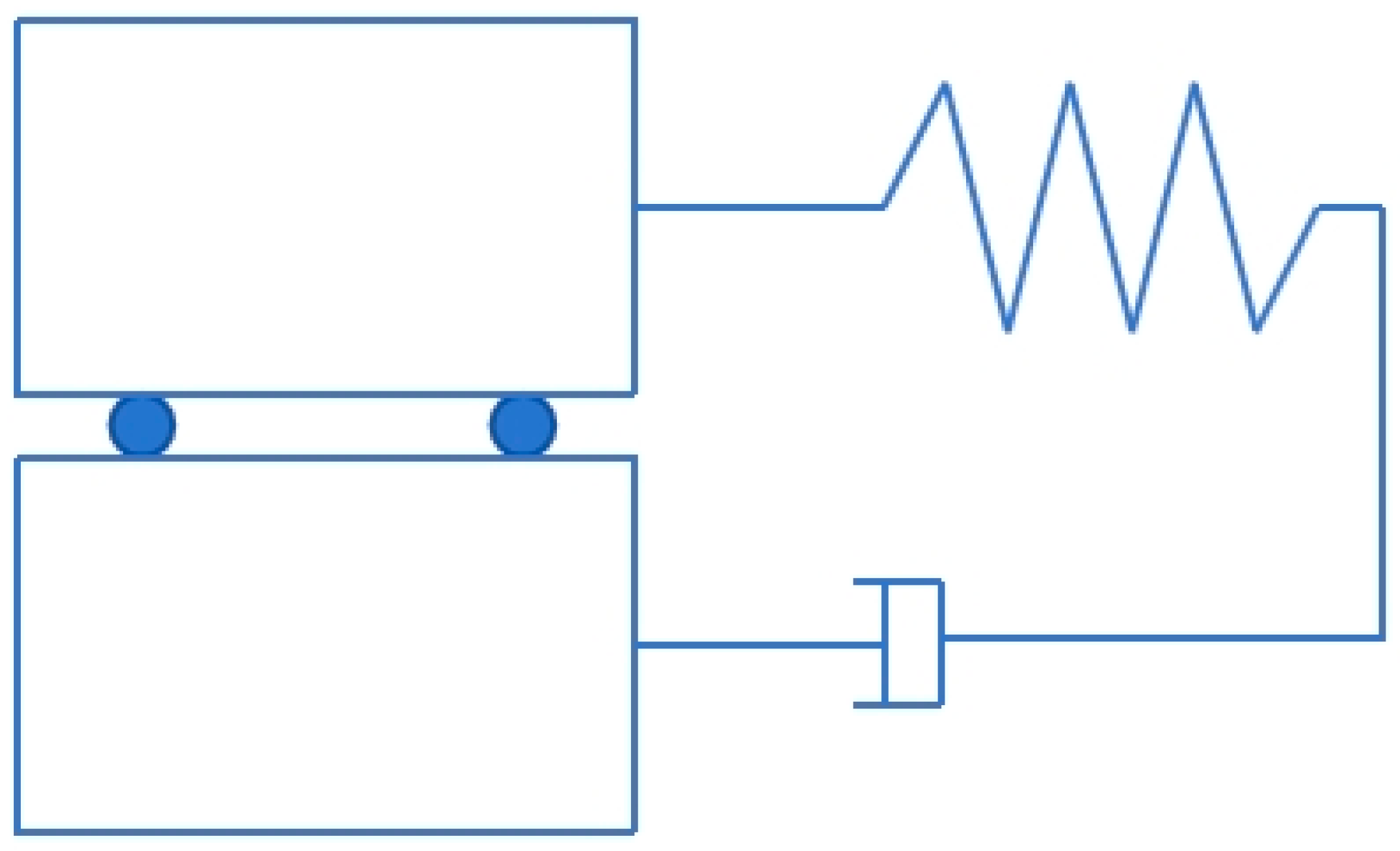
2.4. Simulation of the Seismic Isolation Bearings
2.5. Modal Analysis
2.6. Damping of the Upper Structure
2.6.1. Rayleigh Damping Model
2.6.2. Other Damping Mechanisms
- Material Hysteretic Damping
- 2.
- Frictional Damping at Joints
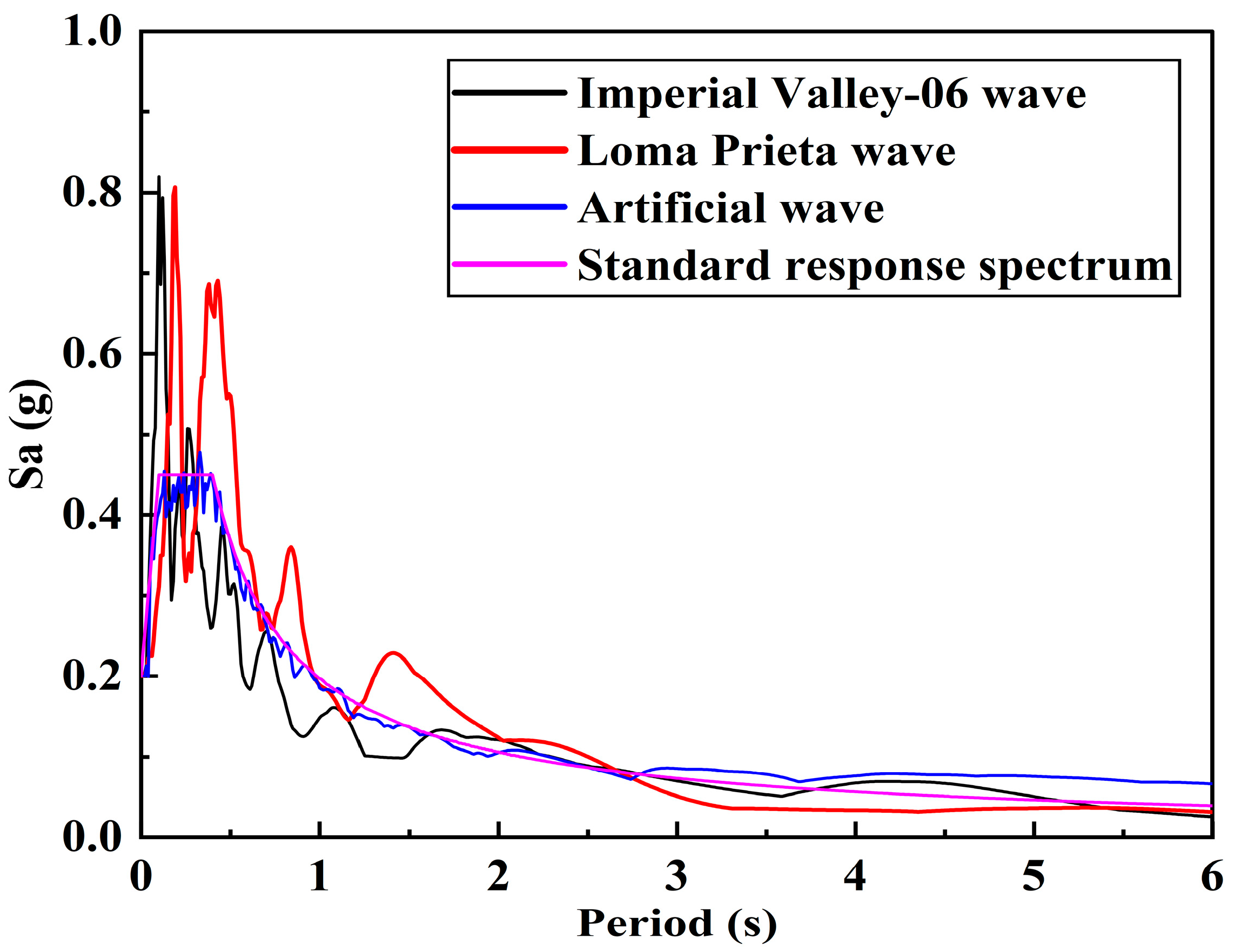
2.7. Selection of Seismic Waves
3. Elasto-Plastic Time History Analysis of Different Isolation Models
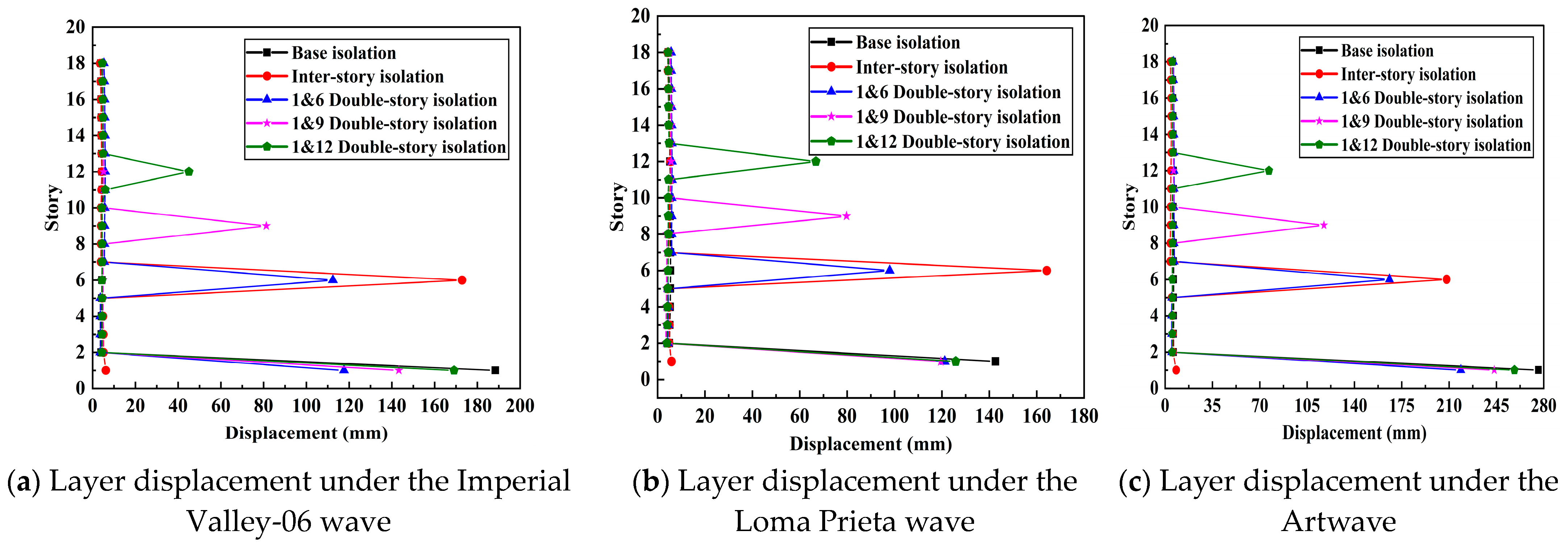
3.1. Inter-Story Displacement
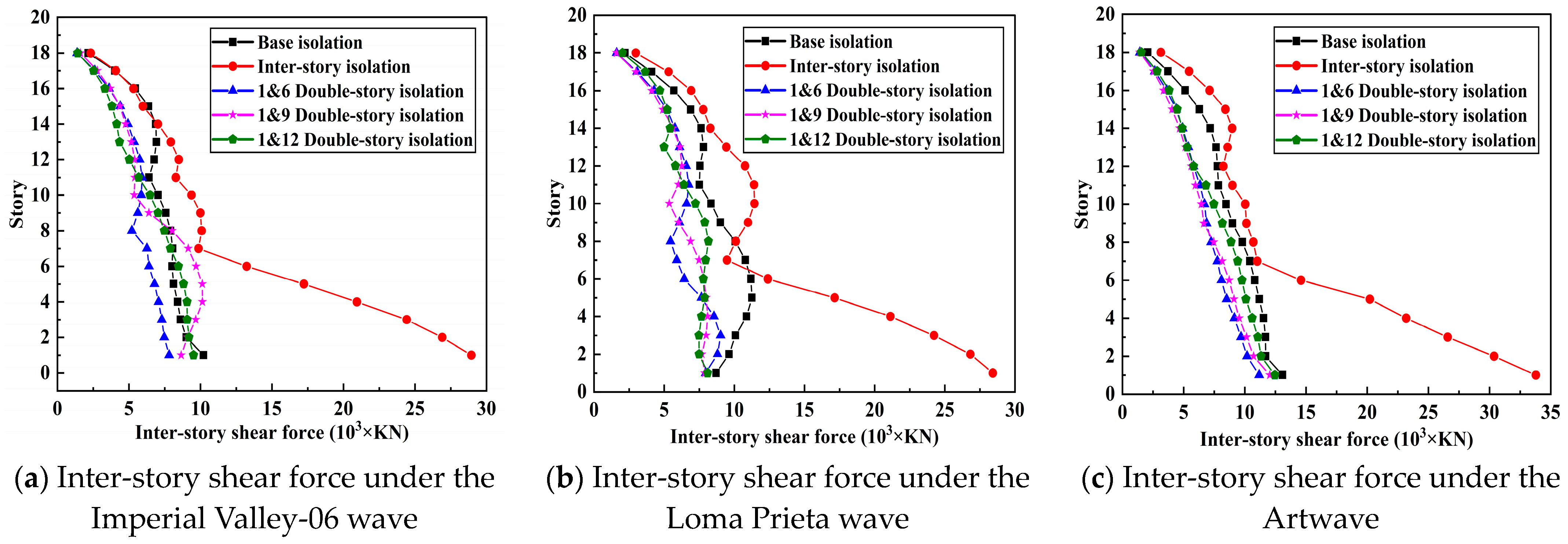
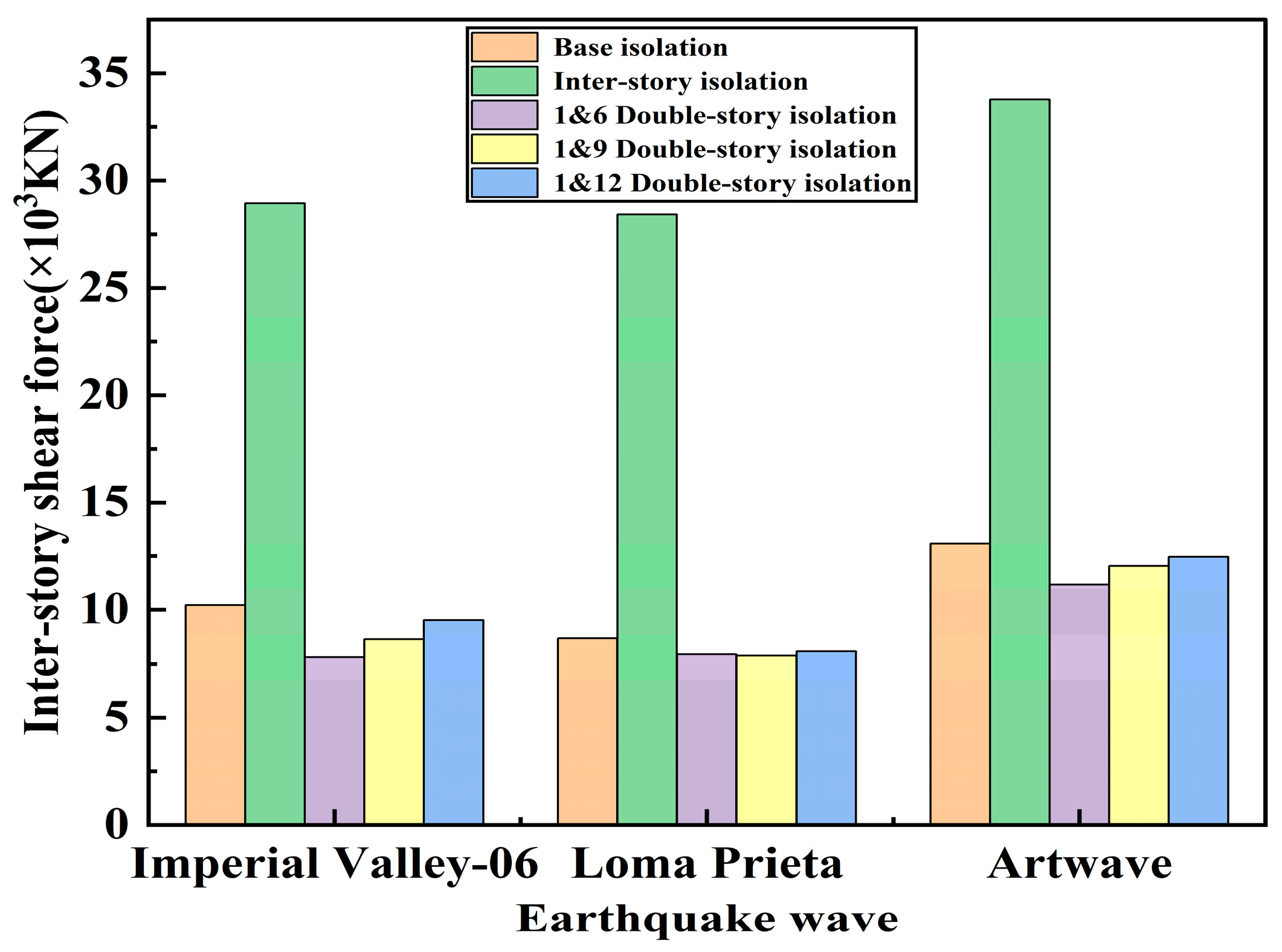
3.2. Inter-Story Shear Force
3.3. Top-Layer Acceleration
4. Stability Analysis
4.1. The Reaction Force of Isolation Bearings
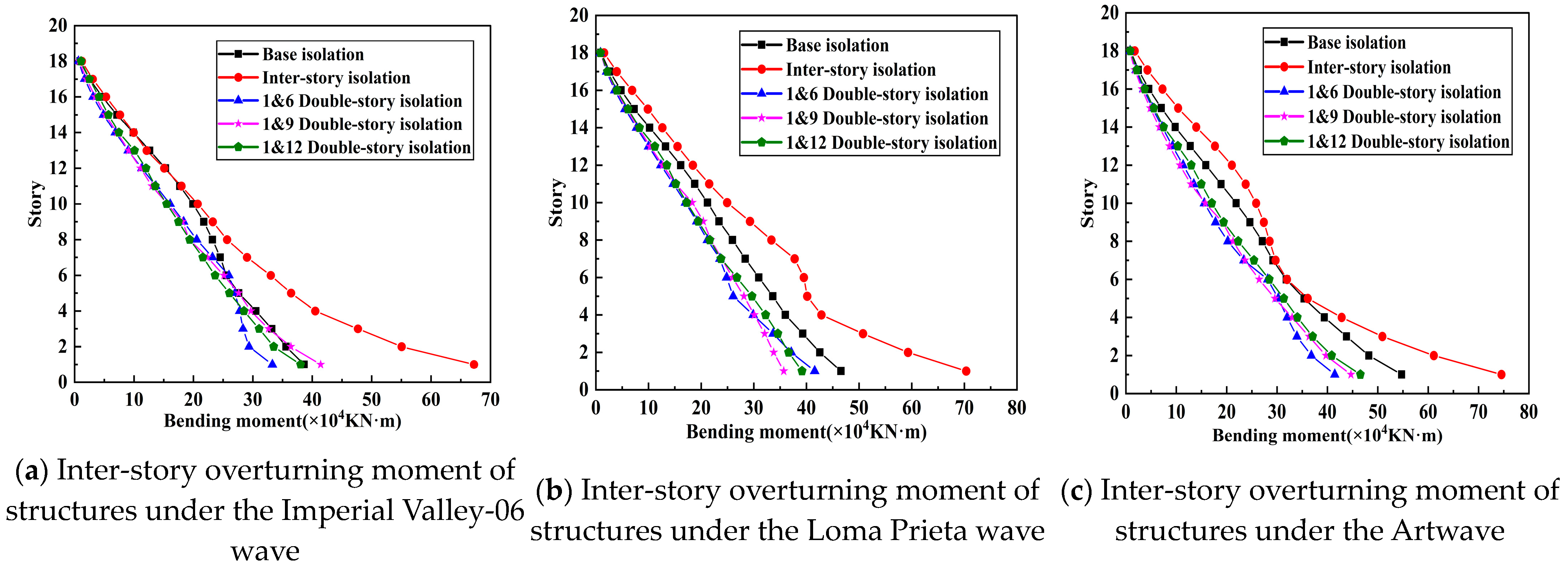
4.2. Overturning Moment of the Structure
5. Conclusions
- (1).
- Modal analysis indicates that a double-layer isolated structure can effectively extend the natural vibration period by adding an inter-story isolation layer, thereby reducing the impact of seismic forces. However, it should be noted that the higher the position of the second isolation layer, the weaker the period-lengthening effect.
- (2).
- The isolation layer can effectively concentrate and absorb inter-story displacement. The installation of an intermediate isolation layer helps distribute the displacement of the base isolation layer, limiting the maximum absolute displacement of the structure under rare earthquakes and preventing the risk of overall overturning.
- (3).
- Compared to single-layer isolation, double-layer isolation significantly reduces the overturning moment of the structure, improving the global stability of super high-rise buildings caused by bending deformation. This is particularly suitable for structures with large height-to-width ratios.
- (4).
- Double-layer isolation can further reduce the acceleration of the upper structure, decreasing inertial force-induced damage while also mitigating the risk of damage to indoor equipment and injuries to occupants. The optimal effect is achieved when the second isolation layer is located in the lower one-third of the building.
- (5).
- Current research on double-layer isolation still has limitations in period control, displacement distribution, applicability, and cost-effectiveness. Future improvements should focus on parametric optimization, multi-hazard analysis, smart isolation technologies, and life-cycle assessment to enhance engineering reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mimura, N.; Yasuhara, K.; Kawagoe, S.; Yokoki, H.; Kazama, S. Damage from the Great East Japan Earthquake and Tsunami-a quick report. Mitig. Adapt. Strateg. Glob. Change 2011, 16, 803–818. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, Y. Study on the distribution of earthquake damage in the Tangshan earthquake. Earthq. Eng. Eng. Vib. 2006, 26, 18–21. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, X. Field-observed phenomena of seismic liquefaction and subsidence during the 2008 Wenchuan earthquake in China. Nat. Hazards 2010, 54, 839–850. [Google Scholar] [CrossRef]
- Chen, M. Ying County Wooden Pagoda; Cultural Relics Publishing House: Beijing, China, 2001. [Google Scholar]
- Nakahara, K.O.J.I.; Hisatoku, T.; Nagase, T.; Takahashi, Y. Earthquake response of ancient five-story pagoda structure of Horyu-Ji temple in Japan. In Proceedings of the WCEE 2000, Auckland, New Zeland, 30 January–4 February 2020. [Google Scholar]
- Zhou, F.L. Progress of application and development in base isolation and passive energy dissipation for civil and industrial structures. In Proceedings of the International Post-SMiRT Conference Seminar, Cheju, Republic of Korea, 15–20 August 1999; Dongam Publishing: Seoul, Republic of Korea, 1999. [Google Scholar]
- Zhou, F.; Zhang, Y.; Tan, P. Theoretical study of inter layer isolation system. J. Civ. Eng. 2009, 42, 1–8. [Google Scholar]
- Nakai, A.; Sato, D.; Murakami, T.; Kasai, K. Evaluation of the stiffness of the seismic isolation layer and the upper structure based on the seismic observation records of super high-rise seismic isolation buildings. J. Archit. Build. Sci. 2018, 24, 571–576. [Google Scholar]
- Gupta, P.K.; Ghosh, G.; Pandey, D.K. Parametric study of effects of vertical ground motions on base isolated structures. J. Earthq. Eng. 2021, 25, 434–454. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, D.; Guo, Z.; Shan, H.; Huo, Y.; Li, X.; Lei, M. Study on the overturning resistance of a new staggered story isolated structure. Structures 2024, 65, 106709. [Google Scholar] [CrossRef]
- Chai, W.C. Mega-Sub Control of High-Rise Buildings; University of California: Irvine, CA, USA, 1996. [Google Scholar]
- Zhang, Y.; Tan, P.; Zhou, F. Parameter design and seismic performance study of segmented isolation new system. J. Civ. Eng. 2010, 270–275. [Google Scholar]
- Wang, X. New Type of SMA-Laminated Rubber Bearing and Its Segmented Isolation Study in High-Rise Buildings. Ph.D. Thesis, Liaoning Technical University, Fuxin, China, 2006. [Google Scholar]
- Zucca, M.; Reccia, E.; Vecchi, E.; Pintus, V.; Dessì, A.; Cazzani, A. An Evaluation of the Structural Behaviour of Historic Buildings Under Seismic Action: A Multidisciplinary Approach Using Two Case Studies. Appl. Sci. 2024, 14, 10274. [Google Scholar] [CrossRef]
- Zucca, M.; Longarini, N.; Simoncelli, M.; Aly, A.M. Tuned Mass Damper Design for Slender Masonry Structures: A Framework for Linear and Nonlinear Analysis. Appl. Sci. 2021, 11, 3425. [Google Scholar] [CrossRef]
- Acito, M.; Bocciarelli, M.; Chesi, C.; Milani, G. Collapse of the clock tower in Finale Emilia after the May 2012 Emilia Romagna earthquake sequence: Numerical insight. Eng. Struct. 2014, 72, 70–91. [Google Scholar] [CrossRef]
- Jain, A.; Acito, M.; Chesi, C. Seismic sequence of 2016–2017: Linear and non-linear interpretation models for evolution of damage in San Francesco church, Amatrice. Eng. Struct. 2020, 211, 110418. [Google Scholar] [CrossRef]
- Ou, J.; Wu, P.; Guan, X. Large displacement friction pendulum base layer and multi-layer seismic resilience structure. J. Disaster Prev. Mitig. Eng. 2021, 41, 657. [Google Scholar] [CrossRef]
- GB50011-2010; Standard for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2016.
- GB50010-2010; Standard for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2010.
- Du, J.; Sun, M.; Jiang, W.; Zhou, Z.; Wang, X.; Fang, Q. Magneto-mechanical hysteresis damping mechanism in dual-phase iron-based alloy with zero magnetostriction. J. Alloys Compd. 2024, 1005, 176120. [Google Scholar] [CrossRef]
- Qiaopula, X.L.; Lu, D. Structural Dynamics: Theory and Its Application in Earthquake Engineering; Higher Education Press: Beijing, China, 2007. [Google Scholar]
- Yang, G. Introduction to Elastoplastic Mechanics; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Skinner, R.I.; Robinson, W.H.; McVerry, G.H. An Introduction to Seismic Isolation; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- American Society of Civil Engineers. Minimum Design Loads for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2010. [Google Scholar]
- Zeng, D. Stiffness Characteristics of Rubber Isolation Bearings and Experimental Study on Seismic Performance of Isolated Buildings. Ph.D. Thesis, China Academy of Building Research, Beijing, China, 2007. [Google Scholar]
- Han, B.; Du, Y.; Hong, N.; Li, H.; Shi, C. Shaking Table Test Study on Dynamic Performance of a Base-Isolated Frame Structure under an Isolation Bearing Removal Scenario. Structures 2023, 48, 1141–1156. [Google Scholar] [CrossRef]
- Zhai, Z.; Liu, Y.; Guo, W.; Mercan, O.; Chen, H.; Zhou, F. A seismic resilient design method for structures equipped with two-level yielding dampers, accounting for extremely rare earthquakes. Eng. Struct. 2023, 294, 116797. [Google Scholar] [CrossRef]
- Sun, K.; Wang, L.; Su, H.; Geng, J.; Meng, B.; Wei, Z.; Wu, G. Damping properties and mechanism of aluminum matrix composites reinforced with glass cenospheres. Trans. Nonferrous Met. Soc. China 2024, 34, 2743–2755. [Google Scholar] [CrossRef]


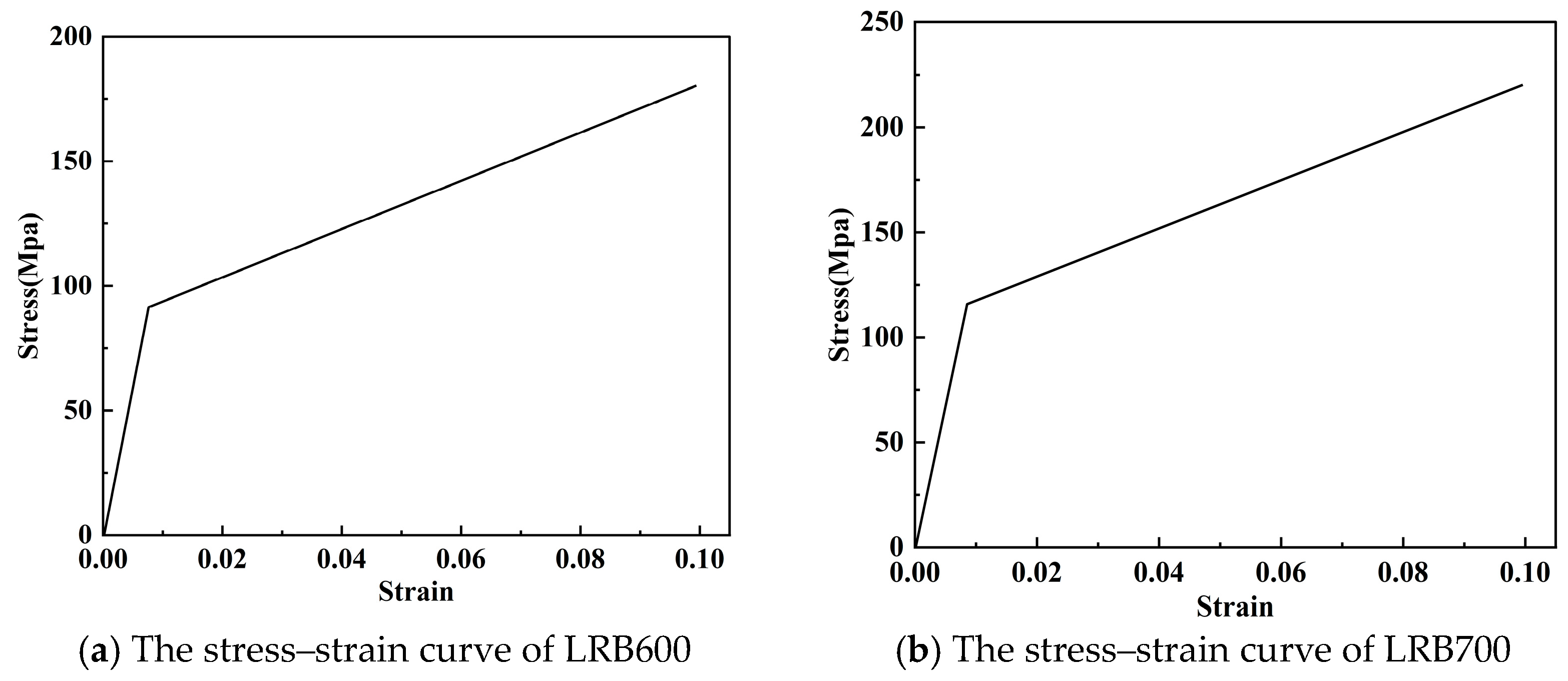




| Type | Effective Diameter (mm) | Total Rubber Thickness (mm) | Vertical Tensile Stiffness (kN/mm) | Vertical Compressive Stiffness (kN/mm) | Horizontal Initial Stiffness (kN/m) | Post-Yield Stiffness Ratio | Yield Force (kN) |
|---|---|---|---|---|---|---|---|
| LRB600 | 600 | 120 | 158.1 | 1581 | 11507 | 0.077 | 91.4 |
| LRB700 | 700 | 140 | 189.4 | 1894 | 13456 | 0.077 | 116.8 |
| Order | Base Isolation | Inter-Layer Isolation | 1&6 Double-Layer Isolation | 1&9 Double-Layer Isolation | 1&12 Double-Layer Isolation |
|---|---|---|---|---|---|
| 1 | 3.712 | 2.925 | 4.423 | 4.128 | 3.915 |
| 2 | 3.692 | 2.884 | 4.405 | 4.108 | 3.893 |
| 3 | 3.201 | 2.537 | 3.853 | 3.571 | 3.372 |
| 4 | 0.914 | 0.569 | 1.192 | 1.144 | 0.942 |
| 5 | 0.894 | 0.568 | 1.186 | 1.126 | 0.927 |
| 6 | 0.602 | 0.416 | 1.163 | 0.995 | 0.551 |
| Event | Time | Tg/g | Magnitude | Station | Soil Type | Vs (m/s) | Arias Intensity (m/s) | Site Class |
|---|---|---|---|---|---|---|---|---|
| Imperial Valley-06 | 1979 | 0.39 | 6.53 | El-Centro Array #1 | Dense soil | 213 | 0.85 | II |
| Loma Prieta | 1989 | 0.42 | 6.93 | Coyote Lake Dam Downst | Rock | 620 | 1.12 | I |
| ArtWave | / | 0.40 | / | / | Synthetic | / | 0.75 | II |
| Event | Isolation Layer | Base Isolation | Inter-Layer Isolation | 1&6 Double-Layer Isolation | 1&9 Double-Layer Isolation | 1&12 Double-Layer Isolation |
|---|---|---|---|---|---|---|
| Imperial Valley-06 | Base isolation layer | 188.4 | / | 117.5 | 143.2 | 169.07 |
| upper isolation layer | / | 172.8 | 112.3 | 81.2 | 45 | |
| Loma Prieta | Base isolation layer | 142.6 | / | 121.1 | 119.5 | 125.8 |
| upper isolation layer | / | 164.2 | 97.9 | 79.7 | 66.8 | |
| ArtWave | Base isolation layer | 276.1 | / | 218.7 | 243.4 | 258.3 |
| upper isolation layer | / | 208.1 | 165.9 | 117.4 | 76.9 |
| Event | Base Isolation | Inter-Layer Isolation | 1&6 Double-Layer Isolation | 1&9 Double-Layer Isolation | 1&12Double-Layer Isolation |
|---|---|---|---|---|---|
| Imperial Valley-06 wave | 2.41257 | 2.8982 | 1.56081 | 1.93322 | 1.67267 |
| Loma Prieta wave | 2.60483 | 3.3493 | 2.17983 | 1.98009 | 2.12722 |
| ArtWave | 2.40728 | 3.43319 | 1.60383 | 1.6527 | 1.56327 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Zhang, L.; Liu, D.; Shen, K. Seismic Response Analysis of Double-Layer Isolation Structures in High-Rise Buildings. Buildings 2025, 15, 1292. https://doi.org/10.3390/buildings15081292
Zhao G, Zhang L, Liu D, Shen K. Seismic Response Analysis of Double-Layer Isolation Structures in High-Rise Buildings. Buildings. 2025; 15(8):1292. https://doi.org/10.3390/buildings15081292
Chicago/Turabian StyleZhao, Guangxing, Lanfang Zhang, Dewen Liu, and Kaoshan Shen. 2025. "Seismic Response Analysis of Double-Layer Isolation Structures in High-Rise Buildings" Buildings 15, no. 8: 1292. https://doi.org/10.3390/buildings15081292
APA StyleZhao, G., Zhang, L., Liu, D., & Shen, K. (2025). Seismic Response Analysis of Double-Layer Isolation Structures in High-Rise Buildings. Buildings, 15(8), 1292. https://doi.org/10.3390/buildings15081292





