Fabrication and Characterization of Pneumatic Unit Cell Actuators
Abstract
:1. Introduction
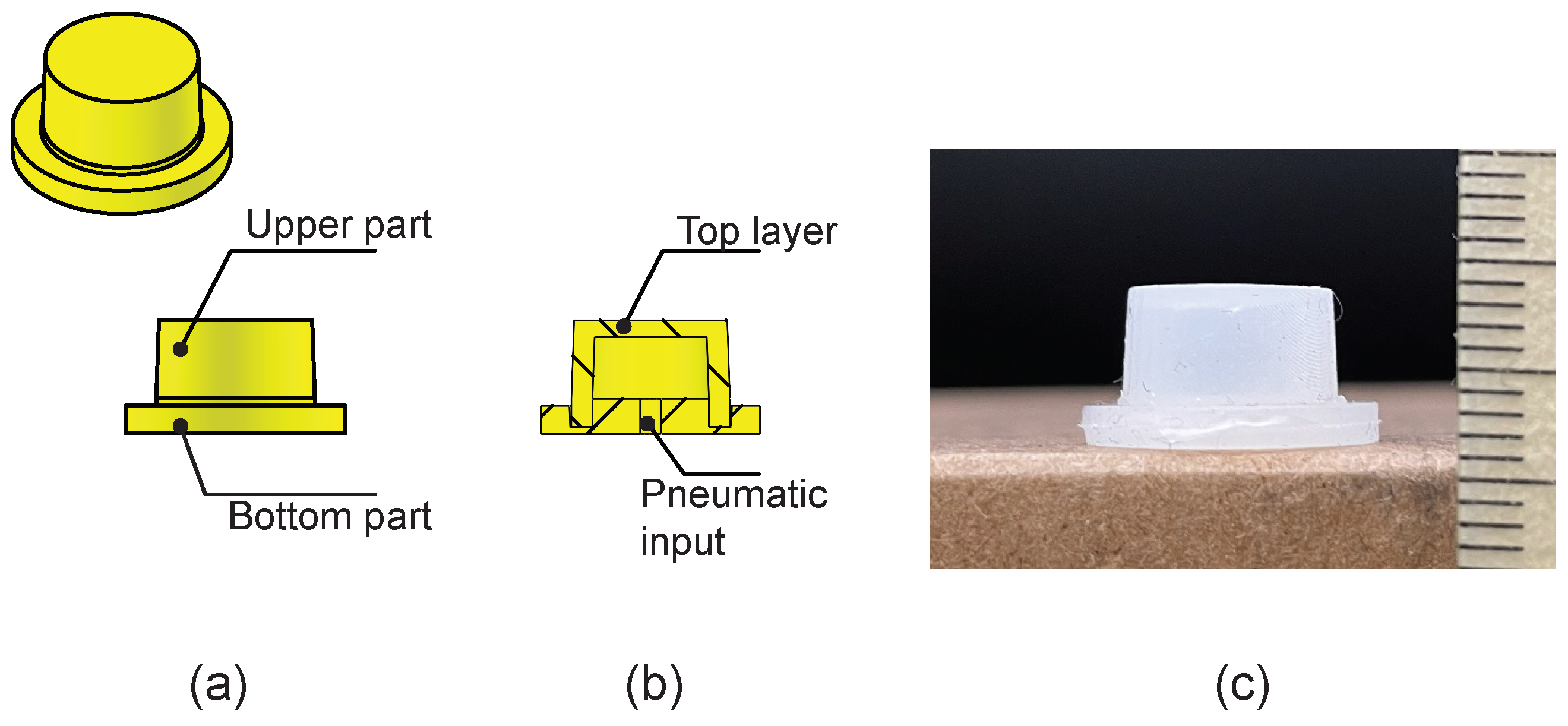
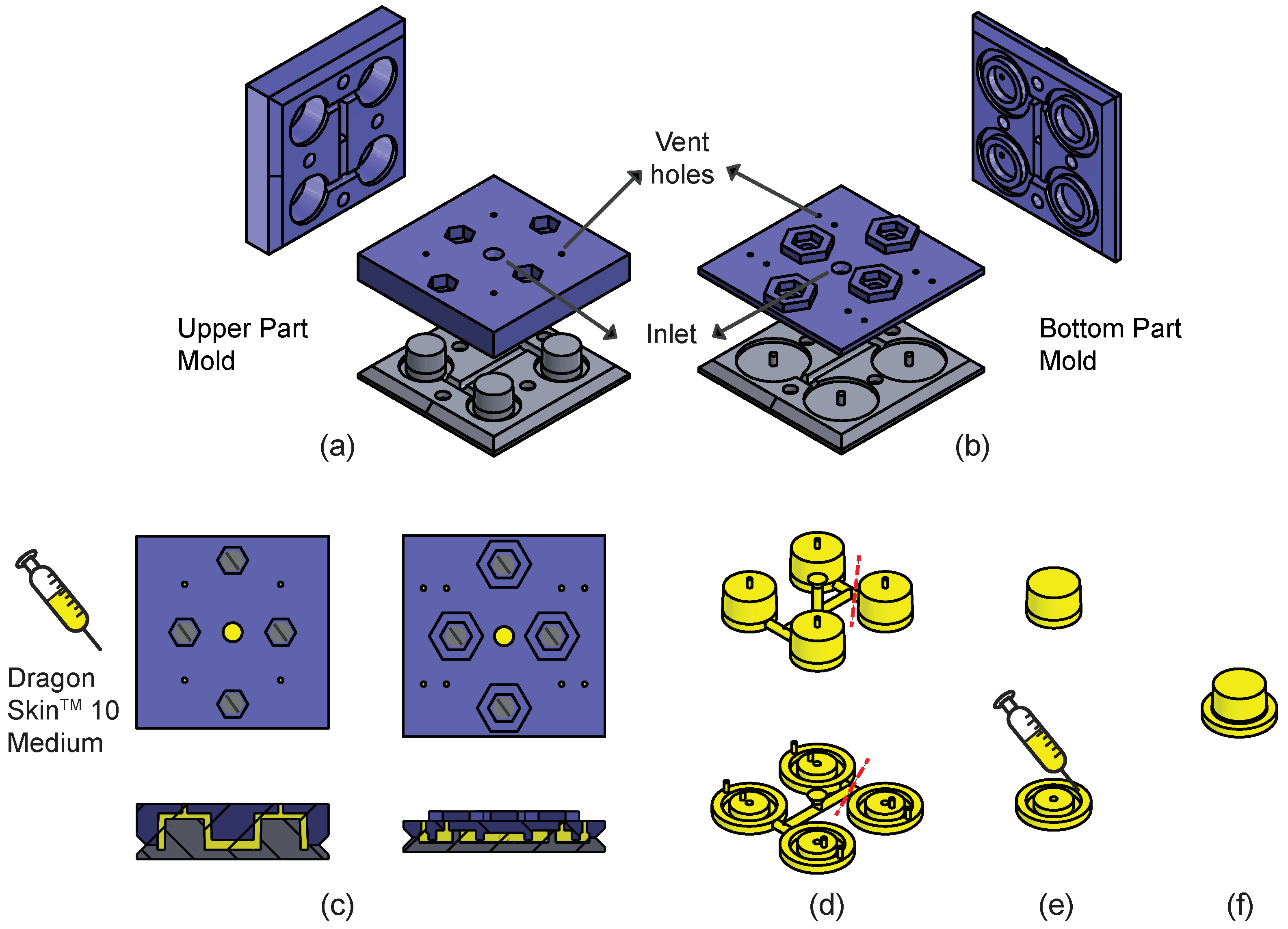
2. Fabrication of Pneumatic Unit Cells
2.1. Design and Fabrication Steps
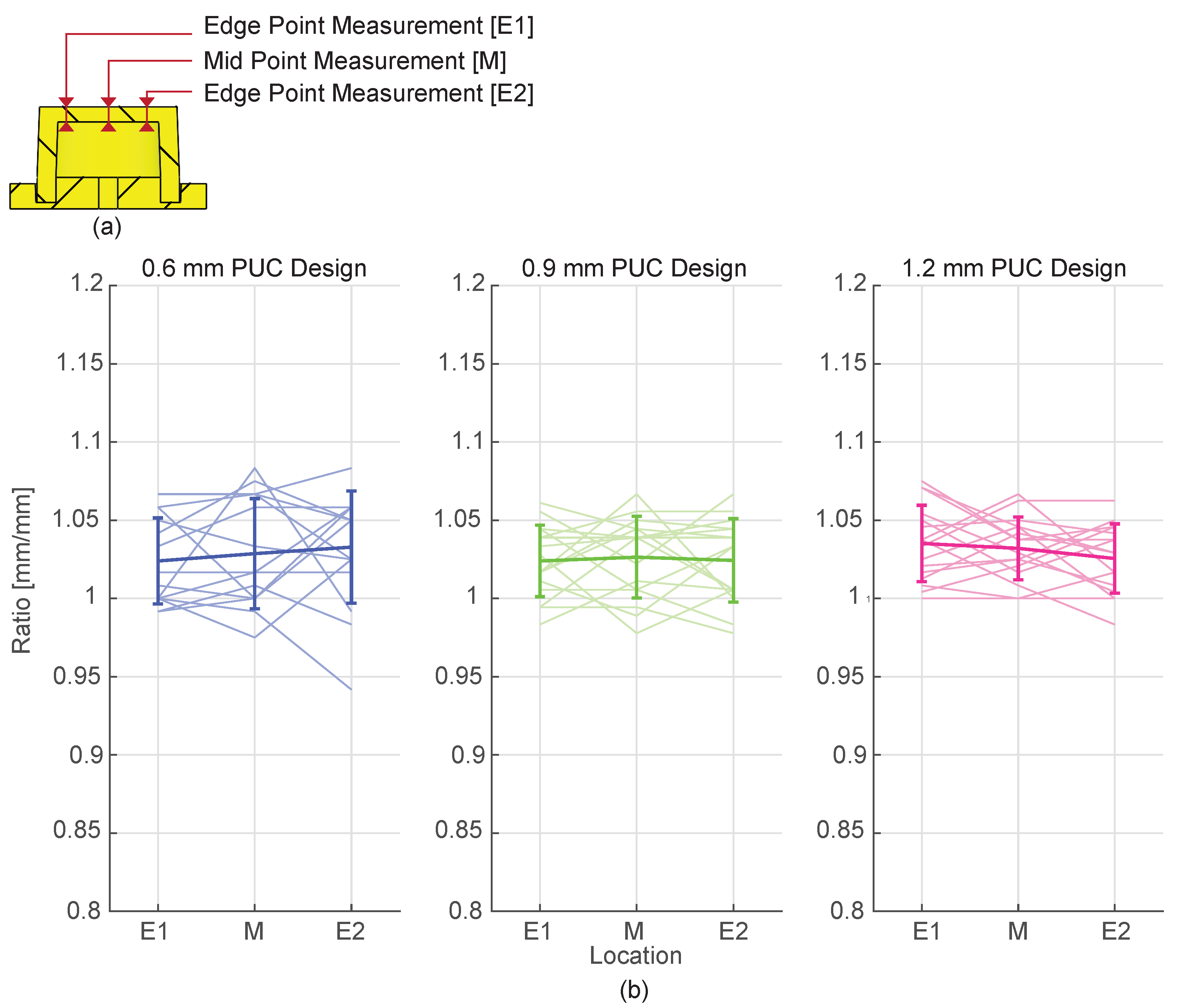
2.2. Method for Dimensional Measurements
2.3. Results
2.4. Discussion
3. Characterization of PUCs
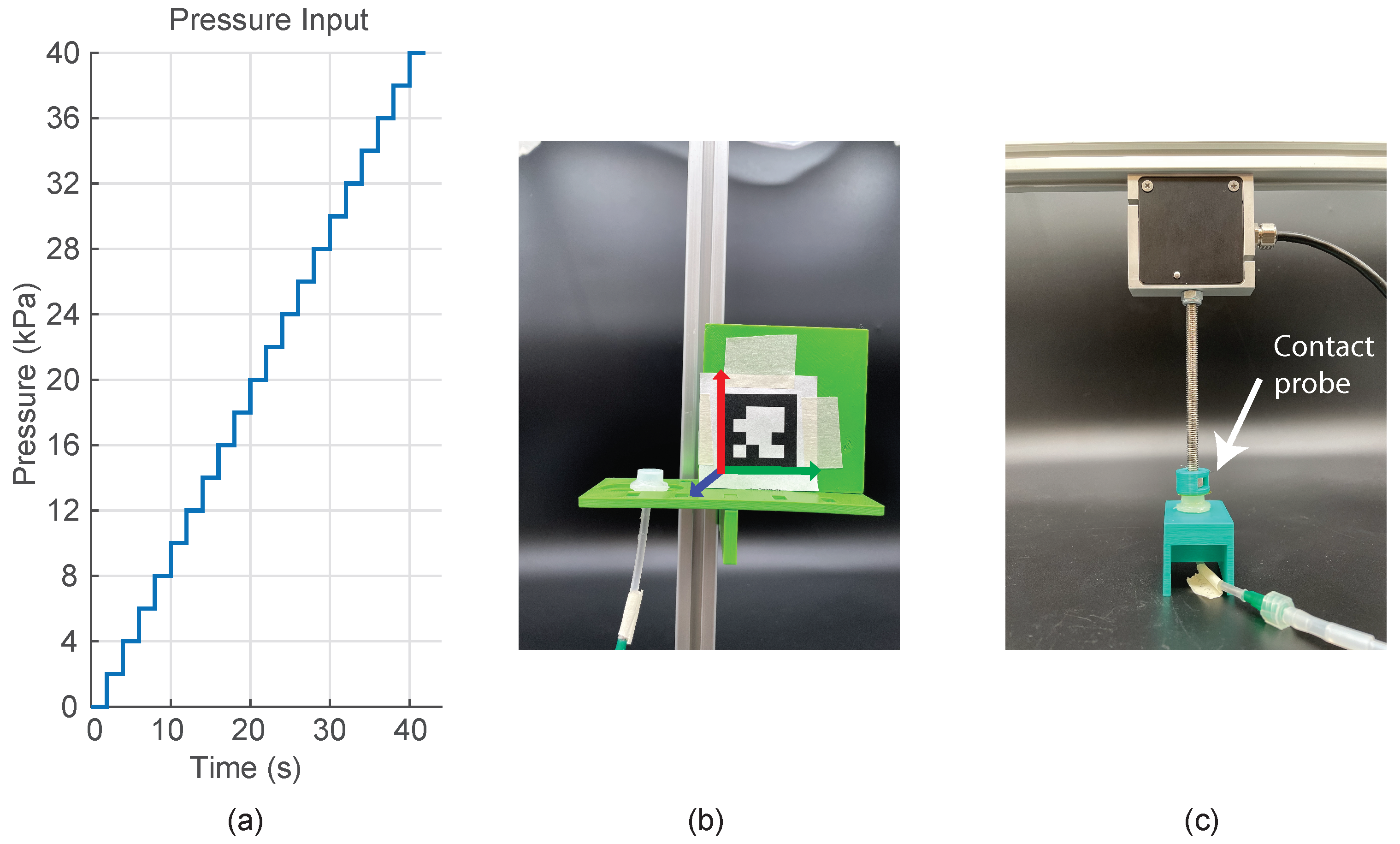
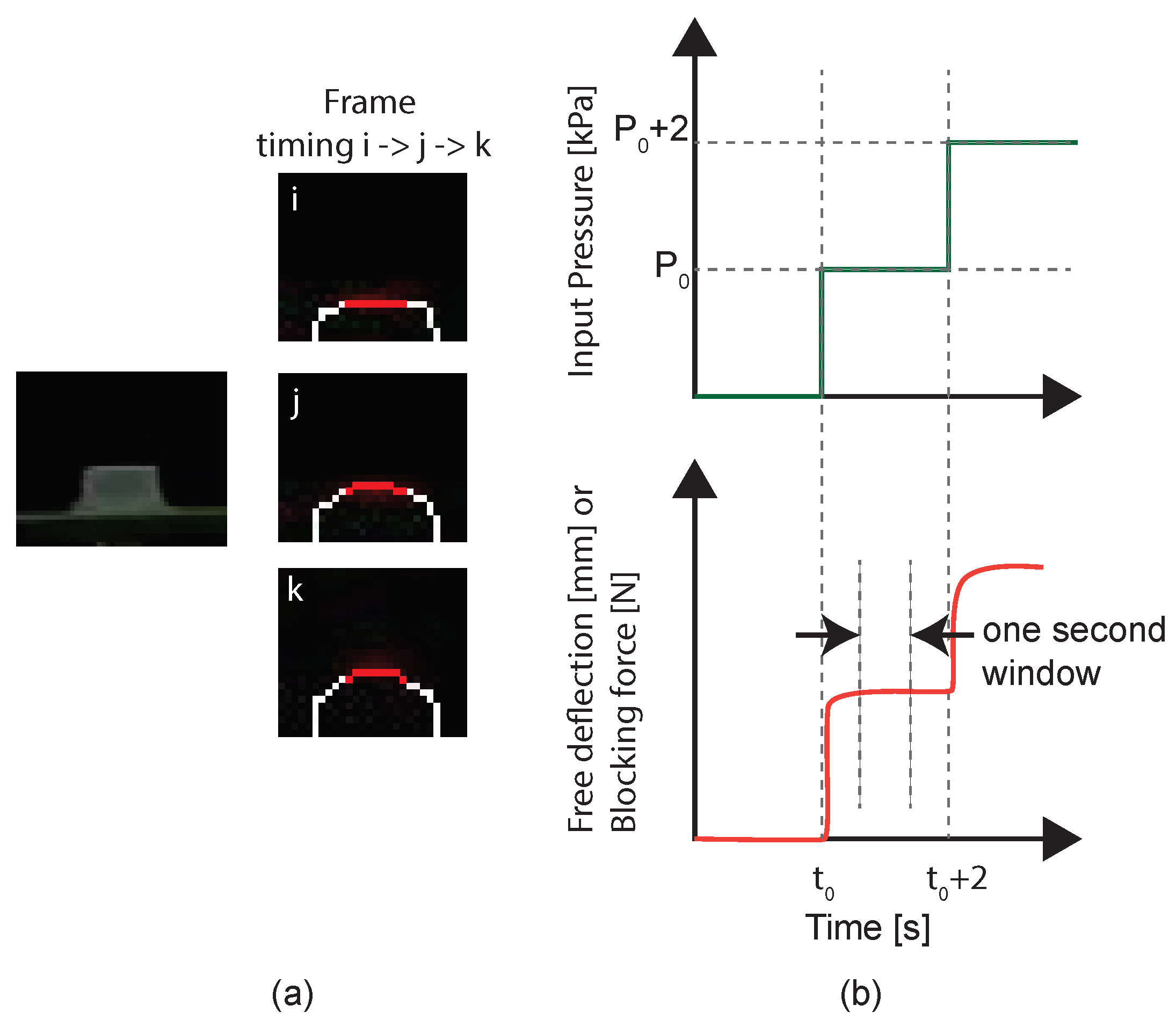
3.1. Hardware Setup
3.2. Static-Pressure Condition—Free-Deflection Measurement
3.2.1. Results
3.2.2. Discussion
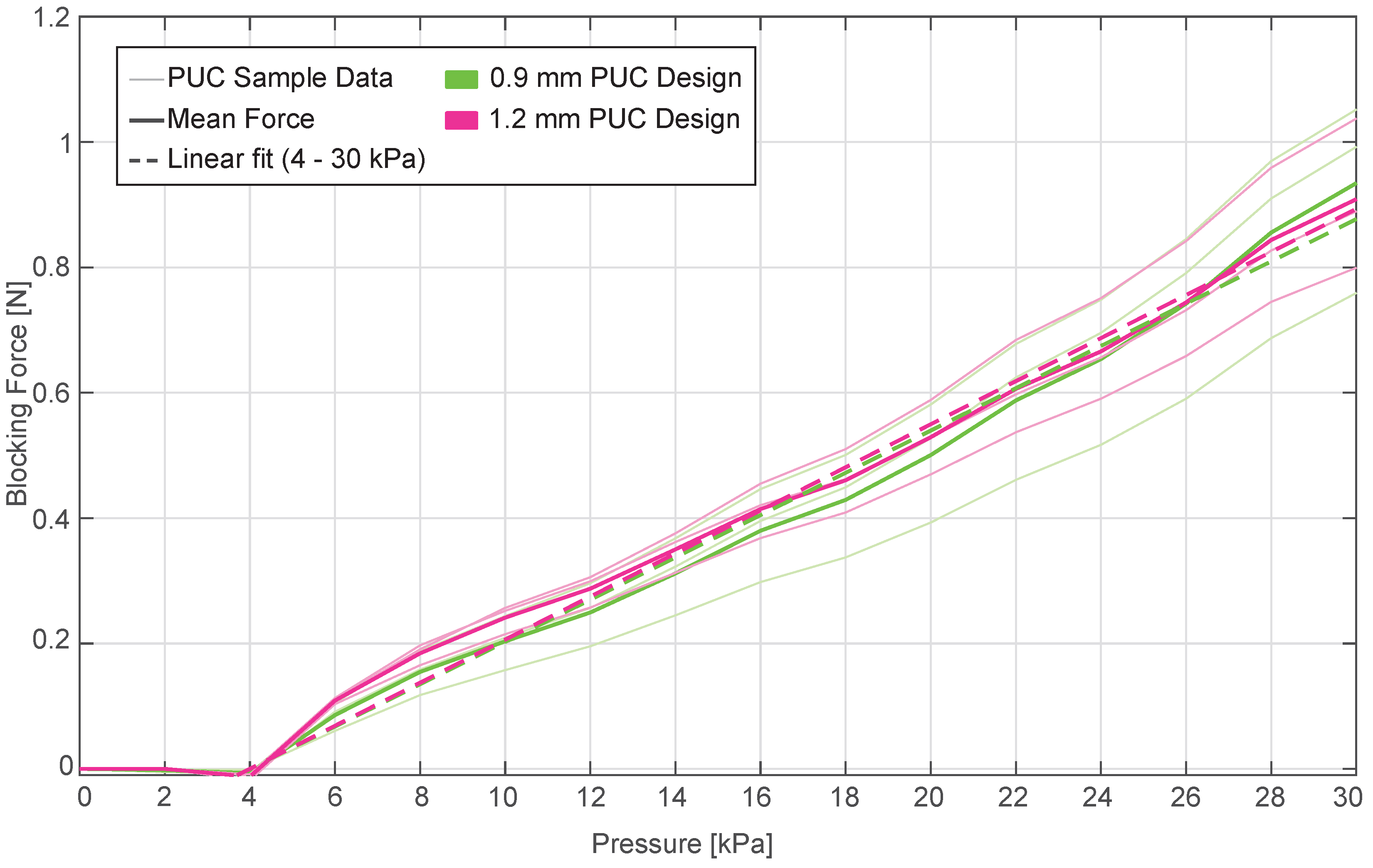
3.3. Static-Pressure Condition—Blocking-Force Measurement
3.3.1. Results
3.3.2. Discussion
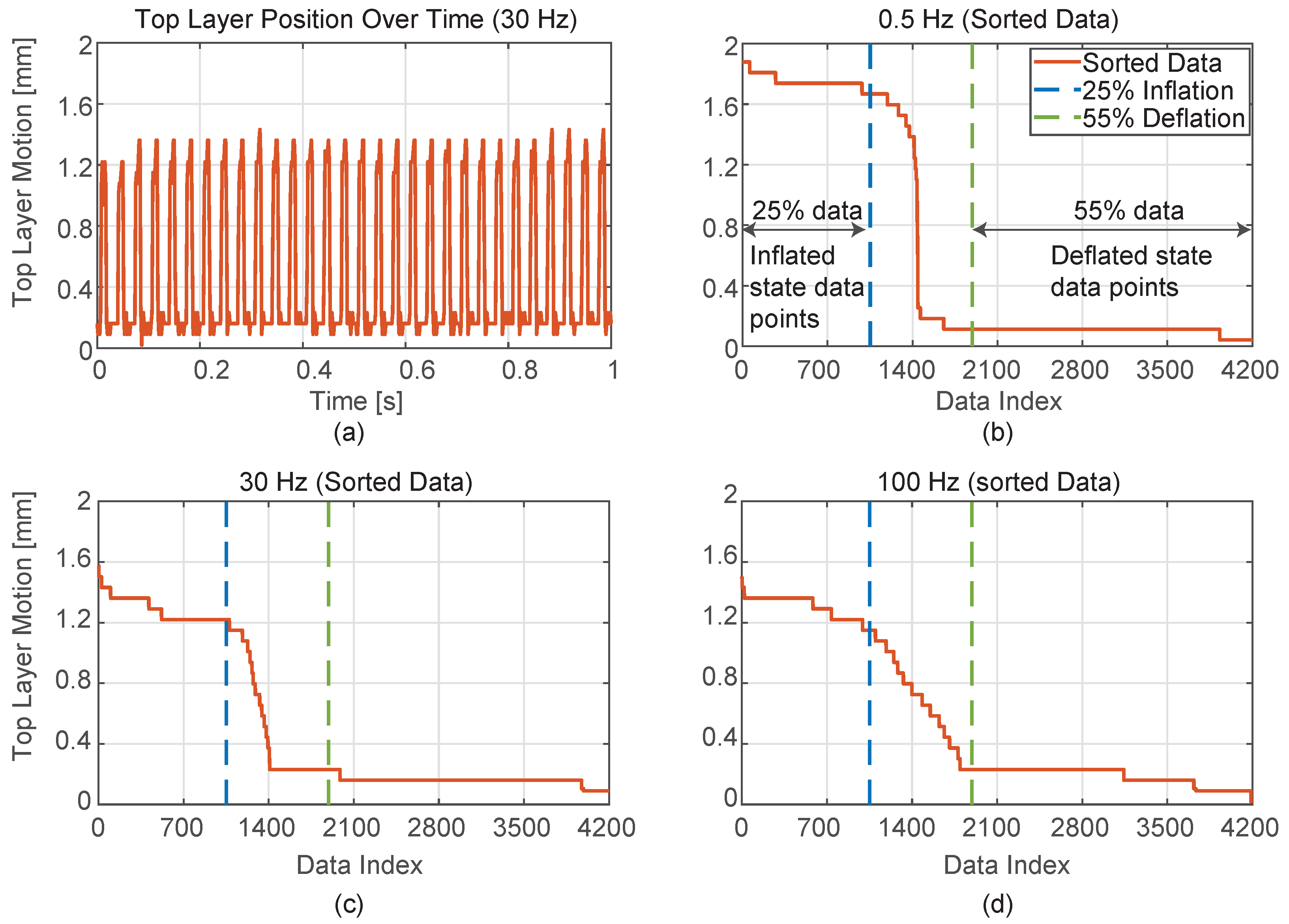
3.4. Frequency Condition—Free-Deflection Measurement
3.4.1. Results
3.4.2. Discussion
4. General Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Escobar-Castillejos, D.; Noguez, J.; Neri, L.; Magana, A.J.; Benes, B. A Review of Simulators with Haptic Devices for Medical Training. J. Med. Syst. 2016, 40, 104. [Google Scholar] [CrossRef] [PubMed]
- Enayati, N.; De Momi, E.; Ferrigno, G. Haptics in Robot-Assisted Surgery: Challenges and Benefits. IEEE Rev. Biomed. Eng. 2016, 9, 49–65. [Google Scholar] [CrossRef] [PubMed]
- Lederman, S.J.; Klatzky, R.L. Haptic perception: A tutorial. Atten. Percept. Psychophys. 2009, 71, 1439–1459. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, S.; Nagano, H.; Yamada, Y. Psychophysical Dimensions of Tactile Perception of Textures. IEEE Trans. Haptics 2013, 6, 81–93. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Ohnishi, K.; Xu, W. Multimodal Haptic Display for Virtual Reality: A Survey. IEEE Trans. Ind. Electron. 2020, 67, 610–623. [Google Scholar] [CrossRef]
- Bai, H.; Li, S.; Shepherd, R. Elastomeric Haptic Devices for Virtual and Augmented Reality. Adv. Funct. Mater. 2021, 31, 2009364. [Google Scholar] [CrossRef]
- Talhan, A.; Kumar, S.; Kim, H.; Hassan, W.; Jeon, S. Multi-mode soft haptic thimble for haptic augmented reality based application of texture overlaying. Displays 2022, 74, 102272. [Google Scholar] [CrossRef]
- Prattichizzo, D.; Pacchierotti, C.; Rosati, G. Cutaneous Force Feedback as a Sensory Subtraction Technique in Haptics. IEEE Trans. Haptics 2012, 5, 289–300. [Google Scholar] [CrossRef]
- Massimino, M.; Sheridan, T. Sensory Substitution for Force Feedback in Teleoperation. IFAC Proc. Vol. 1992, 25, 109–114. [Google Scholar] [CrossRef]
- Pacchierotti, C.; Prattichizzo, D.; Kuchenbecker, K.J. Cutaneous Feedback of Fingertip Deformation and Vibration for Palpation in Robotic Surgery. IEEE Trans. Biomed. Eng. 2016, 63, 278–287. [Google Scholar] [CrossRef]
- Pacchierotti, C.; Sinclair, S.; Solazzi, M.; Frisoli, A.; Hayward, V.; Prattichizzo, D. Wearable Haptic Systems for the Fingertip and the Hand: Taxonomy, Review, and Perspectives. IEEE Trans. Haptics 2017, 10, 580–600. [Google Scholar] [CrossRef] [PubMed]
- Leroy, E.; Hinchet, R.; Shea, H. Multimode Hydraulically Amplified Electrostatic Actuators for Wearable Haptics. Adv. Mater. 2020, 32, 2002564. [Google Scholar] [CrossRef] [PubMed]
- Leroy, E.; Shea, H. Hydraulically Amplified Electrostatic Taxels (HAXELs) for Full Body Haptics. Adv. Mater. Technol. 2023, 8, 2300242. [Google Scholar] [CrossRef]
- Grasso, G.; Rosset, S.; Shea, H. Fully 3D-Printed, Stretchable, and Conformable Haptic Interfaces. Adv. Funct. Mater. 2023, 33, 2213821. [Google Scholar] [CrossRef]
- Youn, J.H.; Mun, H.; Kyung, K.U. A Wearable Soft Tactile Actuator with High Output Force for Fingertip Interaction. IEEE Access 2021, 9, 30206–30215. [Google Scholar] [CrossRef]
- Hassan, W.; Kim, H.; Talhan, A.; Jeon, S. A Pneumatically-Actuated Mouse for Delivering Multimodal Haptic Feedback. Appl. Sci. 2020, 10, 5611. [Google Scholar] [CrossRef]
- Huaroto, J.J.; Suarez, E.; Krebs, H.; Marasco, P.; Vela, E. A Soft Pneumatic Actuator as a Haptic Wearable Device for Upper Limb Amputees: Toward a Soft Robotic Liner. IEEE Robot. Autom. Lett. 2019, 4, 17–24. [Google Scholar] [CrossRef]
- Sonar, H.; Gerratt, A.P.; Lacour, S.; Paik, J. Closed-Loop Haptic Feedback Control Using a Self-Sensing Soft Pneumatic Actuator Skin. Soft Robot. 2020, 7, 22–29. [Google Scholar] [CrossRef]
- Hashem, M.S.; Joolee, J.B.; Hassan, W.; Jeon, S. Soft Pneumatic Fingertip Actuator Incorporating a Dual Air Chamber to Generate Multi-Mode Simultaneous Tactile Feedback. Appl. Sci. 2021, 12, 175. [Google Scholar] [CrossRef]
- Talhan, A.; Kim, H.; Jeon, S. Tactile Ring: Multi-Mode Finger-Worn Soft Actuator for Rich Haptic Feedback. IEEE Access 2020, 8, 957–966. [Google Scholar] [CrossRef]
- Moy, G.; Wagner, C.; Fearing, R. A compliant tactile display for teletaction. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000. [Google Scholar] [CrossRef]
- Ujitoko, Y.; Taniguchi, T.; Sakurai, S.; Hirota, K. Development of Finger-Mounted High-Density Pin-Array Haptic Display. IEEE Access 2020, 8, 145107–145114. [Google Scholar] [CrossRef]
- Suzuki, Y.; Kobayashi, M. Air jet driven force feedback in virtual reality. IEEE Comput. Graph. Appl. 2005, 25, 44–47. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, S.; Ha, T.; Oakley, I.; Woo, W.; Ryu, J. Air-jet button effects in AR. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Lee, E.H.; Kim, S.H.; Yun, K.S. Three-Axis Pneumatic Haptic Display for the Mechanical and Thermal Stimulation of a Human Finger Pad. Actuators 2021, 10, 60. [Google Scholar] [CrossRef]
- Frediani, G.; Carpi, F. Tactile display of softness on fingertip. Sci. Rep. 2020, 10, 20491. [Google Scholar] [CrossRef]
- Fukuda, T.; Tanaka, Y.; Kappers, A.M.; Fujiwara, M.; Sano, A. A Pneumatic Tactile Ring for Instantaneous Sensory Feedback in Laparoscopic Tumor Localization. IEEE Trans. Haptics 2018, 11, 485–497. [Google Scholar] [CrossRef]
- Premarathna, C.P.; Ruhunage, I.; Chathuranga, D.S.; Lalitharatne, T.D. Haptic Feedback System for an Artificial Prosthetic Hand for Object Grasping and Slip Detection: A Preliminary Study. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 2304–2309. [Google Scholar] [CrossRef]
- Lim, S.C.; Lee, H.K.; Doh, E.; Yun, K.S.; Park, J. Tactile display with tangential and normal skin displacement for robot-assisted surgery. Adv. Robot. 2014, 28, 859–868. [Google Scholar] [CrossRef]
- King, C.H.; Franco, M.; Culjat, M.O.; Higa, A.T.; Bisley, J.W.; Dutson, E.; Grundfest, W.S. Fabrication and Characterization of a Balloon Actuator Array for Haptic Feedback in Robotic Surgery. J. Med. Devices 2008, 2, 041006. [Google Scholar] [CrossRef]
- King, C.; Culjat, M.; Franco, M.; Bisley, J.; Dutson, E.; Grundfest, W. Optimization of a Pneumatic Balloon Tactile Display for Robot-Assisted Surgery Based on Human Perception. IEEE Trans. Biomed. Eng. 2008, 55, 2593–2600. [Google Scholar] [CrossRef] [PubMed]
- van Beek, F.E.; Bisschop, Q.P.I.; Kuling, I.A. Validation of a soft Pneumatic Unit Cell (PUC) in a VR experience: A comparison between vibrotactile and soft pneumatic haptic feedback. IEEE Trans. Haptics 2023, 16, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Caasenbrood, B.J.; Van Beek, F.E.; Chu, H.K.; Kuling, I.A. A Desktop-sized Platform for Real-time Control Applications of Pneumatic Soft Robots. In Proceedings of the 2022 IEEE 5th International Conference on Soft Robotics, Edinburgh, UK, 4–8 April 2022; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2022; pp. 217–223. [Google Scholar] [CrossRef]
- OpenCV: Camera Calibration—docs.opencv.org. Available online: https://docs.opencv.org/4.x/dc/dbb/tutorial_py_calibration.html (accessed on 22 August 2023).



| Experiment | Measuring | Design | Pressure | Frequency |
|---|---|---|---|---|
| Static-Pressure Condition | Free Deflection | 0.6 mm | 0 to 40 kPa | - |
| 0.9 mm | 0 to 40 kPa | - | ||
| 1.2 mm | 0 to 40 kPa | - | ||
| Static-Pressure Condition | Blocking Force | 0.6 mm | - | - |
| 0.9 mm | 0 to 30 kPa | - | ||
| 1.2 mm | 0 to 30 kPa | - | ||
| Frequency Condition | Free Deflection | 0.6 mm | - | - |
| 0.9 mm | 10, 20, 30 kPa | 0.5 to 100 Hz | ||
| 1.2 mm | 10, 20, 30 kPa | 0.5 to 100 Hz |
| Design | Pressure Range (kPa) | Coefficient (mm/kPa) | Confidence Bounds (mm/kPa) | RMSE (mm) |
|---|---|---|---|---|
| 0.6 mm | 4 to 40 kPa | 0.23 | (0.21, 0.25) | 1.96 |
| 4 to 30 kPa | 0.16 | (0.15, 0.17) | 0.58 | |
| 0.9 mm | 4 to 40 kPa | 0.13 | (0.12, 0.14) | 0.93 |
| 4 to 30 kPa | 0.094 | (0.09, 0.098) | 0.21 | |
| 1.2 mm | 4 to 40 kPa | 0.068 | (0.066, 0.07) | 0.19 |
| 4 to 30 kPa | 0.065 | (0.062, 0.067) | 0.14 |
| Top Layer Thickness | Pressure Range (kPa) | Coefficient () | Confidence Bounds () | RMSE (N) |
|---|---|---|---|---|
| 0.9 mm | 4 to 30 | 33.7 | (32.04, 35.4) | 0.08 |
| 1.2 mm | 4 to 30 | 34.4 | (33.18, 35.54) | 0.058 |
| Design | Pressure (kPa) | Frequency () | Coefficient | Confidence Bound | RMSE (mm) | ||
|---|---|---|---|---|---|---|---|
(mm/kPa) | (mm × S/kPa) | (mm/kPa) | (mm × S/kPa) | ||||
| 0.9 mm | 10, 20, 30 | 0.5 to 100 | 0.079 | 0.36 | (0.077, 0.081) | (0.3, 0.4) | 0.22 |
| 1.2 mm | 10, 20, 30 | 0.5 to 100 | 0.052 | 0.17 | (0.05, 0.054) | (0.1, 0.2) | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kommuri, K.D.; Van Beek, F.E.; Kuling, I.A. Fabrication and Characterization of Pneumatic Unit Cell Actuators. Actuators 2024, 13, 45. https://doi.org/10.3390/act13020045
Kommuri KD, Van Beek FE, Kuling IA. Fabrication and Characterization of Pneumatic Unit Cell Actuators. Actuators. 2024; 13(2):45. https://doi.org/10.3390/act13020045
Chicago/Turabian StyleKommuri, Krishna Dheeraj, Femke E. Van Beek, and Irene A. Kuling. 2024. "Fabrication and Characterization of Pneumatic Unit Cell Actuators" Actuators 13, no. 2: 45. https://doi.org/10.3390/act13020045
APA StyleKommuri, K. D., Van Beek, F. E., & Kuling, I. A. (2024). Fabrication and Characterization of Pneumatic Unit Cell Actuators. Actuators, 13(2), 45. https://doi.org/10.3390/act13020045








