Development of the Anthropomorphic Arm for Collaborative and Home Service Robot CHARMIE
Abstract
:1. Introduction
2. Methodologies
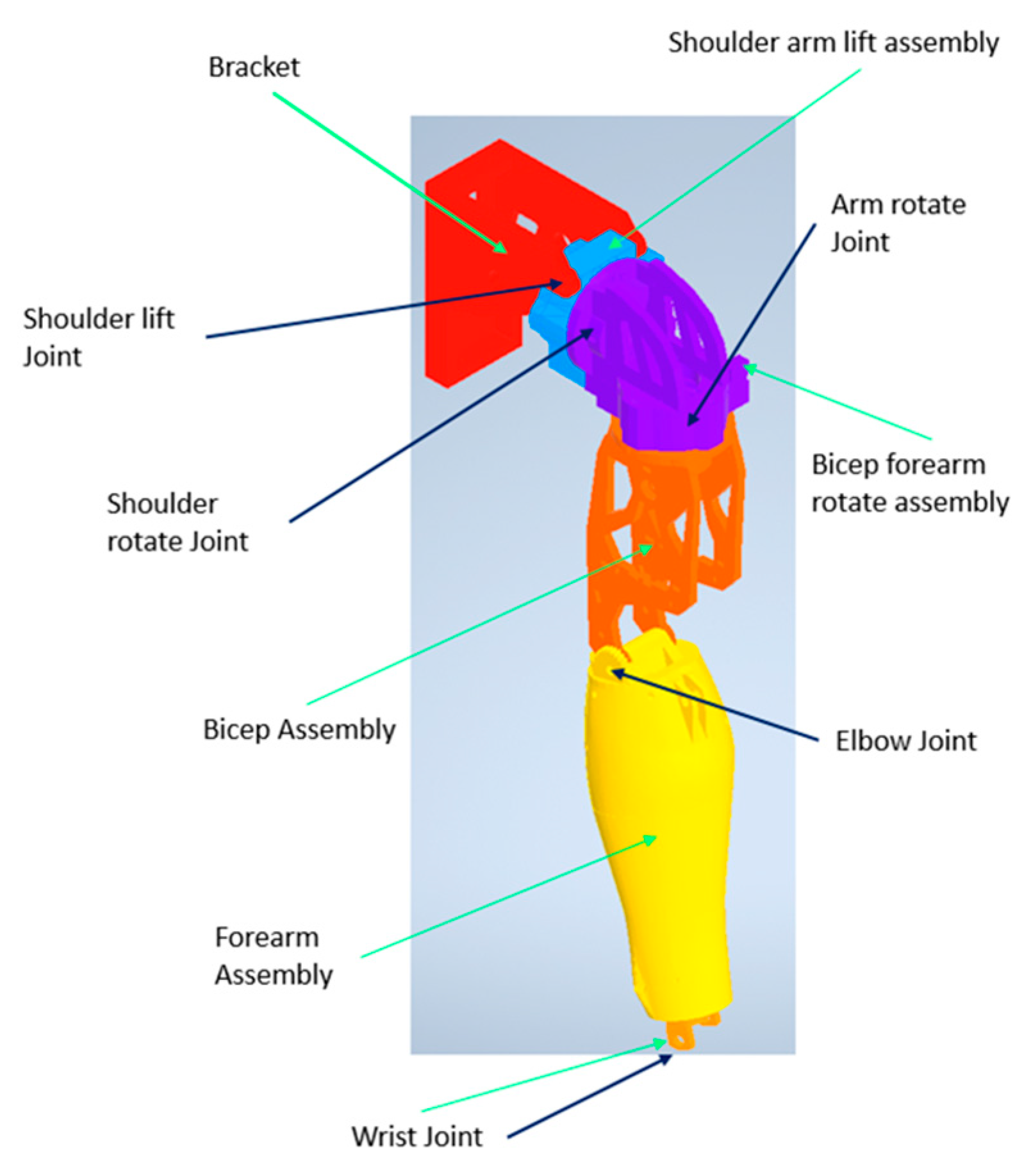
2.1. Electromechanical Build
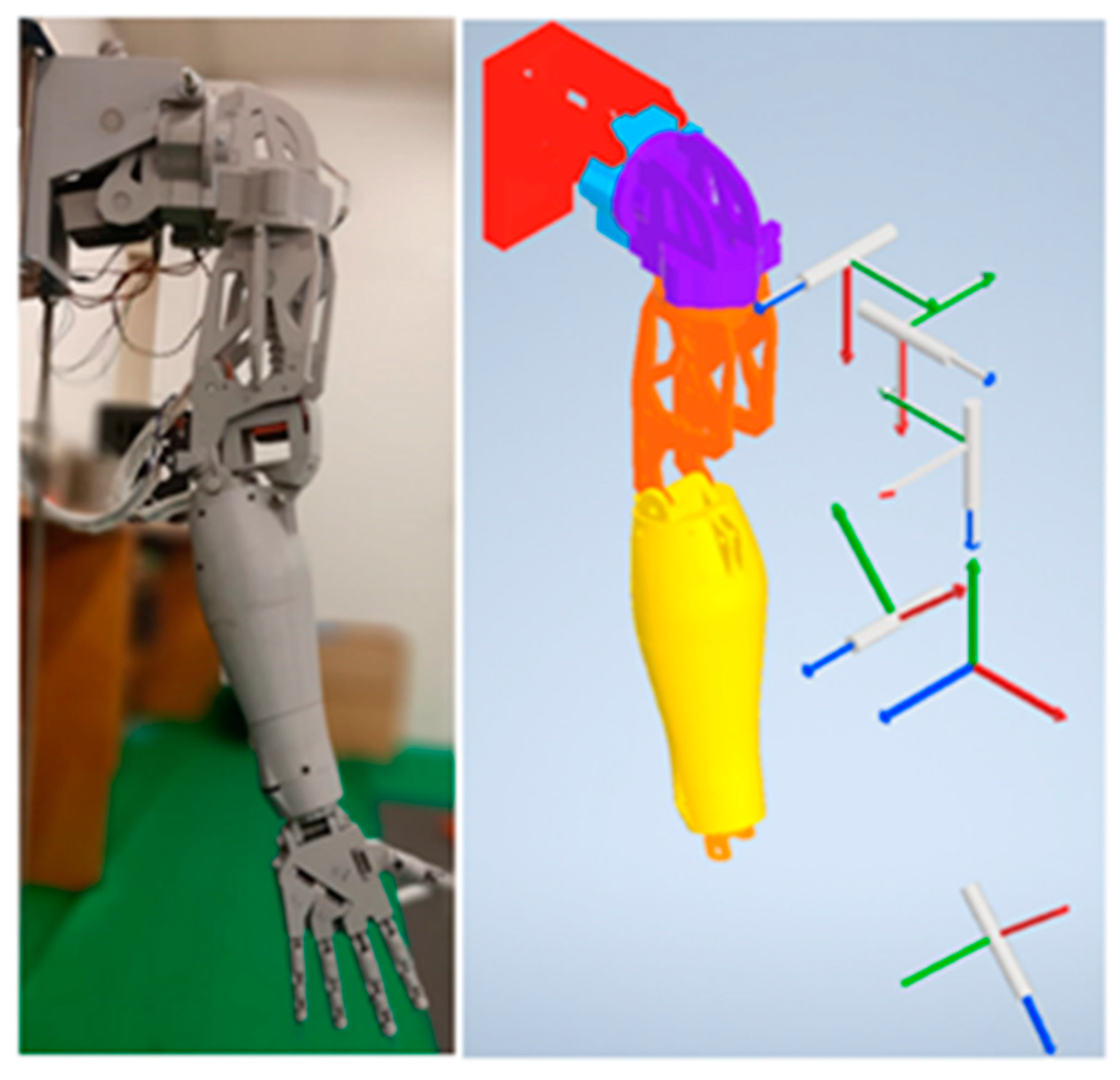
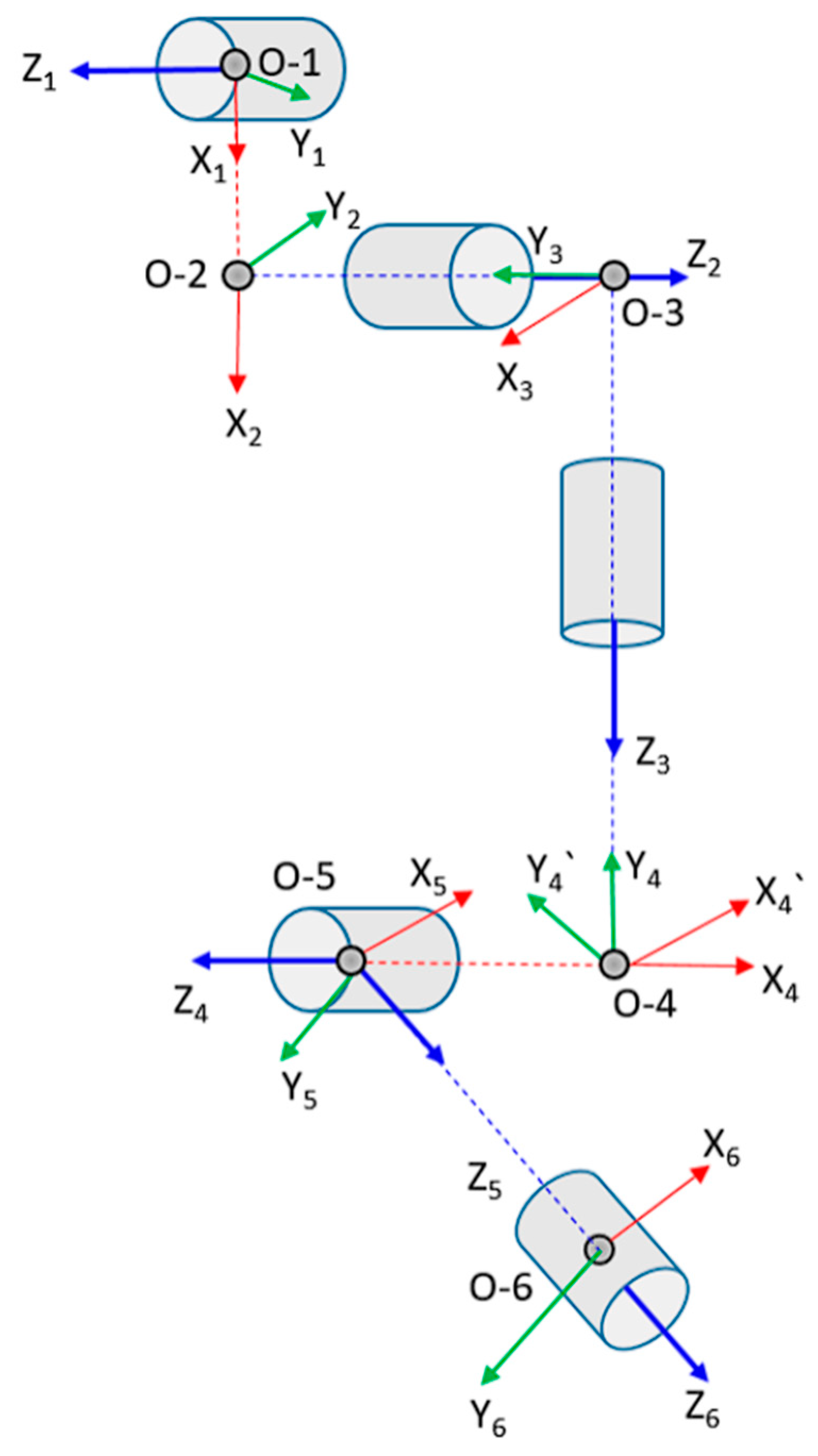
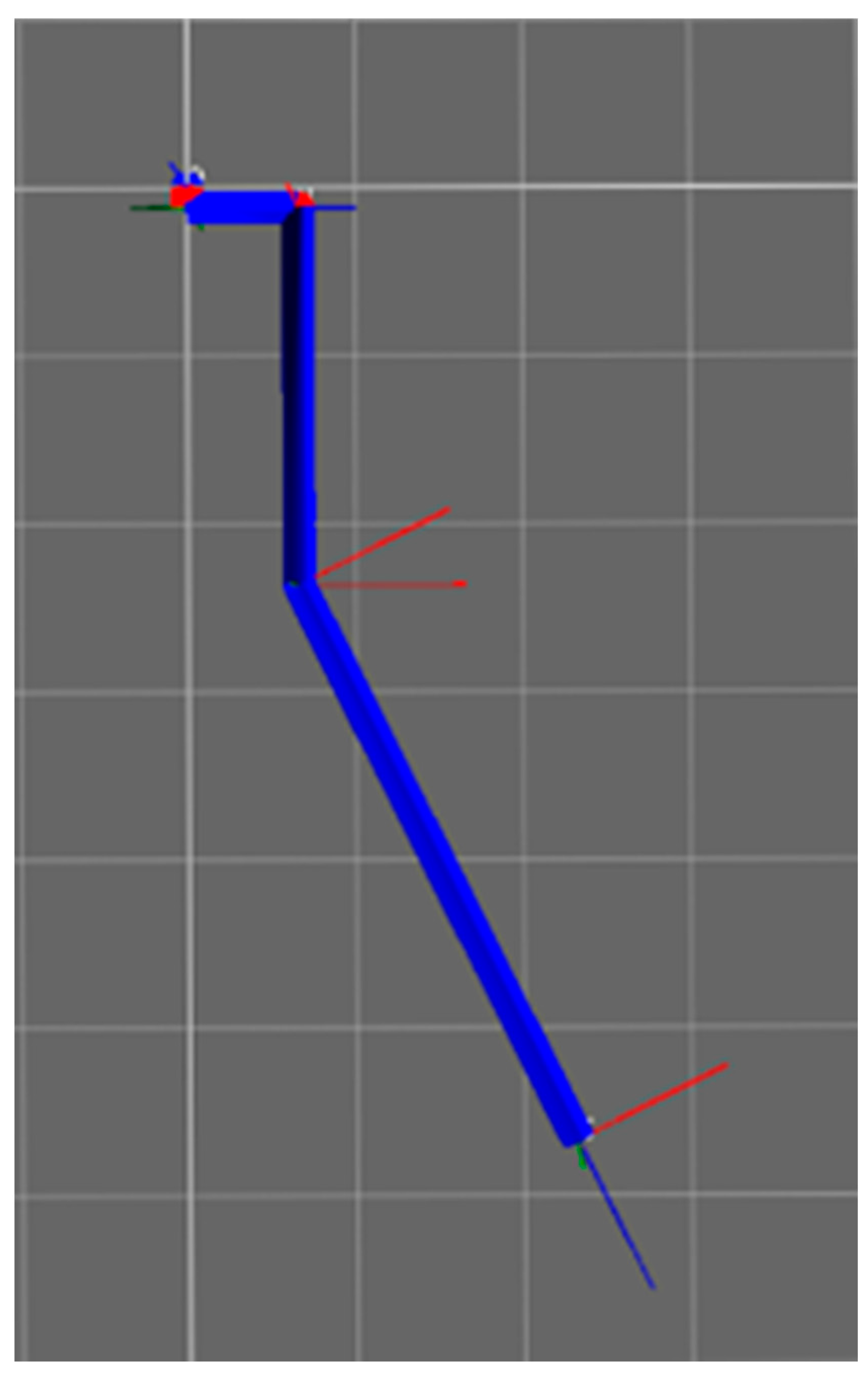
2.2. Forward Kinematics
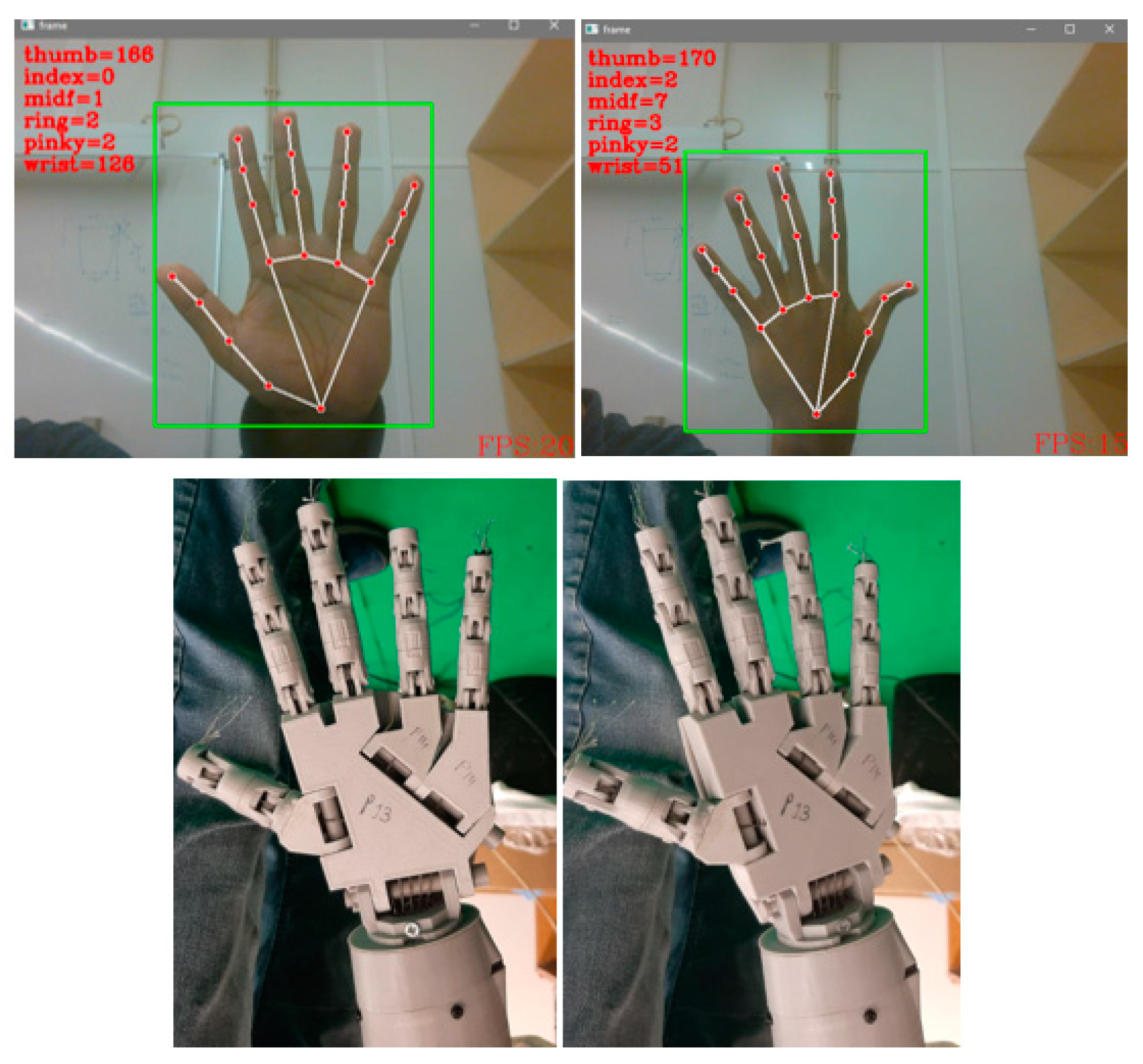
2.3. Mimicking through Vision
3. Results and Discussion
3.1. Electromechanical Build
3.2. Forward Kinematics
3.3. Mimicking through Vision
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paik, J.K.; Shin, B.H.; Bang, Y.B.; Shim, Y.B. Development of an anthropomorphic robotic arm and hand for interactive humanoids. J. Bionic Eng. 2012, 9, 133–142. [Google Scholar] [CrossRef]
- Asfour, T.; Regenstein, K.; Azad, P.; Schroder, J.; Bierbaum, A.; Vahrenkamp, N.; Dillmann, R. ARMAR-III: An integrated humanoid platform for sensory-motor control. In Proceedings of the 2006 6th IEEE-RAS international conference on humanoid robots, Genova, Italy, 4–6 December 2006; pp. 169–175. [Google Scholar]
- Song, H.; Kim, Y.S.; Yoon, J.; Yun, S.H.; Seo, J.; Kim, Y.J. Development of low-inertia high-stiffness manipulator LIMS2 for high-speed manipulation of foldable objects. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4145–4151. [Google Scholar]
- Borst, C.; Ott, C.; Wimbock, T.; Brunner, B.; Zacharias, F.; Bauml, B.; Hillenbrand, U.; Haddadin, S.; Albu- Schaffer, A.; Hirzinger, G. A humanoid upper body system for two-handed manipulation. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 2766–2767. [Google Scholar]
- Cybernetic Zoo Home Page. Available online: http://cyberneticzoo.com/tag/belgrade-hand/ (accessed on 10 May 2024).
- Pellerin, C. The salisbury hand. Ind. Robot. 1991, 18, 25–26. [Google Scholar] [CrossRef]
- Dimery, Rob. 1993: First Bionic Arm. Available online: https://www.guinnessworldrecords.com/world-records/first-bionic-arm-fitted-on-an-individual-(male) (accessed on 10 May 2024).
- OpenAI Solving Rubik’s Cube with a Robot Hand. Available online: https://openai.com/blog/solving-rubiks-cube/ (accessed on 5 June 2024).
- Kim, Y.J. Design of low inertia manipulator with high stiffness and strength using tension amplifying mechanisms. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5850–5856. [Google Scholar]
- Xu, Z.; Todorov, E. Design of a highly biomimetic anthropomorphic robotic hand towards artificial limb regeneration. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3485–3492. [Google Scholar]
- Ribeiro, T.; Gonçalves, F.; Garcia, I.S.; Lopes, G.; Ribeiro, A.F. CHARMIE: A collaborative healthcare and home service and assistant robot for elderly care. App. Sci. 2021, 11, 7248. [Google Scholar] [CrossRef]
- Laboratory of Automation Robotics Development of Anthropomorphic Arm for Collaborative Home Service Robot, C.H.A.R.M.I.E. Available online: https://www.youtube.com/watch?v=XTWzT82S9b4 (accessed on 5 June 2024).
- Mabrouk, Y.; Shehata, O.M.; Morgan, E.I. Development of a Robotic Framework for Modeling and Simulation of an Upper Humanoid Robot. In Proceedings of the 2023 5th Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 21–23 October 2023; pp. 205–210. [Google Scholar]
- InMoov. Available online: https://inmoov.fr/ (accessed on 5 June 2024).
- Denavit, J.; Hartenberg, R.S. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices. ASME J. Appl. Mech. 1955, 77, 215–221. [Google Scholar] [CrossRef]
- Mobile Robot Programming Toolkit. MRPT: Mobile Robot Programming Toolkit. Available online: https://www.mrpt.org/ (accessed on 5 June 2024).
- Google. MediaPipe. Available online: https://google.github.io/mediapipe/ (accessed on 5 June 2024).
- Firmata. Protocol. Available online: https://github.com/firmata/protocol (accessed on 5 June 2024).
- Demonstration of the Anthropomorphic Arm. YouTube Video. Available online: https://www.youtube.com/watch?v=XTWzT82S9b4 (accessed on 5 June 2024).
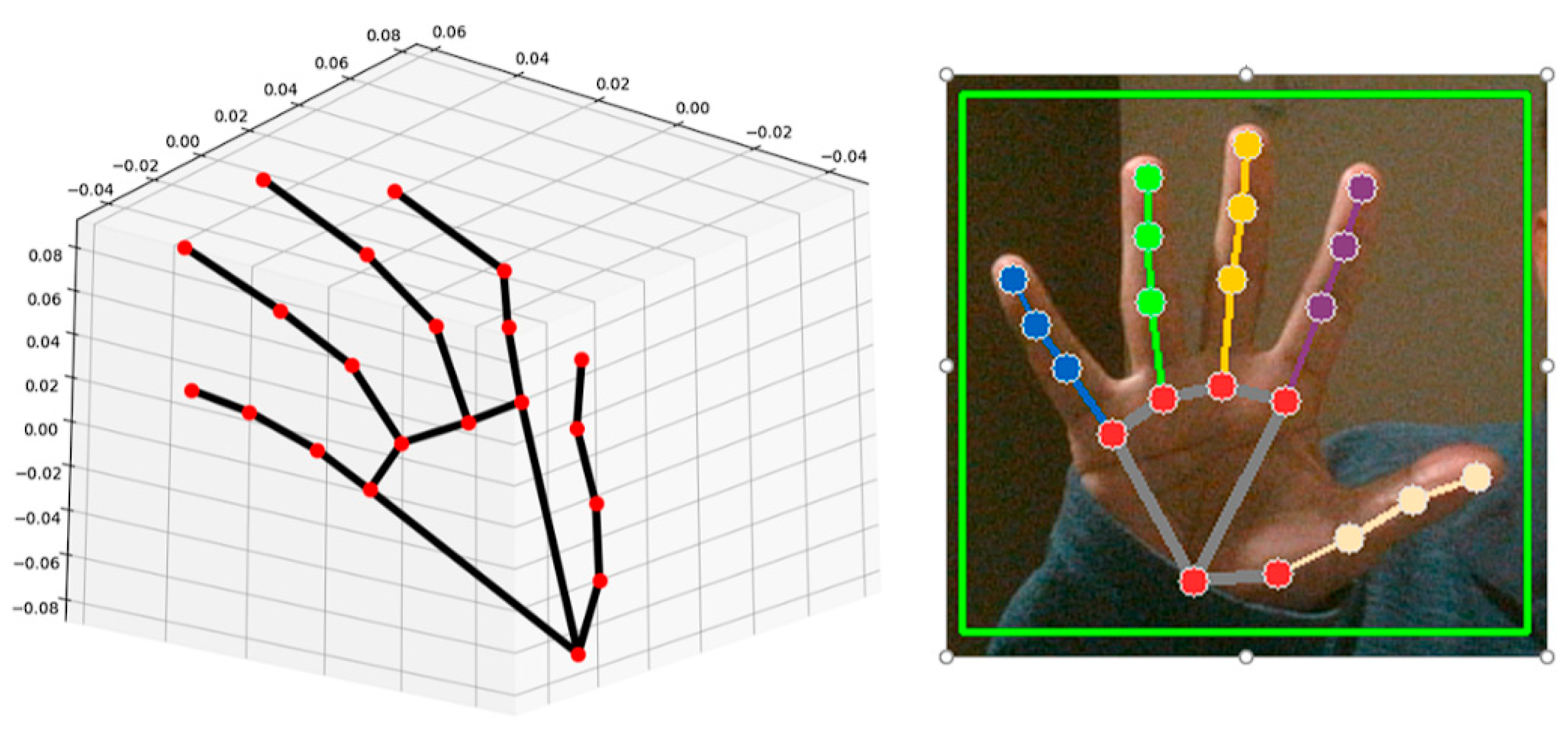



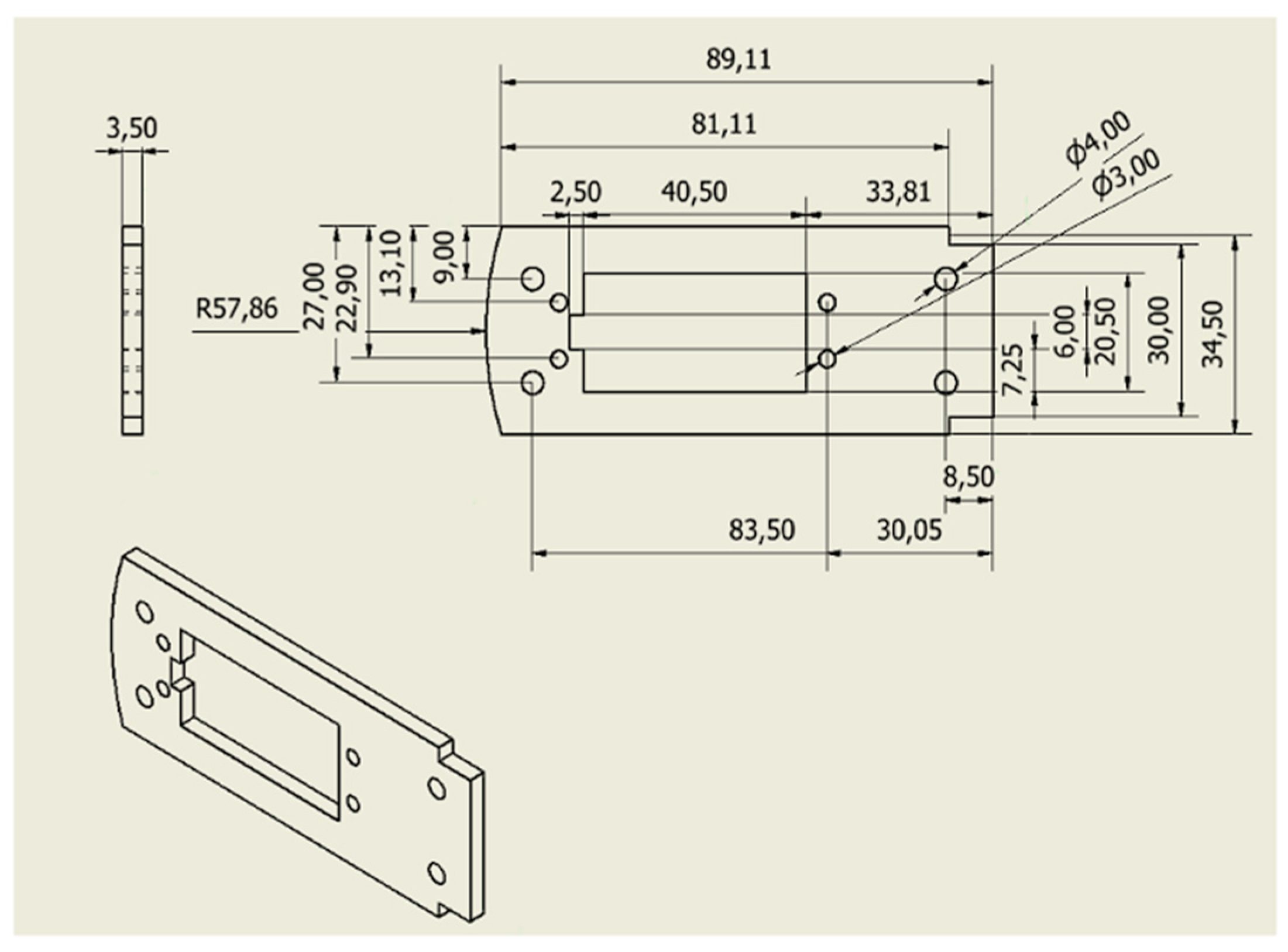


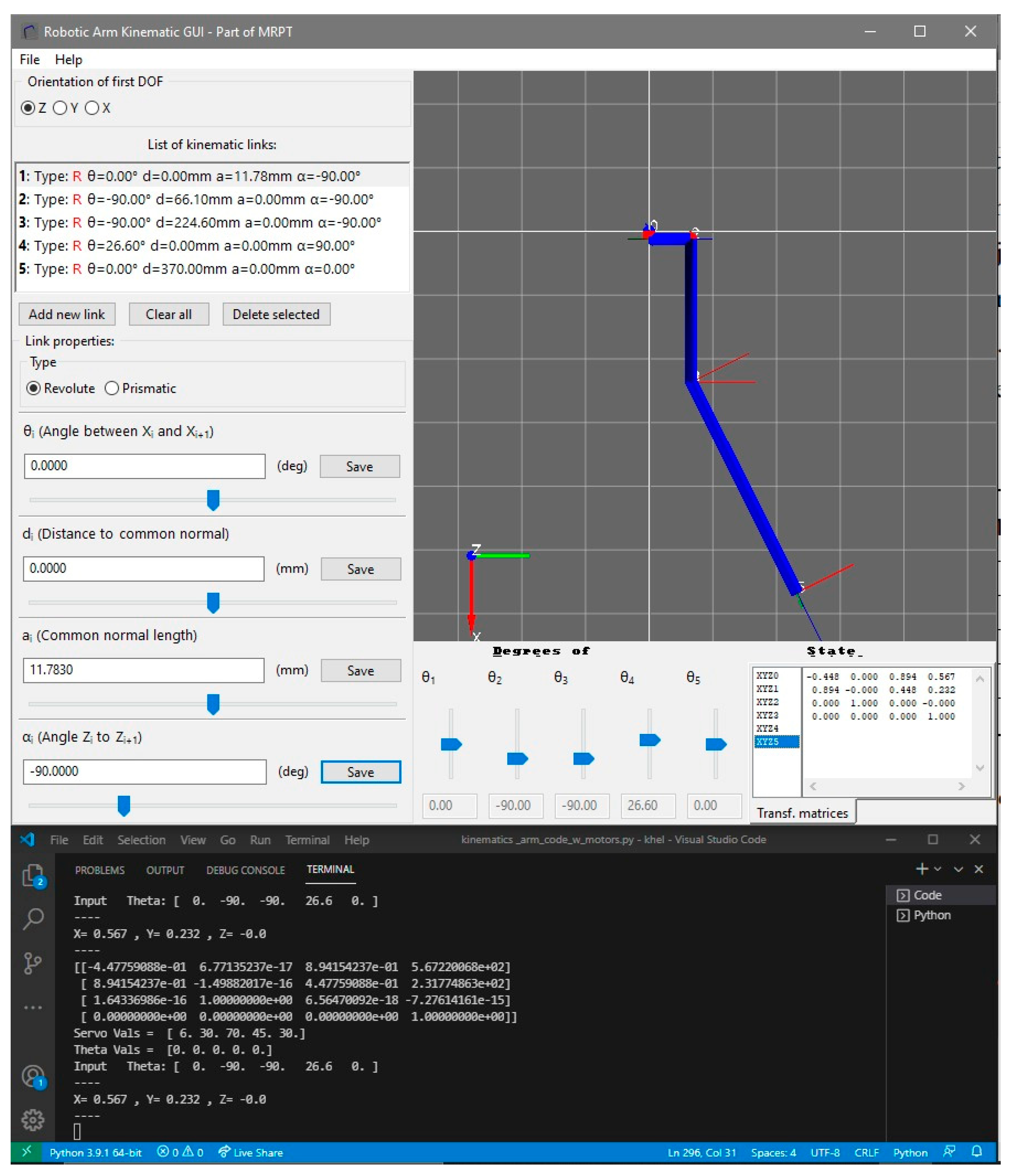


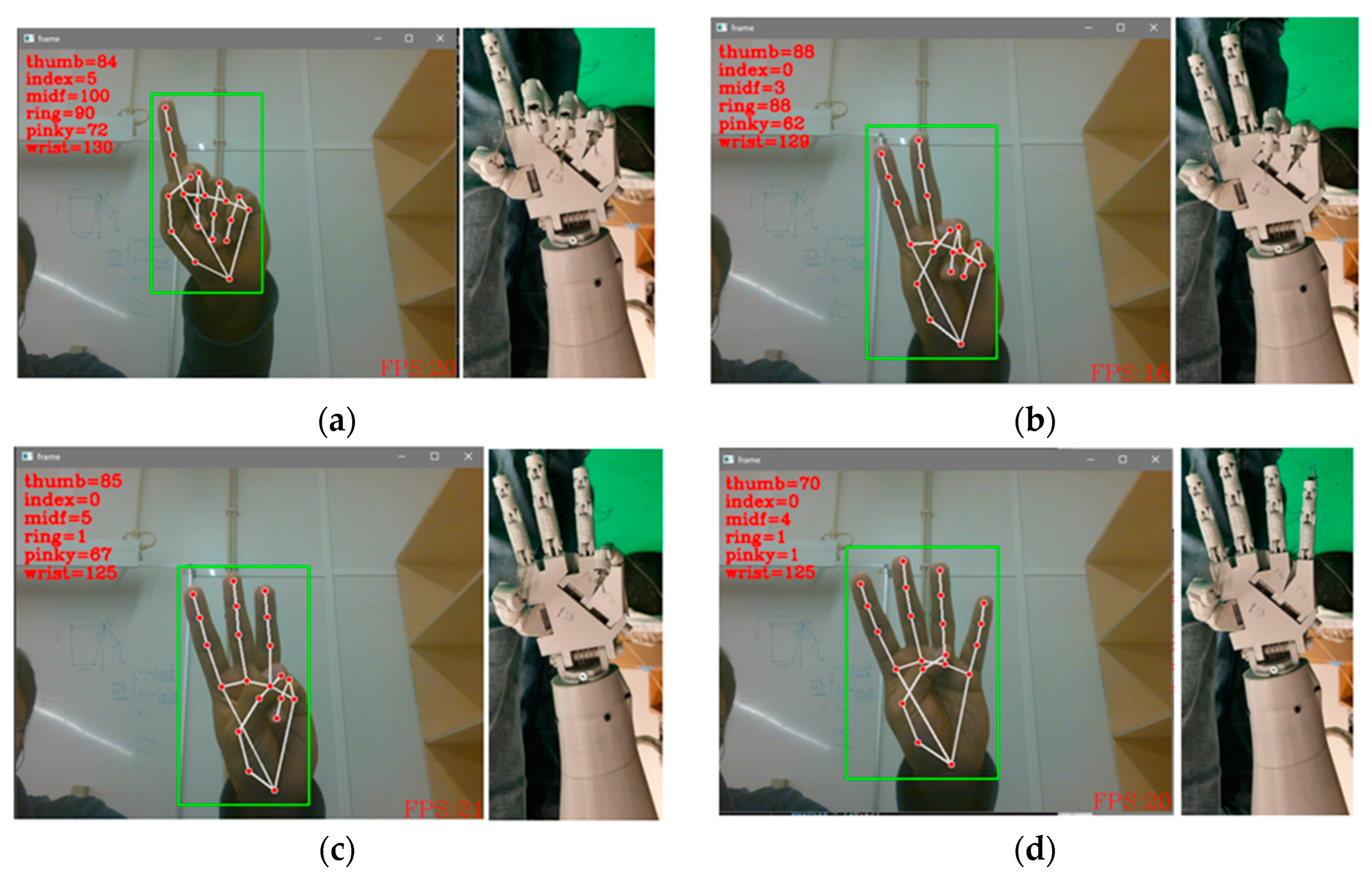
| Joint Name | Minimum Angle Value (rad) | Maximum Angle Value (rad) |
|---|---|---|
| Shoulder Lift | 0.105 | 0.960 |
| Arm Rotate | 0.524 | 2.793 |
| Bicep Rotate | 1.222 | 2.094 |
| Elbow | 2.356 | 0.785 |
| Wrist | 0.524 | 2.618 |
| Finger name | Min Angle Value (rad) | Max Angle Value (rad) |
|---|---|---|
| Thumb | 1.222 | 2.967 |
| Index | 2.184 | 0.436 |
| Middle | 2.356 | 0.523 |
| Ring | 1.094 | 0.523 |
| Small | 1.920 | 0.523 |
| Link i | θ | d | a | α |
|---|---|---|---|---|
| 1 | θ1 | 0 | 11.783 | |
| 2 | 66.104 | 0 | ||
| 3 | 224.60 | 0 | ||
| 4 | θ4 + 0.464 | 0 | 0 | |
| 5 | θ5 | 289.5 + 80.5 = 370 | 0 | 0 |
| POS | Joint Variables (rad) | MRPT | Python | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| θ1 | θ2 | θ3 | θ4 | θ5 | X | Y | Z | X | Y | Z | |
| 1 | 0 | 0.464 | 0 | 0.567 | 0.232 | 0 | 0.567 | 0.232 | 0 | ||
| 2 | 0.349 | 0.464 | 0 | 0.454 | 0.412 | 0 | 0.454 | 0.412 | 0 | ||
| 3 | 0 | −2.356 | 0.464 | 0 | 0.405 | 0.232 | 0.393 | 0.405 | 0.232 | 0.393 | |
| 4 | 0 | −2.356 | −0.698 | 0.464 | 0 | 0.315 | 0.173 | 0.482 | 0.315 | 0.173 | 0.482 |
| 5 | 0.611 | −3.753 | −0.698 | 1.163 | 0 | −0.503 | −0.005 | 0.155 | −0.503 | −0.005 | 0.155 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syed, F.A.; Lopes, G.; Ribeiro, A.F. Development of the Anthropomorphic Arm for Collaborative and Home Service Robot CHARMIE. Actuators 2024, 13, 239. https://doi.org/10.3390/act13070239
Syed FA, Lopes G, Ribeiro AF. Development of the Anthropomorphic Arm for Collaborative and Home Service Robot CHARMIE. Actuators. 2024; 13(7):239. https://doi.org/10.3390/act13070239
Chicago/Turabian StyleSyed, Fawad A., Gil Lopes, and A. Fernando Ribeiro. 2024. "Development of the Anthropomorphic Arm for Collaborative and Home Service Robot CHARMIE" Actuators 13, no. 7: 239. https://doi.org/10.3390/act13070239
APA StyleSyed, F. A., Lopes, G., & Ribeiro, A. F. (2024). Development of the Anthropomorphic Arm for Collaborative and Home Service Robot CHARMIE. Actuators, 13(7), 239. https://doi.org/10.3390/act13070239









