An Optimized Position Control via Reinforcement-Learning-Based Hybrid Structure Strategy
Abstract
1. Introduction
- 1.
- Development of an RL-based hybrid control structure that synthesizes the strengths of different conventional controllers into a single framework, thereby enhancing overall system performance without compromising any performance metrics.
- 2.
- Performance validation of the proposed scheme through both computer simulations and experiments using an electric motor drive system.
2. System Model and Motivations
2.1. System Description and Problem Definition
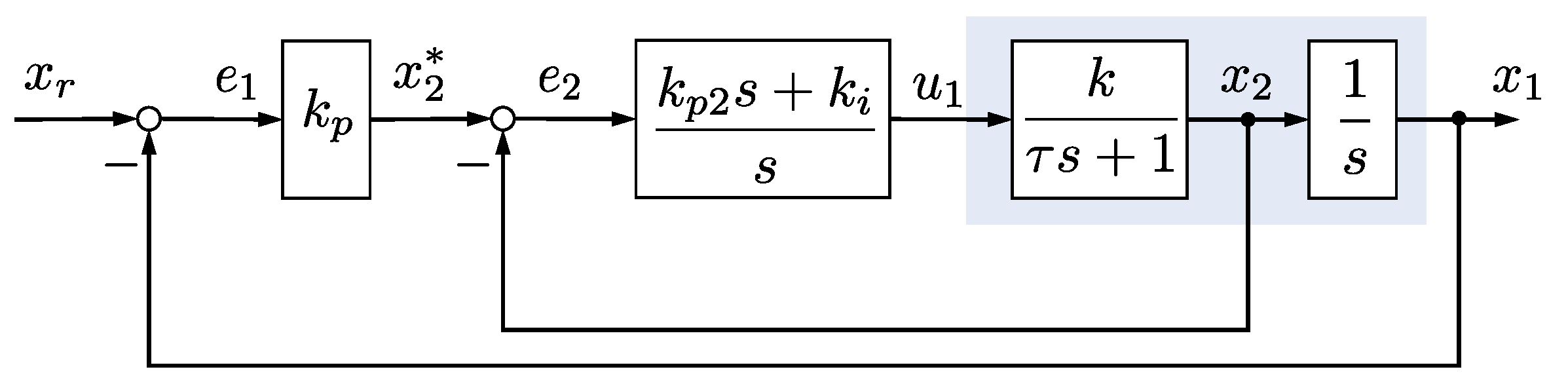
2.2. Cascade Controller Design and Performance
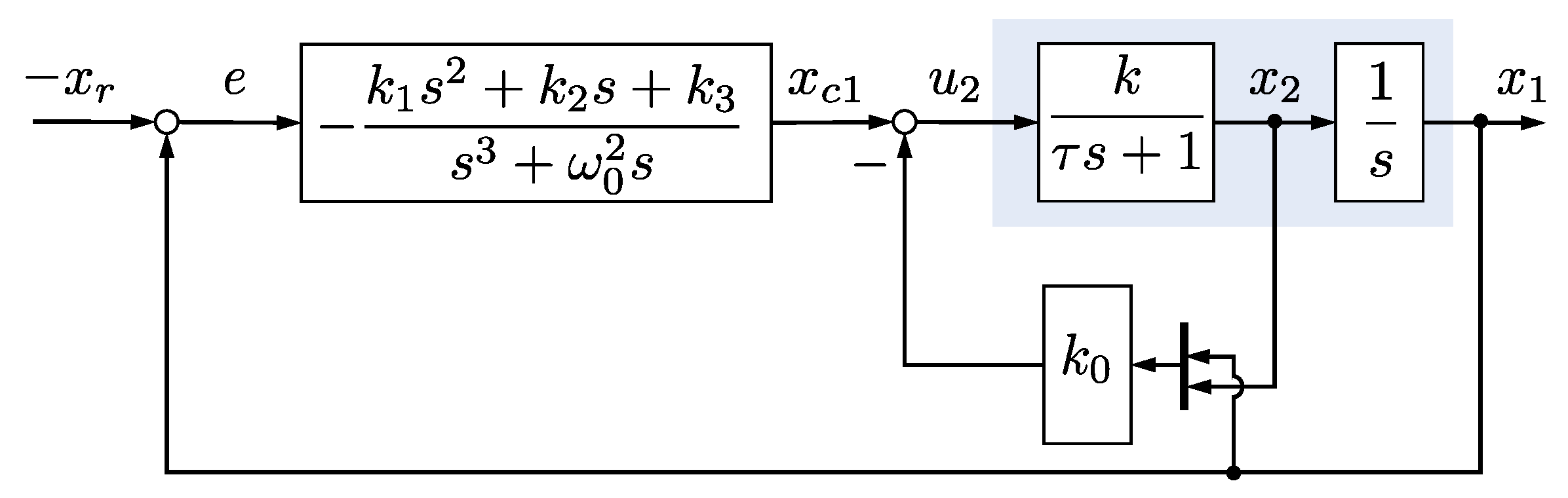
2.3. IMP-Based Controller Design and Performance
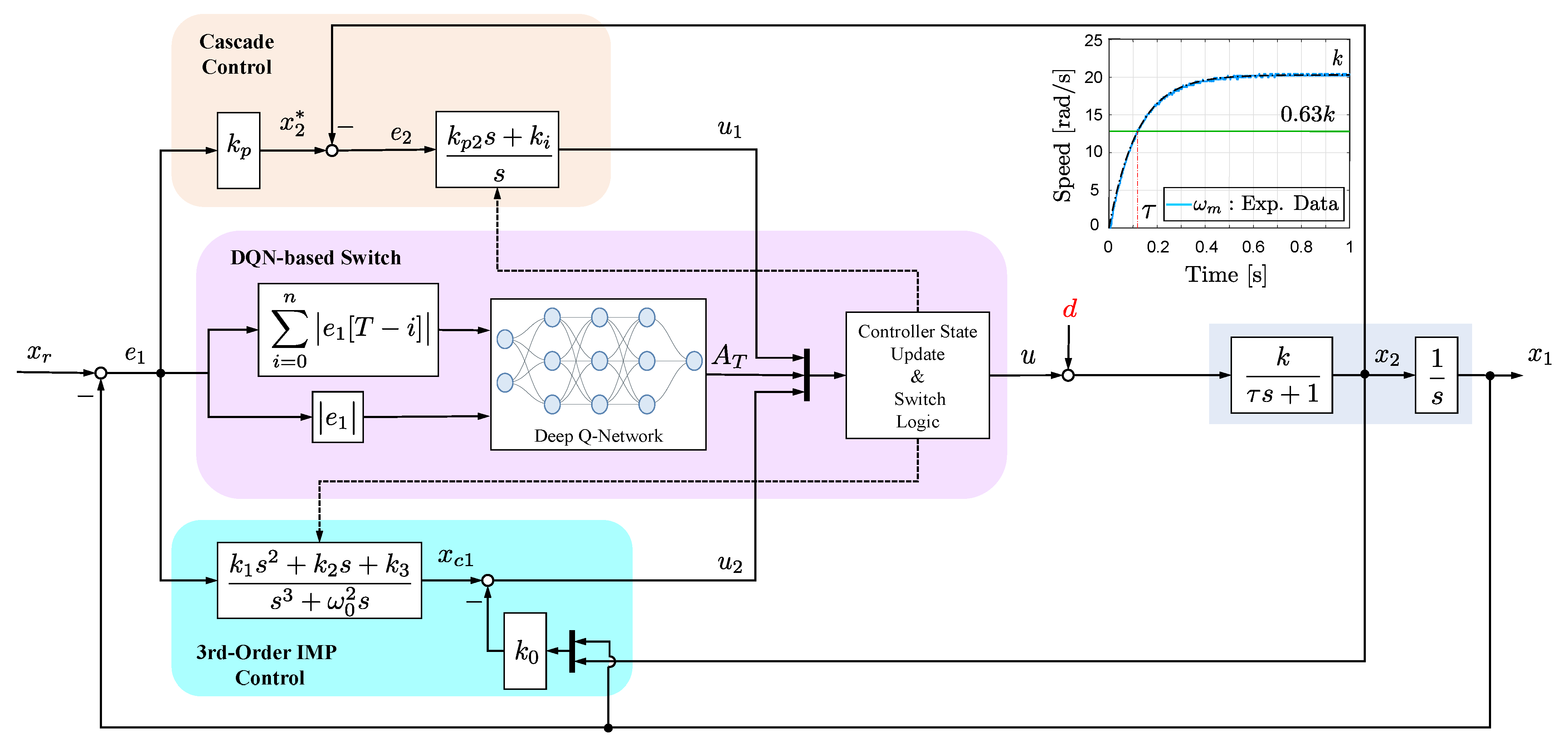
3. DQN-Based Hybrid Controller Design
3.1. Hybrid Structure Controller
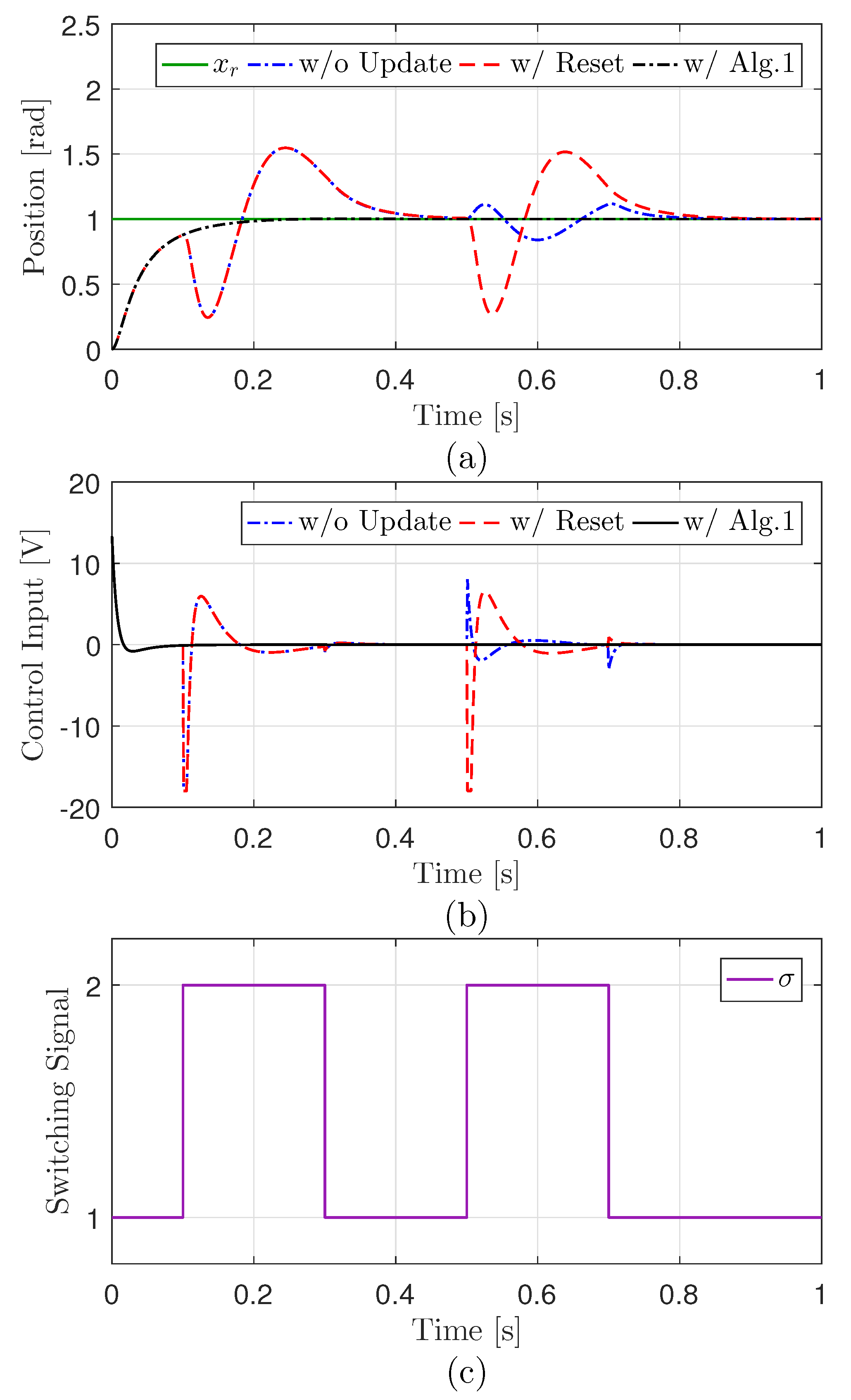
3.2. Controller State Update and Switch Logic
| Algorithm 1 Controller state update and switch logic |
|
3.3. Reinforcement-Learning-Based Switching Function
- State: The state at time step T was constructed aswith and taken as additional tuning parameters. The state was constructed using only , as this parameter highlighted key performance disparities between the two subcontrollers.
- Action: The action available at any time step is the discrete control effort of either (7) or (18), allowing the action space to be formulated as the binary space where 0 and 1 represent the saturated and , respectively, with saturation at V. Hence, in the context of the DQN-based controller, at any given time step T.
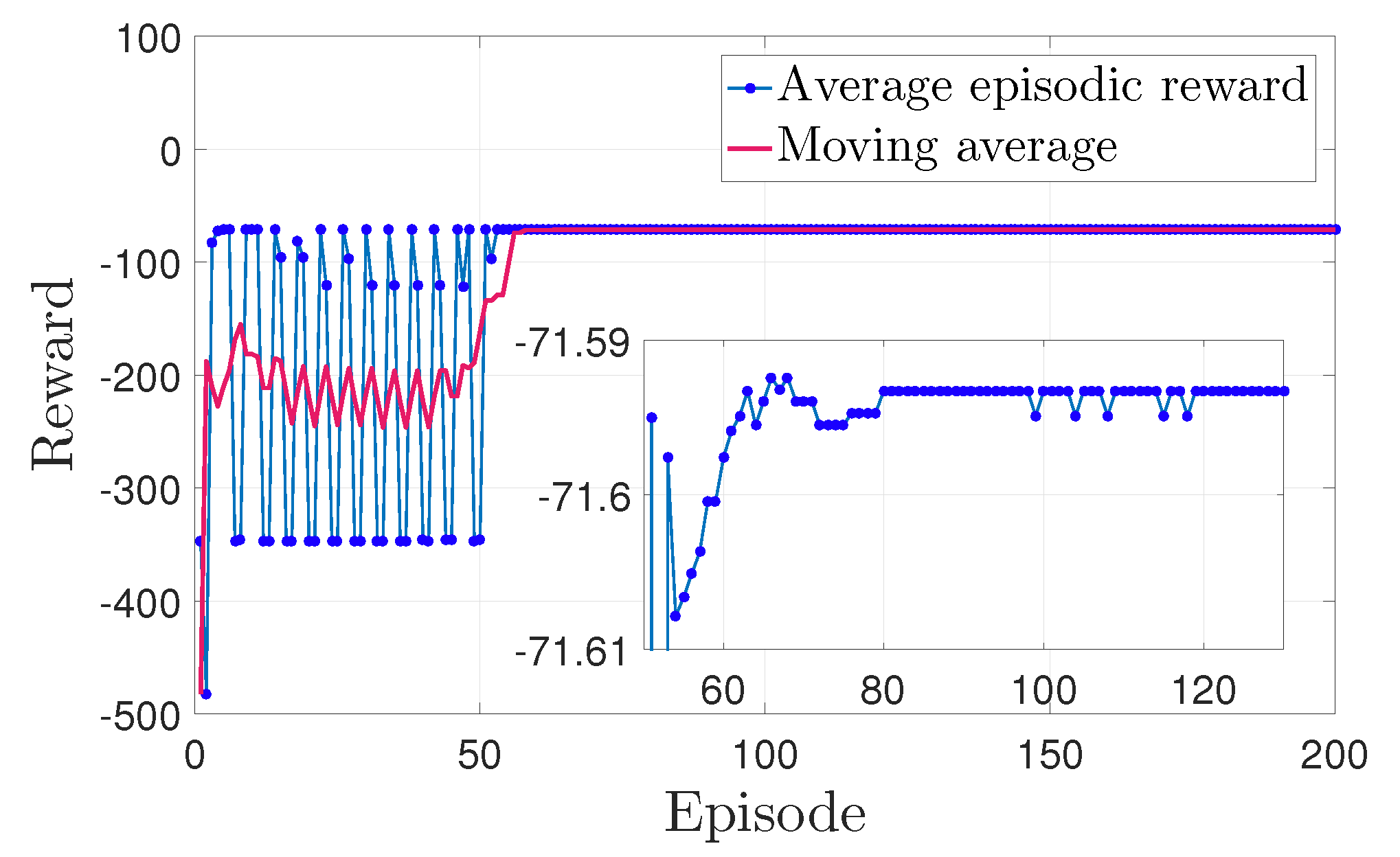
- Reward: As the design objective of the hybrid structure controller is to minimize , the reward function is constructed as the linearly scaled value of the current time step squared error as . To ensure , we set , with . Constructing solely based on offers a clear objective that facilitates straightforward training.
| Algorithm 2 DQN training for hybrid controller |
|
3.4. Discussion on Stability
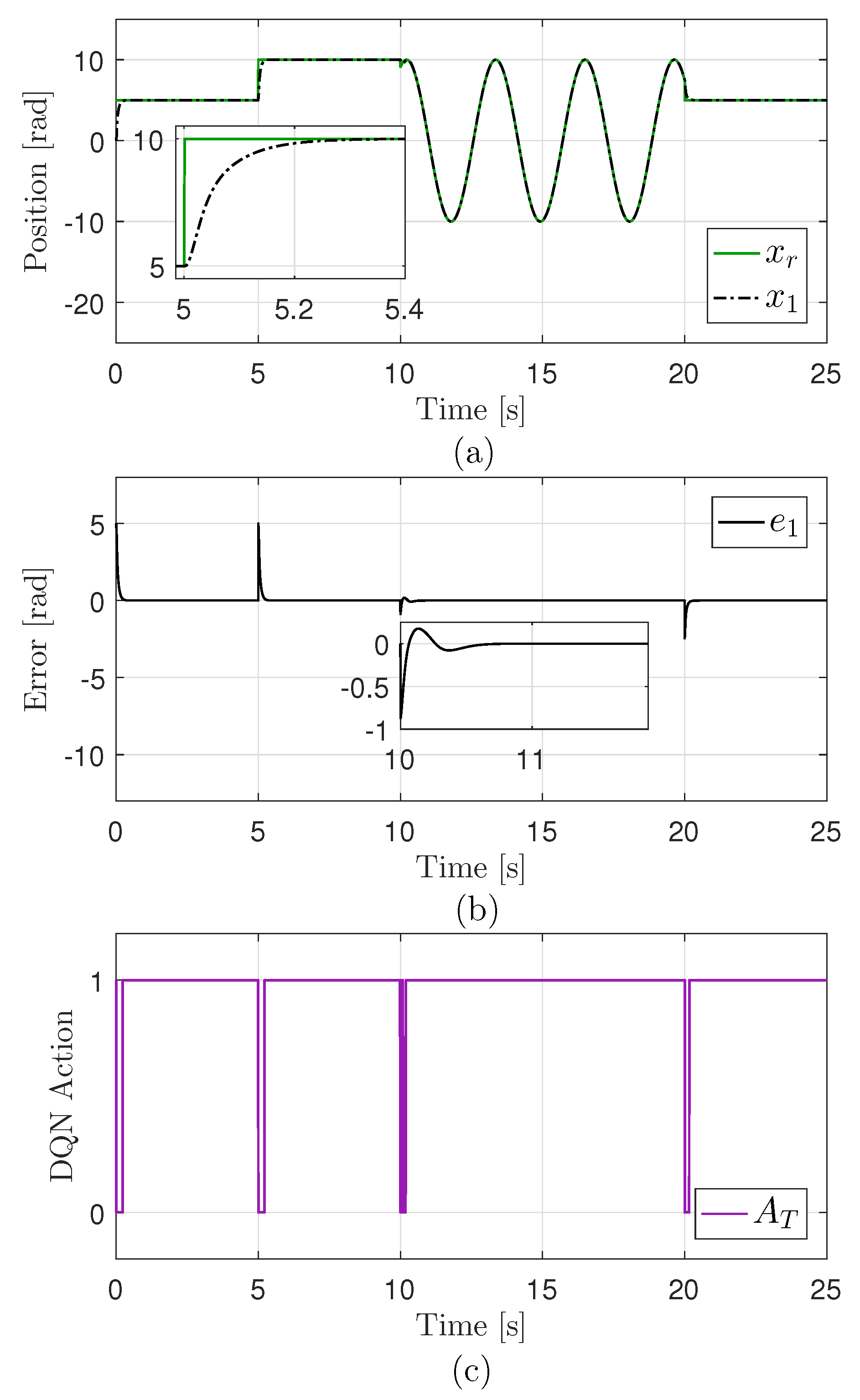
3.5. DQN Training Result and Hybrid Controller Nominal Performance
4. Robust Performance Test
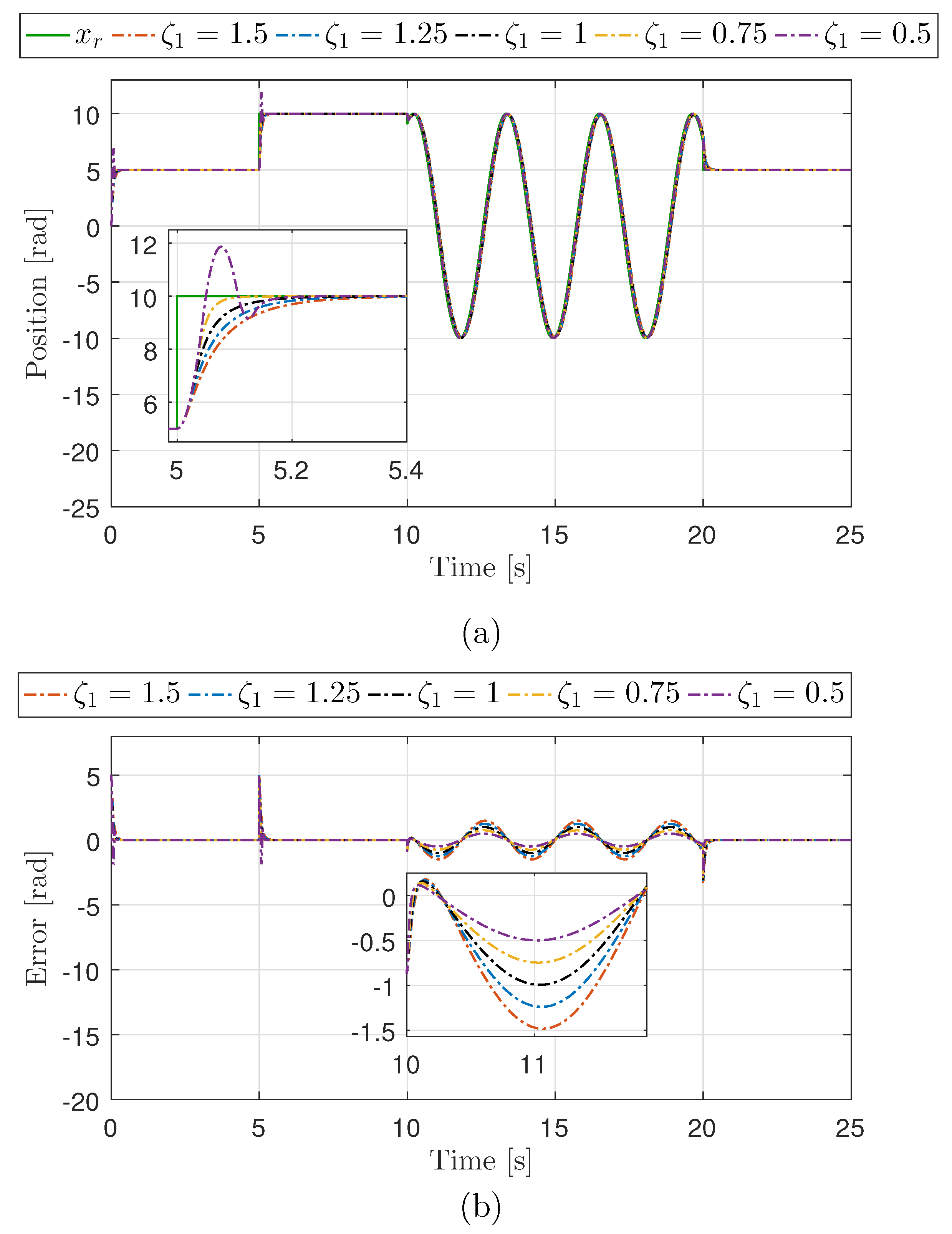
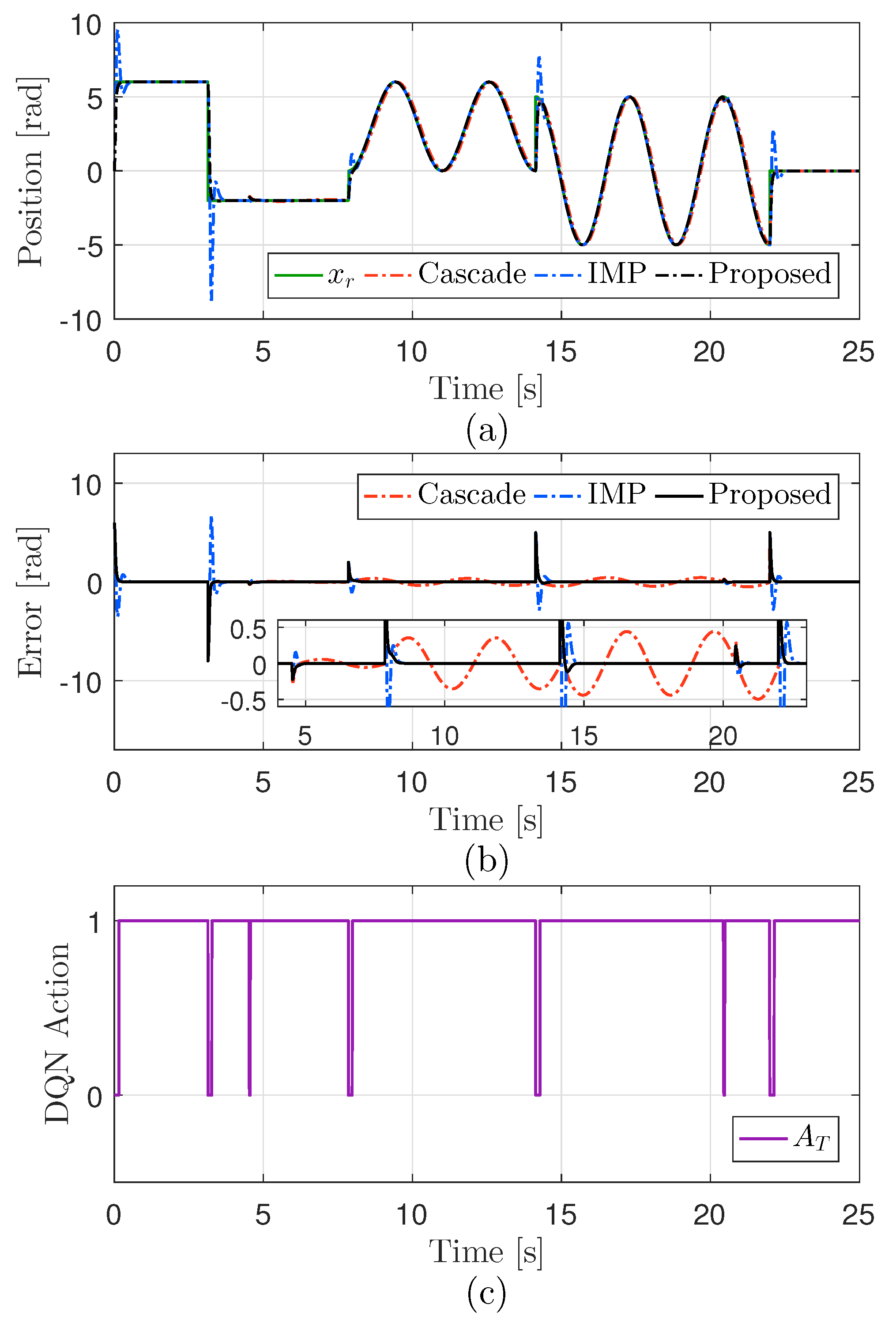
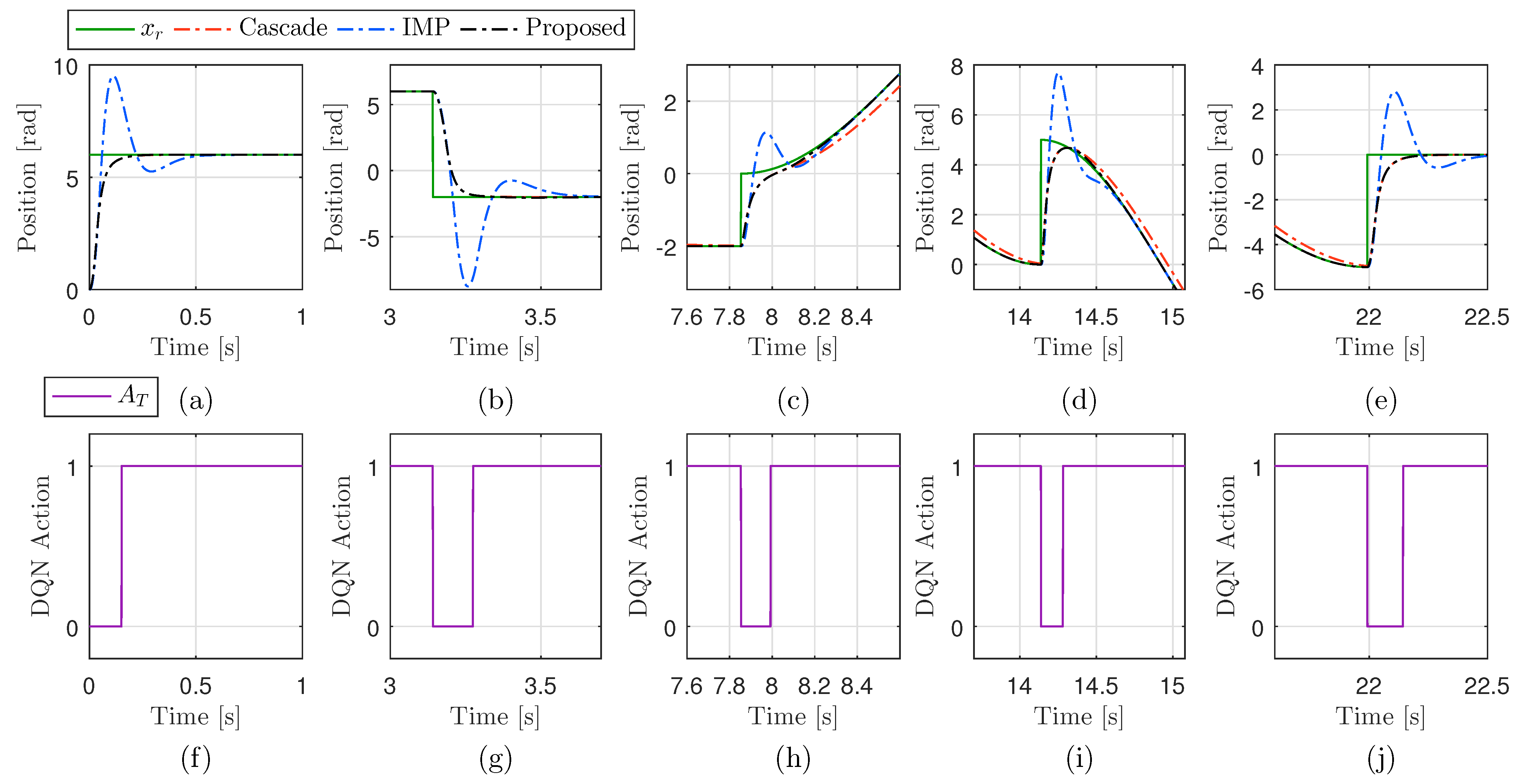
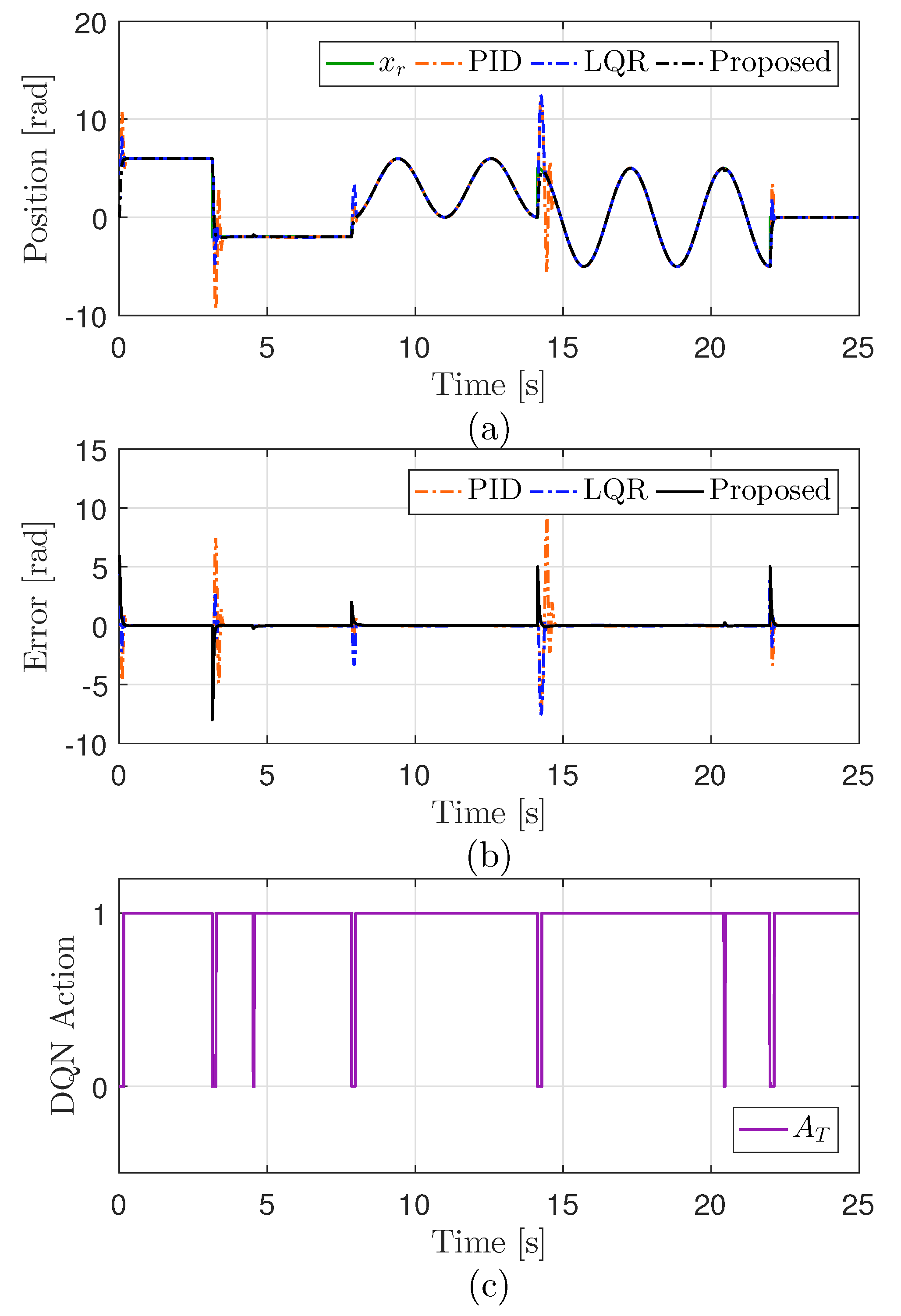
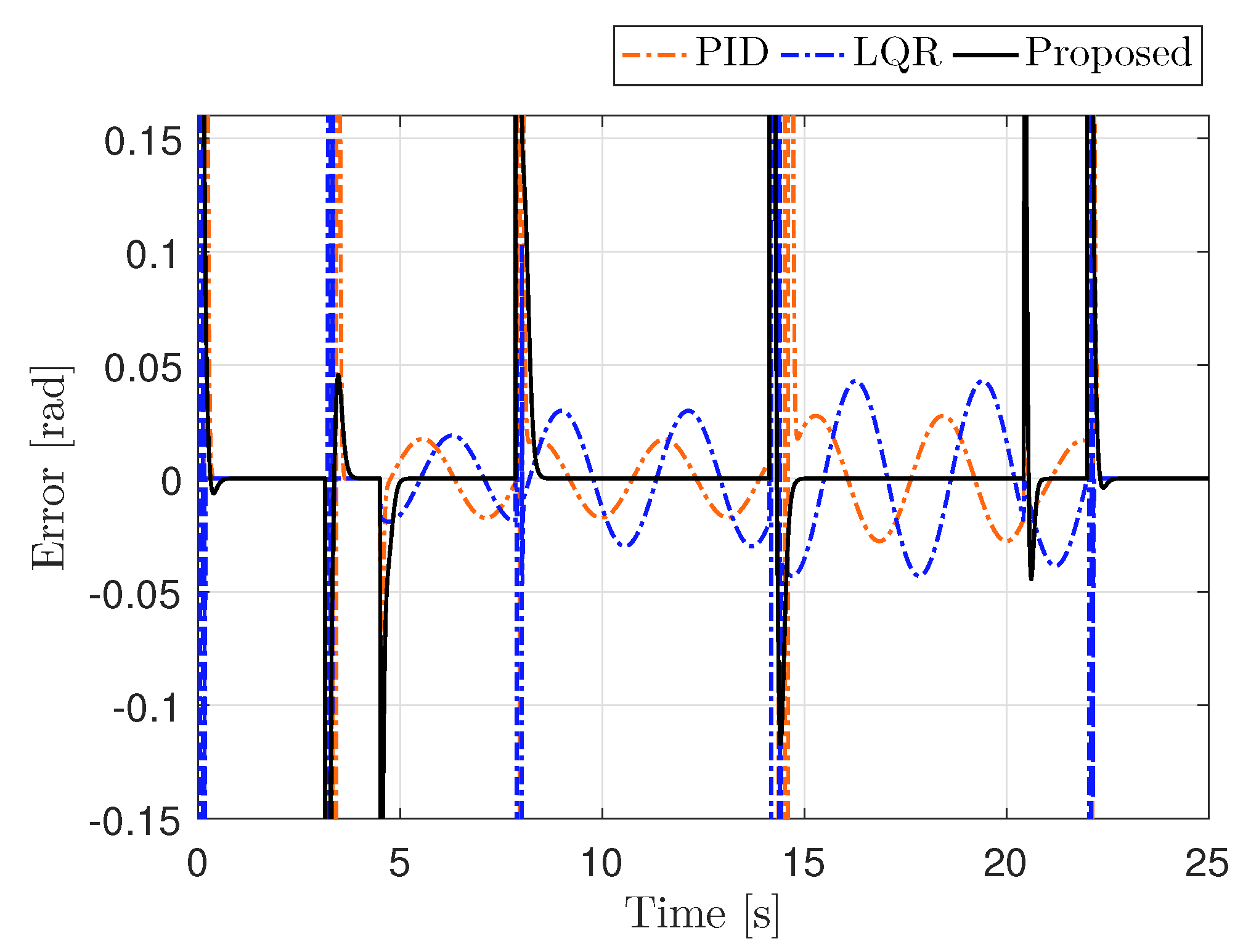
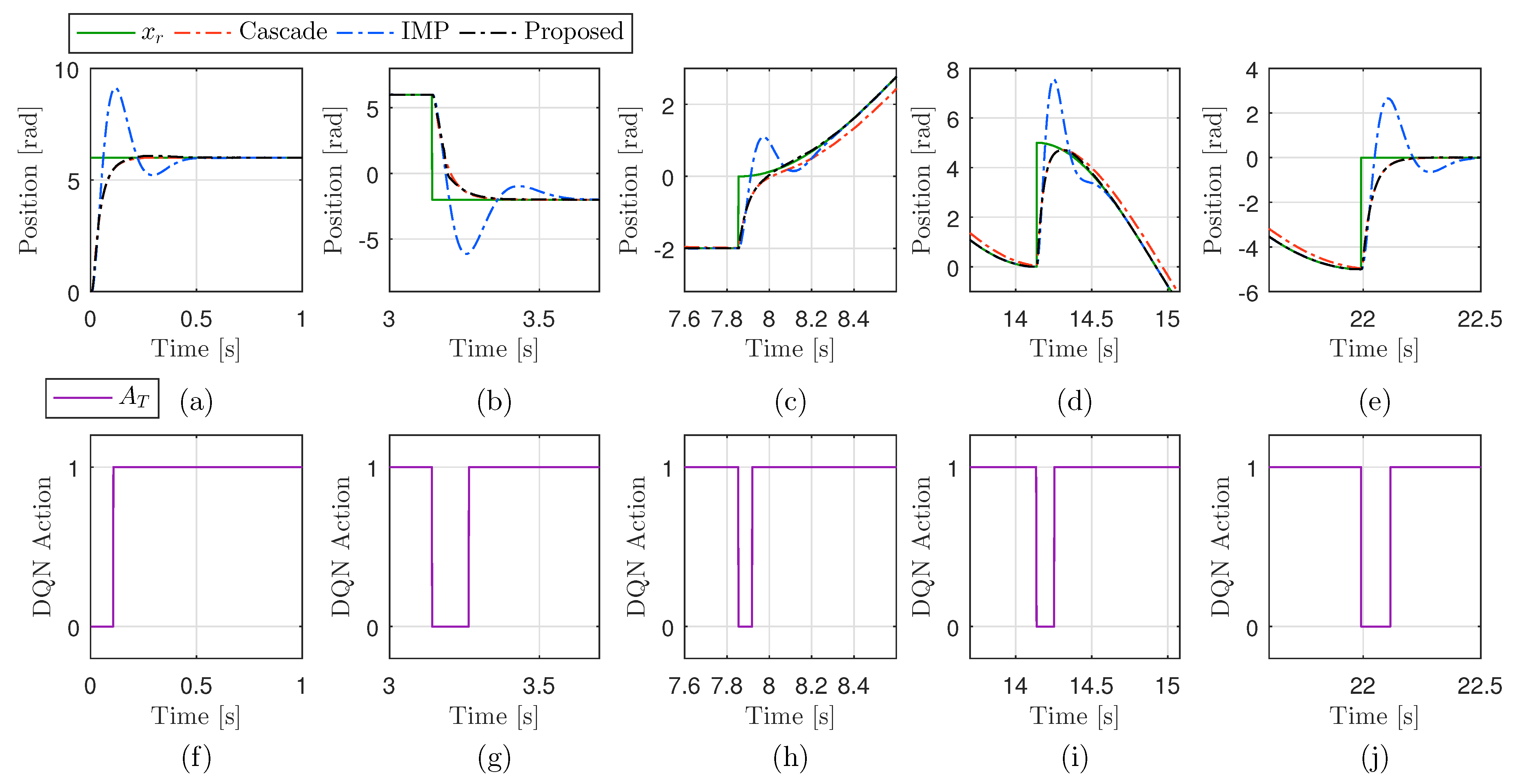
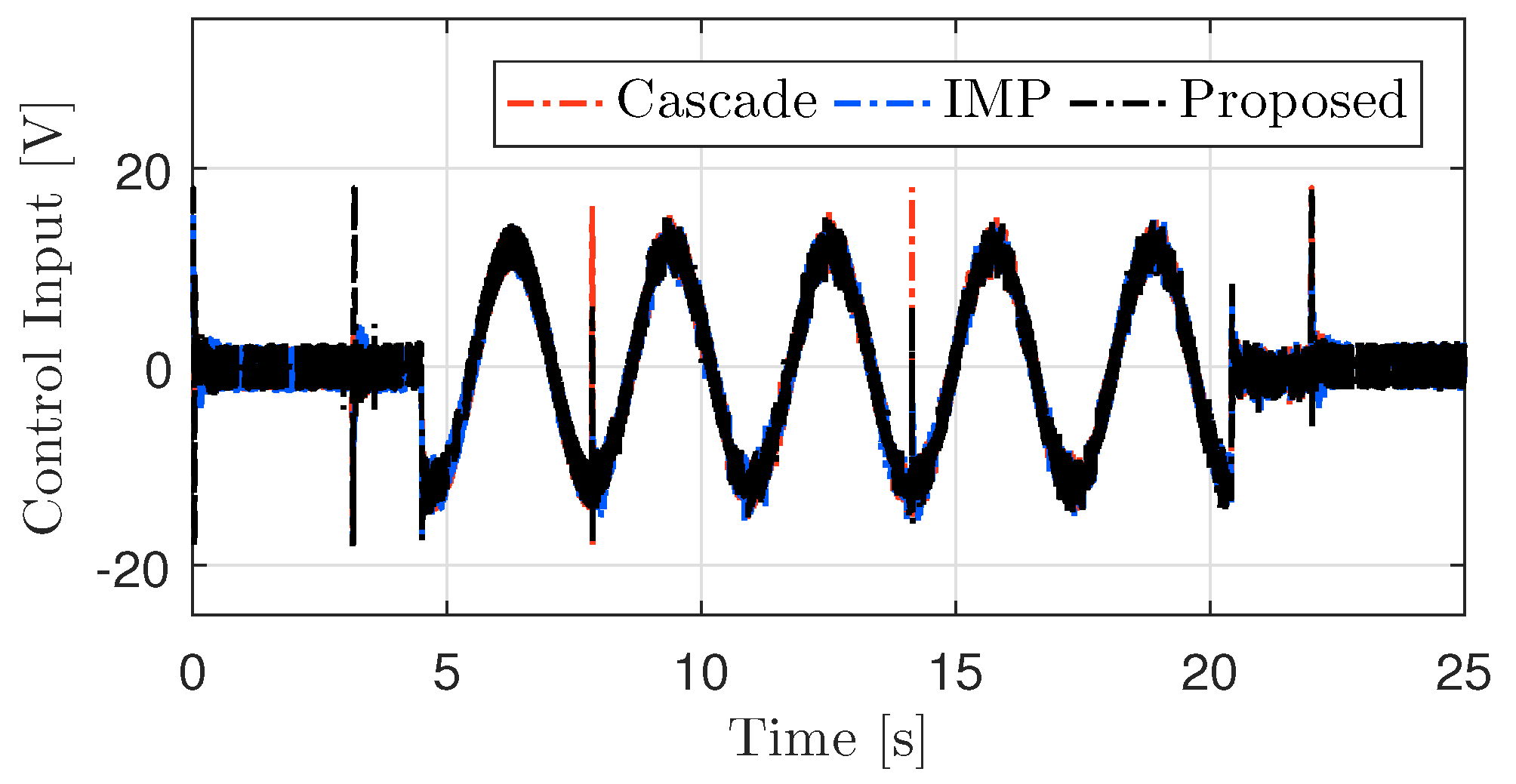
4.1. Performance Validation in Simulations
4.2. Performance Validation in Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IMP | Internal Model Principle |
| RL | Reinforcement learning |
| DQN | Deep Q-Network |
| DC | Direct current |
| DOBC | Disturbance observer-based control |
| BT | Bumpless transfer |
| SAC | Soft actor–critic |
| DDPG | Deep deterministic policy gradient |
References
- Sariyildiz, E.; Oboe, R.; Ohnishi, K. Disturbance observer-based robust control and its applications: 35th anniversary overview. IEEE Trans. Ind. Electron. 2020, 67, 2042–2053. [Google Scholar] [CrossRef]
- Francis, B.A.; Wonham, W.M. The internal model principle of control theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 8th ed.; Pearson: New York, NY, USA, 2019. [Google Scholar]
- Yuz, J.I.; Salgado, M.E. From classical to state feedback-based controllers. IEEE Control Syst. Mag. 2003, 23, 58–67. [Google Scholar]
- Pupadubsin, R.; Chayopitak, N.; Taylor, D.G.; Nulek, N.; Kachapornkul, S.; Jitkreeyarn, P.; Somsiri, P.; Tungpimolrut, K. Adaptive integral sliding-mode position control of a coupled-phase linear variable reluctance motor for high-precision applications. IEEE Trans. Ind. Appl. 2012, 48, 1353–1363. [Google Scholar] [CrossRef]
- Pei, X.; Li, K.; Li, Y. A survey of adaptive optimal control theory. Math. Biosci. Eng. 2022, 19, 12058–12072. [Google Scholar] [CrossRef]
- Ren, B.; Zhong, Q.C.; Dai, J. Asymptotic reference tracking and disturbance rejection of UDE-based robust control. IEEE Trans. Ind. Electron. 2017, 64, 3166–3176. [Google Scholar] [CrossRef]
- Cordero, R.; Estrabis, T.; Brito, M.A.; Gentil, G. Development of a resonant generalized predictive controller for sinusoidal reference tracking. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 1218–1222. [Google Scholar] [CrossRef]
- Salton, A.T.; Zheng, J.; Flores, J.V.; Fu, M. High-precision tracking of periodic signals: A macro–micro approach with quantized feedback. IEEE Trans. Power Electron. 2022, 69, 8325–8334. [Google Scholar] [CrossRef]
- Wu, S.-T. Dynamic transfer between sliding control and the internal model control. Automatica 1999, 35, 1593–1597. [Google Scholar] [CrossRef]
- Lu, Y.-S. Sliding-mode controller design with internal model principle for systems subject to periodic signals. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 1952–1957. [Google Scholar]
- Liberzon, D. Switching in Systems and Control; Springer Science & Business Media: New York, NY, USA, 2003. [Google Scholar]
- Shi, Y.; Zhao, J.; Sun, X.M. A bumpless transfer control strategy for switched systems and its application to an aero-engine. IEEE Trans. Ind. Informat. 2021, 17, 52–62. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, J. Adaptive switching control of active suspension systems: A switched system point of view. IEEE Trans. Control Syst. Technol. 2024, 32, 663–670. [Google Scholar] [CrossRef]
- Kim, I.H.; Son, Y.I. A practical finite-time convergent observer against input disturbance and measurement noise. IEICE Trans. Fundamentals 2015, E98-A, 1973–1976. [Google Scholar]
- Cheong, S.Y.; Safonov, M.G. Slow-fast controller decomposition bumpless transfer for adaptive switching control. IEEE Trans. Autom. Control 2012, 57, 721–726. [Google Scholar] [CrossRef]
- Li, J.; Zhao, J. Bumpless transfer control for switched linear systems: A hierarchical switching strategy. IEEE Trans. Circuits Syst. I Reg. Pap. 2023, 70, 4539–4548. [Google Scholar] [CrossRef]
- Wang, F.; Long, L.; Xiang, C. Event-triggered state-dependent switching for adaptive fuzzy control of switched nonlinear systems. IEEE Trans. Fuzzy Syst. 2024, 32, 1756–1767. [Google Scholar] [CrossRef]
- Lu, S.; Wu, T.; Zhang, L.; Yang, J.; Liang, Y. Interpolated bumpless transfer control for asynchronously switched linear systems. IEEE/CAA J. Autom. Sin. 2024, 11, 1579–1590. [Google Scholar] [CrossRef]
- Wu, F.; Wang, D.; Lian, J. Bumpless transfer control for switched systems via a dynamic feedback and a bump-dependent switching law. IEEE Trans. Cybern. 2023, 53, 5372–5379. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, K.; Yang, J.; Han, M.; Yuan, S. Transition-dependent bumpless transfer control synthesis of switched linear systems. IEEE Trans. Autom. Control 2023, 68, 1678–1684. [Google Scholar] [CrossRef]
- Zeng, Z.-H.; Wang, Y.-W.; Liu, X.-K.; Yang, W. Event-triggered control of switched two-time-scale systems with asynchronous switching. IEEE Control Syst. Lett. 2024, 8, 2075–2080. [Google Scholar] [CrossRef]
- Qi, S.; Zhao, J. Output Regulation Bumpless Transfer Control for Discrete-Time Switched Linear Systems. IEEE Trans. Circuits Syst. II Exp. Briefs 2024, 70, 4181–4185. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, Y.; Yang, D.; Zhang, J. Bumpless transfer control for switched systems: A dual design of controller and switching signal. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 251–261. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Lewis, F.L.; Liu, D. Reinforcement Learning and Approximate Dynamic Programming for Feedback Control; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Vamvoudakis, K.G. Reinforcement learning and feedback control: Using natural decision methods to design optimal adaptive controllers. IEEE Control Syst. Mag. 2012, 32, 76–105. [Google Scholar]
- Lv, L.; Zhang, S.; Ding, D.; Wang, Y. Path planning via an improved DQN-based learning policy. IEEE Access 2019, 7, 67319–67330. [Google Scholar] [CrossRef]
- Rio, A.d.; Jimenez, D.; Serrano, J. Comparative analysis of A3C and PPO algorithms in reinforcement learning: A survey on general environments. IEEE Access 2024, 12, 146795–146806. [Google Scholar] [CrossRef]
- Gao, J.; Li, Y.; Chen, Y.; He, Y.; Guo, J. An improved SAC-based deep reinforcement learning framework for collaborative pushing and grasping in underwater environments. IEEE Trans. Instrum. Meas. 2024, 73, 2512814. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Gao, Z.; He, X. An improved DDPG, and its application based on the double-layer BP neural network. IEEE Access 2020, 8, 177734–177744. [Google Scholar] [CrossRef]
- Goncalves, T.R.; Cunha, R.F.; Varma, V.S.; Elayoubi, S.E. Fuel-efficient switching control for platooning systems with deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 13989–13999. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Song, Y.; Scaramuzza, D. Policy search for model predictive control with application to agile drone flight. IEEE Trans. Robot. 2022, 38, 2114–2130. [Google Scholar] [CrossRef]
- Sul, S.-K. Control of Electric Machine Drive Systems; Wiley: Hoboken, NJ, USA, 2011; Volume 88. [Google Scholar]
- Son, Y.I.; Kim, I.H.; Choi, D.S.; Shim, H. Robust cascade control of electric motor drives using dual reduced-order PI observer. IEEE Trans. Ind. Electron. 2015, 62, 3672–3682. [Google Scholar] [CrossRef]
- Kim, I.H.; Son, Y.I. Regulation of a DC/DC boost converter under parametric uncertainty and input voltage variation using nested reduced-order PI observers. IEEE Trans. Ind. Electron. 2017, 64, 552–562. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Hwangbo, J.; Lee, J.; Dosovitskiy, A.; Bellicoso, D.; Lee, J.; Tsounis, V.; Koltun, V.; Hutter, M. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 2019, 4, eaau5872. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W.; Shim, H.; Yang, I. On improving the robustness of reinforcement learning-based controllers using disturbance observer. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 847–852. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2019, arXiv:1509.02971v6. [Google Scholar]
- Ding, W.; Liu, G.; Li, P. A hybrid control strategy of hybrid-excitation switched reluctance motor for torque ripple reduction and constant power extension. IEEE Trans. Ind. Electron. 2020, 67, 38–48. [Google Scholar] [CrossRef]
- Zhuang, W.; Zhang, X.; Yin, G.; Peng, H.; Wang, L. Mode shift schedule and control strategy design of multimode hybrids powertrain. IEEE Trans. Control Syst. Technol. 2020, 28, 804–815. [Google Scholar] [CrossRef]
- Sussman, H.J.; Kokotovic, P.V. The peaking phenomenon and the global stabilization of nonlinear systems. IEEE Trans. Autom. Control 1991, 36, 424–440. [Google Scholar] [CrossRef]
- Hui, J.; Lee, Y.-K.; Yuan, J. Fractional-order sliding mode load following control via disturbance observer for modular high-temperature gas-cooled reactor system with disturbances. Asian J. Control 2023, 25, 3513–3523. [Google Scholar] [CrossRef]
- Hui, J.; Lee, Y.-K.; Yuan, J. Load following control of a PWR with load-dependent parameters and perturbations via fixed-time fractional-order sliding mode and disturbance observer techniques. Renew. Sustain. Energy Rev. 2023, 184, 113550. [Google Scholar] [CrossRef]
- Hui, J. Fixed-time fractional-order sliding mode controller with disturbance observer for U-tube steam generator. Renew. Sustain. Energy Rev. 2024, 205, 114829. [Google Scholar] [CrossRef]









| Hyperparameter | Value | Hyperparameter | Value |
|---|---|---|---|
| 0.01 | Learning Rate () | ||
| 0.995 | Episodes | 200 | |
| Discount Factor () | 0.4 | Soft Update Parameter | 0.05 |
| Replay Memory Size | Batch Size | ||
| Optimizer | Adam | Loss Function | L1 Loss |
| Parameter | Nominal Value | Uncertain Value | Physical Representation |
|---|---|---|---|
| k | 20.2981 | 25.3726 | |
| 0.1192 | 0.0953 |
| Transient | Cascade Convergence [s] | IMP Convergence [s] | PID Convergence [s] | LQR Convergence [s] | Proposed Convergence [s] |
|---|---|---|---|---|---|
| 1 | 0.17 | 0.46 | 0.25 | 0.17 | 0.17 |
| 2 | 0.13 | 0.44 | 0.37 | 0.20 | 0.13 |
| 3 | Does Not Converge | 0.47 | Does Not Converge | Does Not Converge | 0.38 |
| 4 | Does Not Converge | 0.47 | Does Not Converge | Does Not Converge | 0.32 |
| 5 | 0.17 | 0.47 | 0.21 | 0.13 | 0.18 |
| Average | - | 0.46 | - | - | 0.23 |
| Transient | Cascade Overshoot [%] | IMP Overshoot [%] | PID Overshoot [%] | LQR Overshoot [%] | Proposed Overshoot [%] |
|---|---|---|---|---|---|
| 1 | 0 | 58.63 | 77.81 | 36.63 | 0.11 |
| 2 | 0 | 84.53 | 92.49 | 35.39 | 0.57 |
| 3 | Does Not Converge | 56.52 | Does Not Converge | Does Not Converge | 0 |
| 4 | Does Not Converge | 53.81 | Does Not Converge | Does Not Converge | 2.34 |
| 5 | 0 | 56.27 | 67.21 | 37.98 | 0.082 |
| Average | - | 61.95 | - | - | 0.62 |
| Reference Type | Cascade Avg. Err. [rad] | IMP Avg. Err. [rad] | PID Avg. Err. [rad] | LQR Avg. Err. [rad] | Proposed Avg. Err. [rad] |
|---|---|---|---|---|---|
| Constant (1 s 2 s) | |||||
| Sinusoidal (9 s 12 s) |
| Transient | Cascade Convergence [s] | IMP Convergence [s] | Proposed Convergence [s] |
|---|---|---|---|
| 1 | 0.18 | 0.44 | 0.17 |
| 2 | 0.17 | 0.43 | 0.18 |
| 3 | Does Not Converge | 0.43 | 0.32 |
| 4 | Does Not Converge | 0.44 | 0.28 |
| 5 | 0.17 | 0.43 | 0.18 |
| Average | – | 0.43 | 0.22 |
| Transient | Cascade Overshoot [%] | IMP Overshoot [%] | Proposed Overshoot [%] |
|---|---|---|---|
| 1 | 0.16 | 51.89 | 1.49 |
| 2 | 0.12 | 51.62 | 0.12 |
| 3 | Does Not Converge | 54.41 | 2.53 |
| 4 | Does Not Converge | 53.60 | 2.21 |
| 5 | 0.19 | 52.95 | 0.19 |
| Average | – | 52.91 | 1.31 |
| Reference Type | Cascade Avg. Err. [rad] | IMP Avg. Err. [rad] | Proposed Avg. Err. [rad] |
|---|---|---|---|
| Constant (1 s 2 s) | |||
| Sinusoidal (9 s 12 s) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amare, N.D.; Yang, S.J.; Son, Y.I. An Optimized Position Control via Reinforcement-Learning-Based Hybrid Structure Strategy. Actuators 2025, 14, 199. https://doi.org/10.3390/act14040199
Amare ND, Yang SJ, Son YI. An Optimized Position Control via Reinforcement-Learning-Based Hybrid Structure Strategy. Actuators. 2025; 14(4):199. https://doi.org/10.3390/act14040199
Chicago/Turabian StyleAmare, Nebiyeleul Daniel, Sun Jick Yang, and Young Ik Son. 2025. "An Optimized Position Control via Reinforcement-Learning-Based Hybrid Structure Strategy" Actuators 14, no. 4: 199. https://doi.org/10.3390/act14040199
APA StyleAmare, N. D., Yang, S. J., & Son, Y. I. (2025). An Optimized Position Control via Reinforcement-Learning-Based Hybrid Structure Strategy. Actuators, 14(4), 199. https://doi.org/10.3390/act14040199






