Development of a Magnetorheological Damper with Self-Powered Ability for Washing Machines
Abstract
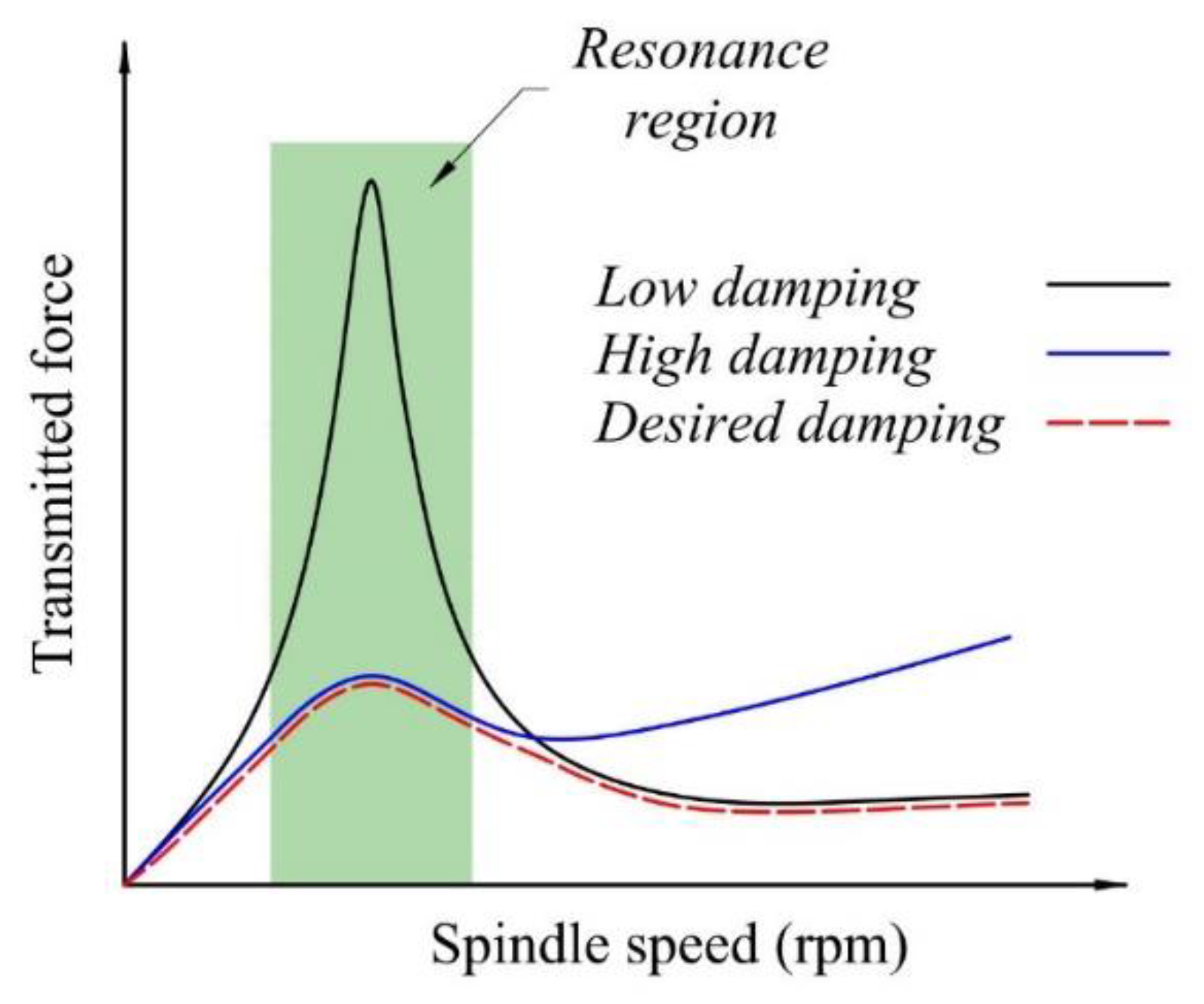
:1. Introduction
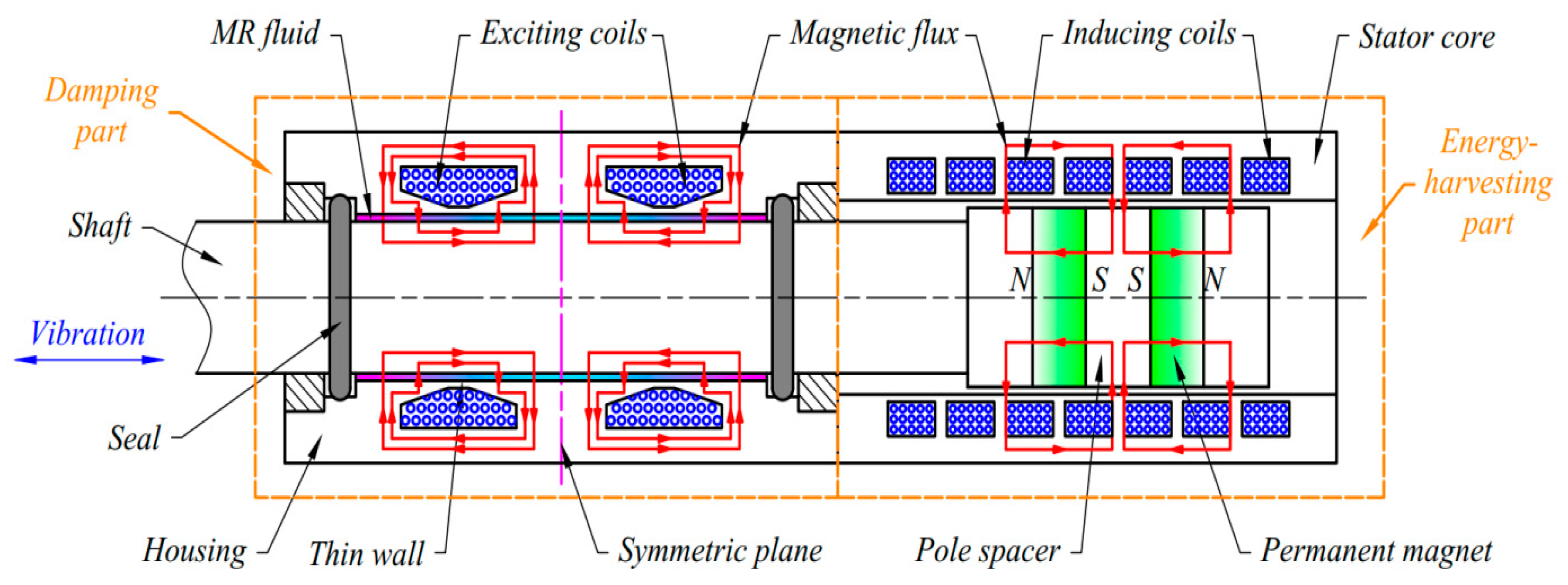
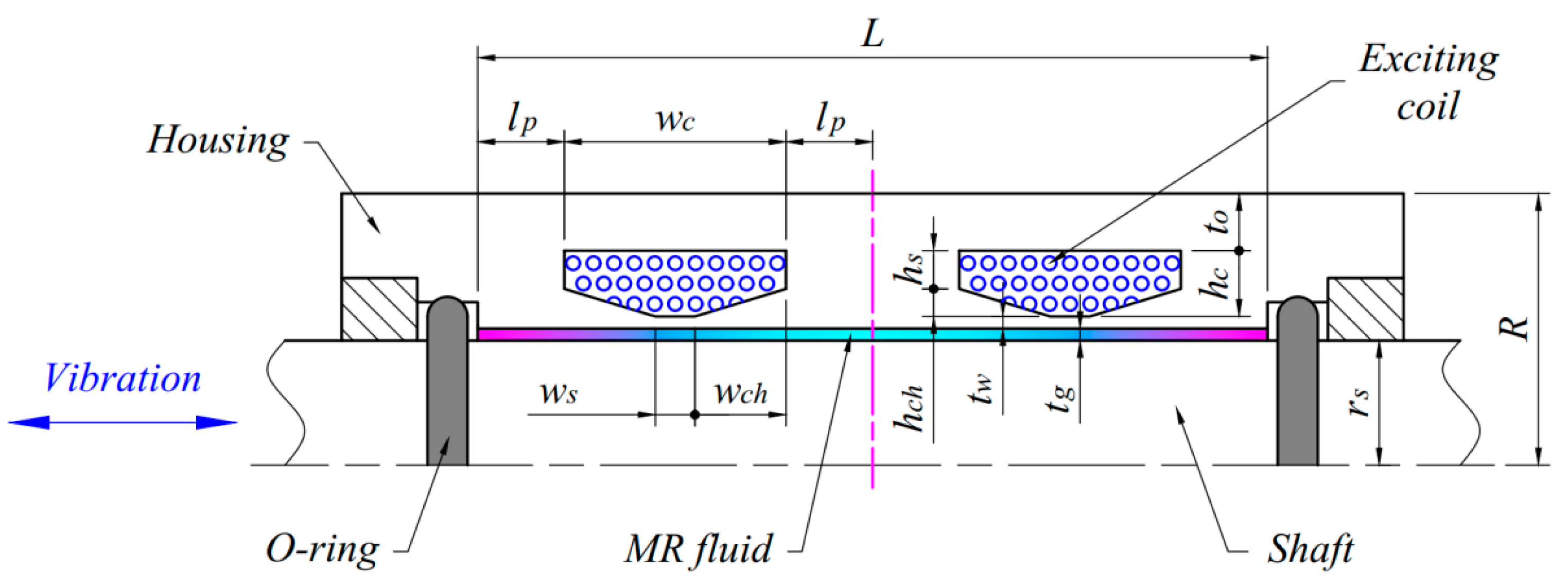
2. Configuration and Operating Principles
3. Energy-Harvesting Part
3.1. Modeling of the Energy-Harvesting Part
3.2. Optimal Design of the Energy-Harvesting Part
4. MR Damping Part
4.1. Modeling of the MR Damping Part
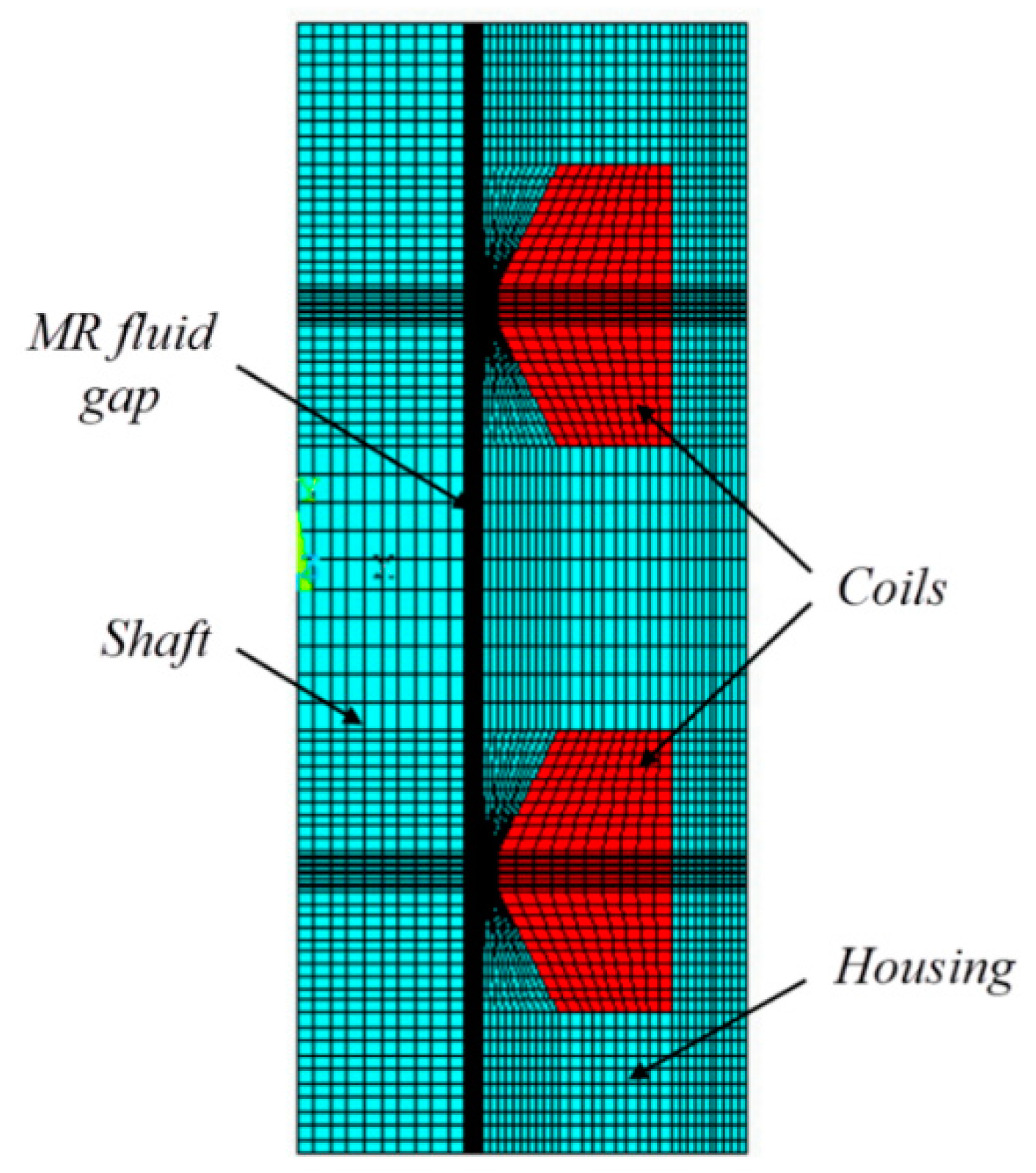
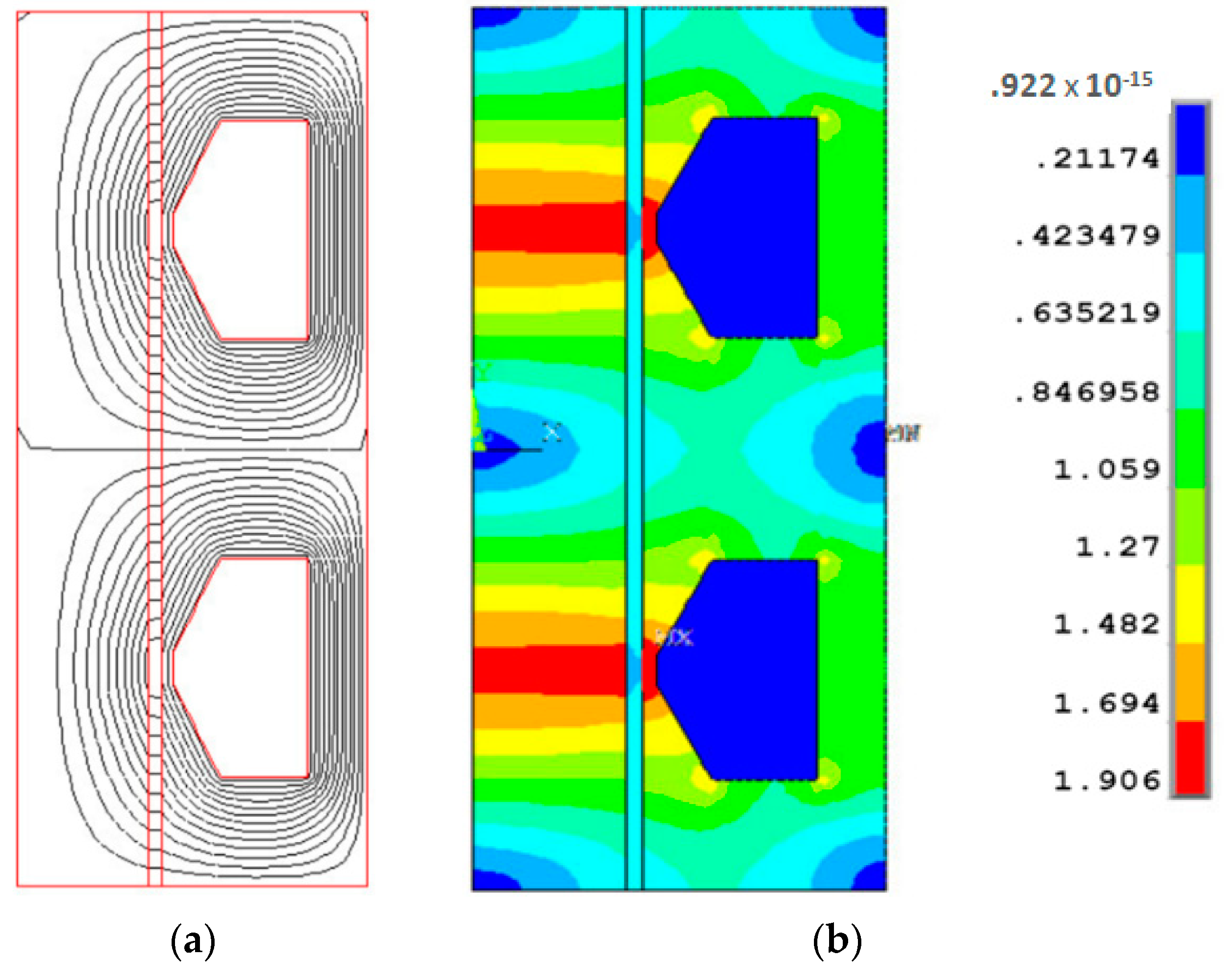
4.2. Optimal Design of the MR Damping Part
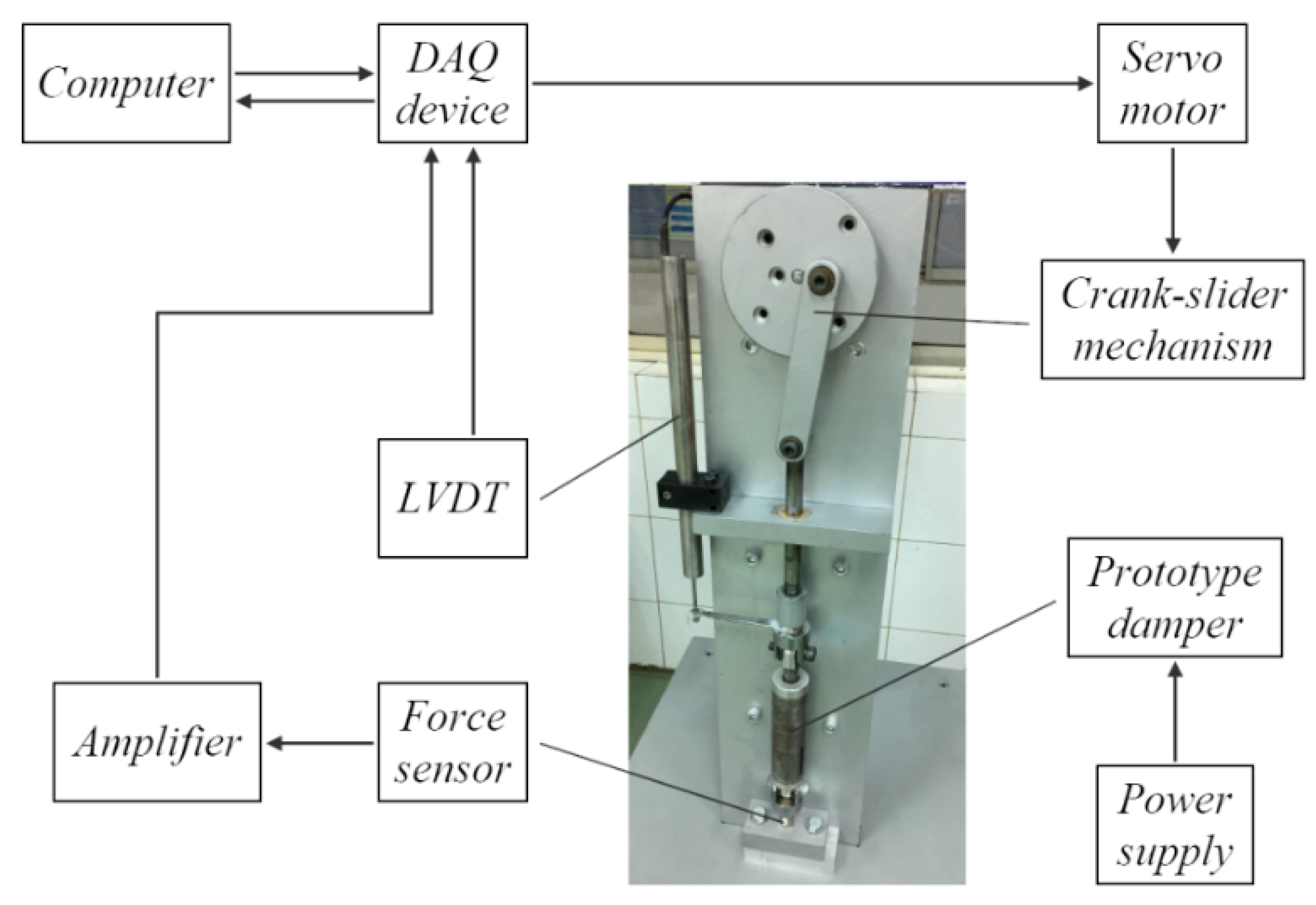
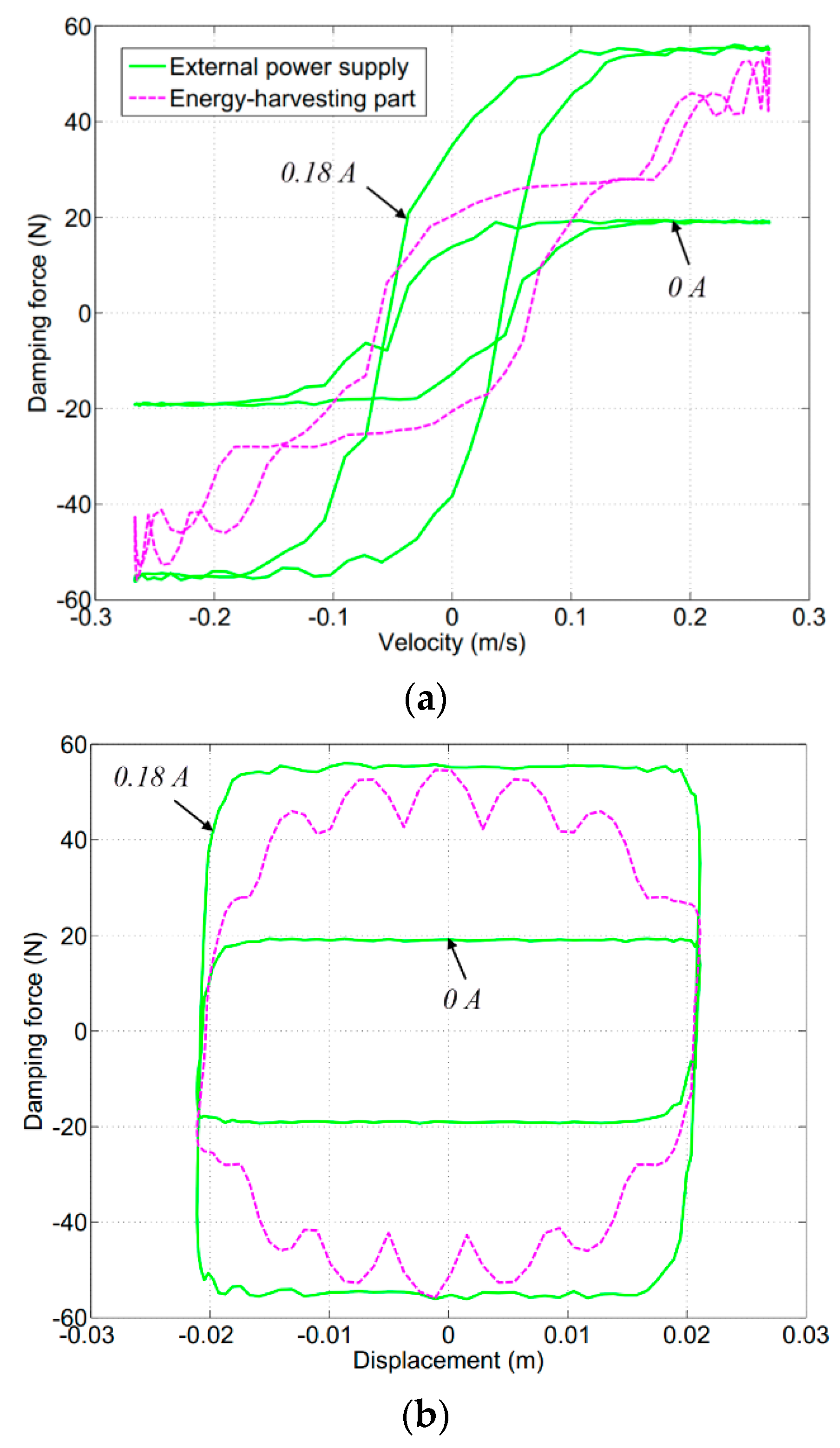
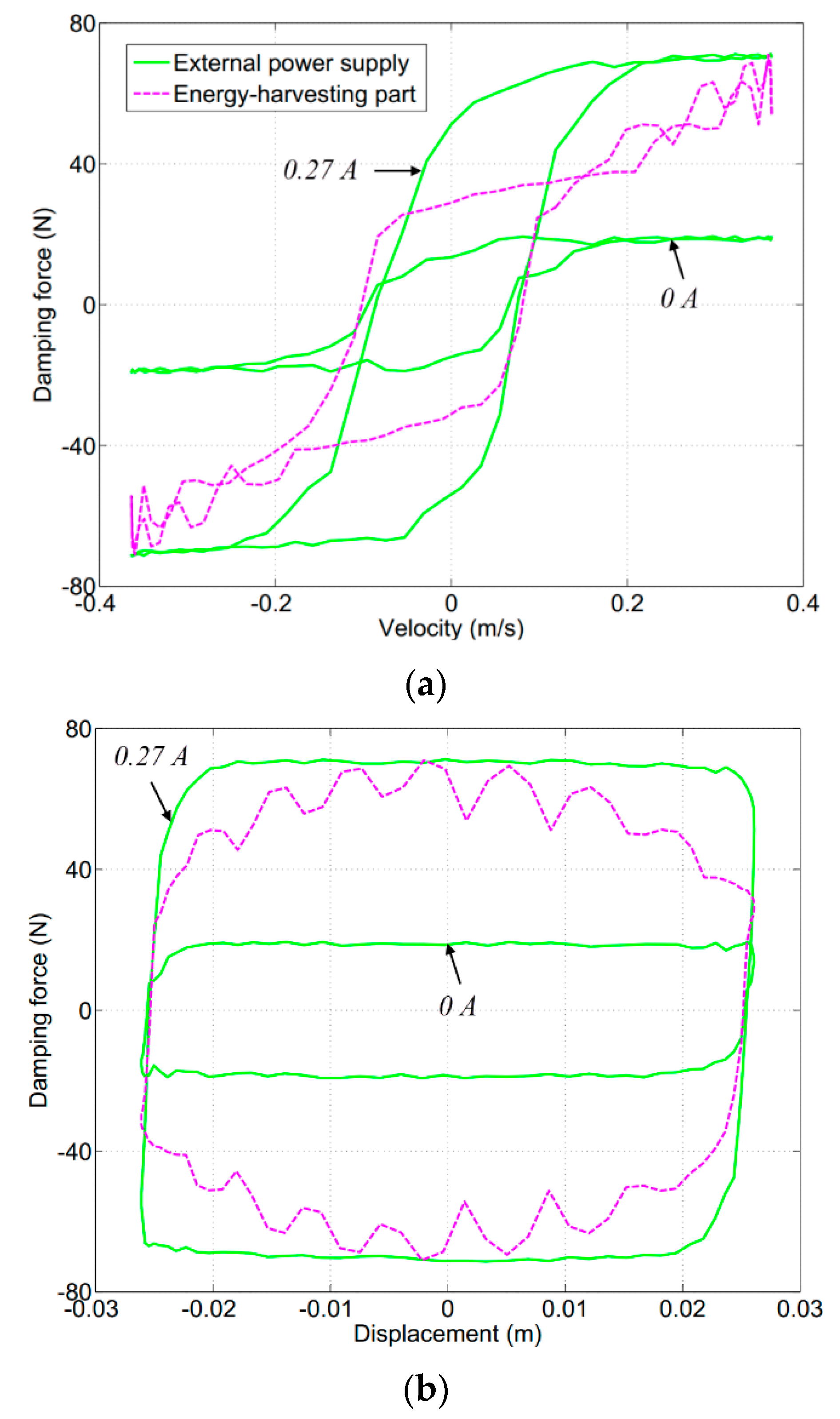
5. Experimental Validation
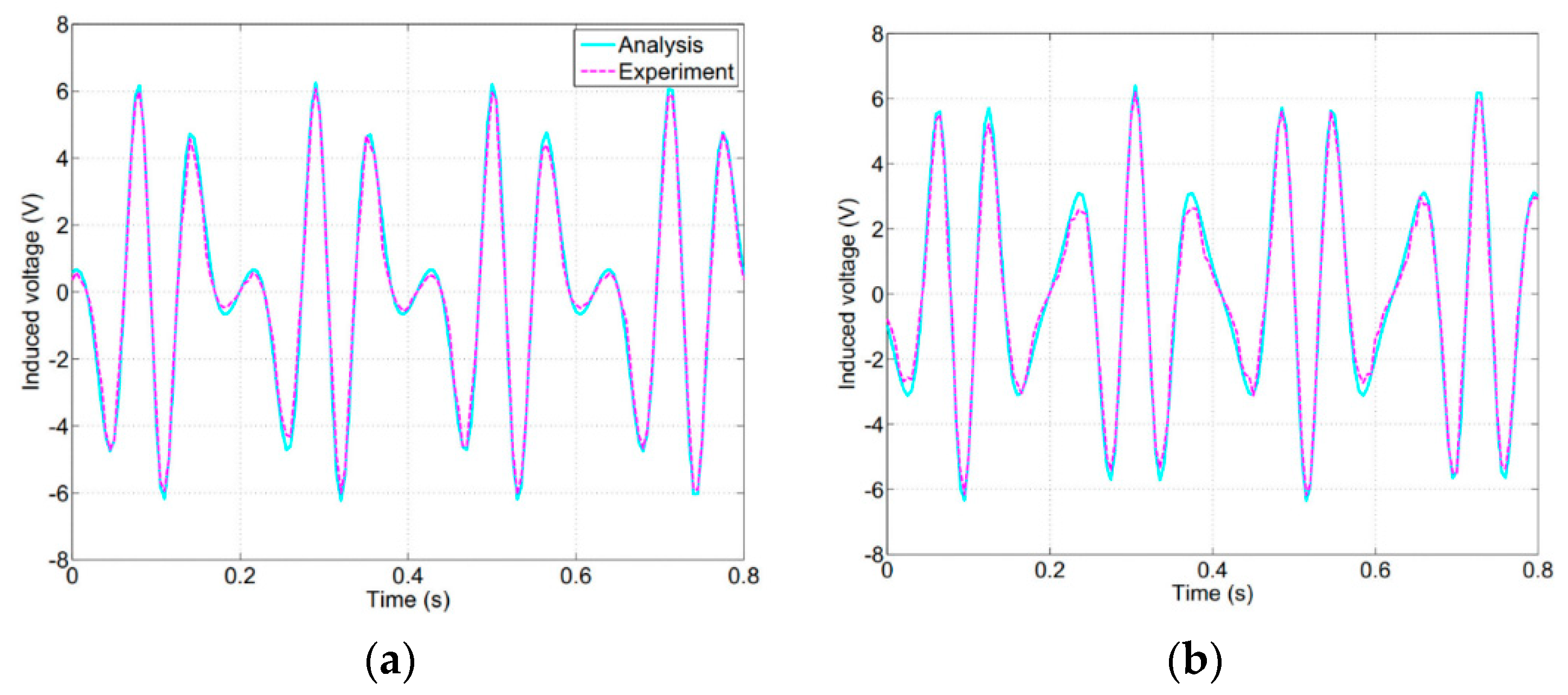
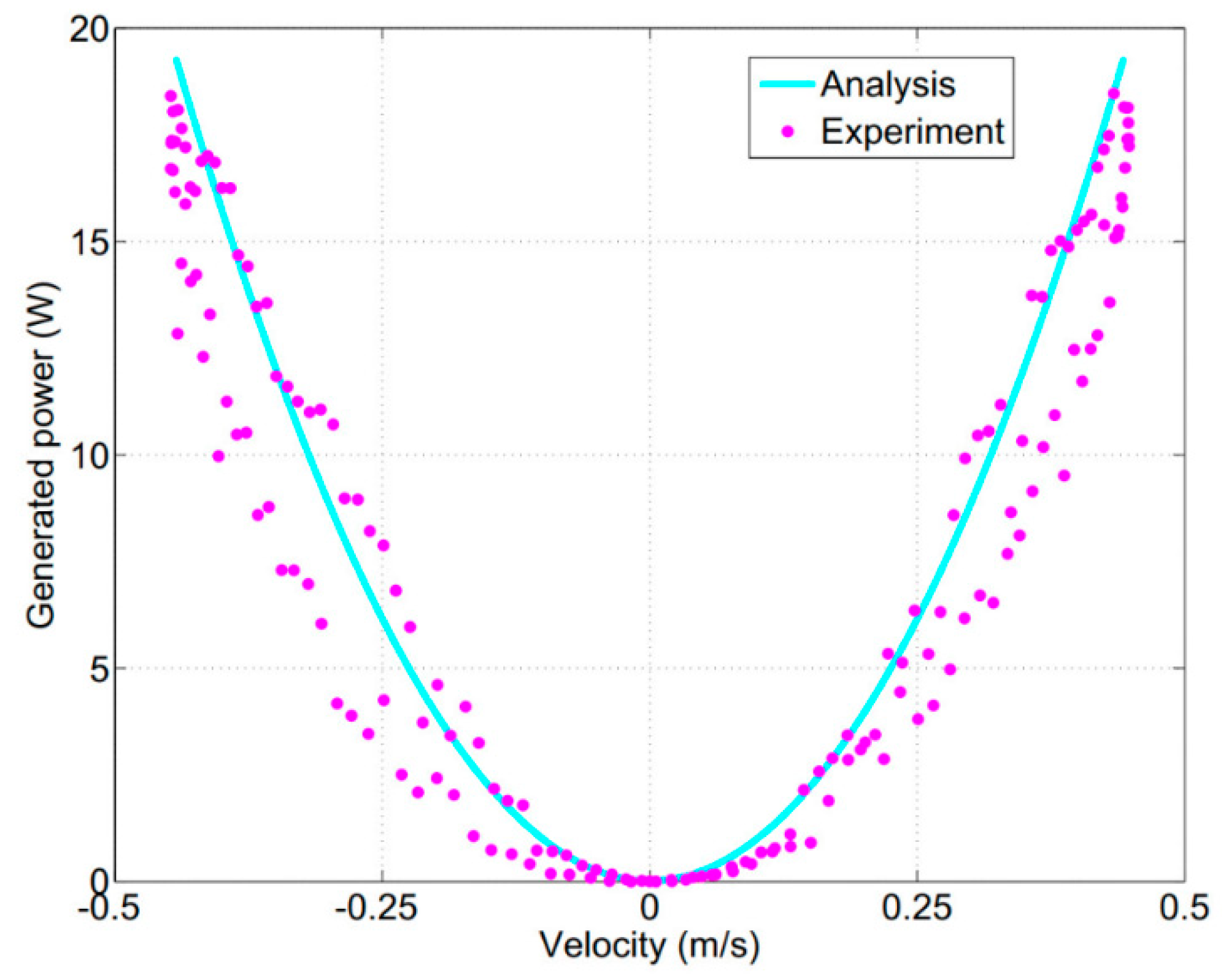
5.1. Performance of the Energy-Harvesting Part
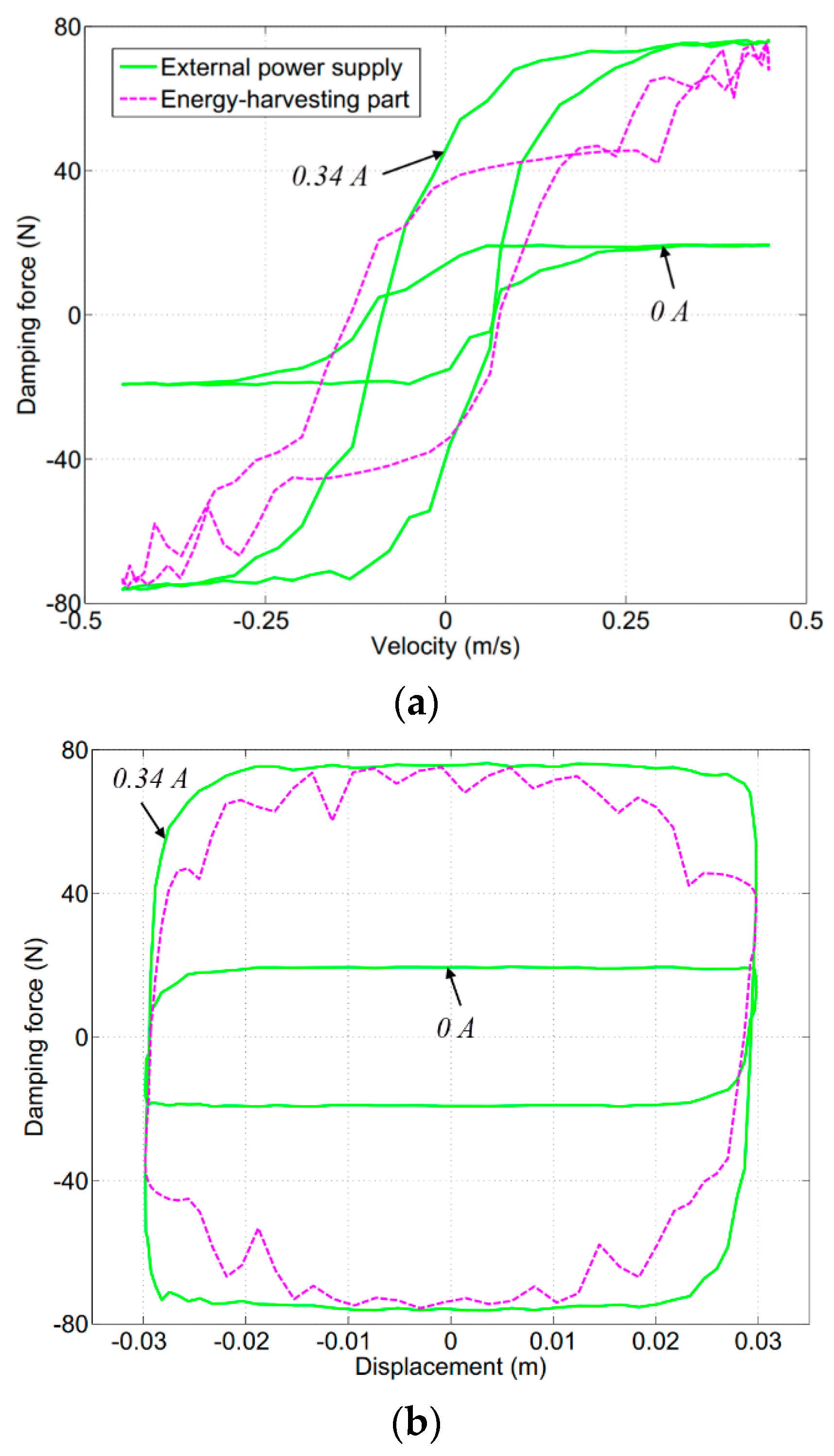
5.2. Damping Force under Constant Magnetic Field
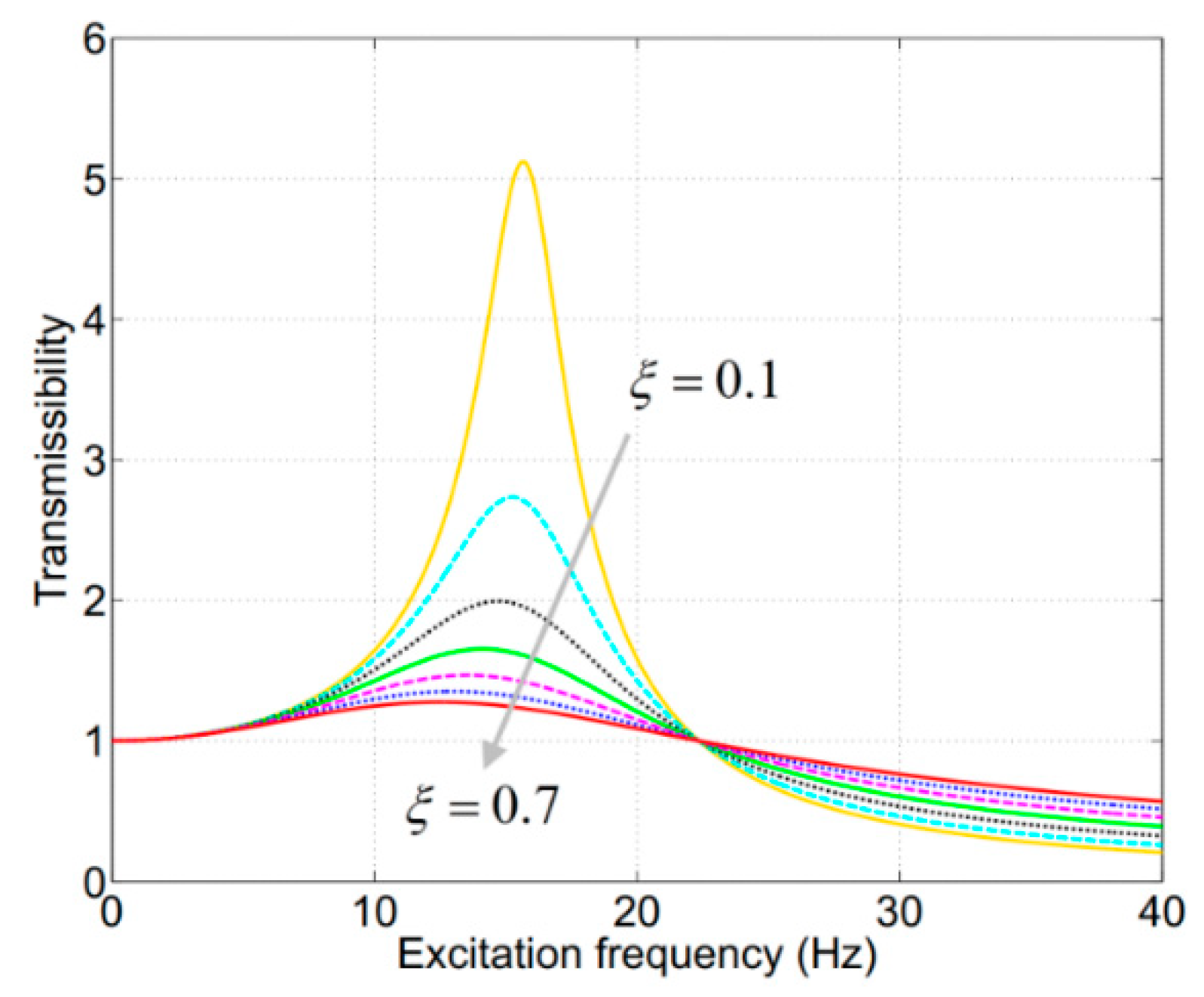
5.3. Self-Adaptability of the Damping Force
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclatures
| Ac | Sectional area of the inducing coil |
| Agm | Cylindrical surface area of the air gap |
| Am | Sectional area of the magnet |
| Ar | Projected area of the seal |
| B | Applied magnetic density |
| Brem | Magnet remanent flux density |
| c | Damping coefficient |
| dw | Diameter of the copper wire |
| E | Induced voltage in the inducing coil |
| Ei | Induced voltages in the i active coil |
| EH | Energy-harvesting |
| F0 | Zero-field friction force |
| Fd | Damping force |
| For | Coulomb friction force between the shaft and the O-ring |
| Fr | Required damping force for the MR damping part |
| Fu | Exciting force due to an unbalanced mass in the u direction |
| Fu0 | Magnitude of the exciting force |
| fc | Friction per unit length caused by the compression of the O-ring |
| fh | Friction force caused by the fluid pressure on a unit projected area of the O-ring |
| Hcoe | Magnetic coercivity of the magnet |
| hc | Height of the exciting coil |
| hch, wch | Chamfer dimensions of the exciting coil |
| hcm | Height of the inducing coil |
| I | Applied current |
| k | Stiffness of each spring |
| L | Length of the MR fluid gap |
| Le | Effective length of the active MR fluid in the gap |
| Lr | Length of the seal rubbing surface |
| Ls | Length of the shaft end |
| lm | Length of the magnet |
| lp | Length of the pole of the MR damping part |
| MRF | Magnetorheological fluid |
| m | Mass of the suspended tub assembly |
| mu | Unbalanced mass |
| N | Number of winding turns of each inducing coil |
| P | Power of four active coils |
| P1, P2 | Powers of coil 1 and coil 2 |
| pc | Pitch of the coil slot of the EH part |
| pm | Pitch of the pole pair of the EH part |
| R | Outer radius of the self-powered MR damper |
| Rc | Resistance of each inducing coil |
| Rs | Radius of the shaft |
| Ru | Radius from the rotation axis of the unbalanced mass |
| ri | Inner radius of the magnet |
| ro | Outer radius of the magnet |
| rs | Radius of the shaft |
| rω | Frequency ratio |
| Tf | Force transmissibility from the tub assembly to the cabinet |
| t | Time |
| tg | Thickness of the MR fluid gap |
| tgm | Thickness of the air gap |
| to | Thickness of the outer housing of the MR damping part |
| tom | Thickness of the housing of the EH part |
| tw | Thickness of the thin wall of the MR damping part |
| twm | Thickness of the thin wall of the EH part |
| v | Velocity of the shaft |
| wc | Width of the exciting coil |
| wcm | Width of the inducing coil |
| X | Amplitude of the tub vibration |
| x | Displacement of the shaft |
| Y | MR fluid rheological property such as postyield viscosity or yield stress |
| α1, α2 | Angle between the spring and the y-axis |
| αSY | Saturation moment of the Y property |
| β1, β2 | Angle between the damper and the y-axis |
| ∆u | Displacement of the center of the tube assembly in the u direction |
| η | Postyield viscosity of the active MR fluid in the gap |
| λ | Efficiency of the magnetic flux considering leakage effect |
| µ0 | Relative magnetic permeability |
| ξ | Damping ratio |
| τy | Field-dependent yield stress of the active MR fluid in the gap |
| Φg | Magnetic flux of the air gap between the magnets and the stator core |
| φ | Angle of the u direction |
| φ0 | Initial phase angle of the inducing coil |
| ωd | Damped frequency |
| ωn | Natural frequency |
References
- Stone, E.J.; Cebon, D. Control of semi-active anti-roll systems on heavy vehicles. Veh. Syst. Dyn. 2010, 48, 1215–1243. [Google Scholar] [CrossRef]
- Erkus, B.; Johnson, E.A. Dissipativity analysis of the base isolated benchmark structure with magnetorheological fluid dampers. Smart Mater. Struct. 2011, 20, 105001. [Google Scholar] [CrossRef]
- Makowski, M.; Knap, L. Investigation of an off-road vehicle equipped with magnetorheological dampers. Adv. Mech. Eng. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Seong, M.S.; Choi, S.B.; Kim, C.H. Design and Performance Evaluation of MR Damper for Integrated Isolation Mount. J. Intell. Mater. Syst. Struct. 2011, 22, 1729–1738. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Papadimitriou, I. Modeling, design and control of a portable washing machine during the spinning cycle. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Como, Italy, 8–12 July 2001; pp. 899–904. [Google Scholar]
- Koizumi, T.; Tsujiuchi, N.; Matsumoto, S.; Hirasawa, Y. Noise prediction of a washing machine considering panel vibration. In Proceedings of the IMAC-XXIV Conference and Exposition on Structural Dynamics, St. Louis, MO, USA, 30 January–2 February 2006. [Google Scholar]
- Lim, H.T.; Jeong, W.B.; Kim, K.J. Dynamic modeling and analysis of drum-type washing machine. Int. J. Precis. Eng. Manuf. 2010, 11, 407–417. [Google Scholar] [CrossRef]
- Carlson, J.D. Low-cost MR fluid sponge devices. J. Intell. Mater. Syst. Struct. 1999, 10, 589–594. [Google Scholar] [CrossRef]
- Aydar, G.; Evrensel, C.A.; Gordaninejad, F.; Fuchs, A. A low force magneto-rheological (MR) fluid damper: Design, fabrication and characterization. J. Intell. Mater. Syst. Struct. 2007, 18, 1155–1160. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Nguyen, N.D.; Choi, S.B. Optimal design and performance evaluation of a flow-mode MR damper for front-loaded washing machines. Asia Pac. J. Comput. Eng. 2014, 1, 3. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, Q.H.; Choi, S.B.; Woo, J.K. Optimal design of magnetorheological fluid-based dampers for front-loaded washing machines. Proc. Inst. Mech. Eng. C-J. Mec. Eng. Sci. 2014, 228, 294–306. [Google Scholar] [CrossRef]
- Bui, D.Q.; Hoang, V.L.; Le, H.D.; Nguyen, Q.H. Design and evaluation of a shear-mode MR damper for suspension system of front-loading washing machines. In Proceedings of the International Conference on Advances in Computational Mechanics, Phu Quoc Island, Vietnam, 2–4 August 2017; pp. 1061–1072. [Google Scholar]
- Ulasyar, A.; Lazoglu, I. Design and analysis of a new magneto rheological damper for washing machine. J. Mech. Sci. Technol. 2018, 32, 1549–1561. [Google Scholar] [CrossRef]
- Cho, S.W.; Jung, H.J.; Lee, I.W. Smart passive system based on magnetorheological damper. Smart Mater. Struct. 2005, 14, 707–714. [Google Scholar] [CrossRef]
- Choi, K.M.; Jung, H.J.; Lee, H.J.; Cho, S.W. Feasibility study of an MR damper-based smart passive control system employing an electromagnetic induction device. Smart Mater. Struct. 2007, 16, 2323–2329. [Google Scholar] [CrossRef]
- Kim, I.H.; Jung, H.J.; Koo, J.H. Experimental evaluation of a self-powered smart damping system in reducing vibrations of a full-scale stay cable. Smart Mater. Struct. 2010, 19, 115027. [Google Scholar] [CrossRef]
- Chen, C.; Liao, W.H. A self-sensing magnetorheological damper with power generation. Smart Mater. Struct. 2012, 21, 025014. [Google Scholar] [CrossRef]
- Hu, G.; Lu, Y.; Sun, S.; Li, W. Performance analysis of a magnetorheological damper with energy harvesting ability. Shock Vib. 2016, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Xinchun, G.; Yonghu, H.; Yi, R.; Hui, L.; Jinping, O. A novel self-powered MR damper: Theoretical and experimental analysis. Smart Mater. Struct. 2015, 24, 105033. [Google Scholar] [CrossRef]
- Ebrahimi, B.; Khamesee, M.B.; Golnaraghi, M.F. Feasibility study of an electromagnetic shock absorber with position sensing capability. In Proceedings of the 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 2988–2991. [Google Scholar]
- Nguyen, Q.H.; Han, Y.M.; Choi, S.B.; Wereley, N.M. Geometry optimization of MR valves constrained in a specific volume using the finite element method. Smart Mater. Struct. 2007, 16, 2242–2252. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Choi, S.B.; Wereley, N.M. Optimal design of magneto-rheological valves via a finite element method considering control energy and a time constant. Smart Mater. Struct. 2008, 17, 1–12. [Google Scholar] [CrossRef]
- Cleveland, O.H. Parker O-Ring handbook. Parker Hannifin Corporation: Cleveland, OH, USA, 2018. [Google Scholar]
- Zubieta, M.; Eceolaza, S.; Elejabarrieta, M.J.; Ali, M.M.B. Magnetorheological fluids: Characterization and modeling of magnetization. Smart Mater. Struct. 2009, 18, 095019. [Google Scholar] [CrossRef]
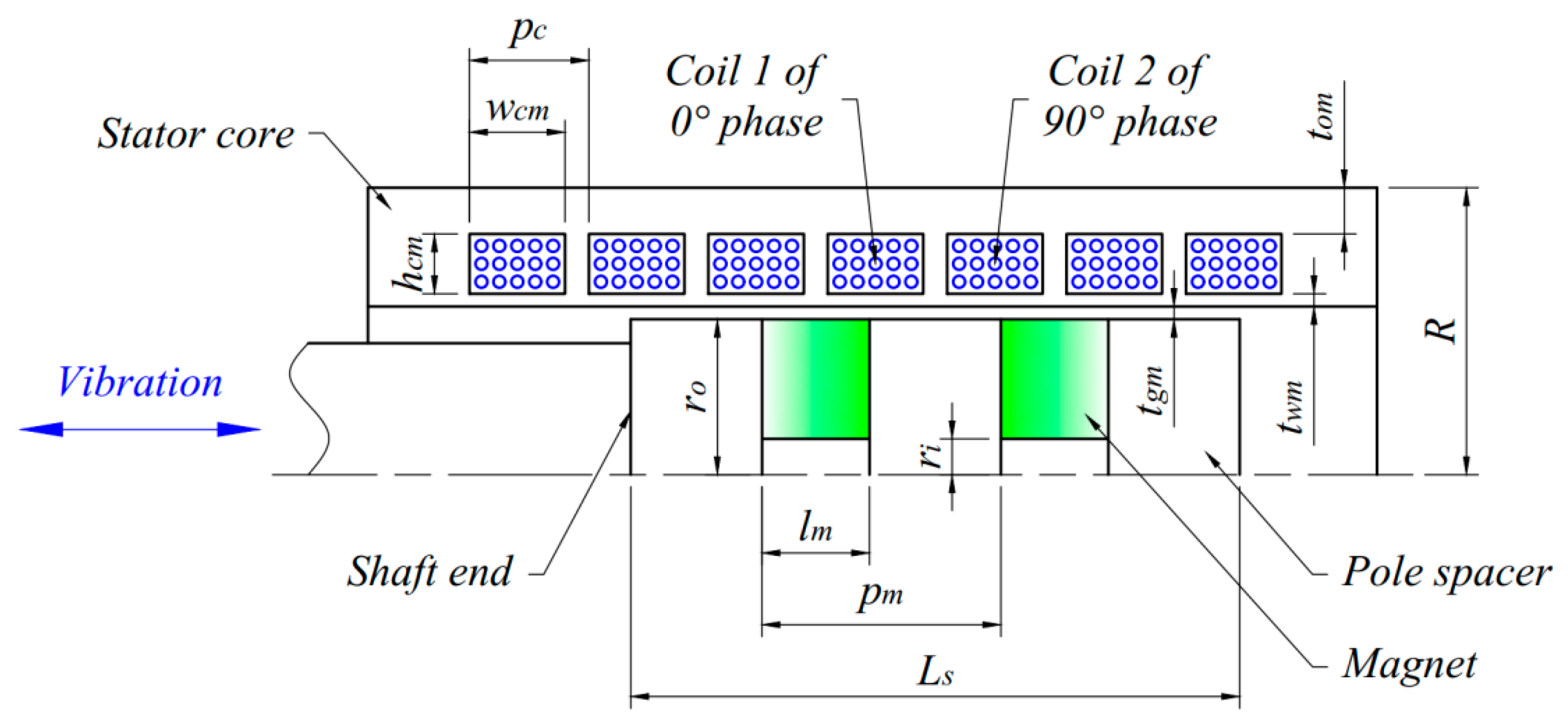

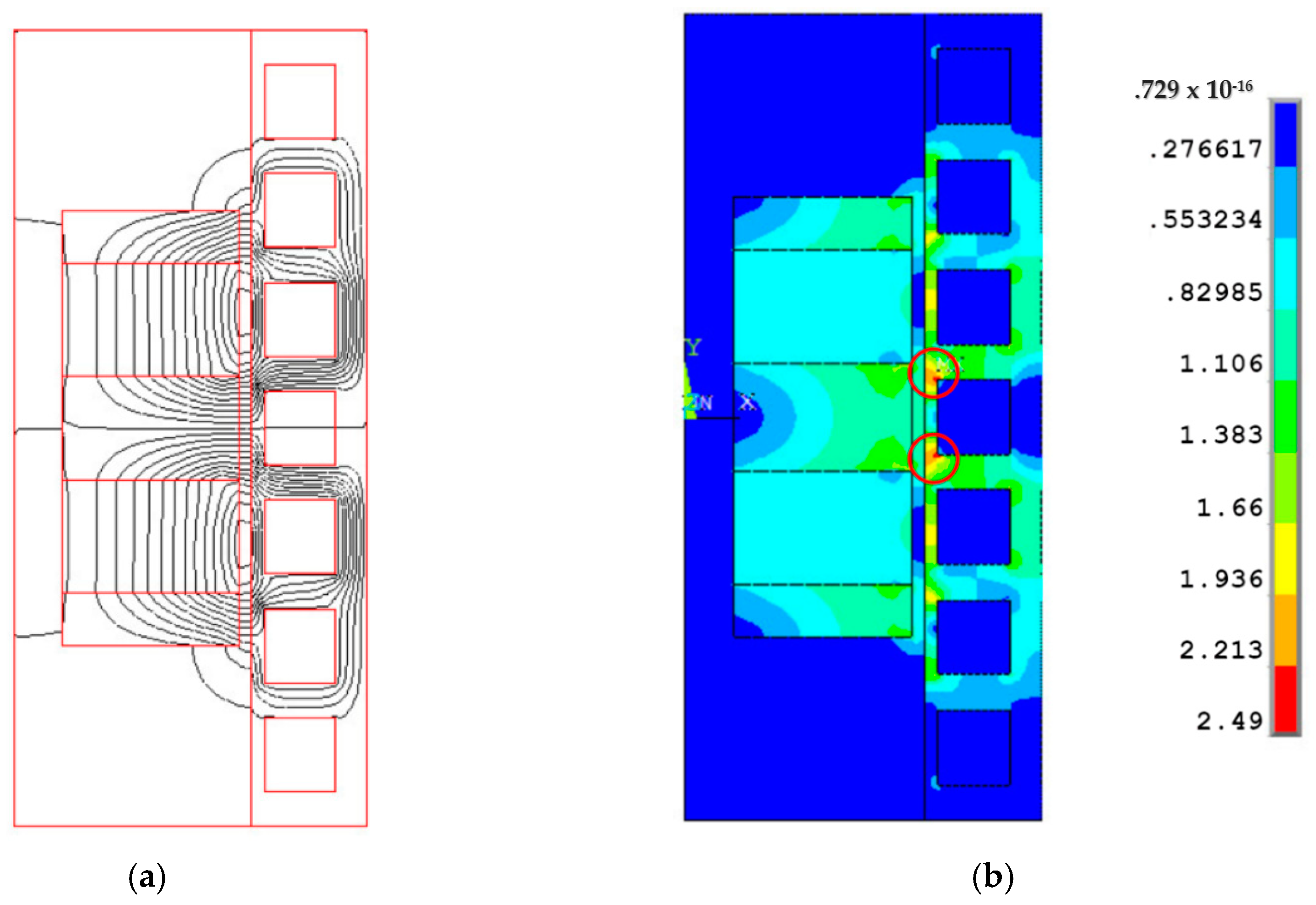



| Parameter (mm) | Value | Parameter (mm) | Value |
|---|---|---|---|
| Coil height hcm | 4.4 | Air gap thickness tgm | 0.8 |
| Coil width wcm | 4.56 | Thin wall thickness twm | 0.8 |
| Coil pitch pc | 6.74 | Housing thickness tom | 2 |
| Magnet length lm | 7 | Outer radius R | 22 |
| Pole pair pitch pm | 13.48 | Generated power P (W) | 19.3 |
| Parameters | ||
|---|---|---|
| η0 = 0.1 Pa·s | τy0 = 15 Pa | αSη = 4.5 T−1 |
| η∞ = 3.8 Pa·s | τy∞ = 40,000 Pa | αSτy = 2.9 T−1 |
| Parameter (mm) | Value | Parameter (mm) | Value |
|---|---|---|---|
| Coil height hc | 8.57 | Thin wall thickness tw | 0.8 |
| Coil width wc | 13.81 | Housing thickness to | 3.58 |
| Coil height chamfer hch | 3.05 | Shaft radius rs | 8.25 |
| Coil width chamfer wch | 5.9 | Outer radius R | 22 |
| Pole length lp | 6.88 | Max. current intensity I (A) | 0.34 |
| MR fluid gap length L | 55.13 | Max. damping force Fd (N) | 80.2 |
| MR fluid gap thickness tg | 0.8 | Zero-field friction force Fo (N) | 18.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bui, Q.-D.; Nguyen, Q.H.; Nguyen, T.T.; Mai, D.-D. Development of a Magnetorheological Damper with Self-Powered Ability for Washing Machines. Appl. Sci. 2020, 10, 4099. https://doi.org/10.3390/app10124099
Bui Q-D, Nguyen QH, Nguyen TT, Mai D-D. Development of a Magnetorheological Damper with Self-Powered Ability for Washing Machines. Applied Sciences. 2020; 10(12):4099. https://doi.org/10.3390/app10124099
Chicago/Turabian StyleBui, Quoc-Duy, Quoc Hung Nguyen, Tan Tien Nguyen, and Duc-Dai Mai. 2020. "Development of a Magnetorheological Damper with Self-Powered Ability for Washing Machines" Applied Sciences 10, no. 12: 4099. https://doi.org/10.3390/app10124099




