Hybrid NOMA/OMA-Based Dynamic Power Allocation Scheme Using Deep Reinforcement Learning in 5G Networks

Abstract

Non-orthogonal multiple access (NOMA) is considered a potential technique in fifth-generation (5G). Nevertheless, it is relatively complex when applying NOMA to a massive access scenario. Thus, in this paper, a hybrid NOMA/OMA scheme is considered for uplink wireless transmission systems where multiple cognitive users (CUs) can simultaneously transmit their data to a cognitive base station (CBS). We adopt a user-pairing algorithm in which the CUs are grouped into multiple pairs, and each group is assigned to an orthogonal sub-channel such that each user in a pair applies NOMA to transmit data to the CBS without causing interference with other groups. Subsequently, the signal transmitted by the CUs of each NOMA group can be independently retrieved by using successive interference cancellation (SIC). The CUs are assumed to harvest solar energy to maintain operations. Moreover, joint power and bandwidth allocation is taken into account at the CBS to optimize energy and spectrum efficiency in order to obtain the maximum long-term data rate for the system. To this end, we propose a deep actor-critic reinforcement learning (DACRL) algorithm to respectively model the policy function and value function for the actor and critic of the agent (i.e., the CBS), in which the actor can learn about system dynamics by interacting with the environment. Meanwhile, the critic can evaluate the action taken such that the CBS can optimally assign power and bandwidth to the CUs when the training phase finishes. Numerical results validate the superior performance of the proposed scheme, compared with other conventional schemes.

1. Introduction

Recently, fourth-generation (4G) systems reached maturity, and will evolve into fifth-generation (5G) systems where limited amounts of new spectrum can be utilized to meet the stringent demands of users. However, critical challenges will come from explosive growth in devices and data volumes, which require more efficient exploitation of valuable spectrum. Therefore, non-orthogonal multiple access (NOMA) is one of the potential candidates for 5G and upcoming cellular network generations [1,2,3].

According to NOMA principles, multiple users are allowed to share time and spectrum resources in the same spatial layer via power-domain multiplexing, in contrast to conventional orthogonal multiple access (OMA) techniques consisting of frequency-division multiple access (FDMA) and time division multiple access (TDMA) [4]. Interuser interference can be alleviated by performing successive interference cancellation (SIC) on the receiver side. There has been a lot of research aimed at sum rate maximization, and the results showed that higher spectral efficiency (SE) can be obtained by using NOMA, compared to baseline OMA schemes [5,6,7,8]. Zeng et al. [5] investigated a multiple-user scenario in which users are clustered and share the same transmit beamforming vector. Di et al. [6] proposed a joint sub-channel assignment and power allocation scheme to maximize the weighted total sum rate of the system while adhering to a user fairness constraint. Timotheou et al. [7] studied a decoupled problem of user clustering and power allocation in NOMA systems in which the proposed user clustering approach is based on exhaustive search with a high required complexity. Liang et al. [8] studied solutions for user pairing, and investigated the power allocation problem by using NOMA in cognitive radio (CR) networks.

Nowadays, energy consumption for wireless communications is becoming a major social and economic issue, especially with the explosive amounts of data traffic. However, limited efforts have been devoted to the energy-efficient resource allocation problem in NOMA-enabled systems [9,10,11]. The authors in [9] maximized energy efficiency subject to a minimum required data rate for each user, which leads to a nonconvex fractional programming problem. Meanwhile, a power allocation solution aiming to maximize the energy efficiency under users’ quality of service requirements was investigated [10]. Fang et al. [11] proposed a gradient-based binary search power allocation approach for downlink NOMA systems, but it requires high complexity. NOMA was also applied to future machine-to-machine (M2M) communications in [12], and it was shown that the outage probability of the system can be improved when compared with OMA. Additionally, by jointly studying beamforming, user scheduling, and power allocation, the system performance of millimeter wave (mmWave) networks was studied [13].

On the other hand, CR (one of the promising techniques to improve SE), has been extensively investigated for decades. In it, cognitive users (CUs) can utilize the licensed spectrum bands of the primary users (PUs) as long as the interference caused by the CUs is tolerable [14,15,16]. Goldsmith et al. in [17] proposed three operation models (opportunistic spectrum access, spectrum sharing, and sensing-based enhanced spectrum sharing) to exploit the CR technique in practice. It is conceivable that the combination of CR with NOMA technologies is capable of further boosting the SE in wireless communication systems. Therefore, many studies on the performance of spectrum-sharing CR combined with NOMA have been analyzed [18,19].

Along with the rapid proliferation of wireless communication applications, most battery-limited devices become useless if their battery power is depleted. As one of the remedies, energy harvesting (EH) exploits ambient energy resources to replenish batteries, such as solar energy [20], radio frequency (RF) signals [21], and both non-RF and RF energy harvesting [22], etc. Among various kinds of renewable energy resources, solar power has been considered one of the most effective energy sources for wireless devices. However, solar power density highly depends on the environment conditions, and may vary over time. Thus, it is critical to establish proper approaches to efficiently utilize harvested energy for wireless communication systems.

Many early studies regarding NOMA applications have mainly focused on the downlink scenario. However, there are fewer contributions investigating uplink NOMA, where an evolved NodeB (eNB) has to receive different levels of transmitted power from all user devices using NOMA. Zhang et al. in [23] proposed a novel power control scheme, and the outage probability of the system was derived. Besides, the user-pairing approach was studied in many predefined power allocation schemes in NOMA communication systems [24] in which internet of things (IoT) devices first harvest energy from BS transmissions in the harvesting phase, and they then utilize the harvested energy to perform data transmissions using the NOMA technique during the transmission phase. The pricing and bandwidth allocation problem in terms of energy efficiency in heterogeneous networks was investigated in [25]. In addition, the authors in [20] proposed joint resource allocation and transmission mode selection to maximize the secrecy rate in cognitive radio networks. Nevertheless, most of the existing work on resource allocation assumes that the amount of harvested energy is known, or that traffic loads are predictable, which is hard to obtain in practical wireless networks.

Since the information regarding network dynamics (e.g., harvested energy distribution, primary user’s behavior) is sometimes unavailable in the cognitive radio system, researchers usually formulate optimization problems as the framework of a Markov decision process (MDP) [20,22,26,27]. Reinforcement learning is one of the potential approaches to obtaining the optimal solution for an MDP problem by interacting with the environment without having prior information about the network dynamics or without any supervision [28,29,30]. However, it is a big issue for reinforcement learning to have to deal with large-state-space optimization problems. For this reason, deep reinforcement learning (DRL) is being investigated extensively these days in wireless communication systems where deep neural networks (DNNs) work as function approximators and are utilized to learn the optimal policy [31,32,33]. Meng et al. proposed a deep reinforcement learning method for a joint spectrum sensing and power control problem in a cognitive small cell [31]. In addition, deep Q-learning was studied for a wireless gateway that is able to derive the optimal policy to maximize throughput in cognitive radio networks [32]. Zhang et al. [33]  proposed an asynchronous advantage, deep actor-critic-based scheme to optimize spectrum sharing efficiency and guarantee the QoS requirements of PUs and CUs.

To the best of our knowledge, there has been little research into resource allocation using deep reinforcement learning under a non-RF energy-harvesting scenario in uplink cognitive radio networks. Thus, we propose a deep actor-critic reinforcement learning framework for efficient joint power and bandwidth allocation by adopting hybrid NOMA/OMA in uplink cognitive radio networks (CRNs). In them, solar energy-powered CUs are assigned the proper transmission power and bandwidth to transmit data to a cognitive base station in every time slot in order to maximize the long-term data transmission rate of the system. Specifically, the main contributions of this paper are as follows.

• We study a model of a hybrid NOMA/OMA uplink cognitive radio network adopting energy harvesting at the CUs, where solar energy-powered CUs opportunistically use the licensed channel of the primary network to transmit data to a cognitive base station using NOMA/OMA techniques. Beside that, a user-pairing algorithm is adopted such that we can assign orthogonal frequency bands to each NOMA group after pairing. We take power and bandwidth allocation into account such that the transmission power and bandwidth are optimally utilized by each CU under energy constraints and environmental uncertainty. The system is assumed to work on a time-slotted basis.
• We formulate the problem of long-term data transmission rate maximization as the framework of a Markov decision process (MDP), and we obtain the optimal policy by adopting a deep actor-critic reinforcement learning (DACRL) framework under a trial-and-error learning algorithm. More specifically, we use DNNs to approximate the policy function and the value function for the actor and critic components, respectively. As a result, the cognitive base station can allocate the appropriate transmission power and bandwidth to the CUs by directly interacting with the environment, such that the system reward can be maximized in the long run by using the proposed algorithm.
• Lastly, extensive numerical results are provided to assess the proposed algorithm performance through diverse network parameters. The simulation results of the proposed scheme are shown to be superior to conventional schemes where decisions on transmission power and bandwidth allocation are taken without long-term considerations.

The rest of this paper is structured as follows. The system model is presented in Section 2. We introduce the problem formulation in Section 3, and we describe the deep actor-critic reinforcement learning scheme for resource allocation in Section 4. The simulation results and discussions are in Section 5. Finally, we conclude the paper in Section 6.

2. System Model

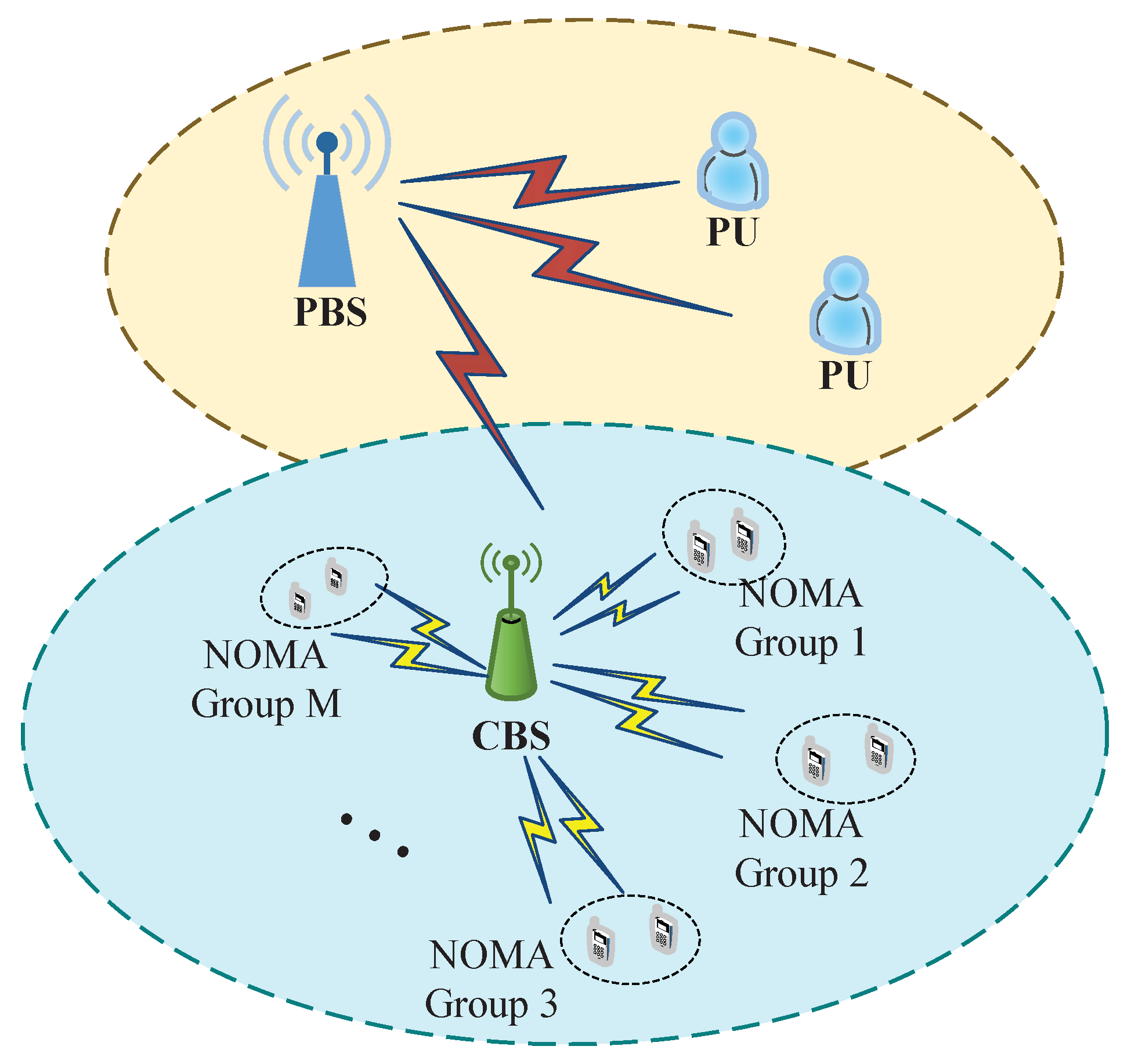
We consider an uplink CRN that consists of a cognitive base station (CBS), a primary base station (PBS), multiple primary users, and $2M$ cognitive users as illustrated in Figure 1. Each CU is outfitted with a single antenna to transmit data to the CBS, and each is equipped with an energy-harvesting component (i.e., solar panels). The PBS and PUs have the license to use the primary channel at will. However, they do not always have data to transmit on the primary channel. Meanwhile, the CBS and the CUs can opportunistically utilize the primary channel by adopting a hybrid NOMA/OMA technique when the channel is sensed as free. To this end, the CBS divides the set of CUs into pairs according to Algorithm 1 where the CU having the highest channel gain will be coupled with the CU having the lowest channel gain, and one of available channels will be assigned to these pairs. More specifically, the CUs are arranged into M NOMA groups, and the primary channel is divided into multiple subchannels to apply hybrid NOMA/OMA for the transmissions between the CUs and the CBS, with $\mathcal{G}=\left\{{\mathrm{G}}_1,{\mathrm{G}}_2,{\mathrm{G}}_3,\dots ,{\mathrm{G}}_{\mathrm{M}}\right\}$ denoting the set of NOMA groups. Additionally, M NOMA groups are assigned to M orthogonal subchannels, $\mathcal{S}\mathcal{C}=\left\{\mathrm{S}{\mathrm{C}}_1,\mathrm{S}{\mathrm{C}}_2,\mathrm{S}{\mathrm{C}}_3,\dots ,\mathrm{S}{\mathrm{C}}_{\mathrm{M}}\right\}$, of the primary channel such that the CUs in each NOMA group can transmit on the same subchannel and will not interfere with the other groups. In this paper, successive interference cancellation (SIC) [34] is applied at the CBS for decoding received signals, which are transmitted from the CUs. Moreover, we assume that the CUs always have data to transmit, and the CBS has complete channel state information (CSI) of all the CUs.

Algorithm 1 User-pairing Algorithm

1: Input: channel gain, number of groups, M, number of CUs, $2M$.   2: Sort the channel gain of all CUs in decending order: $g_1\ge g_2\ge \dots \ge g_{2M}$   3: Define set of channel gains $U=\left\{g_1,g_2,\dots ,g_{2M}\right\}$   4: for$j=1:M$   5:     $G_j=\left\{\varnothing \right\}$   6:     $G_{max}=max\left\{U\right\},G_{min}=min\left\{U\right\}$   7:     $G_j=G_j\cup G_{max}\cup G_{min}$   8:     $U=U\backslash G_{max}\backslash G_{min}$   9: end for    10: Output: Set of CU pairs.

The network system operation is illustrated in Figure 2. In particular, at the beginning of a time slot, with duration ${\tau }_{ss}$, all CUs concurrently perform spectrum sensing and report their local results to the CBS. Based on these sensing results, the CBS first decides the global sensing result as to whether the primary channel is busy or not following the combination rule [35,36], and then allocates power and bandwidth to all CUs for uplink data transmission. As a consequence, according to the allocated power and bandwidth of the NOMA groups, the CUs in each NOMA group can transmit their data to the CBS through the same subchannel without causing interference with other groups within duration ${\tau }_{Tr}=T_{tot}-{\tau }_{ss}$, where $T_{tot}$ is the total time slot duration. Information regarding the remaining energy in all the CUs is updated to the CBS at the end of each time slot. Each data transmission session of the CUs may take place in more than one time slot until all their data have been transmitted successfully.

During data transmission, the received composite signal at the CBS on subchannel $S{C}_m$ is given by

$$\begin{array}{c}\hfill y_m\left(t\right)=\sqrt{P_{{}_{1m}}\left(t\right)}{x}_{1m}\left(t\right)h_{1m}+\sqrt{P_{{}_{2m}}\left(t\right)}{x}_{2m}\left(t\right)h_{2m}+{\mathit{\omega }}_m,\end{array}$$

(1)

where $P_{im}\left(t\right)=e_{im}^{tr}\left(t\right)/{\tau }_{Tr}$ | i ∈ {1,2}, m ∈{1,2,…,M} is the transmission power of CU_i in NOMA group G_m, in which $e_{im}^{tr}$(t) is the transmission energy assigned for CU_im in time slot t; x_im(t) denotes the transmit signal of CU_im in time slot t, (𝔼{|x_im(t)|²} = 1); ω_m is the additive white Gaussian noise (AWGN) at the CBS on subchannel SC_m with zero mean and variance σ²; and h_im is the channel coefficient between CU_im and the CBS. The overall received signal at the CBS in time slot t is given by

$$\begin{array}{c}\hfill y\left(t\right)=\sum _{m=1}^M{y}_m\left(t\right).\end{array}$$

(2)

The received signals at the CBS on different sub-channels are independently retrieved from composite signal $y_m\left(t\right)$ using the SIC technique. In particular, the CU’s signal with the highest channel gain is firstly decoded, and then it will be removed from composite signal at the CBS, in a successive manner. The CU’s signal with the lower channel gain in the sub-channel is treated as noise of the CU with the higher channel gain. We assume perfect SIC implementation at the CBS. The achievable transmission rate for the CUs in NOMA group $G_m$ are

$$\begin{array}{c}\hfill \begin{array}{c}{R}_{1m}\left(t\right)=\frac{{\tau }_{Tr}}{T_{tot}}\times b_m\left(t\right)\times {log}_2\left[1+\frac{P_{1m}\left(t\right)g_{1m}}{P_{2m}\left(t\right)g_{2m}+{\sigma }^2}\right]\hfill \\ R_{2m}\left(t\right)=\frac{{\tau }_{Tr}}{T_{tot}}\times b_m\left(t\right)\times {log}_2\left[1+\frac{P_{2m}\left(t\right)g_{2m}}{{\sigma }^2}\right],\hfill \end{array}\end{array}$$

(3)

where $b_m\left(t\right)$ is the amount of bandwidth allocated to subchannel $S{C}_m$ in time slot t, $g_{im}={\left|h_{im}\right|}^2$ is the channel gain of $C{U}_{im}$ on subchannel m, and $g_{1m}\ge g_{2m}$. Since the channel gain of $C{U}_{1m}$, $g_{1m}$, is higher, $C{U}_{1m}$ has a higher priority for decoding. Consequently, the signal of $C{U}_{1m}$ is decoded first by treating the signal of $C{U}_{2m}$ as interference. Next, user $C{U}_{1m}$ is removed from signal $y_m\left(t\right)$, and the signal of user $C{U}_{2m}$ is decoded as interference-free. The sum achievable transmission rate of NOMA group $G_m$ can be calculated as:

$$\begin{array}{c}\hfill R_m\left(t\right)=R_{1m}\left(t\right)+R_{2m}\left(t\right).\end{array}$$

(4)

The sum achievable transmission rate at the CBS can be given as follows:

$$\begin{array}{c}\hfill R\left(t\right)=\sum _{m=1}^M{R}_m\left(t\right).\end{array}$$

(5)

Energy Arrival and Primary User Models

In this paper, the CUs have a finite capacity battery, $E_{bat}$, which can be constantly recharged by the solar energy harvesters. Therefore, the CUs can perform their other operations and harvest solar energy simultaneously. For many reasons (such as the weather, the season, different times of the day), the harvested energy from solar resources may vary in practice. Herein, we take into account a practical case, where the harvested energy of $C{U}_i$ in NOMA group $G_m$ (denoted as $e_{im}^h$) follows a Poisson distribution with mean value ${\xi }_{avg}$, as studied in [37]. The arrival energy amount that $C{U}_{im}$ can harvest during time slot t can be given as $e_{im}^h\left(t\right)\in \left\{e_1^h,e_2^h,\dots ,e_{\upsilon }^h\right\}$ where $0<e_1^h<e_2^h<\dots <e_{\upsilon }^h<E_{bat}$. The cumulative distribution function can be given as follows:

$$\begin{array}{c}\hfill F\left(e_{im}^h\left(t\right);{\xi }_{avg}\right)=\sum _{k=0}^{e_{im}^h\left(t\right)}{e}^{-{\xi }_{avg}}\frac{{\left({\xi }_{avg}\right)}^k}{k!}.\end{array}$$

(6)

Herein, we use a two-state Markov discrete-time process to model the state of the primary channel, as depicted in Figure 3. We assume that the state of the primary channel does not change during the time slot duration, $T_{tot}$, and the primary channel can switch states between two adjacent time slots. The state transition probabilities between two time slots are denoted as $P_{ij}\left|i,j\in \left\{F,B\right\}\right.$, in which F stands for the free state, and B stands for the $busy$ state. In this paper, we consider cooperative spectrum sensing, in which all CUs collaboratively detect spectrum holes based on an energy detection method, and they send these local sensing results to the CBS. Subsequently, the final decision on the primary users’ activities is attained by combining the local sensing data at the CBS [36]. The performance of the cooperative sensing scheme can be evaluated based on probability of detection $P_d$ and probability of false alarm $P_f$. $P_d$ is denoted as the probability that the PU’s presence is correctly detected (i.e., the primary channel is actually used by the PUs). Meanwhile, $P_f$ is denoted as the probability that the PU’s is detected to be active, but it is actually inactive (i.e., the sensing result of the primary channel is busy, but the primary channel is actually free).

3. Long-Term Transmission Rate Maximization Problem Formulation

In this section, we aim at maximizing the long-term data transmission rate for uplink NOMA/OMA. The $2M$ users in the CRN can be decoupled into pairs according to their channel gain, as described in Algorithm 1. After user pairing, the joint power allocation and bandwidth allocation problem can be formulated as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\mathit{a}}^{*}\left(t\right)=\underset{\mathit{a}\left(t\right)}{argmax}{\displaystyle \sum _{k=t}^{\infty }}{\displaystyle \sum _{m=1}^M}{R}_m\left(k\right)\\ s.t.0\le e_{im}^{tr}\le e_{max}^{tr}\\ {\displaystyle \sum _{m=1}^M}{\mathit{b}}_m\left(t\right)=W\end{array},\end{array}$$

(7)

where $\mathit{a}\left(t\right)=\left\{\mathit{b}\left(t\right),\mathit{\epsilon }\left(t\right)\right\}$ represents the action that the CBS assigns to the CUs in time slot t; $\mathit{b}\left(t\right)$ indicates a vector of the allocated bandwidth portions assigned to the corresponding sub-channel, where $\mathit{b}\left(t\right)=\left\{b_1\left(t\right),b_2\left(t\right),\dots .,b_M\left(t\right)\right\}\left|{\displaystyle \sum _{m=1}^M}{b}_m\left(t\right)=W\right.$ is the assigned bandwidth amount for $m^{th}$ sub-channel; $\mathit{\epsilon }\left(t\right)=\left[\begin{array}{c}{e}_{11}^{tr}\left(t\right),e_{21}^{tr}\left(t\right),,e_{12}^{tr}\left(t\right),e_{22}^{tr}\left(t\right),\dots ,e_{1\mathrm{M}}^{tr}\left(t\right),e_{2\mathrm{M}}^{tr}\left(t\right)\hfill \end{array}\right]$ refers to a transmission energy vector of the CUs, where $e_{im}^{tr}\left(t\right)\in \left\{0,e_1^{tr},e_2^{tr},\dots ,e_{max}^{tr}\right\}$ is the transmission energy value for $C{U}_{im}$, and $e_{max}^{tr}$ represents the upper-bounded value of transmission energy for each CU in time slot t.

4. Deep Reinforcement Learning-Based Resource Allocation Policy

In this section, we first reformulate the joint power and bandwidth allocation problem, which is aimed at maximizing the long-term data transmission rate of the system as the framework of an MDP. Then, we apply a DRL approach to solve the problem, in which the agent (i.e., the CBS) learns to create the optimal resource policy via trial-and-error interactions with the environment. One of the disadvantages of reinforcement learning is that the high computational costs can be imposed due to the long time learning process of a system with high state space and action space. However, the proposed scheme requires less computation overhead by adopting deep neural networks, as compared to other algorithms such as value iteration-based dynamic programming in partially observable Markov decision process (POMDP) framework [20] in which the transition probability of the energy arrival is required for obtaining the solution. Thus, the complex in formulation and computation can be relieved regardless of the dynamic properties of the environment by using the proposed scheme, as compared to POMDP scheme.

Furthermore, the advantage of a deep reinforcement learning scheme as compared with the POMDP scheme is that the unknown harvested energy distribution can be estimated to create the optimal policy by interacting with the environment over the time horizon. In addition, the proposed scheme can work effectively in a large-state-and-space system by adopting deep neural networks. However, other reinforcement learning schemes such as Q-learning  [38], actor-critic learning [39] might not be appropriate to large-state-and-space systems. In the proposed scheme, a deep neural network was trained to obtain the optimal policy where the reward of the system converges to optimal value. Then, the system can choose an optimal action at every state according to that policy learned from the training phase without re-training. Thus, deep actor-critic reinforcement learning can be more applicable to the wireless communication system.

4.1. Markov Decision Process

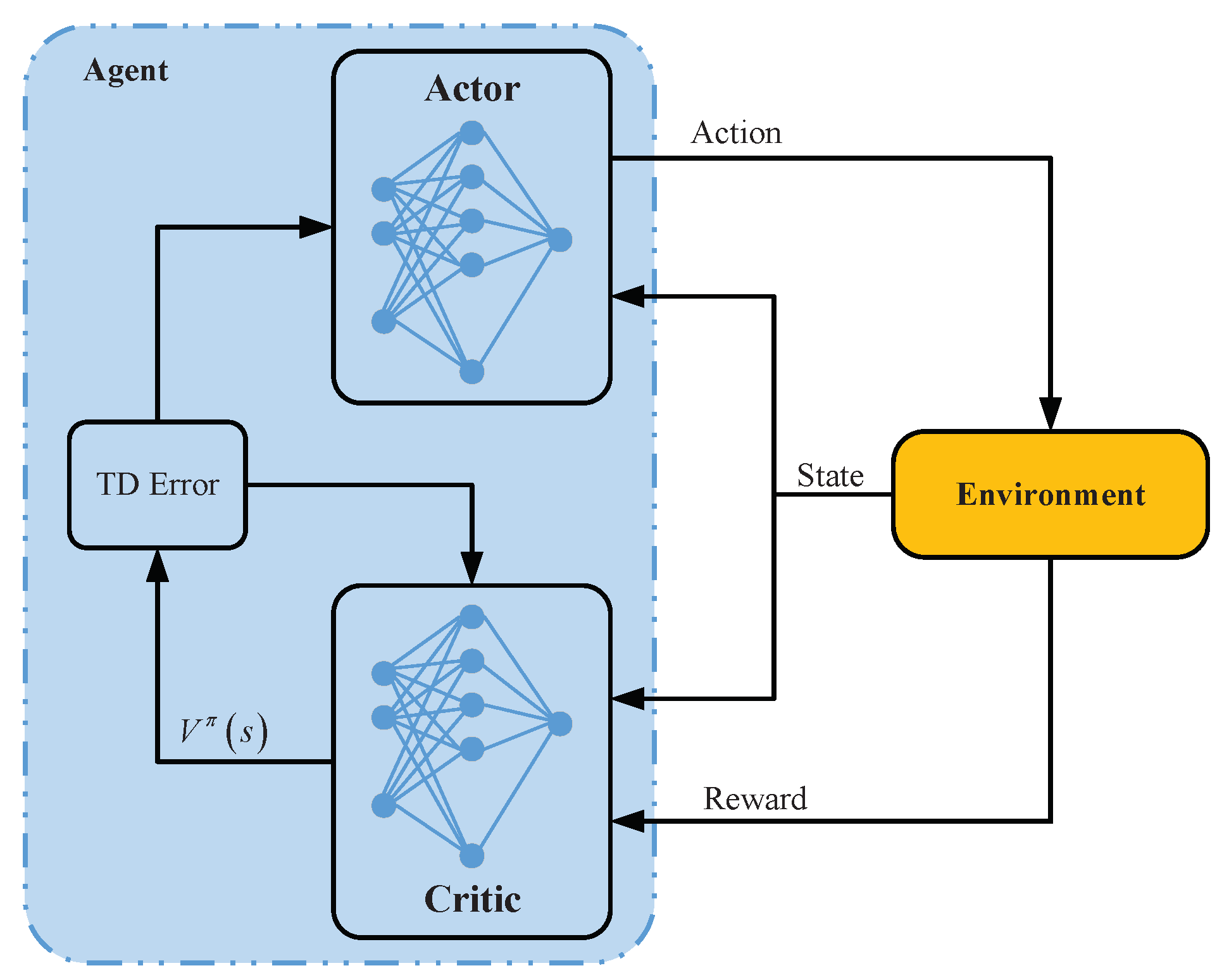
Generally, the purpose of reinforcement learning is for the agent to learn how to map each system state to an optimal action through a trial-and-error learning process. In this way, the accumulated sum of rewards can be maximized after a number of training time slots. Figure 4 illustrates the traditional reinforcement learning via agent–environment interaction. In particular, the agent observers the system state and then chooses an action at the beginning of a time slot. After that, the system receives the corresponding reward at the end of the time slot, and transfers to the next state based on the performed action. The system will be updated and will then go into the next interaction between agent and environment.

We denote the state space and action space of the system in this paper as $\mathbb{S}$ and $\mathbb{A}$, respectively; $s\left(t\right)=\left\{\mu \left(t\right),{\mathit{e}}^{\mathit{re}}\left(t\right)\right\}\in \mathbb{S}$ represents the state of the network in time slot t, where $\mu \left(t\right)$ is the probability ($belief$) that the primary channel is free in that time slot, and ${\mathit{e}}^{\mathit{re}}\left(t\right)=\left[\begin{array}{c}{e}_{11}^{re}\left(t\right),e_{21}^{re}\left(t\right),e_{12}^{re}\left(t\right),e_{22}^{re}\left(t\right),e_{1\mathrm{M}}^{re}\left(t\right),e_{2\mathrm{M}}^{re}\left(t\right)\hfill \end{array}\right]$ denotes a vector of remaining energy of CUs, where $0\le e_{im}^{re}\le E_{bat}$ represents the remaining energy value of $C{U}_{im}$. The action at the CBS is denoted as $\mathit{a}\left(t\right)=\left\{\mathit{b}\left(t\right),\mathit{\epsilon }\left(t\right)\right\}\in \mathbb{A}$. In this paper, we define the reward as the sum data rate of the system, as presented in Equation (5).

The decision-making process can be expressed as follows. At the beginning of time slot t, the agent observes the state, $s\left(t\right)\in \mathbb{S}$, from information about the environment, and then chooses action $\mathit{a}\left(t\right)\in \mathbb{A}$ following a stochastic policy, $\pi \left(a\left|s\right.\right)=Pr\left(a\left(t\right)=a\left|s\left(t\right)=s\right.\right)$, which is mapped from the environment state to the probability of taking an action. In this work, the network agent (i.e, the CBS) determines the transmission power for each CU and decides whether to allocate the bandwidth portion to the NOMA groups in each time slot. Then, the CUs perform their operations (transmit data or stay silent) according to the assigned action from the CBS. Afterward, the instant reward, $R\left(t\right)$, which is defined in Equation (5), is fed back to the agent, and the environment transforms to the next state, $s\left(t+1\right)$. At the end of the time slot, the CUs report information about the current remaining energy level in each CU to the CBS for network management. In the following, we describe the way to update information about the belief and the remaining energy based on the assigned actions at the CBS.

4.1.1. Silent Mode

The global sensing decision shows that the primary channel is busy in the current time slot, and thus, the CBS trusts this result and has all CUs stay silent. As a consequence, there is no reward in this time slot, i.e., $R\left(t\right)=0$. The belief in current time slot t can be calculated according to Bayes’ rule [40], as follows:

$$\begin{array}{c}\hfill \mu \left(t\right)=\frac{\mu \left(t\right)P_f}{\mu \left(t\right)P_f+\left(1-\mu \left(t\right)\right)P_d}.\end{array}$$

(8)

Belief $\mu \left(t+1\right)$ for the next time slot is updated as follows:

$$\begin{array}{c}\hfill \mu \left(t+1\right)=\mu \left(t\right)P_{FF}+\left(1-\mu \left(t\right)\right)P_{BF}.\end{array}$$

(9)

The remaining energy of $C{U}_{im}$ for the next time slot is updated as

$$\begin{array}{c}\hfill e_{im}^{re}\left(t+1\right)=min\left(e_{im}^{re}\left(t\right)+e_{im}^h\left(t\right)-e_{ss},E_{bat}\right),\end{array}$$

(10)

where $e_{ss}$ is the consumed energy from the spectrum sensing process.

4.1.2. Transmission Mode

The global sensing decision indicates that the primary channel is free in the current time slot, and then, the CBS assigns transmission power levels to the CUs for transmitting their data to the CBS. We assume that the data of the CUs will be successfully decoded if the primary channel is actually free; otherwise, no data can be retrieved due to collisions between the signals of the PUs and CUs. In this case, there are two possible observations, as follows.

Observation 1 $\left({\Phi }_1\right)$: All data are successfully received and decoded at the CBS at the end of the time slot. This result means the primary channel was actually free during this time slot, and the global sensing result was correct. The total reward for the network is calculated as

$$\begin{array}{c}\hfill R\left(s\left(t\right)\left|{\Phi }_1\right.\right)={\displaystyle \sum _{m=1}^M}{R}_m\left(t\right),\end{array}$$

(11)

where the immediate data transmission rate of NOMA group $G_m$, $R_m\left(t\right)$, can be computed with Equation (4). Belief $\mu \left(t+1\right)$ for the next time slot is updated as

$$\begin{array}{c}\hfill \mu \left(t+1\right)=P_{FF}.\end{array}$$

(12)

The remaining energy in $C{U}_{im}$ for the next time slot will be

$$\begin{array}{c}\hfill e_{im}^{re}\left(t+1\right)=min\left(e_{im}^{re}\left(t\right)+e_{im}^h\left(t\right)-e_{ss}-e_{im}^{tr}\left(t\right),E_{bat}\right),\end{array}$$

(13)

where $e_{im}^{tr}\left(t\right)$ denotes the transmission energy assigned to $C{U}_{im}$ in time slot t.

Observation 2 $\left({\Phi }_2\right)$: The CBS can not successfully decode the data from the CUs at the end of time slot t due to collisions between the signals of the CUs and the PUs. It implies that the primary channel was occupied, and misdetection happened. In this case, no reward is achieved, i.e., $R\left(s\left(t\right)\left|{\Phi }_2\right.\right)=0$. Belief $\mu \left(t+1\right)$ for the next time slot can be updated as

$$\begin{array}{c}\hfill \mu \left(t+1\right)=P_{BF}.\end{array}$$

(14)

The remaining energy in $C{U}_{im}$ for the next time slot is updated by

$$\begin{array}{c}\hfill e_{im}^{re}\left(t+1\right)=min\left(e_{im}^{re}\left(t\right)+e_{im}^h\left(t\right)-e_{ss}-e_{im}^{tr}\left(t\right),E_{bat}\right).\end{array}$$

(15)

In reinforcement learning, the agent is capable of improving the policy based on the recursive lookup table of state-value functions. The state-value function, $V^{\pi }\left(s\right)$, is defined as the maximum expected value of the accumulated reward starting from current state s with the given policy, which is written as [28]:

$$\begin{array}{c}\hfill V^{\pi }\left(s\right)=E\left\{{\displaystyle \sum _{t=1}^{\infty }}{\gamma }^{t}R\left(t\right)\left|s\right.\left(t\right)=s,\pi \right\},\end{array}$$

(16)

where $E\left\{.\right\}$ denotes the expectation, in which $\gamma \in \left(0,1\right)$ is the discount factor, which can affect the agent’s decisions on myopic or foresighted operations; $\pi$ is the stochastic policy, which maps environment state space $\mathbb{S}$ to action space $\mathbb{A}$, $\pi \left(a\left|s\right.\right)=Pr\left(\mathit{a}\left(t\right)=a\left|s\left(t\right)=s\right.\right)$. The objective of the resource allocation problem is to find optimal policy ${\pi }^{*}$ that provides the maximum discounted value function in the long run, which can satisfy the Bellman equation as follows [41]:

$$\begin{array}{c}\hfill {\pi }^{*}\left(a\left|s\right.\right)=\underset{\pi }{argmax}{V}^{\pi }\left(s\right).\end{array}$$

(17)

The policy can be explored by using an $ϵ-greedy$ policy in which a random action is chosen with probability $ϵ$, or an action can be selected based on the current policy with probability $(1-ϵ)$ during the training process [42]. As a result, the problem of joint power and bandwidth allocation in Equation (7) can be rewritten as Equation (17), and the solution to deep actor-critic reinforcement learning will be presented in the following section.

4.2. Deep Actor-Critic Reinforcement Learning Algorithm

The maximization problem in Equation (17) can be solved by using the actor-critic method, which is derived by combining the value-based method [43] and the policy-based method [44]. The actor-critic structure involves two neural networks (actor and critic) and an environment, as shown in Figure 5. The actor can determine the action according to the policy, and the critic evaluates the selected actions based on value functions and instant rewards that are fed back from the environment. The input of the actor is the state of the network, and the output is the policy, which directly affect how the agent chooses the optimal action. The output of the critic is a state-value function $V^{\pi }\left(s\right)$, which is used to calculate the temporal difference (TD) error. Thereafter, the TD error is used to update the actor and the critic.

Herein, both the policy function in the actor and the value function in the critic are approximated with parameter vectors $\mathit{\theta }$ and $\mathit{\omega }$, respectively, by two sequential models of a deep neural network. Both value function parameter $\mathit{\omega }$ and policy parameter $\mathit{\theta }$ are stochastically initialized and updated constantly by the critic and the actor, respectively, during the training process.

4.2.1. The Critic with a DNN

Figure 6 depicts the DNN at the critic, which is composed of an input layer, two hidden layers, and an output layer. The critic network is a feed-forward neural network that evaluates the action taken by the actor. Then, the evaluation of the critic is used by the actor to update its control policy. The input layer of the critic is an environment state, which contains $\left(2M+1\right)$ elements. Each hidden layer is a fully connected layer, which involves $H_C$ neurons and uses a rectified linear unit (ReLU) activation function [45,46] as follows:

$$\begin{array}{c}\hfill f_{ReLU}\left(z\right)=max\left(0,z\right),\end{array}$$

(18)

where $z={\displaystyle \sum _{i=1}^{2M+1}}{\mathit{\omega }}_i{s}_i\left(t\right)$ is the estimated output of the layer before applying the activation function, in which $s_i\left(t\right)$ indicates the ith element of the input state, $s\left(t\right)$, and ${\mathit{\omega }}_i$ is the weight for the ith input. The output layer of the DNN at the critic contains one neuron and uses the linear activation function to estimate the state-value function, $V^{\pi }\left(s\right)$. In this paper, the value function parameter is optimized by adopting stochastic gradient descent with a back-propagation algorithm to minimize the loss function, defined as the mean squared error, which is computed by

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathit{\omega }}={\delta }^2\left(t\right),\end{array}$$

(19)

where $\delta \left(t\right)$ is the TD error between the target value and the estimated value, which is given by

$$\begin{array}{c}\hfill \delta \left(t\right)=E\left[R\left(t\right)+\gamma V_{\mathit{\omega }}\left(s\left(t+1\right)\right)-V_{\mathit{\omega }}\left(s\left(t\right)\right)\right],\end{array}$$

(20)

and it is utilized to evaluate selected action $\mathit{a}\left(t\right)$ of the actor. If the value of $\delta \left(t\right)$ is positive, the tendency to choose action $\mathit{a}\left(t\right)$ in the future, when the system is in the same state, will be strengthened; otherwise, it will be weakened. The critic parameter can be updated in the direction of the gradient, as follows:

$$\begin{array}{c}\hfill \Delta \mathit{\omega }={\alpha }_c\delta \left(t\right){\nabla }_{\mathit{\omega }}{V}_{\mathit{\omega }}^{\pi }\left(s\left(t\right)\right),\end{array}$$

(21)

where ${\alpha }_c$ is the learning rate of the critic.

4.2.2. The Actor with a DNN

The DNN in the actor is shown in Figure 7, which includes an input layer, two hidden layers, and an output layer. The input layer of the actor is the current state of the environment. There are two hidden layers in the actor, where each hidden layer is comprised of $H_A$ neurons. The output layer of the actor provides the probabilities of selecting actions in a given state. Furthermore, the output layer utilizes the soft-max activation function [28] to compute the policy of each action in the action space, which is given as:

$$\begin{array}{c}\hfill {\pi }_{\mathit{\theta }}\left(a\left|s\right.\right)=\frac{e^{z_{\mathit{a}}}}{{\displaystyle \sum _{{\mathit{a}}^{{}^{\prime }}\in \mathbb{A}}}{e}^{z_{{\mathit{a}}^{{}^{\prime }}}}},\end{array}$$

(22)

where $z_a$ is the estimated value for the preference of choosing action $\mathit{a}$. In the actor, the policy can be enhanced by optimizing the state-value function as follows:

$$\begin{array}{c}\hfill \begin{array}{c}J\left({\pi }_{\mathit{\theta }}\right)=E\left[V^{\pi }\left(s\right)\right]\hfill \\ ={\displaystyle \sum _{s\in \mathbb{S}}}{d}^{\pi }\left(s\right)V^{\pi }\left(s\right),\hfill \end{array}\end{array}$$

(23)

where $d^{\pi }\left(s\right)$ is the state distribution. Policy parameter $\mathit{\theta }$ can be updated toward the gradient ascending to maximize the objective function [39], as follows:

$$\begin{array}{c}\hfill \Delta \mathit{\theta }={\alpha }_a{\nabla }_{\mathit{\theta }}J\left({\pi }_{\mathit{\theta }}\right),\end{array}$$

(24)

where ${\alpha }_a$ denotes the learning rate of actor network, and policy gradient ${\nabla }_{\mathit{\theta }}J\left({\pi }_{\mathit{\theta }}\right)$ can be computed by using the TD error [47]:

$$\begin{array}{c}\hfill {\nabla }_{\mathit{\theta }}J\left({\pi }_{\mathit{\theta }}\right)=E\left[{\nabla }_{\mathit{\theta }}log{\pi }_{\mathit{\theta }}\left(s,\mathit{a}\right)\delta \left(t\right)\right].\end{array}$$

(25)

It is worth noting that TD error $\delta \left(t\right)$ is supplied by the critic. The training procedure of the proposed DACRL approach is summarized in Algorithm 2. In the algorithm, the agent interacts with the environment and learns to select optimal action in each state. The convergence of the proposed algorithm depends on number of steps per episode, the number of training episodes and the learning rate, which is discussed in the following section.

Algorithm 2 The training procedure of the deep actor-critic reinforcement learning algorithm

1: Input:$\mathbb{S}$, $\mathbb{A}$, $\gamma$, ${\alpha }_a$, ${\alpha }_c$, ${\mathit{e}}^{\mathit{re}}\left(t\right)$, $\mu \left(t\right)$, $E_{ca}$, ${\xi }_{avg}$, T, W, ${ϵ}_{min}$, ${ϵ}_{max}$, ${ϵ}_d$.   2: Initialize network parameters of the actor and the critic: $\mathit{\theta },\mathit{\omega }$.   3: Initialize $ϵ={ϵ}_{max}$.   4: for each episode $e=1,2,3,\dots ,L:$   5:     Sample an initial state $s\in \mathbb{S}$.   6:     for each time step $t=0,1,2,3\dots ,T-1$:   7:         Observe current state $s\left(t\right)$, and estimate state value $V_{\mathit{\omega }}^{\pi }\left(s\left(t\right)\right)$.   8:         Choose an action:   9:      10:         $\mathit{a}\left(t\right)=\left\{\begin{array}{cc}argmax{\pi }_{\mathit{\theta }}\left(a\left(t\right)\left|s\left(t\right)\right.\right)\hfill & \mathrm{w}.\mathrm{p}1-\mathrm{ffl}\hfill \\ \mathrm{random}\mathrm{action}a\left(t\right)\in \mathbb{A}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$    11:         Execute action $\mathit{a}\left(t\right)$, observe current reward $R\left(t\right)$.    12:         Update epsilon rate $ϵ=max\left(ϵ.{ϵ}_d,{ϵ}_{min}\right)$    13:         Update next state $s\left(t+1\right)$    14:         Critic Process:    15:         Estimate next state value $V_{\mathit{\omega }}^{\pi }\left(s\left(t+1\right)\right)$.    16:         Critic calculates TD error $\delta \left(t\right)$    17:         if episode is end at time slot t:    18:            $\delta \left(t\right)=R\left(t\right)-V_{\mathit{\omega }}\left(s\left(t\right)\right).$    19:         else    20:            $\begin{array}{c}\delta \left(t\right)=R\left(t\right)+\gamma V_{\mathit{\omega }}\left(s\left(t+1\right)\right)-V_{\mathit{\omega }}\left(s\left(t\right)\right).\hfill \end{array}$    21:         end if    22:         Update parameter of critic network $\mathit{\omega }\leftarrow \mathit{\omega }+\Delta \mathit{\omega }$    23:         Actor Process:    24:         Update parameter of actor network $\mathit{\theta }\leftarrow \mathit{\theta }+\Delta \mathit{\theta }$    25:     end for    26: end for    27: Output: Final policy ${\pi }_t^{*}\left(\mathit{a}\left(t\right)\left|s\left(t\right)\right.\right)$.

5. Simulation Results

In this section, we investigate the performance of uplink NOMA systems using our proposed scheme. The simulation results are compared with other myopic schemes [48] (Myopic-UP, Myopic-Random, and Myopic-OMA) in terms of average data transmission rate and energy efficiency. In the myopic schemes, the system only maximizes the reward in the current time slot, and the system bandwidth is allocated to the group only if it has at least one active CU in the current time slot. In particular, with the Myopic-UP scheme, the CBS arranges the CUs into different pairs based on Algorthim 1. In the Myopic-Random scheme, the CBS randomly decouples the CUs into pairs. In the Myopic-OMA scheme, the total system bandwidth is divided equally into sub-channels in order to assign them to each active CU without applying user pairing. In the following, we analyze the influence of the network parameters on the schemes through the numerical results.

In this paper, we used Python 3.7 with the TensorFlow deep learning library to implement the DACRL algorithm. Herein, we consider a network based on different channel gain values between the CUs and the CBS, such as $h_1=-20$ dB, $h_2=-25$ dB, $h_3=-30$ dB, $h_4=-35$ dB, $h_5=-40$ dB, $h_6=-45$ dB, where $h_1,h_2,h_3,h_4,h_5,h_6$ are the channel gains between $C{U}_1,C{U}_2,C{U}_3,C{U}_4,C{U}_5,C{U}_6$ and the CBS, respectively. Two sequential DNNs are utilized to model the value function and the policy function in the proposed algorithm. Each DNN is designed with an input layer, two hidden layers and an output layer as described in Section 4. The number of neurons in each hidden layer of the value function DNN in the critic, and the policy function in the actor, are set at $H_C=24$ and $H_A=24$, respectively. For the training process, value function parameter $\mathit{\omega }$ and the policy parameter $\mathit{\theta }$ are stochastically initialized by using uniform Xavier initialization [49]. The other simulation parameters for the system are shown in

Table 1. Simulation Parameters.

Parameter	Description	Value
M	Number of groups	3
$T_{tot}$	Time slot duration	200 ms
${\tau }_{ss}$	Sensing duration	2 ms
W	Total system bandwidth	1 Hz
$E_{bat}$	Battery capacity	30 $\mathsf{\mu }$J
$e_{ss}$	Sensing cost	1 $\mathsf{\mu }$J
$e^{tr}$	Transmission energy	$0,10,20$$\mathsf{\mu }$J
${\xi }_{avg}$	Mean value of harvested energy	5 $\mathsf{\mu }$J
$\mu$	Initial belief that the primary channel is free	0.5
$P_{FF}$	Transition probability of the primary channel from state F to itself	0.8
$P_{BF}$	Transition probability of the primary channel from state B to state F	0.2
$P_d$	Probability of detection	0.9
$P_f$	Probability of false alarm	0.1
${\sigma }^2$	Noise variance	−80 dB
$\gamma$	Discount factor	0.9
${\alpha }_a$	Learning rate of the actor	$0.001$
${\alpha }_c$	Learning rate of the critic	$0.005$
$ϵ$	Epsilon rate	$1\to 0.01$
${ϵ}_d$	Epsilon decay	$0.9999$
L	Number of episodes	300
T	Number of iterations per episode	2000

.

We first examine the average transmission rates of the the DACRL scheme under different training iterations, T, while the number of episodes, L, increases from 1 to 400. We achieved the results by calculating the average transmission rate after separately running the simulation 20 times, as shown in Figure 8. The curves sharply increase in the first 50 training episodes, and then gradually converge to the optimal value. We can see that the agent needs more than 350 episodes to learn the optimal policy at $T=1000$ iterations per episode. However, with the increment in T, the algorithm begins to converge faster. For instance, the proposed scheme learns the optimal policy in less than 300 episodes when $T=2000$. Nevertheless, it might take a very long time for the training process if each episode uses too many iterations, and the algorithm evenly converges to a locally optimal policy. As a result, the number of training iterations per episode and the number of training episodes should not be too large or too small. In the rest of the simulations, we set training episodes at 300 and training iterations at 2000.

Figure 9 shows the convergence rate of the proposed scheme according to various values of actor learning rate ${\alpha }_a$ and critic learning rate ${\alpha }_c$. The figure shows that the reward converges faster with increments in the learning rates. In addition, we can observe that the proposed scheme with actor learning rate ${\alpha }_a=0.001$ and critic learning rate ${\alpha }_c=0.005$ provides the best performance after 300 episodes. When the learning rates of the actor and the critic increase to ${\alpha }_a=0.01$ and ${\alpha }_c=0.005$, respectively, the algorithm converges very fast, but does not bring a good reward due to underfitting. Therefore, we set the actor and critic learning rates at ${\alpha }_a=0.001$ and ${\alpha }_c=0.005$, respectively, for the rest of the simulations.

Figure 10 illustrates the average transmission rates under the influence of mean harvested energy. We can see that the average transmission rate of the system increases when the mean value of harvested energy grows. The reason is that with an increase in ${\xi }_{avg}$, the CUs can harvest more solar energy, and thus, the CUs have a greater chance to transmit data to the CBS. In addition, the average transmission rate of the proposed scheme dominates the conventional schemes because the conventional schemes focus on maximizing the current reward, and they ignore the impact of the current decision on the future reward. Thus, whenever the primary channel is free, these conventional schemes allow all CUs to transmit their data by consuming most of the energy in the battery in order to maximize the instant reward. This makes the CUs stay silent in the future due to energy shortages. Although the Myopic-Random scheme had lower performance than the Myopic-UP scheme, it still had greater rewards than Myopic-OMA. This outcome demonstrates the efficiency of the hybrid NOMA/OMA approach, compared with the OMA approach, in terms of average transmission rate.

In Figure 11, the energy efficiency of the schemes was compared with respect to the mean value of the harvested energy. In this paper, we define energy efficiency as the transmission data rate obtained at the CBS over the total energy consumption of the CUs during the operations. We can see that the energy efficiency declines as ${\xi }_{avg}$ rises. The reason is that when the harvested energy goes up, the CUs can gather more energy for their operations; however, the amount of energy overflowing the CUs’ batteries also increases. The curves show that the performance of the proposed scheme outperforms the other conventional schemes because the DACRL agent can learn about the dynamic arrival of harvested energy from the environment. Thus, the proposed scheme can make proper decision in each time slot.

In Figure 12 and Figure 13, we plot the average transmission rate and the energy efficiency, respectively, based on differing noise variance at the CBS. The curves show that system performance notably degrades when noise variance increases. To explain this, noise variance will degrade the data transmission rate, as shown in Equation (3). As a consequence, energy efficiency also decreases with an increment in noise variance. Based on noise variance at the CBS, the figures verify that the proposed scheme dominates the myopic schemes.

6. Conclusions

In this paper, we investigated a deep reinforcement learning framework for joint power and bandwidth allocation by adopting both hybrid NOMA/OMA and user pairing in uplink CRNs. The DACRL algorithm was employed to maximize the long-term transmission rate under the energy constraint in the CUs. A DNN was applied to approximate the policy function and the value function such that the algorithm can work in the system with large state and action spaces. The agent of the DACRL can explore the optimal policy by interacting with the environment. As a consequence, the CBS can effectively allocate bandwidth and power to the CUs based on the current network state in each timeslot. The simulation results verified the advantages of the proposed scheme in improving network performance under various network conditions in the long run, compared to the conventional schemes.