Structural Damage Features Extracted by Convolutional Neural Networks from Mode Shapes
Abstract
1. Introduction
2. Method
2.1. Finite Element Simulations
2.2. Training Samples
2.3. Structural Damage Detection
2.4. CNN Architecture
3. Results
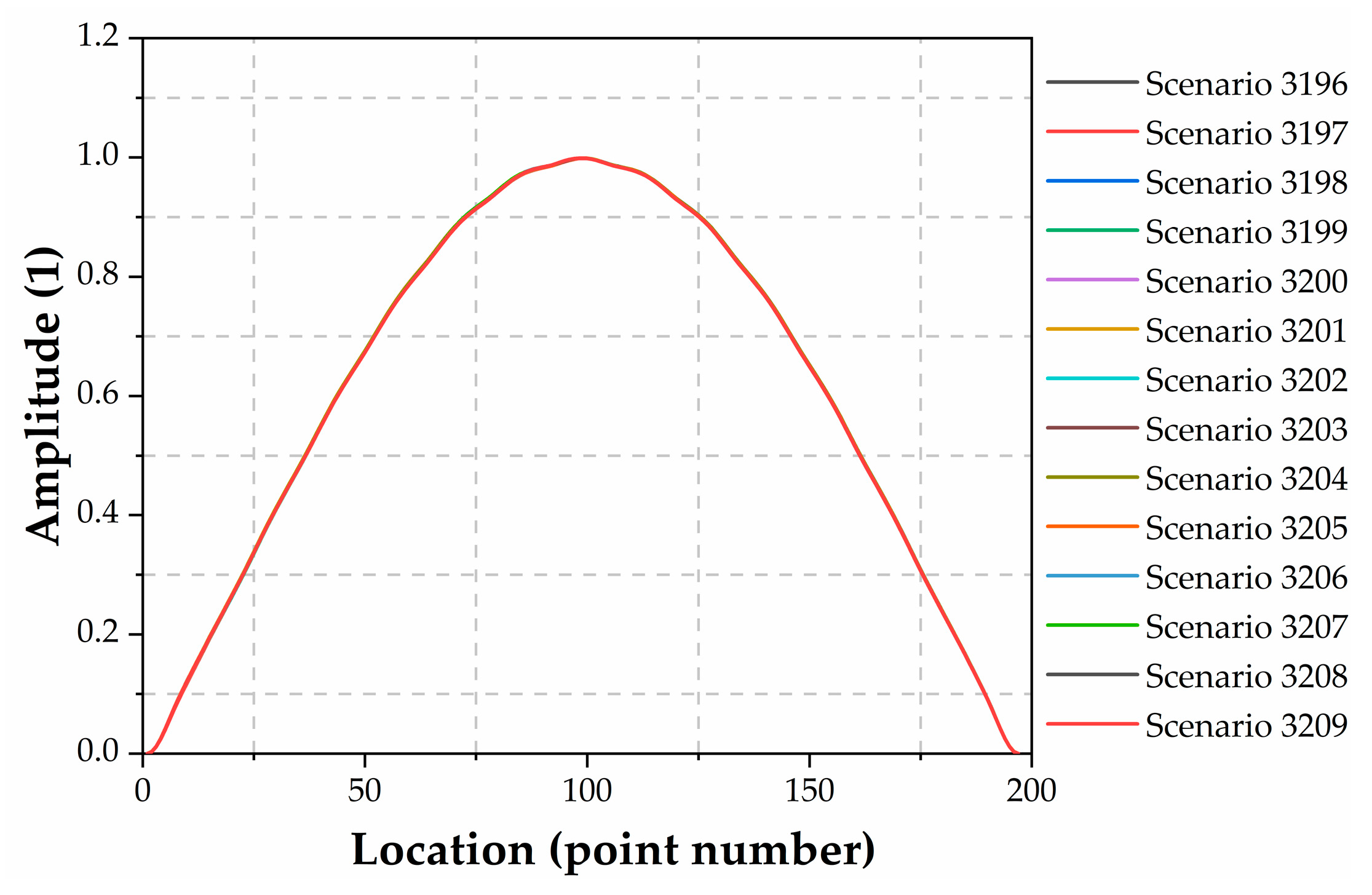
3.1. First Order Mode Shape as CNN Input
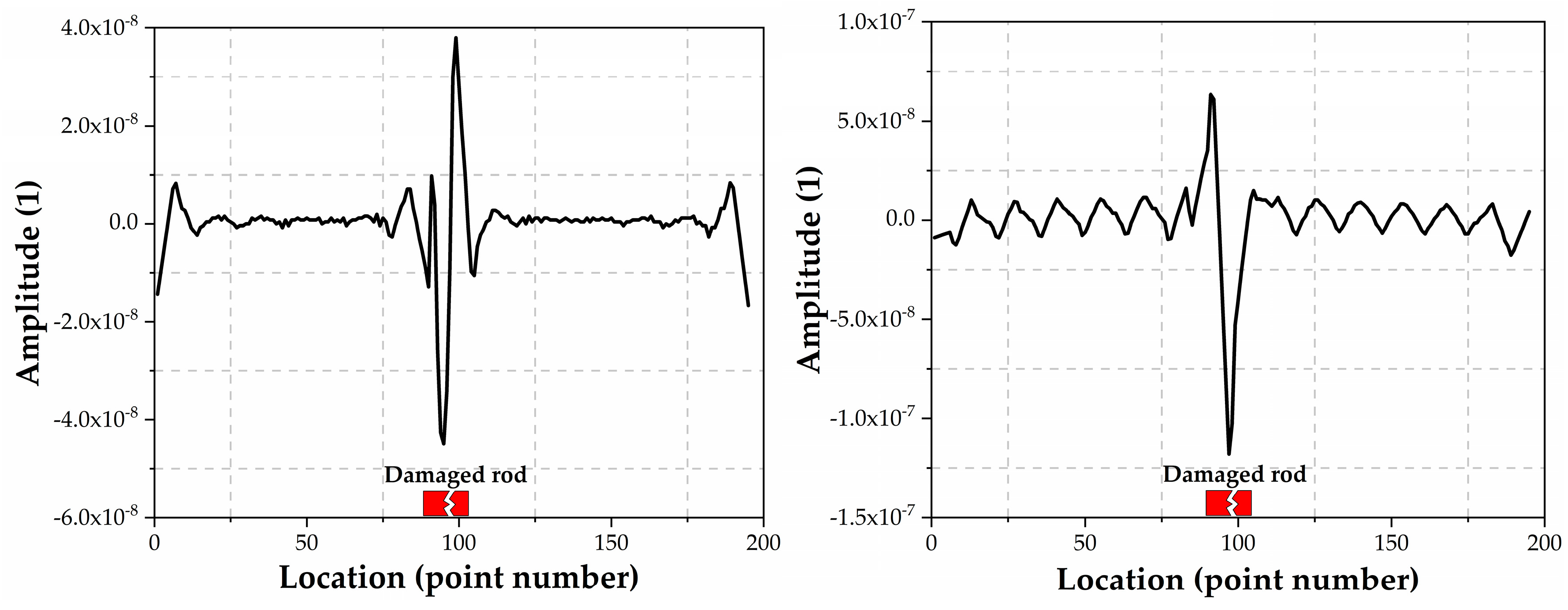
3.2. Mode Curvature Difference as CNN Input
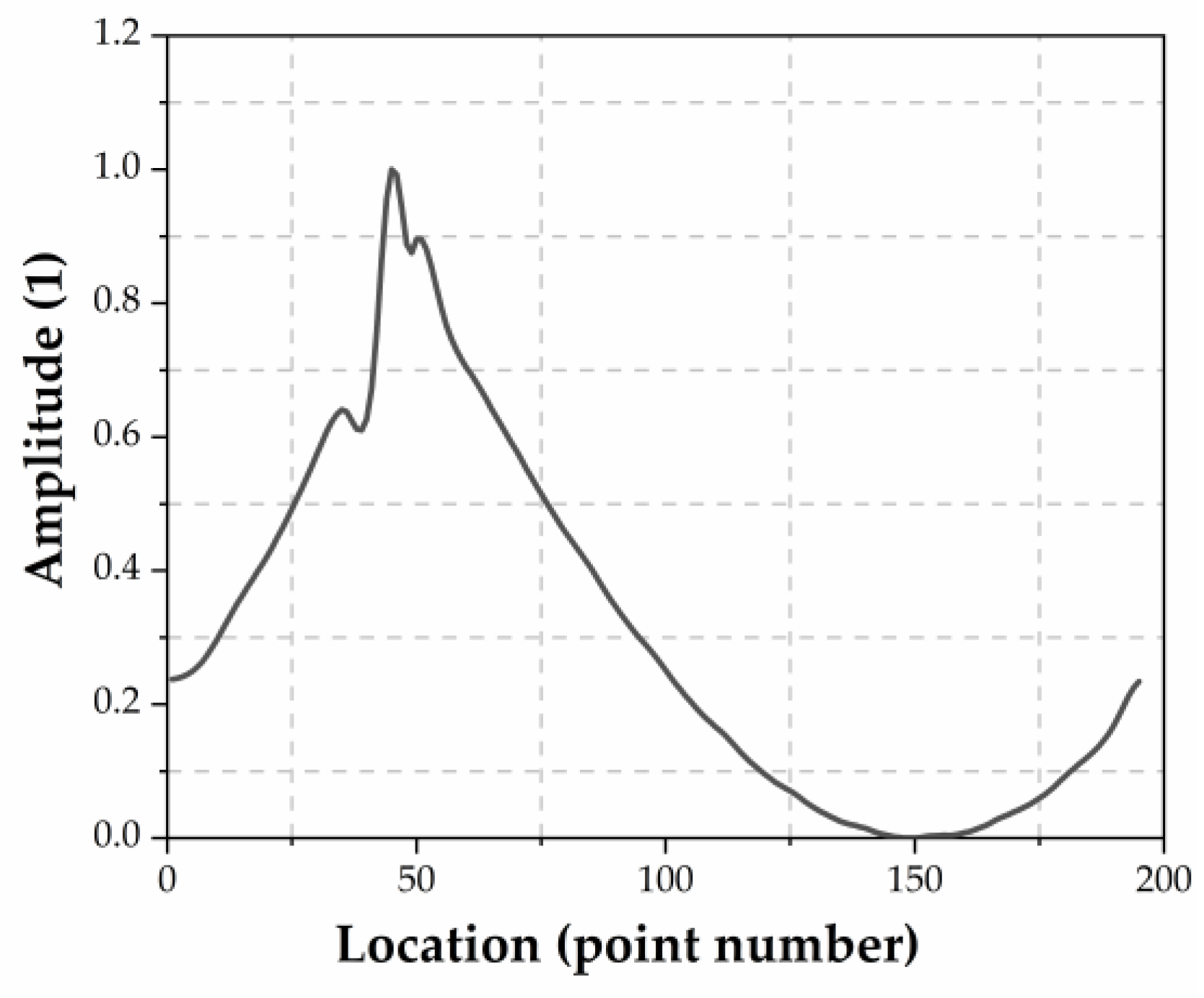
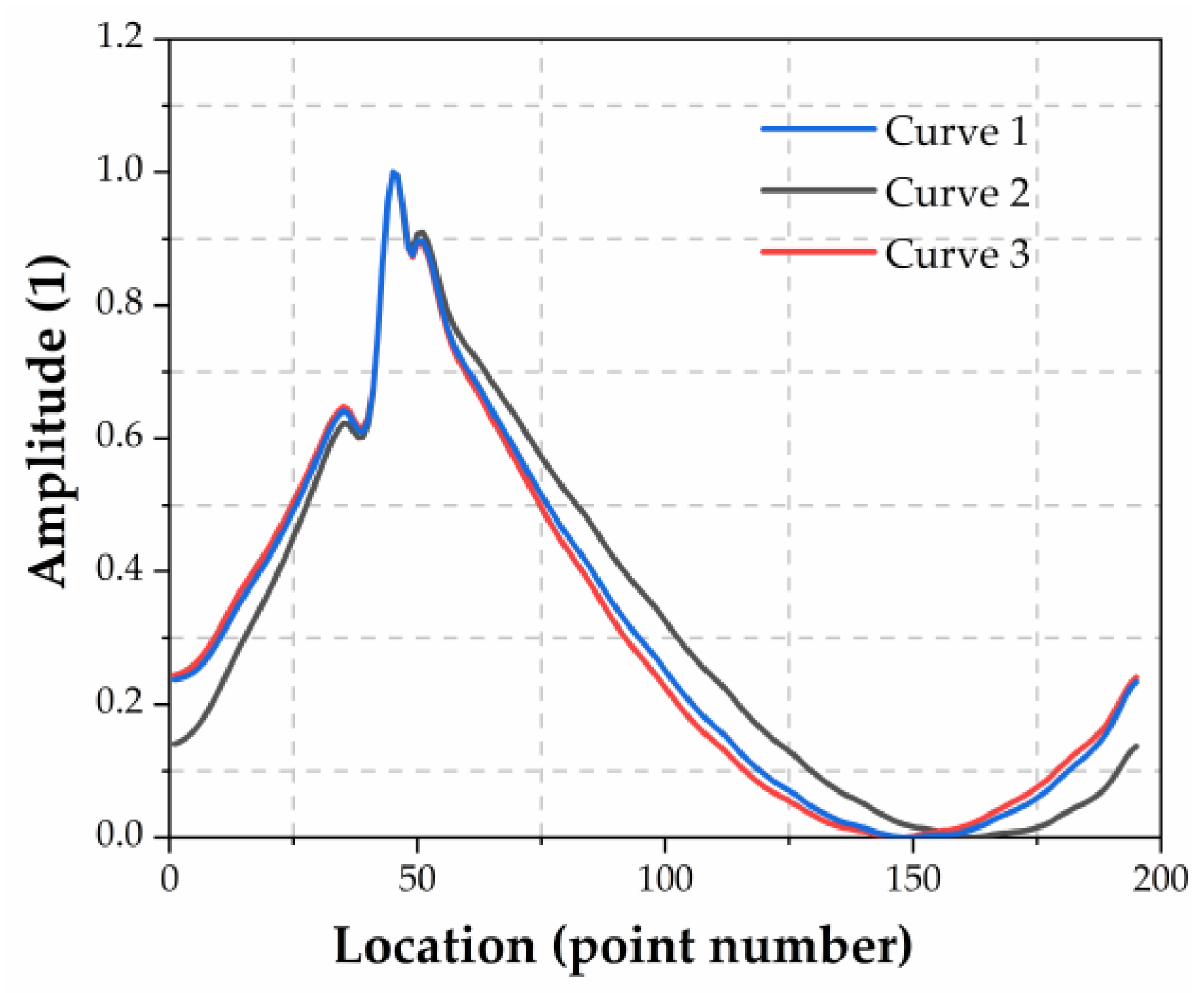
3.3. Data Feature Visualization
3.3.1. Sample Features
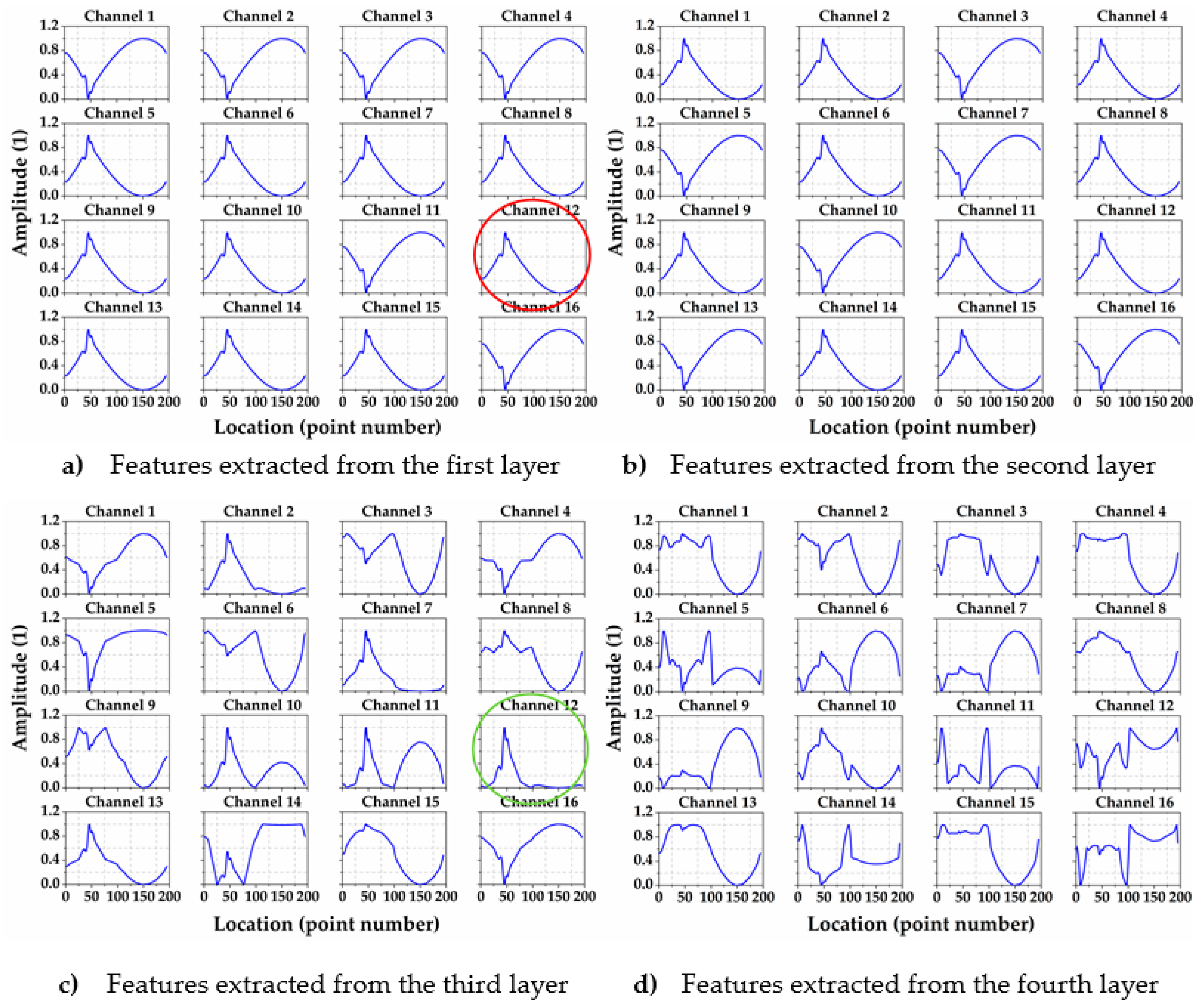
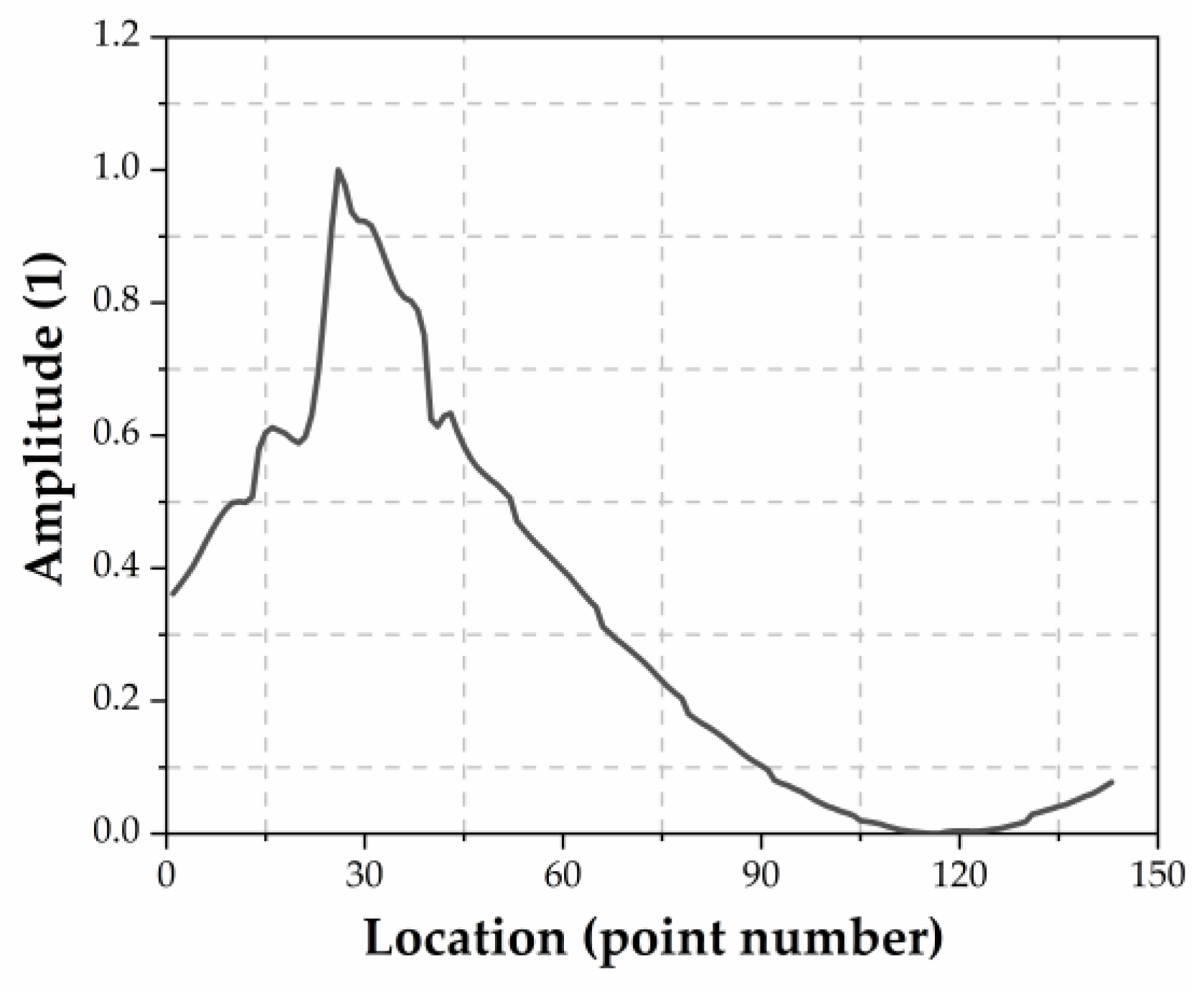
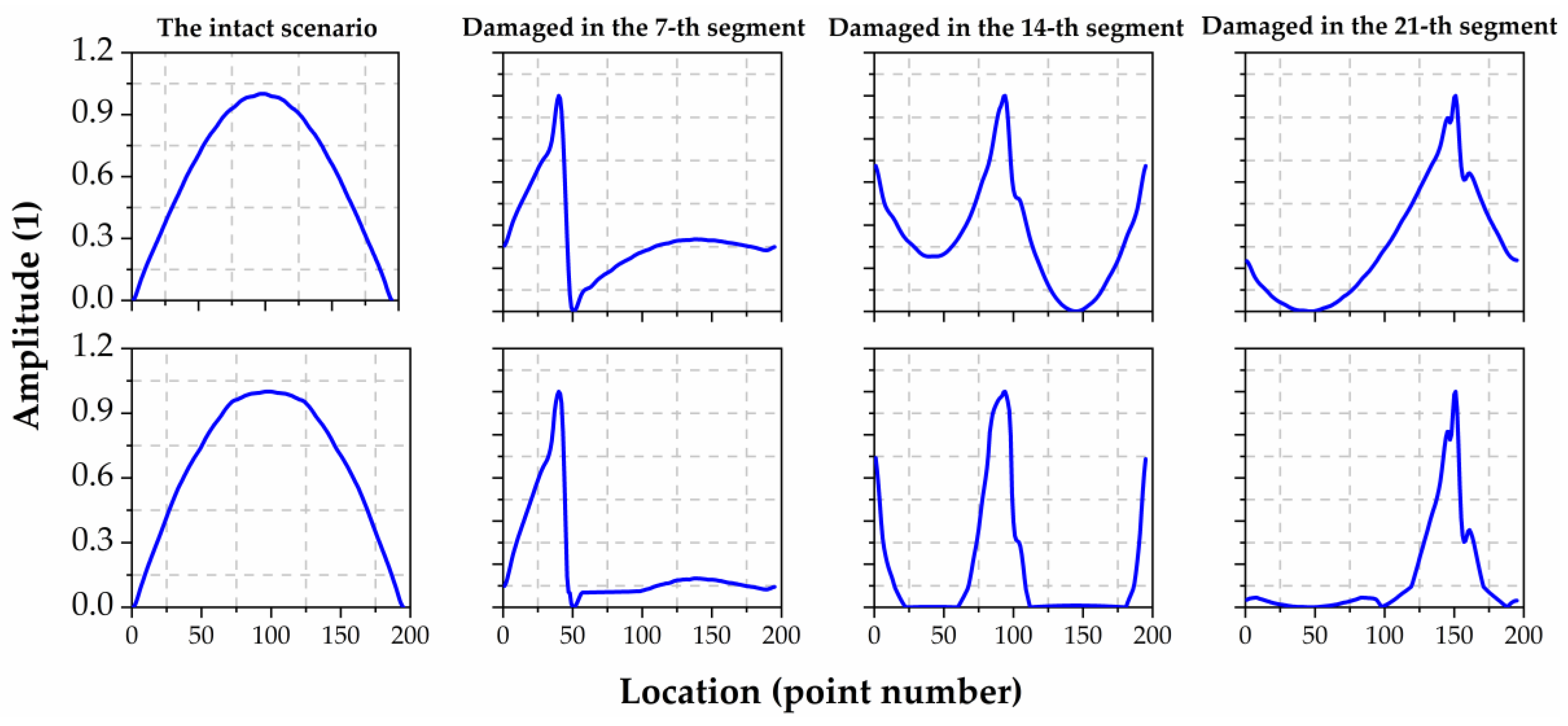
3.3.2. Features Extracted by the CNN
4. Discussions and Conclusions
- the CNN method based on the mode shape has a good prediction accuracy of damaged rods, but there are always some rods with low prediction accuracy. Due to the different sensitivity of modal data to the damage of different types of rods, their prediction accuracies are also different;
- the CNN method based on the mode curvature difference has similar good prediction accuracy to the mode shape when locating the rod with high damage degree. However, the prediction accuracy is low when locating the rods with small damage degree. Like the mode shape, there are always some rods with low prediction accuracy due to the different sensitivity of modal data to the damage of different rods;
- the origin data has more damage information for the CNN. Though the first order mode shapes look indistinguishable, the multi-layer CNN can extract the damage information from the data, which are indistinguishable for naked eyes;
- using the first order mode shape as the input of the CNN to locate the damaged rod, the partial work of the CNN is to update its internal weights to get the difference between the input sample and the weighted average of the training samples in shallow layers, then the data will produce a distinguishable peak feature in the damaged segment after processed by multiple convolutional layers behind. This CNN process is similar to calculating the difference between the sample to be classified and the weighted average of the training samples and then mapping it via a quadratic function.
Author Contributions
Funding
Conflicts of Interest
References
- Ni, H.; Li, M.H.; Zuo, X. Review on Damage Identification and Diagnosis Research of Civil Engineering Structure. Adv. Mat. Res. 2014, 1006–1007, 34–37. [Google Scholar] [CrossRef]
- Graybeal, B.A.; Phares, B.M.; Rolander, D.D.; Moore, M.; Washer, G. Visual Inspection of Highway Bridges. J. Nondestruct. Eval. 2002, 21, 67–83. [Google Scholar] [CrossRef]
- Aguilar, R.; Zonno, G.; Lozano, G.; Boroschek, R.; Lourenço, P.B. Vibration-Based Damage Detection in Historical Adobe Structures: Laboratory and Field Applications. Int. J. Archit. Herit. 2019, 13, 1005–1028. [Google Scholar] [CrossRef]
- Molina-Viedma, A.J.; Felipe-Ses, E.L.; López-Alba, E.; Díaz, F.A. Full-field modal analysis during base motion excitation using high speed 3D digital image correlation. Meas. Sci. Technol. 2017, 28. [Google Scholar] [CrossRef]
- Lee, J.H.; Yoon, S.S.; Kim, I.H.; Jung, H.J. Diagnosis of crack damage on structures based on image processing techniques and R-CNN using unmanned aerial vehicle (UAV). In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, Denver, CO, USA, 27 March 2018; p. 1059811. [Google Scholar] [CrossRef]
- Xiong, C.; Li, Q.; Lu, X. Automated regional seismic damage assessment of buildings using an unmanned aerial vehicle and a convolutional neural network. Autom. Constr. 2020, 109. [Google Scholar] [CrossRef]
- Cawley, P.; Adams, R.D. The Location of defects in structures from measurements of natural frequencies. J. Strain Anal. Eng. Des. 1979, 14. [Google Scholar] [CrossRef]
- Sundermeyer, J.N.; Weaver, R.L. On crack identification and characterization in a beam by non-linear vibration analysis. J. Sound Vib. 1995, 183, 857–871. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Structural damage localization from modal strain energy change. J. Sound Vib. 1998, 218, 825–844. [Google Scholar] [CrossRef]
- Zou, Y.; Tong, L.; Steven, G.P. Vibration-based model-dependent damage (delamination) and health monitoring for composite structures—a review. J. Sound Vib. 2000, 230, 357–378. [Google Scholar] [CrossRef]
- Palacz, M.; Krawczuk, M. Vibration parameters for damage detection in structures. J. Sound Vib. 2002, 249, 999–1010. [Google Scholar] [CrossRef]
- Xu, Z.D.; Wu, Z. Energy damage detection strategy based on acceleration responses for long-span bridge structures. Eng. Struct. 2006, 29, 609–617. [Google Scholar] [CrossRef]
- Wu, X.; Ghaboussi, J.; Garrett, J.H. Use of neural networks in detection of structural damage. Comput. Struct. 1992, 42, 649–659. [Google Scholar] [CrossRef]
- Zang, C.; Imregun, M. Structural Damage Detection Using Artificial Neural Networks and Measured Frf Data Reduced via Principal Component Projection. J. Sound Vib. 2001, 242, 813–827. [Google Scholar] [CrossRef]
- Yao, W. The Researching Overview of Evolutionary Neural Networks. Comput. Sci. 2004, 31, 125–129. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, Z.; Bao, Y.; Li, H. Convolutional neural network-based data anomaly detection method using multiple information for structural health monitoring. Struct. Control. Health Monit. 2018, 26, e2296. [Google Scholar] [CrossRef]
- Modarres, C.; Astorga, N.; Droguett, E.L.; Meruane, V. Convolutional neural networks for automated damage recognition and damage type identification. Struct. Control. Health Monit. 2018, 25, e2230. [Google Scholar] [CrossRef]
- Zhang, Y.; Miyamori, Y.; Mikami, S.; Saito, T. Vibration-based structural state identification by a 1-dimensional convolutional neural network. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 1–18. [Google Scholar] [CrossRef]
- Teng, S.; Chen, G.; Gong, P.; Liu, G.; Cui, F. Structural damage detection using convolutional neural networks combining strain energy and dynamic response. Meccanica 2019, 0, 1–15. [Google Scholar] [CrossRef]
- Teng, S.; Chen, G.; Liu, G.; Lv, J.; Cui, F. Modal Strain Energy-Based Structural Damage Detection Using Convolutional Neural Networks. Appl. Sci. 2019, 9, 3376. [Google Scholar] [CrossRef]
- Frans, R.; Arfiadi, Y.; Parung, H. Comparative Study of Mode Shapes Curvature and Damage Locating Vector Methods for Damage Detection of Structures. Procedia Eng. 2017, 171, 1263–1271. [Google Scholar] [CrossRef]
- Poudel, U.P.; Fu, G.; Ye, J. Wavelet transformation of mode shape difference function for structural damage location identification. Earthq. Eng. Struct. Dyn. 2007, 36, 1089–1107. [Google Scholar] [CrossRef]









| Prediction Accuracies | ||||||||
|---|---|---|---|---|---|---|---|---|
| Type | Damage Degree | |||||||
| 0% | 4% | 6% | 10% | 30% | 50% | 70% | 90% | |
| Front lower rod | 100% | 100% | 100% | 100% | 100% | 92% | 89% | |
| Front upper rod | 100% | 100% | 100% | 100% | 100% | 96% | 92% | |
| Front vertical rod | 100% | 92% | 100% | 100% | 100% | 100% | 100% | |
| Front diagonal rod | 100% | 100% | 100% | 100% | 100% | 100% | 96% | |
| Rear lower rod | 100% | 100% | 100% | 100% | 100% | 100% | 96% | |
| Rear upper rod | 50% | 46% | 38% | 42% | 46% | 42% | 46% | |
| Rear vertical rod | 63% | 77% | 81% | 96% | 92% | 92% | 92% | |
| Rear diagonal rod | 92% | 92% | 100% | 100% | 100% | 100% | 100% | |
| Transverse lower rod | 58% | 58% | 44% | 65% | 48% | 58% | 34% | |
| Horizontal upper diagonal rod | 96% | 92% | 96% | 100% | 100% | 100% | 100% | |
| Transverse upper rod | 14% | 25% | 37% | 63% | 81% | 77% | 40% | |
| Horizontal lower diagonal rod | 84% | 96% | 80% | 92% | 96% | 92% | 100% | |
| Transverse diagonal rod | 66% | 63% | 55% | 55% | 51% | 85% | 74% | |
| Overall | 100% | 79% | 80% | 79% | 85% | 85% | 87% | 81% |
| Prediction Accuracies | ||||||||
|---|---|---|---|---|---|---|---|---|
| Type | Damage Degree | |||||||
| 0% | 4% | 6% | 10% | 30% | 50% | 70% | 90% | |
| Front lower rod | 57% | 100% | 100% | 100% | 100% | 92% | 100% | |
| Front upper rod | 76% | 96% | 100% | 100% | 100% | 100% | 100% | |
| Front vertical rod | 18% | 44% | 55% | 100% | 100% | 100% | 100% | |
| Front diagonal rod | 57% | 78% | 89% | 100% | 100% | 100% | 100% | |
| Rear lower rod | 21% | 17% | 53% | 92% | 100% | 100% | 100% | |
| Rear upper rod | 38% | 38% | 38% | 57% | 92% | 92% | 92% | |
| Rear vertical rod | 66% | 74% | 74% | 59% | 81% | 59% | 44% | |
| Rear diagonal rod | 7% | 25% | 10% | 78% | 96% | 100% | 100% | |
| Transverse lower rod | 10% | 13% | 13% | 37% | 44% | 55% | 27% | |
| Horizontal upper diagonal rod | 32% | 35% | 50% | 71% | 89% | 85% | 100% | |
| Transverse upper rod | 18% | 33% | 48% | 74% | 92% | 74% | 18% | |
| Horizontal lower diagonal rod | 26% | 26% | 19% | 65% | 92% | 84% | 92% | |
| Transverse diagonal rod | 7% | 22% | 44% | 48% | 88% | 100% | 92% | |
| Overall | 0% | 33% | 46% | 53% | 75% | 90% | 87% | 82% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, K.; Teng, S.; Liu, G.; Chen, G.; Cui, F. Structural Damage Features Extracted by Convolutional Neural Networks from Mode Shapes. Appl. Sci. 2020, 10, 4247. https://doi.org/10.3390/app10124247
Zhong K, Teng S, Liu G, Chen G, Cui F. Structural Damage Features Extracted by Convolutional Neural Networks from Mode Shapes. Applied Sciences. 2020; 10(12):4247. https://doi.org/10.3390/app10124247
Chicago/Turabian StyleZhong, Kefeng, Shuai Teng, Gen Liu, Gongfa Chen, and Fangsen Cui. 2020. "Structural Damage Features Extracted by Convolutional Neural Networks from Mode Shapes" Applied Sciences 10, no. 12: 4247. https://doi.org/10.3390/app10124247
APA StyleZhong, K., Teng, S., Liu, G., Chen, G., & Cui, F. (2020). Structural Damage Features Extracted by Convolutional Neural Networks from Mode Shapes. Applied Sciences, 10(12), 4247. https://doi.org/10.3390/app10124247






