Vibration Diagnosis of Sand Units in a Stone Crusher Plant: An On-Site Field Test
Abstract
:1. Introduction
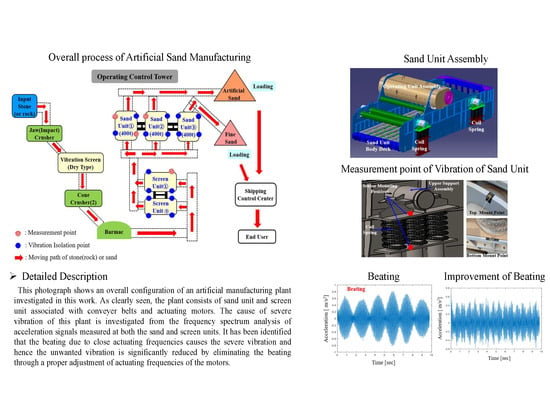
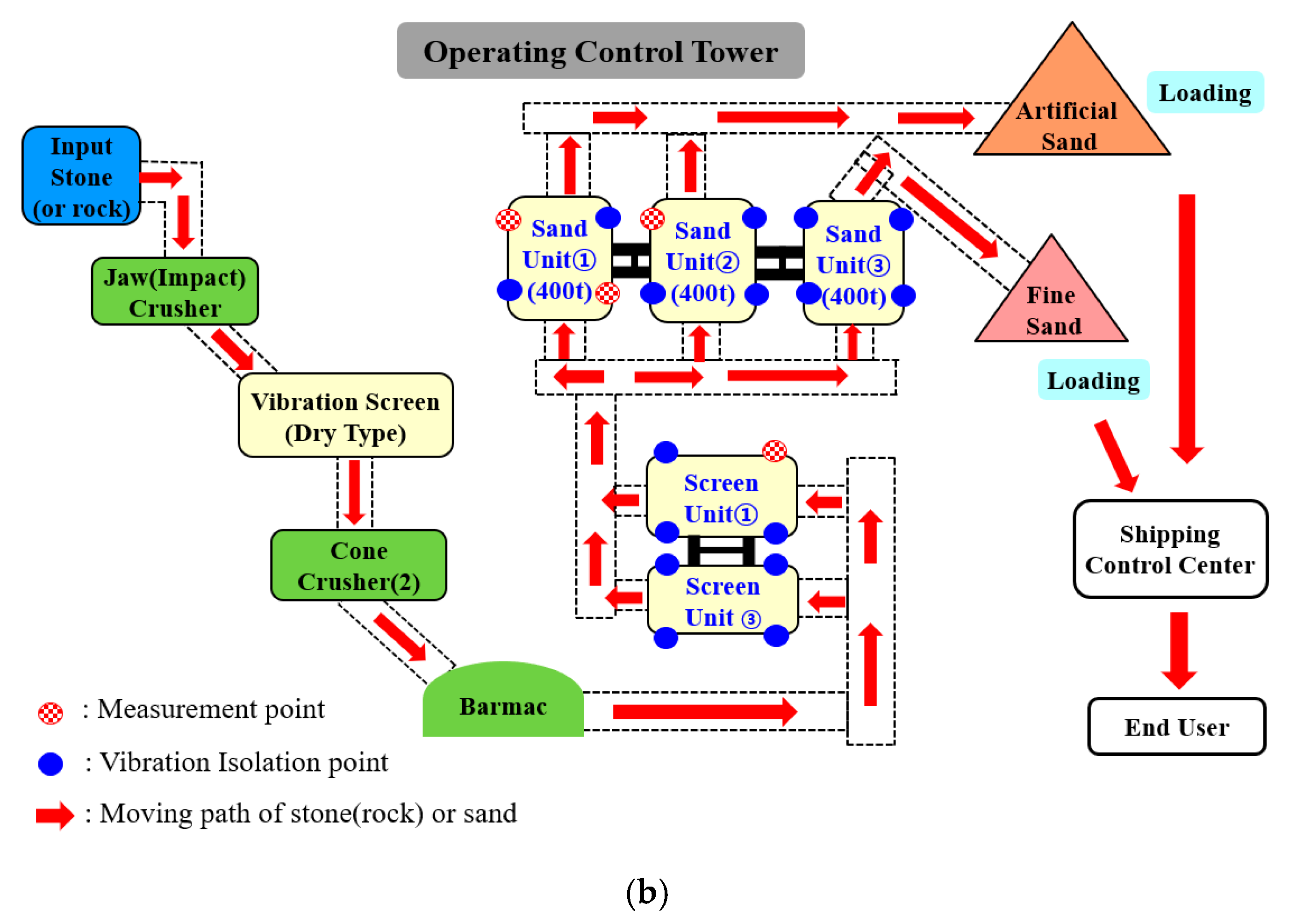
2. Artificial Sand Production Plant
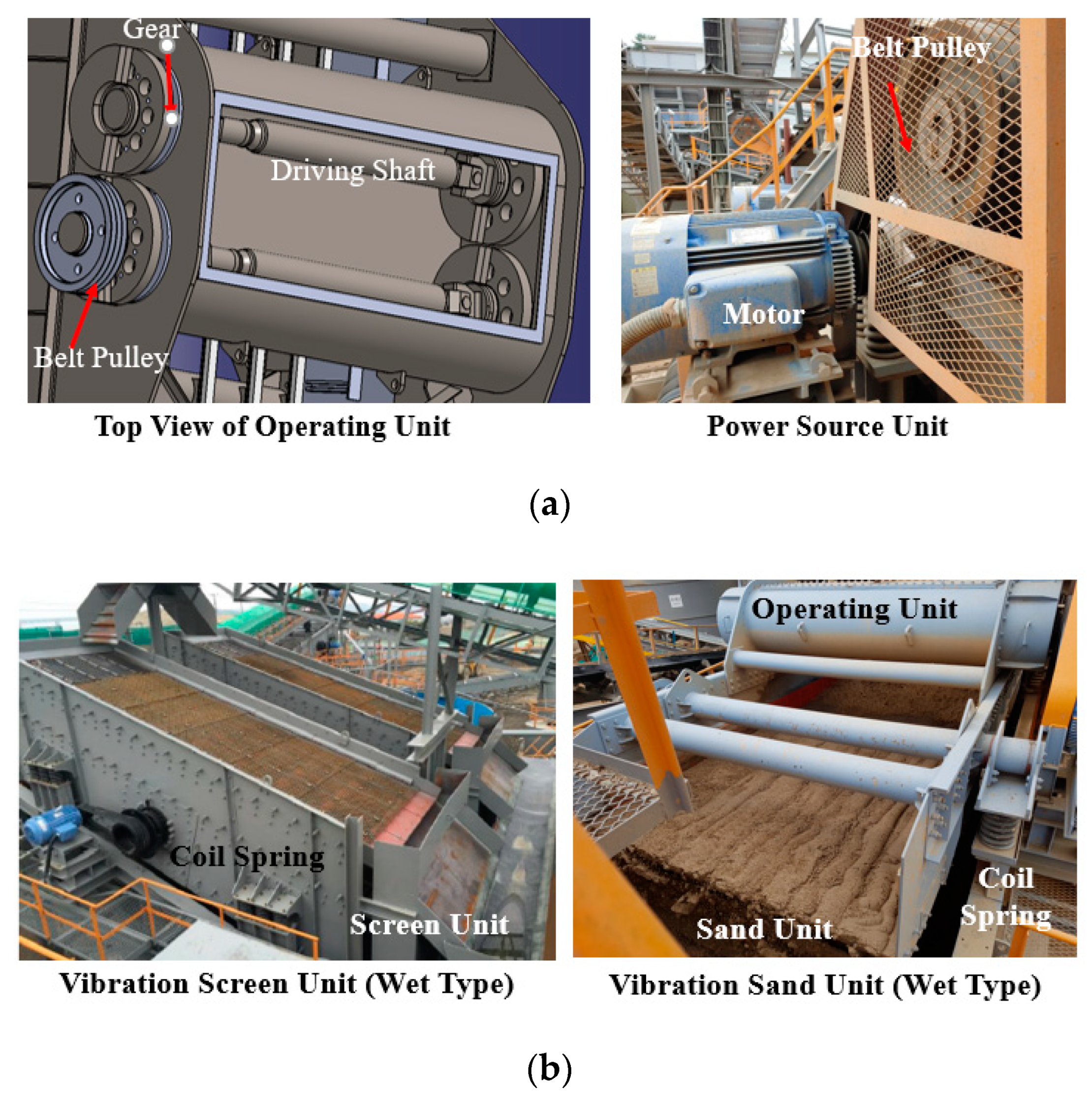
2.1. Overall Structure
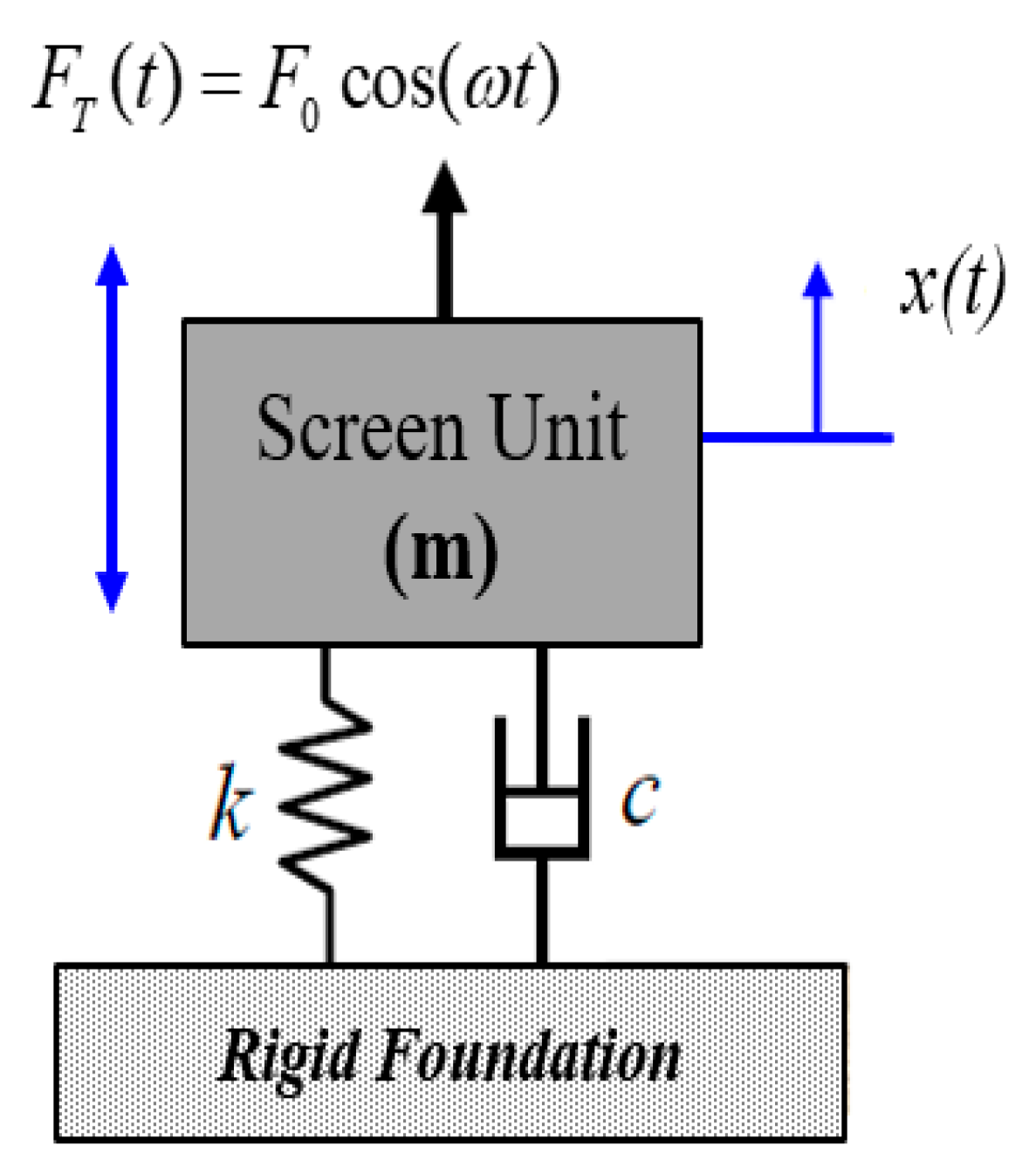
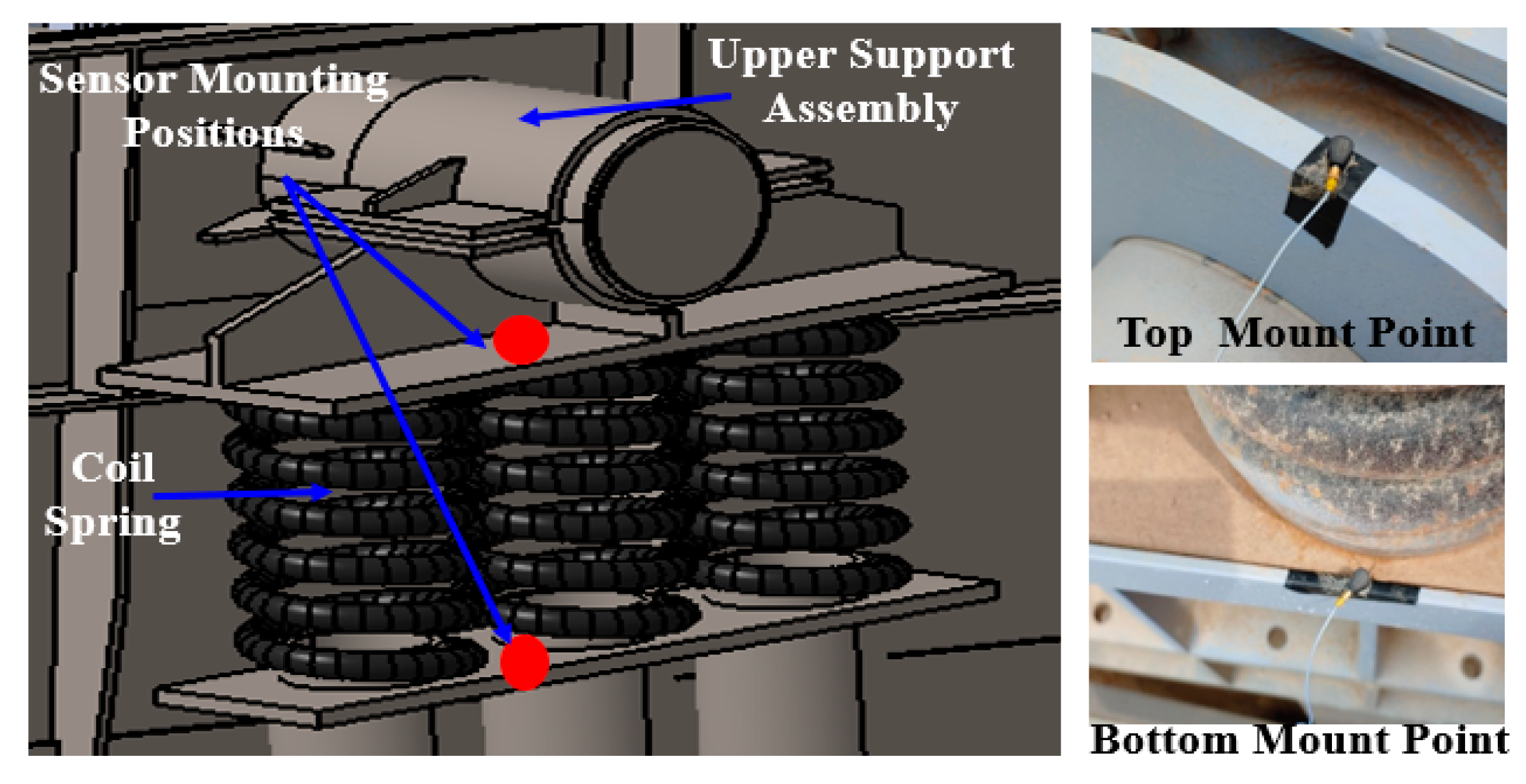
2.2. Vibration Isolation
2.3. Vibration Sources
3. On-Site Vibration Measurement
3.1. Vibration Level
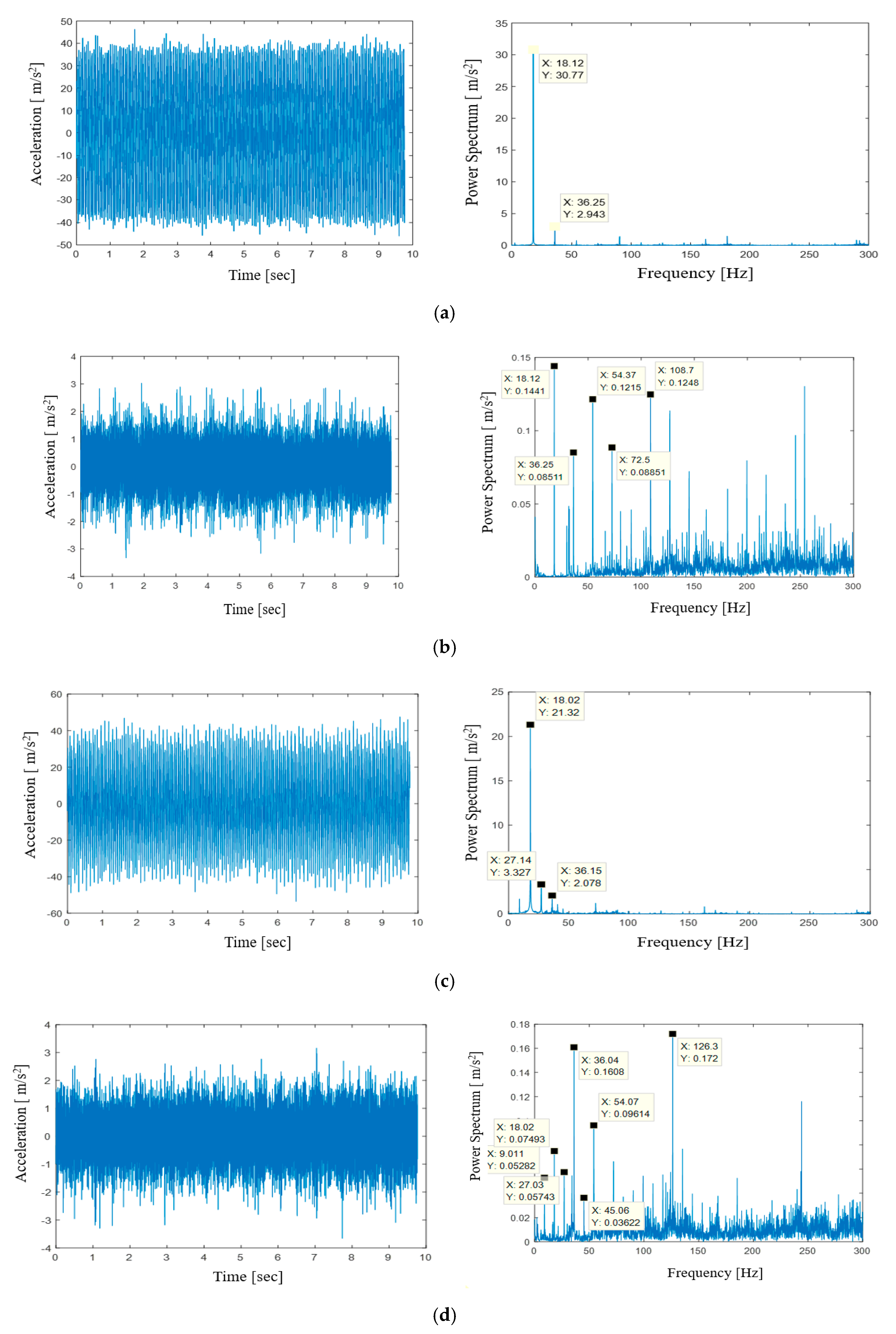
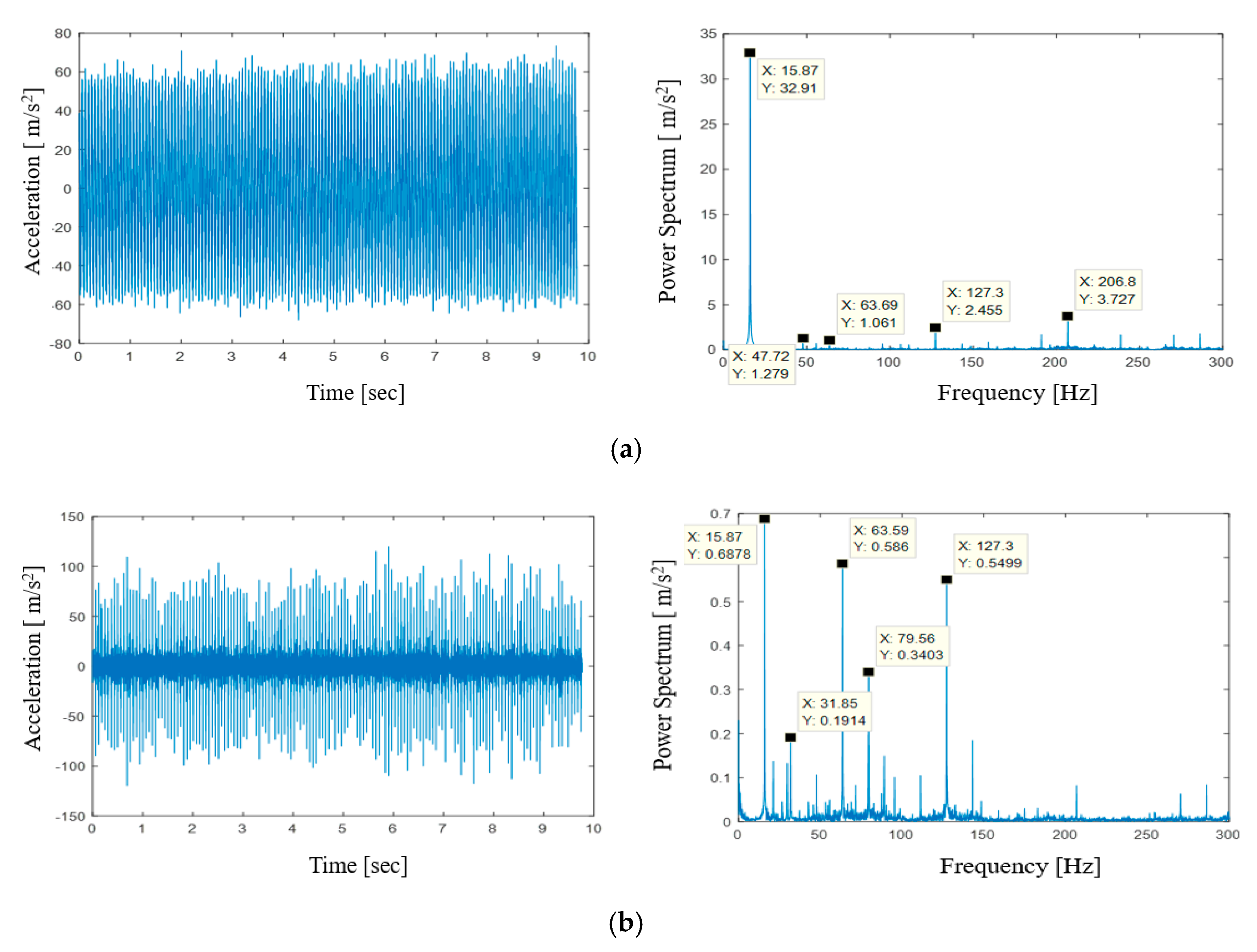
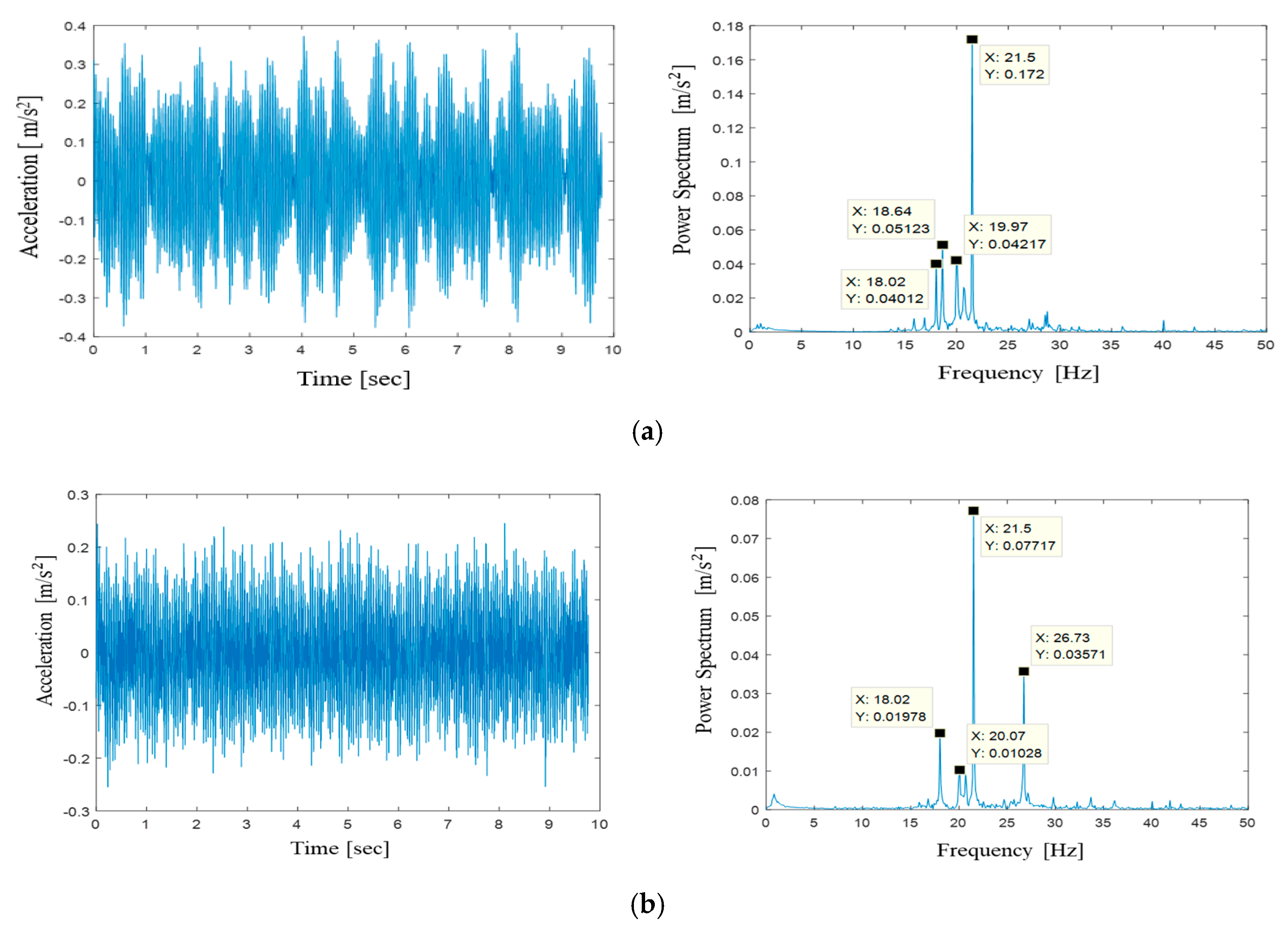
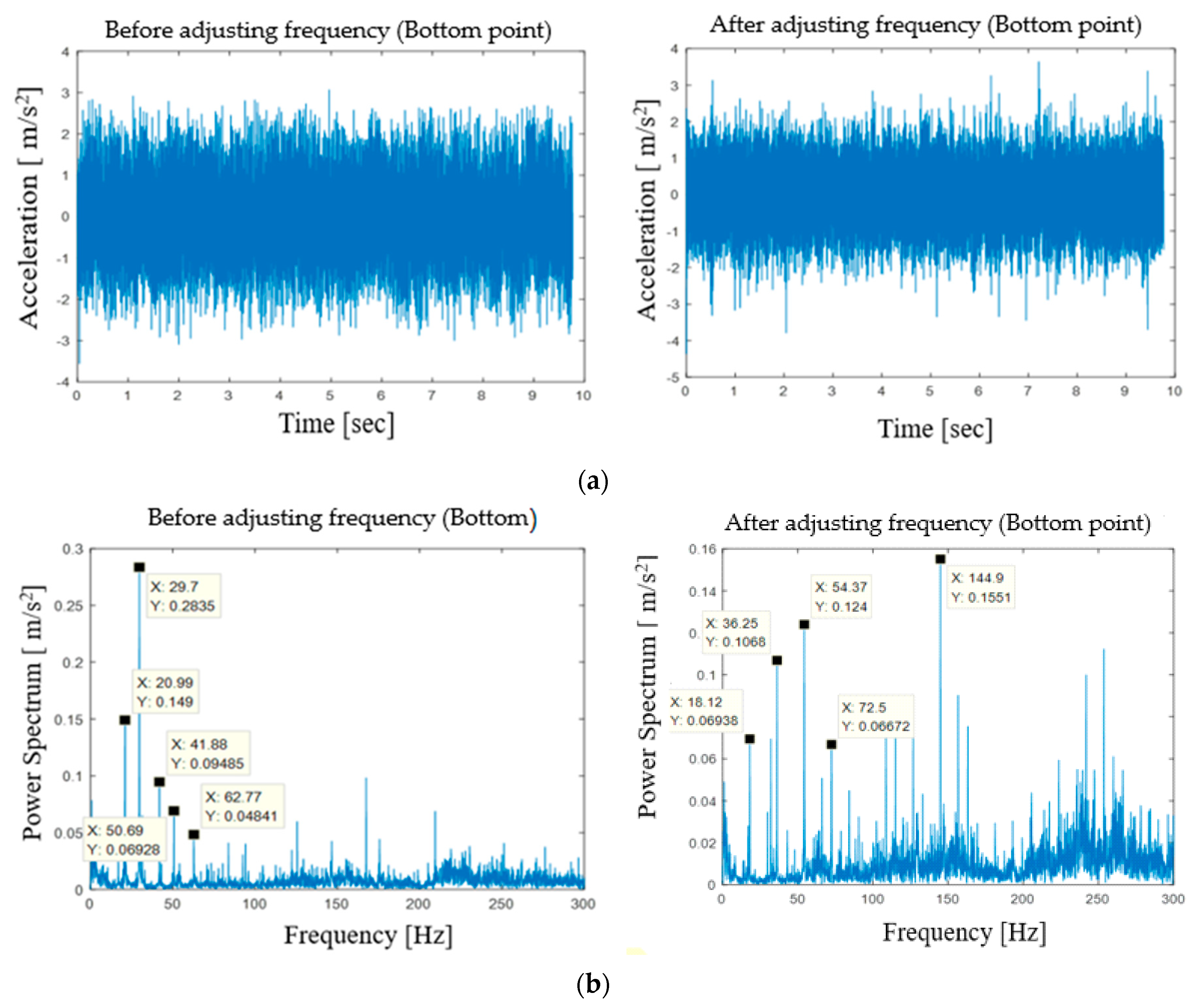
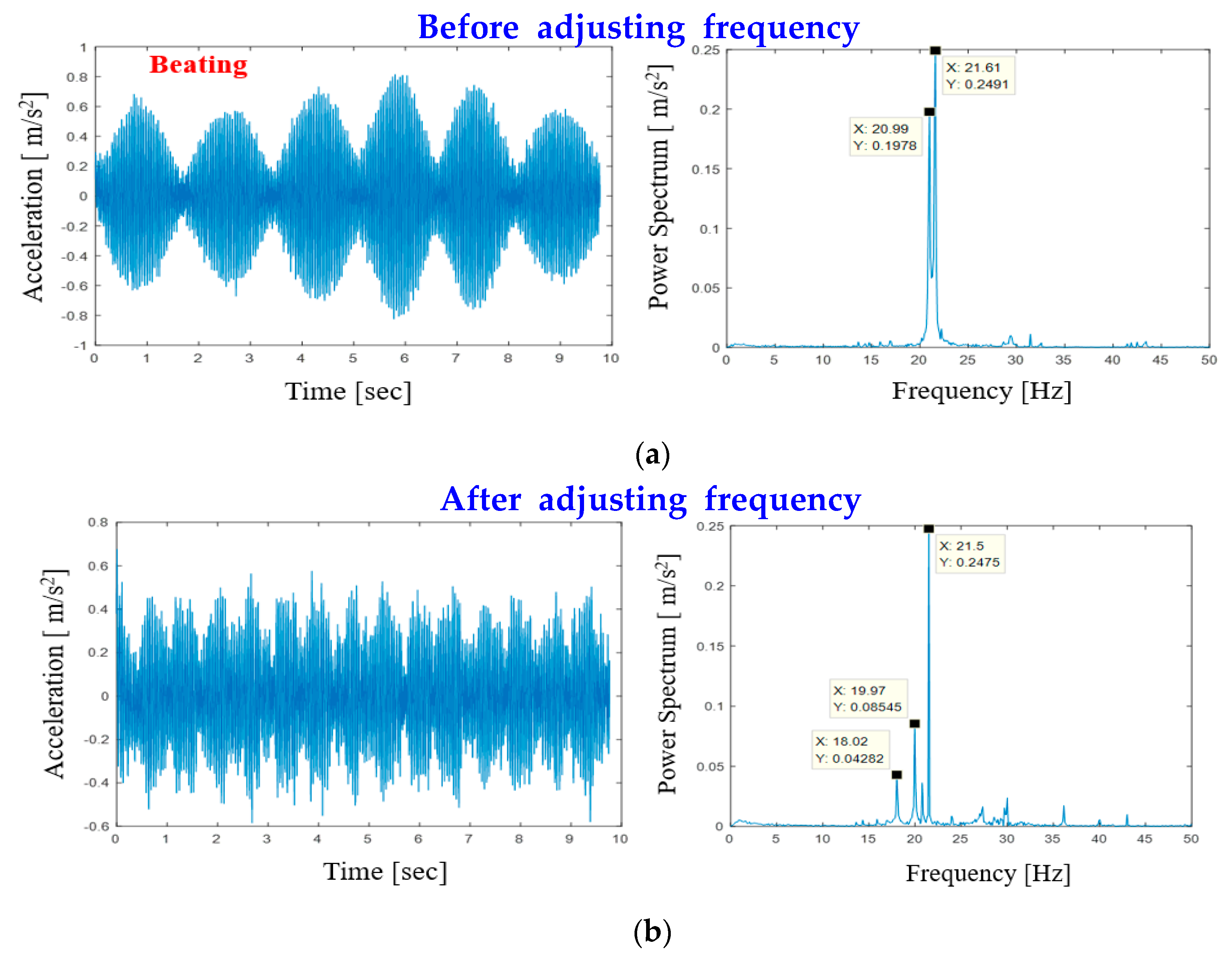
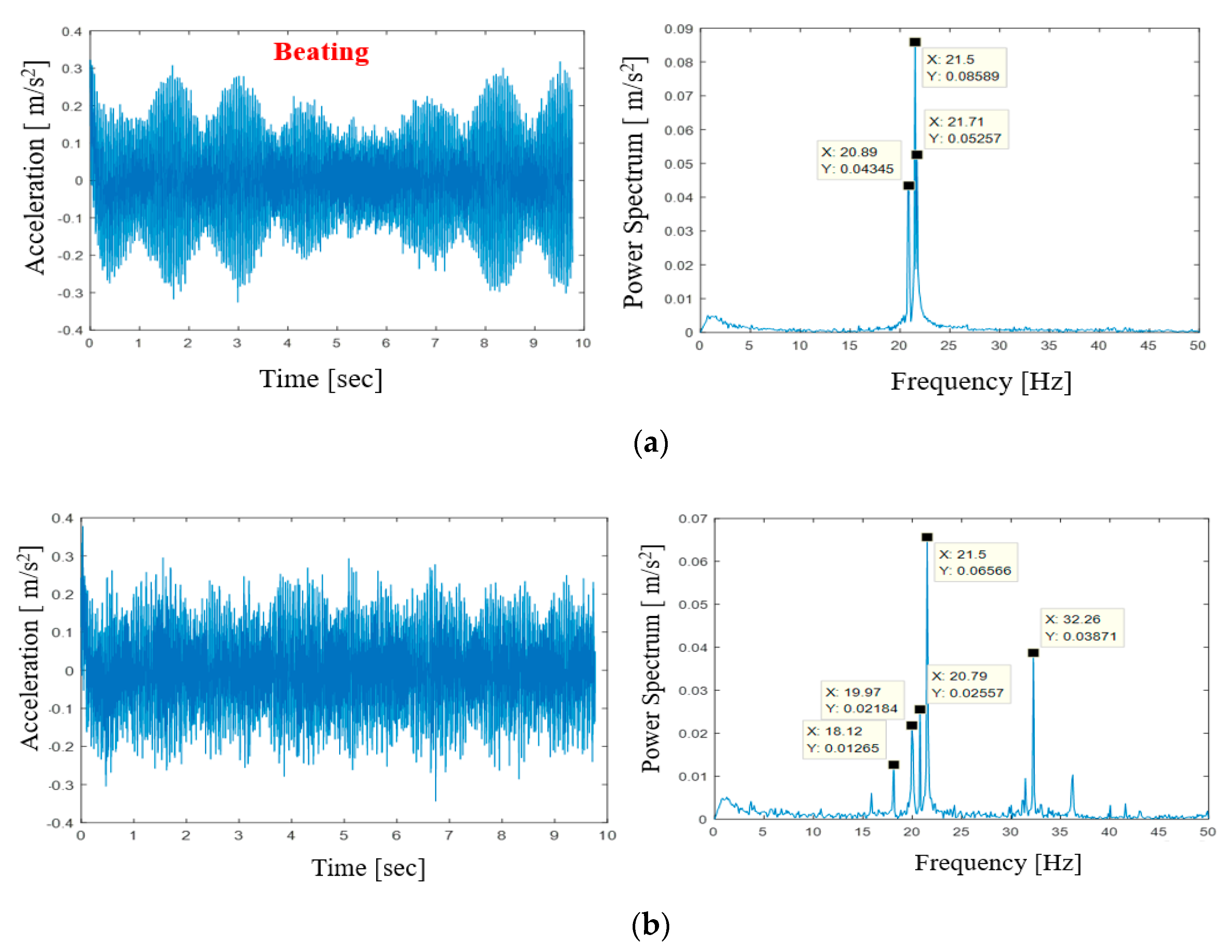
3.2. Vibration Analysis
4. Vibration Reduction
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dalyander, P.S.; Plant, N.G.; Long, J.W.; McLaughlin, M. Nearshore dynamics of artificial sand and oil agglomerates. J. Mar. Pollut. Bull. 2015, 96, 344–355. [Google Scholar] [CrossRef] [PubMed]
- Band, S.R.; Malkhede, S.D. Effect of replacement of natural sand by artificial sand on strength of concrete. Int. J. Adv. Eng. Res. Dev. 2017, 4, 415–419. [Google Scholar]
- Purohit, N.; Chawda, A. Experimental study of effect of artificial sand and aggregates on compressive strength and workability of concrete. Int. J. Eng. Res. Technol. 2016, 5, 730–735. [Google Scholar]
- Bajad, M.N.; Sakhare, S. Influence of artificial sand on the properties of concrete and mortar. Int. J. Civ. Eng. Technol. 2018, 9, 447–454. [Google Scholar]
- Mogre, R.P.; Parbat, D.K. Optimum replacement of natural sand with artificial sand in concrete. Int. J. Civ. Struct. Environ. Infrastruct. Eng. Res. Dev. 2013, 3, 93–100. [Google Scholar]
- Ingale, P.S.; Kawade, N.S.; Jadhav, A.V.; Pawal, B.B.; Pradhan, G.G.; Gawatre, D.w. Optimization of artificial sand in concrete. Int. J. Adv. Mech. Civ. Eng. 2016, 3, 68–70. [Google Scholar]
- Chitlange, M.R.; Pajgade, P.S.; Nagarnaik, P.B. Experimental study of artificial sand concrete. In Proceedings of the International conference on Emerging Trends in Engineering and Technology (ICETET), Maharashtra, India, 16–18 July 2008; pp. 1050–1054. [Google Scholar]
- Zhao, Y.M.; Liu, C.S.; He, X.M.; Zhang, C.Y.; Wang, Y.B.; Ren, Z.T. Dynamic design theory and application of large vibrating screen. Procedia Earth Planet. Sci. 2009, 1, 776–784. [Google Scholar]
- Mali, A.V.; Morey, N.N.; Khtri, A.P. Improvement in the efficiency of the Stone crusher, Generic vibration criteria for vibration-sensitive equipment. Int. J. Sci. Eng. Technol. Res. 2016, 5, 2265–2271. [Google Scholar]
- Leiva, C.A.; Arcos, K.V.; Poblete, D.A.; Serey, E.A.; Toress, C.M.; Ghorabani, Y. Design and evaluation of an expert system in crushing plant. J. Miner. 2018, 8, 469. [Google Scholar] [CrossRef] [Green Version]
- Asbjoernsson, G.; Hulthen, E.; Eversson, M. Modeling and simulation of dynamic crushing plant behavior with MATLAB/Simulink. J. Miner. Eng. 2013, 43–44, 112–120. [Google Scholar] [CrossRef]
- Slepyan, L.I.; Slepyan, V.I. Coupled mode parametric resonance in a vibration screen model. J. Mech. Syst. Signal Process. 2014, 43, 295–304. [Google Scholar] [CrossRef] [Green Version]
- Bessason, B.; Madshus, C.; Frøysteinand, H.A.; Kolbjørnsen, H. Vibration criteria for metrology laboratories. Meas. Sci. Technol. 1999, 10, 1009–1014. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Huang, Y.J.; Xu, S. Trispectrum and correlation dimension analysis of magnetorheological damper in vibration screen. J. Cent. South Univ. 2012, 19, 1832–1838. [Google Scholar] [CrossRef]
- Raczka, W.; Sibielak, M.; Kowal, J.; Konieczny, J. Application and SMA spring for vibration screen control. J. Mech. Low Freq. Noise Vib. Act. Control 2013, 32, 117–132. [Google Scholar] [CrossRef] [Green Version]
- Maleun Environment Co. Ltd. Available online: http://www.maleun.co.kr (accessed on 16 June 2020).
- Yongwon Crusher Co. Ltd. Available online: http://ywcrusher.com/home/?lang=en (accessed on 16 June 2020).
- Samyoung Plant Co. Ltd. Available online: http://www.syplant.co.kr/index.html (accessed on 16 June 2020).
- Kwang San Mining Machinery Co. Ltd. Available online: http://www.mmco.kr/html/sub02.html (accessed on 16 June 2020).
- Metso Mining Machinery com. Available online: https://www.metso.com/products/screens/horizontal-screens/metso-es-series-horizontal-screens (accessed on 17 June 2020).
- Sandvik Machinery. Available online: https://www.rocktechnology.sandvik/en/products/stationary-crushers-and-screens (accessed on 16 June 2020).
- Carting, B. Beating frequency and amplitude modulation of the piano tone due to coupling of tones. J. Acoust. Soc. Am. 2005, 117, 2259–2267. [Google Scholar] [CrossRef] [PubMed]
- Chae, S.I.; Kim, B.S.; Lim, W.S.; Yang, B.S. Vibration reduction of reciprocating compressor. In Proceedings of the Korean Society for Noise and Vibration Engineering 2012 Autumn Annual Conference, Won-Joo, Korea, 25–27 October 2012; pp. 779–783. [Google Scholar]
- Choi, Y.C.; Park, J.H.; Yoon, D.B. Structure excitation by using beating. Trans. Korean Soc. Noise Vib. Eng. 2009, 19, 1028–1033. [Google Scholar]
- Lee, H.C. Robust damage diagnostic method using short time Fourier transform and beating. Trans. Korean Soc. Noise Vib. Eng. 2005, 15, 1108–1117. [Google Scholar]
- Kim, S.H.; Park, S.G.; Park, G.Y.; Suh, B.S. Beat maps of a slightly asymmetric ring. Trans. Korean Soc. Noise Vib. Eng. 2002, 12, 685–693. [Google Scholar]
- Kim, S.H.; Cui, C.X. A study on the control of the beat clarity and the beat period in a ring structure. Trans. Korean Soc. Noise Vib. Eng. 2008, 18, 1170–1176. [Google Scholar]
- Park, J.H.; Ahn, S.J.; Jeong, W.B. Study on ride comfort of idle vibration declined by beating phenomenon on passenger vehicle. In Proceedings of the Korean Society for Noise and Vibration Engineering 2015 Spring Annual Conference, Jeju, Korea, 22–25 April 2015; pp. 871–874. [Google Scholar]
- Physics and Radio Electronics/Physics. Available online: https://www.physics-and-radio-electronics.com/physics/beats-waves-physics.html (accessed on 16 June 2020).
- Topper/guides/physics/beat. Available online: https://www.toppr.com/guides/physics-formulas/beat-frequency-formula (accessed on 16 June 2020).
- RP Photonics Encyclopedia/Beats Note. Available online: https://www.rp-photonics.com/beat_note.html (accessed on 16 June 2020).
- Lee, C.J.; Asia Noise and Vibration Institute. Noise and Vibration Control for Workplace; Ybook: Seoul, Korea, 2013; ISBN 978-89-967735-7-3. [Google Scholar]
- The Committee of Korean Society for Noise and Vibration Engineering. A Handbook of Noise and Vibration; the KSNVE Compilation Committee: Seoul, Korea, 1995. [Google Scholar]
- Irwin, J.D.; Graf, E.R. Industrial Noise and Vibration Control; Prentice Hall INC.: Englewood Cliff, NJ, USA, 1996; pp. 154–196. [Google Scholar]
- Jung, I.R.; Kim, J.Y.; Yoon, S.C.; Lee, T.H. Theory and Practice of Noise and Vibration; Shinkwang Munhwa Sa: Seoul, Korea, 2006; pp. 137–187. ISBN 978-89-7432-131-4. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 4th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Thomson, W. Theory of Vibration with Applications; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Dimarogonas, A.D. Vibration for Engineers, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001; ISBN 0-13-456229-1. [Google Scholar]
- Shin, K.H.; Hammond, J. Fundamental of Signal Processing for Sound and Vibration Engineers; John Wiely & Sons. Ltd: Hoboken, NJ, USA, 2008; ISBN 978-0-47051188-6. [Google Scholar]
- Yang, B.S. Condition Monitoring and Diagnostics of Rotational Machinery; Inter Vison: Seoul, Korea, 2006; ISBN 89-5667-320-9. [Google Scholar]


| Devices No. | Before Adjusting Frequency | After Adjusting Frequency | ||||
|---|---|---|---|---|---|---|
| Power Efficiency | Operating Speed (rpm) | Fundamental Frequency | Power Efficiency | Operating Speed (rpm) | Fundamental Frequency | |
| Sand Unit #1 | 100% | 1320 rpm | 22.0 Hz | 80% | 1050 rpm | 17.5 Hz |
| Sand Unit #2 | 100% | 1320 rpm | 22.0 Hz | 100% | 1320 rpm | 22.0 Hz |
| Sand Unit #3 | 100% | 1320 rpm | 22.0 Hz | 90% | 1180 rpm | 19.6 Hz |
| Screen Unit #1 | 100% | 1320 rpm | 22.0 Hz | 73% | 960 rpm | 16 Hz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-H.; Kim, B.-G.; Jung, D.-S.; Choi, S.-B.; Lee, J.-M.; Lee, K.-B. Vibration Diagnosis of Sand Units in a Stone Crusher Plant: An On-Site Field Test. Appl. Sci. 2020, 10, 4327. https://doi.org/10.3390/app10124327
Kim S-H, Kim B-G, Jung D-S, Choi S-B, Lee J-M, Lee K-B. Vibration Diagnosis of Sand Units in a Stone Crusher Plant: An On-Site Field Test. Applied Sciences. 2020; 10(12):4327. https://doi.org/10.3390/app10124327
Chicago/Turabian StyleKim, Seong-Hwan, Bo-Gyu Kim, Dong-Soo Jung, Seung-Bok Choi, Jong-Mu Lee, and Kyu-Bong Lee. 2020. "Vibration Diagnosis of Sand Units in a Stone Crusher Plant: An On-Site Field Test" Applied Sciences 10, no. 12: 4327. https://doi.org/10.3390/app10124327
APA StyleKim, S.-H., Kim, B.-G., Jung, D.-S., Choi, S.-B., Lee, J.-M., & Lee, K.-B. (2020). Vibration Diagnosis of Sand Units in a Stone Crusher Plant: An On-Site Field Test. Applied Sciences, 10(12), 4327. https://doi.org/10.3390/app10124327