Thermal Mapping of Power Semiconductors in H-Bridge Circuit †
Abstract
:1. Introduction
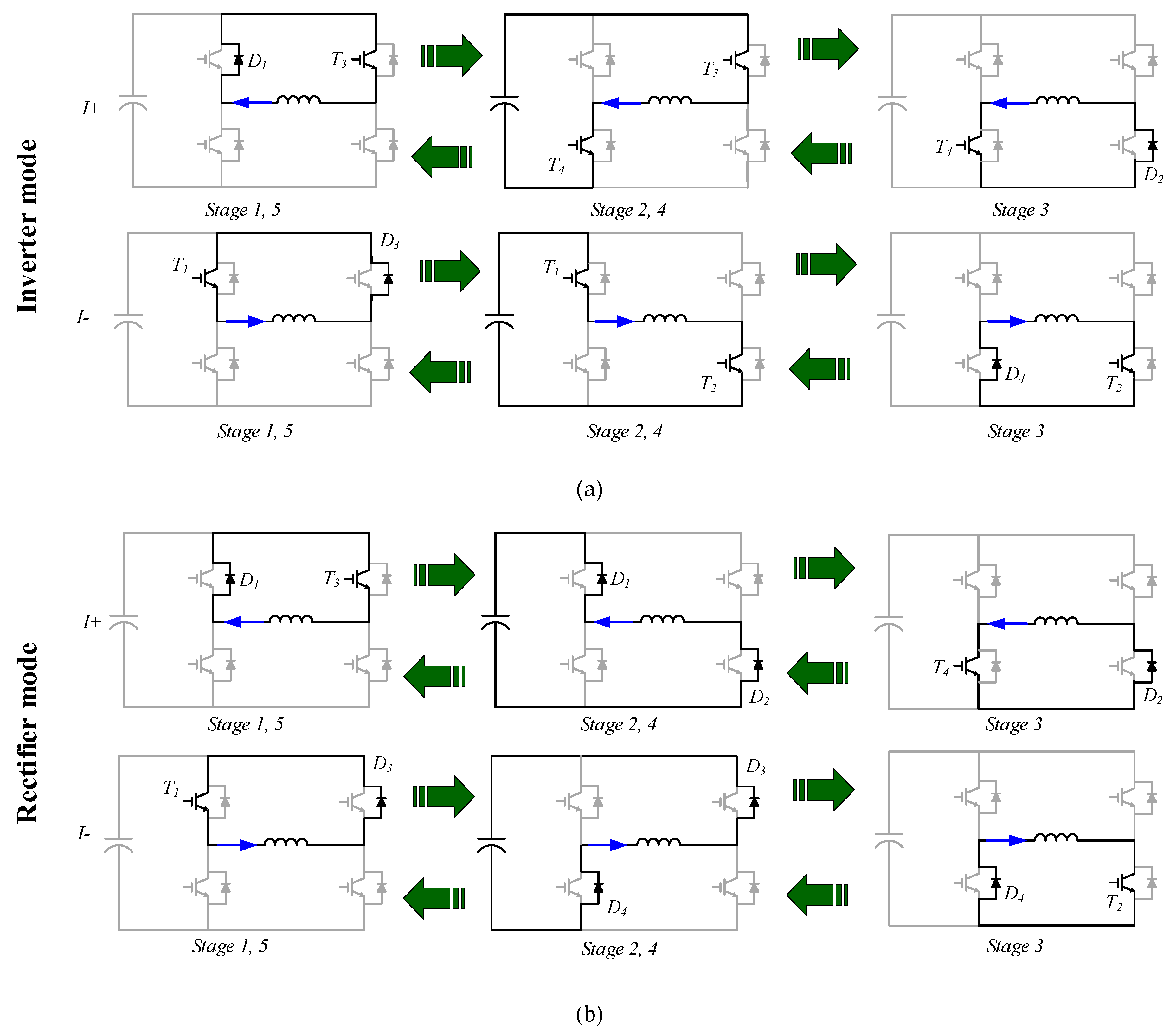
2. Operation Principle of H-Bridge Circuit
3. Loss Dissipation and Junction Temperature of Power Devices
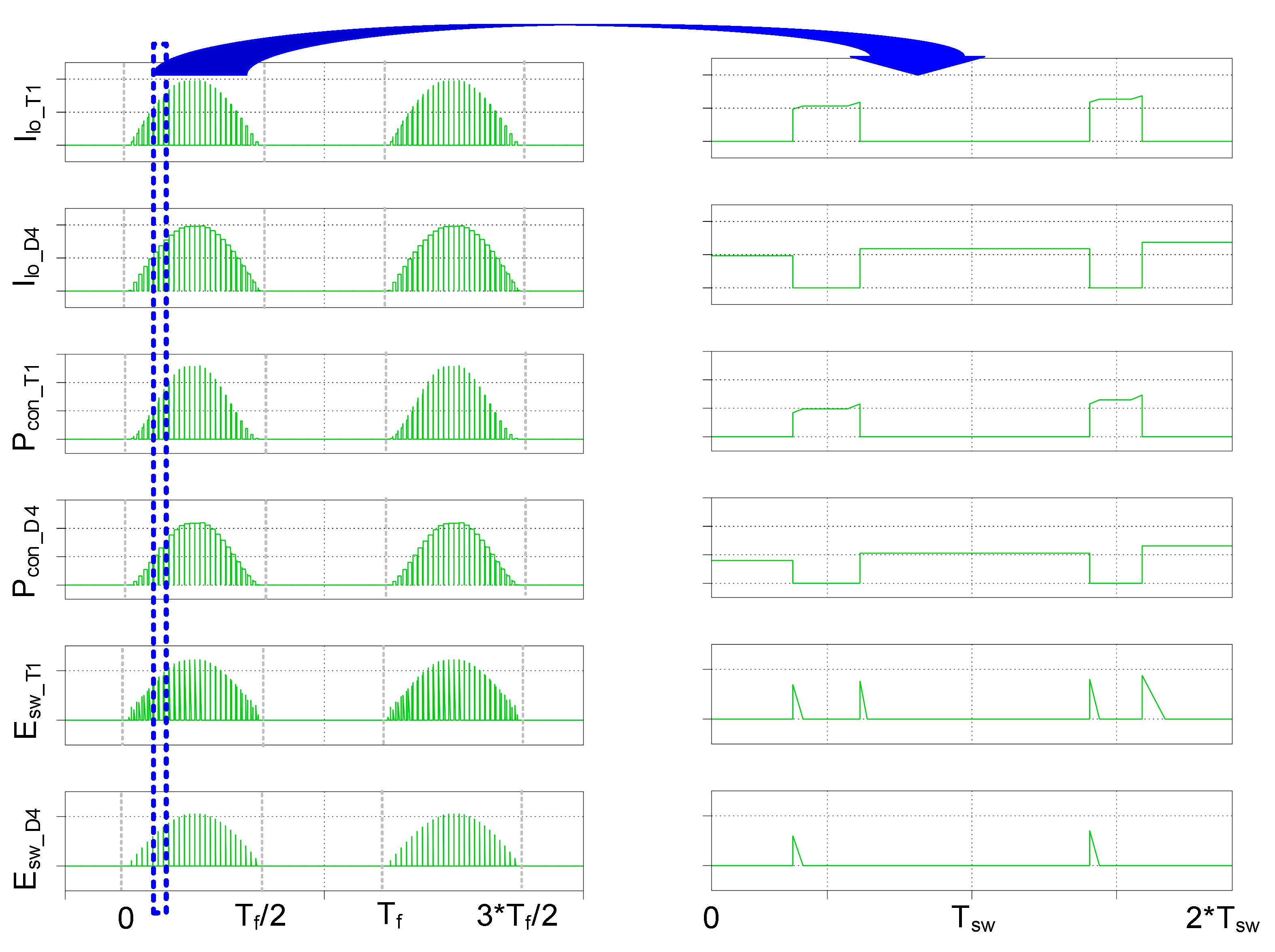
3.1. Loss Dissipation
3.2. Junction Temperaute Estimation
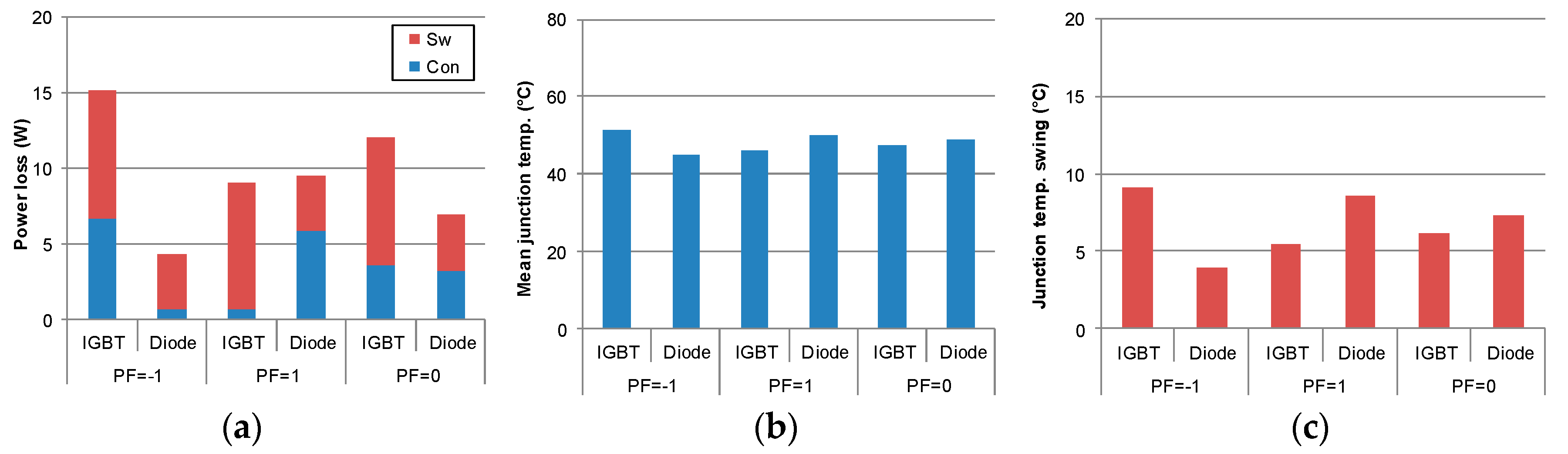
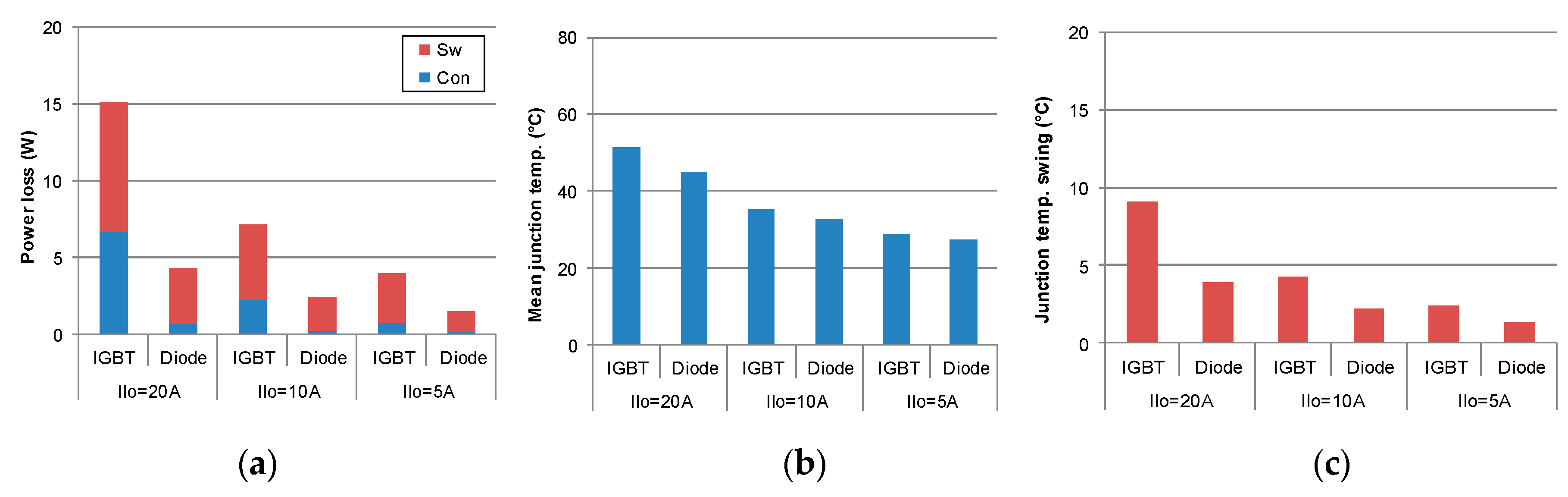
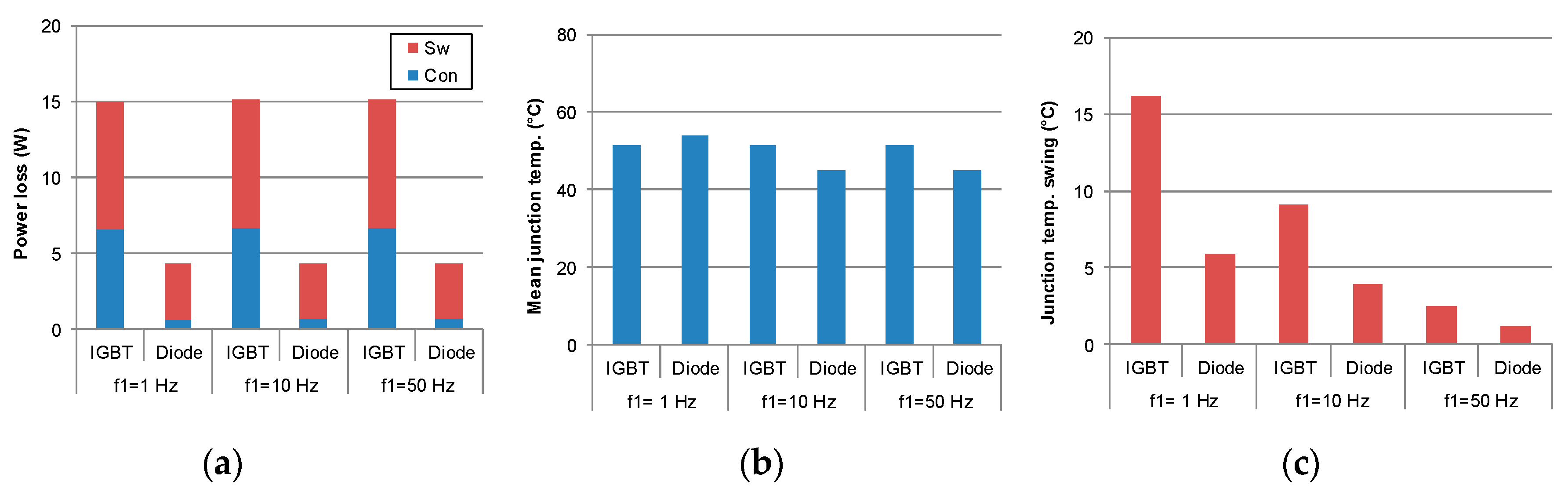
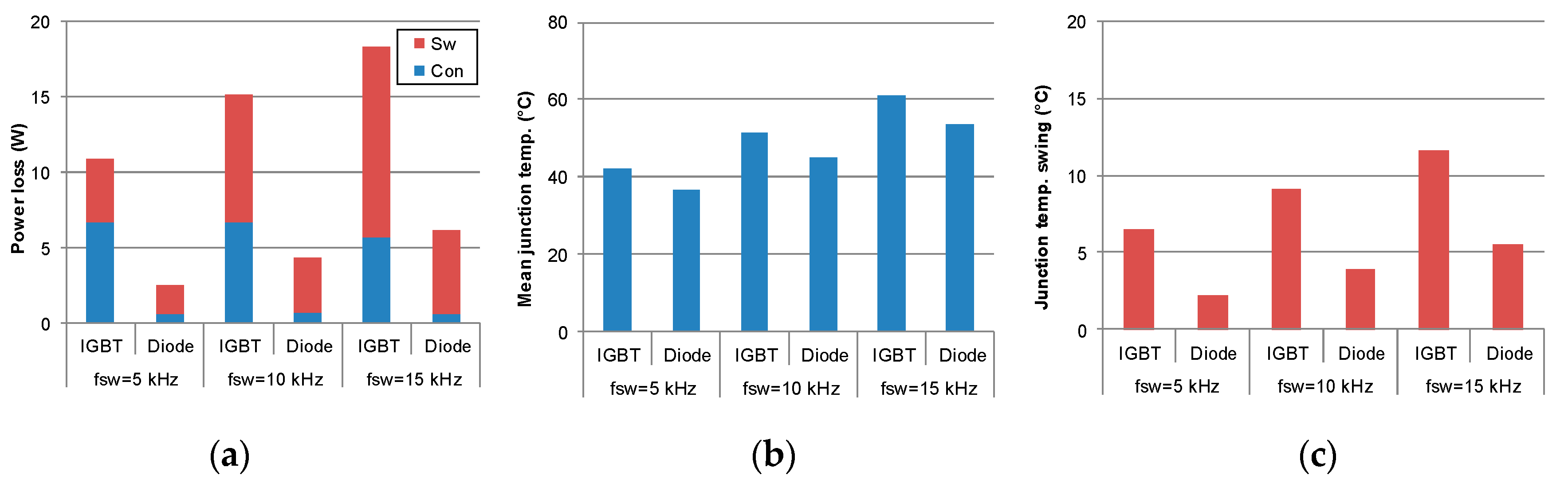
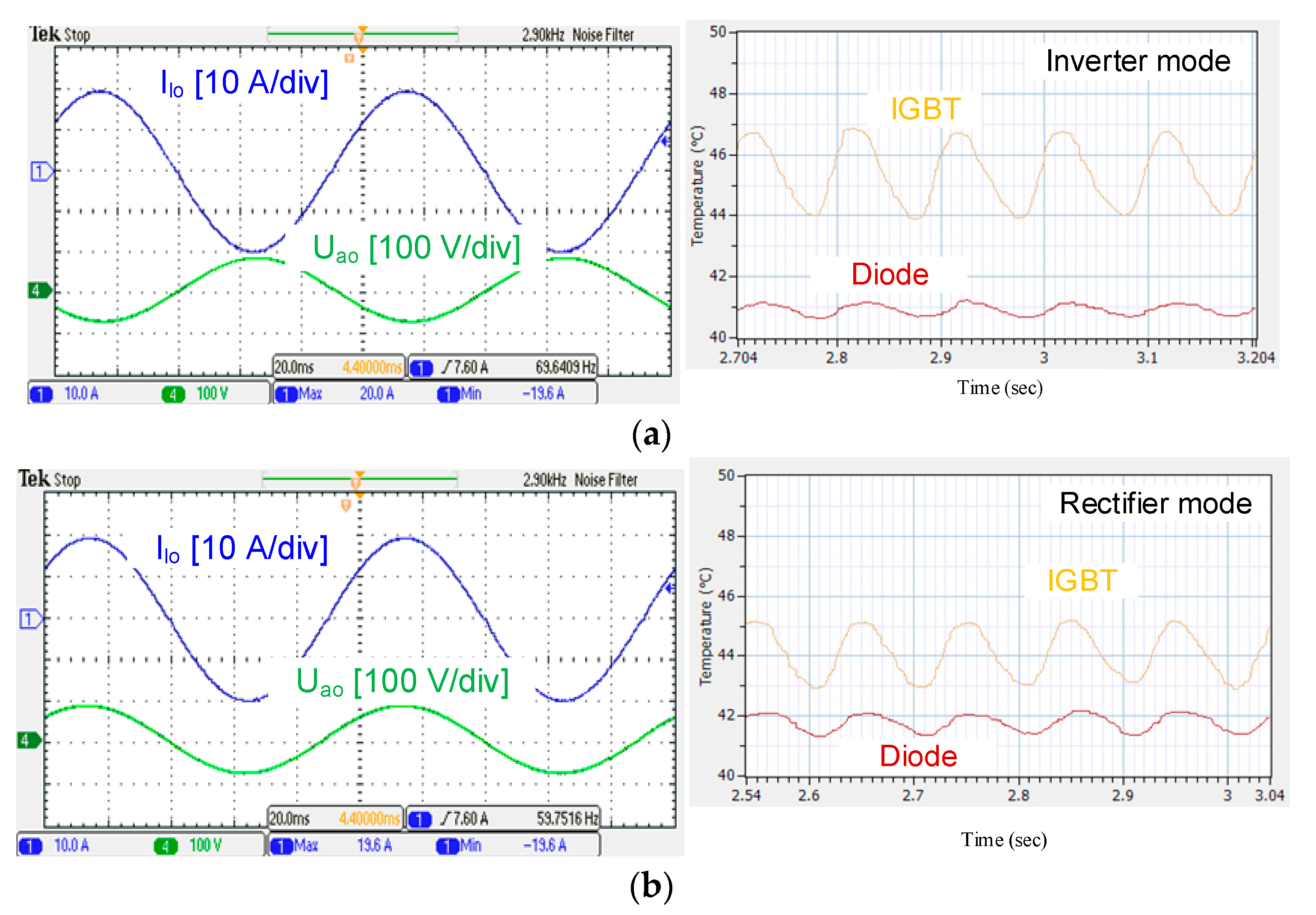
4. Thermal Stresses of Power Devices at Various Loading Conditions
4.1. Dominating Factors for Device Loading
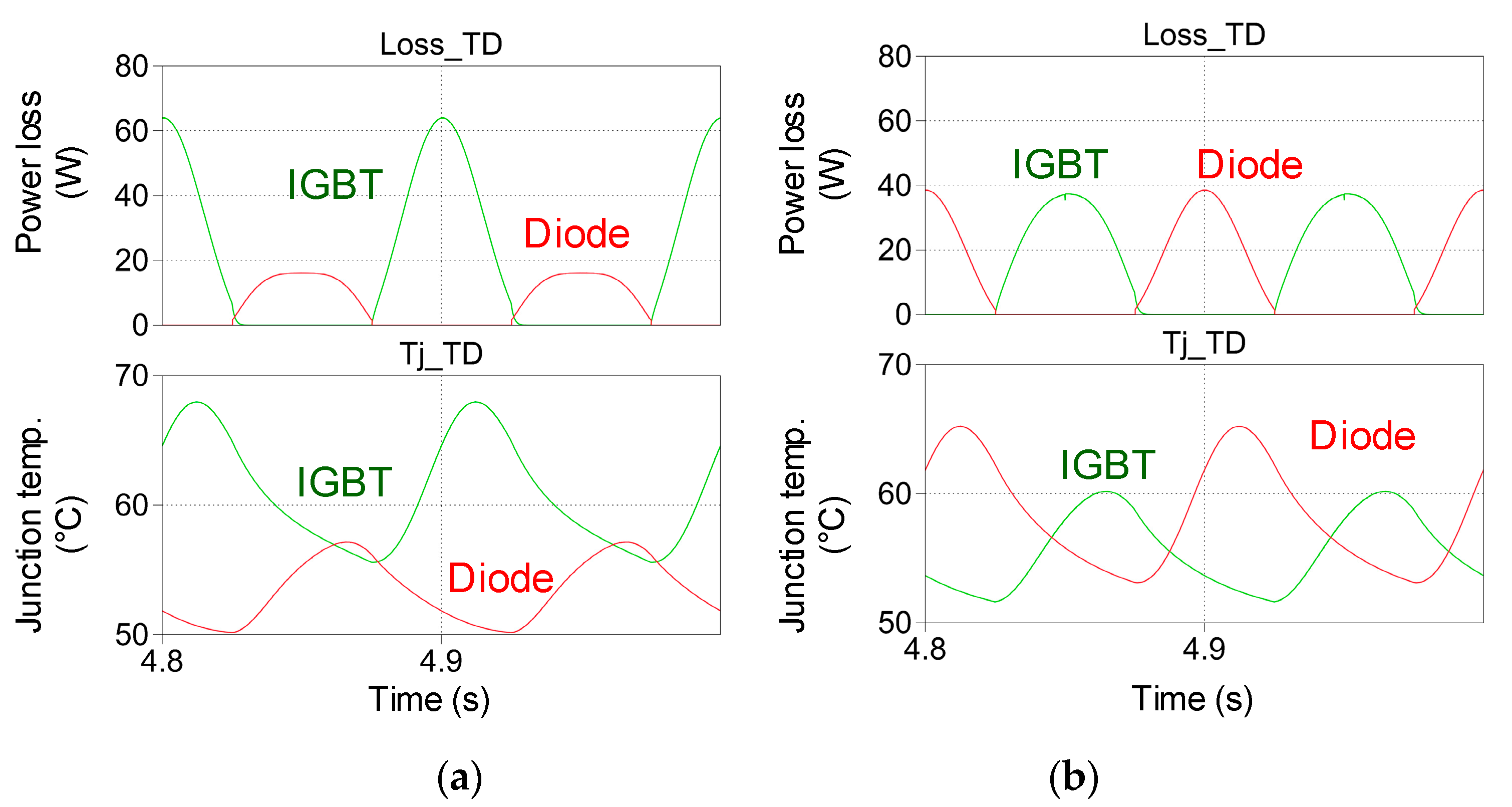
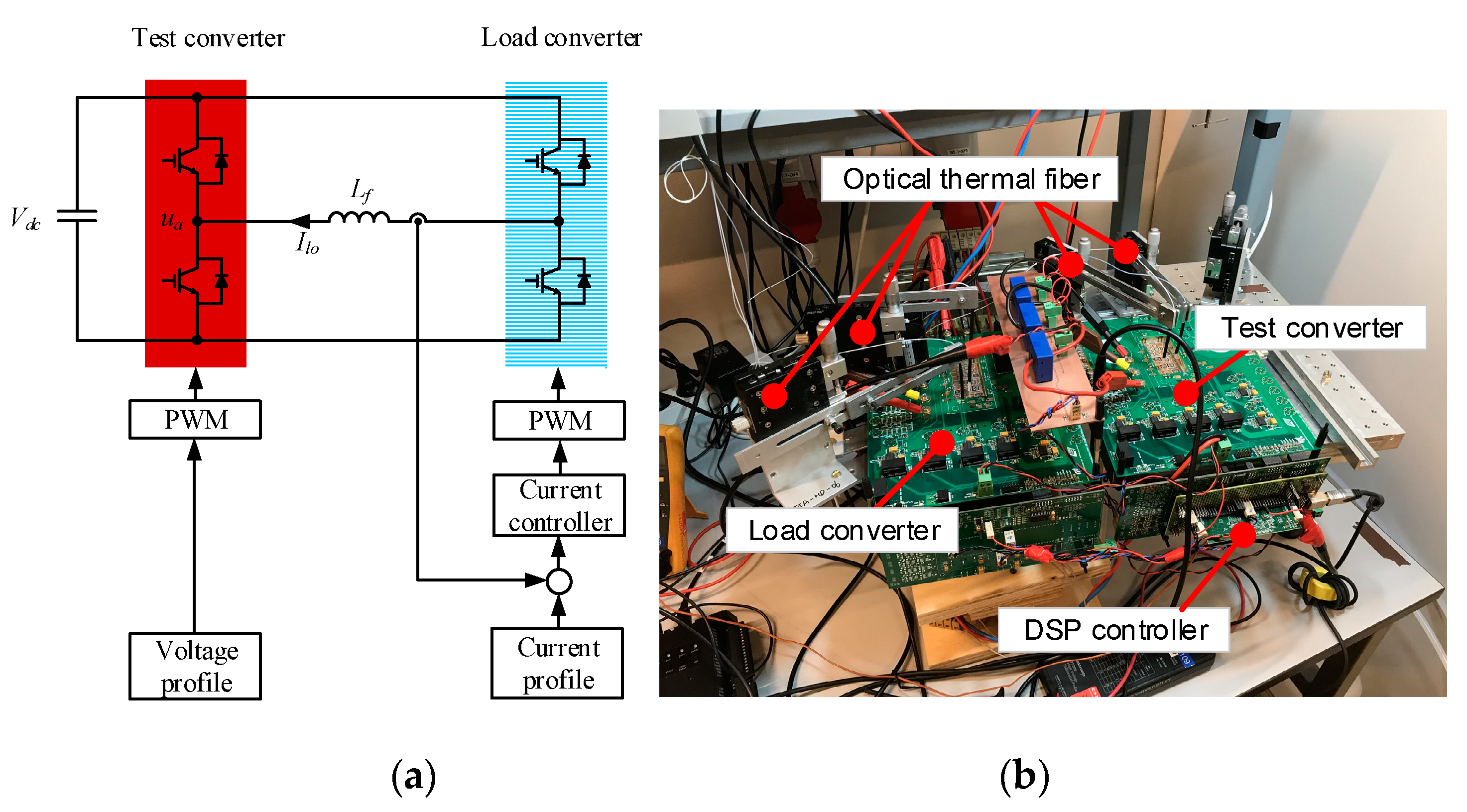
4.2. Simulation and Experimental Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blaabjerg, F.; Ma, K. Future on Power Electronics for Wind Turbine Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 139–152. [Google Scholar] [CrossRef]
- Wang, H.; Liserre, M.; Blaabjerg, F.; Rimmen, P.D.P.; Jacobsen, J.B.; Kvisgaard, T.; Landkildehus, J. Transitioning to Physics-of-Failure as a Reliability Driver in Power Electronics. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 2, 97–114. [Google Scholar] [CrossRef]
- Xiong, Y.; Cheng, X.; Shen, Z.; Mi, C.; Wu, H.; Garg, V. Prognostic and Warning System for Power-Electronic Modules in Electric, Hybrid Electric, and Fuel-Cell Vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2268–2276. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.T.; Mawby, P.A.; Xiang, D.; Ran, L.; Tavner, P. An industry based survey of reliability of power electronic converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Ji, B.; Song, X.; Sciberras, E.; Cao, W.; Hu, Y.; Pickert, V. Multi-objective design optimization of IGBT power modules considering power cycling and thermal cycling. IEEE Trans. Power Electron. 2015, 30, 2493–2504. [Google Scholar] [CrossRef] [Green Version]
- Gopireddy, L.R.; Tolbert, L.M.; Ozpineci, B. Power Cycle Testing of Power Switches: A Literature Survey. IEEE Trans. Power Electron. 2014, 30, 1. [Google Scholar] [CrossRef]
- Luo, H.; Iannuzzo, F.; Blaabjerg, F.; Turnaturi, M.; Mattiuzzo, E. Aging precursors and degradation effects of SiC-MOSFET modules under highly accelerated power cycling conditions. In Proceedings of the IEEE ECCE 2017, Cincinnati, OH, USA, 1–5 October 2017; pp. 2506–2511. [Google Scholar]
- Choi, U.-M.; Joergensen, S.; Blaabjerg, F. Advanced Accelerated Power Cycling Test for Reliability Investigation of Power Device Modules. IEEE Trans. Power Electron. 2016, 31, 8371–8386. [Google Scholar] [CrossRef]
- Czerny, B.; Lederer, M.; Nagl, B.; Trnka, A.; Khatibi, G.; Thoben, M. Thermo-mechanical analysis of bonding wires in IGBT modules under operating conditions. Microelectron. Reliab. 2012, 52, 2353–2357. [Google Scholar] [CrossRef]
- Wei, L.; Lukaszewski, R.; Lipo, T. Analysis of Power-Cycling Capability of IGBT Modules in a Conventional Matrix Converter. IEEE Trans. Ind. Appl. 2009, 45, 1443–1451. [Google Scholar]
- Oates, C. Accelerated life testing of a traction inverter. Power Eng. J. 1999, 13, 263–271. [Google Scholar] [CrossRef]
- Song, Y.; Cheng, R.; Ma, K. A Mission Profile Emulator for Permanent Magnet Synchronous Machine Drive System Based on Single-Phase H-Bridge Circuit. In Proceedings of the IEEE ECCE 2018, Portland, OR, USA, 23–27 September 2018; pp. 4972–4978. [Google Scholar]
- Ko, Y.; Andresen, M.; Buticchi, G.; Liserre, M. Thermally Compensated Discontinuous Modulation Strategy for Cascaded H-Bridge Converters. IEEE Trans. Power Electron. 2018, 33, 2704–2713. [Google Scholar] [CrossRef]
- Broeck, C.V.D.; Zeng, H.; Lorenz, R.D.; Doncker, R.W.D. A test bench for thermal characterization of IGBT power modules over mission profiles. In Proceedings of the PCIM Europe 2018, Nuremberg, Germany, 5–7 June 2018; pp. 1–8. [Google Scholar]
- Lai, W.; Chen, M.; Ran, L.; Alatise, O.; Xu, S.; Mawby, P. mLow dT stress cycle effect in IGBT power module die-attach lifetime modeling. IEEE Trans. Power Electron. 2018, 31, 6575–6585. [Google Scholar] [CrossRef]
- Hung, T.-Y.; Liao, L.-L.; Wang, C.C.; Chi, W.H.; Chiang, K.-N. Life Prediction of High-Cycle Fatigue in Aluminum Bonding Wires Under Power Cycling Test. IEEE Trans. Device Mater. Reliab. 2013, 14, 484–492. [Google Scholar] [CrossRef]
- Ghirmire, P.; Beczkowski, S.; Munk-Neilson, S.; Rannestad, B.; Thogersen, P.B. A review on real time physical measurement techniques and their attempt to predict wear-out status of IGBT. In Proceedings of the EPE 2013, Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Zhou, D.; Song, Y.; Blaabjerg, F. Thermal stress mapping of power semiconductors in H-bridge test bench. In Proceedings of the IEEE CPE-PWERENG 2019, Sonderborg, Denmark, 23–25 April 2019; pp. 1–6. [Google Scholar]
- Wintrich, A.; Ulrich, N.; Werner, T.; Reimann, T. Application Manual Power Semiconductors; Semikron: Nuremberg, Germany, 2015. [Google Scholar]
- Backlund, B.; Schnell, R.; Schlapbach, U.; Fischer, R.; Tsyplakov, E. Applying IGBTs; ABB. Semiconductors: Lenzburg, Switzerland, 2007. [Google Scholar]
- Zhou, D.; Blaabjerg, F.; Gae, F.B. Optimized Demagnetizing Control of DFIG Power Converter for Reduced Thermal Stress during Symmetrical Grid Fault. IEEE Trans. Power Electron. 2018, 33, 10326–10340. [Google Scholar] [CrossRef]
- Zhou, D.; Blaabjerg, F.; Lau, M.; Tonnes, M. Optimized Reactive Power Flow of DFIG Power Converters for Better Reliability Performance Considering Grid Codes. IEEE Trans. Ind. Electron. 2014, 62, 1552–1562. [Google Scholar] [CrossRef]
- Infineon IGBT Power Module FP50R12KT4. Available online: https://www.infineon.com/cms/en/product/power/igbt/igbt-modules/fp50r12kt4/ (accessed on 1 April 2020).
- PLECS User Manual. Available online: https://www.plexim.com/sites/default/files/plecsmanual.pdf/ (accessed on 1 April 2020).
- TI Application Note, TMS320F2833x Digital Signal Controllers. Available online: http://www.ti.com/lit/ds/symlink/tms320f28335.pdf/ (accessed on 1 April 2020).
- OTG-F Fiber Optic Temperature Sensor. Available online: https://opsens-solutions.com/products/fiber-optic-temperature-sensors/otg-f// (accessed on 1 April 2020).


| Rating of Power Device | 1200 V/50 A |
| Filter inductor Lf | 300 μH |
| DC-link voltage Vdc | 400 V |
| Rated power factor PF | −1 |
| Rated peak current Ilo | 20 A |
| Rated fundamental frequency f1 | 10 Hz |
| Rated switching frequency fsw | 10 kHz |
| IGBT | Diode | ||
|---|---|---|---|
| Loss model | VCE @ 50 A, Tj = 150 °C (V) | 2.25 | / |
| VF @ 50 A, Tj = 150 °C (V) | / | 1.65 | |
| Eon @ 50 A, Tj = 150 °C (mJ) | 7.7 | / | |
| Eoff @ 50 A, Tj = 150 °C (mJ) | 4.8 | / | |
| Err @ 50 A, Tj = 150 °C (mJ) | / | 3.7 | |
| Thermal model | Fourth order thermal resistance Rth (°C/kW) | 0.0324 | 0.0486 |
| 0.1782 | 0.2673 | ||
| 0.1728 | 0.2592 | ||
| 0.1566 | 0.2349 | ||
| Fourth order thermal time constant τth (s) | 0.01 | 0.01 | |
| 0.02 | 0.02 | ||
| 0.05 | 0.05 | ||
| 0.1 | 0.1 |
| IGBT | Diode | ||||||
|---|---|---|---|---|---|---|---|
| Sim. | Exp. | Error | Sim. | Exp. | Error | ||
| Inverter mode | Junction temperature swing (°C) | 53.8~67.7 | 43.9~46.9 | / | 50.1~56.1 | 40.8~41.3 | / |
| Mean temperature (°C) | 60.8 | 45.4 | 15.4 | 53.1 | 41.1 | 12.0 | |
| Temperature deviation (°C) | 13.9 | 3.0 | 10.9 | 6.0 | 0.5 | 5.5 | |
| Rectifier mode | Junction temperature swing (°C) | 52.2~60.2 | 42.8~45.2 | / | 53.0~63.5 | 41.2~42.2 | / |
| Mean temperature (°C) | 57.2 | 44.0 | 13.2 | 58.3 | 41.7 | 16.6 | |
| Temperature deviation (°C) | 10.0 | 2.4 | 7.6 | 10.5 | 1.0 | 9.5 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Peng, Y.; Iannuzzo, F.; Hartmann, M.; Blaabjerg, F. Thermal Mapping of Power Semiconductors in H-Bridge Circuit. Appl. Sci. 2020, 10, 4340. https://doi.org/10.3390/app10124340
Zhou D, Peng Y, Iannuzzo F, Hartmann M, Blaabjerg F. Thermal Mapping of Power Semiconductors in H-Bridge Circuit. Applied Sciences. 2020; 10(12):4340. https://doi.org/10.3390/app10124340
Chicago/Turabian StyleZhou, Dao, Yingzhou Peng, Francesco Iannuzzo, Michael Hartmann, and Frede Blaabjerg. 2020. "Thermal Mapping of Power Semiconductors in H-Bridge Circuit" Applied Sciences 10, no. 12: 4340. https://doi.org/10.3390/app10124340
APA StyleZhou, D., Peng, Y., Iannuzzo, F., Hartmann, M., & Blaabjerg, F. (2020). Thermal Mapping of Power Semiconductors in H-Bridge Circuit. Applied Sciences, 10(12), 4340. https://doi.org/10.3390/app10124340








