A Simplified Method for Real-Time Prediction of Temperature in Mass Concrete at Early Age

Featured Application

An early warning system for maximum concrete temperature control was established based on the temperature forecasting method in this paper and the real-time monitoring system for the Baihetan arch dam and Wudongde arch dam.

Abstract

According to the practice of temperature control in dam concrete, within a few days after a concrete block is poured, the temperature at the core of the concrete rises rapidly. The maximum temperature may still exceed the standard even under a relatively perfect post-cooling system, which is mostly caused by failure to quickly and correctly judge the development of the early-age temperature. This study investigates concrete temperature at an early age via in situ monitoring data collected from Baihetan arch dam and Wudongde arch dam. A simplified algorithm of temperature prediction is formed, which only considers the heat released by cement hydration and the cooling effect of cooling pipes. The influence of a cooling pipe on the measuring point of the thermometer is investigated, and a simple empirical formula to calculate the cooling effect is obtained. An equation for the rate of hydration temperature rise is achieved by combining measured data and the formula used to calculate the cooling effect. Furthermore, through the explorations of the related data, it is determined that the cement hydration ratio of the two dams is quite low during concreting. On the basis of the data collected from the field, the method to predict temperature proposed in this study is tested and proven.

1. Introduction

With the rapid development of damming technology, the construction scale of concrete dams is also increasing, resulting in higher dam heights, faster construction speeds, and larger volumes of concrete. Owing to the vast quantity of heat released by cement hydration and the poor thermal conductivity of concrete, heat in the core of dam concrete in unlikely to dissipate in time without effective cooling measures, resulting in high thermal stress and even cracks. Temperature control of mass concrete was, is, and remains to be the key concern of concrete dams. Fly ash and superplasticizer are often used to reduce the heat of cement hydration. Limestone fines added as a filler to concrete also effectively suppress the adiabatic temperature rise, but the degree of hydration of the cement is improved owing to related chemical reactions, thus strengthening the concrete [1]. The application of low-heat cement fundamentally reduces the heat of cement hydration; its successful utilization in Hoover dam further promoted the development of low-heat cement concrete [2]. However, a postcooling system is also necessary to prevent thermal cracks. To achieve precise temperature control, an accurate real-time prediction system is needed.

Temperature rises in concrete are caused by the hydration of cementitious materials. Over recent years, many studies were carried out regarding the hydration mechanism and the temperature development of concrete. The adiabatic temperature rise measured by adiabatic calorimetry is a common way of reflecting the heat-release process of cement hydration; on this basis, many methods for temperature prediction were developed. As a simplified finite difference method proposed in the 1930s, Schmidt’s method mainly considers heat generation and heat transfer of concrete, playing an important role in the era of manual calculation and performing better than the traditional empirical methods [3,4]. However, Schmidt’s method assumes that the thermal conductivity and specific heat of all nodes are the same and constant, which is not consistent with reality. With the development of the finite element method (FEM), the spatial and temporal distributions of a temperature field could be obtained [5,6,7,8,9,10,11,12,13]. Owing to the related properties assigned to each element, the temperature variations of concrete are simulated more accurately using this method, but the more refined the model is, the longer it takes to calculate. In addition, a number of researchers developed a numerical simulation of the exothermic process of cement hydration according to the chemical reaction of each composition [14,15,16,17], with the microstructure model being established based on molecular dynamics to simulate cement hydration in a certain environment [18]. Alongside the progression of experimental methods and the deepening of applicable research, a series of micromonitoring experiments regarding cement hydration were also performed. Combined with the micromonitoring results, changes in cement hydration properties, such as temperature and elastic modulus, were analyzed [19,20,21,22]. The arrival of the information age emphasized the significance of data utilization. Usually, it is suitable for extremely complex problems to find hidden rules in large amounts of data through mathematical statistics or deep learning algorithms, among others. Naturally, data mining technology to predict concrete temperature and other properties was also realized [23,24,25], but was not greatly integrated or developed in terms of engineering practice.

Many predictions were achieved in regard to concrete temperature, however, because the models used in the calculation are often complex and time-consuming, such as using FEM for a comprehensive simulation, it is not easy to make fast, real-time predictions during the process of construction. Via in situ monitoring of the Baihetan arch dam and Wudongde arch dam, this paper studies the relevant data of dam concrete at an early age. With the aim to develop rapid and real-time predictions and to facilitate the verification of the method, this paper directly targets the temperatures at the measuring points of thermometers without considering the temperature distribution of the entire concrete block. A simplified method for predicting the early-age temperature of concrete is formed, only considering the effects of cooling pipes and cement hydration, and the feasibility of this technique is proven. The main impact of the concrete temperature during concreting is determined to be the environment rather than cement hydration, and a real-time forecasting and warning system is established based on the real-time monitoring system of the two dams, thereby successfully providing reference and convenience for the maximum temperature control of dam concrete at an early age.

2. Field Experimental Program

2.1. Materials

Low heat Portland cement with a strength grade of 42.5 was used in both the Baihetan arch dam and Wudongde arch dam. The mixing proportions of concrete of the two dams used in this study are listed in

Table 1. Mixing proportions of the concrete.

Dam	Cement $(\mathrm{kg}/{\mathrm{m}}^3)$	Water $(\mathrm{kg}/{\mathrm{m}}^3)$	Fly Ash $(\mathrm{kg}/{\mathrm{m}}^3)$	Fine Aggregates $(\mathrm{kg}/{\mathrm{m}}^3)$	Coarse Aggregates $(\mathrm{kg}/{\mathrm{m}}^3)$
Baihetan	120	85	65	535	1695
Wudongde	108	83	58	574	1740

. There were four gradations of the coarse aggregate, which were divided into 5–20 mm, 20–40mm, 40–80 mm, and 80–120 mm. The material of cooling pipes selected for the two dams was high density polyethylene (HDPE), which possesses high thermal conductivity.

Table 2. Specifications of the cooling pipes.

Cooling Pipe	Inner Diameter (mm)	Wall Thickness (mm)	Outer Diameter (mm)
Main pipe	32.6	3.7	40
Branch pipe	28	2	32

shows the specifications of the cooling pipes.

2.2. Layout of Cooling Pipes and Thermometers

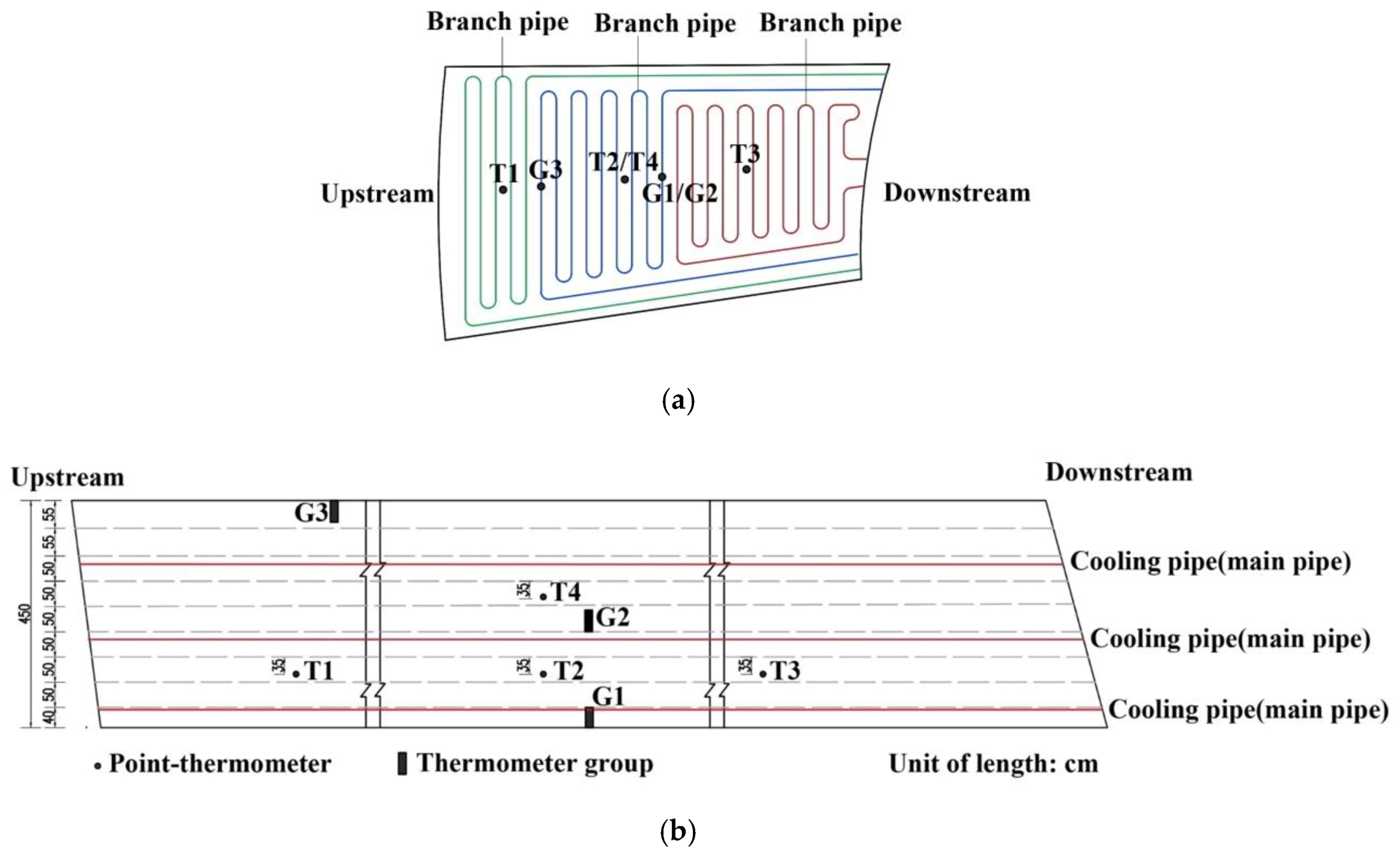
The cooling pipes of the two dams were arranged in the same way, with each main pipe connected to two or three branches outside the dam, and the branch pipe was arranged in a serpentine shape, as shown in Figure 1a. The length of each branch pipe was similar and not more than 300 m, and the layouts were mainly 1.5 m (vertical) × 1.5 m (horizontal). This paper only investigates this situation. The cooling pipes were buried in concrete pouring layers, as shown in Figure 1b. The water flow rate and temperature of each main pipe were monitored, but the data concerning each branch pipe were not collected. Figure 1 shows the locations of four point-thermometers (T1–T4) used to monitor the temperature of the concrete in the middle of the two layers of cooling pipes, with different thermometers corresponding to different branches. A digital temperature sensor (DS18B20) was used for each point-thermometer with an accuracy of ±0.3 °C. Data were uploaded to the database automatically with an acquisition frequency of 3 hours.

A dense array of platinum resistance thermometers (PT1000) with a precision of ±0.1 °C was designed to explore the influence of the heat exchange between the concrete boundary and the external environment on the internal temperature. Data were uploaded to the database automatically with an acquisition frequency of 5 min. Figure 2a illustrates the arrangement of the five sensors in a string of thermometers, with each thermometer placed in the precast concrete column according to the arrangement shown in Figure 2b. Three groups of thermometer strings (G1–G3), as mentioned above, were used to test the temperature distribution near the surface, interior, and bottom of the concrete. The buried positions of each thermometer string are shown in Figure 1. Thermometer string G1 was located at the bottom of the concrete pouring block, in which the first thermometer was placed on the bottom, and the last thermometer was close to the first layer of the cooling pipe. Thermometer string G2 was located in the fifth pouring layer, in which the first thermometer was close to the second layer of the cooling pipe. Thermometer string G3 was located in the ninth pouring layer, in which the first thermometer was 5 cm away from the surface of the concrete pouring block.

3. Components of the Predictive Formula

3.1. Effect of Cooling Pipes

Owing to the point-thermometers located in the middle of the two layers of cooling pipes, the cooling effects of the upper and lower cooling pipes at the measuring point of the thermometer were reflected by related data. Therefore, the data at a later age were suitable for this study, with the rate of hydration being very slow during this period and the temperature decreases inside the concrete almost definitely caused by the cooling pipes. According to practical experience, when the difference between the temperatures of the concrete and the water is large, the cooling effect is more obvious; the same is true for the water flow rate. However, when the flow rate increases to a certain point, the increasing rate of the cooling effect slows down as the flow rate increases [26].

The factors that affect cooling also include the material, section size, length, and spacing of the cooling pipes [26,27,28,29,30]. Because the specifications of the cooling pipes were determined and the length of the cooling pipes in the Baihetan and Wudongde dams were required to be as similar as possible, the impacts mentioned above are not considered in this study for simplification reasons. According to the analysis above, Equation (1) was established to reflect the cooling effect of the upper or lower cooling pipe on the thermometer located in the middle of the two layers of pipes, and the least square fitting method was used to calculate the parameters based on the field data.

$$\Delta {\mathrm{T}}_{\mathrm{w}}={\mathrm{p}}_1\times \left({\mathrm{T}}_{\mathrm{c}}-{\mathrm{T}}_{\mathrm{w}}\right)\times \frac{\mathrm{q}}{{\mathrm{p}}_2+\mathrm{q}}\times \Delta \mathrm{t},$$

(1)

where $\Delta {\mathrm{T}}_{\mathrm{w}}$ is the temperature falling caused by cooling pipe during the time of $\Delta \mathrm{t}(°\mathrm{C})$; ${\mathrm{T}}_{\mathrm{c}}$is the concrete temperature at the beginning of the time period $\Delta \mathrm{t}(°\mathrm{C})$; ${\mathrm{T}}_{\mathrm{w}}$ is the average temperature of the cooling water at the inlet of the cooling pipe during the time period $\Delta \mathrm{t}(°\mathrm{C})$, which was measured by the thermometer located inside the cooling pipe; q is the average flow rate of the cooling water during the time period $\Delta \mathrm{t}$(L/min); and ${\mathrm{p}}_1$ and ${\mathrm{p}}_2$ are parameters to be determined. The time represented by $\Delta \mathrm{t}$ is either one or two days herein. The data of each branch pipe were unable to be obtained; therefore, for the point-thermometers located in the same pouring layer and between the same main pipes, the average values of these thermometer readings were used to fit the data. The superposition of the cooling effect of the upper and lower cooling pipes was taken into account in the fitting procedure.

The parameter values are listed in

Table 3. Parameter values in Equation (1).

Dam	${\mathrm{p}}_1$	${\mathrm{p}}_2$
Baihetan	−0.0156	21.5197
Wudongde	−0.0268	15.6441

, which were obtained by fitting according to the data of the two dams. The fitted results and measured values are depicted in Figure 3. From the comparison, the fitting results of the formula were in good agreement with the measured values. In addition to the systematic error, some results with relatively large differences from the actual values may have resulted from uneven distribution of flow from the main pipes to the branch pipes. Further, the cooling effect of the Baihetan dam was relatively weaker than that of the Wudongde dam according to Equation (1) and the parameter values of the two dams, as listed in Table 3, owing to the Baihetan dam being thicker than the Wudongde dam.

3.2. Effect of Outside Environment and Old Concrete Blocks

Concrete pouring blocks are much smaller in height than they are in length and width, and the point-thermometers are far away from the upstream and downstream surfaces and the transverse joints. Therefore, their influence is not considered at an early age in this study. Three groups of thermometer strings (G1–G3), as shown in Figure 1, were used to explore the temperature distribution near the top and bottom surface and interior of the concrete block. Data regarding all the point-thermometers and thermometer strings are presented in Figure 4.

Combining the positions of the thermometers shown in Figure 1 and the temperature distribution depicted in Figure 4, the fifth temperature sensor in the G1 thermometer string (G1–5) was found to be close to the cooling pipe and was significantly affected by the cooling water, with the data proving obviously different from the other thermometers. Thermometers in G1 were affected by the cooling pipe and heat transfer from the old concrete pouring block; the closer the thermometer was to the cooling pipe, the greater the influence of the cooling water and the less influence the old concrete demonstrated. The temperatures of the point-thermometers (T1–T3) showed a completely different trend from G1, and the three point-thermometers (T1–T3) and G1 were blocked by the first layer of the cooling pipe. Hence, it was determined that the old concrete block had no obvious influence on the internal temperature of the new concrete block at an early age. According to the data from G2, G3, T4, and the air temperature, the surface temperature of the concrete was obviously affected by ambient temperature, with the effect decreasing with increasing depth. G3–5 was 45 cm away from the surface, and its fluctuation with ambient temperature was weak. G2 and T4 were located between the second and third layers of cooling pipes, which were mainly affected by the cooling pipes shown in Figure 4, but not by ambient temperature, as the poor thermal conductivity of concrete and cooling pipes plays an important role in regulating concrete temperature.

For concrete, cooling pipes are regarded as a negative heat source, and affect the upper and lower parts of concrete. In the short term, the depth and range of heat transfer of air temperature through the concrete surface are limited. Therefore, for this simplified method of predicting the early-age temperature of concrete, it is feasible to not consider the effect of air temperature and old concrete blocks. Therefore, the prediction model can be simplified into two parts, namely temperature rise caused by cement hydration and the cooling effect of the cooling pipes.

3.3. Temperature Rise Caused by Hydration

Temperature rise caused by cement hydration is often expressed by an adiabatic temperature rise formula, which is commonly used in exponential, composite exponential, and hyperbolic forms, only considering the age of concrete. In fact, the rate of the hydration reaction is also related to the concrete temperature and its own cumulative hydration degree [31,32,33]. Moreover, the values tested in the field and in a laboratory are different. To reflect reality, the rate of hydration temperature rise in each period was determined via in situ monitoring. The formula of hydration temperature rise is represented in Equation (2), and the least square fitting method was used to calculate the parameters. The hydration temperature rise in each period was determined by combining the measured data and Equation (1).

$$\Delta {\mathrm{T}}_{\mathrm{c}}={\mathrm{m}}_1\times \exp \left[-{\mathsf{\tau }}^{{\mathrm{m}}_2}\right]\times {\mathsf{\tau }}^{{\mathrm{m}}_3}\times {\mathrm{T}}_{\mathrm{c}}{}^{{\mathrm{m}}_4}\times \Delta \mathrm{t},$$

(2)

where $\Delta {\mathrm{T}}_{\mathrm{c}}$ is the hydration temperature rise during the time of $\Delta \mathrm{t}(°\mathrm{C})$; ${\mathrm{T}}_{\mathrm{c}}$is the temperature of concrete at the beginning of the time $\Delta \mathrm{t}(°\mathrm{C})$; $\mathsf{\tau }$ is the age of concrete at the beginning of the time $\Delta \mathrm{t}\left(\mathrm{day}\right)$; and ${\mathrm{m}}_1,{\mathrm{m}}_2,{\mathrm{m}}_3$, and ${\mathrm{m}}_4$ are parameters to be determined.

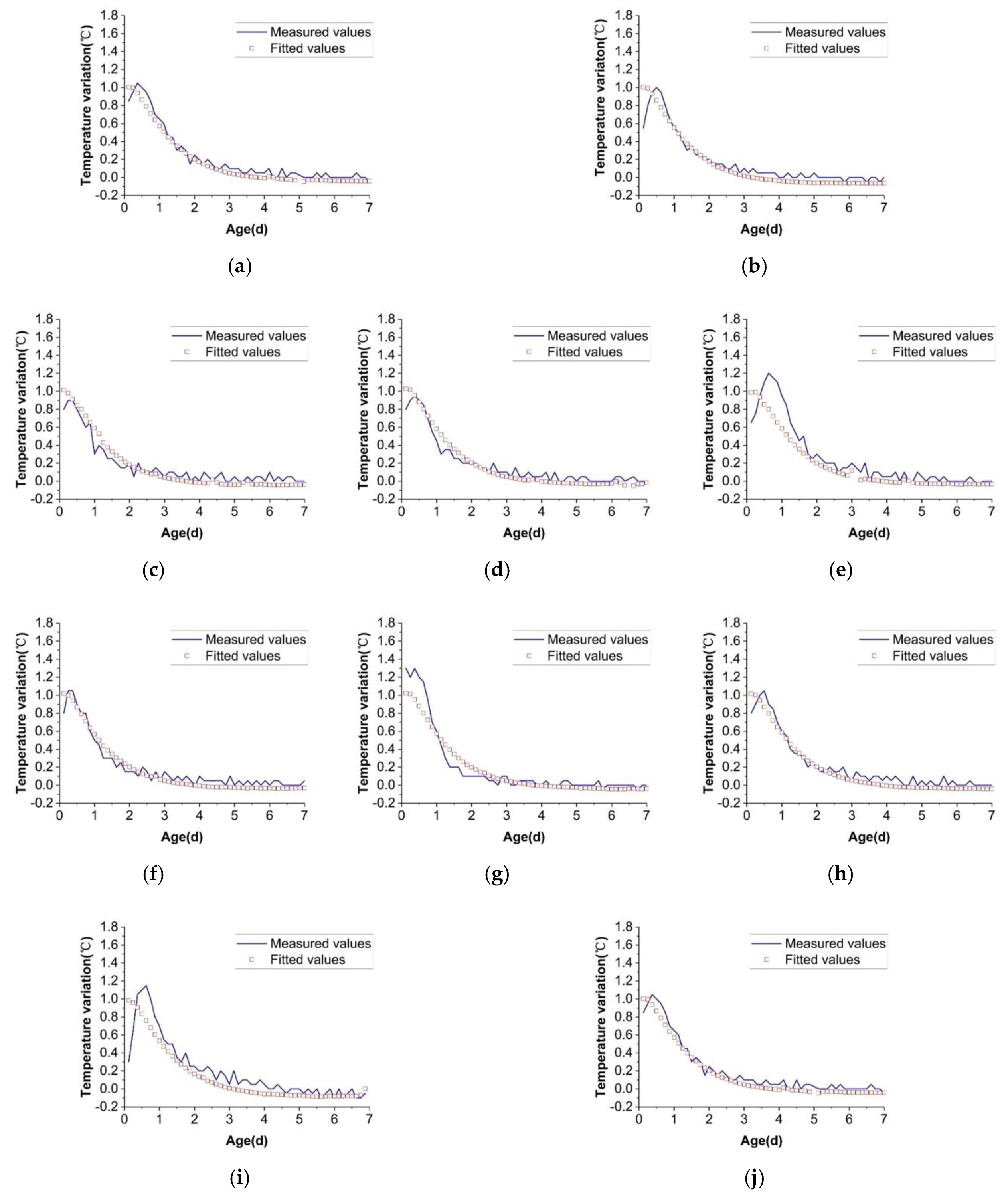
Data regarding 14 concrete blocks were selected from each of the two dams, 10 of which were used for fitting and the remaining 4 were used to verify the accuracy of the prediction method. The parameter values were obtained and are listed in

Table 4. Parameter values in Equation (2).

Dam	${\mathrm{m}}_1$	${\mathrm{m}}_2$	${\mathrm{m}}_3$	${\mathrm{m}}_4$
Baihetan	9.3748	1.0106	0.2259	0.1382
Wudongde	9.1067	1.0401	0.1483	0.1160

. Comparisons between fitted results and measured values for the Baihetan dam and the Wudongde dam are drawn in Figure 5 and Figure 6, respectively. The fitted and measured values generally agreed well with each other, but larger deviations were observed at the beginning when the pouring process was generally unfinished or had just been completed.

4. Results and Discussions

4.1. Accuracy of Prediction Formula

On the basis of Equation (1) and Equation (2), Equation (3) can be formed for predictive purposes.

$${\mathrm{T}}_{\mathrm{p}}={\mathrm{T}}_{\mathrm{c}}+\Delta {\mathrm{T}}_{\mathrm{c}}+\Delta {\mathrm{T}}_{\mathrm{w}1}+\Delta {\mathrm{T}}_{\mathrm{w}2},$$

(3)

where ${\mathrm{T}}_{\mathrm{p}}$ is the predicted value of the concrete temperature at the end of the time period $\Delta \mathrm{t}(°\mathrm{C})$; ${\mathrm{T}}_{\mathrm{c}}$is temperature of concrete at the beginning of the time period $\Delta \mathrm{t}(°\mathrm{C})$; $\Delta {\mathrm{T}}_{\mathrm{c}}$ is the temperature rise caused by hydration during the time period $\Delta \mathrm{t}(°\mathrm{C})$; and $\Delta {\mathrm{T}}_{\mathrm{w}1}$ and $\Delta {\mathrm{T}}_{\mathrm{w}2}$ are the temperature fallings caused by the upper and lower cooling pipes, respectively, during the time period $\Delta \mathrm{t}(°\mathrm{C})$.

In light of the in situ monitoring data collected from main pipe (1) and G1, as shown in Figure 4, after the start of water supply, the time for each thermometer in G1 affected by the cooling pipe decreased as distance increased, and the response time of the cooling effect of the thermometers located in the middle of the two cooling pipes with a vertical space of 1.5 m was about 3 h. Therefore, the temperature at 3 h after the current time could be calculated using the cooling water data within the last 3 h. To verify the accuracy of the prediction model, the actual cooling water data were regarded as known variables. Using the data of the remaining four concrete blocks from the two dams, temperatures at 3 and 12 h were calculated and compared with the measured values, as depicted in Figure 7 and Figure 8. Equation (2) takes into account the influence of concrete temperature, therefore, the method of superimposing the calculation according to the time period was used to reduce the error caused by excessive change in the temperature of the concrete during the calculation period. The temperature was predicted after 12 h by splitting 12 h into four 3 h parts, that is, the procedure to predict the temperature was repeated four times every 3 hours, with the results of the previous prediction used in the next calculation.

As seen from Figure 7 and Figure 8, the accuracy of this method was desirable to some extent, and the predicted values were generally in good agreement with the actual values. The overall precision of predicting the temperature every 3 h was higher than using a single 12 h block. Usually, at the beginning, when the pouring was not or had just been completed, large discrepancies appeared under the influence of various factors. Meanwhile, because the water flow from one main pipe allocated to each branch may not be similar and only data from the main pipes were obtained, error occurred. The prediction algorithm also relies on real-time, updated data, so data interruptions or lagging had the potential to increase the prediction error.

The calculation processes ran in the system constantly. Owing to the time intervals of the data used for the fitting generally being 3 h, if the temperature after a longer period of time was forecasted using this model, larger deviations could have appeared owing to failure to obtain accurate data from the cooling water or the accumulation of prediction errors over long periods. In this case, the time interval of the original data could be adjusted to achieve the corresponding purpose.

4.2. Analysis of Concrete Temperature Changes during the Pouring Process

Owing to large forecasting errors existing in the initial stage, it was necessary to explore the main factors affecting the concrete temperature during this period. Data regarding the pouring temperature and placement temperature of the concrete were analyzed. In this study, the pouring temperature was the concrete temperature at 10 cm below the concrete surface after the concrete was put down and before vibration, whereas the placement temperature was the concrete temperature at 10 cm below the concrete surface after the concrete was vibrated and before the new concrete was covered. The first records regarding thirteen point-thermometers and the average pouring temperature and placement temperature in the same concrete layer are presented in Figure 9, showing that the initial records of the point-thermometers were basically between the pouring temperature and placement temperature. This indicated that the initial recording time of the point-thermometer was usually after the concrete was put down and before it was vibrated. Figure 9 also shows that the placement temperature was higher than the pouring temperature; the difference between these two temperatures was named the pouring temperature rise (PTR). The magnitude of the PTR may be related to both the environment and the hydration heat of concrete, and the duration of the heat exchange between the concrete and the external environment was related to the construction speed. However, the construction speed fluctuated within a certain range; under this condition, the main influencing factors of the PTR could be obtained based on a large amount of data.

This study collected all relevant data from the Baihetan and Wudongde dams since construction started. The relationship between the PTR and the difference between air temperature and pouring temperature (DAP) is plotted in Figure 10, showing that the relationships for both dams are basically linear, thereby verifying the previous speculation of the influence of ambient temperature. Meanwhile, Figure 10 displays the trend line of each month, and the slopes of these trend lines are also plotted in Figure 11.

Figure 10a and Figure 11a show that the slope of the trend line for each month for Baihetan dam is divided into two sides. The slopes of the trend lines from April to September are relatively small, but are larger from October to March of the following year, following the variation law of hot and cold seasons. Figure 11a presents the monthly averages of the related temperature data during the concreting of Baihetan dam, showing that the pouring temperature of Baihetan dam was strictly controlled according to the season. From April to September, pouring temperature was low and air temperature was high; consequently, PTR was large, but the slope of the trend line was relatively small. This situation was reversed from October to March of the following year. Compared with Baihetan dam, the relevant data of Wudongde dam are irregular, as shown in Figure 10b and Figure 11b; the pouring temperature of Wudongde dam was not strictly controlled according to the season, and the slopes of the trend lines do not change according to season. Ultimately, no correlation between the slope of the trend line and pouring temperature was observed.

Through comparison, the influence of the hydration heat of cement was ruled out. During this period, the hydration rate was still slow and made few contributions to PTR, thus, the large error during this period did not affect the later prediction. Therefore, it was determined that the main factors affecting the slope of the trend line (the change rate of PTR with DAP) during the concrete pouring period included the effect of cooling measures, such as a spray cooling system. The Baihetan and Wudongde projects maintain spraying cooling systems throughout the year. Wind speed also affects the spraying system, an area that requires further study.

5. Conclusions

On the basis of in situ monitoring data, the development of concrete temperature at an early age was studied and a simplified method for real-time prediction of early-age temperature was obtained. The relevant conclusions are summarized as follows:

(1) At an early age, the external environment and old concrete blocks demonstrated no obvious influences on the internal temperature of new concrete. The heat released by cement hydration and a postcooling system were found to be the main factors that control the internal temperature development of concrete. For rapid prediction of early-age temperature in mass concrete, it is feasible to only consider the contribution of hydration heat and the cooling effect of cooling pipes on the development of concrete temperature.

(2) Under the same construction background, a linear relationship was observed between PTR (the difference between the placement temperature and the pouring temperature) and DAP (the difference between the air temperature and the pouring temperature) during concrete pouring, and the rate of change of PTR according to DAP is mainly affected by the effect of cooling measures, such as a spray cooling system. The cement hydration rate was found to be quite slow, with few contributions to temperature variation during this stage.

(3) A simple empirical formula for calculating the cooling effect of the cooling pipes was formed, which well reflected the influence of the cooling pipes at the measuring point of the point-thermometer. However, other layouts of cooling pipes were not considered; further research is needed to improve this formula.

(4) Owing to the Baihetan arch dam being thicker than the Wudongde arch dam, successful application of the forecasting method in the two dams and different sized concrete blocks between the two dams indicated that the process of this predictive formula could be used for other, similar projects. This method may be more suitable for larger concrete blocks because the interior of the block is closer to the adiabatic environment. Although it was proven to be a convenient method to achieve real-time temperature warning system predictions, this method still needs to be applied and improved in further practice.