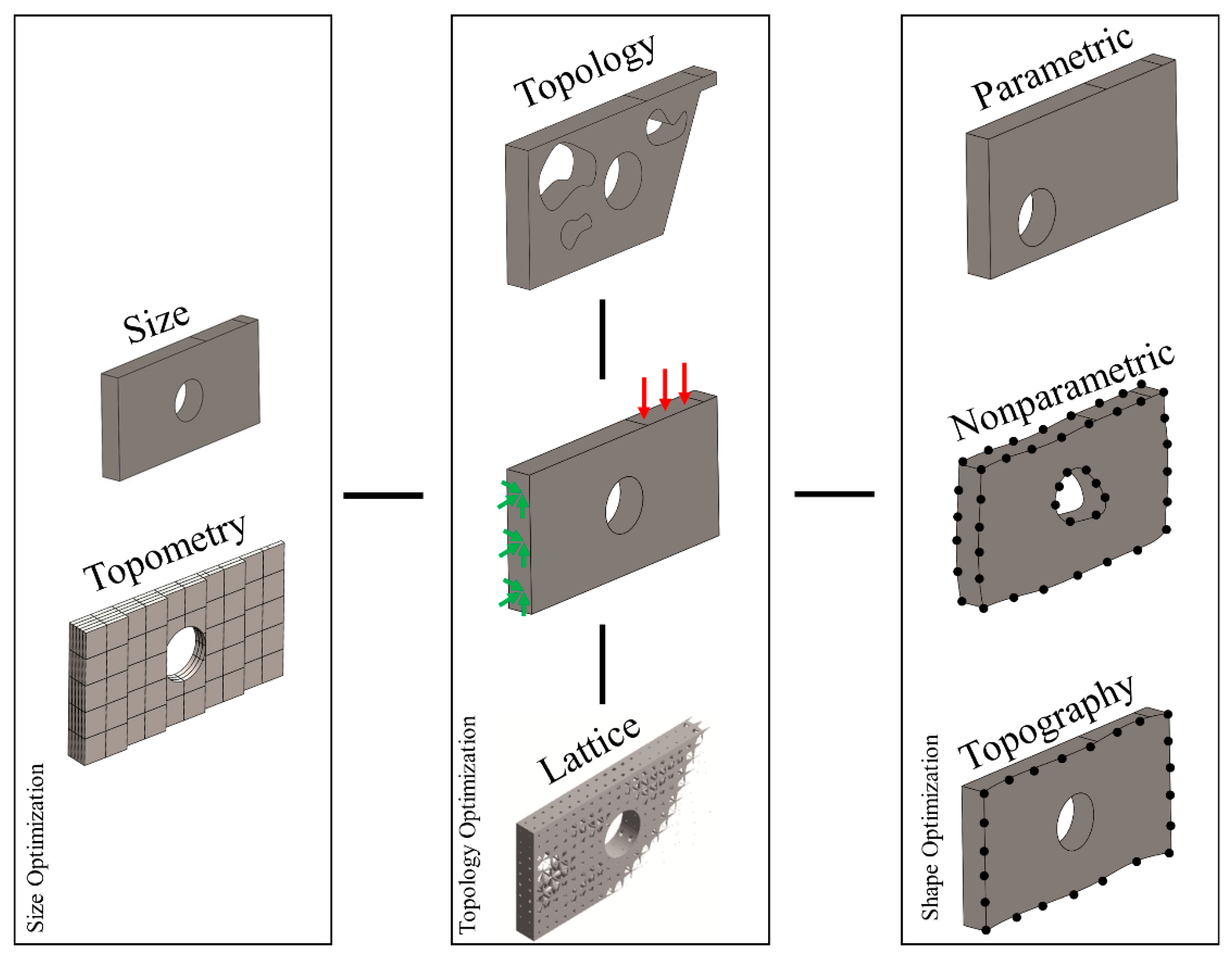
Figure 1.
The different Structural Optimization (SO) types of a Hollow Plate.
Figure 1.
The different Structural Optimization (SO) types of a Hollow Plate.
Figure 2.
The level set function and its domains adapted from Jia, Beom [
20].
Figure 2.
The level set function and its domains adapted from Jia, Beom [
20].
Figure 3.
The ten design processes and their categorization based on the design workflow as well as the production method.
Figure 3.
The ten design processes and their categorization based on the design workflow as well as the production method.
Figure 4.
The experimental design process in ANSYS software.
Figure 4.
The experimental design process in ANSYS software.
Figure 5.
Examples of response surface plots: (a) Response surface plot of a first-order regression model, and (b) response surface plot of a second-order regression model.
Figure 5.
Examples of response surface plots: (a) Response surface plot of a first-order regression model, and (b) response surface plot of a second-order regression model.
Figure 6.
An example of a Latin Hypercube Sampling (LHS) with two factors and both nine design points and factor levels.
Figure 6.
An example of a Latin Hypercube Sampling (LHS) with two factors and both nine design points and factor levels.
Figure 7.
An example of a sensitivity analysis diagram.
Figure 7.
An example of a sensitivity analysis diagram.
Figure 8.
(a) The original design of the Hollow Plate, as well as the finite element model, (b) the Finite Element Analysis (FEA) of the Hollow Plate (σmax = 33.2 MPa), and (c) the design space for the Topology Optimization (TO).
Figure 8.
(a) The original design of the Hollow Plate, as well as the finite element model, (b) the Finite Element Analysis (FEA) of the Hollow Plate (σmax = 33.2 MPa), and (c) the design space for the Topology Optimization (TO).
Figure 9.
The three design processes in the TO workflow: (1) Topology optimization with no redesign (TO_NR), (2) topology optimization with redesign (TO_R), and (3) topology optimization with redesign and parametric shape optimization (TO_R_PO).
Figure 9.
The three design processes in the TO workflow: (1) Topology optimization with no redesign (TO_NR), (2) topology optimization with redesign (TO_R), and (3) topology optimization with redesign and parametric shape optimization (TO_R_PO).
Figure 10.
Unfeasible design solutions: (a) L ≤ 2 × r, (b) L ≤ FA, (c) r ≥ l1 ≥ L − r, (d) H ≤ 2 × r, and (e) r ≥ h1 ≥ H − r.
Figure 10.
Unfeasible design solutions: (a) L ≤ 2 × r, (b) L ≤ FA, (c) r ≥ l1 ≥ L − r, (d) H ≤ 2 × r, and (e) r ≥ h1 ≥ H − r.
Figure 11.
(a) Sensitivity analysis of the Hollow Plate, (b) response surface plot presented the impact of the thickness and length to the mass, and (c) response surface plot showed the effect of the thickness and the radius to the maximum equivalent stress.
Figure 11.
(a) Sensitivity analysis of the Hollow Plate, (b) response surface plot presented the impact of the thickness and length to the mass, and (c) response surface plot showed the effect of the thickness and the radius to the maximum equivalent stress.
Figure 12.
The four design processes in the PO workflow: (4) parametric size/shape optimization (PO), (5) parametric size/shape, and topology optimization with no redesign (PO_TO_NR), (6) parametric size/shape, and topology optimization with redesign (PO_TO_R), and (7) parametric size/shape, topology optimization with redesign, and parametric shape optimization (PO_TO_R_PO).
Figure 12.
The four design processes in the PO workflow: (4) parametric size/shape optimization (PO), (5) parametric size/shape, and topology optimization with no redesign (PO_TO_NR), (6) parametric size/shape, and topology optimization with redesign (PO_TO_R), and (7) parametric size/shape, topology optimization with redesign, and parametric shape optimization (PO_TO_R_PO).
Figure 13.
The optimized design by the PO within the simultaneous PO and TO workflow, as well as its design results: (8) simultaneous parametric size/shape and topology optimization with no redesign (PO + TO_NR), (9) simultaneous parametric size/shape and topology optimization with redesign (PO + TO_R), and (10) simultaneous parametric size/shape and topology optimization with redesign, and parametric shape optimization PO + TO_R_PO.
Figure 13.
The optimized design by the PO within the simultaneous PO and TO workflow, as well as its design results: (8) simultaneous parametric size/shape and topology optimization with no redesign (PO + TO_NR), (9) simultaneous parametric size/shape and topology optimization with redesign (PO + TO_R), and (10) simultaneous parametric size/shape and topology optimization with redesign, and parametric shape optimization PO + TO_R_PO.
Figure 14.
(a) The initial design of the L-Bracket, as well as the finite element model, (b) the FEA of the L-Bracket (σmax = 19.7 MPa), and (c) the design space for the TO.
Figure 14.
(a) The initial design of the L-Bracket, as well as the finite element model, (b) the FEA of the L-Bracket (σmax = 19.7 MPa), and (c) the design space for the TO.
Figure 15.
The design solutions of the L-Bracket.
Figure 15.
The design solutions of the L-Bracket.
Figure 16.
(a) The initial design of the Messerschmitt–Bölkow–Blohm Beam (MBB-Beam), as well as the finite element model, (b) the FEA of the MBB-Beam (σmax = 32.9 MPa), and (c) the design space for the TO.
Figure 16.
(a) The initial design of the Messerschmitt–Bölkow–Blohm Beam (MBB-Beam), as well as the finite element model, (b) the FEA of the MBB-Beam (σmax = 32.9 MPa), and (c) the design space for the TO.
Figure 17.
The design results of the MBB-Beam.
Figure 17.
The design results of the MBB-Beam.
Figure 18.
Presentation of the results clustered in the TO, PO, and PO + TO workflows: (a) Mass, (b) maximum stress, (c) optimization time, and (d) interval plot for the three case studies.
Figure 18.
Presentation of the results clustered in the TO, PO, and PO + TO workflows: (a) Mass, (b) maximum stress, (c) optimization time, and (d) interval plot for the three case studies.
Figure 19.
(a) The mass reduction in TO, PO, and PO + TO workflows, and (b) an illustration of the mass reduction in the three workflows vs. the size and design complexity, as well as typical examples in each workflow.
Figure 19.
(a) The mass reduction in TO, PO, and PO + TO workflows, and (b) an illustration of the mass reduction in the three workflows vs. the size and design complexity, as well as typical examples in each workflow.
Table 1.
The ten implemented design processes, their name, description, and production method.
Table 1.
The ten implemented design processes, their name, description, and production method.
| Design Workflow | Design Process | Description | Production Method |
|---|
| Topology Optimization | (1) TO_NR | topology optimization with no redesign | AM |
| (2) TO_R | topology optimization with redesign | AM + CMP |
| (3) TO_R_PO | topology optimization with redesign and parametric shape optimization | AM + CMP |
| Parametric Optimization | (4) PO | parametric size/shape optimization | AM + CMP |
| (5) PO_TO_NR | parametric size/shape, and topology optimization with no redesign | AM |
| (6) PO_TO_R | parametric size/shape, and topology optimization with redesign | AM + CMP |
| (7) PO_TO_R_PO | parametric size/shape, topology optimization with redesign, and parametric shape optimization | AM + CMP |
| Simultaneous Parametric and Topology Optimization | (8) PO + TO_NR | simultaneous parametric size/shape and topology optimization with no redesign | AM |
| (9) PO + TO_R | simultaneous parametric size/shape and topology optimization with redesign | AM + CMP |
| (10) PO + TO_R_PO | simultaneous parametric size/shape and topology optimization with redesign, and parametric shape optimization | AM + CMP |
Table 2.
The used design parameters (factors) in the optimization of the hollow plate, their description, initial value, allowable range, and value increment (step) in parentheses.
Table 2.
The used design parameters (factors) in the optimization of the hollow plate, their description, initial value, allowable range, and value increment (step) in parentheses.
| Symbol | Description | Initial Value (mm) | Range (Step) (mm) |
|---|
| L | Length | 100 | 50–150 (5) |
| H | Height | 50 | 40–60 (5) |
| t | thickness | 30 | 10–50 (5) |
| r | hole radius | 10 | 5–15 (5) |
| hhp | allowable range for the hole at horizontal direction | 50 | 10%–90% (5) |
| l1 | horizontal distance of the hole | 50 | dependent parameter |
| hvp | allowable range for the hole at vertical direction | 50 | 10–90% (10) |
| h1 | vertical distance of the hole | 25 | dependent parameter |
| FA | Force Area | 30 | 20–40 (5) |
| fcp | allowable range for the force placement | 90 | 10–90% (10) |
| d1 | force placement | 63 | dependent parameter |
Table 3.
The results of all design processes of the Hollow Plate optimization.
Table 3.
The results of all design processes of the Hollow Plate optimization.
| Parameter | Initial | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|
| Mass (g) | 1103.5 | 450.7 | 448.1 | 285.9 | 101.5 | 66.6 | 65.6 | 55.5 | 45.0 | 39.8 | 34.7 |
| Max Stress (MPa) | 34.7 | 120.1 | 60.2 | 109.4 | 55.7 | 94.8 | 106.5 | 115.4 | 75.2 | 115.4 | 114.6 |
| Optimization time (min) | - | 5.5 | 20.1 | 70.4 | 75.9 | 76.9 | 86.8 | 124.7 | 275.5 | 285.5 | 323.4 |
Table 4.
The used design parameters (factors) in the optimization of the L-Bracket, their description, initial value, allowable range, and value increment (step) in parentheses.
Table 4.
The used design parameters (factors) in the optimization of the L-Bracket, their description, initial value, allowable range, and value increment (step) in parentheses.
| Symbol | Description | Initial Value (mm) | Range (Step) (mm) |
|---|
| t1 | thickness 1 | 20 | 10–30 (5) |
| l1 | length 1 | 100 | 50–150 (5) |
| t2 | thickness 2 | 20 | 10–30 (5) |
| l2 | length 2 | 100 | 50–150 (5) |
| w | width | 30 | 10–50 (5) |
| r | Radius of fillet | 5 | 1–19 (1) |
Table 5.
The results of all design processes of the L-Bracket optimization.
Table 5.
The results of all design processes of the L-Bracket optimization.
| Parameter | Initial | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|
| Mass (g) | 849.1 | 344.6 | 343.4 | 318.5 | 71.1 | 65.1 | 63.9 | 55.9 | 28.8 | 27.1 | 23.2 |
| Max Stress (MPa) | 19.7 | 101.0 | 115.4 | 106.4 | 95.9 | 121.0 | 96.3 | 114.0 | 84.3 | 81.8 | 105.6 |
| Optimization time (min) | - | 7.4 | 17.1 | 63.3 | 67.4 | 68 | 73 | 106.7 | 374.6 | 379.6 | 413.2 |
Table 6.
The used design parameters (factors) in the optimization of the MBB-Beam, their description, initial value, allowable range, and value increment (step) in parentheses.
Table 6.
The used design parameters (factors) in the optimization of the MBB-Beam, their description, initial value, allowable range, and value increment (step) in parentheses.
| Symbol | Description | Initial Value (mm) | Range (mm) |
|---|
| L | Length | 100 | 50–150 (5) |
| H | Height | 30 | 10–50 (5) |
| t | thickness | 20 | 10–30 (5) |
| fcp1 | allowable range for the placement of F1 | 60 | 10–90% (10) |
| fcp2 | allowable range for the placement of F1 | 40 | 10–90% (10) |
| d1 | placement of F1 | 30 | dependent parameter |
| d2 | placement of F2 | 70 | dependent parameter |
Table 7.
The results of all design processes of the MBB-Beam optimization.
Table 7.
The results of all design processes of the MBB-Beam optimization.
| Parameter | Initial | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|
| Mass (g) | 471 | 113.9 | 113.6 | 52.8 | 39.3 | 14.9 | 14.7 | 10.6 | 9.9 | 8.9 | 4.2 |
| Max Stress (MPa) | 32.9 | 65.3 | 26.2 | 27.6 | 85.6 | 103.1 | 101.4 | 110.3 | 100.2 | 61.6 | 92.0 |
| Optimization time (min) | - | 3.1 | 22.9 | 64.9 | 65.6 | 66.3 | 81.3 | 114.1 | 167.1 | 182.1 | 214.9 |
Table 8.
An overview of the simulations’ results in the three case studies.
Table 8.
An overview of the simulations’ results in the three case studies.
| Design Workflow | Design Process | Mass | Mass Reduction (g) | Mass Reduction (%) | Mass Reduction Rate (g/min) | Max Stress (MPa) | Time (min) |
|---|
| Hollow Plate |
| | Initial | 1103.5 | | | | | |
| TO | 1 | 450.7 | 652.8 | 59.2% | 118.7 | 120.1 | 5.5 |
| 2 | 448.1 | 655.4 | 59.4% | 32.6 | 60.2 | 20.1 |
| 3 | 285.9 | 817.6 | 74.1% | 11.6 | 109.4 | 70.4 |
| PO | 4 | 101.5 | 1002 | 90.8% | 13.2 | 55.7 | 75.9 |
| 5 | 66.6 | 1036.9 | 94.0% | 13.5 | 94.8 | 76.9 |
| 6 | 65.6 | 1037.9 | 94.1% | 12.0 | 106.5 | 86.8 |
| 7 | 55.5 | 1048 | 95.0% | 8.4 | 115.4 | 124.7 |
| PO + TO | 8 | 45 | 1058.5 | 95.9% | 3.8 | 75.2 | 275.5 |
| 9 | 39.8 | 1063.7 | 96.4% | 3.7 | 115.4 | 285.5 |
| 10 | 34.7 | 1068.8 | 96.9% | 3.3 | 114.6 | 323.4 |
| L-Bracket |
| | Initial | 849.1 | | | | | |
| TO | 1 | 344.6 | 504.5 | 59.4% | 68.2 | 101 | 7.4 |
| 2 | 343.4 | 505.7 | 59.6% | 29.6 | 115.4 | 17.1 |
| 3 | 318.5 | 530.6 | 62.5% | 8.4 | 106.4 | 63.3 |
| PO | 4 | 71.1 | 778 | 91.6% | 11.5 | 95.9 | 67.4 |
| 5 | 65.1 | 784 | 92.3% | 11.5 | 121 | 68 |
| 6 | 63.9 | 785.2 | 92.5% | 10.8 | 96.3 | 73 |
| 7 | 55.9 | 793.2 | 93.4% | 7.4 | 114 | 106.7 |
| PO + TO | 8 | 28.8 | 820.3 | 96.6% | 2.2 | 84.3 | 374.6 |
| 9 | 27.1 | 822 | 96.8% | 2.2 | 81.8 | 379.6 |
| 10 | 23.2 | 825.9 | 97.3% | 2.0 | 105.6 | 413.2 |
| MBB-Beam |
| | Initial | 471 | | | | | |
| TO | 1 | 113.9 | 357.1 | 75.8% | 115.2 | 65.3 | 3.1 |
| 2 | 113.6 | 357.4 | 75.9% | 15.6 | 26.2 | 22.9 |
| 3 | 52.8 | 418.2 | 88.8% | 6.4 | 27.6 | 64.9 |
| PO | 4 | 39.3 | 431.7 | 91.7% | 6.6 | 85.6 | 65.6 |
| 5 | 14.9 | 456.1 | 96.8% | 6.9 | 103.1 | 66.3 |
| 6 | 14.7 | 456.3 | 96.9% | 5.6 | 101.4 | 81.3 |
| 7 | 10.6 | 460.4 | 97.7% | 4.0 | 110.3 | 114.1 |
| PO + TO | 8 | 9.9 | 461.1 | 97.9% | 2.8 | 100.2 | 167.1 |
| 9 | 8.9 | 462.1 | 98.1% | 2.5 | 61.6 | 182.1 |
| 10 | 4.2 | 466.8 | 99.1% | 2.2 | 92 | 214.9 |
Table 9.
The essential statistics of the workflows.
Table 9.
The essential statistics of the workflows.
| Design Workflow | N | Mean | StDev | 95% CI |
|---|
| TO | 9 | 533.3 | 152.8 | (376.7–689.8) |
| PO | 12 | 755.8 | 248.6 | (620.2–891.4) |
| PO + TO | 9 | 783.2 | 261.7 | (626.7–939.8) |