Bearing Capacity of Ring Foundations on Sand Overlying Clay
Abstract
:1. Introduction
2. Problem Definition
3. Finite Element Limit Analysis
4. Comparisons of Previous Studies
4.1. For Circular Footings on Homogeneous Clay
4.2. For Circular Footings on Homogeneous Sand
4.3. For Strip and Circular Footings on Sand Overlying Clay
5. Results and Discussion
5.1. Effect of the Undrained Shear Strength of the Clay (cu/γR0)
5.2. Effect of the Ratio of the Internal Radius to the External Radius of the Footing (Ri/R0)
5.3. Effect of the Thickness of the Sand Layer (H/R0)
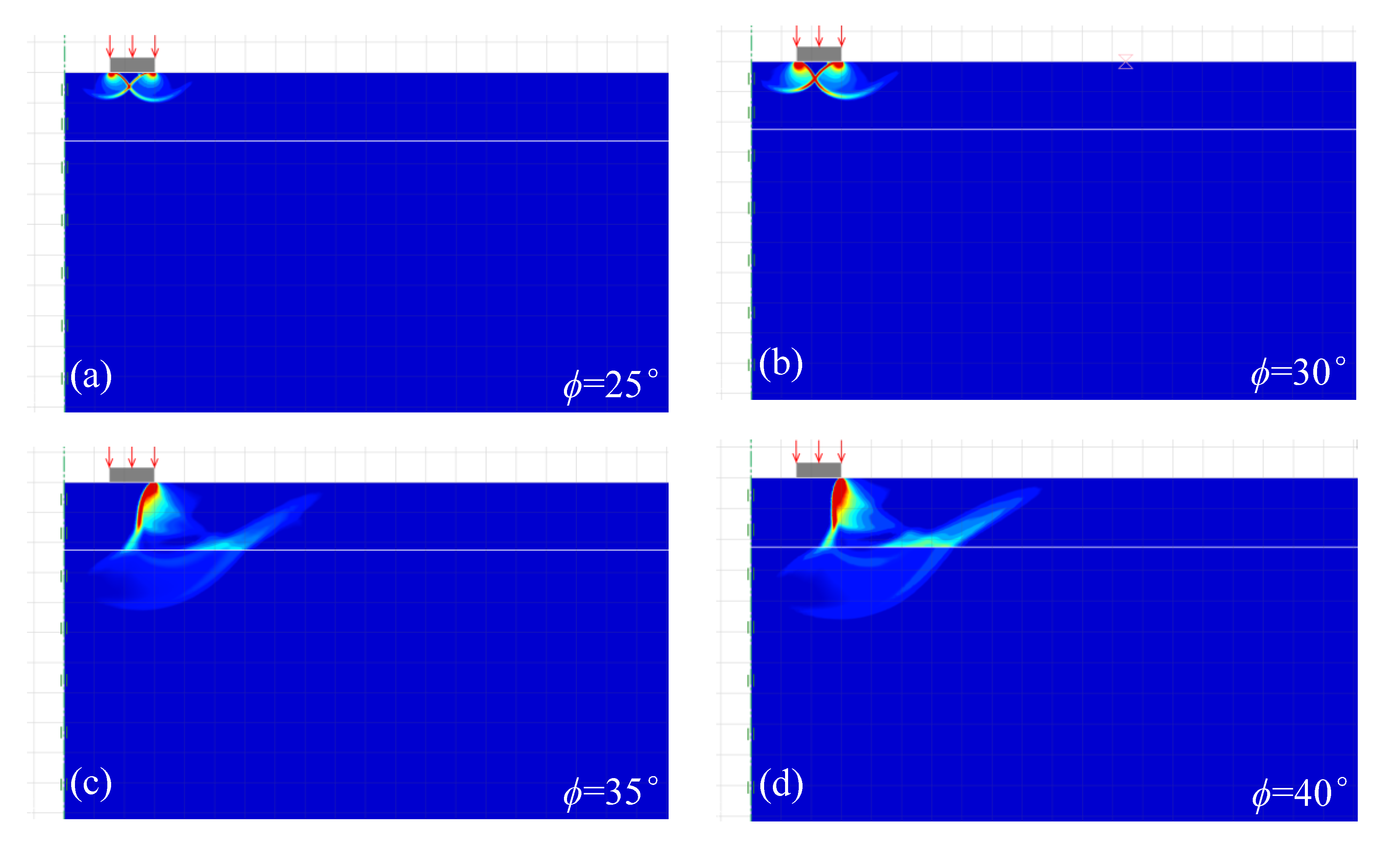
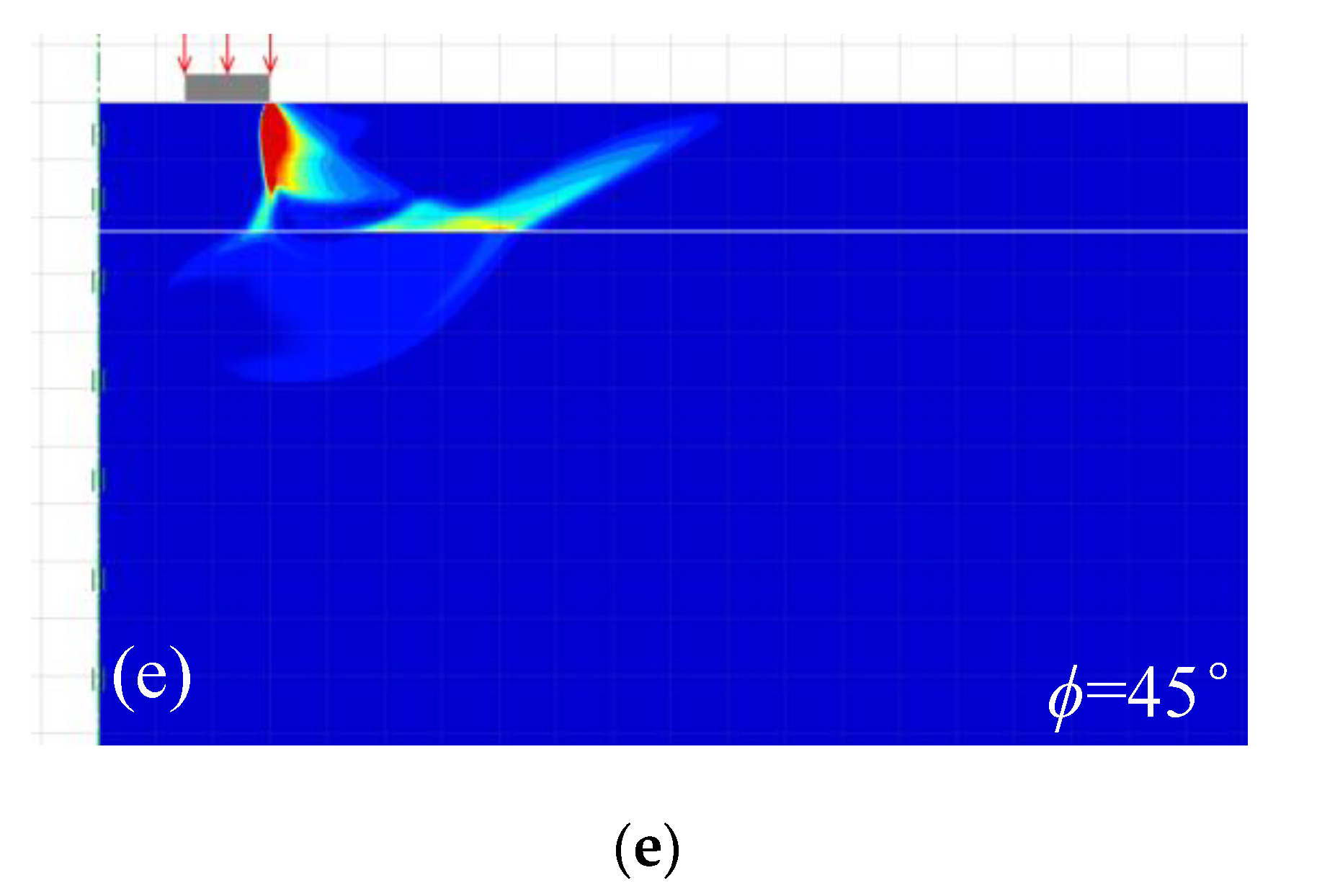
5.4. Failure Mechanisms
6. Conclusions
- (1)
- The bearing capacity reaches a constant value when H/R0 exceeds the critical thickness Hc/R0, which depends on the magnitudes of φ, Ri/R0, and cu/(γR0). In general, the value of Hc/R0 decreases with decreases in φ and increases in Ri/R0 and cu/(γR0). For H/R0 < Hc/R0, the bearing capacity increases continuously with an increase in the value of cu/(γR0), H/R0, and φ.
- (2)
- For H/R0 < Hc/R0, the values of p/(γR0) tend to become maximum corresponding to a certain value of Ri/R0. The magnitude of Ri/R0 for the bearing capacity reaching the maximum value decreases with increasing cu/(γR0), H/R0, and φ. On the other hand, with smaller values of cu/(γR0), H/R0, and φ, the value of p/(γR0) increases continuously with increasing Ri/R0 and decreases continuously with increasing Ri/R0 for larger values of cu/(γR0), H/R0, and φ.
- (3)
- For H/R0 ≥ Hc/R0, the collapse mechanism is confined only within the sand layer, which is similar to the classical shallow footing mechanism. For H/R0 < Hc/R0, the punching shear failure occurs in the sand layer, and the log-spiral rupture lines develop from the clayey strata to the upper sand layer.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Meyerhof, G.G. Some recent research on the bearing capacity of foundations. Can. Geotech. J. 1963, 1, 16–26. [Google Scholar] [CrossRef]
- Hansen, J.B. A Revised and Extended Formula for Bearing Capacity; Bulletin No. 28; Danish Geotechnical Institute: Copenhagen, Denmark, 1970; p. 21. [Google Scholar]
- Vesic, A.S. Analysis of ultimate loads of shallow foundations. J. Soil Mech. Found. Div. 1973, 99, 45–73. [Google Scholar] [CrossRef]
- Shiau, J.S.; Lyamin, A.V.; Sloan, S.W. Bearing capacity of a sand layer on clay by finite element limit analysis. Can. Geotech. 2003, 40, 900–915. [Google Scholar] [CrossRef] [Green Version]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice, 1st ed.; John Wiley and Sons: New York, NY, USA, 1948. [Google Scholar]
- Meyerhof, G.G. Ultimate bearing capacity of footings on sand layer overlying clay. Can. Geotech. J. 1974, 11, 223–229. [Google Scholar] [CrossRef]
- Hanna, A.M.; Meyerhof, G.G. Design charts for ultimate bearing capacity of foundations on sand overlying soft clay. Can. Geotech. J. 1980, 17, 300–303. [Google Scholar] [CrossRef]
- Okamura, M.; Takemura, J.; Kimura, T. Bearing capacity predictions of sand overlying clay based on limit equilibrium methods. Soil Found. 1998, 38, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.K.; Cassidy, M.J.; Randolph, M.F. Bearing capacity on sand overlying clay soils: Experimental and finite-element investigation of potential punch-through failure. Geotechnique 2013, 63, 1271–1284. [Google Scholar] [CrossRef] [Green Version]
- Florkiewicz, A. Upper bound to bearing capacity of layered soils. Can. Geotech. J. 1989, 26, 730–736. [Google Scholar] [CrossRef]
- Michalowski, R.L.; Shi, L. Bearing capacity of footings over two-layer foundation soils. J. Geotech. Eng. 1995, 121, 421–428. [Google Scholar] [CrossRef]
- Huang, M.; Qin, H.L. Upper-bound multi-rigid-block solutions for bearing capacity of two-layered soils. Comput. Geotech. 2009, 36, 525–529. [Google Scholar] [CrossRef]
- Burd, H.J.; Frydman, S. Bearing capacity of plane-strain footings on layered soils. Can. Geotech. J. 1997, 34, 241–253. [Google Scholar] [CrossRef]
- Ornek, M.; Demir, A.; Laman, M.; Yildiz, A. Numerical analysis of circular footings on natural clay stabilized with a granular fill. Acta Geotech. Slov. 2012, 1, 61–75. [Google Scholar]
- Park, J.S.; Park, D. Vertical bearing capacity of bucket foundation in sand overlying clay. Ocean Eng. 2017, 134, 62–76. [Google Scholar] [CrossRef]
- Kumar, J.; Chakraborty, M. Bearing capacity of a circular foundation on layered sand–clay media. Soils Found. 2015, 55, 1058–1068. [Google Scholar] [CrossRef] [Green Version]
- Craig, W.H.; Chua, K. Deep penetration of spud-can foundations on sand and clay. Geotechnique 1990, 40, 541–556. [Google Scholar] [CrossRef]
- Okamura, M.; Takemura, J.; Kimura, T. Centrifuge model tests on bearing capacity and deformation of sand layer overlying clay. Soils Found. 1997, 37, 73–88. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.K.; Randolph, M.F.; Cassidy, M.J. Bearing capacity on sand overlying clay soils: A simplified conceptual model. Geotechnique 2013, 63, 1285–1297. [Google Scholar] [CrossRef]
- Ohri, M.; Purhit, D.; Dubey, M. Behavior of ring footing on dune sand overlying dense sand. In Proceedings of the International Conference on Civil Engineering, Tehran, Iran, 12 August 1997; pp. 22–24. [Google Scholar]
- Hataf, N.; Razav, I.M. Behavior of ring footings on sand. Iran. J. Sci. Technol. Trans. B 2003, 27, 47–56. [Google Scholar]
- Kumar, J.; Ghosh, P. Bearing capacity factor Nγ for ring footings using the method of characteristics. Can. Geotech. J. 2005, 42, 1474–1484. [Google Scholar] [CrossRef]
- Keshavarz, A.; Kumar, J. Bearing capacity computation for a ring foundation using the stress characteristics method. Comput. Geotech. 2017, 89, 33–42. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.H. Vertical bearing capacity for ring footings. Comput. Geotech. 2008, 35, 292–304. [Google Scholar] [CrossRef]
- Benmebarek, S.; Remadna, M.S.; Benmebarek, N.; Belounar, L. Numerical evaluation of the bearing capacity factor of ring footings. Comput. Geotech. 2012, 44, 132–138. [Google Scholar] [CrossRef]
- Choobbasti, A.J.; Hesami, S.; Najafi, A.; Pirzadeh, S.; Farrokhzad, F.; Zahmatkesh, A. Numerical evaluation of bearing capacity and settlement of ring footing; case study of Kazeroon cooling towers. Int. J. Res. Rev. Appl. Sci. 2010, 4, 263–271. [Google Scholar]
- Boushehrian, J.H.; Hataf, N. Experimental and numerical investigation of the bearing capacity of model circular and ring footings on reinforced sand. Geotext. Geomembr. 2003, 21, 241–256. [Google Scholar] [CrossRef]
- Naderi, E.; Hataf, N. Model testing and numerical investigation of interference effect of closely spaced ring and circular footings on reinforced sand. Geotext. Geomembr. 2014, 42, 191–200. [Google Scholar] [CrossRef]
- Kumar, J.; Chakraborty, M. Bearing capacity factors for ring foundations. J. Geotech. Geoenviron. Eng. 2015, 141, 06015007. [Google Scholar] [CrossRef]
- Benmebarek, S.; Saifi, I.; Benmebarek, N. Undrained vertical bearing capacity factors for ring shallow footings. Geotech. Geol. Eng. 2017, 35, 1–10. [Google Scholar] [CrossRef]
- Lee, J.K.; Jeong, S.; Lee, S. Undrained bearing capacity factors for ring footings in heterogeneous soil. Comput. Geotech. 2016, 75, 103–111. [Google Scholar] [CrossRef]
- Lee, J.K.; Jeong, S.; Shang, J.Q. Undrained bearing capacity of ring foundations on two-layered clays. Ocean Eng. 2016, 119, 47–57. [Google Scholar] [CrossRef]
- Lee, J.K.; Jeong, S. Immediate settlement of ring footing resting on inhomogeneous finite stratum. Appl. Sci. 2018, 8, 225. [Google Scholar] [CrossRef] [Green Version]
- Sargazi, O.; Hosseininia, E.S. Bearing capacity of ring footings on cohesionless soil under eccentric load. Comput. Geotech. 2017, 92, 169–178. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Lyamin, A.; Krabbenhoft, J. Optum Computational Engineering (OptumG2). 2020. Available online: www.optumce.com (accessed on 19 March 2020).
- Lyamin, A.V.; Sloan, S.W. Lower bound limit analysis using non-linear programming. Int. J. Numer. Anal. Methods Eng. 2002, 55, 573–611. [Google Scholar] [CrossRef]
- Lyamin, A.V.; Sloan, S.W. Upper bound limit analysis using linear finite elements and non-linear programming. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 181–216. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Lyamin, A.V.; Hjiaj, M.; Sloan, S.W. A new discontinuous upper bound limit analysis formulation. Int. J. Numer. Anal. Methods Eng. 2005, 63, 1069–1088. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Lyamin, A.V.; Sloan, S.W. Formulation and solution of some plasticity problems as conic programs. Int. J. Solids Struct. 2007, 44, 1533–1549. [Google Scholar] [CrossRef] [Green Version]
- Sloan, S.W. Geotechnical stability analysis. Geotechnique 2013, 63, 531–571. [Google Scholar] [CrossRef] [Green Version]
- Potts, D.M.; Zdravkovic, L.; Zdravković, L. Finite Element Analysis in Geotechnical Engineering: Application; Thomas Telford: London, UK, 2001. [Google Scholar]
- Salgado, R.; Lyamin, A.V.; Sloan, S.W.; Yu, H.S. Two-and three-dimensional bearing capacity of foundations in clay. Geotechnique 2004, 54, 297–306. [Google Scholar] [CrossRef]
- Meyerhof, G.G. The ultimate bearing capacity of foudations. Geotechnique 1951, 2, 301–332. [Google Scholar] [CrossRef]
- Tani, K.; Craig, W. Bearing capacity of circular foundations on soft clay of strength increasing with depth. Soils Found. 1995, 35, 21–35. [Google Scholar]
- Houlsby, G.T.; Martin, C.M. Undrained bearing capacity factors for conical footings on clay. Geotechnique 2003, 53, 513–520. [Google Scholar] [CrossRef]
- Martin, C.M. ABC-Analysis of Bearing Capacity. 2004. Available online: www-civil.eng.ox.ac.uk/people/cmm/software/abc (accessed on 26 March 2020).
- Skempton, A.W. The bearing capacity of clays. In Proceedings of the Building Research Congress, London, UK, 9 September 1951; Part 1. pp. 180–189. [Google Scholar]
- Edwards, D.H.; Zdravkovic, L.; Potts, D.M. Depth factors for undrained bearing capacity. Geotechnique 2005, 55, 755–758. [Google Scholar] [CrossRef]
- Gourvenec, S.; Randolph, M.; Kingsnorth, O. Undrained bearing capacity of square and rectangular footings. J. Geomech. 2006, 6, 147–157. [Google Scholar] [CrossRef]
- Taiebat, H.A.; Carter, J.P. A failure surface for circular footings on cohesive soils. Geotechnique 2010, 60, 265–273. [Google Scholar] [CrossRef] [Green Version]
- Kusakabe, O.; Suzuki, H.; Nakase, A. An upper bound calculation on bearing capacity of a circular footing on a non-homogeneous clay. Soils Found. 1986, 26, 143–148. [Google Scholar] [CrossRef] [Green Version]
- Khatri, V.N.; Kumar, J. Bearing capacity factor Nγ for a rough conical footing. Geomech. Eng. 2009, 1, 205–218. [Google Scholar] [CrossRef]
- De Simone, P. Bearing capacity of a circular footing on a Coulomb medium. In Proceedings of the 5th International Conference Numerical Methods Geomechanics, Nayoya, Japan, 1–5 April 1985; Volume 2, pp. 829–836. [Google Scholar]
- Erickson, H.L.; Drescher, A. Bearing capacity of circular footings. J. Geotech. Geoenviron. Eng. 2002, 128, 38–43. [Google Scholar] [CrossRef]
- Lyamin, A.V.; Salgado, R.; Sloan, S.W.; Prezzi, M. Two-and three-dimensional bearing capacity of footings in sand. Geotechnique 2007, 57, 647–662. [Google Scholar] [CrossRef] [Green Version]
- Kumar, J.; Khatri, V.N. Bearing capacity factors of circular foundations for a general c–φ soil using lower bound finite elements limit analysis. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 393–405. [Google Scholar] [CrossRef]
- Loukidis, D.; Salgado, R. Bearing capacity of strip and circular footings in sand using finite elements. Comput. Geotech. 2009, 36, 871–879. [Google Scholar] [CrossRef]














| Meyerhof (1951) a | 6.05 | Salgado et al. (2004) c | 6.227 |
| Skempton (1951) b | 6.00 | Edwards et al. (2005) f | 6.09 |
| Hansen (1970) b | 6.17 | Gourvenec et al. (2006) f | 5.96 |
| Vesic (1973) b | 6.17 | Khatri and Kumar (2009) e | 6.00 |
| Kusakabe et al. (1986) c | 6.31 | Taiebat and Carter (2010) f | 6.166 |
| Tani and Craig (1995) d | 6.34 | Kumar and Chakraborty (2015) e | 6.00 |
| Houlsby and Martin (2003) d | 6.05 | Lee et al. (2016) f | 6.08 |
| Martin (2004) d | 6.05 | Present study e | 6.025 |
| Salgado et al. (2004) e | 5.856 | Present study c | 6.058 |
| φ = 30° | φ = 35° | φ = 40° | φ = 45° | |
|---|---|---|---|---|
| De Simone (1985) a | 15.73 | 42.38 | 124.46 | 418.93 |
| Erickson and Drescher (2002) b | -- | 45.00 | 130.00 | 456.00 |
| Martin (2004) a | 15.54 | 41.97 | 124.10 | 419.44 |
| Lyamin et al. (2007) c | 14.10 | 37.18 | 106.60 | 338.00 |
| Lyamin et al. (2007) d | 19.84 | 52.51 | 157.20 | 539.20 |
| Loukidis and Salgado (2009) e | 15.80 | 42.00 | 122.20 | 405.50 |
| Kumar and Khatri (2011) c | 14.65 | 39.97 | 116.20 | 379.79 |
| Kumar and Chakraborty (2015) c | 14.80 | 40.10 | 116.57 | 380.08 |
| Present study c | 15.06 | 40.15 | 115.03 | 373.37 |
| Present study d | 15.62 | 42.21 | 124.97 | 422.68 |
| cu/γB | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | |
| Hanna and Meyerhof (1980) a | 18.28 | 27.00 | 41.55 | 51.23 | 59.62 | 67.69 |
| Michalowski and Shi (1995) b | 20.06 | 26.36 | 41.06 | 52.21 | 61.24 | 68.82 |
| Shiau et al. (2003) b | 20.71 | 27.81 | 38.80 | 48.97 | 57.84 | 66.39 |
| Shiau et al. (2003) c | 16.17 | 23.44 | 34.59 | 43.95 | 52.34 | 59.43 |
| Present study b | 16.85 | 24.79 | 36.90 | 46.91 | 55.89 | 64.09 |
| Present study c | 15.59 | 23.15 | 34.43 | 43.59 | 51.74 | 59.97 |
| R0 (m) | H/R0 | cu/γR0 | Present Study a | Present Study b | Kumar and Chakraborty (2015) b | Okamura et al. (1997) c | Okamura et al. (1998) d |
|---|---|---|---|---|---|---|---|
| 1.5 | 0 | 1.61 | 9.70 | 9.76 | 9.71 | 10.00 | 10.71 |
| 3.01 | 18.14 | 18.24 | 18.09 | -- | 19.27 | ||
| 5.15 | 30.03 | 31.21 | 30.97 | -- | 32.88 | ||
| 6.26 | 37.71 | 37.94 | 37.59 | -- | 39.12 | ||
| 1 | 0.75 | 11.82 | 12.04 | 14.07 | -- | 10.69 | |
| 3.05 | 26.47 | 27.14 | 29.78 | 28.90 | 31.57 | ||
| 5.19 | 36.60 | 37.66 | 44.17 | -- | 52.45 | ||
| 6.26 | 41.08 | 42.27 | 51.30 | -- | 62.61 | ||
| 2 | 0.80 | 33.98 | 34.85 | 46.92 | 31.95 | 25.23 | |
| 1.20 | 40.42 | 41.51 | 55.79 | 37.01 | 31.98 | ||
| 3.21 | 60.34 | 62.40 | 78.14 | 58.30 | 58.43 | ||
| 5.15 | 73.29 | 76.05 | 96.86 | 73.30 | 87.12 | ||
| 3 | 2.45 | 106.62 | 111.14 | 109.02 | -- | 84.65 | |
| 3.54 | 111.53 | 125.53 | 118.52 | 103.00 | 103.75 | ||
| 5.84 | 114.89 | 125.80 | 131.73 | 141.00 | 152.05 | ||
| 4 | 1.63 | 114.67 | 124.82 | 131.13 | 129.31 | 112.54 | |
| 1.85 | 115.01 | 125.19 | 134.62 | 133.80 | 117.04 | ||
| 3.67 | 114.53 | 124.93 | 132.46 | 125.00 | -- |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Zhu, Z.; Xiao, Y. Bearing Capacity of Ring Foundations on Sand Overlying Clay. Appl. Sci. 2020, 10, 4675. https://doi.org/10.3390/app10134675
Yang C, Zhu Z, Xiao Y. Bearing Capacity of Ring Foundations on Sand Overlying Clay. Applied Sciences. 2020; 10(13):4675. https://doi.org/10.3390/app10134675
Chicago/Turabian StyleYang, Chaowei, Zhiren Zhu, and Yao Xiao. 2020. "Bearing Capacity of Ring Foundations on Sand Overlying Clay" Applied Sciences 10, no. 13: 4675. https://doi.org/10.3390/app10134675
APA StyleYang, C., Zhu, Z., & Xiao, Y. (2020). Bearing Capacity of Ring Foundations on Sand Overlying Clay. Applied Sciences, 10(13), 4675. https://doi.org/10.3390/app10134675





