Tolerance Design and Robust Study for The Joint Clearances of Landing Gear Retraction Mechanisms
Abstract
:Featured Application
Abstract
1. Introduction
2. Related Theory
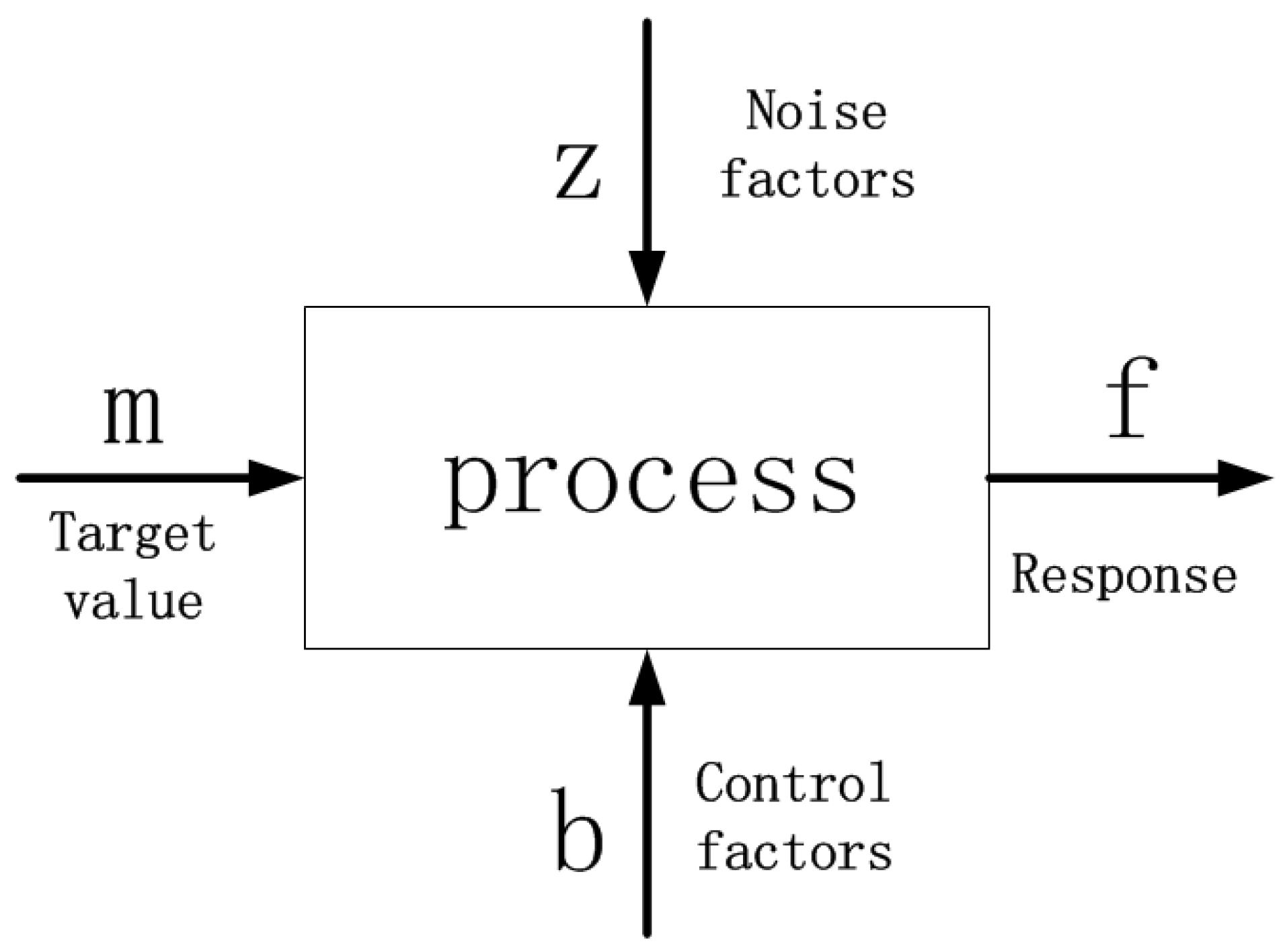
2.1. The Basic Concepts of Jacobian Model
2.2. Traditional Tolerance Analysis
2.3. Robust Analysis with Doe
3. An Integrated Tolerance Theory for the Kinematic Accuracy Analysis of Landing Gear Mechanisms
3.1. Kinematic Accuracy Model Derived from Jacobian–Torsor Model in a Mechanism
3.2. Analysis of Variance and Ratios for Tolerance Analysis
3.3. The Integrated Tolerance Analysis Procedure
- Establish the kinematic accuracy model of a mechanism and deduce the propagation function for the FR,
- According to the experience and engineering handbook, conduct primary tolerance design and analysis,
- Select control factors and their corresponding levels, and choose an orthogonal array as an experiment matrix,
- Perform the experiments and calculate ratios,
- Analyze the ratios, and obtain the optimum setting of control factors,
- Verify the obtained factors and conduct tolerance redesign and reanalysis.
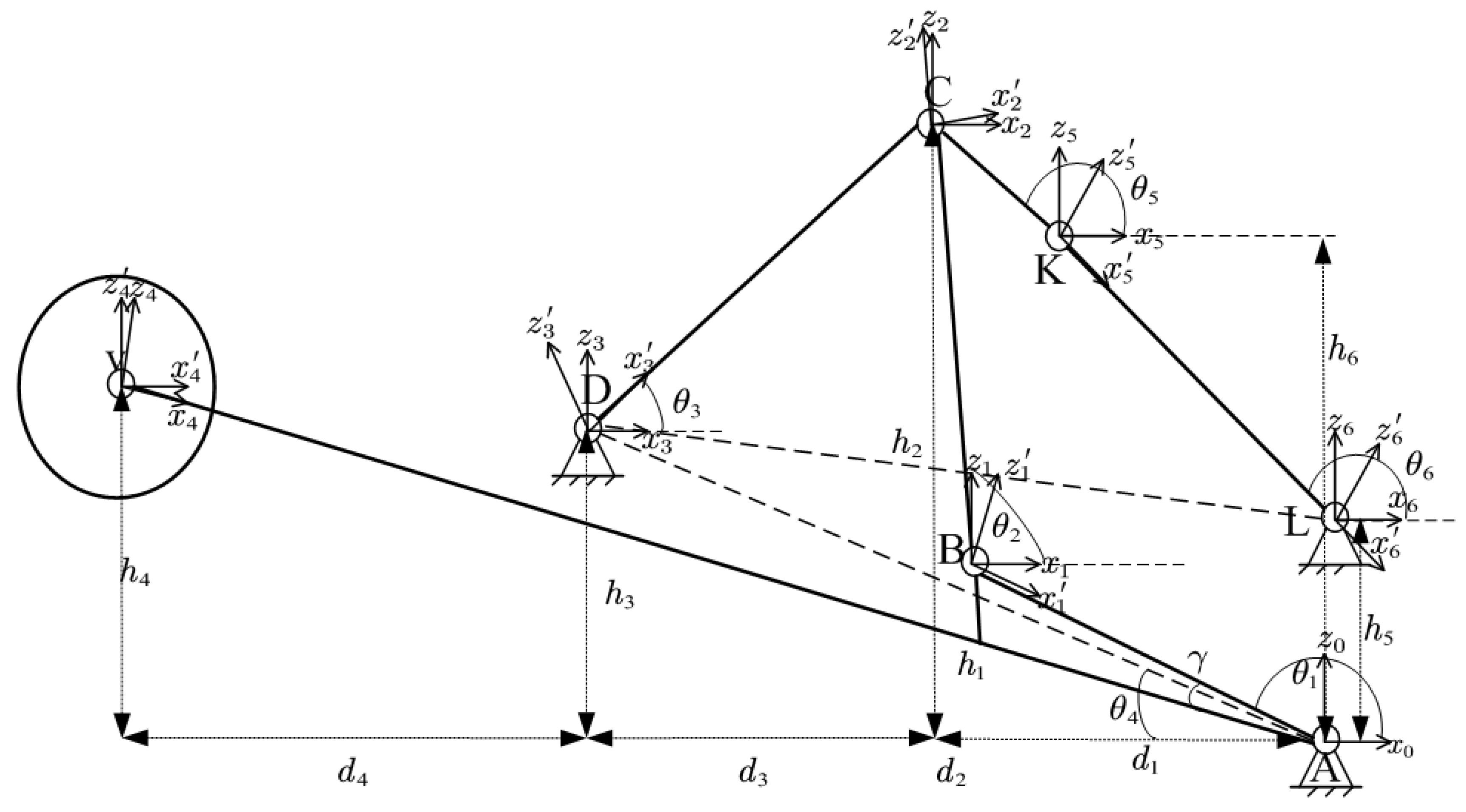
4. The Tolerance Design and Robust Study for the Joint Clearances of a Landing Gear Retraction Mechanism
- There is no deformation because of contacts in joints.
- Contacts between the hole and shaft are supposed to be line contact.
4.1. Primary Clearance Design and Tolerance Analysis of the Mechanism
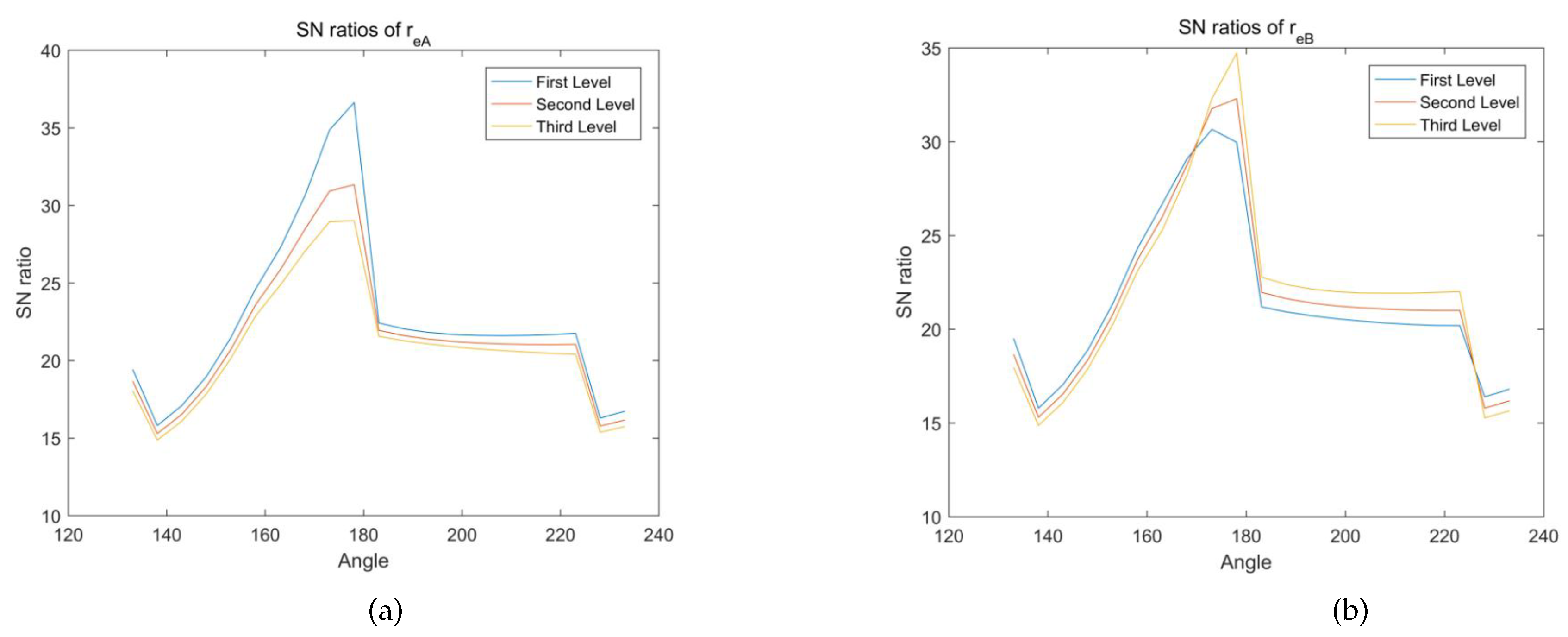
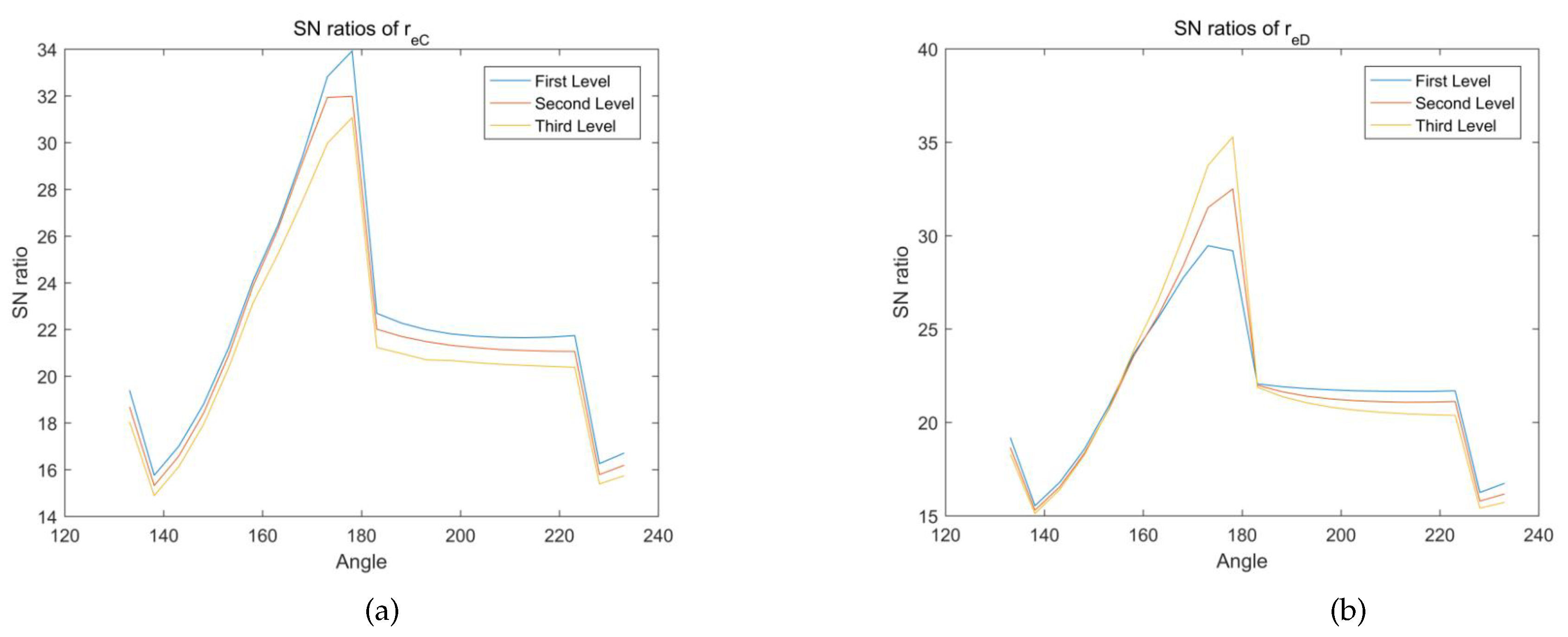
4.2. Robust Analysis
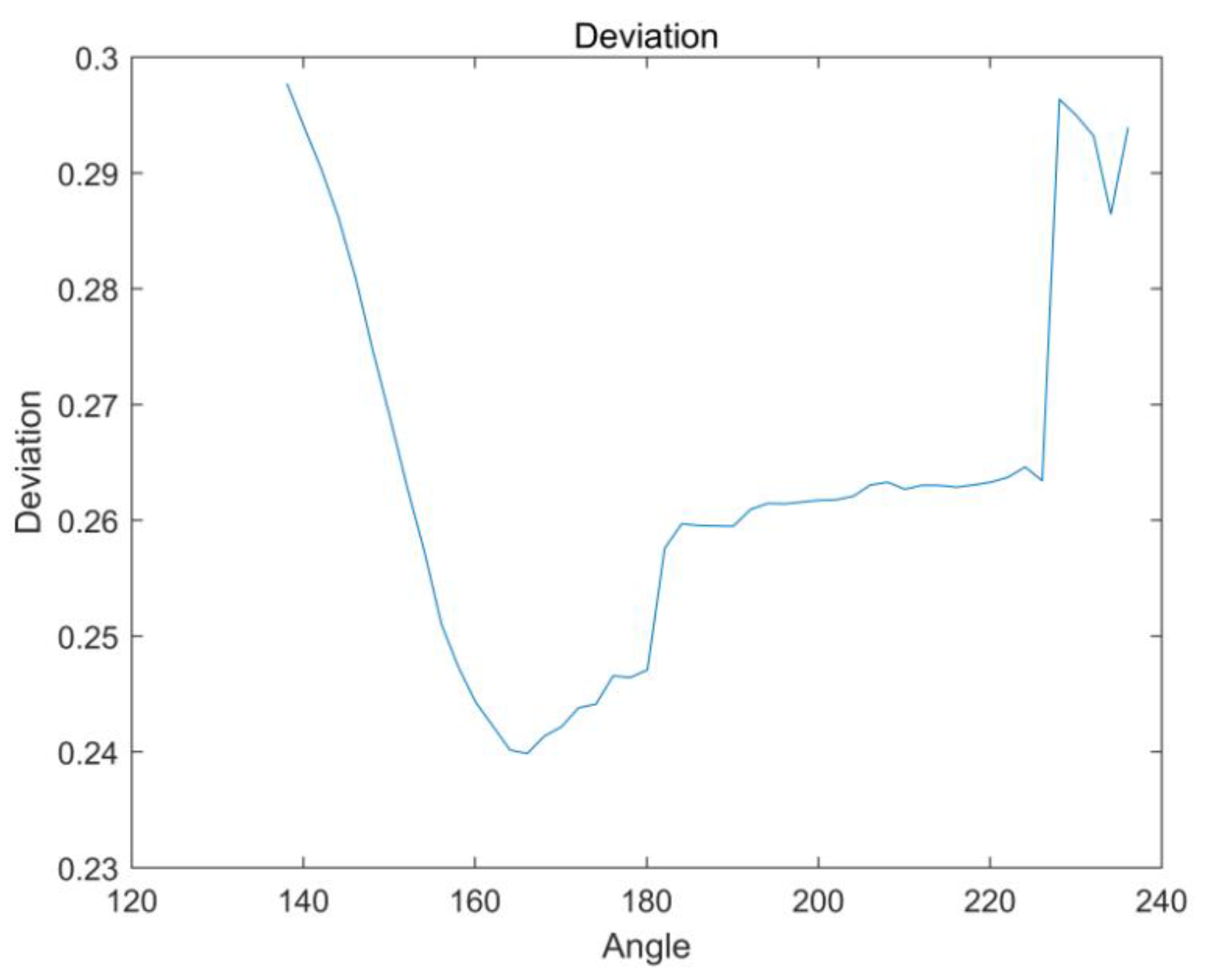
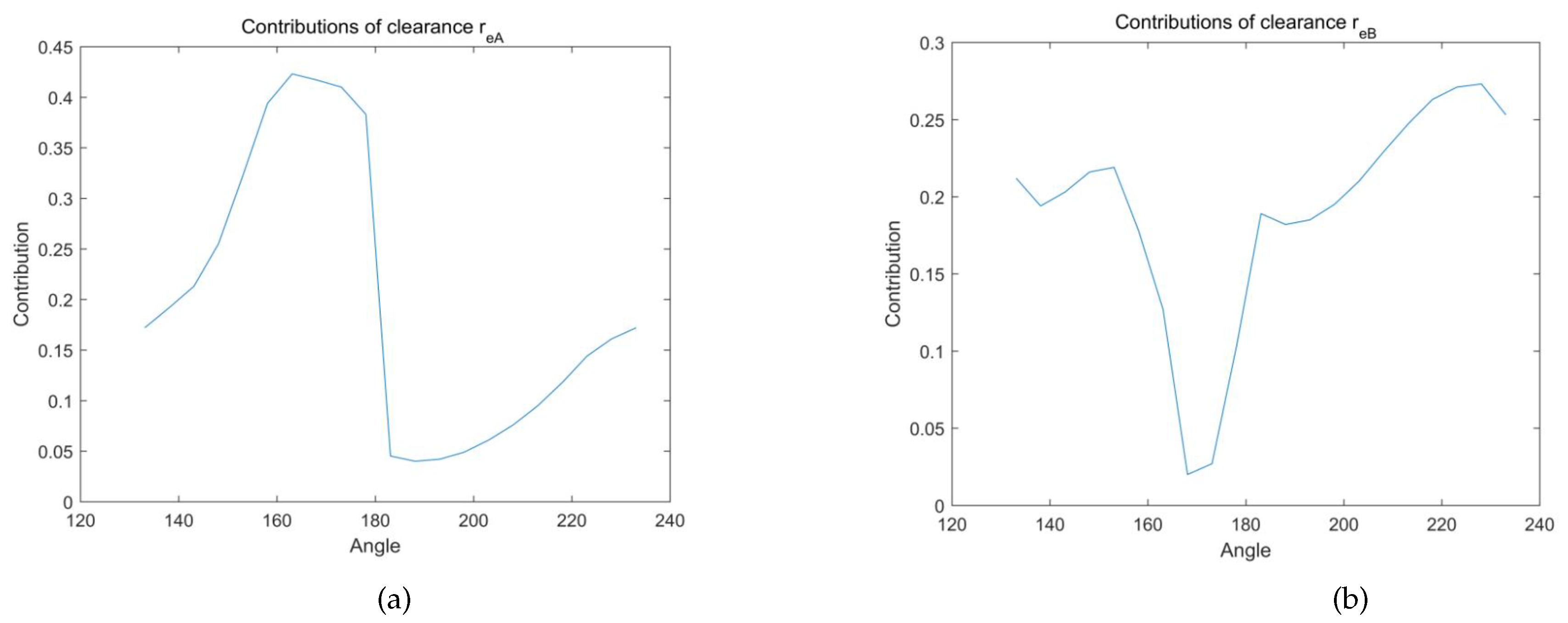
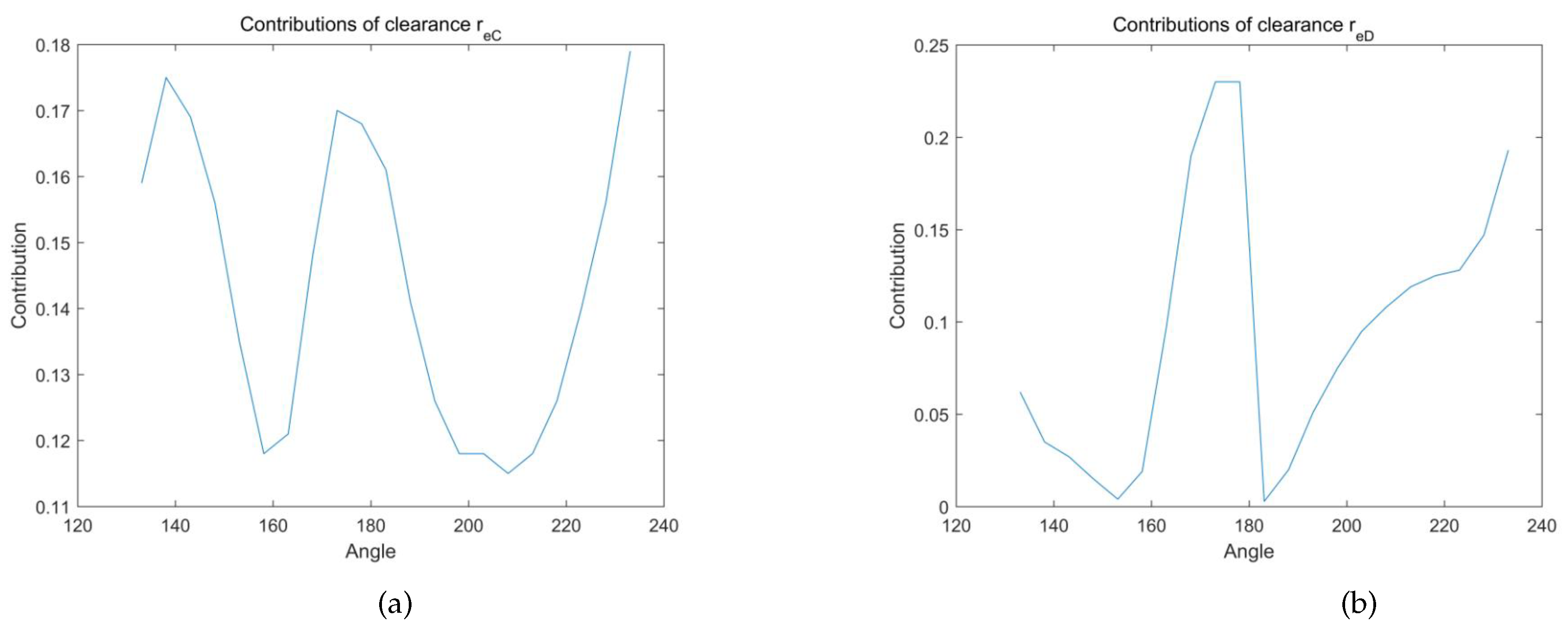
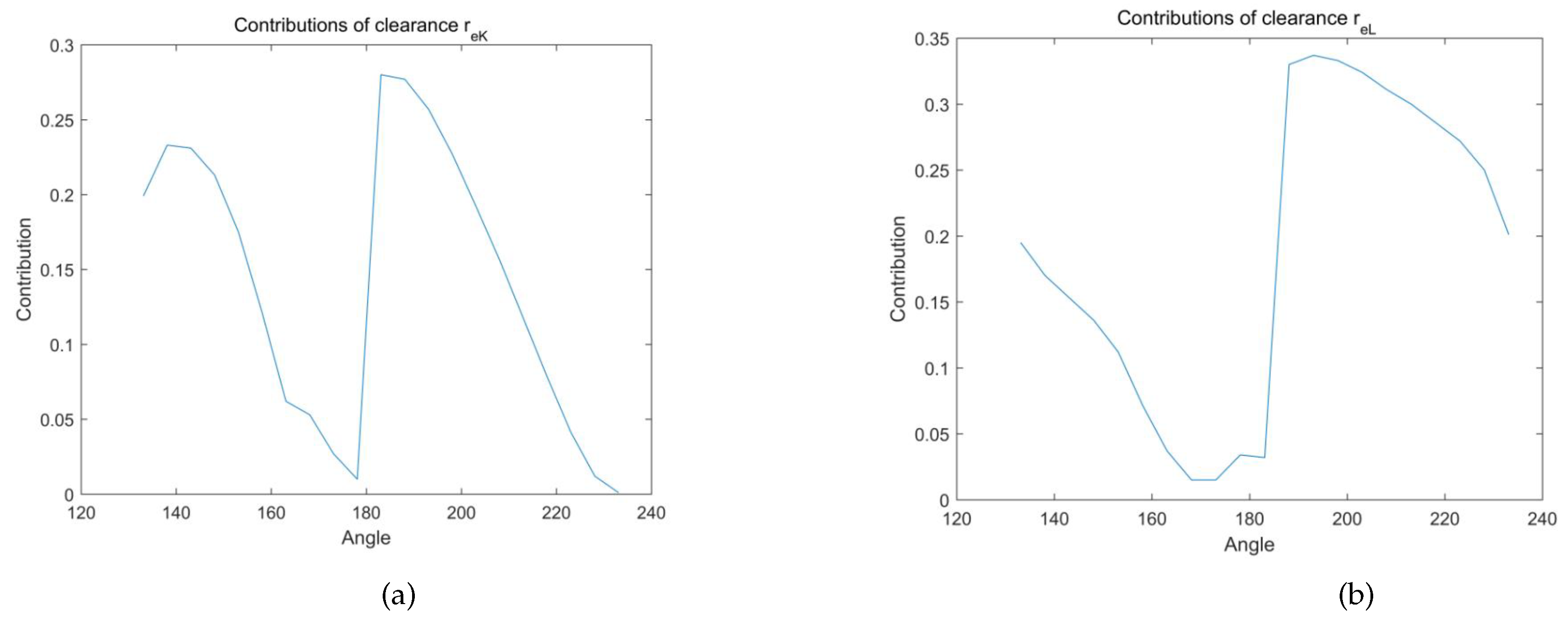
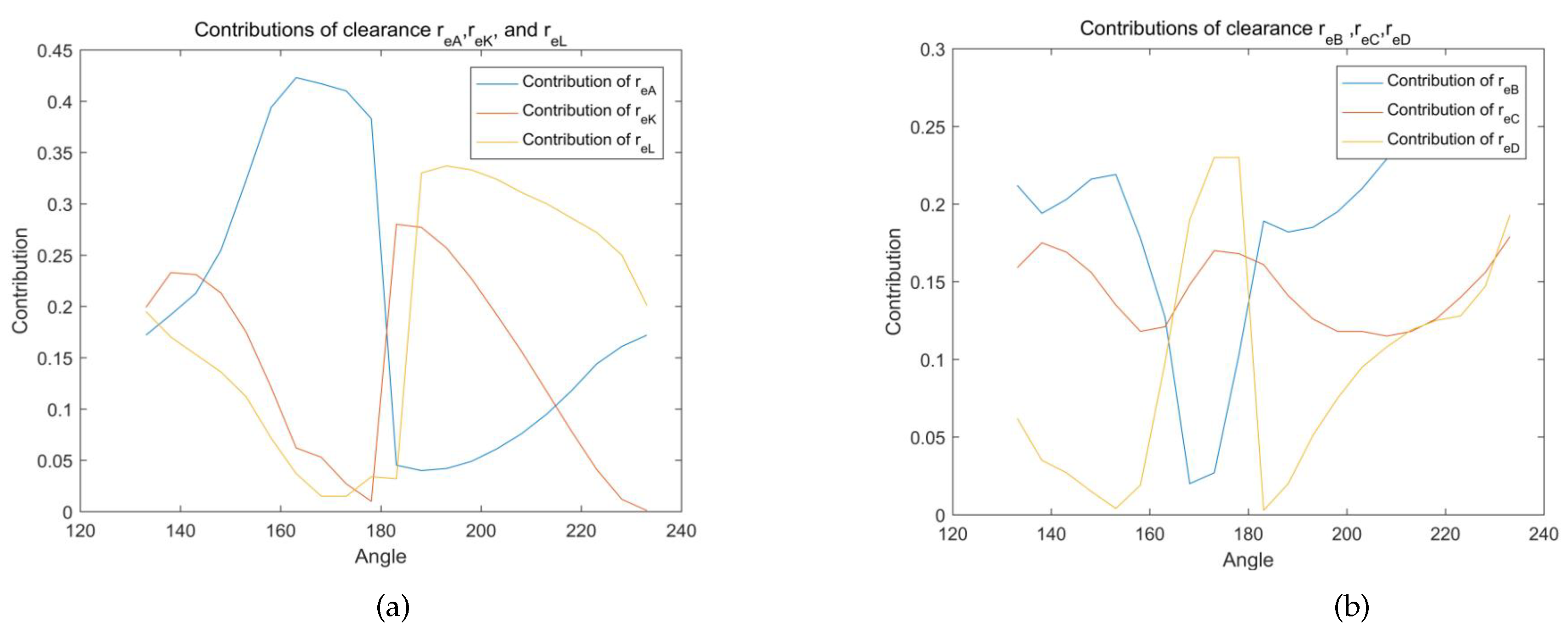
- All six clearances have significant effects on final results, however, different clearances have different effects.
- When the input variable is within the range of 153°∼223°, fluctuations exist for six curves of the contributions, indicating that the effects of six clearances can not be overlooked.
- Referring to the results, the order of the effects can be given as: . , and have negative effects on final results, and output deviation decrease as they increase. For most of the time, and have negative influences. However, when is during the periods of 168°∼223° and 163°∼183° respectively, they have positive influences.
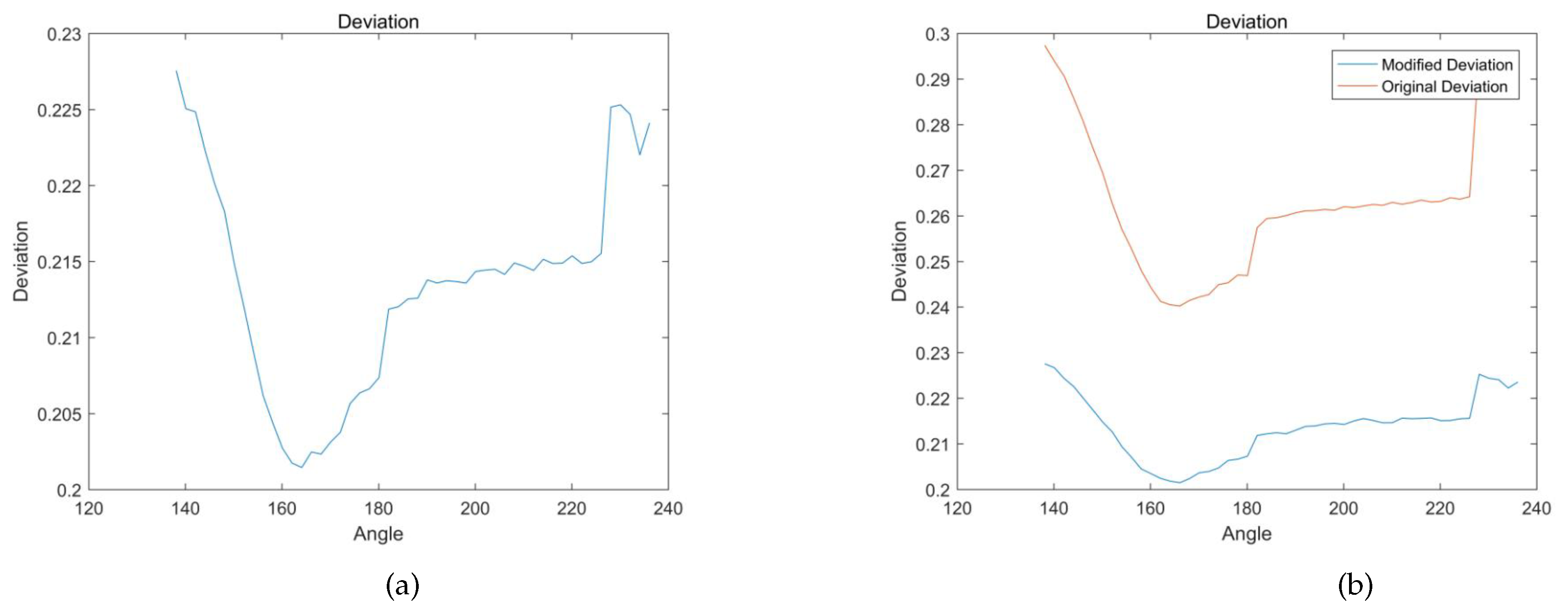
4.3. Modified Tolerance Design for Joint Clearances
5. Conclusions
- A new integrated theory composed of tolerance design and robust analysis was presented. The Jacobian tolerance theories were adopted to deduce the kinematic accuracy model, while robust theories are used to analyze the tolerance effects of a mechanism. The procedures of the theory are also given.
- A typical landing gear retraction mechanism was taken as a case to study the joint clearance effects. Using the presented theory, joint clearances were seen as tolerances. Through the procedures of tolerance design, robust analysis, and tolerance redesign, final results showed that modified deviations of the landing gear retraction mechanism were significantly reduced, which suggests that the integrated theory presented is a valid way to estimate the influences of joint clearances and keep the robustness of a mechanism.
- The study has have found that the inner tendencies of joint clearances could be observed. This finding provides designers assistance for sound decisions and researchers’ insights for future studies on joint clearances. According to the finding and the results of the study case, the designers are planning to modify the tolerance parameters to obtain a more robust mechanism and further research will continue.
- Regarding landing gear retraction mechanism, the integrated theory and the study presented contribute in several ways to our understanding of tolerance design and robust analysis. This is the first study to integrate tolerance and robust theories and analyze the clearance effects on landing gear kinematic accuracy. The theory and the findings will be of great use for landing gears in the future design.
- The jacobian model has the advantage of simplicity and clarity. This is also the first study to use the jacobian model for the tolerance analysis of the landing gear mechanism. Future studies regarding the role of the jacobian model are strongly recommended.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FE | Functional element |
| FR | Functional requirement |
| FE pair | Functional element pair |
| GRF | Global reference frame |
| LRF | Local reference frame |
Appendix A
| Experiments | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.027 | 0.027 | 0.027 | 0.027 | 0.027 | 0.027 |
| 2 | 0.027 | 0.027 | 0.027 | 0.027 | 0.037 | 0.037 |
| 3 | 0.027 | 0.027 | 0.027 | 0.027 | 0.047 | 0.047 |
| 4 | 0.027 | 0.037 | 0.037 | 0.037 | 0.027 | 0.027 |
| 5 | 0.027 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 |
| 6 | 0.027 | 0.037 | 0.037 | 0.037 | 0.047 | 0.047 |
| 7 | 0.027 | 0.047 | 0.047 | 0.047 | 0.027 | 0.027 |
| 8 | 0.027 | 0.047 | 0.047 | 0.047 | 0.037 | 0.037 |
| 9 | 0.027 | 0.047 | 0.047 | 0.047 | 0.047 | 0.047 |
| 10 | 0.037 | 0.027 | 0.037 | 0.047 | 0.027 | 0.037 |
| 11 | 0.037 | 0.027 | 0.037 | 0.047 | 0.037 | 0.047 |
| 12 | 0.037 | 0.027 | 0.037 | 0.047 | 0.047 | 0.027 |
| 13 | 0.037 | 0.037 | 0.047 | 0.027 | 0.027 | 0.037 |
| 14 | 0.037 | 0.037 | 0.047 | 0.027 | 0.037 | 0.047 |
| 15 | 0.037 | 0.037 | 0.047 | 0.027 | 0.047 | 0.027 |
| 16 | 0.037 | 0.047 | 0.027 | 0.037 | 0.027 | 0.037 |
| 17 | 0.037 | 0.047 | 0.027 | 0.037 | 0.037 | 0.047 |
| 18 | 0.037 | 0.047 | 0.027 | 0.037 | 0.047 | 0.027 |
| 19 | 0.047 | 0.027 | 0.047 | 0.037 | 0.027 | 0.047 |
| 20 | 0.047 | 0.027 | 0.047 | 0.037 | 0.037 | 0.027 |
| 21 | 0.047 | 0.027 | 0.047 | 0.037 | 0.047 | 0.037 |
| 22 | 0.047 | 0.037 | 0.027 | 0.047 | 0.027 | 0.047 |
| 23 | 0.047 | 0.037 | 0.027 | 0.047 | 0.037 | 0.027 |
| 24 | 0.047 | 0.037 | 0.027 | 0.047 | 0.047 | 0.037 |
| 25 | 0.047 | 0.047 | 0.037 | 0.027 | 0.027 | 0.047 |
| 26 | 0.047 | 0.047 | 0.037 | 0.027 | 0.037 | 0.027 |
| 27 | 0.047 | 0.047 | 0.037 | 0.027 | 0.047 | 0.037 |
References
- Committee of Aircraft. Aircraft Design Manual Book 14: Taking-off and Landing Devices Design; Aviation Industry Press: Beijing, China, 2002. [Google Scholar]
- Currey, N. Aircraft Landing Gear Design: Principle and Practice; AIAA: Washington, DC, USA, 1988. [Google Scholar]
- Chen, B. Aircraft Manufacturing coordination Accuracy and Tolerance Allocation; Aviation Industry Press: Beijing, China, 1987. [Google Scholar]
- Laperrière, L.; Lafond, P. Tolerance Analysis And Synthesis Using Virtual Joints; Springer: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Laperrière, L.; ElMaraghy, H.A. Tolerance Analysis and Synthesis Using Jacobian Transforms. CIRP Ann. 2000, 49, 359–362. [Google Scholar] [CrossRef]
- Lafond, P.; Laperriere, L. Jacobian-based modeling of dispersions affecting pre-defined functional requirements of mechanical assemblies. In Proceedings of the 1999 IEEE International Symposium on Assembly and Task Planning (ISATP’99) (Cat.No.99TH8470), Porto, Portugal, 24 July 1999; pp. 20–25. [Google Scholar]
- Desrochers, A.; Riviere, A. A matrix approach to the representation of tolerance zones and clearances. Int. J. Adv. Manuf. Technol. 1998, 13, 630–636. [Google Scholar] [CrossRef]
- Chase, K.W.; Jinsong, G.; Magleby, S.P. Generalized 3D tolerance analysis of mechanical assemblies with small kinematic adjustments. IIE Trans. 2000, 30, 367–377. [Google Scholar]
- Desrochers, A.; Clement, A. A dimensioning and tolerancing assistance model for CAD/CAM systems. Int. J. Adv. Manuf. Technol. 2000, 9, 352–361. [Google Scholar] [CrossRef]
- Laperrière, L.; Ghie, W.; Desrochers, A. Statistical and Deterministic Tolerance Analysis and Synthesis Using a Unified Jacobian–Torsor Model. CIRP Ann. 2002, 51, 417–420. [Google Scholar] [CrossRef]
- Frisoli, A.; Solazzi, M.; Pellegrinetti, D.; Bergamasco, M. A new screw theory method for the estimation of position accuracy in spatial parallel manipulators with revolute joint clearances. Mech. Mach. Theory 2011, 46, 1929–1949. [Google Scholar] [CrossRef]
- Ghie, W.; Laperrière, L.; Desrochers, A. Statistical tolerance analysis using the unified Jacobian–Torsor model. Int. J. Prod. Res. 2009, 48, 4609–4630. [Google Scholar] [CrossRef]
- Franciosa, P.; Gerbino, S.; Patalano, S. Variational modeling and assembly constraints in tolerance analysis of rigid part assemblies: Planar and cylindrical features. Int. J. Adv. Manuf. Technol. 2009, 49, 239–251. [Google Scholar]
- Asante, J.N. A small displacement torsor model for tolerance analysis in a workpiece-fixture assembly. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 1005–1020. [Google Scholar] [CrossRef]
- Desrochers, A.; Ghie, W.; Laperriere, L. Application of a unified Jacobian–Torsor model for tolerance analysis. J. Comput. Inf. Sci. Eng. 2003, 3, 2–14. [Google Scholar] [CrossRef]
- Adams, J.D.; Whitney, D.E. Application of screw theory to constraint analysis of mechanical assemblies joined by features. J. Mech. Des. 2001, 123, 26–32. [Google Scholar] [CrossRef]
- Tobon, S.A.; Teissandier, D.; Delos, V. Applying screw theory for summing sets of constraints in geometric tolerancing. Mech. Mach. Theory 2017, 112, 255–271. [Google Scholar] [CrossRef]
- Li, H.; Zhu, H.; Zhou, X.; Li, P.; Yu, Z. A new computer-aided tolerance analysis and optimization framework for assembling processes using DP-SDT theory. Int. J. Adv. Manuf. Technol. 2016, 86, 1299–1310. [Google Scholar] [CrossRef]
- Jin, S.; Chen, H.; Li, Z.M.; Lai, X.M. A small displacement torsor model for 3D tolerance analysis of conical structures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2514–2523. [Google Scholar] [CrossRef]
- Zuo, X.; Li, B.; Yang, J.; Jiang, X. Application of the Jacobian–torsor theory into error propagation analysis for machining processes. Int. J. Adv. Manuf. Technol. 2013, 69, 1557–1568. [Google Scholar] [CrossRef]
- Chen, H.; Jin, S.; Li, Z.M.; Lai, X.M. A solution of partial parallel connections for the unified Jacobian–Torsor model. Mech. Mach. Theory 2015, 91, 39–49. [Google Scholar] [CrossRef]
- Chen, H.; Jin, S.; Li, Z.; Lai, X. A modified method of the unified Jacobian–Torsor model for tolerance analysis and allocation. Int. J. Precis. Eng. Manuf. 2015, 16, 1789–1800. [Google Scholar] [CrossRef]
- Chen, H.; Jin, S.; Li, Z.M.; Lai, X.M. A comprehensive study of three dimensional tolerance analysis methods. Comput.-Aided Des. 2014, 53, 1–13. [Google Scholar] [CrossRef]
- Zhou, X.; Li, H.; Zhu, H.P. A novel kinematic accuracy analysis method for a mechanical assembly based on DP-SDT theory. Int. J. Adv. Manuf. Technol. 2018, 94, 4301–4315. [Google Scholar] [CrossRef]
- Taguchi, G. Systems of Experimental Design Kraus International; Kraus International Pub & American Supplier Institute: New York, NY, USA, 1987. [Google Scholar]
- Erkaya, S.; Uzmay, I. Determining link parameters using genetic algorithm in mechanisms with joint clearance. Mech. Mach. Theory 2009, 44, 222–234. [Google Scholar] [CrossRef]
- Stander, N.; Craig, K.J. On the robustness of a simple domain reduction scheme for simulation-based optimization. Eng. Comput. 2002, 19, 431–450. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.H.; Park, G.J. Robust optimization in discrete design space for constrained problems. Aiaa J. 2002, 40, 774–780. [Google Scholar] [CrossRef]
- Zhu, J.M.; Ting, K.L. Performance distribution analysis and robust design. J. Mech. Des. 2001, 123, 11–17. [Google Scholar] [CrossRef]
- Gong, C.; Kao, I. Design for accuracy and repeatability for robots using Taguchi methods. Concurrent. Eng. Res. A 1997, 5, 263–277. [Google Scholar]
- Ting, K.; Long, Y. Performance Quality and Tolerance Sensitivity of Mechanisms. J. Mech. Des. 1996, 118, 144–150. [Google Scholar] [CrossRef]
- Tsui, K.L. An overview of Taguchi method and newly developed statistical methods for robust design. IIE Trans. 1992, 24, 44–57. [Google Scholar] [CrossRef]
- Caro, S.; Bennis, F.; Wenger, P. Tolerance synthesis of mechanisms: A robust design approach. J. Mech. Des. 2005, 127, 86–94. [Google Scholar] [CrossRef] [Green Version]
- Rout, B.K.; Mittal, R.K. Tolerance design of robot parameters using Taguchi method. Mech. Syst. Signal Process. 2006, 20, 1832–1852. [Google Scholar] [CrossRef]
- Dua, X.P.; Venigella, P.K.; Liu, D.S. Robust mechanism synthesis with random and interval variables. Mech. Mach. Theory 2009, 44, 1321–1337. [Google Scholar] [CrossRef]
- Luo, K.; Wang, J.G.; Du, X.P. Robust mechanism synthesis with truncated dimension variables and interval clearance variables. Mech. Mach. Theory 2012, 57, 71–83. [Google Scholar] [CrossRef]
- Huang, X.Z.; Zhang, Y.M. Robust tolerance design for function generation mechanisms with joint clearances. Mech. Mach. Theory 2010, 45, 1286–1297. [Google Scholar] [CrossRef]
- Huang, X.Z.; Zhang, Y.M.; Lu, H.; Tang, L.; Li, H. Tolerance Design for Four-Bar Function Generating Mechanisms with Joint Clearances Using Taguchi Method; Trans Tech Publications Ltd: Stafa-Zurich, Switzerland, 2010. [Google Scholar]
- Armillotta, A. A static analogy for 2D tolerance analysis. Assem. Autom. 2014, 34, 182–191. [Google Scholar] [CrossRef] [Green Version]
- Park, G.J.; Lee, T.H.; Lee, K.H.; Hwang, K.H. Robust design: An overview. Aiaa J. 2006, 44, 181–191. [Google Scholar] [CrossRef]
Sample Availability: Samples of the paper are available from the authors. |



| Parameter | Definition |
|---|---|
| Functional element (FE): | Point, curve, or surface that belongs to a part in the assembly. A FE can be real, e.g., the plane surface of a block, or constructed, e.g., the axis of a cylinder or a median plane. |
| Functional requirement (FR): | An important condition to be satisfied between two FEs on different parts, e.g., a fitting condition. |
| Virtual joints | For tolerancing purposes, we associate coordinate frames to the toleranced FE in a pair, assuming there exists a set of virtual joints that can make the toleranced FE of the pair “move” relative to the other FE of the pair, to simulate manufacturing inaccuracies. |
| Functional element pair (FE pair) | Two FES on different parts or on the same part; includes a kinematic pair and internal pair. |
| small-displacement screw model | An expression which contains potential variations along and about all three Cartesian axes. |
| Global reference frame (GRF) | Frame in which the functional requirement and total dimensional chain is established. |
| Local reference frame (LRF) | Frame in which each functional element pair is established. |
| Characteristic Type | Ratios |
|---|---|
| Nominal the best | With scale factor With adjustment factor |
| Smaller the better | |
| Larger the better |
| Components | Length(mm) | Angle | Scope |
|---|---|---|---|
| AB | 451.77 | 133.14∼234.30 (input variable) | |
| BC | 315.8 | 86.257∼62.389 | |
| CD | 465 | 43.481∼−62.389 | |
| AD | 704.89 | 152.544 | |
| AV | 1334.437 | 24.203 | |
| KL | 305 | 122.004∼−141.98 | |
| CK | 195 | 122.004∼−141.98 | |
| LD | 615.359 | 9.453 |
| Components | Tolerances (mm) |
|---|---|
| Components | Tolerances (mm) |
|---|---|
| Level 1: (rough) Level 2: (medium) Level 3: (precise) | |
| Level 1: (rough) Level 2: (medium) Level 3: (precise) | |
| Level 1: (rough) Level 2: (medium) Level 3: (precise) | |
| Level 1: (rough) Level 2: (medium) Level 3: (precise) | |
| Level 1: (rough) Level 2: (medium) Level 3: (precise) | |
| Level 1: (rough) Level 2: (medium) Level 3: (precise) |
| Components | Tolerances (mm) |
|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Nie, H.; Wei, X. Tolerance Design and Robust Study for The Joint Clearances of Landing Gear Retraction Mechanisms. Appl. Sci. 2020, 10, 4856. https://doi.org/10.3390/app10144856
Zhang L, Nie H, Wei X. Tolerance Design and Robust Study for The Joint Clearances of Landing Gear Retraction Mechanisms. Applied Sciences. 2020; 10(14):4856. https://doi.org/10.3390/app10144856
Chicago/Turabian StyleZhang, Li, Hong Nie, and Xiaohui Wei. 2020. "Tolerance Design and Robust Study for The Joint Clearances of Landing Gear Retraction Mechanisms" Applied Sciences 10, no. 14: 4856. https://doi.org/10.3390/app10144856
APA StyleZhang, L., Nie, H., & Wei, X. (2020). Tolerance Design and Robust Study for The Joint Clearances of Landing Gear Retraction Mechanisms. Applied Sciences, 10(14), 4856. https://doi.org/10.3390/app10144856






