Theoretical and Experimental Study on Contact Characteristics of Spiral Bevel Gears under Quasi-Static and Large Loading Conditions
Abstract
:1. Introduction
2. Theoretical Tooth Surface Modeling
2.1. Tooth Surface Modeling of the Gear
2.2. Tooth Surface Modeling of the Pinion
2.3. Meshing Contact Modeling
3. Solid Modeling and Finite Element Model
3.1. Examples of Calculation
3.2. Constructing Solid Geometry Model
3.3. Transmission System Model
3.4. Material Property and Mesh Generation
4. Simulation Results
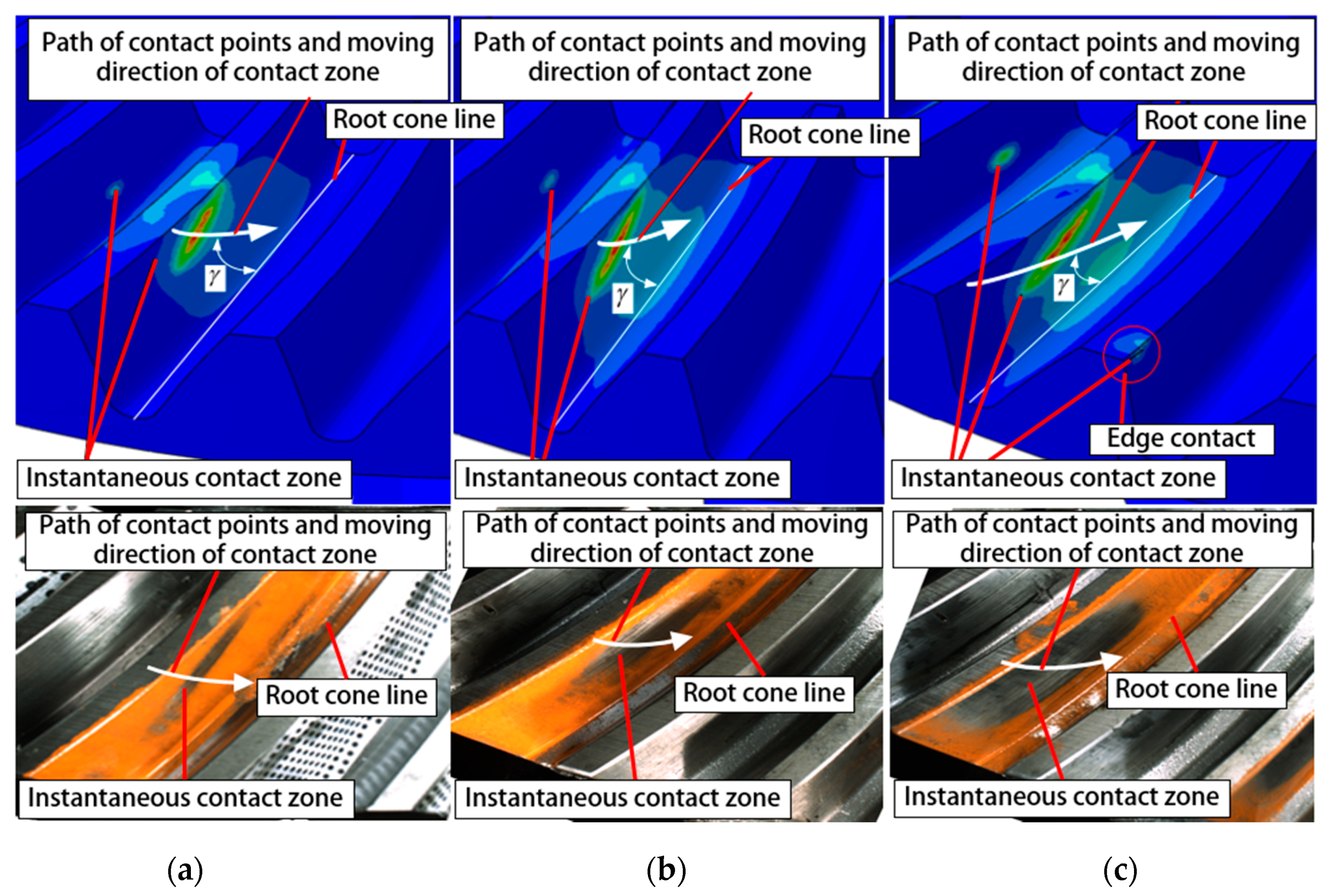
4.1. Tooth Surface Contact Pattern
4.2. Tooth Surface Contact Stress
4.3. Tooth Root Bending Stress
4.4. Transmission Error
5. Verification Test
5.1. Construction of Test Bench
5.2. Tooth Contact Pattern Test
5.3. Tooth Root Bending Stress Test
5.4. Transmission Error Test
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004; pp. 3–11. [Google Scholar]
- Shojaei, A.; Tajmir, R.H.; Hirmand, M. Finite element modeling of incremental bridge launching and study on behavior of the bridge during construction stages. Int. J. Civ. Eng. 2015, 13, 112–125. [Google Scholar]
- Litvin, F.L.; Fuentes, A.; Fan, Q.; Handschuh, R.F. Computerized design, simulation of meshing, and contact and stress analysis of face-milled formate generated spiral bevel gears. Mech. Mach. Theory 2002, 37, 441–459. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A.; Hayasaka, K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears. Mech. Mach. Theory 2006, 41, 83–118. [Google Scholar] [CrossRef]
- He, D.; Ding, H.; Tang, J.Y. A new analytical identification approach to the tooth contact points considering misalignments for spiral bevel or hypoid gears. Mech. Mach. Theory 2018, 121, 785–803. [Google Scholar] [CrossRef]
- Simon, V. Optimization of face-hobbed hypoid gears. Mech. Mach. Theory 2014, 77, 164–181. [Google Scholar] [CrossRef]
- Simon, V. Design and manufacture of spiral bevel gears with reduced transmission errors. J. Mech. Des. 2009, 131, 041007. [Google Scholar] [CrossRef]
- Simon, V. Design of face-hobbed spiral bevel gears with reduced maximum tooth contact pressure and transmission errors. Chin. J. Aeronaut. 2013, 26, 777–790. [Google Scholar] [CrossRef] [Green Version]
- Simon, V. Manufacture of optimized face-hobbed spiral bevel gears on computer numerical control hypoid generator. J. Manuf. Sci. Eng. 2014, 136, 031008. [Google Scholar] [CrossRef]
- Simon, V. Computer simulation of tooth contact analysis of mismatched spiral bevel gears. Mech. Mach. Theory 2007, 42, 365–381. [Google Scholar] [CrossRef]
- Artoni, A.; Kolivand, M.; Kahraman, A. An ease-off based optimization of the loaded transmission error of hypoid gears. J. Mech. Des. 2010, 132, 011010. [Google Scholar] [CrossRef]
- Artoni, A.; Bracci, A.; Gabaccini, M.; Guiggiani, M. Optimization of the loaded contact pattern in hypoid gears by automatic topography modification. J. Mech. Des. 2009, 131, 011008. [Google Scholar] [CrossRef]
- Artoni, A.; Gabaccini, M.; Guiggiani, M.; Kahraman, A. Multi objective ease-off optimization of hypoid gears for their efficiency, noise, and durability performances. J. Mech. Des. 2011, 133, 121007. [Google Scholar] [CrossRef]
- Kolivand, M.; Kahraman, A. An ease-off based method for loaded tooth contact analysis of hypoid gears having local and global surface deviations. J. Mech. Des. 2010, 132, 071004. [Google Scholar] [CrossRef]
- Kolivand, M.; Kahraman, A. A load distribution model for hypoid gears using ease-off topography and shell theory. Mech. Mach. Theory 2009, 44, 1848–1865. [Google Scholar] [CrossRef]
- Mu, Y.M.; Fang, Z.D. An ease-off flank modification method for high contact ratio spiral bevel gears with modified curvature motion. J. Adv. Mech. Des. Syst. Manuf. 2017, 11, 0034. [Google Scholar] [CrossRef]
- Nie, S.W.; Deng, J.; Deng, X.Z.; Geng, L.L. A flank modification method for spiral bevel gears based on mismatch topography adjustment. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, 0057. [Google Scholar] [CrossRef]
- De Vaujany, J.P.; Guingand, M.; Remond, D. Numerical and experimental study of the loaded transmission error of a spiral bevel gear. J. Mech. Des. 2007, 129, 195–200. [Google Scholar] [CrossRef]
- Kazumasa, K.; Isamu, T. Analytical and experimental tooth contact pattern of large-sized spiral bevel gears in cyclo-palloid system. J. Mech. Des. 2010, 132, 139–147. [Google Scholar]
- Zhuo, Y.B.; Xiang, X.Y.; Zhou, X.J. A method for the global optimization of the tooth contact pattern and transmission error of spiral bevel and hypoid gears. J. Zhejiang Univ. 2017, 18, 377–392. [Google Scholar] [CrossRef]
- Zhuo, Y.B.; Zhou, X.J.; Lv, H.L. Theoretical and experimental investigation on contact characteristics of hypoid gears under quasi-static condition. Chin. J. Sci. Instrum. 2017, 38, 1285–1295. [Google Scholar]
- Cao, X.M.; Deng, X.Z.; Wei, B.Y. A novel method for gear tooth contact analysis and experimental validation. Mech. Mach. Theory 2018, 126, 1–13. [Google Scholar] [CrossRef]
- Liang, Z.Q.; Huang, D.Q.; Zhou, T.F.; Li, H.W. Simulation and experimental research on grinding surface topography of spiral bevel gear. J. Mech. Eng. 2019, 55, 191–198. [Google Scholar] [CrossRef]
- ISO. 10300-Calculation of Load Capacity of Bevel Gears; International Standard: Geneva, Switzerland, 2014. [Google Scholar]
- ISO. 6336-Calculation of Load Capacity of Spur and Helical Gears; International Standard: Geneva, Switzerland, 2006. [Google Scholar]
- Chen, X.N.; Gu, D.Q. Machine Design; Zhejiang University Press: Hangzhou, China, 2004; pp. 165–172. [Google Scholar]
- Deng, X.Z.; Shu, Y.Q.; Liang, G.M. The Contact ratio of Spiral Bevel Gear for Different Loads. J. Luoyang Inst. Technol. 1994, 15, 47–152. [Google Scholar]
- AGMA. Rating the Pitting Resistance and Bending Strength of Generated Straight Bevel, ZEROL Bevel and Spiral Bevel Gear Teeth; American National Standard: New York, NY, USA, 1997. [Google Scholar]




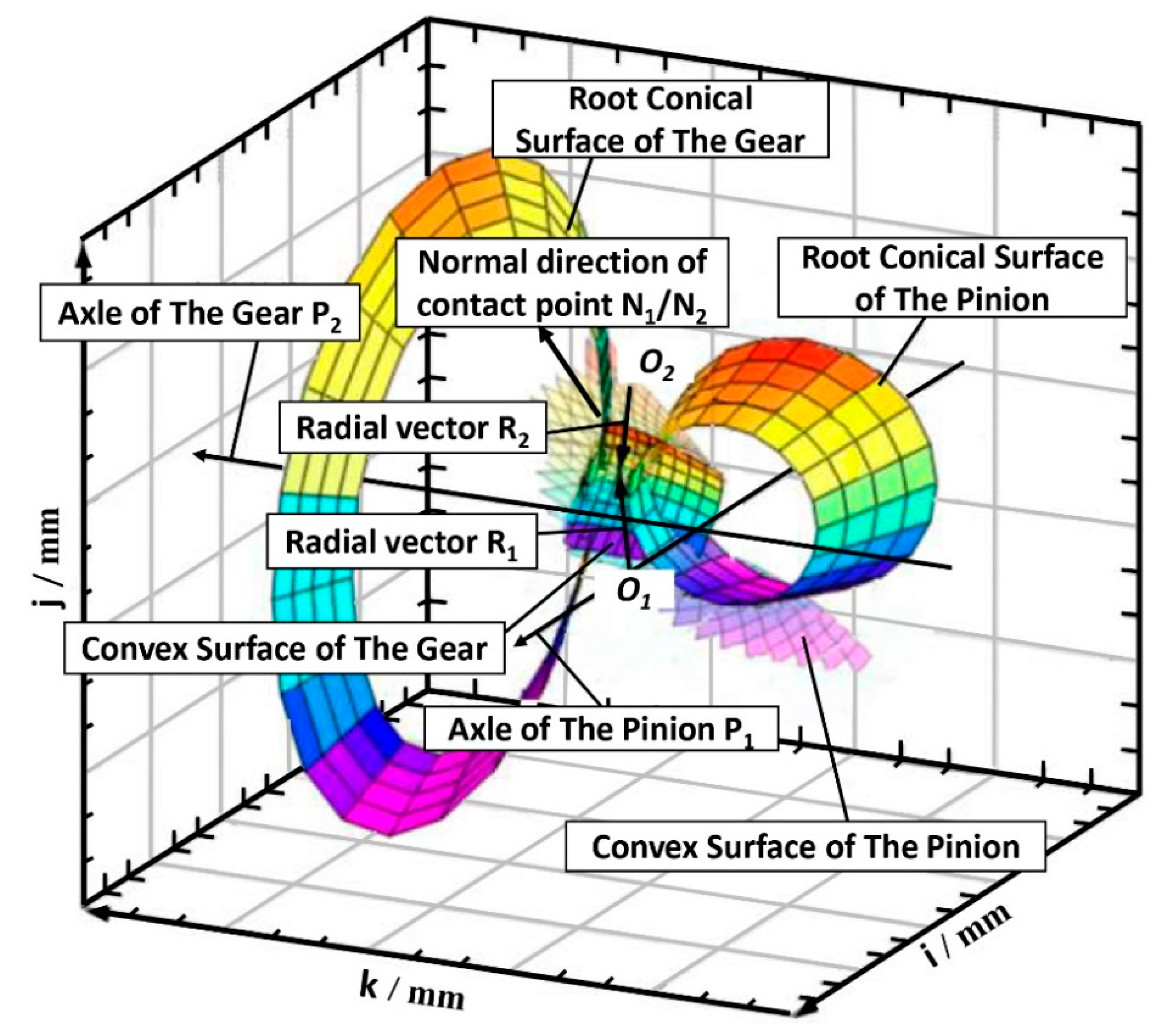
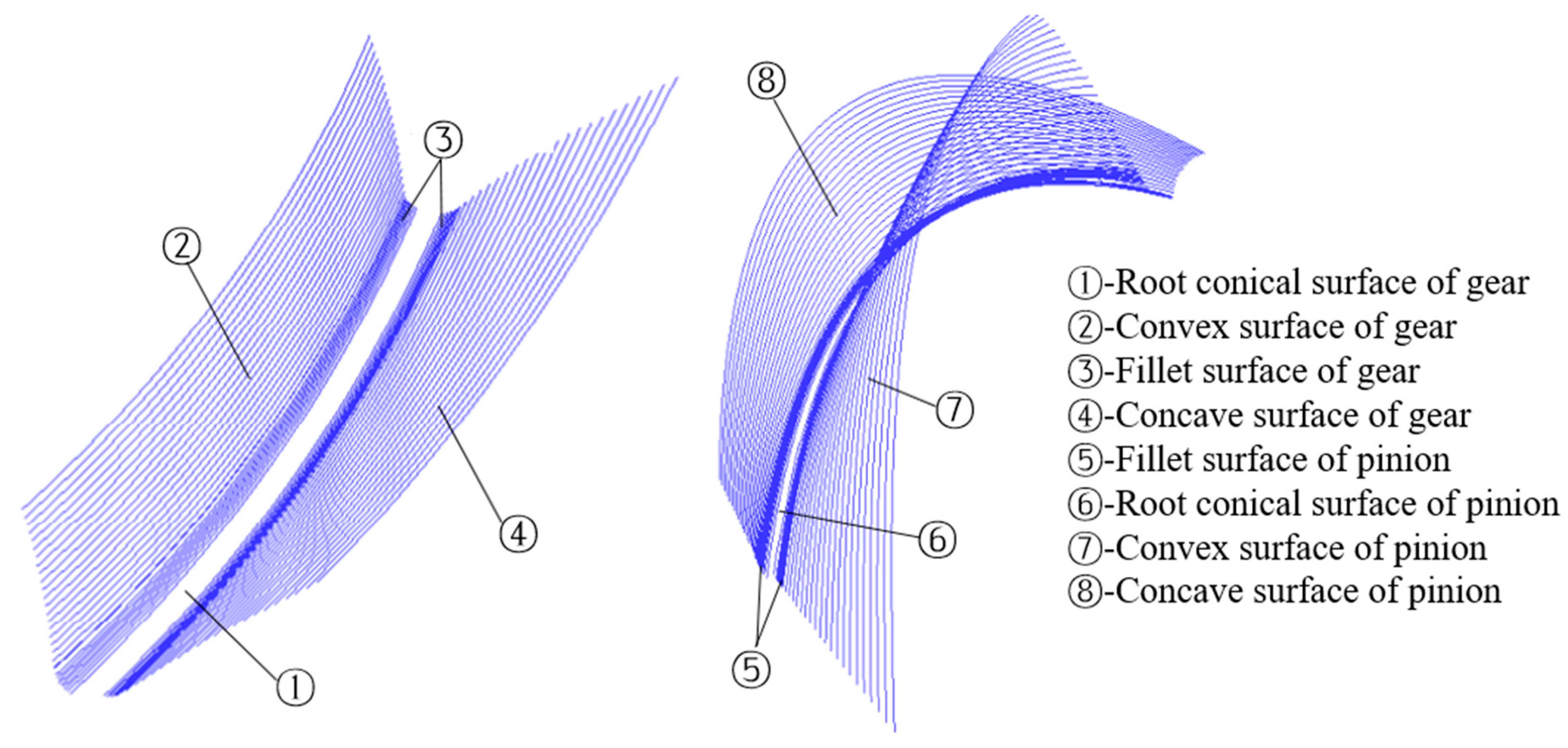













| Geometrical Parameter | Description | |
|---|---|---|
| Pinion | Gear | |
| Number of teeth | 15 | 46 |
| Hand of spiral | Left | Right |
| Modification coefficient | 0.35 | −0.35 |
| Pitch diameter (mm) | 90 | 276 |
| Tip diameter (mm) | 117.48 | 423.28 |
| Module (mm) | 6 | |
| Shaft angle (°) | 90 | |
| Pressure angle(°) | 20 | |
| Tooth width(mm) | 44 | |
| Spiral angle (°) | 35 | |
| Material | v | |||||
|---|---|---|---|---|---|---|
| 20CrMnTiA | 207 | 0.25 | 7800 | 1475 | 415 | 850 |
| Load T/Nm | Values of Differences Δ% | ||
|---|---|---|---|
| 1500 | 632.79 | 573.83 | 9.32 |
| 3000 | 815.48 | 758.25 | 7.02 |
| 4500 | 1045.32 | 914.49 | 12.51 |
| 6000 | 1324.21 | 1138.1 | 14.05 |
| 7500 | 1569.74 | 1331 | 15.21 |
| Load T/Nm | Gear | Pinion | ||||
|---|---|---|---|---|---|---|
| FEM Results | Calculated Results | Values of Differencs Δ% | FEM Results | Calculated Results | Values of Differences Δ% | |
| 1500 | 296 | 343 | 13.71 | 338 | 389 | 13.11 |
| 3000 | 456 | 529 | 13.79 | 567 | 643 | 11.82 |
| 4500 | 621 | 710 | 12.54 | 791 | 883 | 10.42 |
| 6000 | 805 | 890 | 9.55 | 925 | 1039 | 13.86 |
| 7500 | 912 | 1067 | 12.52 | 1183 | 1352 | 12.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Zhuo, Y.; Zhou, X.; Wan, B.; Lv, H.; Wang, Z. Theoretical and Experimental Study on Contact Characteristics of Spiral Bevel Gears under Quasi-Static and Large Loading Conditions. Appl. Sci. 2020, 10, 5109. https://doi.org/10.3390/app10155109
Fu Y, Zhuo Y, Zhou X, Wan B, Lv H, Wang Z. Theoretical and Experimental Study on Contact Characteristics of Spiral Bevel Gears under Quasi-Static and Large Loading Conditions. Applied Sciences. 2020; 10(15):5109. https://doi.org/10.3390/app10155109
Chicago/Turabian StyleFu, Yimeng, Yaobing Zhuo, Xiaojun Zhou, Bowen Wan, Haoliang Lv, and Zhe Wang. 2020. "Theoretical and Experimental Study on Contact Characteristics of Spiral Bevel Gears under Quasi-Static and Large Loading Conditions" Applied Sciences 10, no. 15: 5109. https://doi.org/10.3390/app10155109





