Gaussian Process Modeling of Specular Multipath Components
Abstract
:1. Introduction
- We derive a Gaussian process regression model for describing the spatial non-stationarity of SMC amplitudes in indoor environments.
- We validate the prediction capability of the GP based real measurements acquired in an indoor environment.
- We show that the GP is capable of modeling the angle-dependencies of the SMC amplitudes.
2. System and Signal Models
2.1. Signal Model
2.2. Amplitude Estimation
2.3. GP Modeling of the SMC Amplitudes
3. Gaussian Process Regression
3.1. GP Model
3.2. Prediction
3.3. Learning
3.4. Evaluate the Quality of Prediction
4. Results
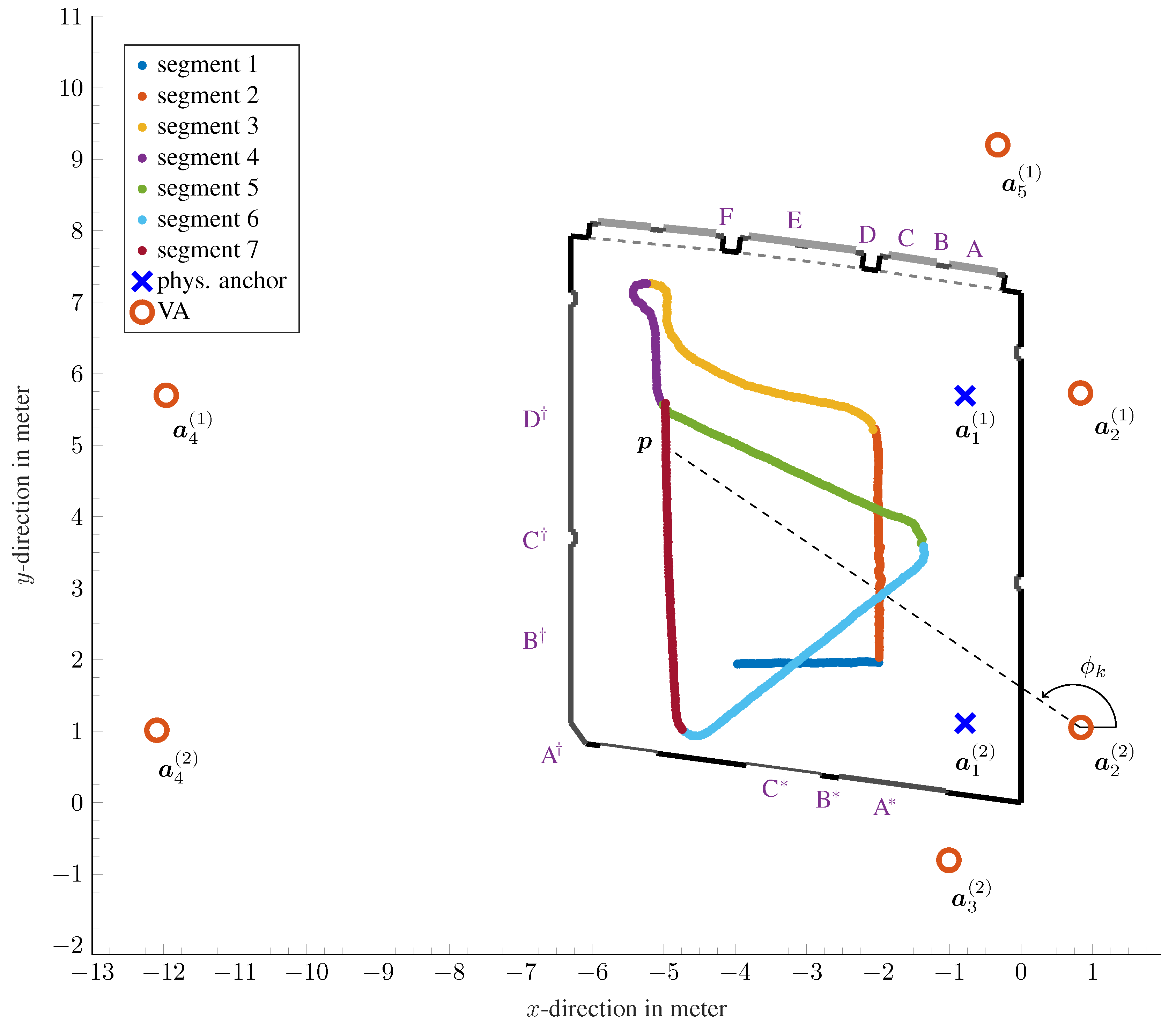
4.1. Experimental Setup
- EPB East plaster board.
- SW South wall.
- WW West wall.
- NGW North glass wall.
4.2. Measurement Pre-Processing
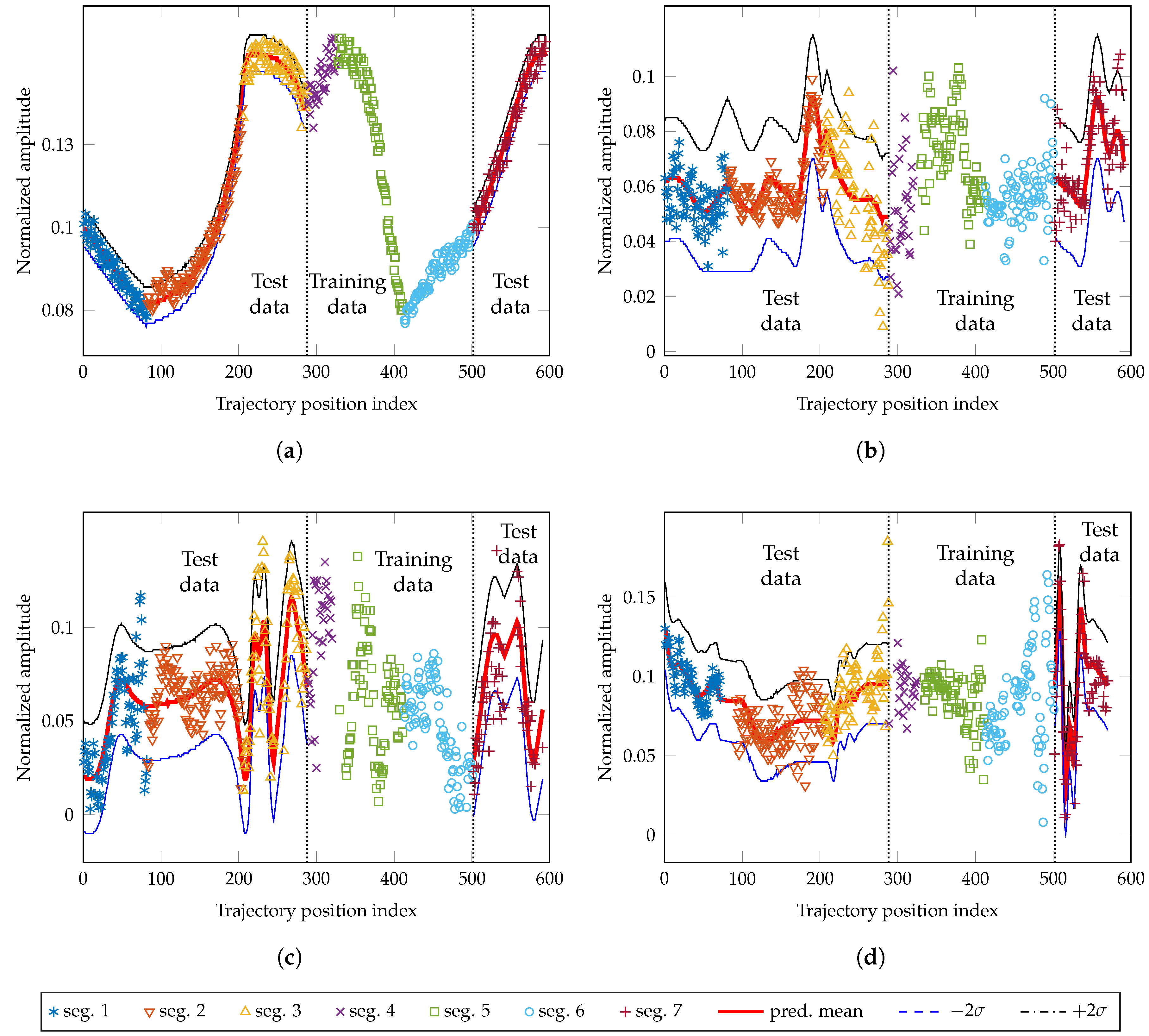
4.3. GPR of SMC Amplitudes
4.3.1. Predictability
4.3.2. Variance Verification
4.4. GPR of SMC Phases
Predictability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Variance of νk
- Assuming a signal with block-spectrum, the effective pulse duration is given as , where is the Nyquist sampling time.
- For root-raised-cosine, raised-cosine, or similar waveforms having a rectangular spectrum with tapered ends, is less than the Nyquist sampling time , under common symmetry conditions. For example, a raised-cosine pulse results in , where is the roll-factor.
Appendix B. Predicted Variance
References
- Boccardi, F.; Heath, R.W.; Lozano, A.; Marzetta, T.L.; Popovski, P. Five disruptive technology directions for 5G. IEEE Commun. Mag. 2014, 52, 74–80. [Google Scholar] [CrossRef] [Green Version]
- Fettweis, G.P. The Tactile Internet: Applications and Challenges. IEEE Veh. Technol. Mag. 2014, 9, 64–70. [Google Scholar] [CrossRef]
- Simsek, M.; Aijaz, A.; Dohler, M.; Sachs, J.; Fettweis, G. 5G-Enabled Tactile Internet. IEEE J. Sel. Areas Commun. 2016, 34, 460–473. [Google Scholar] [CrossRef] [Green Version]
- Di Taranto, R.; Muppirisetty, S.; Raulefs, R.; Slock, D.; Svensson, T.; Wymeersch, H. Location-Aware Communications for 5G Networks: How location information can improve scalability, latency, and robustness of 5G. IEEE Signal Process. Mag. 2014, 31, 102–112. [Google Scholar] [CrossRef] [Green Version]
- Muppirisetty, L.; Svensson, T.; Wymeersch, H. Spatial Wireless Channel Prediction under Location Uncertainty. IEEE Trans. Wirel. Commun. 2016, 15, 1031–1044. [Google Scholar] [CrossRef] [Green Version]
- Fröhle, M.; Charalambous, T.; Nevat, I.; Wymeersch, H. Channel Prediction With Location Uncertainty for Ad Hoc Networks. IEEE Trans. Signal Inf. Process. Netw. 2018, 4, 349–361. [Google Scholar] [CrossRef] [Green Version]
- Gentner, C.; Jost, T.; Wang, W.; Zhang, S.; Dammann, A.; Fiebig, U.C. Multipath Assisted Positioning with Simultaneous Localization and Mapping. IEEE Trans. Wirel. Commun. 2016, 15, 6104–6117. [Google Scholar] [CrossRef] [Green Version]
- Leitinger, E.; Meyer, F.; Hlawatsch, F.; Witrisal, K.; Tufvesson, F.; Win, M.Z. A Belief Propagation Algorithm for Multipath-Based SLAM. IEEE Trans. Wirel. Commun. 2019, 18, 5613–5629. [Google Scholar] [CrossRef] [Green Version]
- Mendrzik, R.; Meyer, F.; Bauch, G.; Win, M.Z. Enabling Situational Awareness in Millimeter Wave Massive MIMO Systems. IEEE J. Sel. Top. Signal Process. 2019, 13, 1196–1211. [Google Scholar] [CrossRef]
- Leitinger, E.; Meyer, F.; Tufvesson, F.; Witrisal, K. Factor graph based simultaneous localization and mapping using multipath channel information. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 652–658. [Google Scholar] [CrossRef]
- Leitinger, E.; Grebien, S.; Witrisal, K. Multipath-Based SLAM Exploiting AoA and Amplitude Information. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Leitinger, E.; Meissner, P.; Rudisser, C.; Dumphart, G.; Witrisal, K. Evaluation of Position-Related Information in Multipath Components for Indoor Positioning. IEEE J. Sel. Areas Commun. 2015, 33, 2313–2328. [Google Scholar] [CrossRef] [Green Version]
- Shahmansoori, A.; Garcia, G.E.; Destino, G.; Seco-Granados, G.; Wymeersch, H. Position and Orientation Estimation Through Millimeter-Wave MIMO in 5G Systems. IEEE Trans. Wirel. Commun. 2018, 17, 1822–1835. [Google Scholar] [CrossRef] [Green Version]
- Mendrzik, R.; Wymeersch, H.; Bauch, G.; Abu-Shaban, Z. Harnessing NLOS Components for Position and Orientation Estimation in 5G Millimeter Wave MIMO. IEEE Trans. Wirel. Commun. 2019, 18, 93–107. [Google Scholar] [CrossRef]
- Gustafsson, F.; Gunnarsson, F. Mobile positioning using wireless networks: Possibilities and fundamental limitations based on available wireless network measurements. IEEE Signal Process. Mag. 2005, 22, 41–53. [Google Scholar] [CrossRef]
- Kumar, S.; Gil, S.; Katabi, D.; Rus, D. Accurate indoor localization with zero start-up cost. In Proceedings of the 20th Annual International Conference on Mobile Computing and Networking, Maui, HI, USA, 7–11 September 2014. [Google Scholar]
- Meissner, P.; Leitinger, E.; Witrisal, K. UWB for Robust Indoor Tracking: Weighting of Multipath Components for Efficient Estimation. Wirel. Commun. Lett. IEEE 2014, 3, 501–504. [Google Scholar] [CrossRef]
- Witrisal, K.; Meissner, P.; Leitinger, E.; Shen, Y.; Gustafson, C.; Tufvesson, F.; Haneda, K.; Dardari, D.; Molisch, A.F.; Conti, A.; et al. High-Accuracy Localization for Assisted Living: 5G systems will turn multipath channels from foe to friend. IEEE Signal Process. Mag. 2016, 33, 59–70. [Google Scholar] [CrossRef]
- Poutanen, J.; Salmi, J.; Haneda, K.; Kolmonen, V.; Vainikainen, P. Angular and Shadowing Characteristics of Dense Multipath Components in Indoor Radio Channels. IEEE Trans. Antennas Propag. 2011, 59, 245–253. [Google Scholar] [CrossRef]
- Karedal, J.; Tufvesson, F.; Czink, N.; Paier, A.; Dumard, C.; Zemen, T.; Mecklenbrauker, C.F.; Molisch, A.F. A geometry-based stochastic MIMO model for vehicle-to-vehicle communications. IEEE Trans. Wirel. Commun. 2009, 8, 3646–3657. [Google Scholar] [CrossRef] [Green Version]
- Virk, U.T.; Haneda, K.; Wagen, J. Dense multipath components add-on for COST 2100 channel model. In Proceedings of the 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 13–17 April 2015; pp. 1–5. [Google Scholar]
- Oestges, C.; Clerckx, B.; Raynaud, L.; Vanhoenacker-Janvier, D. Deterministic channel modeling and performance simulation of microcellular wide-band communication systems. IEEE Trans. Veh. Technol. 2002, 51, 1422–1430. [Google Scholar] [CrossRef]
- Athanasiadou, G.E.; Nix, A.R.; McGeehan, J.P. A microcellular ray-tracing propagation model and evaluation of its narrow-band and wide-band predictions. IEEE J. Sel. Areas Commun. 2000, 18, 322–335. [Google Scholar] [CrossRef] [Green Version]
- Kanatas, A.G.; Kountouris, I.D.; Kostaras, G.B.; Constantinou, P. A UTD propagation model in urban microcellular environments. IEEE Trans. Veh. Technol. 1997, 46, 185–193. [Google Scholar] [CrossRef]
- Nguyen, H.A.; Rath, M.; Leitinger, E.; Hinteregger, S.; Nguyen, V.K.; Witrisal, K. Channel Capacity Analysis of Indoor Environments for Location-Aware Communications. In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Leitinger, E.; Grebien, S.; Li, X.; Tufvesson, F.; Witrisal, K. On the Use of MPC Amplitude Information in Radio Signal Based SLAM. In Proceedings of the IEEE Statistical Signal Processing Workshop (SSP), Freiburg, Germany, 10–13 June 2018; pp. 633–637. [Google Scholar]
- Borish, J. Extension of the Image Model to arbitrary Polyhedra. JASA 1984, 75, 1827–1836. [Google Scholar] [CrossRef]
- Bello, P. Characterization of Randomly Time-Variant Linear Channels. IEEE Trans. Commun. Syst. 1963, 11, 360–393. [Google Scholar] [CrossRef] [Green Version]
- Meissner, P.; Witrisal, K. Analysis of position-related information in measured UWB indoor channels. In Proceedings of the 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 6–10. [Google Scholar]
- Durgin, G. Space-time Wireless Channels, 1st ed.; Prentice Hall Press: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Rasmussen, C.; Williams, C. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2006; p. 248. [Google Scholar]
- Sachs, J.; Herrmann, R.; Kmec, M.; Helbig, M.; Schilling, K. Recent Advances and Applications of M-Sequence based Ultra-Wideband Sensors. In Proceedings of the 2007 IEEE International Conference on Ultra-Wideband, Singapore, 24–26 September 2007; pp. 50–55. [Google Scholar] [CrossRef]
- Molisch, A.F. Wireless Communications, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2010. [Google Scholar]
- Krall, C. Signal Processing for Ultra Wideband Transceivers. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2008. [Google Scholar]





| MPC | Constant Mean | DMC Stdv. | Char. Corr. Angle | GP Stdv. | |
|---|---|---|---|---|---|
| or [Linear or Rad] | or [Linear or Rad] | or [Deg.] | or [Linear or Rad] | ||
| abs. value | EPB—anchor 1 | 0.062 | 0.009 | 2.91 | 0.013 |
| LOS—anchor 1 | 0.099 | 0.003 | 43.11 | 0.035 | |
| NGW—anchor 1 | 0.075 | 0.014 | 1.02 | 0.02 | |
| SW—anchor 2 | 0.09 | 0.013 | 2.17 | 0.03 | |
| phase | EPB—anchor 1 | −0.956 | 0.387 | 9.83 | 1.03 |
| EPB—anchor 2 | −12.74 | 0.779 | 85.99 | 15.57 | |
| NGW—anchor 1 | −3.79 | 0.826 | 3.37 | 1.71 |
| MPC | SMSE | MSLL | |
|---|---|---|---|
| Amplitude | EPB—anchor 1 | 0.35 | −0.381 |
| LOS—anchor 1 | 0.014 | −2.099 | |
| NGW—anchor 1 | 0.46 | −0.175 | |
| SW—anchor 2 | 0.762 | −0.242 | |
| Phase | EPB—anchor 1 | 0.143 | −0.834 |
| EPB—anchor 2 | 0.058 | −1.25 | |
| NGW—anchor 1 | 0.294 | −0.54 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, A.H.; Rath, M.; Leitinger, E.; Nguyen, K.V.; Witrisal, K. Gaussian Process Modeling of Specular Multipath Components. Appl. Sci. 2020, 10, 5216. https://doi.org/10.3390/app10155216
Nguyen AH, Rath M, Leitinger E, Nguyen KV, Witrisal K. Gaussian Process Modeling of Specular Multipath Components. Applied Sciences. 2020; 10(15):5216. https://doi.org/10.3390/app10155216
Chicago/Turabian StyleNguyen, Anh Hong, Michael Rath, Erik Leitinger, Khang Van Nguyen, and Klaus Witrisal. 2020. "Gaussian Process Modeling of Specular Multipath Components" Applied Sciences 10, no. 15: 5216. https://doi.org/10.3390/app10155216





