Stochastic Extreme Wind Speed Modeling and Bayes Estimation under the Inverse Rayleigh Distribution

Abstract

Inverse Rayleigh probability distribution is shown in this paper to constitute a valid model for characterization and estimation of extreme values of wind speed, thus constituting a useful tool of wind power production evaluation and mechanical safety of installations. The first part of this paper illustrates such a model and its validity to interpret real wind speed field data. The inverse Rayleigh model is then adopted as the parent distribution for assessment of a dynamical “risk index” defined in terms of a stochastic Poisson process, based upon crossing a given value with part of the maximum value of wind speed on a certain time horizon. Then, a novel Bayes approach for the estimation of such an index under the above model is proposed. The method is based upon assessment of prior information in a novel way which should be easily feasible for a system engineer, being based upon a model quantile (e.g., the median value) or, alternatively, on the probability that the wind speed is greater than a given value. The results of a large set of numerical simulation—based upon typical values of wind-speed parameters—are reported to illustrate the efficiency and the precision of the proposed method, also with hints to its robustness. The validity of the approach is also verified with respect to the two different methods of assessing the prior information.

1. Introduction

Inverse Rayleigh distribution (IRD) has raised growing interest in modeling positive random variables and especially for its applications in reliability and survival times studies [1,2,3,4,5,6,7,8,9,10,11]. Being also a particular case of the inverse Weibull distribution, which has been adopted as a valid model for the characterization and estimation of extreme values of wind speed (WS) [12,13,14,15,16,17]—or briefly, “extreme wind speed” (EWS)—the IRD model is studied in this paper in relation to such kinds of applications.

Before introducing the above model, its generalization, and their application to EWS analyses, it is recalled that studies on wind speed statistical distribution are more and more largely widespread, since wind energy production strongly depends on such distribution. For instance, the annual electricity production (AEP) indicator is frequently used to quantify the electricity output expected in a particular system. The following expression can be considered for the evaluation of the AEP indicator [15]:

$$AEP=T{\displaystyle \underset{u_{cut,in}}{\overset{u_{cut,off}}{\int }}f\left(u\right)P\left(u\right)du}$$

(1)

where

-

AEP is in MWh,

-

T is the average number of hours per year (8760),

-

f(u) is the wind speed probability density function,

-

P(u) is the power curve of a turbine as function of wind speed, and

-

u_cut-in and u_cut-out are the cut-in and cutoff speed values of a turbine.

Hence, accurate wind speed distribution modeling is the first step to achieving accurate wind energy production estimation. Moreover, as discussed in [16,17,18,19,20], the randomness of WS also has a great impact on the mechanical reliability of wind power systems, since extreme values of wind speed may damage sensible components of the structures, such as towers and wind blades, so that EWS characterization also constitutes a basic tool for an officiate wind turbine design. Furthermore, as also pointed out in [19,20], values of WS that are greater than the “cutoff” value of the wind generator are generally undesirable, since the electric generator has to be disconnected from the wind turbine to not compromise the electrical section of the wind power system; consequently, the “cutoff” value of the generator must be chosen according to the characterization of EWS in the particular location, since it has a great impact on aggregate power production [21,22,23]. Therefore, EWS is also indirectly related to the AEP formulation of Equation (1). However, in this paper, primary reference to the issue of mechanical safety will be dealt with, with emphasis on the most adequate methods for the correct choice or identification of the various probability models involved, which is a delicate step in all applied statistical analysis [24].

Leaving more details on the IRD model to Section 2 and the Appendices, for the subsequent discussion, it is sufficient to report the following definition of the model: given a positive random variable (RV) X (the EWS in this study), the IRD cumulative distribution functions (CDF), F(x), with positive scale parameter α is expressed in the paper by the following equation:

$$F\left(x|\alpha \right)=e^{-\left(\frac{\alpha }{x^2}\right)},\hspace{1em}x>0$$

(2)

to which the following probability density function (PDF) corresponds:

$$f\left(x|\alpha \right)=2\alpha x^{-3}{e}^{-\left(\frac{\alpha }{x^2}\right)},\hspace{1em}x>0$$

(3)

In particular, in this paper, a practical method for the Bayes estimation [7,8,9,10,11,12] of the IRD model for EWS is proposed, in the framework of the assessment of a dynamical “risk index”, to be outlined in the following. The method is also extended to a generalization of the IRD obtained by means of a continuous mixture of its parameter. The mixture of the scale parameter has been recently adopted also for other models [19,20] in order to allow the randomness on environmental conditions of the windfarm under study.

Such a model is adopted as the parent distribution for assessment by means of a novel Bayes approach of a risk index model accounting for the most severe EWS amplitudes as disturbances for wind tower safety [18]. For the definition of such a risk index, this paper follows a probabilistic approach established in some basic literature on stochastic processes but probably not so widespread as it would be opportune in wind energy applications. Under such a stochastic approach—originated by classical studies on risk analysis as the authoritative book by Thompson [25]—safety is evaluated probabilistically in terms of a suitable stochastic counting process, measuring risk in terms of the occurrence of disturbance levels (i.e., EWS amplitude, in the case under study) higher than a prefixed threshold value. The risk index (RI) here adopted is defined with reference to a given time interval (0,t) as the probability that a given EWS amplitude is exceeded at least once in a time interval. As will be discussed with more details in Section 2 and Appendix A, if a threshold value z is assigned to EWS amplitudes, which is large enough, the occurrences of wind speed values which exceed such thresholds are rare events. Therefore, under general hypotheses, the process which counts the number of EWS values of exceeding z in the time interval (0,t) can be described, as deduced in advanced books on extremal processes [21,22,23], by the well-known Poisson stochastic counting process. Denoting by ϕ the parameter of such a Poisson process, i.e., the mean frequency of EWS values exceeding a given “threshold” value z, then, assuming that the EWS values Z_k are statistically independent and identically distributed with the common, time-independent CDF F(z), which is equal to the CDF of (2) according to the supposed model, the above defined RI can be expressed, as it will be shown, by the following:

$$R=R\left(t,z\right)=1-e^{-\phi t\left[1-F\left(z\right)\right]}$$

(4)

With reference to such an RI, this paper also discusses the problem of its statistical estimation in the presence of a few field data with the purpose of efficient assessment of wind tower reliability and safety, not forgetting that such kinds of analyses also allow to obtain useful information for wind power generation statistics, as above outlined.

In brief, the novelty of the proposed procedure discussed in this manuscript is twofold:

• The use of a new wind-speed model, the IRD one, to characterize extreme wind-speed distribution; such a model is proposed for the first time in the literature on the object, and its validity is illustrated with reference to real wind-speed data.
• The use of a new suitable and practical Bayes approach is introduced for the estimation of the above RI with reference to the above IRD wind-speed model. The numerical part of the manuscript shows that such a Bayesian statistical inference approach for the estimation of the above RI from available data possesses a very good level of efficiency and precision, as proven by the very low Root Mean Square errors (RMSE).

It is apparent that such results constitute novelties with respect to the current state-of-art on the subject.

The application of the proposed wind-speed model to real field data is reported in Appendix B. Moreover, in order to better highlight the application of the proposed wind-speed model to real field data, in Section 4, a brief summary of the steps which are necessary to perform the application of the proposed model to real field data is reported.

The rest of this paper is organized as follows. In Section 2, the basic steps leading to the RI of (4) are illustrated, together with the key features of the IRD model, characterizing the CDF F(z) of (4). In Section 3, a summary of the methods for IRD classical estimation is outlined; then, in Section 4, a suitable and practical Bayes approach is introduced for the estimation of the RI, with reference to the IRD model. The method constitutes a “practical” Bayesian statistical inference approach for the estimation of the EWS distribution from available data by using the model quantile or the model CDF as the proper input for the prior assessment of the model. The feasibility, efficiency, and precision of such a Bayes estimation method is finally illustrated in the successive and final Section 5, Section 6 and Section 7 by numerical examples and a broad amount of Monte Carlo simulations performed on the basis of typical values of real EWS data. Such results, illustrated by a large number of tables reported in Section 5 and Section 6, assess the good performance of the proposed approach, especially when compared to “classical” estimation methods, such as the maximum likelihood estimation [26,27,28,29,30,31,32,33].

Appendix A reports some details on the derivation of the RI of (6), while Appendix B reports some details on the IRD model, also with examples of their applications to real EWS data. Other Appendixes are also reported for recalling some basic properties of the statistical distributions mentioned in this paper (Appendix C, Appendix D and Appendix E), while Appendix F recalls useful relations concerning the gamma Probability density function (PDF) as a prior model for the scale parameter of the IRD distribution.

2. A Stochastic Risk Analysis for Extreme Wind Speed Data under the IRD Model

For the purpose of developing a stochastic risk analysis for extreme wind speed data, a stochastic approach established in some literature on extremal processes for safety applications [25] is adopted, also referring to specific application of such extremal processes to wind data [28,29,30]. Let a threshold value z be assigned to the EWS values for safety reasons. If z is large enough, the occurrences of wind speed values which exceed such thresholds (or “exceedances” in the following), are rare events which, under general hypotheses, can be described by the well-known Poisson process, i.e., by the probability law given, as well known, by the following [25,31]:

$$p\left(k,t\right)\equiv P\left[\mathrm{N}\left(t\right)=k\right]=e^{-\varphi t}\frac{{\left(\varphi t\right)}^k}{k!},\hspace{1em}k=0,1,\dots$$

(5)

where

-

N(t) is a process which counts the number of EWS values of exceeding z in the time interval (0,t);

-

p(k,t) is the probability that the number of exceedances in (0,t), N(t), and attains the nonnegative integer value k;

-

$\varphi$ > 0 is the mean frequency of the process N(t), i.e., the expected number of exceedances, over the threshold value z for a unit time or $\varphi =E\left[\mathrm{N}\left(t\right)\right]/t$.

Indeed, mean (or expected) value and variance of N(t) are expressed, as well known [25,31], by the following:

$$E\left[\mathrm{N}\left(t\right)\right]=Var\left[\mathrm{N}\left(t\right)\right]=\varphi t$$

(6)

Moreover, a stronger result holds, almost surely (a.s.) in terms of the so called “strong law” of the renewal processes [25,31]:

$$\varphi =\underset{t\to 0}{\lim }\frac{E\left[\mathrm{N}\left(t\right)\right]}{t}\hspace{1em}\hspace{1em}\left(a.s.\right)$$

(7)

The following developments, leading to the analytical expression of the RI, are discussed with more details in Appendix A. Let u(t,z) denote the probability that z is never exceeded over (0,t), i.e., a “safety” index.

Let the random variable “EWS amplitude occurring at time T_k of the kth exceedance” (k = 1,2, …) be denoted as Z_k. If the RV Z_k is (as typically assumed in the literature [18]) assumed to be statistically independent and identically distributed with the common, time-independent CDF,

$$F\left(x\right)=P\left(Z_k\le x\right),\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}k=1,2,\dots ,n$$

(8)

then, the following compact expression can be obtained for the above function u(t,z), as shown in Appendix A:

$$u\left(t,z\right)=e^{-\phi t\left[1-F\left(z\right)\right]}$$

(9)

Therefore, with the RI defined—as above reported—as the probability of the event that the EWS amplitude z is exceeded at least once, since such event is complementary of the event “z is never exceeded over (0,t)”, the above defined RI is expressed in terms of the function u(t,z) in (9) by the following:

$$R\left(t,z\right)=1-u\left(t,z\right)=1-e^{-\phi t\left[1-F\left(z\right)\right]}$$

(10)

By its very definition and clearly shown in its expression, such RI is intrinsically dynamic, being dependent on the chosen value of time horizon. If the above limit value z is chosen as the maximum value of the EWS that the structure can resist, then the RI is an efficient measure of the failure probability the structure. As discussed in [30], this kind of measure appears to be very significant for predicting the risk values associated with gust occurrence and their effects on real wind power systems.

In this framework, this paper discusses the problem of the statistical estimation of wind probabilistic distribution with the primary purpose of an efficient assessment of wind tower reliability and safety and of wind power generation statistics.

This is performed by assuming an IRD model as the reference model of the CDF F(z) in (10) and then by performing an estimation of the RI based upon the Poisson exceedances process and the above IRD model.

Let us first briefly illustrate the use of the IRD model for the EWS statistics and then the expression of the RI in (10) in terms of such IRD model. In Figure 1, three typical IRD PDF and CDF curves corresponding to the analytical expressions of (1) and (2) are shown, characterized by three different values of the parameter α (15, 45, and 90) (Such values of α correspond, as can be shown afterwards, to the following values of the median (50th percentile) of the wind speed RV: 5, 8, and 11 m/s respectively). The values on the x-axis are WS values in m/s.

The expression of the RI assuming the IRD as the reference model becomes the following:

$$R\left(t,z\right)=1-u\left(t,z\right)=1-e^{-\phi t\left[1-e^{-\left(\frac{\alpha }{z^2}\right)}\right]}$$

(11)

A set of possible curves of the RI in time are depicted in Figure 2, assuming a value α = 90 (corresponding to a median value of 11 m/s for the EWS); a mean frequency of the process N(t): ϕ = 10/year; and three different threshold values z of (22, 33, and 44) m/s, i.e., two, three, and four times the median value. From the three curves, it is apparent—as simply deducible from the meaning of the RI as well as from the general expression of (10)—that the RI always increases with time (given the scale parameter value of α and the threshold value z), while it decreases for a given time interval if z increases (allowing for a greater maximum value z implies decreasing the probability that such a value is exceeded).

Finally, as some figures will confirm in a following section—holding fixed the values of time t and threshold value z—the RI always increases with increasing values of scale parameter α, since both median and mean values (as also apparent from Figure 1) increase with α. Therefore, the PDF curve shifts to the right for increasing values of the parameter α, thus yielding a higher probability that a given threshold value z is exceeded, which means a higher value of the risk index in any given time interval.

3. Hints to the Classical Inference Methods of Estimation and Identification of the IRD Model

While the present paper is focused upon new Bayes estimation methods, the topic of classical estimation has been already discussed in the literature [1,2,3,4,5,6,31], so in this brief section, only hints to the classical ML (Maximum Likelihood) estimation method of the IRD distribution are illustrated with some further discussion on the model identification. The extension to the RI estimation is straightforward and is briefly illustrated here for the ML method: by virtue of the well-known property of invariance of the ML estimation, if ϕ * and F * are respectively the Maximum Likelihood estimates (MLE) of the quantities ϕ and F in (10), then the MLE of the RI in (10) is expressed for any fixed value of time t and threshold z by the following:

$$R^{*}\left(t,z\right)=1-e^{-{\varphi }^{*}t\left[1-F^{*}\left(z\right)\right]}$$

(12)

The MLE of the Poisson frequency is also well known in terms of the number of exceedances in a given interval (0,t) denoted by the random variable M (which counts the number of WS values in the given sample which exceed the value z) and is given by the following [31]:

$${\varphi }^{*}=\frac{M}{t}$$

(13)

Then, let us consider the MLE of the CDF F(z) appearing in (12) for an IRD model. First, we consider the MLE of parameter α of the IRD model in Equations (1) and (2). The log-likelihood function $\mathrm{L}\left(x|\alpha \right)$ of a dataset $x=\left\{x_1,x_2,\dots ,x_n\right\}$ of EWS values from an IRD model is simply deducible as follows:

$$\mathrm{L}\left(x|\alpha \right)=N\log 2+N\log \alpha -\alpha {\displaystyle \sum _{i=1}^N\left[{\left(\frac{1}{x_i}\right)}^3\right]-3{\displaystyle \sum _{i=1}^N\log x_i}}$$

(14)

Equating to zero the partial derivative of the above function with respect to parameter α *, the MLE of such parameter is as follows:

$${\alpha }^{*}=\frac{N}{{\displaystyle \sum _{i=1}^N{x}_k^{-2}}}$$

(15)

It is remarked that each RV 1/X_k follows a Raleigh distribution, so its square obeys an exponential law [1,2,3,4,5,6,31].

It is known that a sum of independent exponentially distributed random variates gives a gamma distributed variable, giving the probability density function of the sum in the denominator of (15) as a gamma PDF with parameters: N (shape) and α (scale).

Finally, since—as already recalled—the MLE is invariant, the MLE of the CDF F(z) appearing in (12) is provided, looking at (2), by the following:

$$F^{*}\left(z\right)=F\left(z|{\alpha }^{*}\right)=e^{-\left(\frac{{\alpha }^{*}}{x^2}\right)}$$

(16)

Let us give a brief hint to the IRD model identification, which is very simple given the basic properties of the inverse Rayleigh model, i.e., the fact that it describes the distribution of X = 1/Y, with Y being a Rayleigh RV, for which identification is a well-established topic. Therefore, the goodness of fit tests for assessing the validity of an IRD model for a given set of EWS data $x=\left\{x_1,x_2,\dots ,x_n\right\}$ is simply performed (as exemplified in the Appendix B) assessing the validity of Weibull model with shape parameter b = 2, i.e., a Rayleigh model, for the data $y=\left\{y_1,y_2,\dots ,y_n\right\}$, where y_k = 1/x_k.

4. A Bayes Method of Inference for the Risk Index Based upon the IRD Model

4.1. A Premise. Bayes Estimation of the Frequency of Exceedances

Bayes method of inference or estimation—as illustrated in its general theory in [26,27] and for some EWS applications in [12,18,20]—is proposed here for the RI under the IRD model. This kind of inference implies the assessment of prior information on the model parameters. In the cases under study, there are two parameters to be estimated:

(1)

The mean frequency ϕ of the process N(t) in (5), i.e., the expected number of exceedances of the EWS per unit time according (6). Briefly, ϕ is denoted as frequency of exceedances.

(2)

The parameter a of the IRD model of (2) and (3) or any other parameter related to these ones.

The above phrase “any other parameter related to the parameter a of the IRD model” means, for instance, the CDF of the above model, denoted as F(x|α) in Section 1.

Indeed, the mentioned relation represents a one-to-one correspondence between the parameter α vs. the IRD CDF F(x) for any given EWS value x. In the proposed approach, the prior information can be assessed equivalently both in terms of the “basic” parameters (α) or of the corresponding CDF of their respective model.

It is remarked that assessing the prior information in terms of the basic parameters (α) is also equivalent to assessing the prior information in terms of the of the quantiles of the model, which are related to α.

Whatever the choice, depending on the available information or past experience, for assessing the above information, the ultimate purpose of the inference is to evaluate the Bayes estimates of the above defined RI, in which time t and threshold z are to be considered known constants:

$$R=R\left(t,z\right)=1-e^{-\phi t\left[1-F\left(z\right)\right]}$$

(17)

It may be convenient in order to simplify some of the following formulations and considering that the time horizon t and threshold z are to be held fixed to express more concisely the RI as follows:

$$R=R\left(t,z\right)=1-e^{-WS}$$

(18)

where

$$W=W\left(t\right)=\phi t\mathrm{and}S=S\left(z\right)=1-F\left(z\right)$$

(19)

are respectively the “expected number of exceedances” (ENE) in (0,t), and the complementary CDF (CCDF) (or “survival function”) of the EWS amplitudes evaluated at z, i.e., S represents the probability that the threshold value z is exceeded by any single EWS values.

Since S(z) = 1 − F(z|α) for the IRD model, the RI to be estimated can be considered as functions of two RVs, R = p(ϕ, α). Moreover, the two input RVs (ϕ and α) for the RI estimation will be considered as statistically independent of each other.

In general terms, denoting by T = (X,Y) the 2-dimensional vector of the two input RV, the problem of the Bayes estimation of the function R = p(X,Y) = p(T) is briefly outlined in the following, leaving the details to the well-established literature on the subject [26,27].

The Bayes estimator (BE) of R requires a joint prior PDF of the RV (X,Y), denoted by p(x,y), expressing prior belief or information about the above parameters. Such a prior PDF on (X,Y) implies—as will be shown for the cases under study—a prior PDF on the RI R and is based upon the well-known Bayes formula used to derive the posterior PDF q(r|D), conditional to data D (the observed EWS data in this application), which has been collected:

$$q\left(r|D\right)=\frac{p\left(r\right)L\left(D|r\right)}{C}$$

(20)

where L is the Likelihood function [26,27], given the observed data w, and C has the following expression:

$$C={\displaystyle \underset{0}{\overset{\infty }{\int }}p\left(r\right)L\left(D|r\right)dr}$$

(21)

Finally, as well known [26,27], the best Bayes estimate—in the mean square error sense—of R is given by its “posterior mean”, evaluable through the posterior PDF of R, q(r|D):

$$R°=\mathrm{E}\left[R|D\right]={\displaystyle \underset{0}{\overset{\infty }{\int }}rq\left(r|D\right)dr}$$

(22)

In practice, due to the nature of R, i.e., the fact that it is a probability, the above integration is confined to the interval (0,1).

Analogous formulations applied to the estimation of the single parameters (ϕ and α) will be illustrated in the following two subsections.

Therefore, before considering the relevant features of the above general formulations to the practical cases of the IRD model, the Bayes estimation of ϕ is illustrated here in a brief summary since, differently from the estimation of α, it is well established in the literature [25,31]. As above recalled, f is the mean frequency of the process N(t) counting the number of exceedances: these are random events which occur at random time,: T₁, T₂, …, T_n, by well-known properties of the Poisson process; such random times instants are gamma random variables [25,31], and the times between two subsequent events, τ_k = T_k+1 − T_k (assuming and T₀ = 0) are Exponential random variables with mean value μ = 1/ϕ. It is well-known [28] that a gamma PDF, also recalled in Appendix C, apart from being very flexible for describing positive random variables is a valid choice for the prior PDF of the RV ϕ, since it is a “conjugate” PDF [26,27], i.e., the posterior PDF is still a gamma PDF. Thus, in this paper, a gamma prior PDF—denoted as “Gampdf (ϕ; p₀,θ₀)”—for ϕ is assumed:

$$p\left(\varphi |{\rho }_0,{\vartheta }_0\right)=\frac{{\varphi }^{{\rho }_0-1}}{\mathsf{\Gamma }\left({\rho }_0\right){\theta }^{{\rho }_0}}{e}^{-\left(\frac{\varphi }{{\theta }_0}\right)}$$

(23)

Then, let a sample of EWS data $x=\left\{x_1,x_2,\dots ,x_n\right\}$ be observed in a given time interval (0,t), and the number of exceedances of z be denoted by M as in the previous section. The likelihood function of the sample, i.e., of data D, is the probability that M exceedances are observed in time interval (0,t), computed by mean of the above Poisson PDF,

$$\mathrm{L}\left(D|\phi \right)=P\left[N(t)=M\right]=e^{-\varphi t}\frac{{\left(\varphi t\right)}^M}{M!}$$

(24)

It is then straightforward to deduce that the product of the gamma prior PDF of (23) and the likelihood function of (24) yields a posterior PDF of ϕ, q(ϕ|D), which is still a gamma PDF, i.e., a Gampdf (ϕ; p₀,θ₀) with updated parameters [26,27]:

$${\mathsf{\rho }}_1={\mathsf{\rho }}_0+M;\hspace{1em}{\mathsf{\theta }}_1=\frac{{\mathsf{\theta }}_0}{1+{\mathsf{\theta }}_0}$$

(25)

Therefore, the BE of ϕ being expressed, the mean of its posterior PDF, is computed as follows (see also Appendix C for the mean of a gamma PDF):

$$\phi °=\mathrm{E}\left(\varphi |D\right)={\mathsf{\nu }}_1{\delta }_1=\frac{{\delta }_0\left({\mathsf{\nu }}_0+n\right)}{1+U{\delta }_0}$$

(26)

Of course, the same arguments apply to the Expected number of exceedances (ENE) RV, W = ϕt. It is easily proved [28] that, if ϕ is a gamma RV with parameters ν and δ, then the RV W = ϕt is still a gamma RV with parameters p’ and θ’ simply related to p and θ as follows: p’ = p; θ’ = θt.

It is also straightforward to verify that the gamma conjugate PDF for ϕ also implies a gamma conjugate PDF for W. Thus, in the paper, a gamma prior PDF Gampdf (ϕ; p₀, θ₀ t) for W is assumed with parameters deduced from the gamma prior PDF of ϕ. As above said, the posterior PDF of W is still a gamma prior PDF Gampdf(ϕ; p₁, θ₁),

$$p\left(w\right)=\frac{w^{\left({\rho }_1-1\right)}}{{\theta }_1^{{\mathsf{\rho }}_1}\mathsf{\Gamma }\left({\rho }_1\right)}{e}^{-\frac{w}{{\mathsf{\theta }}_1}},\hspace{1em}w>0$$

(27)

and the BE of W is as follows:

$$W°=\mathrm{E}\left[W|D\right]={\rho }_1{\theta }_1=\frac{{\theta }_{0}t\left({\rho }_0+n\right)}{1+{\theta }_0}$$

(28)

A final remark seems opportune before concluding this subsection devoted to the estimation of ϕ.

The assessment of the prior PDF on S is dealt with in the following subsections. Once the posterior PDF of S, q_S(s), is also obtained, it can be used together with the posterior PDF of W, q_W(w), for determining the joint posterior PDF of W and S, which—assuming the statistical independence of W and S—will be given by the following:

$$q\left(w,s\right)=q_w\left(w\right)q_s\left(s\right)$$

(29)

Then, an alternative (but equivalent) formulation of the BE of R, instead of (22), can be made in terms of joint posterior PDF of W and S as follows:

$$r°=\mathrm{E}\left[R\left(W,S\right)|D\right]=1-{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-ws}q\left(w,s|D\right)}}drds$$

(30)

It is remarked that, in some cases, the above double integration can be avoided as well as the explicit evaluation of the single integration of (22). First, let us consider the prior PDF assessment.

An opportune method which will be pursued in the following for a feasible estimation of the RI is the one assessing the prior PDF on the CCDF S of (18) in order for—at least in principle—easy evaluation of the implied prior PDF of the product, V = WS, and consequently of the RI:

$$\{\begin{array}{l}R=1-e^{-V}\\ V=WS\end{array}$$

(31)

Therefore, an alternative way to evaluate the BE of R may be obtained by means of a single integrations, as follows: if the PDF of V is computed, then the BE of R can be computed in terms of such a posterior PDF of V, q(v|D), with $R=e^{-V}$:

$$r°=1-\mathrm{E}\left[e^{-\mathrm{V}}|D\right]=1-{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-v}q\left(v|D\right)}dv$$

(32)

It is noticed that the above formulation establishes the BE of the RI in terms of a “Laplace Transform” of the posterior PDF of V.

A useful analytical tool, given that a gamma prior PDF is assumed for W, is the assessment of the prior PDF for the probability S(z) = 1 − F(z) by mean of a model that possesses hopefully the two following properties:

(1)

First, the obvious property that such a model is very manageable analytically and rather flexible for a RV with support in the interval (0,1).

(2)

Moreover, in view of (32), it is opportune that it can render the above product V = WS manageable analytically, i.e., that the PDF of the RV V = WS and R = 1−exp(−V) could be easy computable, at least approximatively, by analytical formulations or simple numerical tools.

This seems to be the case if a beta prior PDF [28] is assumed for S. It is indeed by far the most widely adopted model in Bayes estimation for a RV which is a probability [26,27] since it is well-known that it constitutes the most practical and flexible model to express a prior PDF for a RV confined in the (0,1) interval. It is recalled (see Appendix D for details) that the beta PDF has the following form, in which s is a generic value of the RV S, and a and b are positive parameters:

$$p\left(s;a,b\right)=\frac{\mathsf{\Gamma }\left(a+b\right)}{\mathsf{\Gamma }\left(a\right)\mathsf{\Gamma }\left(b\right)}{s}^{a-1}{\left(1-s\right)}^{b-1},\hspace{0.17em}\hspace{0.17em}0<s<1$$

(33)

The above formulation is denoted by the symbol “p(s)”, as this is adopted in the paper for all prior PDFs. It is possible—as it will be shown in the following—that also the posterior PDF q(s|D) is a beta PDF (or it may be approximated by a beta PDF) which simplifies all the subsequent computations. However, let us continue by examining the prior assessment.

Under the above assumption, the product V = WS has a computable PDF here denoted as a “beta-gamma product” (BGP) PDF, as reported in Appendix E. In some cases, such a product still has a gamma PDF, and in this case also, the RI R possesses a computable prior PDF, i.e., a Negative Log-Gamma distribution (NLGD) PDF (in Appendix C). In some cases, discussed in the following, this also holds for the posterior PDF, at least approximately, as illustrated in the course of the numerical application. This implies that the BE of R, evaluated as the posterior mean of R, is obtained by well-known formulations (reported in the Appendix C), thus avoiding the above integrations.

4.2. Bayes Estimation of the Parameters of the IRD Model

The Bayes estimation of the IRD model implies to estimate the parameter α in the expression of the IRD CDF:

$$F\left(x|\alpha \right)=e^{-\left(\frac{\alpha }{x^2}\right)}$$

(34)

For this estimation, two methods for are considered in the paper in order to establish appropriate prior distributions:

(1)

A gamma prior distribution on α, which is a conjugate distribution (see Appendix F and [26,27]).

(2)

A negative exponential beta distribution (NEBD) on α, (see Appendix D) which is not a conjugate distribution, but has the advantage of implying a beta distribution on S.

The choice of a gamma prior distribution is already reported in the literature and will not be further discussed here but will directly be used in the course of the numerical applications. Before discussing such method, it is recalled that, in the Bayesian setting, also the CDF and other parameter (e.g., moments and quantiles), being functions of α, are themselves RV, described by appropriate distributions. The same also holds for the CCDF:

$$S\left(z\right)=1-F\left(z|\alpha \right)$$

(35)

for which estimation, as outlined above, can directly allow for the estimation of the RI. The assessment of the prior information in terms of the parameter α, a quantile, the CDF, or any other parameter is a matter of convenience, depending on which information is available. Generally, it is advisable to base the estimation upon a parameter which possesses a clear physical meaning, which is not the case for α, which appears to be difficult to interpret. The information on a given quantile should be more easily available and also interpretable, so it is chosen here first how to use this kind of information. In particular, for sake of illustration, the median is chosen as the input RV for assessing the estimation, with no loss of generality, since any quantile X_p is proportional to the median through the following relations, which are simply deducible (see Appendix B):

$${\mathrm{X}}_p=m{\left[\frac{\mathsf{\psi }}{{\mathrm{K}}_p}\right]}^{\frac{1}{2}};\hspace{1em}\mathsf{\psi }=\log \left(2\right)=0.6931;\hspace{1em}{\mathrm{K}}_p=-\log \left(p\right)>0$$

(36)

Therefore, an assessment of the prior information in terms of any quantile is essentially the same as an assessment of the prior information in terms of the median, which in turn implies a prior information in terms of α, since

$$\alpha =\mathsf{\psi }{\left(m\right)}^2$$

(37)

The above relations also imply prior information in terms of IRD CCDF, expressible in terms of the median m as well as in terms of the parameter α:

$$S=S\left(z|m\right)=1-F\left(z|m\right)=1-e^{-\mathsf{\psi }{\left(\frac{m}{z}\right)}^2}=1-F\left(z|\alpha \right)=1-e^{-\left(\frac{\alpha }{z^2}\right)}$$

(38)

It is remarked that the function S(z) reported here, being relevant to a fixed threshold value, z, of EWS has to be regarded as a constant, i.e., a parameter, in view of the estimation process. In the above Equation (34), instead, the CDF F(x) reported there denotes a function of the generic EWS value as a variable argument.

Far from what is above discussed, the peculiar method suggested in this paper is that S, a RV with support in (0,1), is assumed as a beta RV, which implies that the parameter α has an NEBD PDF, as can be deduced from Appendix D, since

$$\alpha =\left[-\log \left(1-S\right)\right]z^2$$

(39)

In practice, assuming an NEBD prior PDF for α implies that the negative exponential function of α in (38) has a beta distribution. This assumption has the advantages already discussed in the previous section and may be put in practice, starting from prior information in terms of the median as follows:

Let a prior guess on the median be given in terms of a “credible interval” (m₁, m₂), i.e., a Bayesian (prior) confidence interval on the median, i.e., an “interval” (m₁, m₂) such that, for a given probability value p,

$$P\left(m_1<m<m_2\right)=p$$

(40)

1)

Since α = ψ (m)², the corresponding quantiles (α₁, α) on α are readily be evaluated as follows:

α₁ = ψ (m₁)²; α₂ = ψ (m₂)²

so that

$$P\left({\alpha }_1<\alpha <{\alpha }_2\right)=p$$

(41)

2)

On the basis of such quantiles of α, the corresponding quantiles of S are readily computed by (38) with S being a one-to-one increasing function of α, as follows:

$$S_1=1-e^{-\left(\frac{{\alpha }_1}{x^2}\right)};S_2=1-e^{-\left(\frac{{\alpha }_2}{x^2}\right)}$$

(42)

This information is sufficient (see [27]) for assessing the beta PDF on S. In any case, the posterior PDF on S must be evaluated numerically. In principle, this also holds for the posterior PDF on R, which is the basic tool for assessing the BE of R, i.e., its posterior mean. Some simplifications are however possible, which will be shown to be numerically acceptable. It was already discussed that, in cases in which S has a beta PDF, V has a computable PDF, the BGP PDF. Apart from such particular cases, the independence of W and S can be used as a basis for evaluating the posterior mean of V:

$$\mathrm{V}°=\mathrm{E}\left[\mathrm{V}|D\right]=\mathrm{E}\left[\mathrm{W}|D\right]\mathrm{E}\left[\mathrm{S}|D\right]={\rho }_1{\theta }_1\mathrm{E}\left[\mathrm{S}|D\right]$$

(43)

where p₁ and θ₁ are the posterior gamma parameters computed in the previous subsection. This shows that only the posterior mean of S is needed in order to evaluate the posterior mean, i.e., the BE, of V°.

This does not imply a direct estimation of the RI, which theoretically requires the integration of (30) or (32).

However, at least as a first-order approximation, with R = e^−V, the following approximation of the BE of R can be evaluated:

$$\mathrm{R}°=1-e^{-\mathrm{V}°}$$

(44)

Finally, if V can be described by a gamma distribution, then R has a “negative log-gamma” distribution (summarized in Appendix D and recalled in the previous subsection) and its posterior mean is evaluable analytically.

5. A Framework for the Numerical Applications of the Bayes Method of Inference for the Risk Index with Reference to Practical Applications

Before illustrating (in the next sections) extensive numerical applications of the Bayes method aimed at evaluating its performances, a framework for such numerical applications is established here in order to better highlight the rationale behind the computations which will be shown afterwards. For the sake of brevity, only the case of a gamma prior PDF on the IRD parameter a will be illustrated here, leaving the case of a of a beta prior PDF on the IRD CCDF S(α) to be illustrated directly in the course of the numerical applications. Section 5.1 here is devoted to the prior assessment analysis, and the following Section 5.2 is devoted to the posterior analysis, still in the case of a gamma prior PDF on the IRD parameter α. the assumption of a gamma prior PDF on the Poisson parameter ϕ is always maintained instead. It is remarked that the two subsections both referred to practical applications, being based upon typical wind-speed data as those reported in the Appendix B.

5.1. The Case of a Gamma Prior PDF on the IRD Parameter α: Prior Analysis

First, for sake of numerical illustration in

Table 1. Some values of the RI corresponding to nine couples of values (ϕ, α), t = 1 year, and z = 22.

ϕ(year−1)	α(m2/s2)
	15	45	90
2.5	0.0735	0.1991	0.3457
5	0.1415	0.3585	0.5719
10	0.2630	0.5885	0.8167

, some values of the RI, computed as

$$\{\begin{array}{l}R=R\left(t,z,\varphi ,\alpha \right)=1-e^{-\mathrm{WS}}\\ \mathrm{W}=\phi \mathrm{t}\\ S=1-F\left(z|\alpha \right)=1-e^{-\left(\frac{\alpha }{x^2}\right)}\end{array}$$

(45)

are shown with reference to a fixed time interval of 1 year, a threshold value z = 22 m/s., and nine couples of values (ϕ, α), shown respectively in the headings of the rows and columns of Table 1.

Also, the following numerical applications will refer to these typical values of the RI and parameters ϕ and α.

As already discussed, the values of the RI increase as both ϕ and α increase, so they increase from left to right, looking through rows, and from top to bottom, looking through columns. In particular, for the sake of brevity, the three cases corresponding to boldface characters in the principal diagonal of Table 1 will be those taken as references in the course of the following numerical applications. Considering that the parameters ϕ and α are RVs in the Bayes method, their values are to be considered expected values of their prior distributions. Therefore, the following three cases are taken as references:

Case A

(“low risk” values): E[ϕ] = 2.5, E[α] = 15, corresponding to an approximate expected value of the RI: E[R] ≈ 0.0735;

Case B

(“medium risk” values): E[ϕ] = 5, E[α] = 45, corresponding to an approximate expected value of the RI: E[R] ≈ 0.3585;

Case C

(“high risk” values): E[ϕ] = 10, E[α] = 90, corresponding to an approximately expected value of the RI: E[R] ≈ 0.8167

The above reported expected values of the RI: (E[R] = 0.0735, 0.3585, and 0.8167), as taken from Table 1, are merely indicative; indeed they are approximate expected values since the RI is a nonlinear function of (ϕ, α):

E [R (ϕ, α)] ≠ R [(E [ϕ], E [α])]

Indeed, for a given prior PDF p(ϕ, α) of (ϕ, α) which—as long as t = 1 year and W = ϕ t—coincides with the prior PDF p(w,α) of (w,α), the mean of R, as already discussed before since $\mathrm{R}=1-e^{-\mathrm{WS}\left(\alpha \right)}$ should be computed as follows:

$$\mathrm{E}\left[R\left(W,S\right)|D\right]=1-{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-ws}q\left(w,s|D\right)}}drds$$

(46)

However, hints on a simpler way to obtain such an expected value of R have already been hinted at before and will be shown here in the course of computations, together with numerical or simulation methods, which are always possible to give a better approximation if the above ones are generally satisfactory, but it is remarked that the primary meaning of the above approximations (such as E[R] ≈ 0.0735, and more) is not to serve as approximate expected values of the true means but only as typical values that one should expect from computations, so that the experimenter can choose the typical values of the parameters to be assigned a prior PDF with a better knowledge of its implications.

As for the choice of the prior PDF p(ϕ, α), i.e., the gamma PDF (on both ϕ and α) and/or beta PDF on S(ϕ, α), their parameters are chosen in order to obtain the expected values of the cases A, B, and C above; moreover, in each of the three cases, different values of the prior coefficient of variation (CV)—i.e., the ratio between standard deviation and mean values of ϕ and a—are chosen in order to show different degrees of prior uncertainty (a larger prior CV value implies a higher degree of prior uncertainty about the random parameter values). Therefore, denoting for a given RV Q, its CV is as follows in terms of its mean value E[Q] and standard deviation STD[Q]:

$$\mathrm{CV}\left[\mathrm{Q}\right]=\frac{\mathrm{STD}\left[\mathrm{Q}\right]}{\mathrm{E}\left[\mathrm{Q}\right]}$$

(47)

The following values of CV for both ϕ and α have been chosen: 0.05 and 0.10, giving rise to four different subcases of the three cases A, B, and C above, each labeled with (i,j) indexes, “i” standing for 1 or 2 according to CV[ϕ] = 0.05 or CV[ϕ] = 0.10 and “j” having the same meaning for CV[α].

In detail, 12 = 3 × 4 sets of combinations of prior values (corresponding to different simulation cases) among the many more performed are shown in the following sections with respect to the mean value and CV of the input RV(ϕ, α), as listed with more details in the next section, while here, they are only exemplified in

Table 2. Combinations of prior values with respect to mean value and coefficient of variation (CV) of the input random variable (RV) (ϕ, α).

Case	E[ϕ]	E[α]	CV[ϕ]	CV[α]
A11	2.5	15	0.05	0.05
A12	2.5	15	0.05	0.10
A21	2.5	15	0.10	0.05
A22	2.5	15	0.10	0.10
B11	5.0	45	0.05	0.05
B12	5.0	45	0.05	0.10
B21	5.0	45	0.10	0.05
B22	5.0	45	0.10	0.10
C11	10	90	0.05	0.05
C12	10	90	0.05	0.10
C21	10	90	0.10	0.05
C22	10	90	0.10	0.10

:

Details on the results of numerous simulations performed for each one of the above cases will be shown in the following sections, while here, some highlights are reported which give some insight on the process of the prior and posterior PDF assessments and on the BE of the RI. For the sake of exemplification, case C11 is examined. Therefore, it is assumed that, concerning the prior PDF assessment,

-

α has a prior gamma PDF with E[α] = 90, CV[α] = 0.05;

-

ϕ has a prior gamma PDF with E[ϕ] = 10, CV[ϕ] = 0.05.

Let us examine first the prior gamma PDF for α: as already reported (see also Appendix C and Appendix F), the mean and variance of such prior PDF with parameters ν₀ and δ₀ are

$$\mathrm{E}\left[\alpha \right]={\nu }_0{\delta }_0;\hspace{1em}\mathrm{VAR}\left[\alpha \right]={\nu }_0{\delta }_0^2$$

(48)

which imply

$$\mathrm{STD}\left[\alpha \right]={\nu }_0^{1/2}{\delta }_0\to \mathrm{CV}\left[\alpha \right]=\frac{\mathrm{STD}\left[\alpha \right]}{\mathrm{E}\left[\alpha \right]}=\frac{1}{{\nu }_0^{1/2}}$$

(49)

Inverting the relations between the desired values of mean (90) and CV (0.05) of α and the above prior parameters (ν₀ and δ₀), the following values are obtained for ν₀ and δ₀: ν₀ = 400; δ₀ = 0.2250.

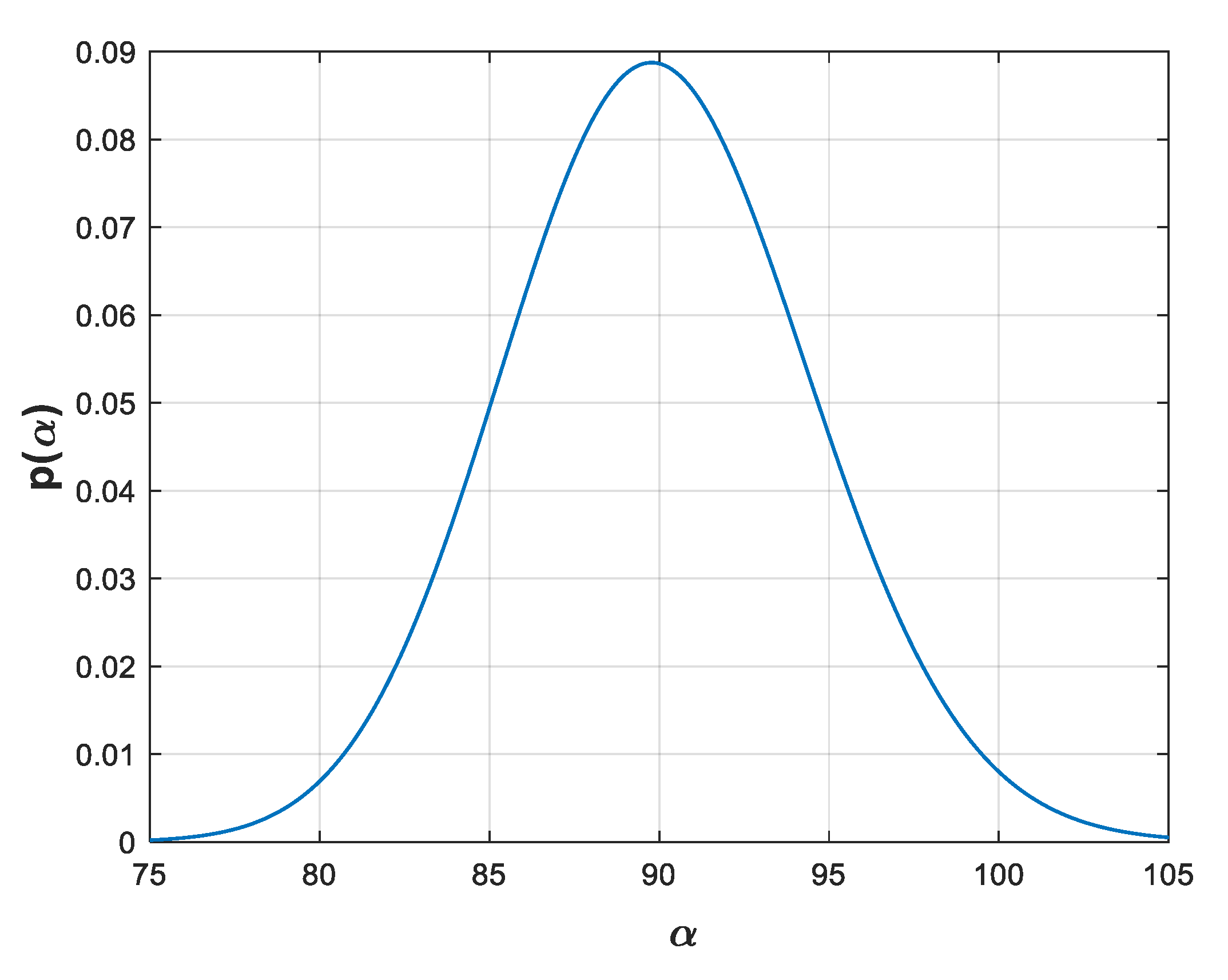
The corresponding prior gamma PDF with such parameters (ν₀ and δ₀), i.e., with mean E[α] = 90 and CV: CV[α] = 0.05, is depicted in Figure 3. Due to the high value of the shape parameter n₀ = 400, such a PDF closely resembles a Gaussian one [28].

Analogous computations for RV ϕ—having a prior gamma PDF with E[f] = 10 and CV[ϕ] = 0.05—show that its prior gamma parameters are p₀ = 400 and θ₀ = 0.02250 (the shape parameter p₀ = 400 is equal to the one, ν₀, of the PDF of α, since it depends only upon the CV, which is the same for both RV). With t = 1 year, also W = ϕt has the same prior gamma PDF. Such a PDF has exactly the same shape as the one of α in Figure 4 but centered on E[W] = 10.

Of course, the primary interest here is not the estimation of the above parameters per se, but they are the input RVs which allow the BE of the RI. Let us first evaluate the prior mean of RI implied by the above assessments on ϕ and α.

By simulation, numerical integration, or following the approximated method illustrated in the previous section, it is not difficult to evaluate such a prior mean and afterwards also the posterior mean based upon the following relations:

$$\{\begin{array}{l}R=1-e^{-V}\\ V=WS\end{array}$$

(50)

First, notice that the RV $S=1-e^{-\left(\frac{\alpha }{z^2}\right)}$ has a prior PDF which can be easily assessed in terms of the NLGD PDF (Appendix C). Indeed, since the RV α has a gamma PDF with parameters ν₀ = 400 and δ₀ = 0.2250, it is easy to verify that also the RV,

$$\beta =\frac{\alpha }{z^2}$$

(51)

has a prior gamma PDF, with parameters ν and δ expressed by ν = ν₀ = 400 and δ = δ₀/z² = 0.2250/z² = 4.6488e-04.

Therefore, by definition of the NLGD model (Appendix C), U = 1 − S = e^−β has an NLGD prior PDF, here denoted by p(u):

$$p\left(u\right)=\frac{1}{\mathsf{\Gamma }\left(\nu \right){\delta }^{\nu }}{u}^{\left(\frac{1}{\mathsf{\delta }}-1\right)}{\left(-\log u\right)}^{\nu -1},\hspace{0.17em}\hspace{0.17em}0\le u\le 1$$

(52)

This implies that S = 1 − U has a prior PDF which can be easily computed from the above NGL PDF, evaluated in u = 1 − s, as follows:

$$p\left(s\right)=\frac{1}{\mathsf{\Gamma }\left(\nu \right){\delta }^{\nu }}{\left(1-s\right)}^{\left(\frac{1}{\mathsf{\delta }}-1\right)}{\left[-\log \left(1-s\right)\right]}^{\nu -1},\hspace{0.17em}\hspace{0.17em}0\le s\le 1$$

(53)

Therefore, utilizing the equations relevant to the NLGD model in Appendix C, prior mean and variance of S are, respectively, equal to

$$\{\begin{array}{l}{\mu }_{S0}=1-\frac{1}{{\left(1+\delta \right)}^{\nu }}\\ {\sigma }_{S0}^2=\frac{1}{{\left(1+2\delta \right)}^{\nu }}-\frac{1}{{\left(1+\delta \right)}^{2\nu }}\end{array}$$

(54)

The values of the mean and variance of S and W allow the computation of the mean and variance of V = WS by simple properties of the product of RV [31], with the following results:

E[V] = 1.6965; VAR[V] = 0.0132→CV[V] = 0.0676

This, in turn, allows the computation of the parameter of the approximating prior gamma PDF of V, which are equal to ν_0ν = 1/(0.0676)² = 218.62 and δ_0V = E[V]/218.6171 = 0.0078.

In Figure 4, two prior gamma PDFs are superimposed:

(1)

The one corresponding to the theoretical approximating prior gamma PDF of V, and

(2)

The one estimated by means of the “smoothed kernel PDF estimator” [31], obtained after generating by Monte Carlo simulation (The Monte Carlo simulation of samples from RV W and S was obtained through the function “gamrnd” of Matlab® used for generating samples of the gamma RV (ϕ, a), and then, the corresponding sample of S was obtained through the function S = S(α) = 1 − exp(−α /z²)) 5000 values of W and S and so of V = WS, according to their above prior PDF.

The prior mean of V, as estimated from the simulated sample data, is equal to 1.6955, while the one obtained from the approximating prior gamma is equal to 1.6965, which confirms the adequacy of the approximation.

Finally (as long as the priori assessment is concerned) the prior mean of R can be evaluated by the simulated sample, i.e., by the sample mean (average value), 0.8155.

If, instead, the above approximating prior gamma is adopted for V, then 1 − R = e^−V has an NLGD prior PDF. Indeed, since the prior gamma PDF of V, as already computed, has parameters ν_0V = 218.6171 and δ_0V = 0.0078, then analogously to what was before illustrated, S − R has a prior PDF which can be approximated by a NGL PDF, as follows:

$$p\left(r\right)=\frac{1}{\mathsf{\Gamma }\left(\nu \right){\delta }^{\nu }}{\left(1-r\right)}^{\left(\frac{1}{\mathsf{\delta }}-1\right)}{\left[-\log \left(1-r\right)\right]}^{\nu -1},\hspace{0.17em}\hspace{0.17em}0\le r\le 1;\hspace{0.17em}\hspace{0.17em}\nu ={\nu }_{0\mathrm{V}}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\mathsf{\delta }={\mathsf{\delta }}_{0\mathrm{V}}$$

(55)

Also, in this case, the theoretical approximating prior NLGD PDF of R and the smoothed kernel PDF estimator of R are perfectly superimposed. Assuming the approximating NLGD prior PDF of R, its mean is equal to

$$\mathrm{E}\left[R\right]=1-\frac{1}{{\left(1+\mathsf{\delta }\right)}^{\nu }}$$

(56)

with ν = ν_0V and δ = δ_0V, which yields 0.8155, the same value computed by simulation.

Also, as hinted at in a previous section, it can be roughly computed by means of the “first order” approximation: E[R] ≈ 1 − e^(−E[V]) = 1 − e ^−1.6955 = 0.8165.

Also, this value is close to the previous one and very close to what reported is in Table 1.

It is well known, however, that the Bayes inference method, differently from the classical ones, produces not only point estimates of the parameters but also the probability distributions describing our uncertainty about their values. In this case, we can assess a whole prior PDF, which, for what concerns its numerical estimation, is shown in Figure 5 in the form of the smoothed kernel PDF estimator of R.

Such a numerical prior PDF, i.e., the quantile estimates associated with the simulated sample, yields, for instance, the following prior 90% credibility interval: (0.7804 0.8483).

P (0.7804 < R < 0.8483) = 0.90

Using the NLGD approximation, taking into account that U = (1−R) is a NLGD RV with parameters (ν = ν_0V; δ = δ_0V), it is easy to see that the p-quantile of R is equal to 1, the (1−p)-quantile of U:

$$R_p=1-{\mathrm{U}}_{\left(1-p\right)}=1-\mathrm{nlginv}\left(1-p,\nu ,\mathsf{\delta }\right)$$

(57)

where nlginv (q, ν, and δ) is the q-quantile of an NLGD RV with parameters ν and δ. (For such a computation, the Matlab® function computing the quantile of a gamma RV, gaminv, was used, since Y = e^(−X) is an NLGD RV when X is a gamma RV, so the p- quantile of Y is given by Y_p = e ^{(−X(1−p))}) This yields the following prior 90% credibility interval (0.7796, 0.8489), which is practically the same interval above found numerically (0.7804, 0.8483), with precision up to the third decimal number.

Of course, since the numerical computations are very reliable, the above gamma or NLGD approximation, as those dealt with in the following, are useful only because they allow easier and faster computations, a sensitivity or robustness analysis with respect to the assumed values of the parameters or the choice of the basic distributions (e.g., one could be interested in evaluating which are the changes in the range of results if the prior gamma PDF, here assumed for the parameters W and S, is changed into, say, a lognormal or a uniform PDF. This is an issue discussed under the topic of “robustness analysis”, briefly dealt with in the final part of the paper). Apart from this remark, in the following, more emphasis will be given to the numerical computations.

5.2. The Case of a Gamma Prior PDF on the IRD Parameter α—Posterior Analysis

Obviously, the basic purpose of Bayes inference is to obtain, once the sample data are observed, the posterior estimates and, also, the probability distributions describing our uncertainty about their values. This can be performed in a relatively straightforward way, which can take advantage of the numerical tools shown in the course of the prior analysis illustrated above. Here, a simple example of how the posterior analysis can be accomplished is illustrated, based upon a small data set produced by simulation from an IRD model, according to the relation (see Appendix F):

$$X={\left[-\frac{\alpha }{\log U}\right]}^{\frac{1}{2}}$$

(58)

which yields an IRD RV if U is a uniform RV in (0,1).

Of course, the posterior analysis requires first that the relevant parameters are generated according their prior distributions; then, that their PDFs are updated in view of the above EWS sample; and then, that the BE of the RI is obtained. This is briefly illustrated here, while the performances of such a BE and their comparison with the one obtained by classical methods are examined in the following sections.

Reference is still made to the above case C11, so that

-

α has a gamma prior PDF with E[α] = 90, CV[α] = 0.05, implying parameters ν₀ = 400 and δ₀ = 0.2250;

-

ϕ has a gamma prior PDF with E[ϕ] = 10 CV[ϕ] = 0.05, implying parameters p₀ = 400 and θ₀ = 0.02250.

In order to illustrate a simple and easily reproducible numerical example and to highlight how the Bayes inference allows a significant update of information also with very few data, a small sample of only 3 EWS values is produced by a single simulation exemplified here as follows:

-

a value of α is generated by its gamma prior PDF; its value is 88.00.

-

a value of ϕ is generated by its gamma prior PDF; its value is 10.00.

The corresponding “true” value of the RI to be estimated is as follows:

$$R=1-e^{-\phi t\left[1-e^{-\left(\alpha /z^2\right)}\right]}=1-e^{-10\left[1-e^{-\left(88/{22}^2\right)}\right]}=0.8103$$

A sample of three EWS values obtained from three uniform variates according to Equation (59), and the above generated value of α is obtained through simulation, resulting in the following sample:

x = (12.07, 45.01, 49.62).

To such a sample, the following observed number of exceedances M is M = 2 (the number of EWS values exceeding the threshold 22), and the Statistics n (sample size) and Σ of Equation (15) and (A31) in Appendix F for evaluating the MLE and the BE for n equals to 3 is 0.0078 and for M equals to 2 is $\Sigma ={\displaystyle \sum _{j=1}^n\frac{1}{x_j^2}}=0.0078$, respectively, so that

-

the MLE of W = φt and α are

W * = M = 2; α * = n/Σ = 384

-

the posterior PDF of α and W, and gamma PDF (A32 in the Appendix F) are described by the following equations respectively:

$$q\left(\alpha |D\right)=Gampdf\left(\alpha ;{\nu }_1,{\mathsf{\delta }}_1\right)$$

(59)

for α, with updated parameters

$$\{\begin{array}{l}{\nu }_1={\nu }_0+n=403;\\ {\mathsf{\delta }}_1=\frac{{\mathsf{\delta }}_0}{1+{\mathsf{\delta }}_0\Sigma }=0.2246\end{array}\hspace{1em}$$

and

$$q\left(\mathrm{W}|D\right)=Gampdf\left(\mathrm{W};{\mathsf{\rho }}_1,{\mathsf{\theta }}_1\right)$$

(60)

for W, with updated parameters

$${\mathsf{\rho }}_1={\mathsf{\rho }}_0+M=402\hspace{0.17em};\hspace{1em}{\mathsf{\theta }}_1=\frac{{\mathsf{\theta }}_0}{1+{\mathsf{\theta }}_0}=0.0220$$

The BE, i.e., the posterior mean estimates of (α, W) are respectively

$$\varphi °=\mathrm{E}\left[\varphi |D\right]={\nu }_1{\mathsf{\delta }}_1=90.52;\hspace{1em}\hspace{1em}W°=\mathrm{E}\left[W|D\right]={\mathsf{\rho }}_1{\mathsf{\theta }}_1=9.805$$

Finally, following the same steps as in the prior assessment, the following computations are performed to evaluate the posterior mean estimate of the RI, R. First, the posterior parameters and PDF of the RV V = WS are computed. Since the numerical computations are very simple, as already noticed, the analytical approximation is shown. Since the RV α has a posterior gamma PDF with parameters ν₁ = 403 and δ₁ = 0.2246, the RV $\beta =\alpha /z^2$ has a posterior gamma PDF with parameters ν and δ expressed by the following:

ν = ν₀ = 403; δ = δ₀/z² = 0.2250/z² = 4.6405e-04

Therefore, U = 1 − S = e^−β has an NLGD posterior PDF, already formulated in (52); S = 1 − U has a posterior PDF which can be computed from the above NLGD PDF, evaluated in u = 1 − s; and posterior mean is as follows:

$${\mu }_{S0}=1-\frac{1}{{\left(1+\mathsf{\delta }\right)}^{\nu }}=0.1705$$

Then, the computation of the mean and variance of V = WS are performed with the following results:

E[V] = 1.6965; VAR[V] = 0.0132→CV[V] = 0.0676

This, in turn, allows the computation of the parameter of the approximating prior gamma PDF of V, and as in the previous subsection, the BE of R is as follows:

R° = 0.8116

which is of course (given also the very little sample size) much closer to the true value (0.8103) of R than the MLE (0.6672). It is also worth mentioning that, as in the previous subsection, the “rough” computation of such BE by means of the “first-order” approximation E[R|D] ≈ 1 − e^−E[V|D] = 1 − e^−1.6955 = 0.8165.

Finally, the numerical computations, both when performed by simulation or numerical computations, give essentially the same result: E[R|D] ≈ 1- e^−E[V|D] = 1-e^−1.6955 = 0.8120. Of course, the merits of the BE are not appreciable by a single simulation, here shown only to highlight the mathematics, but require an overall assessment, which is the object of the next sections.

6. Numerical Application for Performances of the Bayes Approach in the Case of a Gamma Prior PDF on the IRD Parameter α

This and the next section follow the framework illustrated in the previous section, in which only the features of an estimation procedure for a given sample have been reported. Since in practice the Bayes estimate and their relevant features (e.g., their mean square errors) are computable only numerically, in order to assess the overall performance of the proposed Bayes estimation, a large series of Monte Carlo simulations have been carried out, relevant to different sample sizes and extending the same approach. In detail, the Bayesian methodology has been evaluated numerically, as illustrated here, by means of a large set of simulated experiments aiming at assessing the estimation efficiency of the Bayes approach. This is illustrated here in the case of a gamma prior PDF on the IRD parameter α, while the alternative assumption of a beta prior PDF on the IRD parameter S(α) will be briefly illustrated in the next section. Both in this and in the next section, the assumption of a gamma prior PDF on the Poisson parameter (α, ϕ) is maintained, as customary [26,27].

The estimation efficiency of the Bayes estimates is assessed both “per se” (i.e., in “absolute” terms) and in terms of “relative efficiency” [26,27,28] of the Bayes estimates vs. the “classical” Maximum Likelihood (ML) estimators, more widely used in the field of wind speed PDF assessment [13,14,15,16,17].

After a sound investigation, different sets of typical values have been selected for the mean and the standard deviation (or the CV) of the main random parameters (α and ϕ).

Different CV prior values were selected with the same values of prior means, since—as intuitive—the estimation performances are rather sensitive to variations in CV prior values while variations in the prior means are less effective in terms of estimation efficiency. As above said, 12 sets of simulation cases are illustrated here, among the many more performed, and shown in

Table 3. Simulation results for cases Aij.

Parameters	n = 3	n = 10	n = 30	n = 50	n = 3	n = 10	n = 30	n = 50
	Case A11				Case A12
AV(R)	0.0733	0.0735	0.0733	0.0734	0.0735	0.0734	0.0733	0.0735
AV(α)	14.9964	15.0061	14.9767	15.9998	14.9929	14.9980	14.990	15.0057
AV(ϕ)	2.4969	2.5000	2.4986	2.5003	2.5022	2.4982	2.4999	2.5010
AV(RL)	0.0057	0.0115	0.0001	0.0471	0.0068	0.0108	0.0471	0.0470
AV(RB)	0.0730	0.0730	0.0732	0.0733	0.0730	0.0731	0.0732	0.0733
RMSEL	0.0732	0.0661	0.0542	0.0460	0.0740	0.0663	0.0543	0.0467
RMSEB	0.0050	0.0049	0.0048	0.0047	0.0050	0.0049	0.0049	0.0049
RARE	17.7987	16.1190	12.6195	10.2275	17.8265	16.2862	12.3797	10.2125
RMRE	21.8762	9.5639	5.3210	8.8966	36.5525	11.0236	6.3284	8.2127
REFF	14.7407	13.3886	11.2272	9.7079	14.7653	13.5250	10.9862	9. 6030
	Case A21				Case A22
AV(R)	0.0733	0.0735	0.0734	0.0734	0.0734	0.0734	0.0735	0.0735
AV(α)	14.9964	15.0061	14.9767	14.9947	15.0027	15.0038	15.0051	14.9998
AV(ϕ)	2.4969	2.5000	2.4986	2.4993	2.4980	2.5000	2.5007	2.5003
AV(RL)	0.0057	0.0115	0.0001	0.0466	0.0064	0.0115	0.0291	0.0471
AV(RB)	0.0730	0.0730	0.0732	0.0733	0.0730	0.0731	0.0732	0.0733
RMSEL	0.0732	0.0661	0.0546	0.0475	0.0743	0.0662	0.0542	0.0470
RMSEB	0.0050	0.0049	0.0049	0.0049	0.0050	0.0050	0.0049	0.0048
RARE	17.7987	16.1190	12.6776	10.3687	17.9172	16.0920	12.5001	10.3649
RMRE	21.8762	9.5639	8.9712	11.8046	40.5468	11.0576	8.3189	10.7958
REFF	14.7407	13.3886	11.2468	9.7686	14.9604	13.3499	11.0788	9.7256

,

Table 4. Simulation results for cases Bij.

Parameters	n = 3	n = 10	n = 30	n = 50	n = 3	n = 10	n = 30	n = 50
	Case B11				Case B12
AV(R)	0.3581	0.3580	0.3582	0.3581	0.3581	0.3574	0.3581	0.3576
AV(α)	44.9549	44.9780	45.0124	44.9782	44.9782	44.9632	44.9782	45.0137
AV(ϕ)	5.0033	5.0011	4.9994	5.0014	5.0014	5.0004	5.0014	4.9987
AV(RL)	0.0435	0.3169	0.2118	0.3173	0.3173	0.0871	0.3173	0.3227
AV(RB)	0.3551	0.3577	0.3569	0.3579	0.3579	0.3553	0.3579	0.3580
RMSEL	0.3308	0.1388	0.1907	0.1400	0.1408	0.2877	0.1400	0.1396
RMSEB	0.0198	0.0189	0.0195	0.0190	0.0160	0.0294	0.0190	0.0263
RARE	20.5448	7.4852	10.5744	7.4852	7.4852	11.6283	7.4852	5.3642
RMRE	6.4392	5.6895	3.8621	5.6895	5.6895	2.8046	5.6895	3.7746
REFF	16.7142	7.3439	9.9739	7.3539	8.8000	2.8046	7.3539	5.3030
	Case B21				Case B22
AV(R)	0.3581	0.3580	0.3579	0.3581	0.3568	0.3576	0.3576	0.3572
AV(α)	44.9549	44.9780	44.9658	44.9782	44.9622	45.0668	44.9961	45.0137
AV(ϕ)	5.0033	5.0011	4.9987	5.0014	4.9982	5.0003	5.0088	4.9987
AV(RL)	0.0435	0.3169	0.2144	0.3173	0.0426	0.0862	0.2126	0.3227
AV(RB)	0.3551	0.3577	0.3568	0.3579	0.3453	0.3472	0.3519	0.3580
RMSEL	0.3308	0.1388	0.1910	0.1400	0.3308	0.2899	0.1918	0.1459
RMSEB	0.0198	0.0189	0.0191	0.0190	0.0411	0.0396	0.0378	0.0368
RARE	20.5448	7.4852	10.7949	7.4852	9.9445	8.7859	5.4961	4.0660
RMRE	6.4392	5.6895	5.7265	5.6895	2.8095	2.5301	2.1168	2.8898
REFF	16.7142	7.3439	9.9739	7.3539	8.0392	7.3128	5.0740	3.9608

and

Table 5. Simulation results for cases Cij.

Parameters	n = 3	n = 10	n = 30	n = 50	n = 3	n = 10	n = 30	n = 50
	Case C11				Case C12
AV(R)	0.8155	0.8153	0.8156	0.8158	0.8135	0.8140	0.8157	0.8141
AV(α)	90.0238	90.0330	90.0446	89.9848	89.9591	90.2071	90.0450	89.8219
AV(ϕ)	9.9981	9.9923	9.9997	10.0126	9.9989	9.9898	9.9999	10.0296
AV(RL)	0.1209	0.2599	0.5563	0.7371	0.1222	0.2576	0.5548	0.7352
AV(RB)	0.8093	0.8102	0.8128	0.8155	0.8091	0.8101	0.8130	0.8144
RMSEL	0.7178	0.5872	0.3140	0.1571	0.7151	0.5879	0.3200	0.1619
RMSEB	0.0220	0.0217	0.0210	0.0203	0.0328	0.0318	0.0227	0.0275
RARE	39.4869	32.1310	15.8064	7.1391	26.3424	21.7838	15.7704	5.3541
RMRE	9.1652	9.1527	9.5250	7.7309	4.9205	5.8405	9.5310	4.8270
REFF	32.6531	27.0373	14.9798	7.7233	21.8310	18.4877	14.0900	5.8877
	Case C21				Case C22
AV(R)	0.8135	0.8144	0.8134	0.8136	0.8122	0.8113	0.8112	0.8115
AV(α)	89.9999	90.0665	89.9154	89.9523	90.0497	89.9970	89.8842	90.0238
AV(ϕ)	10.0002	10.0210	10.0030	10.0055	10.0119	9.9874	9.9961	9.9981
AV(RL)	0.1194	0.2596	0.5563	0.7360	0.1210	0.2617	0.5556	0.7354
AV(RB)	0.7877	0.7916	0.8020	0.8120	0.7875	0.7912	0.8012	0.8113
RMSEL	0.7175	0.5870	0.3140	0.1598	0.7152	0.5815	0.3137	0.1596
RMSEB	0.0431	0.0411	0.0363	0.0346	0.0487	0.0461	0.0424	0.0400
RARE	19.8357	16.6461	8.9626	4.3247	17.5856	14.7490	7.7339	3.7085
RMRE	4.5298	5.5847	4.2137	3.8440	4.8757	4.1047	3.4221	2.6899
REFF	16.6600	14.2742	8.6463	4.6132	14.6936	12.6104	7.4058	3.9855

cIn detail, 12 = 3 × 4 sets of combinations of prior values (corresponding to different simulation cases), among the many more performed, are shown in this section with respect to mean value and CV of the input RV (ϕ, α), as listed in the previous Table 2. It is recalled that, always maintaining a time horizon of one year.

.

• Cases Aij correspond to “low risk” values (E[R] ≈ 0.0735).
• Cases Bij correspond to “medium risk” values (E[R] ≈ 0.3585).
• Cases Cij correspond to “high risk” values (E[R] ≈ 0.8167).

For each of the above cases, N random samples of size n (with n varying as specified below) of EWS values X_j have been generated according to the assumed IRD PDF of stress X with parameter α and with a Poisson parameter ϕ for the process of exceedances. The parameters (ϕ and α) are in turn RVs generated according to their prior gamma distributions, as shown in a previous section (different priors were also investigated, with similar results to those shown in the following).

For each sample size n, a number N = 10⁴ of replications has been performed; let us refer to each considered couple of values of n and N as a single simulation case study; different simulation case studies were considered by testing different sample sizes. Here, in particular, the results for small (n = 3, n = 10) or moderate (n = 30, n = 50) sample sizes are reported in the tables that follow, among the many more performed. The choice to show also the results for very small sample sizes as n = 3 takes its origin in view of the previously discussed features of Bayesian information updated also in the case of a limited amount of data has mainly a theoretical interest; nonetheless, it can also have a practical aspect when dealing with very high values of WS, so that their occurrence is very rare and only very few data are available.

With reference to the generic parameter ζ to be estimated (which in this case is basically the RI R, but one could be interested also in the BE of ϕ and α), it will be denoted as ζ_j°, the estimate of the “true” value ζ_j of ζ relevant to the particular n-sized sample generated at the jth simulation cycle. The basic statistics—estimated at the end of each simulation case study—which describe the efficiency of the proposed estimates are the following:

• ♦ RMSEB: root mean square error of the Bayes estimator;
• ♦ RMSEL: root mean square error of the ML estimator; and
• ♦ REFF = RMSEL/RMSEB: relative efficiency of the Bayes estimator with respect to the ML estimator.

The REFF index is the most widely adopted measure of the “relative efficiency” [26,27] of the Bayes estimator with respect to the ML estimator: the more it exceeds unity, the more efficient is the Bayes estimate with respect to the ML estimate.

The above-defined quantities are based on the concept of “RMSE”. Given an estimator, ζ°, of the parameter ζ, its RMSE is—as well known—defined as

$$RMSE=\sqrt{\mathrm{E}\left[\right(\mathsf{\zeta }°-\mathsf{\zeta }{)}^2]}$$

(61)

with both ζ° and ζ as random variables in the Bayesian approach, while the latter is an unknown, deterministic constant in the classical statistical approach. The RMSE (which is not analytically computable) is evaluated here at the end of each simulation case study by means of the ordinary large-sample estimator [31] as follows:

$$RMSE={\left[\frac{1}{N}{\displaystyle \sum _{j=1}^N{(\mathsf{\zeta }{°}_j-{\mathsf{\zeta }}_j)}^2}\right]}^{1/2}$$

(62)

While the above measures concern the efficiency of the Bayes estimates, other significant “performance indexes” were also evaluated, as measure of their precision:

• ♦ AREB: Average relative error of the Bayes estimator
• ♦ AREL: Average relative error of the ML estimator
• ♦ MREB: Maximum relative error of the Bayes estimator
• ♦ MREL: Maximum relative error of the ML estimator

The relative error of an estimator, ζ°, of the parameter ζ can be defined as (E[ζ°] − E[ζ])/E[ζ]. Therefore, as an overall “sample” measure of the relative bias, the “Average Relative Error”, AREB, is used here, in which the quantities E[ζ°] and E[ζ] are evaluated through their estimated mean (average) values at the end of each simulation case study:

$$\mathrm{ARE}=\left|\frac{\mathrm{M}\left[\zeta °\right]-\mathrm{M}\left[\zeta \right]}{\mathrm{M}\left[\zeta °\right]}\right|$$

(63)

with M[ζ°] and M[ζ] respectively the average values of the ζ_j° and ζ_j values over the N performed simulations:

$$\{\begin{array}{l}\mathrm{M}[\mathsf{\zeta }°]=(1/N){\displaystyle \sum _{k=1}^N\mathsf{\zeta }{°}_k}\\ \mathrm{M}[\mathsf{\zeta }]=(1/N){\displaystyle \sum _{k=1}^N{\mathsf{\zeta }}_k}\end{array}$$

(64)

With the same notations, the Maximum Relative Error, MRE, of an estimator over N trials is given by the following:

$$\mathrm{MRE}=\max \left|\frac{{\zeta }_j^o-{\zeta }_j}{{\zeta }_j}\right|,\hspace{1em}\hspace{1em}\mathrm{j}=1,\dots ,\mathrm{N}$$

(65)

The values of RMSE, ARE, and MRE can be calculated for each simulation case study for both the ML estimator and the proposed Bayesian approach, thus obtaining the values of quantities RMSEB, RMSEL, AREB, ARELB, MREB, and MREL (defined above). In other words, RMSEB denotes the RMSE value for a BE, RMSEL denotes that for an MLE; AREB denotes the ARE value for a BE; AREL denotes that for an MLE; and so on. Note that, for an easier comparison, both ARE and MRE are evaluated in terms of absolute values.

In addition, the following (dimensionless) ratios are computed as useful synthetic measures in evaluating the precision of the Bayes estimates with respect to the MLE:

• ♦ RARE = AREL/AREB,
• ♦ RMREL = MREL/MREB

As for REFF, RARE and RMREL are also greater than 1 if the Bayes estimate is “better”—in the specified sense—than the ML one.

A summary of the simulation results, in Table 3, Table 4 and Table 5, reported the average value of R, α and f; the average value of the MLE and BE of R; and the measures RMSEL, RMSEB, RARE, RMRE, and REFF.

Any average value is always computed as for indexes ARE and MRE above as the sample mean computed over the N simulations performed for each generated sample. The average values of a random parameter, such as α, should be ideally equal to its mean value (they would be equal if an infinite number of simulations would be possible), e.g., 15 in case A11; in practice, they should be close to the theoretical mean values.

All the above values are reported as a function of the sample size considered in the simulations (see row headings). It is noticed that the values of the RI average value, AV(R), and the ratio REFF (relative efficiency) are boldface, being the most significant measures.

Since they are evaluated through simulation, all the reported quantities must be regarded as sample estimates. The number of digits used for the data representation is purely indicative.

All the results show that the Bayes estimates errors are always acceptably small and much smaller—in particular for very small sample sizes—than those of the traditional ML method. In all cases (as in the many more cases omitted here), the reported results show the good performances of the Bayes estimates, assessing the Bayes estimation robustness, with very high REFF values, especially for small sample sizes. As could be anticipated, cases implying a higher confidence in the prior values (i.e., with minor CV values) are more favorable in terms of efficiency of the Bayes estimates: it is remarkable, however, that also cases corresponding to a relatively high degree of uncertainty in the prior estimates (CV = 10%) are characterized by high values of efficiency. The same conclusions can be drawn about the precision of the Bayes estimators, as measured by the RARE and RMRE index.

In summary, the relative efficiency with respect to the ML estimate—as measured by REFF—is always larger than 1; in particular, it is much larger for small sample sizes, for which the ML estimates are definitively outperformed by the Bayes ones. For example, it can be noticed in Table 5, case C₁₁, that the REFF assumes a value around 7 for n = 50 but increases until 33 about for n = 3. This latter feature is reinforced by the examination of ratios RARE and RMRE, which behave, as could be expected, less regularly from sample to sample.

It is again remarked that the above Bayes estimate must be computed by numerical methods, as above discussed. In particular, both numerical integration of the posterior PDF and simulation were performed, giving essentially the same results.

Finally, it is remarked that the numerical simulations are not (only) theoretical but are based upon typical values of wind-speed parameters which have been found in actual practice. Moreover, a larger series of Monte Carlo simulations carried out for a much wider range of parameter values (prior means and CV) were performed, all with similar results, which are often highlighted in the applications of Bayes estimation [32,33,34,35,36].

7. Numerical Application for Performances of the Bayes Approach in the Case of a Beta Prior PDF on the IR Parameter S(α)

In this section, the topic of the previous section is continued, assuming a beta prior PDF on the IR parameter S(α) while maintaining the customary assumption of a gamma prior PDF for the random parameter ϕ. Also, in this case, interest is focused on the evaluation of the performances of the Bayes approach by numerical methods since, as highlighted in Section 4, also in this case, generally an analytical solution is not available or is very cumbersome [37,38].

In practice, as illustrated in Section 4, a prior guess on the parameter S (α can, as in the case of a prior guess on α, be originated by a prior guess on the median or may be directly expressed on the basis of “credible interval” (S₁, S₂), i.e., a Bayesian (prior) confidence interval on S).

As already discussed (see the discussion after Equation (38)), it is convenient that S, a RV with support in (0,1), is assumed as a beta RV (already introduced in Section 4 and with more details in Appendix D), since this is a very flexible distribution in the interval (0,1), which implies that the parameter α has an NEBD PDF (Appendix D), since:

$$\alpha =\left[-\log \left(1-S\right)\right]z^2$$

(66)

For brevity, here, only three cases are examined. In detail, we start from the same cases examined in previous section, here recalled only in the “most unfavorable” case of both CV = 0.10:

Case

A22 (“low risk” values: E[R] ≈ 0.0735): E[ϕ] = 2.5, E[α] = 15, CV = 0.10 for both ϕ and α;

Case

B22 (“medium risk” values: E[R] ≈ 0. 3585;): E[ϕ] = 5, E[α] = 45, CV = 0.10 for both ϕ and α; corresponding to an approximate expected value of the RI: E[R] ≈ 0. 3585;

Case

C22 (“high risk” values: E[R] ≈ 0.8167: E[ϕ] = 10, E[α] = 90, CV = 0.10 for both ϕ and α.

For easier comparison with the cases examined above, we assume that the beta(r,s) prior PDF for S has the mean value corresponding to the above mean values of α, with the value CV = 0.10 assigned to S, so to obtain the following three cases, denoted with apexes A’22, B’22, and A’22 corresponding respectively to A22, B22, and C22.

Case 

A’22: E[S] = 0.0305 and CV[S] = 0.10 (implying a beta(r,s) PDF with: r = 96.92, s = 3081) and E[ϕ] = 2.5, CV[ϕ] = 0.10;

Case 

B’22: E[S] = 0.0888 and CV[S] = 0.10 (implying a beta(r,s) PDF with: r = 91.03, s = 934.1) and E[ϕ] = 5, CV[ϕ] = 0.10;

Case 

C’22: E[S] = 0.1697 and CV[S] = 0.10 (implying a beta(r,s) PDF with: r = 82.86, s = 405.4) and E[ϕ] = 10, CV[ϕ] = 0.10.

For example, the curve of the prior beta(r,s) PDF of case C’22 (S has mean value 0.1697 and CV = 0.10, implying: r = 82.86, s = 405.4) is depicted in Figure 6.

The results of these 3 cases are reported in

Table 6. Simulation results for cases A’22.

Parameters	n = 3	n = 10	n = 30	n = 50
AV(R)	0.0735	0.0731	0.0734	0.0735
AV(S)	0.0305	0.0304	0.0305	0.0305
AV(ϕ)	2.5031	2.4970	2.5005	2.5009
AV(RL)	0.0071	0.0116	0.0287	0.0467
AV(RB)	0.0718	0.0719	0.0724	0.0728
RMSEL	0.0744	0.0662	0.0551	0.0475
RMSEB	0.0100	0.0098	0.0095	0.0092
RARE	9.0047	8.0724	6.4986	5.4816
RMRE	15.4999	4.4161	3.1576	4.4662
REFF	7.4510	6.7446	5.7911	5.1915

,

Table 7. Simulation results for cases B’22.

Parameters	n = 3	n = 10	n = 30	n = 50
AV(R)	0.3571	0.3573	0.3574	0.3574
AV(S)	0.0888	0.0888	0.0888	0.0884
AV(ϕ)	4.9980	5.0000	5.0009	5.0230
AV(RL)	0.0448	0.0859	0.2140	0.3173
AV(RB)	0.3454	0.3471	0.3521	0.3560
RMSEL	0.2902	0.2902	0.1907	0.1408
RMSEB	0.3308	0.0408	0.0374	0.0374
RARE	9.8376	8.5902	5.4890	3.8759
RMRE	3.7691	1.6688	1.7944	2.1163
REFF	7.9854	7.1147	5.0606	3.7660

and

Table 8. Simulation results for cases C’22.

Parameters	n = 3	n = 10	n = 30	n = 50
AV(R)	0.8112	0.8110	0.8100	0.8125
AV(S)	0.1696	0.1696	0.1696	0.1699
AV(ϕ)	9.9955	10.0037	9.9497	10.012
AV(RL)	0.1198	0.2649	0.5637	0.7316
AV(RB)	0.7875	0.7912	0.8018	0.8110
RMSEL	0.7153	0.5784	0.3023	0.1652
RMSEB	0.0503	0.0485	0.0419	0.0395
RARE	17.0349	14.1524	7.5331	3.8165
RMRE	3.4950	5.1857	3.5330	4.8343
REFF	14.2283	11.9186	7.2107	4.1840

, illustrated as in the previous section, except that, of course, in this section in the 2nd row of the tables, the average value of S, AV(S) is shown instead of that of α, AV(α).

It is apparent that the results are quite comparable and indeed very similar to those of the previous section, confirming the validity of the approach with respect to different methods of assessing the researcher’s prior information.

Finally, it is remarked that an analysis of the robustness of the Bayesian Estimation with respect to the assumed prior hypotheses has been successfully carried out following the same methodology illustrated in [27]. In particular, many different prior PDFs were chosen instead of the assumed ones, e.g., lognormal or uniform prior PDF with the same mean value and CV of the assumed gamma and beta PDF. For reasons of length, these results are not reported here but are available on request from the authors.

8. Conclusions

The correct assessment of the probabilistic distribution for wind and extreme wind speeds is very important for a technical and economical point of view and gives the possibility to optimize the electricity production of a wind farm. In particular, the occurrence of very high values of wind speed is an undesirable event, since wind power systems provide zero power output for values greater than their cutoff thresholds. Also, the mechanical safety of the installations can be seriously compromised by extreme values of wind speed. The IRD is proposed in the paper as a valid model for extreme wind speeds; such a model is proposed for the first time in the literature on the object, and its validity is illustrated with reference to real wind-speed data. Then, this paper investigates the problem of a proper and efficient Bayes estimation of a risk index described in terms of a stochastic process of extreme values of wind speed based upon a practical parameter estimation of the IRD using the gamma and/or the prior beta distribution according to which kind of prior information is available. The methodology proposed is based upon the use of real data of EWS and using different estimation procedures, also comparing such estimation procedures to the ML procedure. The proposed model is verified by means of many numerical simulations. The obtained results show the efficiency and precision of the analyzed model. The considered Bayes estimator appears also to be robust with respect to incorrect prior assumptions.

It is highlighted that, beyond the theoretical aspects which have been developed in the paper, its basic purpose is to address a real engineering problem, since it deals both with wind power production evaluation and the mechanical safety of the installations. This is a clearly basic topic to be addressed both in the planning and the operation of a wind farm and is afforded in the manuscript by a novel risk index which the authors deem to be an important tool in helping a decision making procedure for deciding if a wind farm is worth being installed and whether its operation will be safe or reliable enough in time.

Further extension of the proposed approach is worth being developed, extending the hypotheses assumed for the Poisson process of exceedances, allowing for non-homogeneous Poisson processes [39,40,41,42,43,44].