Dynamic Response of a Bridge–Embankment Transition with Emphasis on the Coupled Train–Track–Subgrade System
Abstract
1. Introduction
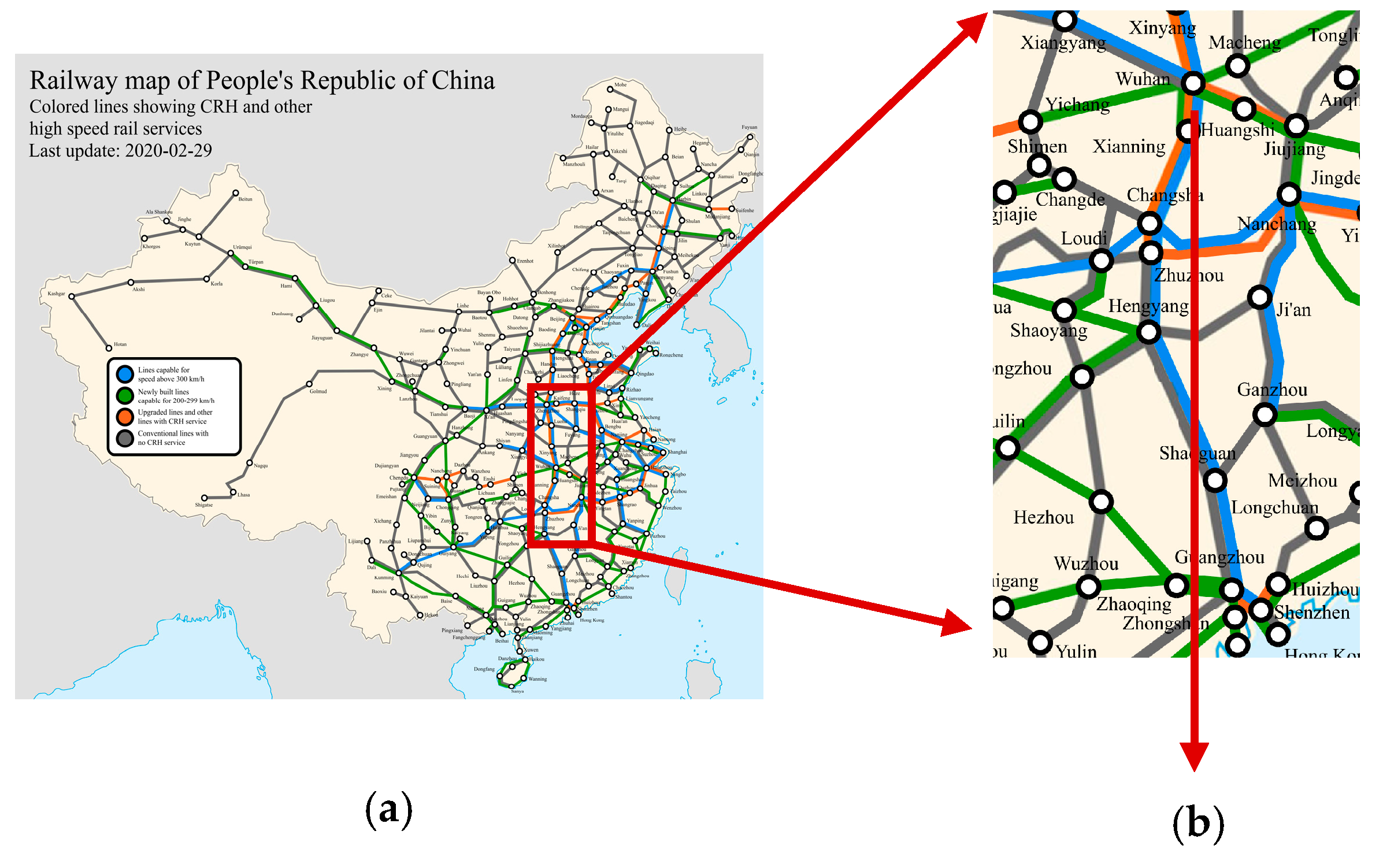
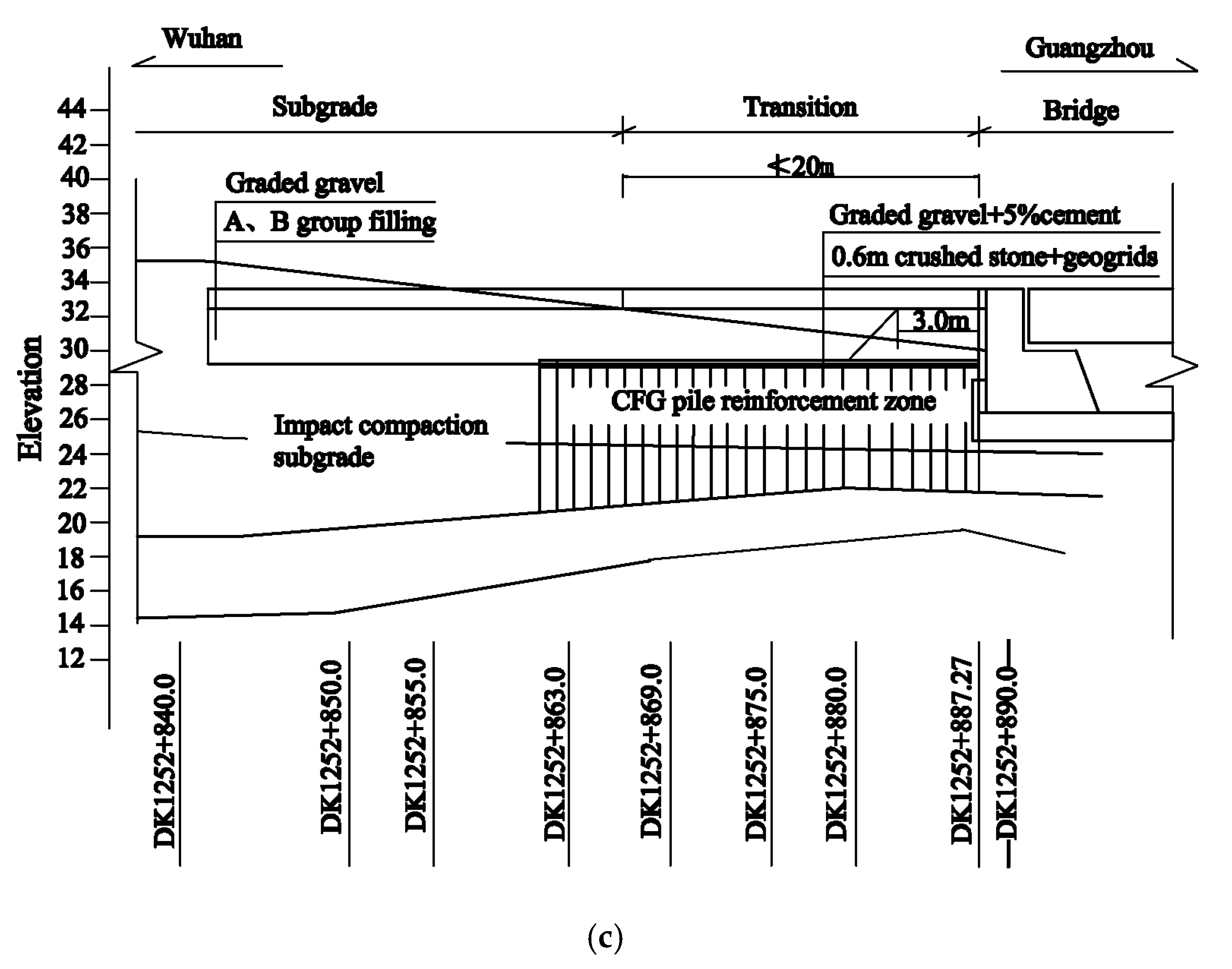
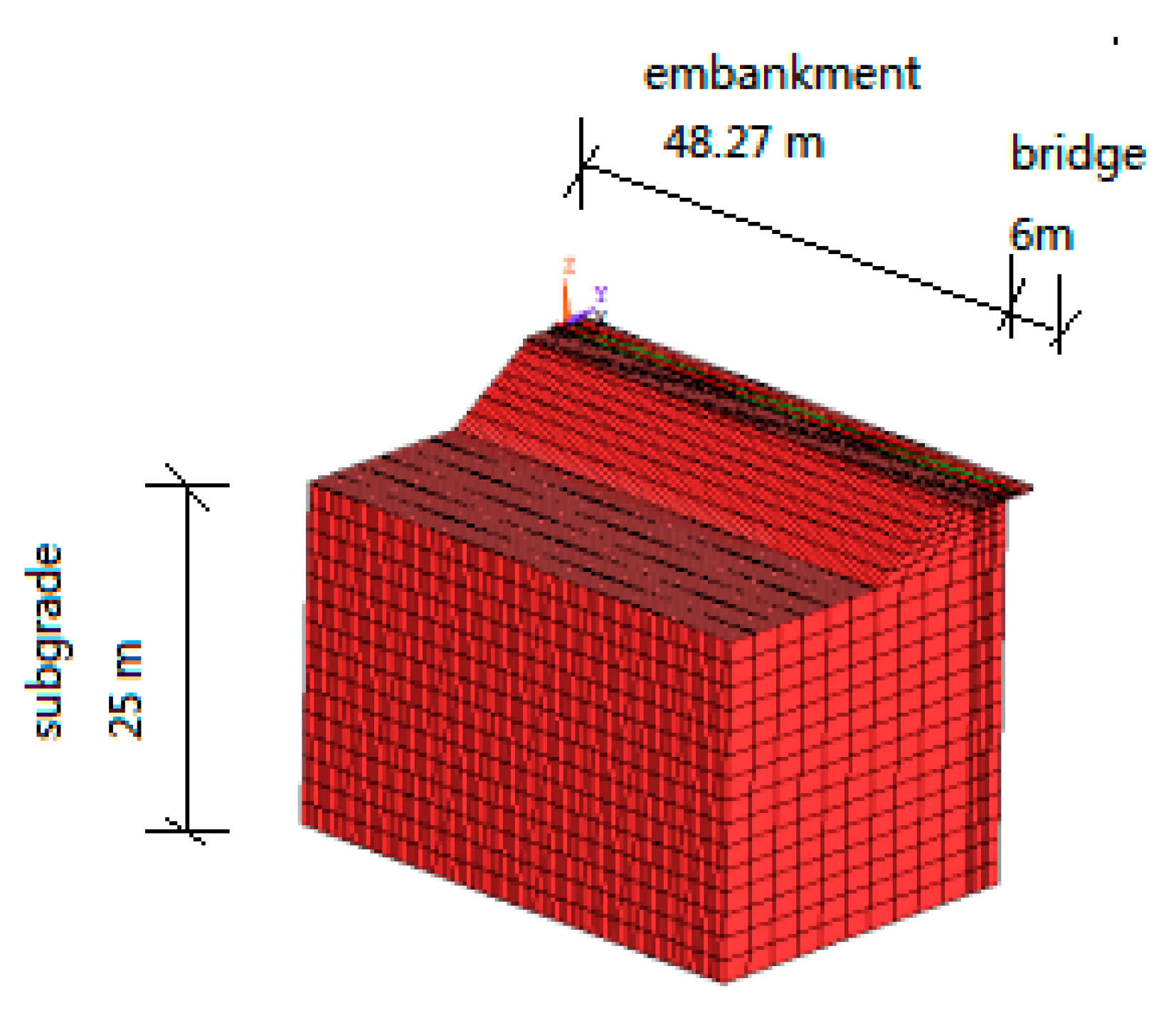
2. Profile of the Bridge–Embankment Transition
3. Establishment of Numerical Analysis Model of Bridge–Embankment Transition Section
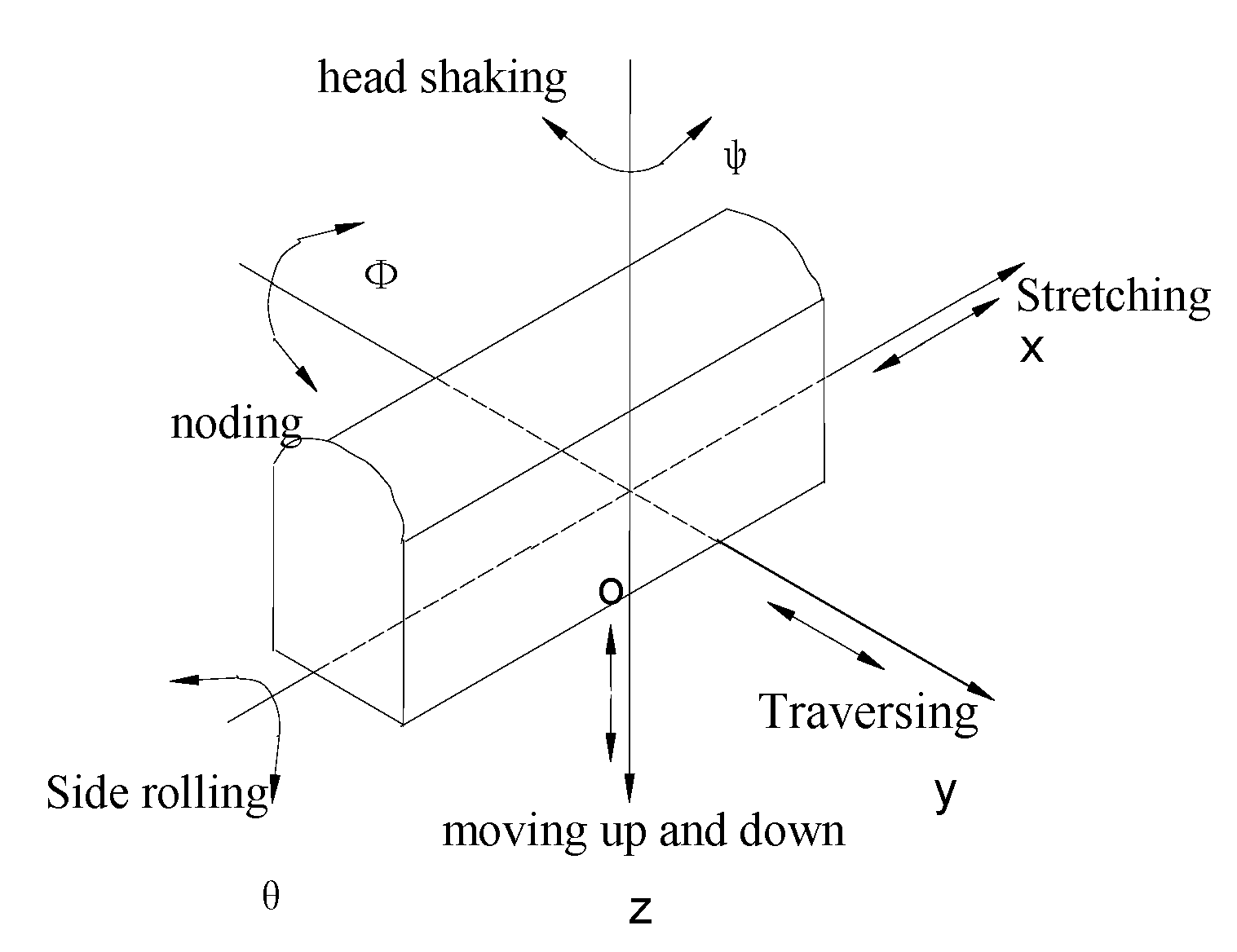
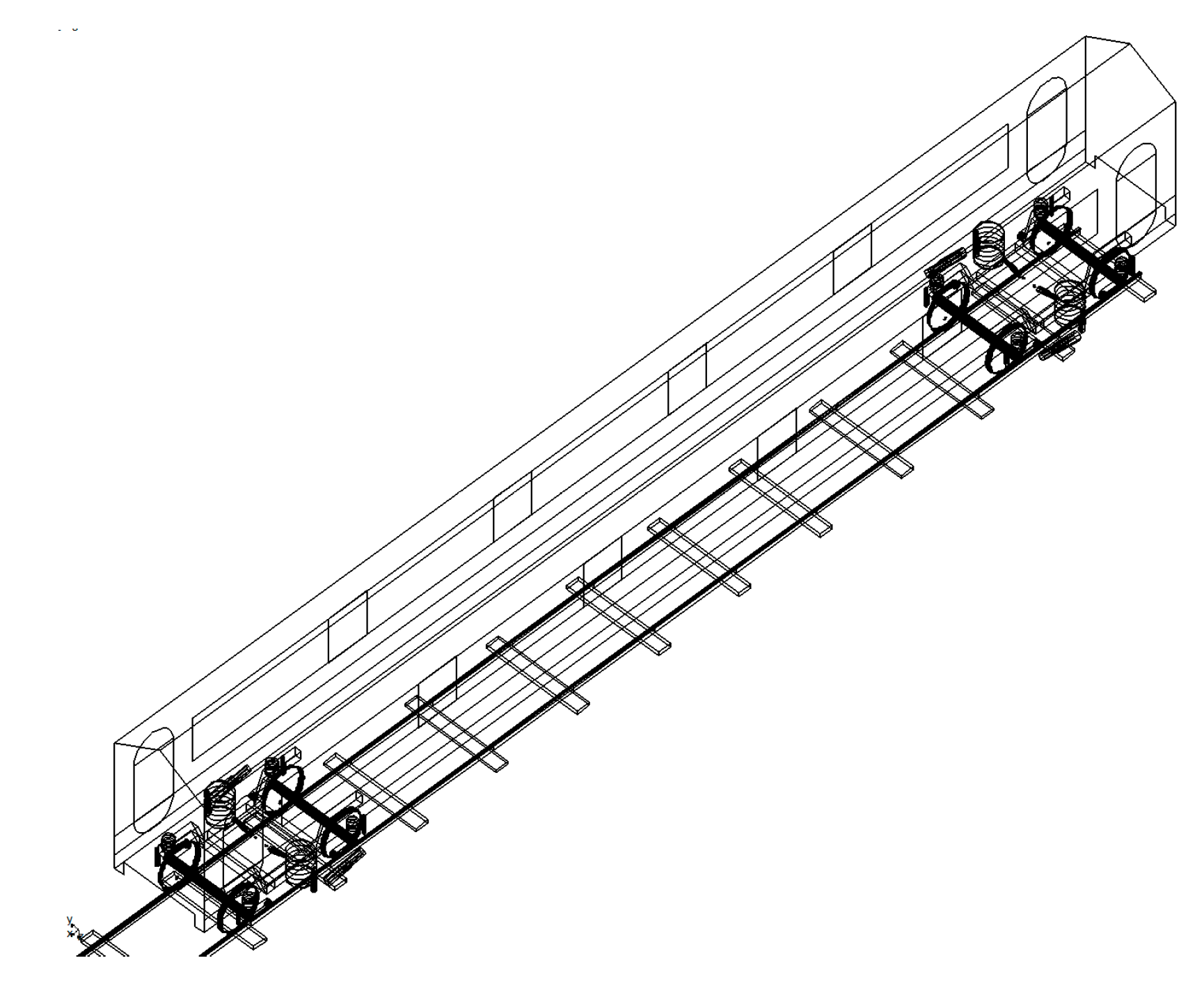
3.1. Vehicle Model
3.2. Coupled Vehicle–Track–Space Time-Varying Model
3.3. Solution of Dynamics of Multi-Rigid Body System
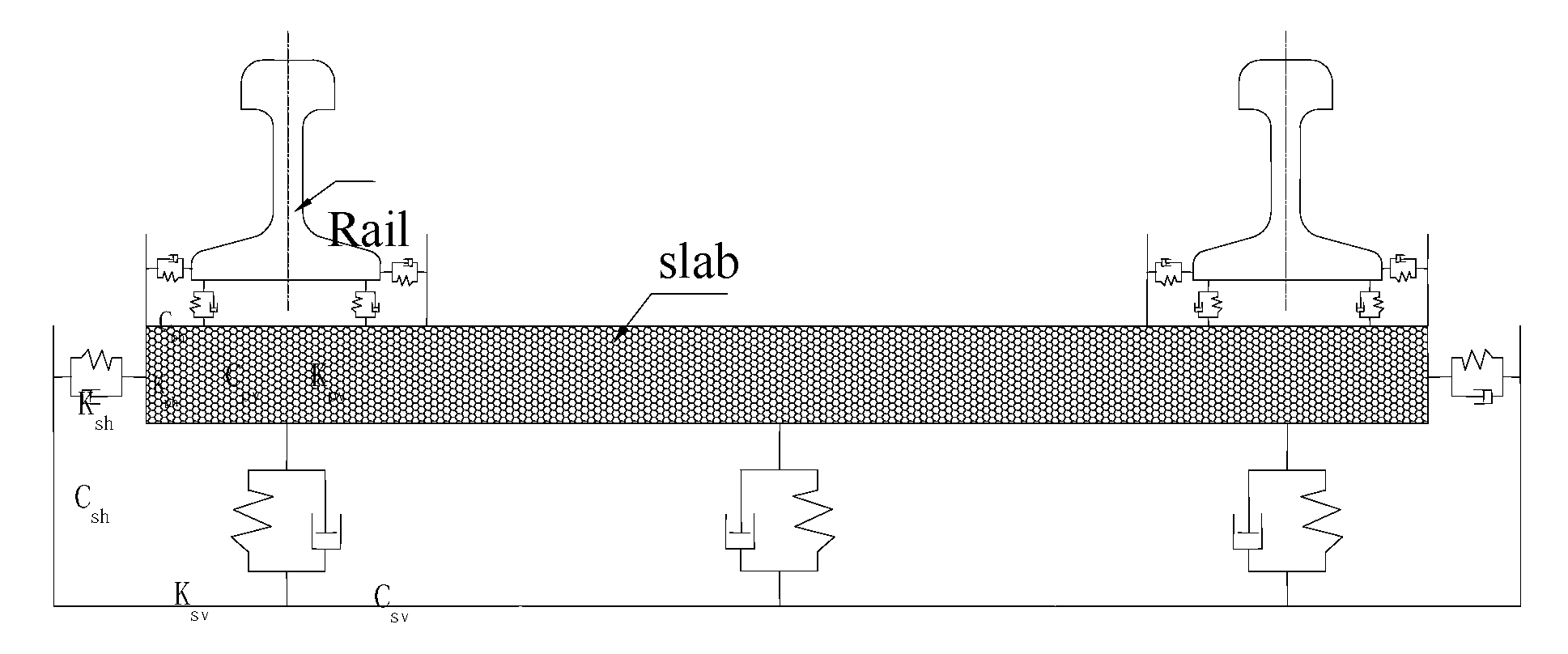
3.4. Finite Element Model of Track Subgrade of Road Bridge Transition Section
3.5. Load Application
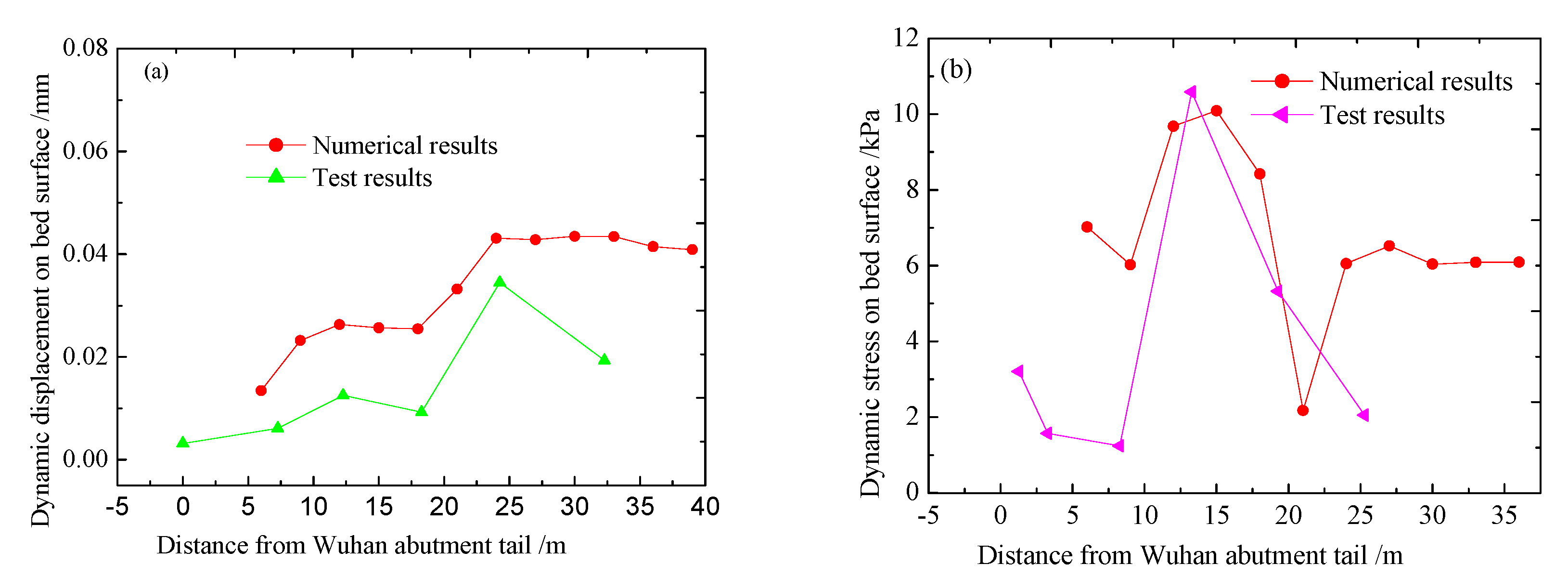
3.6. Model Validation
4. Influence Factors on Dynamic Responses of Vehicle-Track-Subgrade System in Transition Section
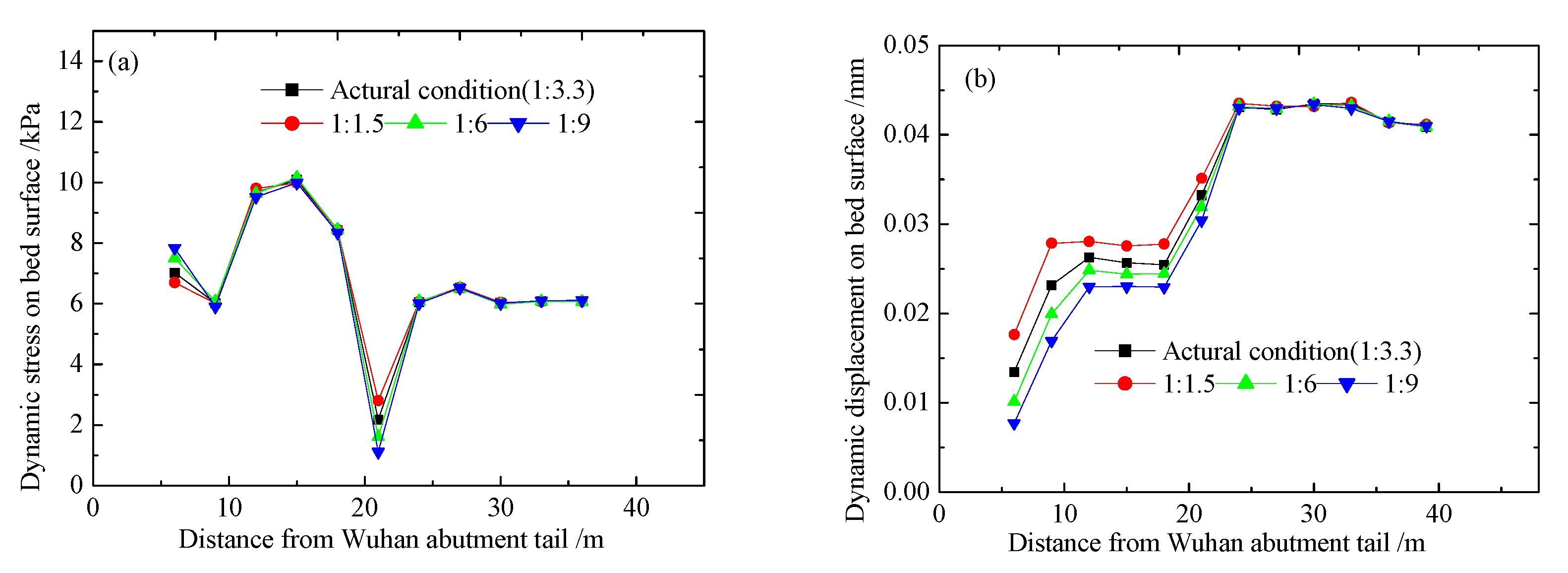
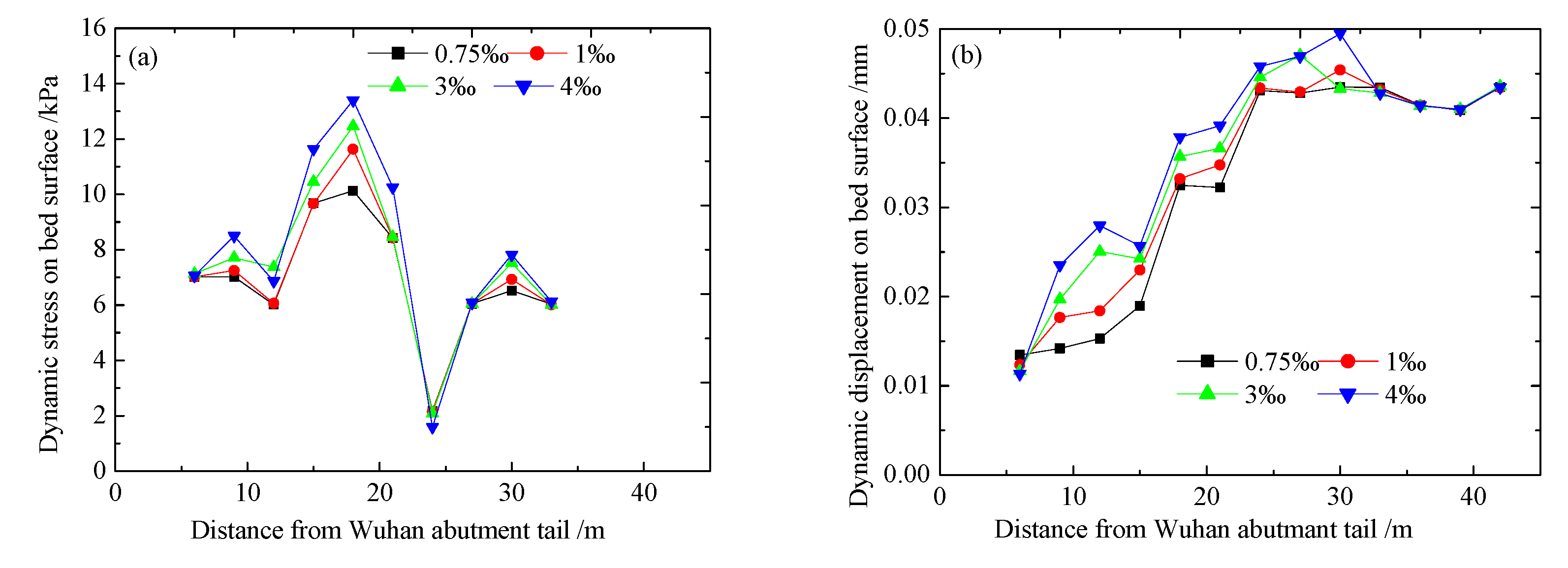
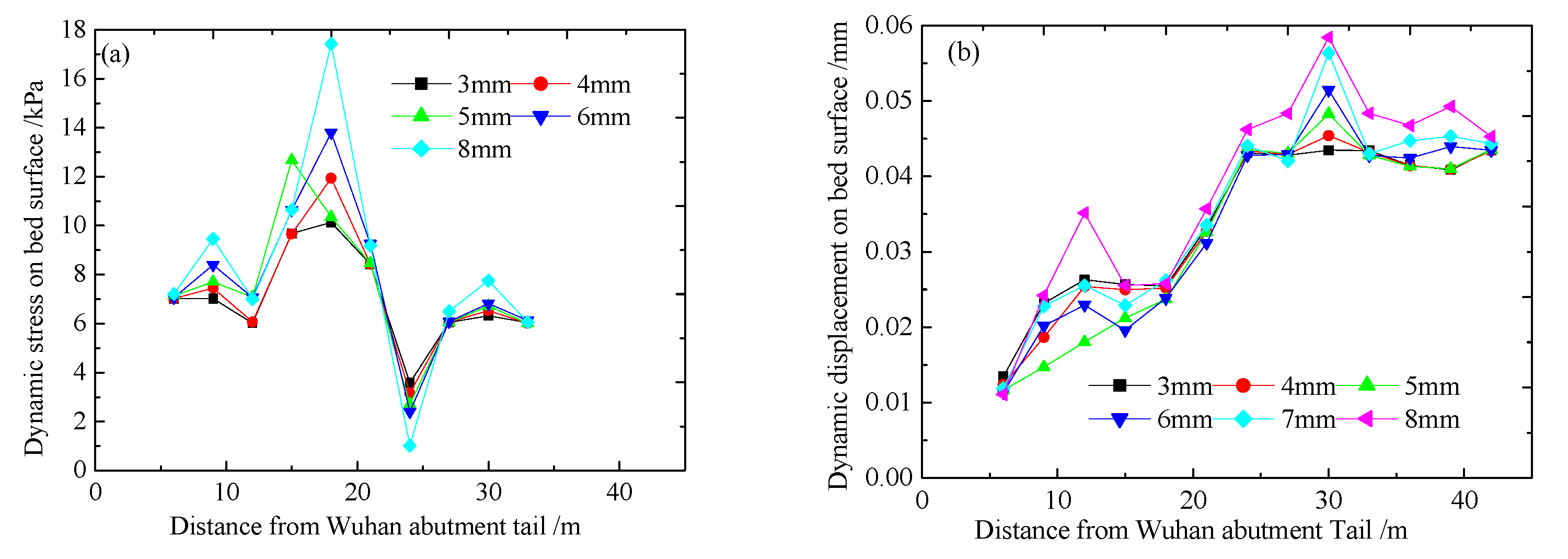
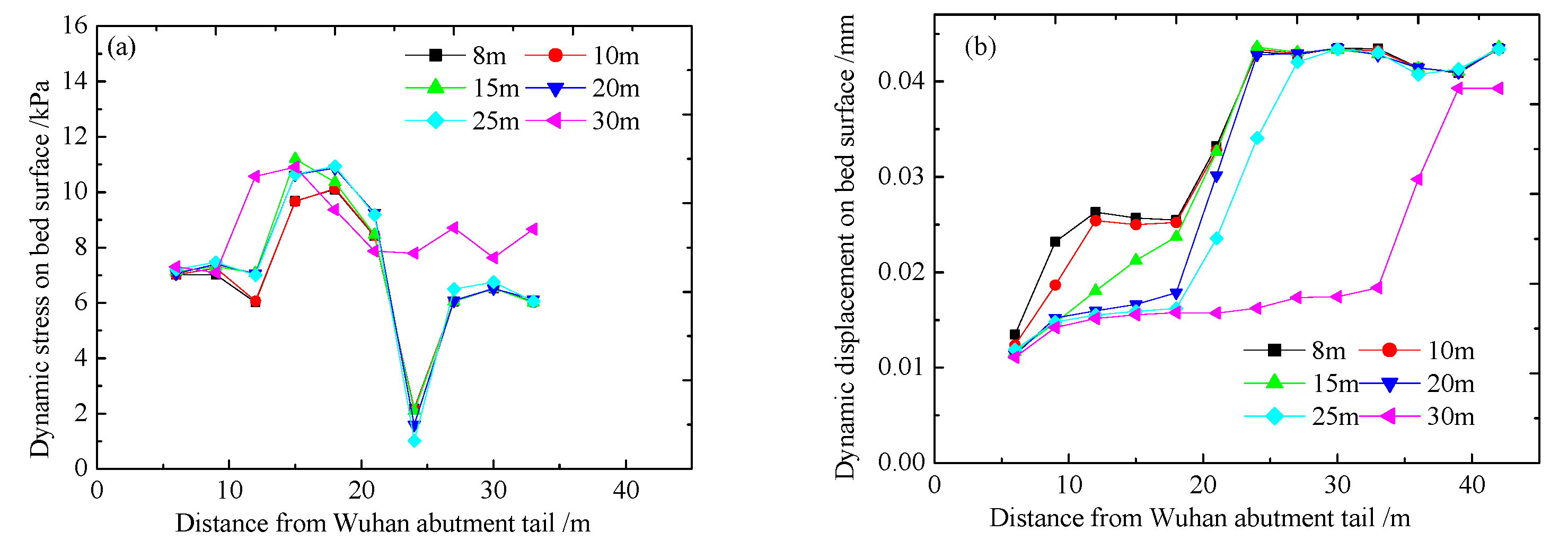
4.1. Change Rule of Dynamic Response along the Longitudinal Direction of the Line
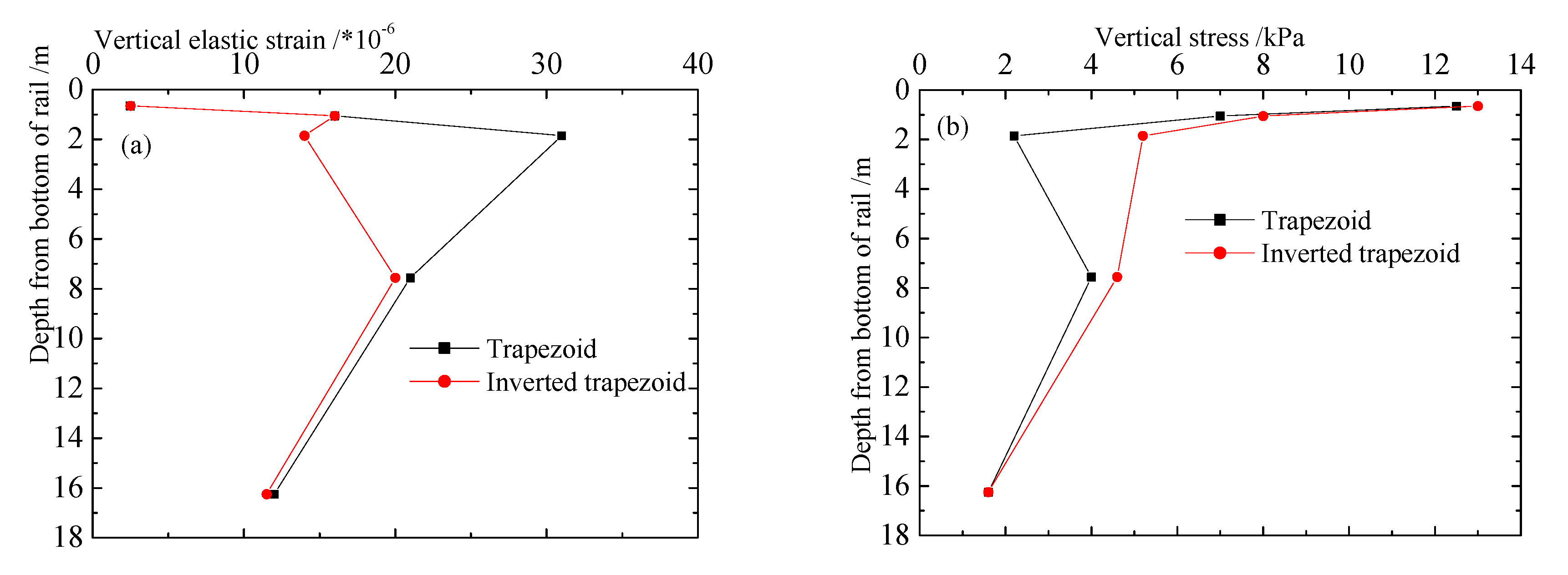
4.2. Law of Dynamic Response along the Depth
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ribeiro, C.A.; Calçada, R.; Delgado, R. Experimental assessment of the dynamic behaviour of the train-track system at a culvert transition zone. Eng. Struct. 2017, 138, 215–228. [Google Scholar] [CrossRef]
- Gou, H.Y.; Ran, Z.W.; Yang, L.C. Mapping vertical bridge deformations to track geometry for high-speed railway. Steel. Compos. Struct. 2019, 32, 467–478. [Google Scholar]
- Zhai, W.M.; Zhao, C.F.; Xia, H.; Xie, Y.J.; Li, G.; Cai, C.; Luo, Q.; Song, X. Basic scientific issues on dynamic performanc evolution of the high-speed railway infrastructure and its service safety. Sci. China Press 2014, 44, 645–666. (In Chinese) [Google Scholar]
- Varandas, J.N.; Hölscher, P.; Silva, M.A.G. Dynamic behavior of railway tracks on transitions zones. Comput. Struct. 2011, 89, 1468–1479. [Google Scholar] [CrossRef]
- Heydari-Noghabi, H.; Varandas, J.N.; Esmaeili, M.; Zakeri, J.A. Investigating the Influence of Auxiliary Rails on Dynamic Behavior of Railway Transition Zone by a 3D Train-Track Interaction Model. Lat. Am. J. Solids Struct. 2017, 14, 2000–2018. [Google Scholar] [CrossRef]
- Armstrong, M.A.; Ravasio, M.; Versteijlen, W.G.; Verschuur, D.J.; Metrikine, A.V.; Van Dalen, K.N. Seismic inversion of soil damping and stiffness using multichannel analysis of surface wave measurements in the marine environment. Geophys. J. Int. 2020, 221, 1439–1449. [Google Scholar] [CrossRef]
- Liang, L.; Li, X.; Zheng, J.; Lei, K.; Gou, H. Structure-borne noise from long-span steel truss cable-stayed bridge under damping pad floating slab: Experimental and numerical analysis. Appl. Acoust. 2020, 157, 106988. [Google Scholar] [CrossRef]
- Shan, Y.; Zhou, S.; Shu, Y. Differential Settlement and Soil Dynamic Stress of a Culvert-embankment Transition Zone Due to an Adjacent Shield Tunnel Construction. KSCE J. Civ. Eng. 2018, 22, 2325–2333. [Google Scholar] [CrossRef]
- Fu, Q.; Wu, Y. Three-dimensional finite element modelling and dynamic response analysis of track-embankment-ground system subjected to high-speed train moving loads. Geomech. Eng. 2019, 19, 241–254. [Google Scholar]
- Matthias, G.; Geert, D.; Geert, L. A track model for railway-induced ground vibration resulting from a transition zone. Proc. I Mech. E Part F J. Rail Rapid Transit. 2018, 232, 1703–1717. [Google Scholar]
- Sheng, X.; Zhong, T.-S.; Li, Y. Vibration and sound radiation of slab high-speed railway tracks subject to a moving harmonic load. J. Sound Vib. 2017, 395, 160–186. [Google Scholar] [CrossRef]
- Shan, Y.; Shu, Y.; Zhou, S. Finite-infinite element coupled analysis on the influence of material parameters on the dynamic properties of transition zones. Constr. Build. Mater. 2017, 148, 548–558. [Google Scholar] [CrossRef]
- Zhang, X.; Shan, Y.; Yang, X. Effect of Bridge-Pier Differential Settlement on the Dynamic Response of a High-Speed Railway Train-Track-Bridge System. Math. Probl. Eng. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Chen, M.; Sun, Y.; Zhai, W. High efficient dynamic analysis of vehicle–track–subgrade vertical interaction based on Green function method. Veh. Syst. Dyn. 2019, 58, 1076–1100. [Google Scholar] [CrossRef]
- Hu, P.; Zhang, C.; Chen, S.; Wang, Y.; Wang, W.; Zhuang, J. Dynamic responses of bridge–embankment transitions in high speed railway: Field tests and data analyses. Eng. Struct. 2018, 175, 565–576. [Google Scholar] [CrossRef]
- Hu, P.; Zhang, C.; Wen, S.; Wang, Y. Dynamic responses of high-speed railway transition zone with various subgrade fillings. Comput. Geotech. 2019, 108, 17–26. [Google Scholar] [CrossRef]


| Working Condition | Acceleration of Train Body (m/s2) | Rate of Wheel Load Reduction Q/P | Y/YDerailment | Rail Wheel Force (kN) | ||||
|---|---|---|---|---|---|---|---|---|
| Lateral ay | Vertical az | Vertical | Lateral | |||||
| Rigid | Transition length | 10 | -- | 0.893 | 0.120 | 0.010 | 115.3 | -- |
| 15 | 0.582 | 0.110 | 0.010 | 115.8 | ||||
| 20 | -- | 0.424 | 0.105 | 0.010 | 116.4 | -- | ||
| 25 | -- | 0.405 | 0.063 | 0.010 | 118.2 | -- | ||
| 30 | 0.018 | 0.406 | 0.054 | 0.011 | 121.3 | -- | ||
| Bending angle * | 1/1000 | 0.033 | 1.035 | 0.124 | 0.015 | 123.8 | -- | |
| 3/1000 | −0.145 | 4.413 | 0.330 | 0.050 | 142.7 | -- | ||
| 4/1000 | 0.152 | 4.327 | 0.522 | 0.069 | 150.2 | -- | ||
| PSD & | 0.349 | 0.500 | 1.469 | 2.041 | 140.6 | 193.7 | ||
| Flexible | PSD | 0.341 | 0.520 | 0.448 | 0.229 | 135.7 | 41.9 | |
| Bending angle of 0.75/1000 | 0.153 | 0.733 | 0.142 | 0.215 | 117.7 | -- | ||
| Differential Settlement | Acceleration of Train Body (m/s2) | Rate of Wheel Load Reduction Q/P | Y/YDerailment | Wheelset Vertical Displacement (mm) | Rail Wheel Force (kN) | ||
|---|---|---|---|---|---|---|---|
| Lateral ay | Lateral ay | Vertical | Lateral | ||||
| 3 | 0.07 | 0.45 | 0.53 | 0.19 | 40.4 | 2.9 | 226.6 |
| 4 | 0.12 | 0.67 | 0.79 | 0.25 | 57.7 | 3.7 | 238.0 |
| 5 | 0.12 | 0.87 | 0.96 | 0.33 | 87.5 | 7.3 | 283.2 |
| 6 | 0.19 | 3.49 | 2.88 | 1.46 | 139.2 | 9.4 | 294.2 |
| 7 | 0.26 | 3.79 | 4.37 | 1.66 | 168.6 | 15.4 | 344.9 |
| 7.4 | 0.50 | 4.93 | 8.48 | 2.21 | 183.3 | 56.1 | 558.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, P.; Zhang, C.; Guo, W.; Wang, Y. Dynamic Response of a Bridge–Embankment Transition with Emphasis on the Coupled Train–Track–Subgrade System. Appl. Sci. 2020, 10, 5982. https://doi.org/10.3390/app10175982
Hu P, Zhang C, Guo W, Wang Y. Dynamic Response of a Bridge–Embankment Transition with Emphasis on the Coupled Train–Track–Subgrade System. Applied Sciences. 2020; 10(17):5982. https://doi.org/10.3390/app10175982
Chicago/Turabian StyleHu, Ping, Chunshun Zhang, Wei Guo, and Yonghe Wang. 2020. "Dynamic Response of a Bridge–Embankment Transition with Emphasis on the Coupled Train–Track–Subgrade System" Applied Sciences 10, no. 17: 5982. https://doi.org/10.3390/app10175982
APA StyleHu, P., Zhang, C., Guo, W., & Wang, Y. (2020). Dynamic Response of a Bridge–Embankment Transition with Emphasis on the Coupled Train–Track–Subgrade System. Applied Sciences, 10(17), 5982. https://doi.org/10.3390/app10175982





