Grousers Effect in Tracked Vehicle Multibody Dynamics with Deformable Terrain Contact Model
Abstract
:1. Introduction
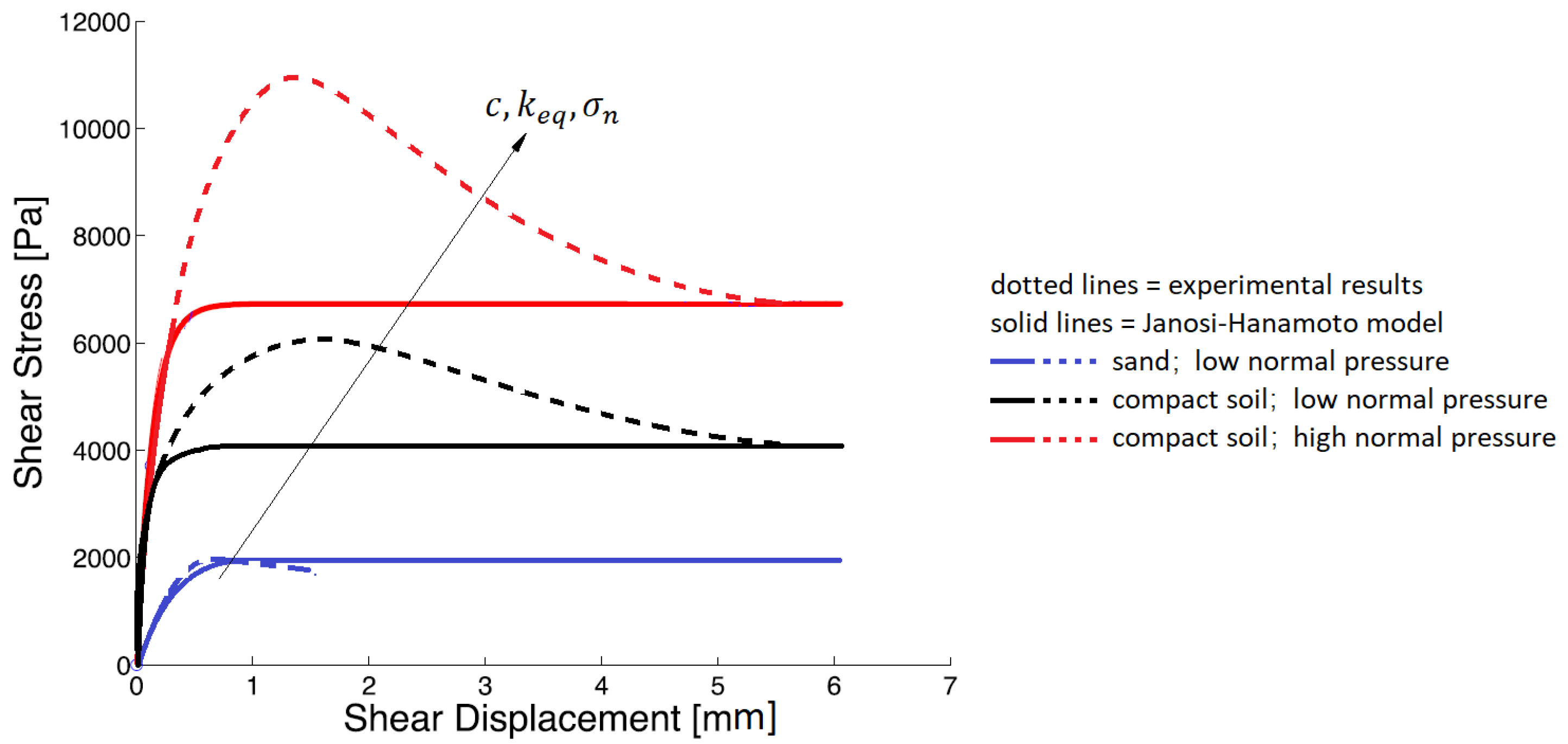
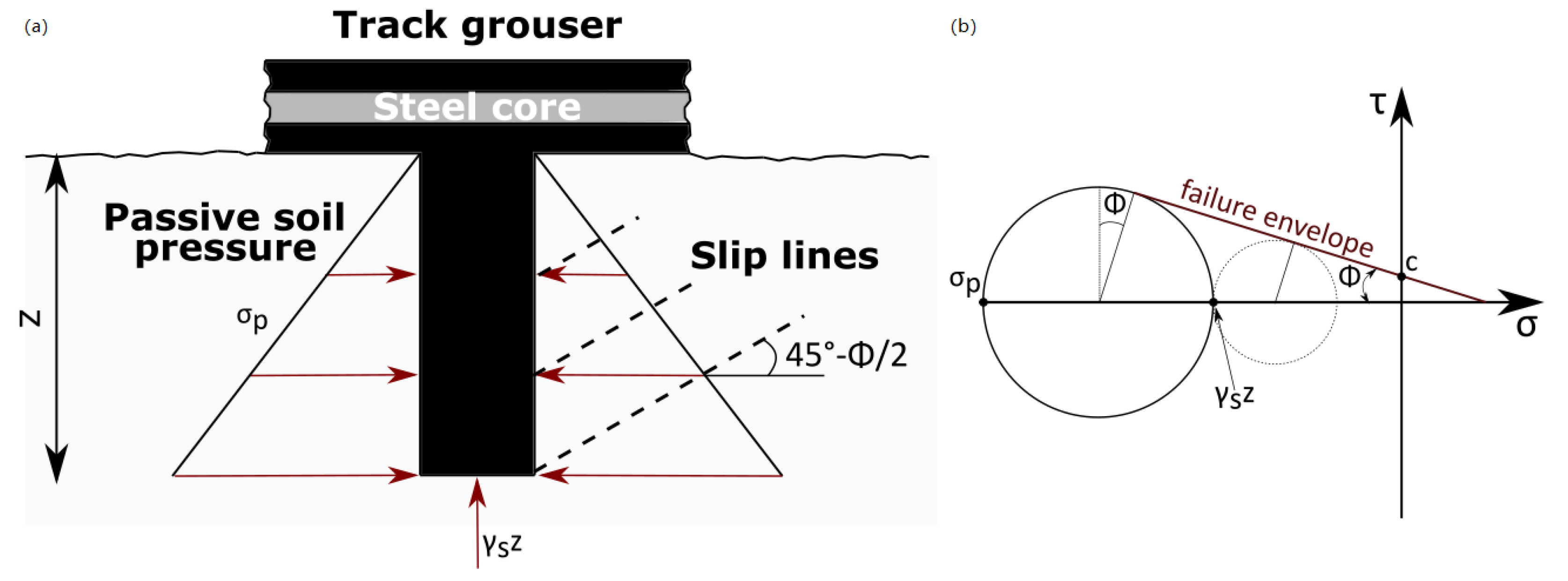
2. Soil Mechanics
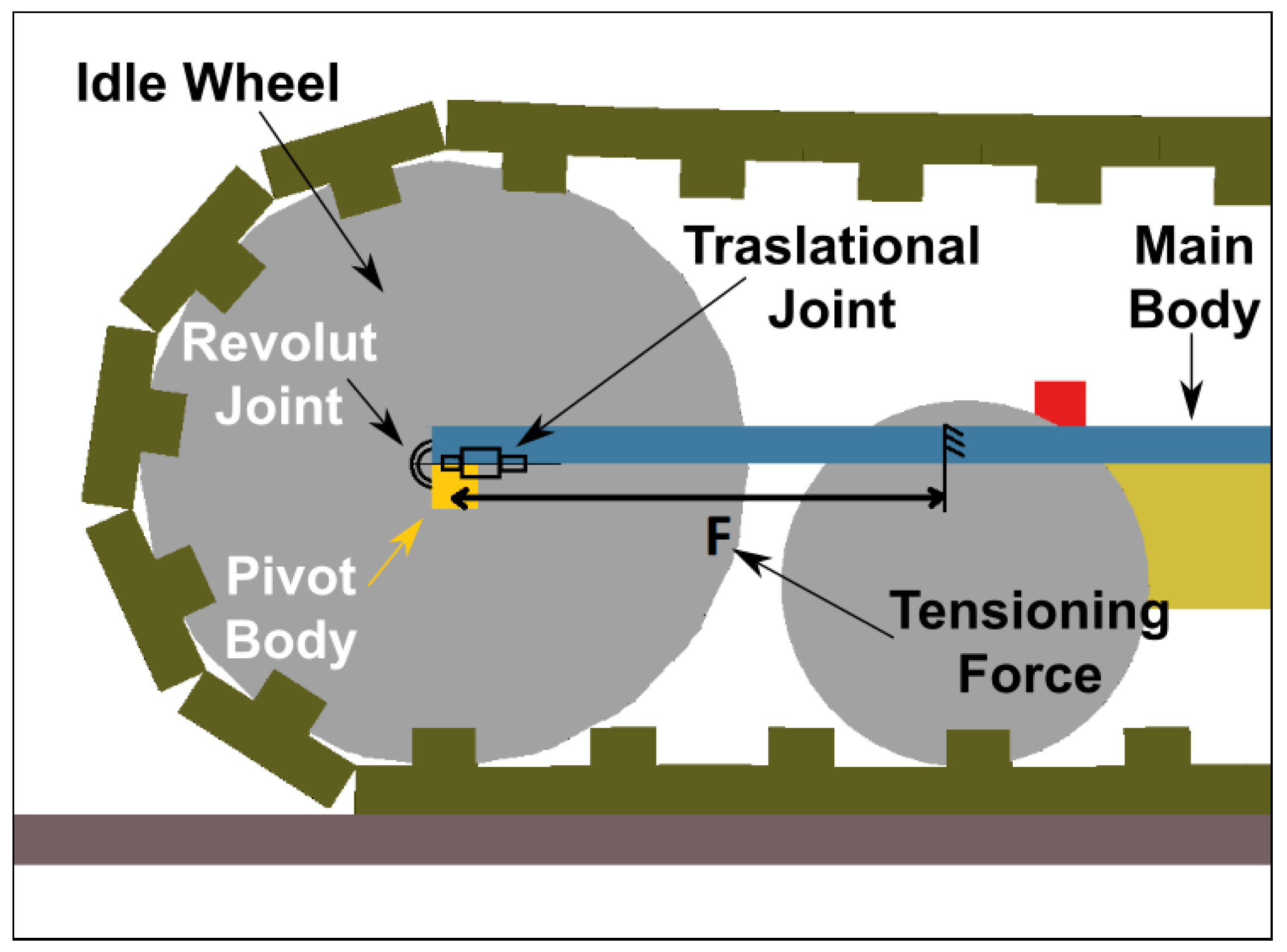
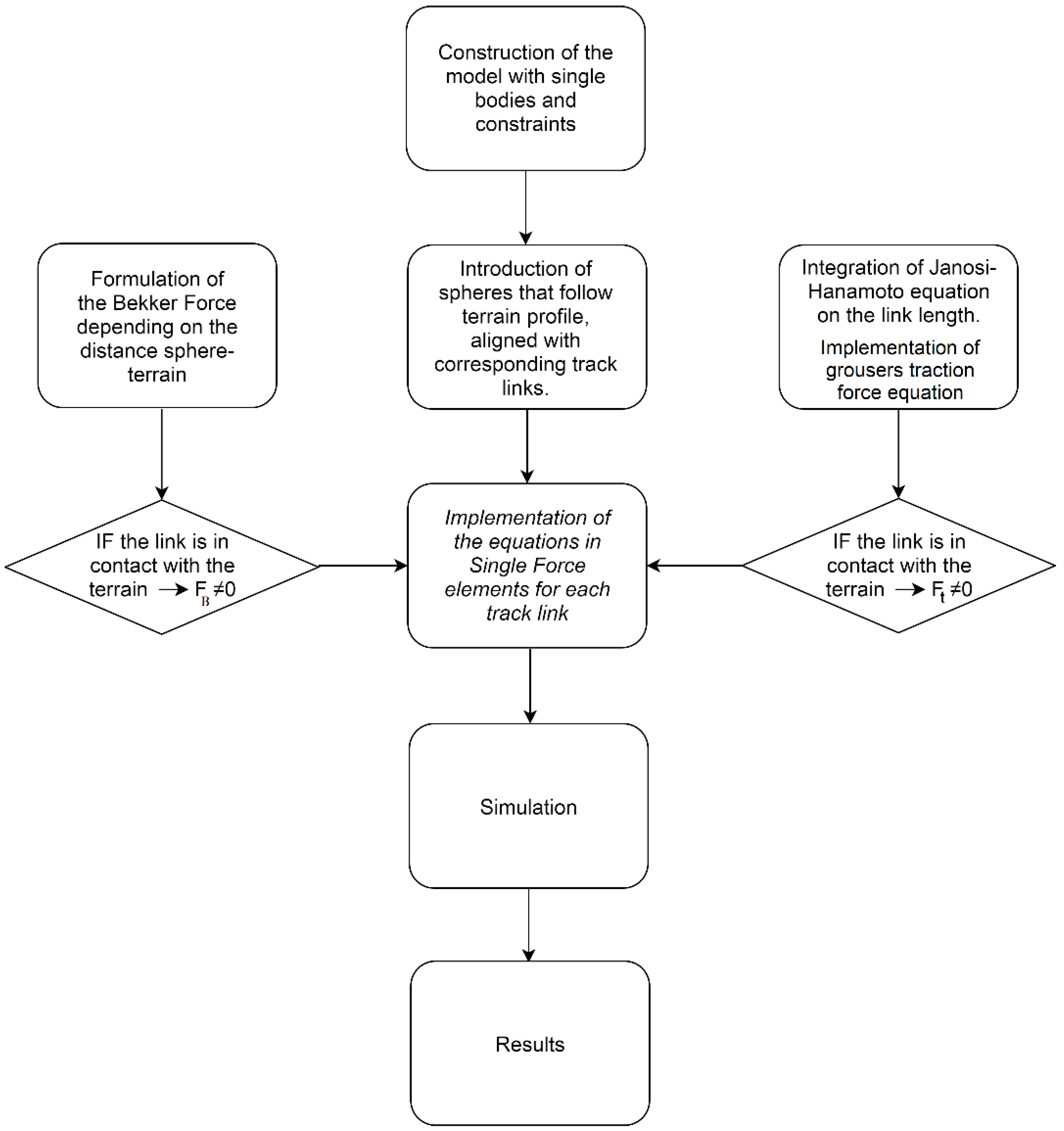
3. Methods: Multibody Modelling
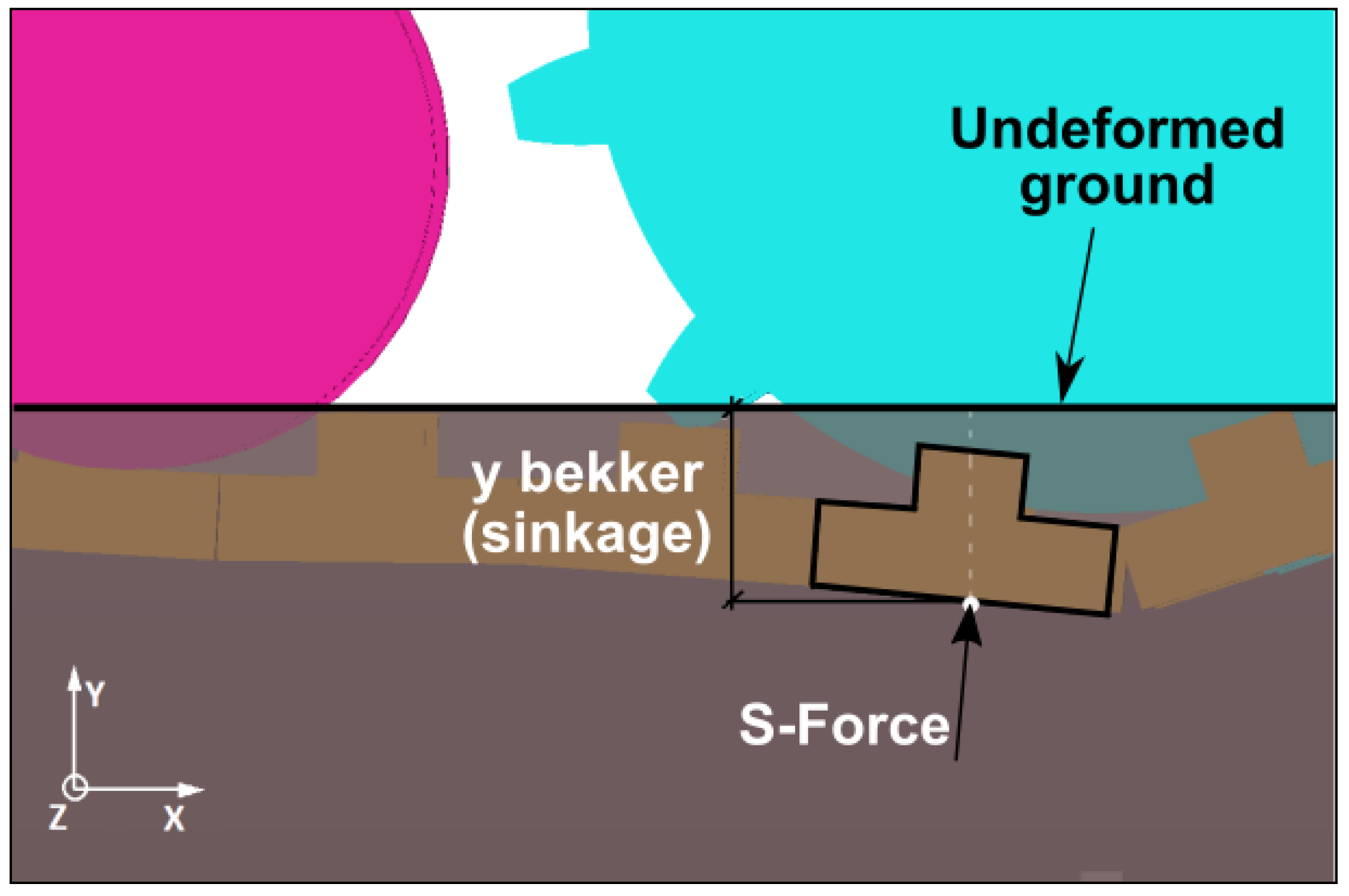
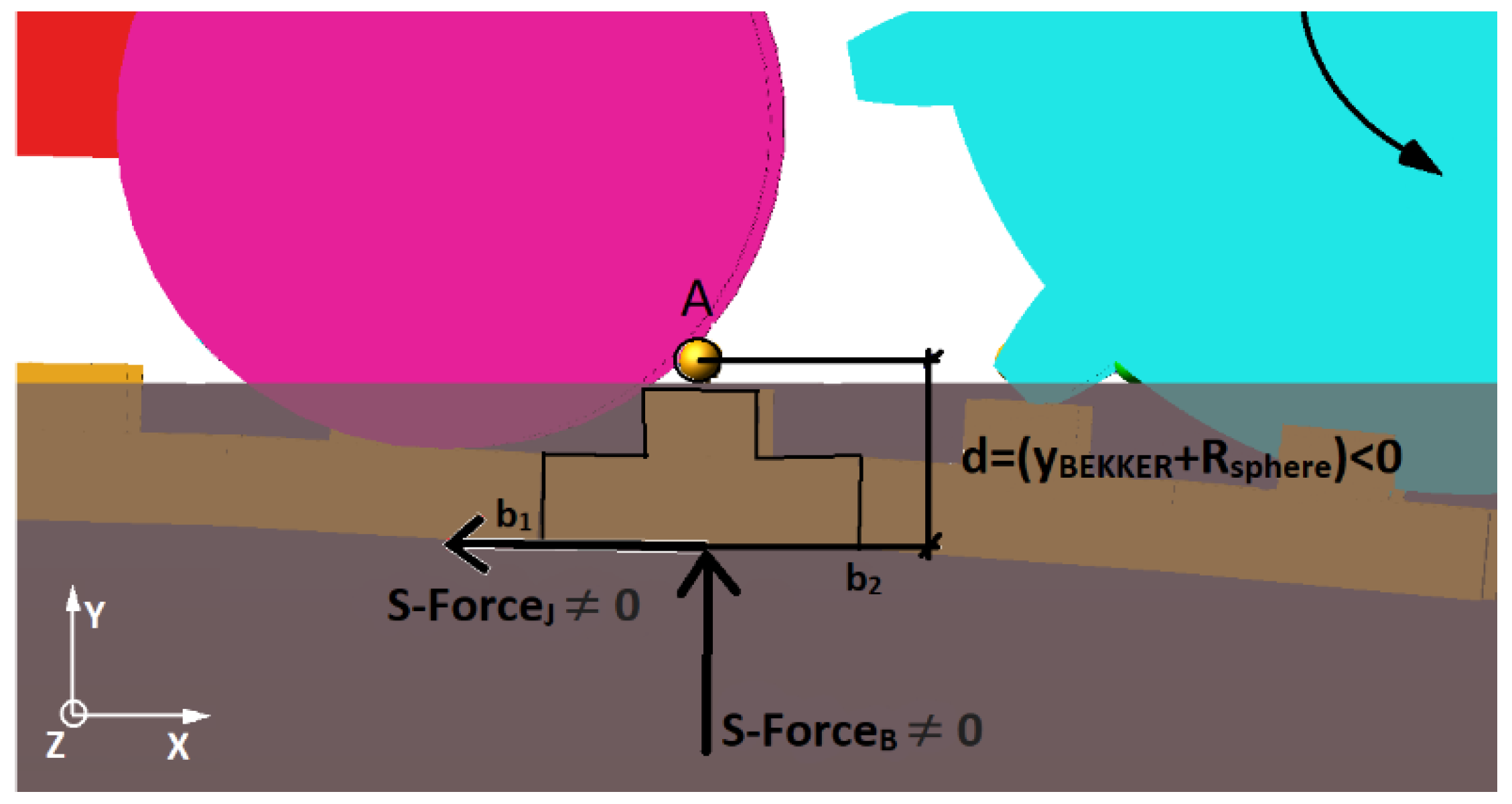
3.1. Deformable Ground Contact Model
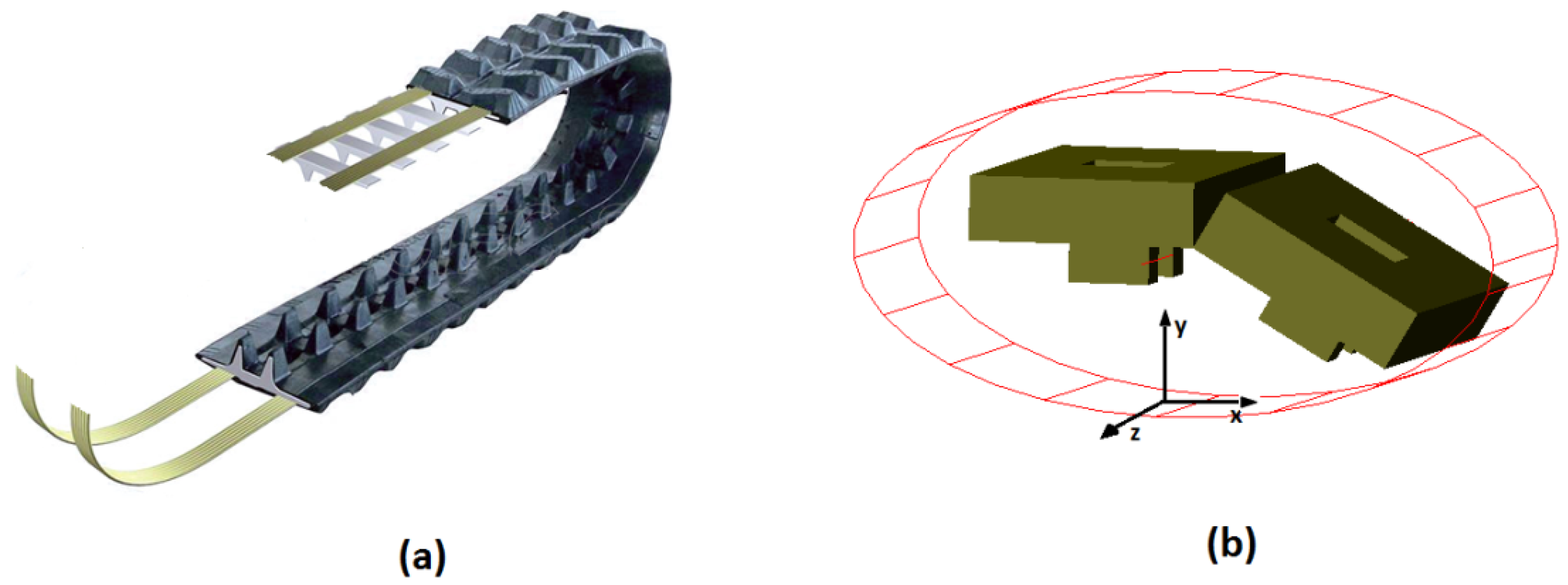
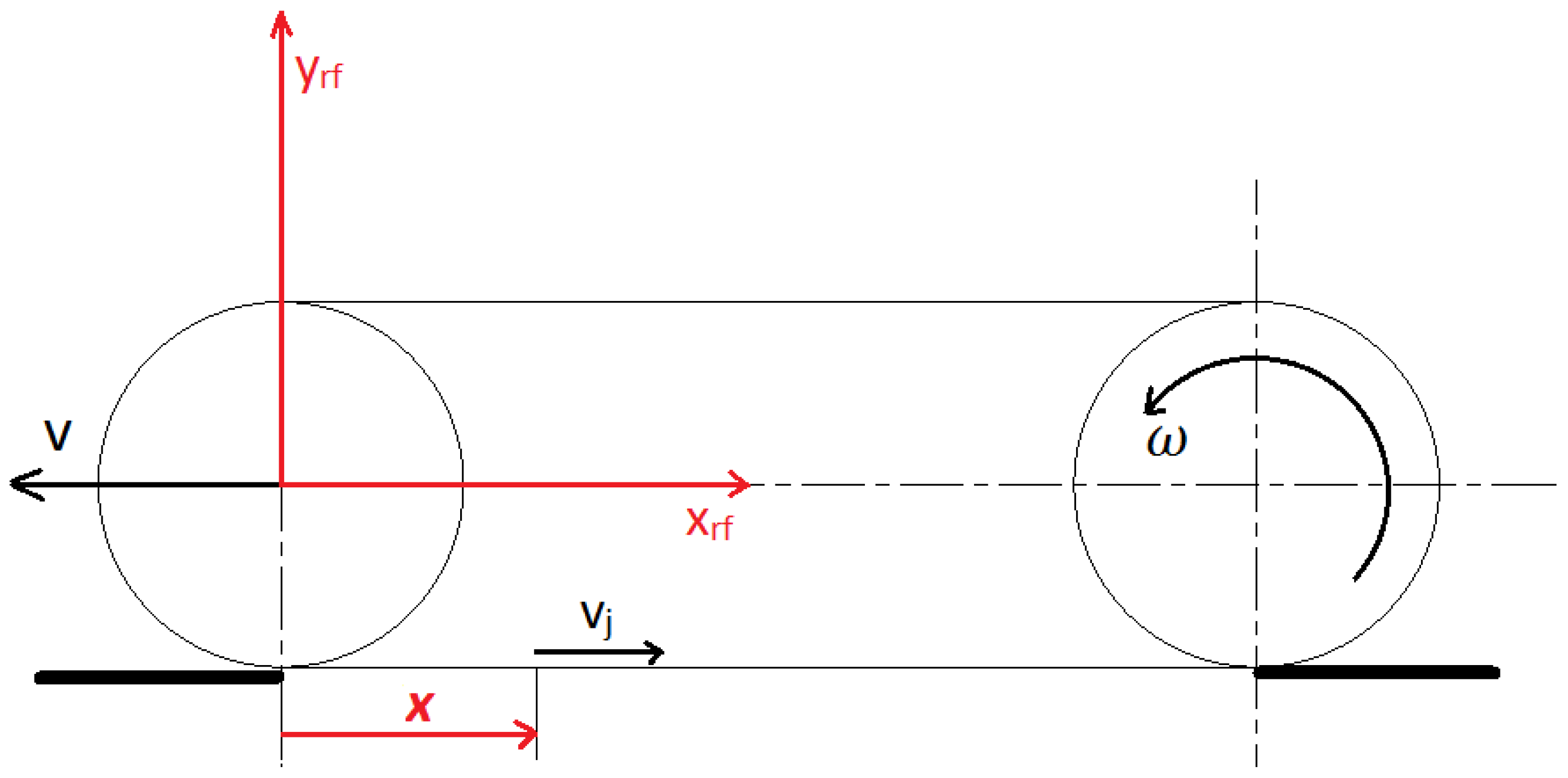
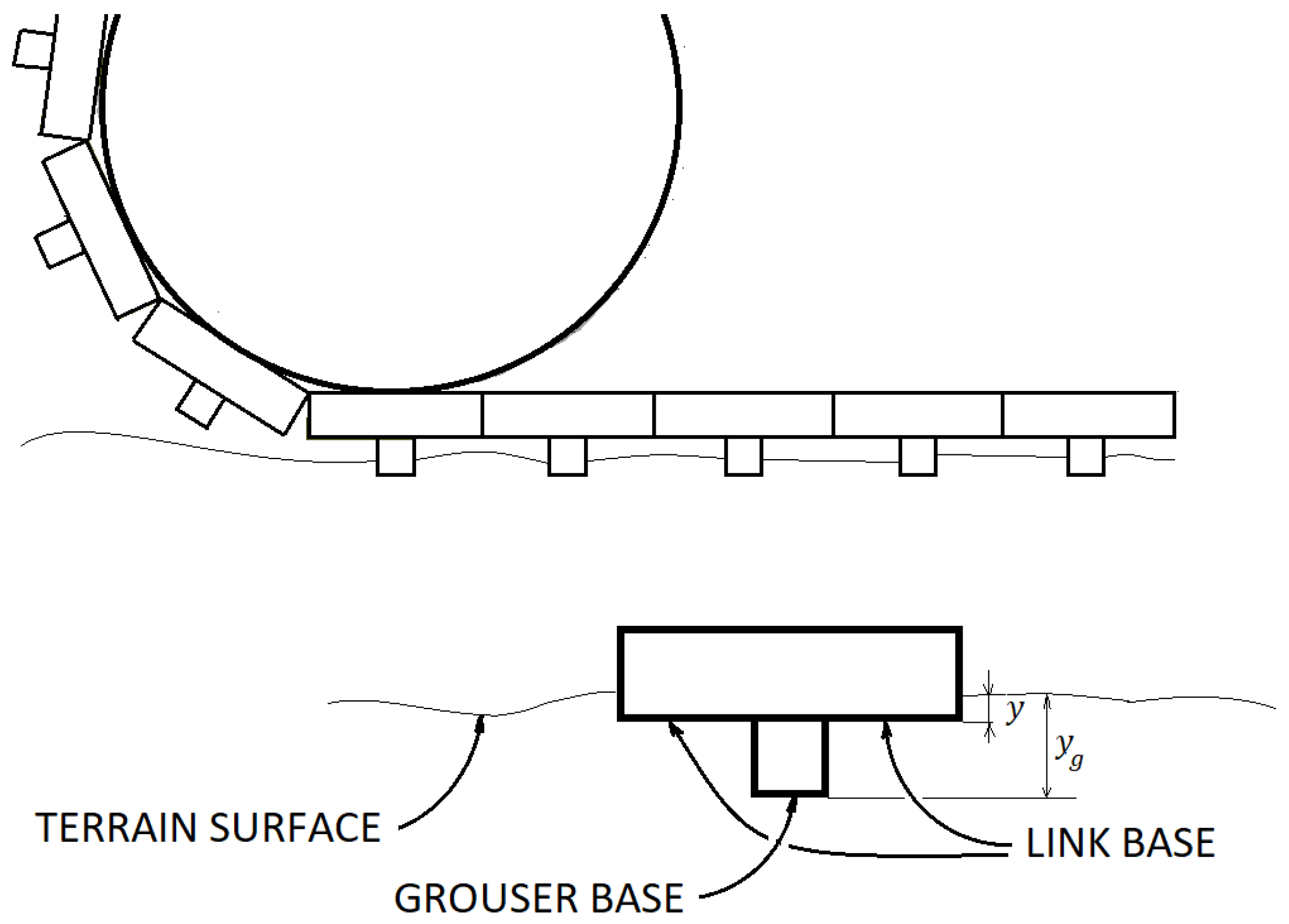
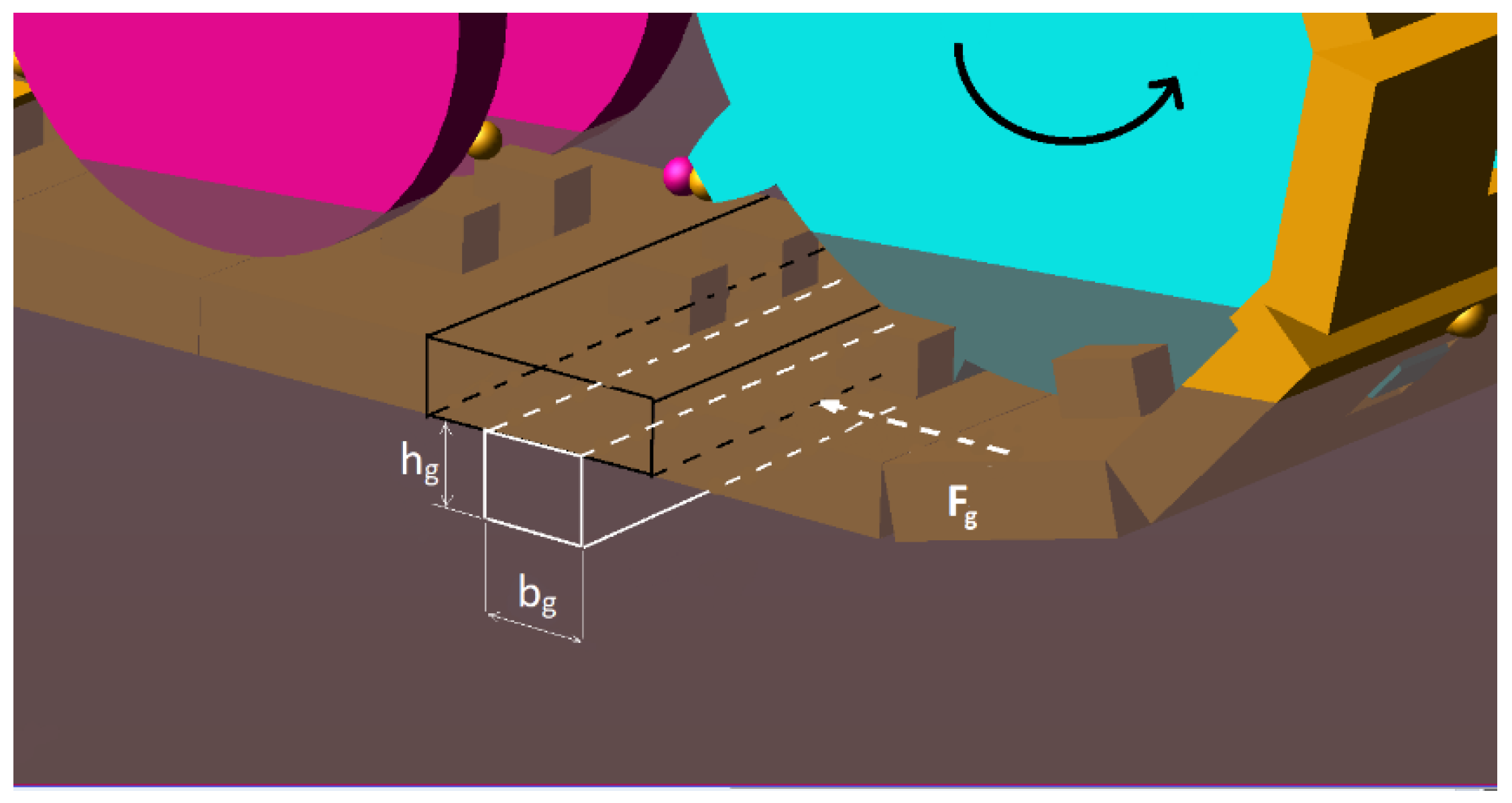
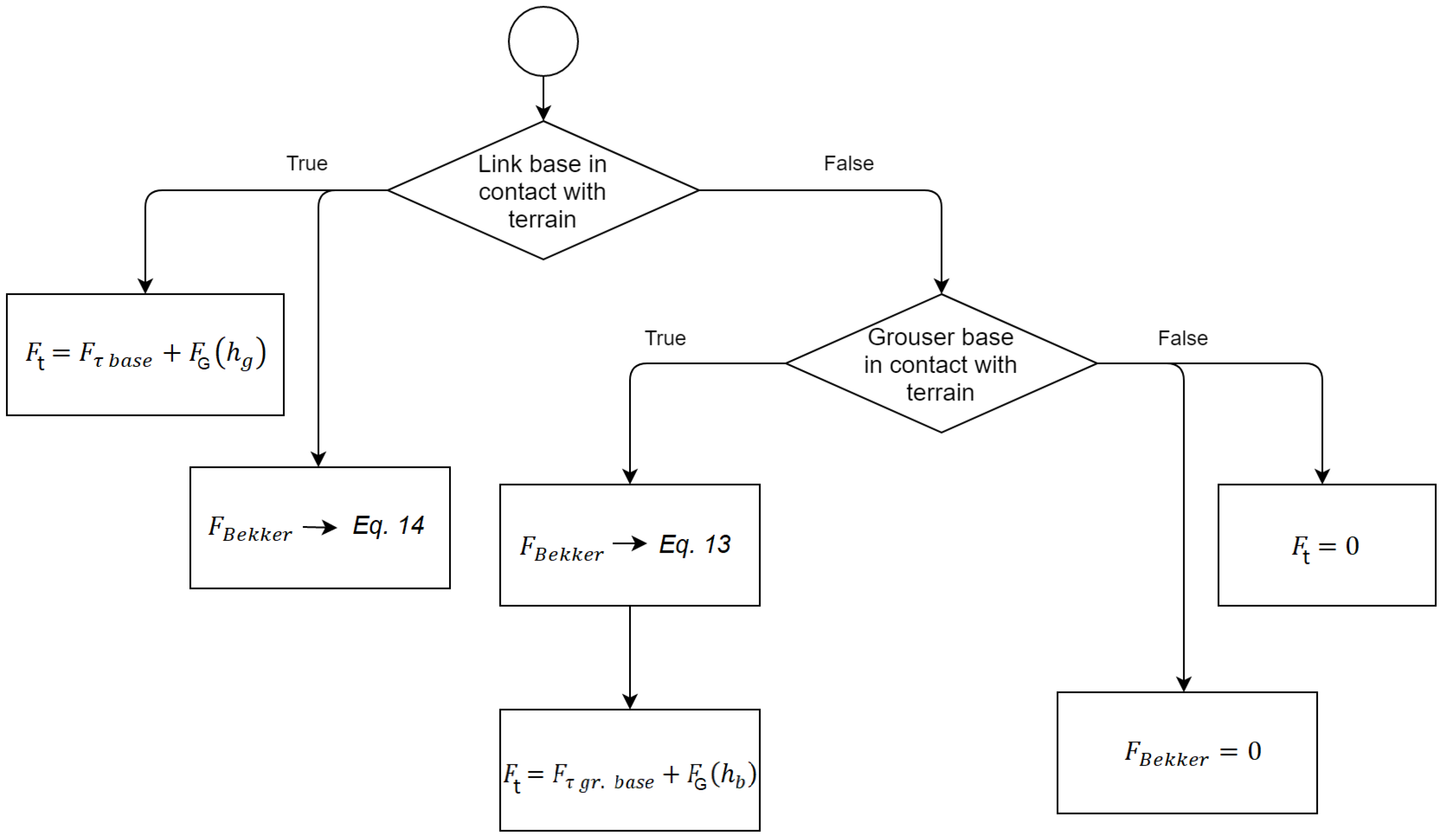
3.2. Grousers Modelling
4. Simulations and Results
4.1. Smooth Tracks
4.1.1. Normal Pressure Distribution and Track Sinkage
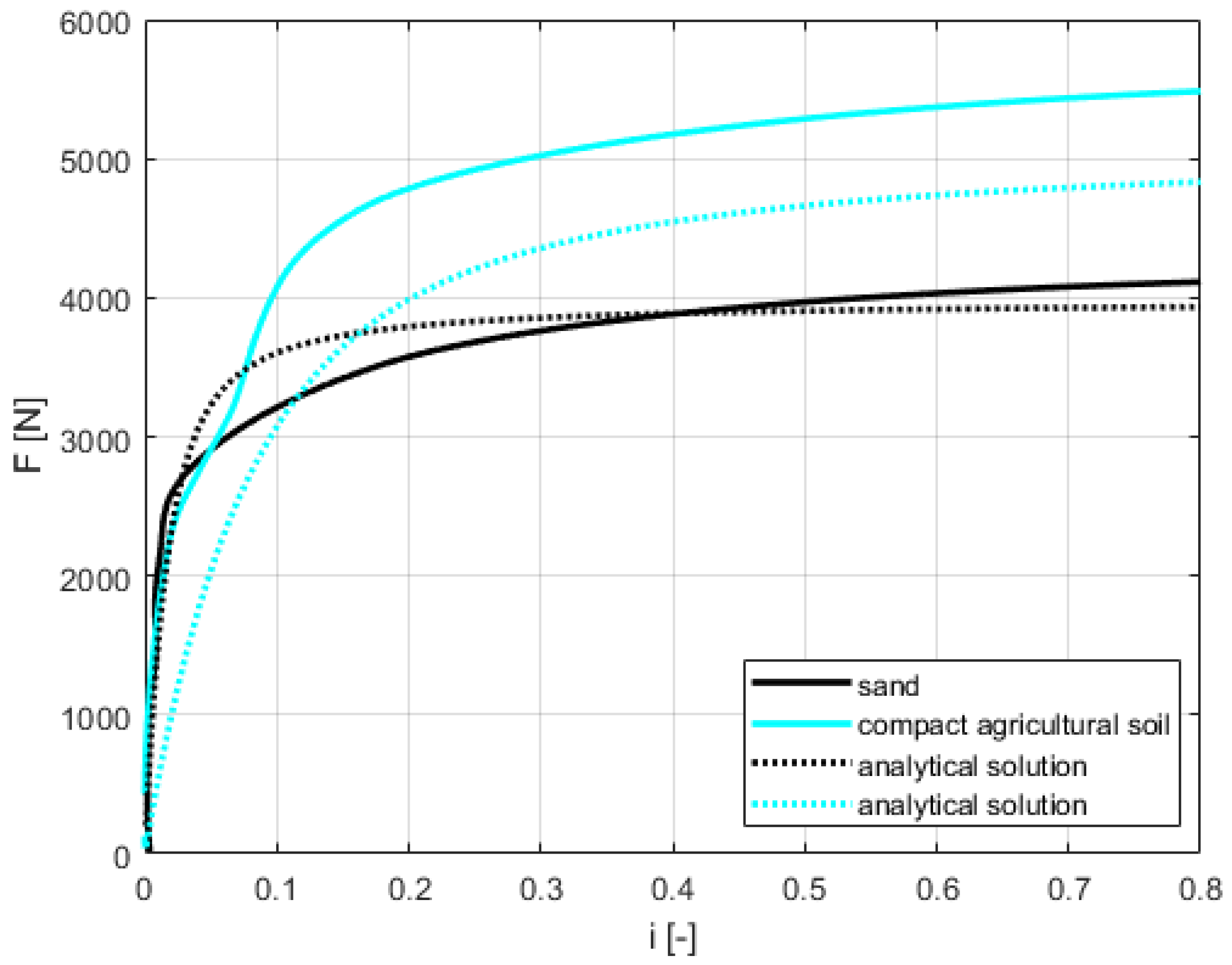
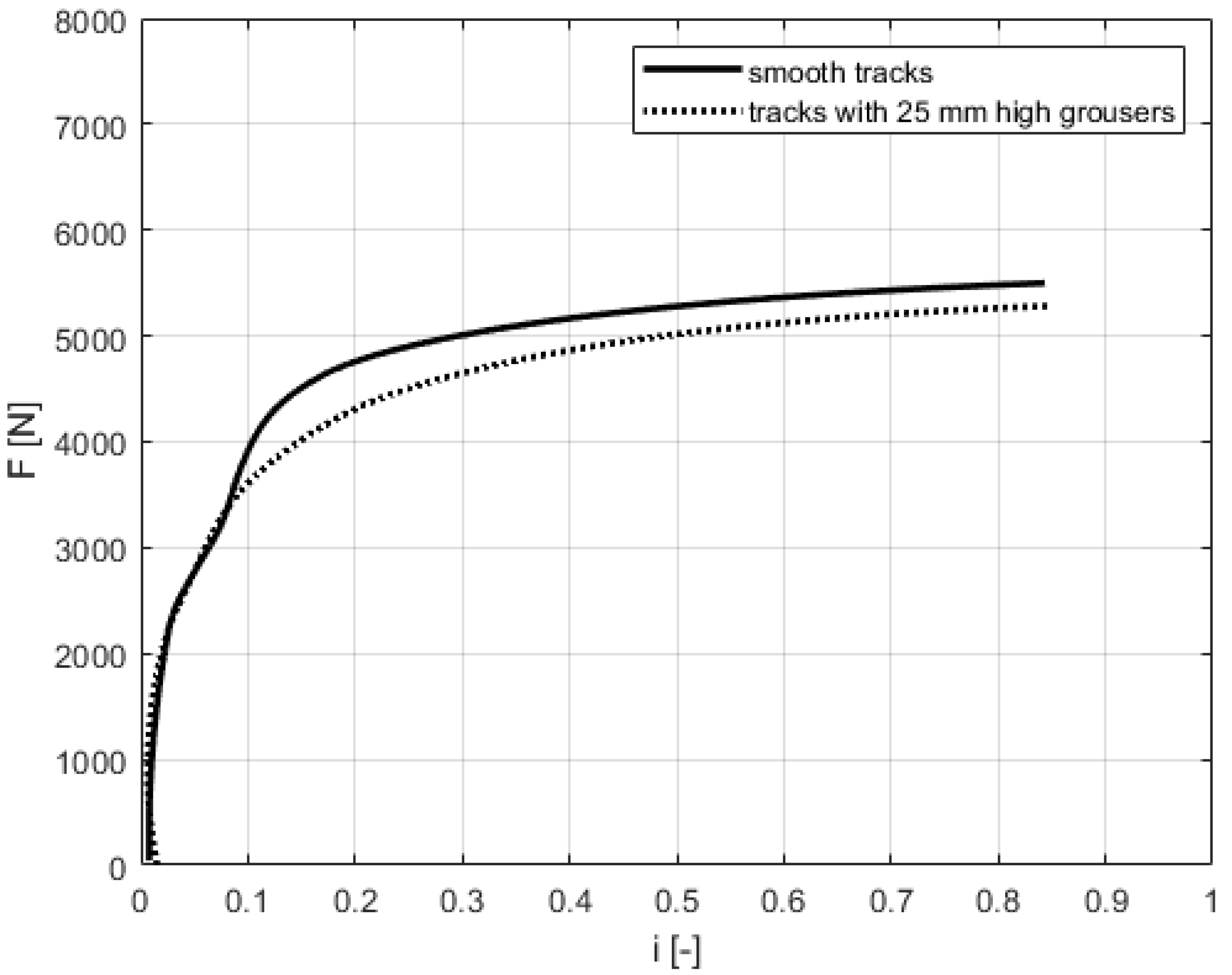
4.1.2. Traction Force-Slip Curves
4.2. Tracks with Grousers
4.2.1. Sinkage
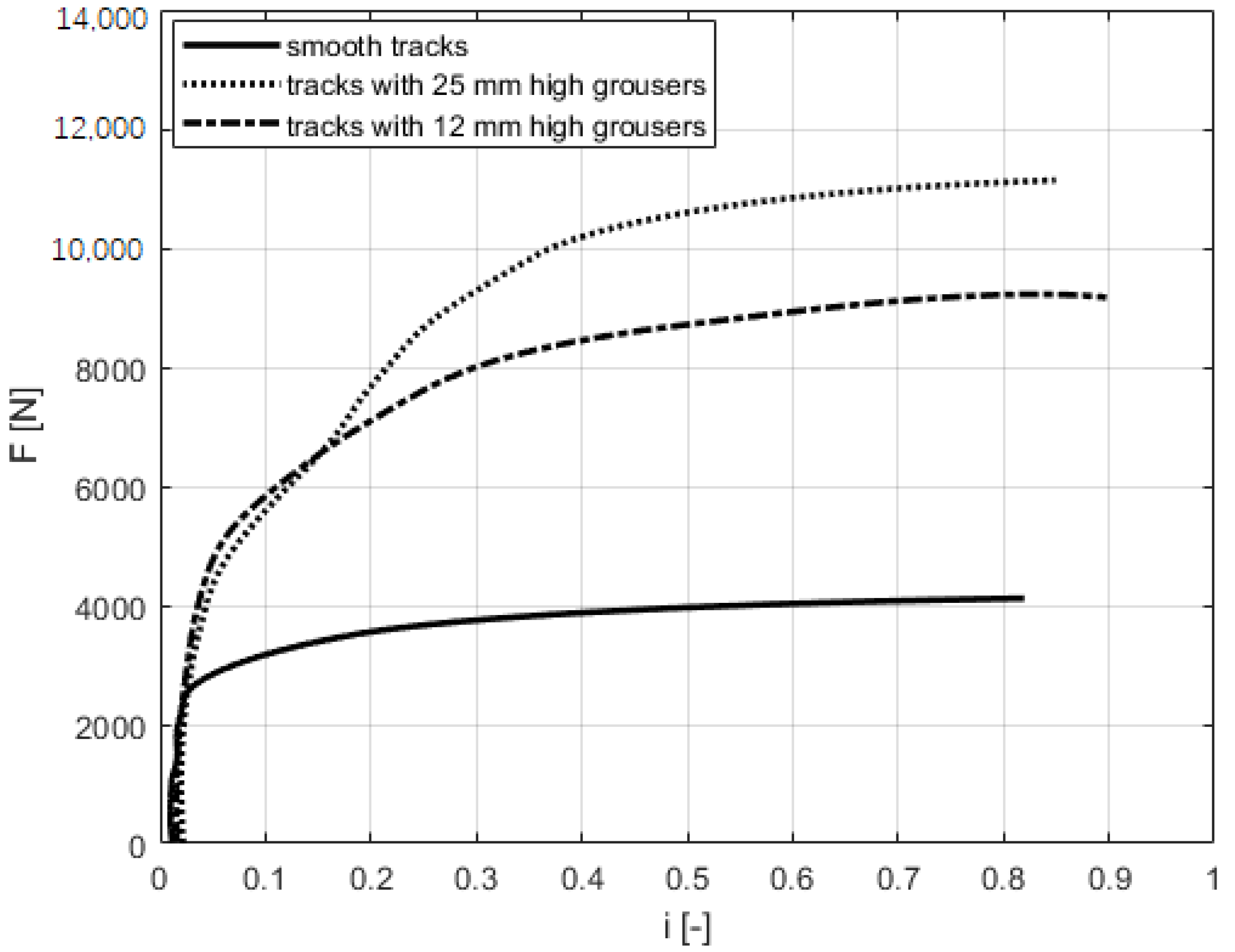
4.2.2. Traction Force-Slip Curves
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blundell, M.; Harty, D. The Multibody Systems Approach to Vehicle Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Pascuzzi, S. A multibody approach applied to the study of driver injuries due to a narrow-track wheeled tractor rollover. J. Agric. Eng. 2015, 46, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Melzi, S.; Sabbioni, E.; Vignati, M.; Cutini, M.; Brambilla, M.; Bisaglia, C.; Cavallo, E. Multibody model of fruit harvesting trucks: Comparison with experimental data and rollover analysis. J. Agric. Eng. 2015, 49, 92–99. [Google Scholar] [CrossRef] [Green Version]
- Yong, R.N. Track-soil interaction. J. Terramech. 1984, 21, 133–152. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tyre and Vehicle Dynamics; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Bekker, M.G. Theory of Land Locomotion; University of Michigan Press: Ann Arbor, MI, USA, 1962. [Google Scholar]
- Wong, J.Y.; Preston-Thomas, J. On the characterization of the shear stress-displacement relationship of terrain. J. Terramech. 1982, 19, 225–234. [Google Scholar] [CrossRef]
- Wong, J.Y. Data processing methodology in the characterization of the mechanical properties of terrain. J. Terramech. 1980, 17, 13–41. [Google Scholar] [CrossRef]
- Taheri, S.; Sandu, C.; Taheri, S.; Pinto, E.; Gorsich, D. A technical survey on terramechanics models for tire–terrain interaction used in modeling and simulation of wheeled vehicles. J. Terramech. 2014, 57, 1–22. [Google Scholar] [CrossRef]
- Wong, J.Y. Some recent developments in the computer-aided methods for design evaluation of off-road vehicles. Proc. Symp. Transp. Syst. 1990, 28, 269–288. [Google Scholar]
- Wong, J.Y. On the study of wheel-soil interaction. J. Terramech. 1984, 21, 117–131. [Google Scholar] [CrossRef]
- Senatore, C.; Iagnemma, K. Analysis of stress distributions under lightweight wheeled vehicles. J. Terramech. 2013, 51, 1–17. [Google Scholar] [CrossRef]
- Shabana, A.A. ANCF Tire Assembly Model for Multibody System Applications. J. Comput. Nonlinear Dyn. 2015, 10, 024504. [Google Scholar] [CrossRef]
- Patel, M.; Orzechowski, G.; Tian, Q.; Shabana, A.A. A New Multibody System Approach for Tire Modeling Using ANCF Finite Elements. Proc. Inst. Mech. Eng. Part K J. Multi Body Dyn. 2016, 230, 69–84. [Google Scholar] [CrossRef]
- Sivo, S.; Stio, A.; Mocera, F.; Somà, A. A study of a rover wheel for Martian explorations, based on a flexible multibody approach. Proc. Inst. Mech. Eng. Part J. Multi Body Dyn. 2019, 234, 306–321. [Google Scholar] [CrossRef]
- Reece, A.R. Principles of soil-vehicle mechanics. Proc. Inst. Mech. Eng. Automob. Div. 1965, 108, 45–66. [Google Scholar] [CrossRef]
- Harnisch, C.; Lach, B.; Jakobs, R.; Troulis, M.; Nehls, O. A new tyre–soil interaction model for vehicle simulation on deformable ground. Veh. Syst. Dyn. 2005, 3, 384–394. [Google Scholar] [CrossRef]
- Sharaf, A.M.; Rahnejat, H.; King, P.D. Analysis of handling characteristics of all-wheel-drive off-road vehicles. Int. J. Heavy Veh. Syst. 2008, 15, 89–106. [Google Scholar] [CrossRef]
- Rubinstein, D.; Hitron, R. A detailed multibody model for dynamic simulation of off-road tracked vehicles. J. Terramech. 2004, 41, 163–173. [Google Scholar] [CrossRef]
- Madsen, J.; Heyn, T.; Negrut, D. Methods for Tracked Vehicle System Modelling and Simulation; Technical Report 2010–01; Department of Mechanical Engineering, University of Wisconsin: Madison, WI, USA, 2010. [Google Scholar]
- Frimpong, S.; Thiruvengadam, M. Contact and joint forces modeling and simulation of crawler-formation interactions. J. Powder Metall. Min. 2015, 4, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Frimpong, S.; Thiruvengadam, M. Rigid multi-body kinematics of shovel crawler-formation interactions. Int. J. Mining Reclam. Environ. 2016, 30, 347–369. [Google Scholar] [CrossRef]
- Baik, D.K. Systems Modeling and Simulation: Theory and Applications; Springer: Jeju Island, Korea, 2005; pp. 553–558. [Google Scholar]
- Matej, J. Tracked mechanism simulation of mobile machine in MSC.ADAMS/View. Res. Agric. Eng. 2010, 56, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.H.; Wong, J.Y.; Mang, H.A. Large strain finite element analysis of sand: Model, algorithm and application to numerical simulation of tire-sand interaction. Comput. Struct. 1999, 74, 253–265. [Google Scholar] [CrossRef]
- Krenn, R.; Hirzinger, G. Simulation of rover locomotion on sandy terrain-modeling, verification and validation. In Proceedings of the 10th ESA Workshop on Advanced Space Technologies for Robotics and Automation—ASTRA 2008, Noordwijk, The Netherlands, 11–13 November 2018. [Google Scholar]
- Gao, Y.; Wong, J.Y. The development and validation of a computer aided method for design evaluation of tracked vehicles with rigid links. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1994, 208, 207–215. [Google Scholar] [CrossRef]
- Nakanishi, T.; Shabana, A.A. Contact forces in the non-linear dynamic analysis of tracked vehicles. Int. J. Numer. Methods Eng. 1994, 37, 1251–1275. [Google Scholar] [CrossRef]
- Omar, M.A. Modular multibody formulation for simulating off-road tracked vehicles. Stud. Eng. Technol. 2014, 1, 77–100. [Google Scholar] [CrossRef] [Green Version]
- Ryu, H.S.; Bae, D.S.; Choi, J.H.; Shabana, A.A. A compliant track link model for high-speed, high-mobility tracked vehicles. Int. J. Numer. Methods Eng. 2000, 48, 1481–1502. [Google Scholar] [CrossRef]
- Bando, K.; Yoshida, K.; Hori, K. The development of the rubber track for small size bulldozers. SAE Trans. Sect. 2 J. Commer. Veh. 1991, 100, 339–347. [Google Scholar]
- Bosso, N.; Spiryagin, M.; Gugliotta, A.; Somà, A. Mechatronic Modeling of Real-Time Wheel-Rail Contact; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Nicolini, A.; Mocera, F.; Somà, A. Multibody simulation of a tracked vehicle with deformable ground contact model. Proc. Inst. Mech. Eng. Part K J. Multi Body Dyn. 2019, 233, 152–162. [Google Scholar] [CrossRef]
- Hettiaratchi, D.R.P.; Reece, A.R. The calculation of passive soil resistance. Geotecnique 1974, 24, 289–310. [Google Scholar] [CrossRef]
- Wong, J.Y.; Garber, M.; Preston-Thomas, J. Theoretical prediction and experimental substantiation of the ground pressure distribution and tractive performance of tracked vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1984, 198, 265–285. [Google Scholar] [CrossRef]
- Janosi, Z.J.; Hanamoto, B. The analytical determination of drawbar pull as a function of slip for tracked vehicles in deformable soils. In Proceedings of the 1st International Conference on the Mechanics of Soil Systems, Torino, Italy, 12–16 June 1961. [Google Scholar]
- Wong, J.Y. Terramechanics and Off-Road Vehicles Engineering, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2010. [Google Scholar]
- Hutangkabodee, S.; Zweiri, Y.H.; Seneviratne, L.D.; Althoefer, K. Validation of soil parameter identification for track-terrain interaction dynamics. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–22 November 2007. [Google Scholar]
- Neal, M.S. Friction and adhesion between soil and rubber. J. Agric. Eng. Res. 1966, 11, 108–112. [Google Scholar] [CrossRef]
- Jayakumar, P.; Melanz, D.; MacLennan, J.; Gorsich, D.; Senatore, C.; Iagnemma, K. Scalability of classical terramechanics models for lightweight vehicle applications incorporating stochastic modeling and uncertainty propagation. J. Terramech. 2014, 54, 37–57. [Google Scholar] [CrossRef]
- Grecenko, A. Binomic slip-thrust equation for tractors in predominantly frictional soil. J. Terramech. 1967, 4, 37–54. [Google Scholar] [CrossRef]
- Reece, A.R. The fundamental equation of earthmoving mechanics. In Proceedings of the Institution of Mechanical Engineers, Conference Proceedings; Sage: London, UK, 1964; Volume 179, pp. 16–22. [Google Scholar]
- Mocera, F.; Nicolini, A. Multibody simulation of a small size farming tracked vehicle. Procedia Struct. Integr. 2018, 8, 118–125. [Google Scholar] [CrossRef]
- Rubinstein, D.; Coppock, J.L. A detailed single-link track model for multi-body dynamic simulation of crawlers. J. Terramech. 2007, 44, 355–364. [Google Scholar] [CrossRef]
- Grecenko, A. A Re-examined principles of thrust generation by a track on soft ground. J. Terramech. 2006, 44, 123–131. [Google Scholar] [CrossRef]
- Keller, T.; Arvidsson, J. A model for prediction of vertical stress distribution near the soil surface below rubber-tracked undercarriage systems fitted on agricultural vehicles. Soil Tillage Res. 2016, 155, 116–123. [Google Scholar] [CrossRef]






| Vehicle Properties | |
|---|---|
| Mass | 750 kg |
| Length | 1500 mm |
| Width | 700 mm |
| Height | 1130 mm |
| Track width | 180 mm |
| Top speed | 4 km/h |
| x | y | z | |
|---|---|---|---|
| Translational Stiffness N/mm | |||
| Rotational Stiffness Nmm/deg | 200 |
| Symbol | |
|---|---|
| Grouser height | |
| Grouser height sunk into the soil | |
| Traction force related to Janosi-Hanamoto law | |
| (first term of Equation (15)) acting on the grouser base | |
| Traction force related to Janosi-Hanamoto law | |
| (first term of Equation (14)) acting on the total link base area (grouser base + link base) | |
| Traction force developed by a grouser, equal to | |
| Total traction force developed by a track link. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mocera, F.; Somà, A.; Nicolini, A. Grousers Effect in Tracked Vehicle Multibody Dynamics with Deformable Terrain Contact Model. Appl. Sci. 2020, 10, 6581. https://doi.org/10.3390/app10186581
Mocera F, Somà A, Nicolini A. Grousers Effect in Tracked Vehicle Multibody Dynamics with Deformable Terrain Contact Model. Applied Sciences. 2020; 10(18):6581. https://doi.org/10.3390/app10186581
Chicago/Turabian StyleMocera, Francesco, Aurelio Somà, and Andrea Nicolini. 2020. "Grousers Effect in Tracked Vehicle Multibody Dynamics with Deformable Terrain Contact Model" Applied Sciences 10, no. 18: 6581. https://doi.org/10.3390/app10186581
APA StyleMocera, F., Somà, A., & Nicolini, A. (2020). Grousers Effect in Tracked Vehicle Multibody Dynamics with Deformable Terrain Contact Model. Applied Sciences, 10(18), 6581. https://doi.org/10.3390/app10186581






