Optimal Design and Control of a Two-Speed Planetary Gear Automatic Transmission for Electric Vehicle
Abstract
:1. Introduction
2. Topology Structure of The Drivetrain
3. Gear Ratio Optimization Problem
3.1. Feasible Regions of Gear Ratio
3.2. Objective Functions
3.2.1. The Acceleration Time
3.2.2. The Electric Energy Consumption
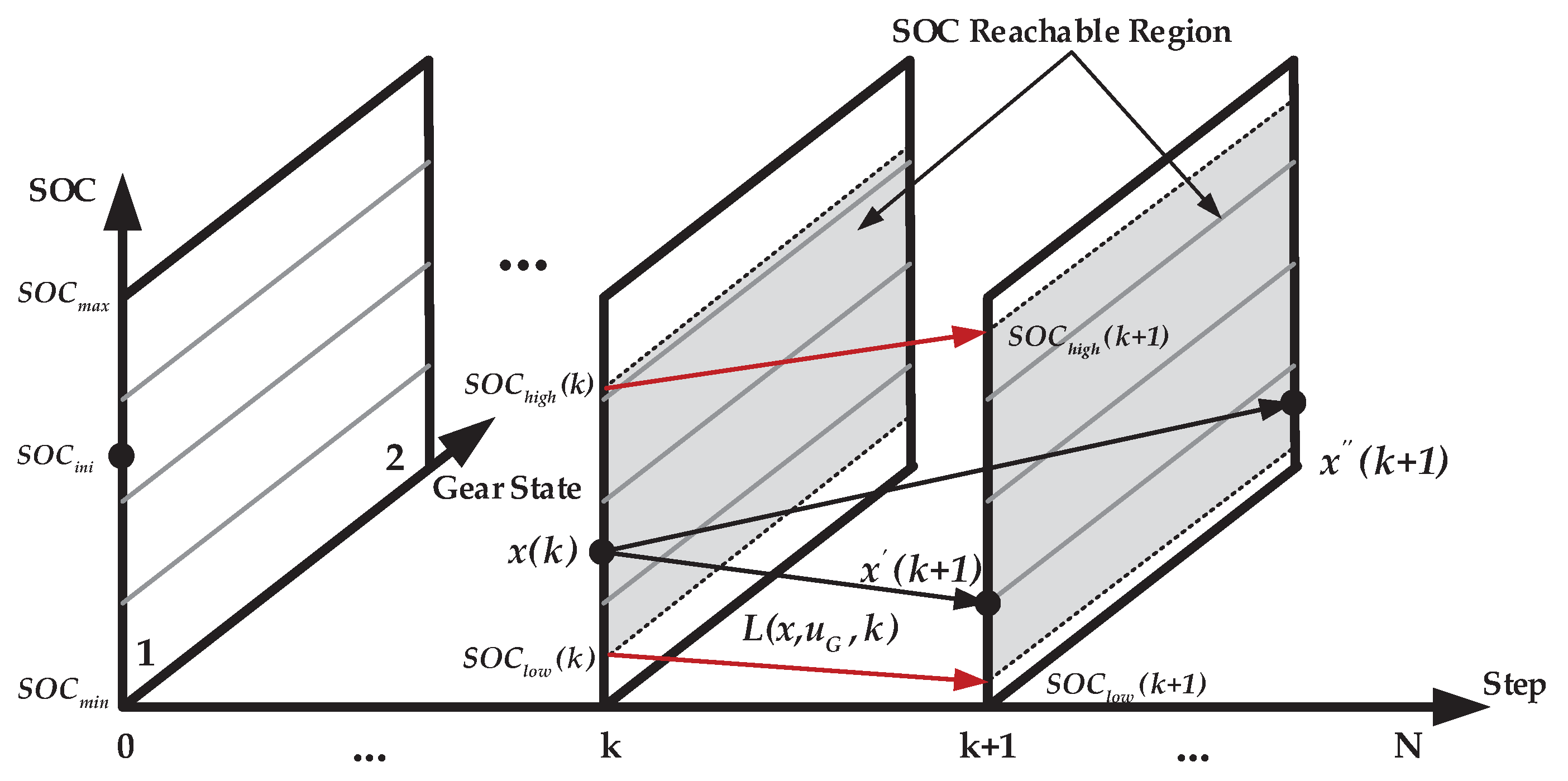
- The global optimization problem formulation
- The DP calculation processAccording to Bellman’s optimality principle [25], the global optimization problem can be decomposed into a series of simple minimization problems as follows:
- (a)
- Cost calculation at step
- (b)
- Intermediate calculation step for to 0where represents the minimum objective function from the state variable at the step to the state variable at the step. The DP calculation process consists of the backward calculation and forward calculation parts. First, starting from the step, based on Equations (14) and (15), the minimum objective function for each state variable at the previous step can be derived in an iterative way and the optimal control policy corresponding to this state variable is stored. In the forward calculation process, starting from the initial time and state variable, the optimal control variable at step can be obtained from the optimal control policy stored in the above backward calculation process. Combining Equations (8) and (9), the state variable at the next step on the optimal path can be calculated and the above process is repeated until the final step is reached.
3.3. Optimization Results and Analysis
4. Gearshift Control Problem
- Duration of the whole process can be easily manipulated.
- Jerks on both the input and output shaft are small enough so as to protect the motor shaft and ensure riding comfort.
- Friction work of the two brakes are small enough so as to protect the two components.
- Output torque of the transmission can be arbitrarily shaped (within the capability and constraint of components) during the shifting process so as to ensure drivability on some high-performance models.
4.1. Mathematical Model of the Electrified Power-Train
4.2. Torque Phase Control
- The off-going brake should be kept engaged during the whole process and no slip occurs.
- The load and the pressure on the off-going brake should be reduced to zero at the same time.
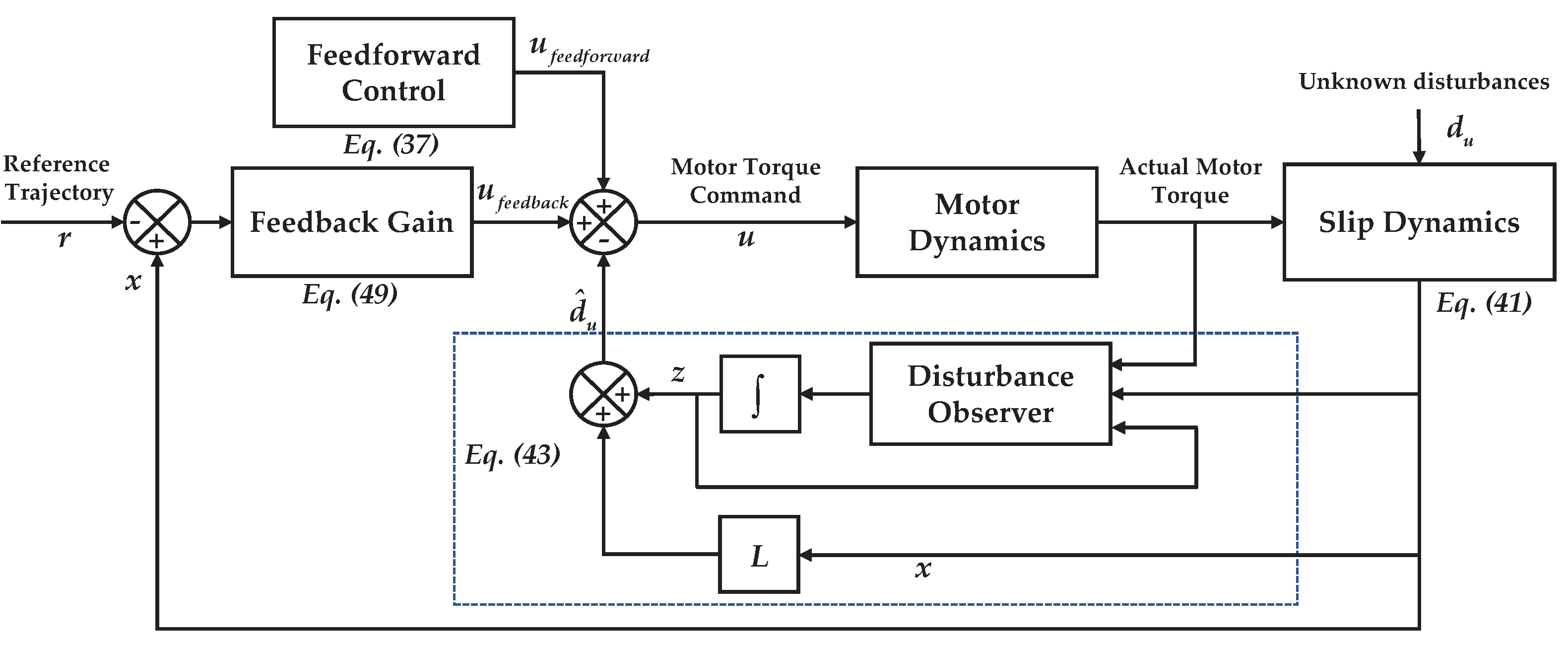
4.3. Inertia Phase Control
4.3.1. Feedforward Control
4.3.2. Feedback Control
4.4. Simulation Results
5. Summary and Conclusions
- From the Pareto front graph obtained using the NSGA-II approach, the dynamic and economic performance of the two-speed transmission is conflicted with the other. Thus, a compromise solution is chosen as the final gear ratio combination.
- Simulation results demonstrate that the two-speed transmission has much better performance in terms of acceleration time and electric energy consumption compared with the fixed-ratio transmission.
- Compared with the conventional constant-input-torque control (CITC), the proposed constant-output-torque control (COTC) comes with advantages of keeping the driving torque on the output shaft constant during the whole gearshift process.
- The disturbance observer is integrated to the feedforward–feedback slip speed controller to enhance the robustness, and the effectiveness is validated through comparison with the non-disturbance-compensation method. Thus, the controller is suitable for practical engineering use.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EV | Electric vehicle |
| NSGA-II | Nondominated sorting genetic algorithm-II |
| DP | Dynamic programming |
| COTC | Constant-output-torque control |
| DCT | Equivalent inertia of the transmission output shaft |
| CVT | Continuous variable transmission |
| AT | Automatic transmission |
| AMT | Automatic manual transmission |
| HMP | Hybrid minimum principle |
| PGTs | Planetary-gear-based transmissions |
| DOF | Degree of freedom |
| NEDC | New European Drive Cycle |
| WLTP | World Light Vehicle Test Procedure |
| SOC | State-of-charge |
| BMS | Battery management system |
| VCU | Vehicle controller unit |
| MCU | Motor controller unit |
| DO | Disturbance observer |
| CITC | Constant-input-torque control |
| PID | Proportional-integral-derivative |
| PI | Proportional–integral |
References
- Wang, N.; Tang, L.; Pan, H. A global comparison and assessment of incentive policy on electric vehicle promotion. Sustain. Cities Soc. 2019, 44, 597–603. [Google Scholar] [CrossRef]
- Ruan, J.; Walker, P.D.; Zhang, N. A comparative study energy consumption and costs of battery electric vehicle transmissions. Appl. Energy 2016, 165, 119–134. [Google Scholar] [CrossRef] [Green Version]
- Roberts, S. Multispeed transmission for electric vehicles. ATZ Worldw. 2012, 114, 8–11. [Google Scholar] [CrossRef]
- Nicola, F.D.; Sorniotti, A.; Holdstock, T.; Viotto, F.; Bertolotto, S. Optimization of a multiple-speed transmission for downsizing the motor of a fully electric vehicle. SAE Int. J. Altern. Powertrains 2012, 1, 134–143. [Google Scholar] [CrossRef]
- Bottiglione, F.; De Pinto, S.; Mantriota, G.; Mantriota, A. Energy Consumption of a Battery Electric Vehicle with Infinitely Variable Transmission. Energies 2014, 7, 8317–8337. [Google Scholar] [CrossRef] [Green Version]
- Gao, B.; Liang, Q.; Xiang, Y.; Guo, L.; Chen, H. Gear ratio optimization and shift control of 2-speed I-AMT in electric vehicle. Mech. Syst. Signal Proc. 2015, 50, 615–631. [Google Scholar] [CrossRef]
- Ahssan, R.; Ektesabi, M.; Gorji, S.A. Electric Vehicle with Multi-Speed Transmission: A Review on Performances and Complexities. SAE Int. J. Altern. Powertrains 2018, 7, 169–181. [Google Scholar] [CrossRef]
- Walker, P.D.; Zhu, B.; Zhang, N. Powertrain dynamics and control of a two speed dual clutch transmission for electric vehicles. Mech. Syst. Signal Proc. 2017, 85, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Son, H.; Lee, S.; Park, J.; Kim, K.; Kim, H. Shift control of a dry-type two-speed dual-clutch transmission for an electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 308–321. [Google Scholar] [CrossRef]
- Pakniyat, A.; Caines, P.E. Hybrid optimal control of an electric vehicle with a dual-planetary transmission. Nonlinear Anal. Hybrid Syst. 2017, 25, 263–282. [Google Scholar] [CrossRef]
- Mo, W.; Walker, P.D.; Fang, Y.; Wu, J.; Ruan, J.; Zhang, N. A novel shift control concept for multi-speed electric vehicles. Mech. Syst. Signal Proc. 2018, 112, 171–193. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, H.; Xi, J.; Wang, J.; Fang, Z. Robust speed synchronization control for clutchless automated manual transmission systems in electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 229, 424–436. [Google Scholar] [CrossRef]
- Walker, P.D.; Fang, Y.; Zhang, N. Dynamics and Control of Clutchless Automated Manual Transmissions for Electric Vehicles. J. Vib. Acoust. 2017, 139, 61005–61017. [Google Scholar] [CrossRef]
- Sorniotti, A.; Subramanyan, S.; Turner, A.; Cavallino, C.; Viotto, F.; Bertolotto, S. Selection of the Optimal Gearbox Layout for an Electric Vehicle. SAE Int. J. Engines 2011, 4, 1267–1280. [Google Scholar] [CrossRef]
- Schwarzer, V.; Ghorbani, R. Drive Cycle Generation for Design Optimization of Electric Vehicles. IEEE Trans. Veh. Technol. 2013, 62, 89–97. [Google Scholar] [CrossRef]
- Mousavi, M.S.R.; Pakniyat, A.; Boulet, B. Dynamic modeling and controller design for a seamless two-speed transmission for electric vehicles. In Proceedings of the IEEE International Conference on Control Applications (CCA), Antibes, France, 8–10 October 2014; pp. 635–640. [Google Scholar]
- Mousavi, M.S.R.; Pakniyat, A.; Wang, T.; Boulet, B. Seamless dual brake transmission for electric vehicles: Design, control and experiment. Mech. Mach. Theory 2015, 94, 96–118. [Google Scholar] [CrossRef]
- Roozegar, M.; Angeles, J. A two-phase control algorithm for gear-shifting in a novel multi-speed transmission for electric vehicles. Mech. Syst. Signal Proc. 2018, 104, 145–154. [Google Scholar] [CrossRef]
- Gao, B.; Xiang, Y.; Chen, H.; Liang, Q.; Guo, L. Optimal Trajectory Planning of Motor Torque and Clutch Slip Speed for Gear Shift of a Two-Speed Electric Vehicle. J. Dyn. Syst. Meas. Control 2015, 137, 61016–61024. [Google Scholar] [CrossRef] [Green Version]
- Roozegar, M.; Angeles, J. The optimal gear-shifting for a multi-speed transmission system for electric vehicles. Mech. Mach. Theory 2017, 116, 1–13. [Google Scholar] [CrossRef]
- Mousavi, M.S.R.; Pakniyat, A.; Helwa, M.K.; Boulet, B. Observer-Based Backstepping Controller Design for Gear Shift Control of a Seamless Clutchless Two-Speed Transmission for Electric Vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar]
- Kahraman, A.; Ligata, H.; Kienzle, K.; Zini, D.M. A Kinematics and Power Flow Analysis Methodology for Automatic Transmission Planetary Gear Trains. J. Mech. Des. 2004, 126, 1071–1081. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Naunheimer, H.; Fietkau, P. Automotive Transmissions. Fundamentals, Selection, Design and Application; Springer: Heidelberg, Germany, 2011. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming and Optimal Control: Volumes I and II; Athena Scientific: Belmont, MA, USA, 2005. [Google Scholar]
- Garofalo, F.; Glielmo, L.; Iannelli, L.; Vasca, F. Smooth engagement for automotive dry clutch. In Proceedings of the IEEE Conference on Decision & Control (CDC), Orlando, FL, USA, 4–7 December 2001; pp. 529–534. [Google Scholar]
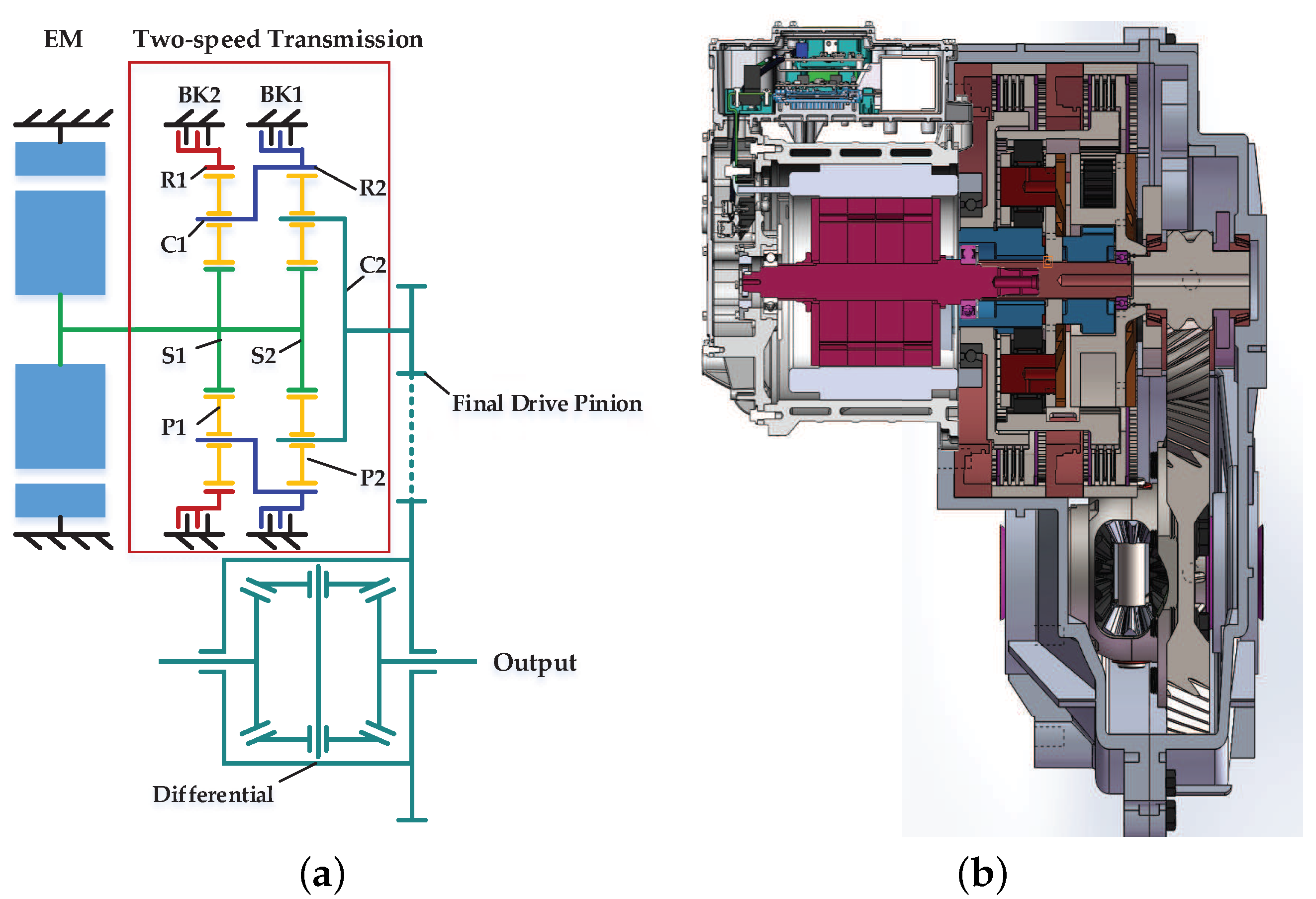









| Gear State | Brake Status | Level Analogy | Gear Ratio |
|---|---|---|---|
| 1st Gear | BK1:engaged BK2:disengaged |  | |
| 2nd Gear | BK1:disengaged BK2:engaged |  |
| Parameter | Description | Quantity (Unit) |
|---|---|---|
| m | Vehicle mass | 1865 kg |
| r | Wheel radius | 0.35 m |
| f | Coefficient of rolling resistance | 0.011 |
| Coefficient of aerodynamic drag | 0.24 | |
| A | Frontal area | 2.34 m |
| Overall power-train efficiency | 0.96 | |
| Final drive ratio | 3.91 | |
| Maximum vehicle speed | 220 km/h | |
| Maximum ascendable grade | 35% | |
| Adhesion coefficient | 0.75 | |
| Maximum motor speed | 12,000 rpm | |
| Maximum motor torque | 290 Nm | |
| Battery rated capacity (cell) | 50 Ah | |
| Number of the cell | 384 |
| Transmission Type | Gear Ratio | Acceleration Time (s) | Electricity Consumption (kWh/100km) | |
|---|---|---|---|---|
| *[c]NEDC | *[c]WLTP | |||
| fixed-ratio Transmission | 8.18 | 12.23 | 13.83 | |
| Two-speed Transmission | 7.03 (−1.15) | 11.66 (−4.66%) | 13.22 (−4.41%) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Huang, J.; Yin, C. Optimal Design and Control of a Two-Speed Planetary Gear Automatic Transmission for Electric Vehicle. Appl. Sci. 2020, 10, 6612. https://doi.org/10.3390/app10186612
Huang W, Huang J, Yin C. Optimal Design and Control of a Two-Speed Planetary Gear Automatic Transmission for Electric Vehicle. Applied Sciences. 2020; 10(18):6612. https://doi.org/10.3390/app10186612
Chicago/Turabian StyleHuang, Wei, Jianfeng Huang, and Chengliang Yin. 2020. "Optimal Design and Control of a Two-Speed Planetary Gear Automatic Transmission for Electric Vehicle" Applied Sciences 10, no. 18: 6612. https://doi.org/10.3390/app10186612
APA StyleHuang, W., Huang, J., & Yin, C. (2020). Optimal Design and Control of a Two-Speed Planetary Gear Automatic Transmission for Electric Vehicle. Applied Sciences, 10(18), 6612. https://doi.org/10.3390/app10186612





