A Novel Comprehensive Method for Modeling and Analysis of Mesh Stiffness of Helical Gear
Abstract
:1. Introduction
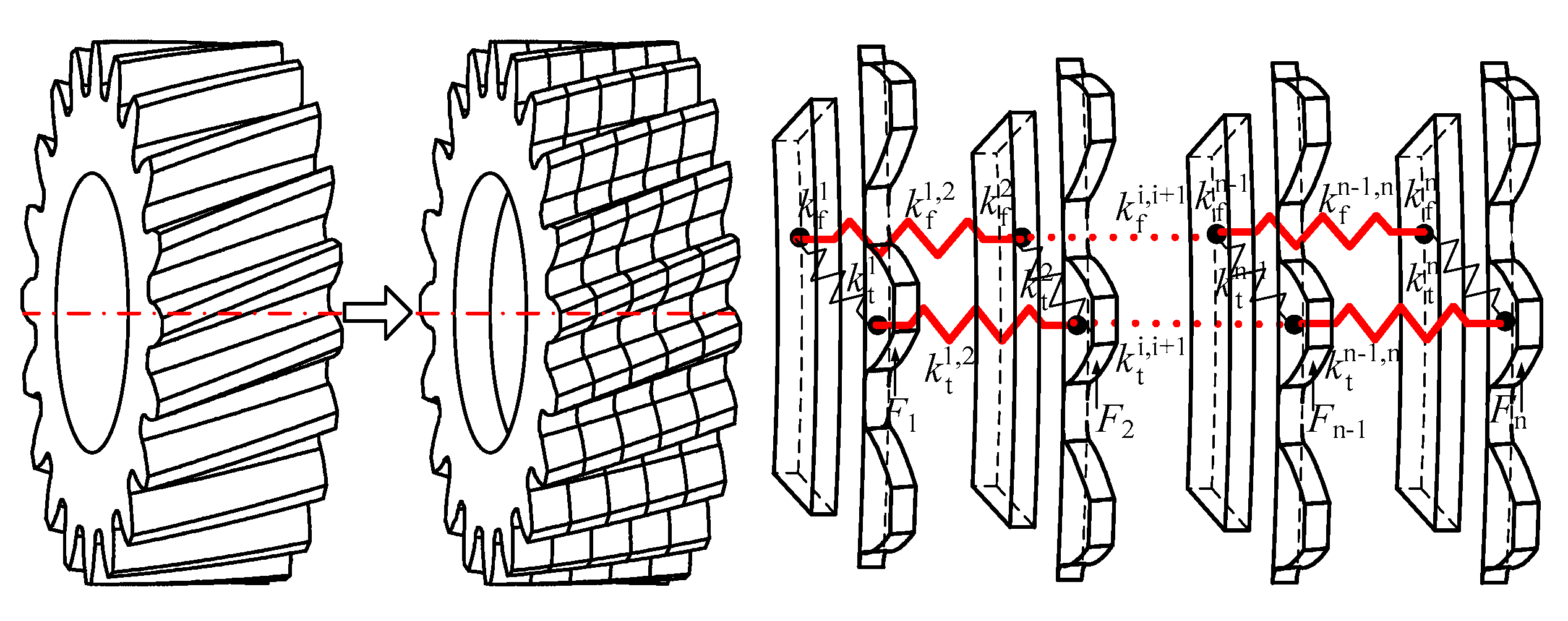
2. The Analytical Model of Mesh Stiffness of Helical Gear
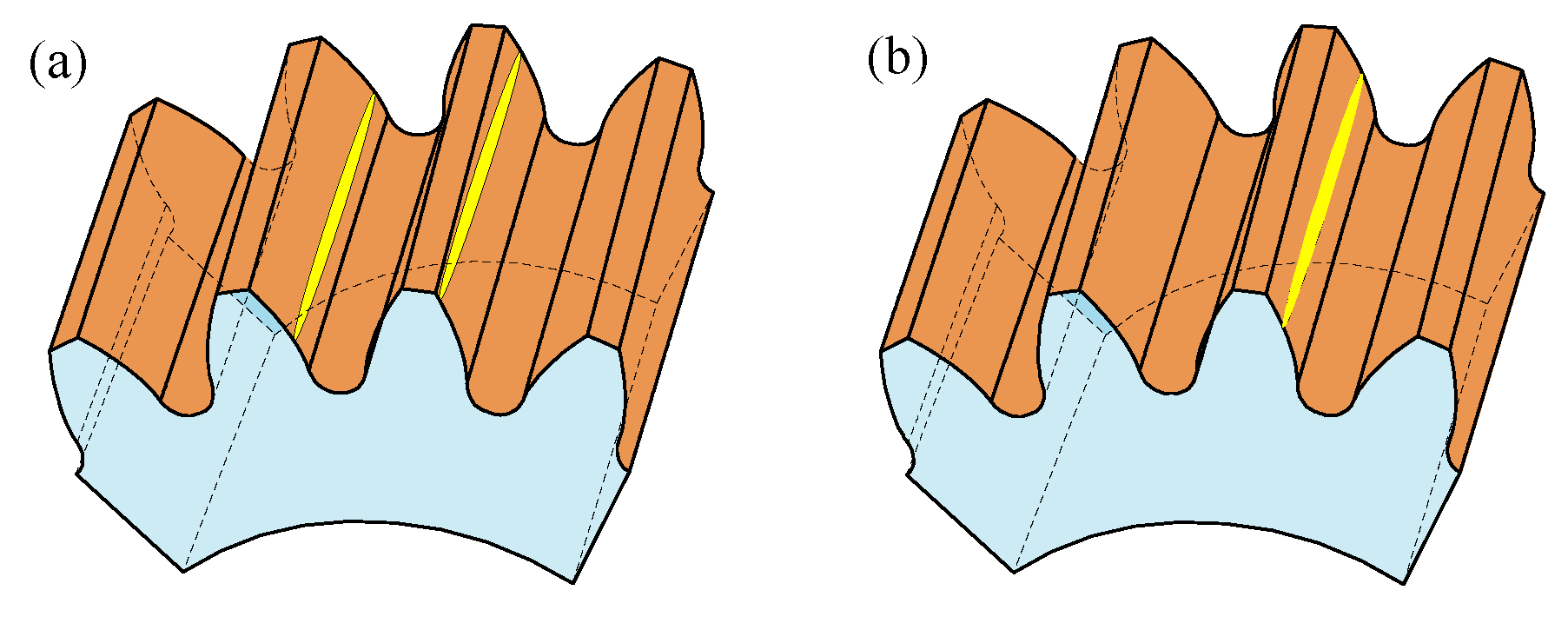
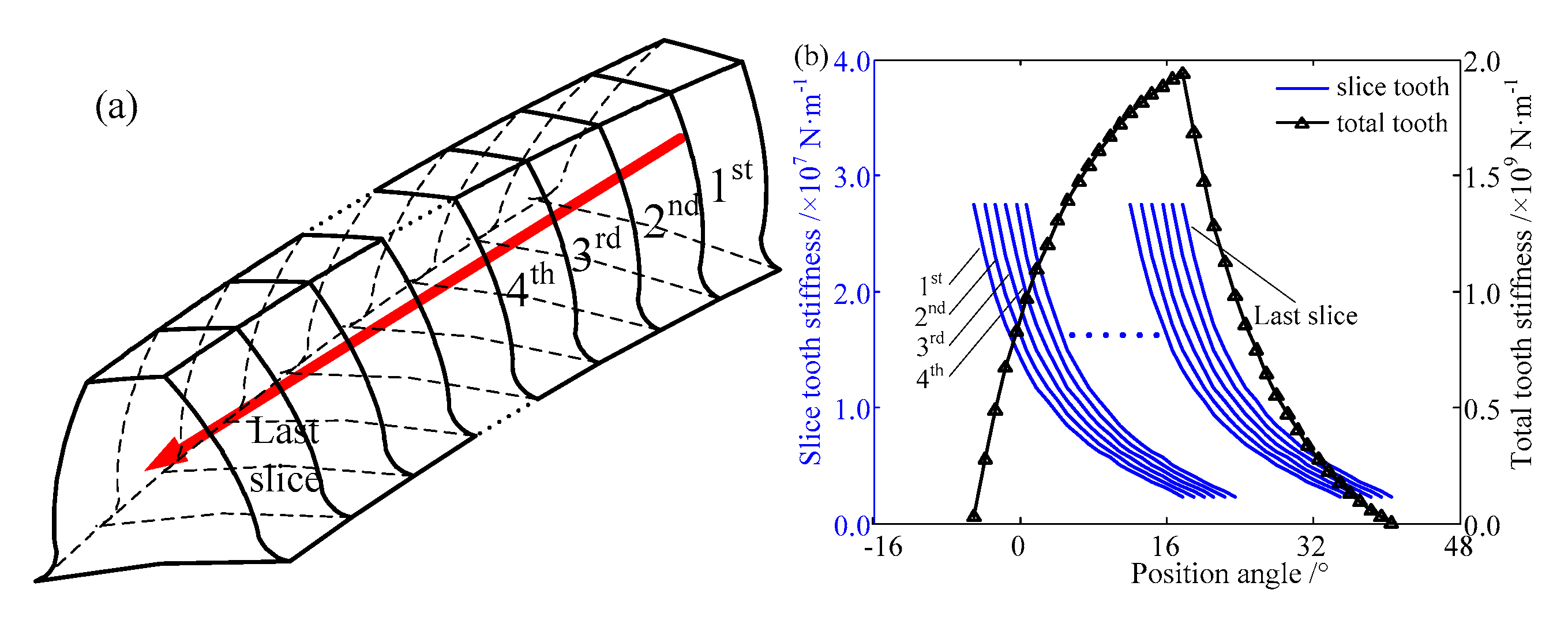
2.1. The Relationship between Neighboring Sliced Gears
2.2. The Stiffness of Each Sliced Gear
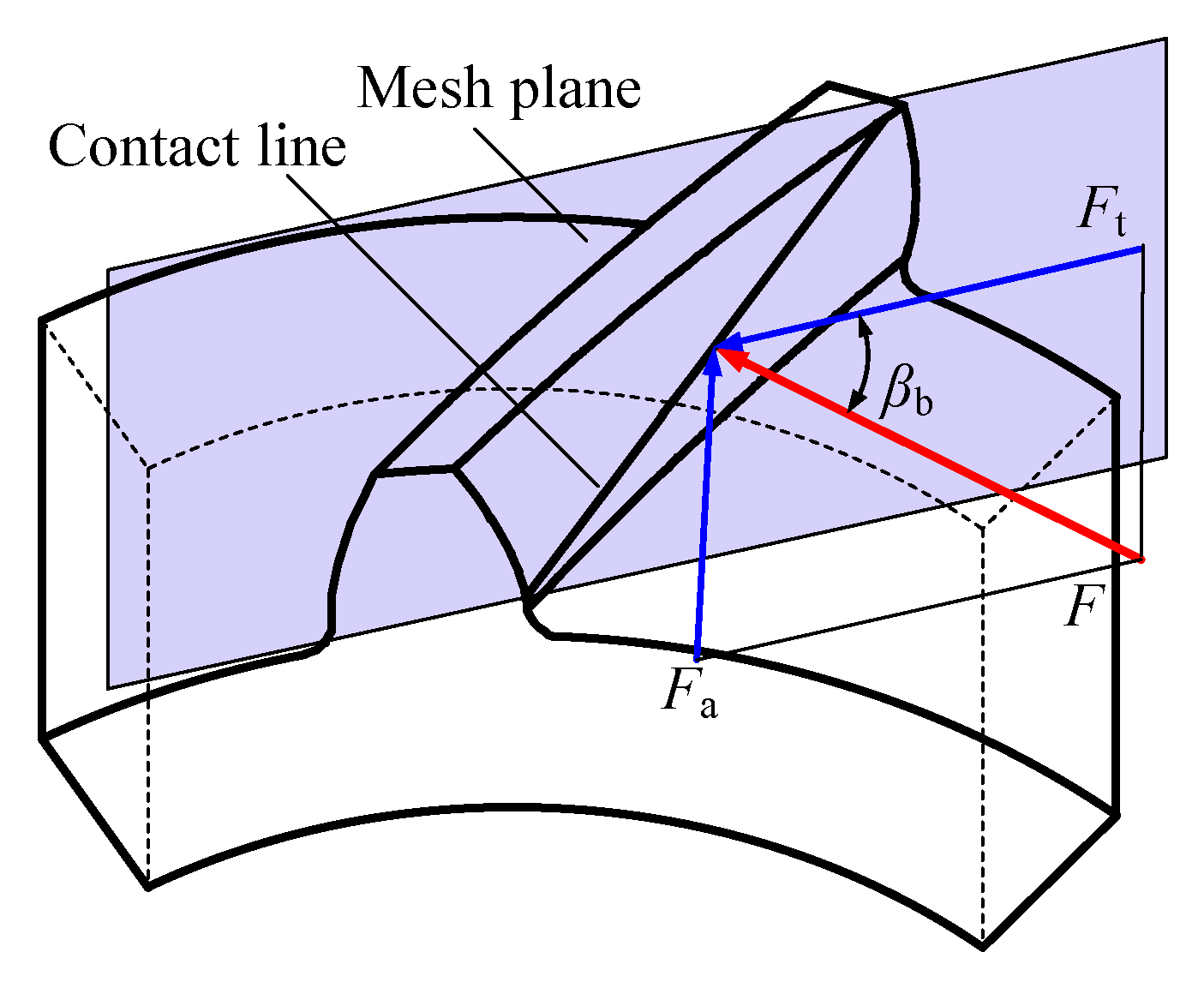
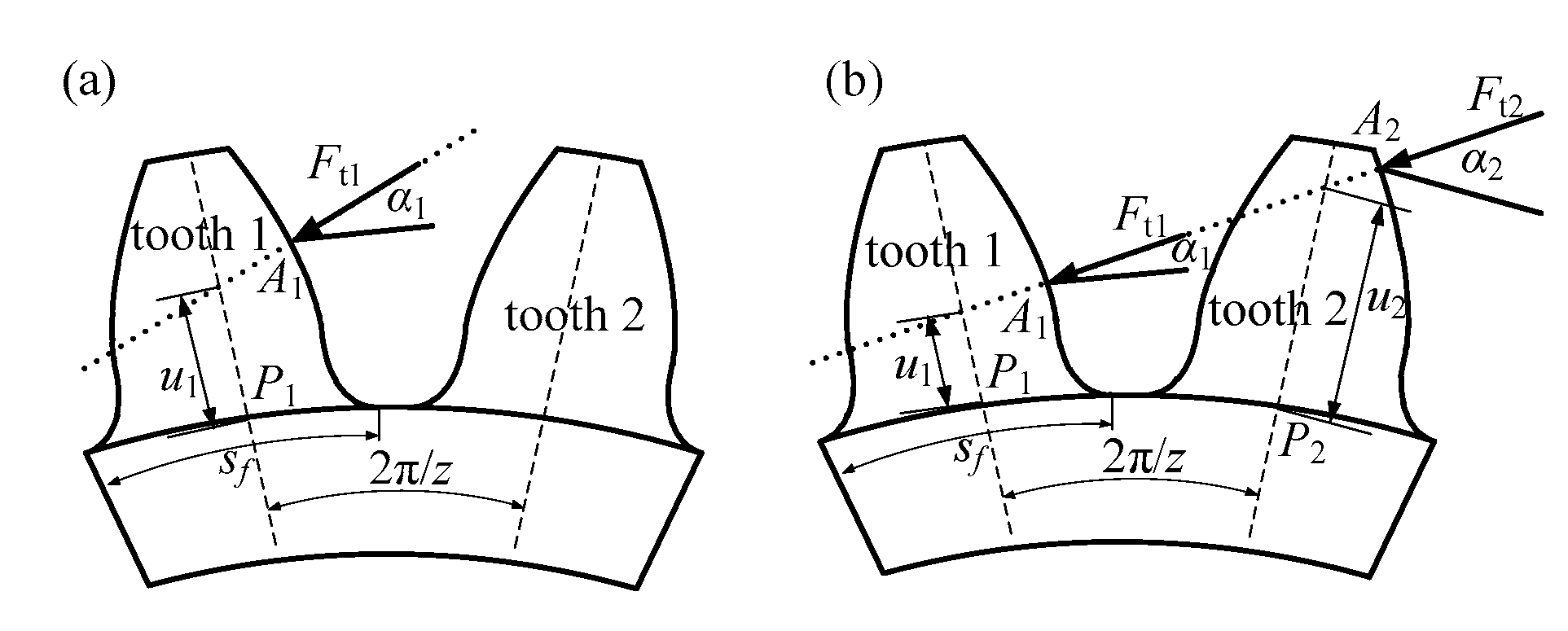
2.2.1. Tooth Stiffness
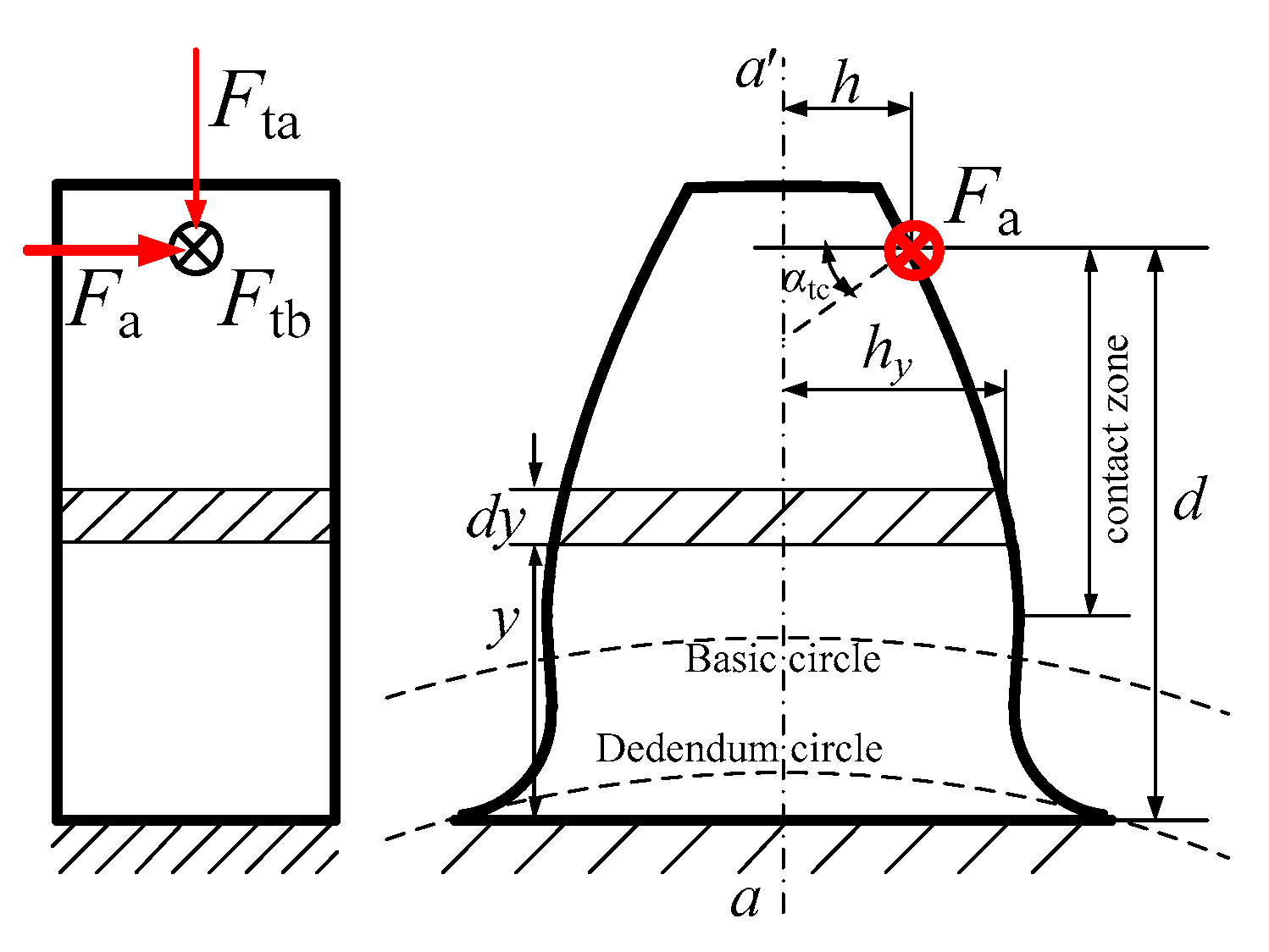
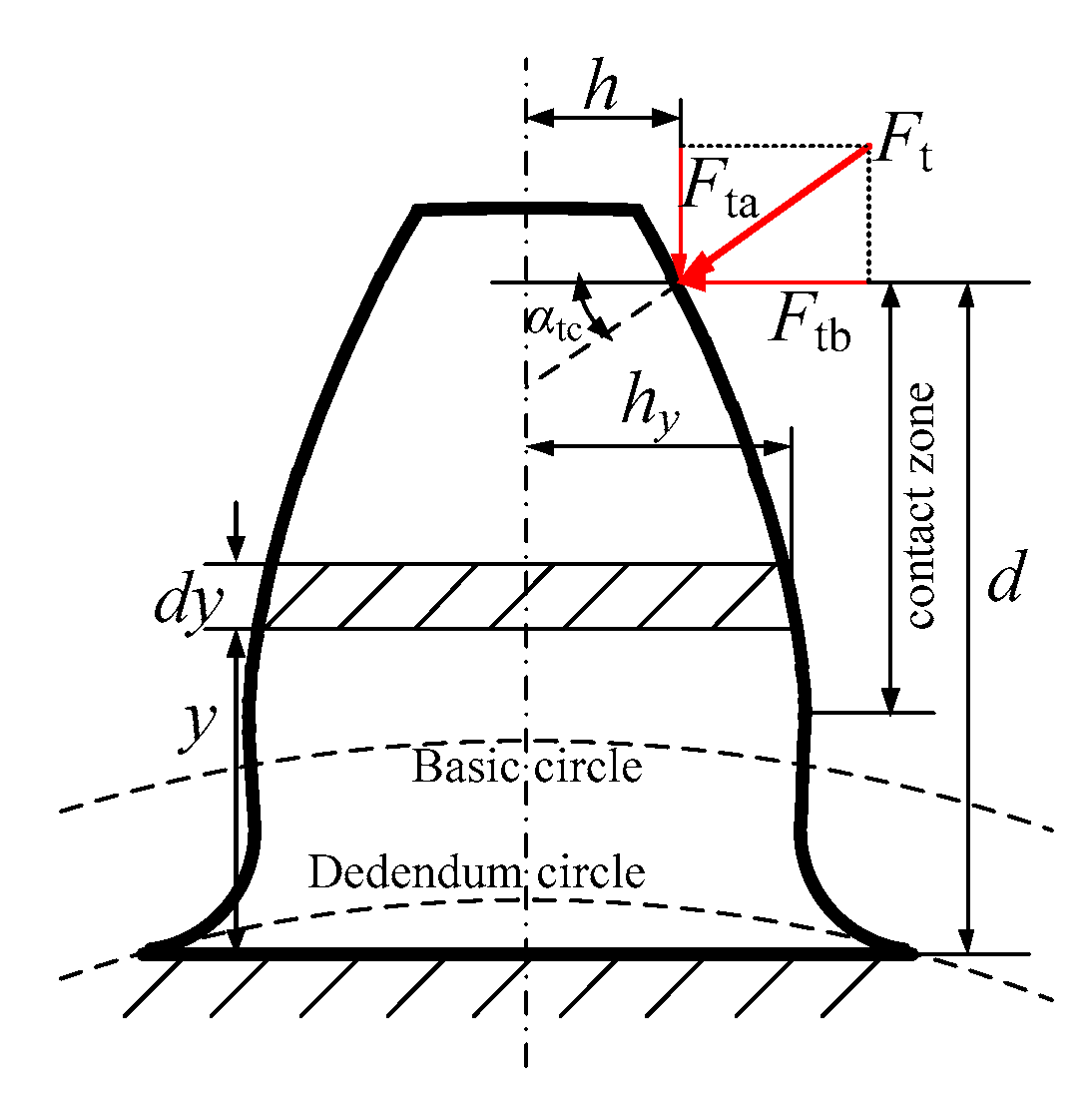
2.2.2. Fillet-Foundation Stiffness
2.2.3. Hertzian Contact Stiffness
2.3. The Helical Gear with Addendum Modification
3. The Model Validation
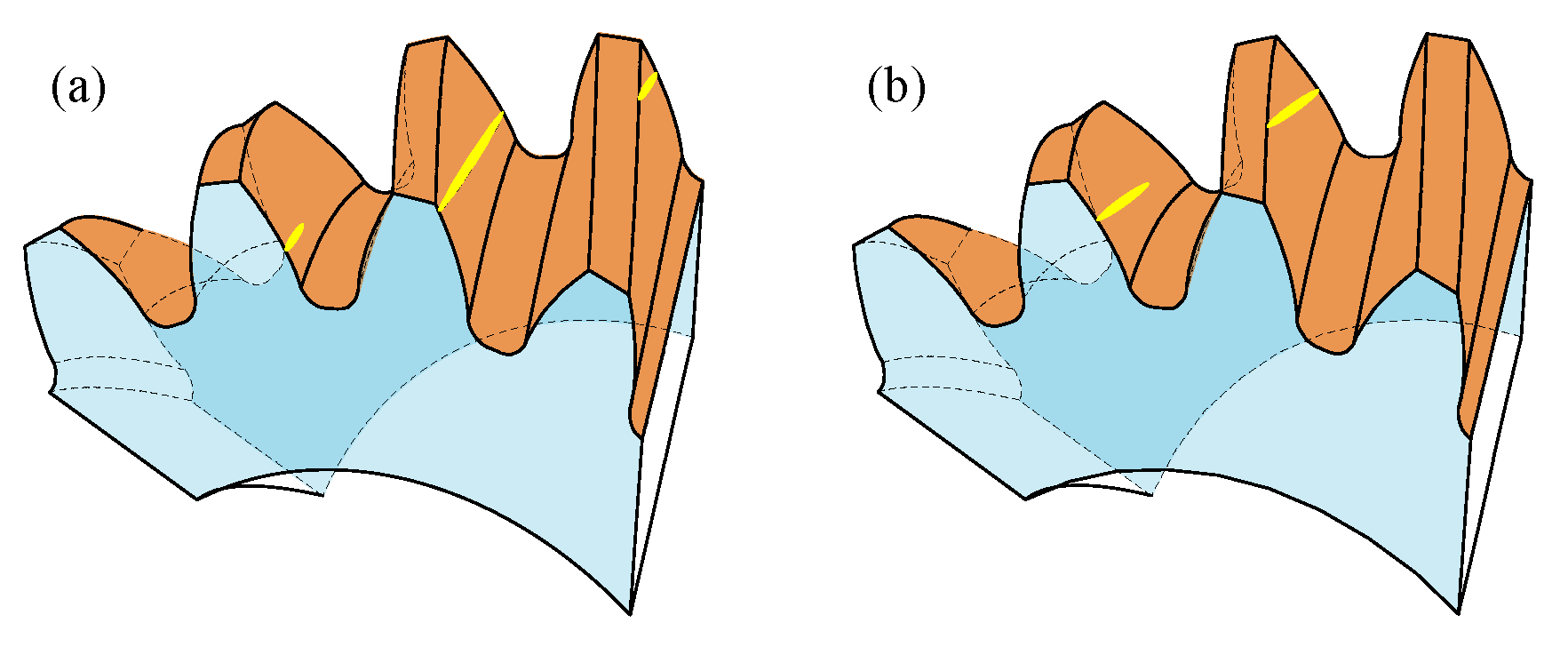
3.1. The Computational Method of the Finite Element Model
3.2. Gear Parameters
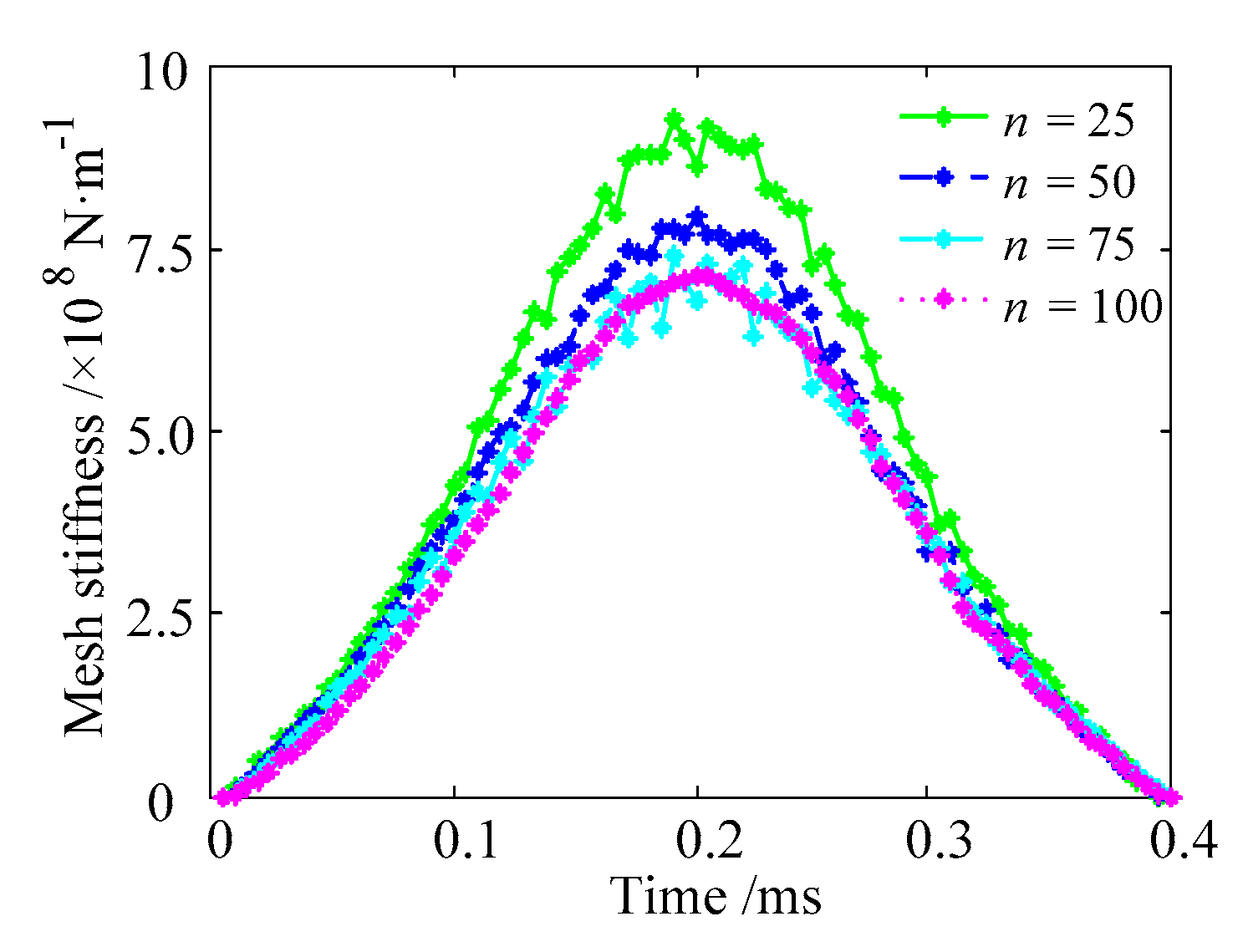
3.3. Finite Element Mesh Sensitive Analysis
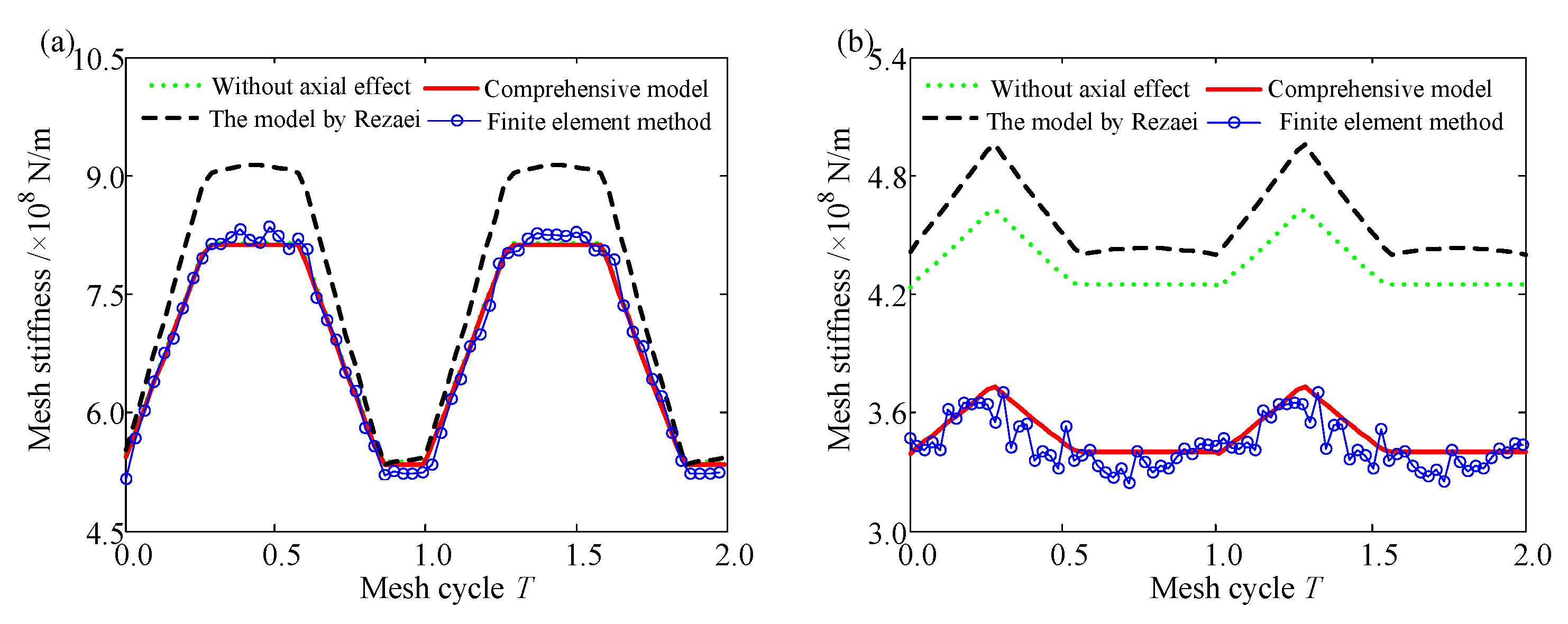
3.4. Stiffness Contrast
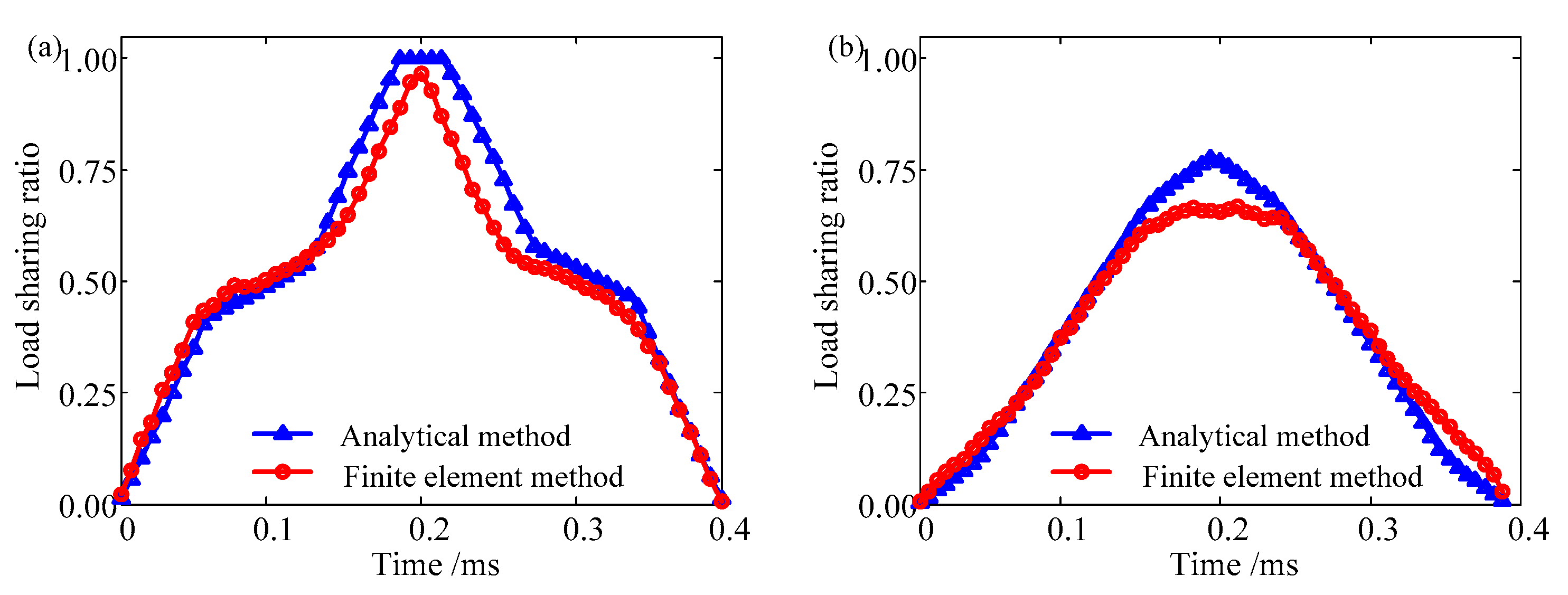
3.5. Load Sharing Ratio Contrast
4. Results and Discussion
4.1. Helical Angle
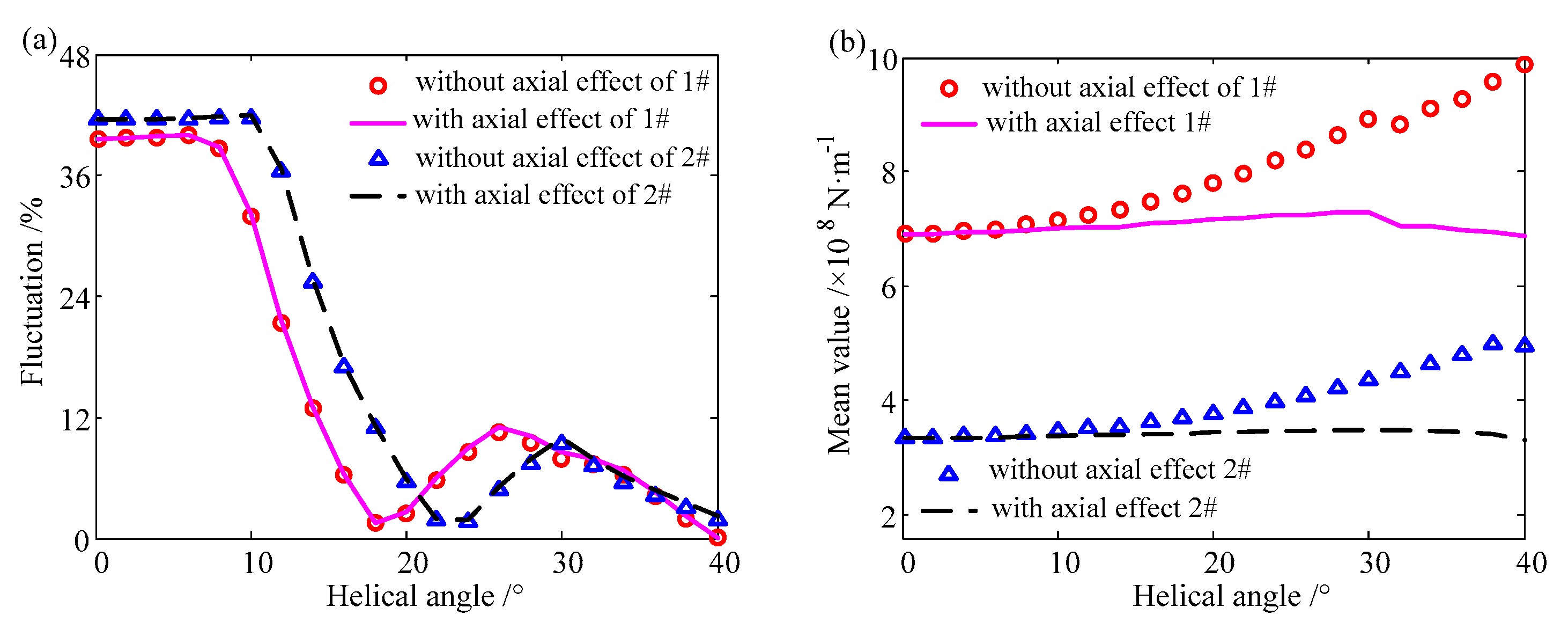
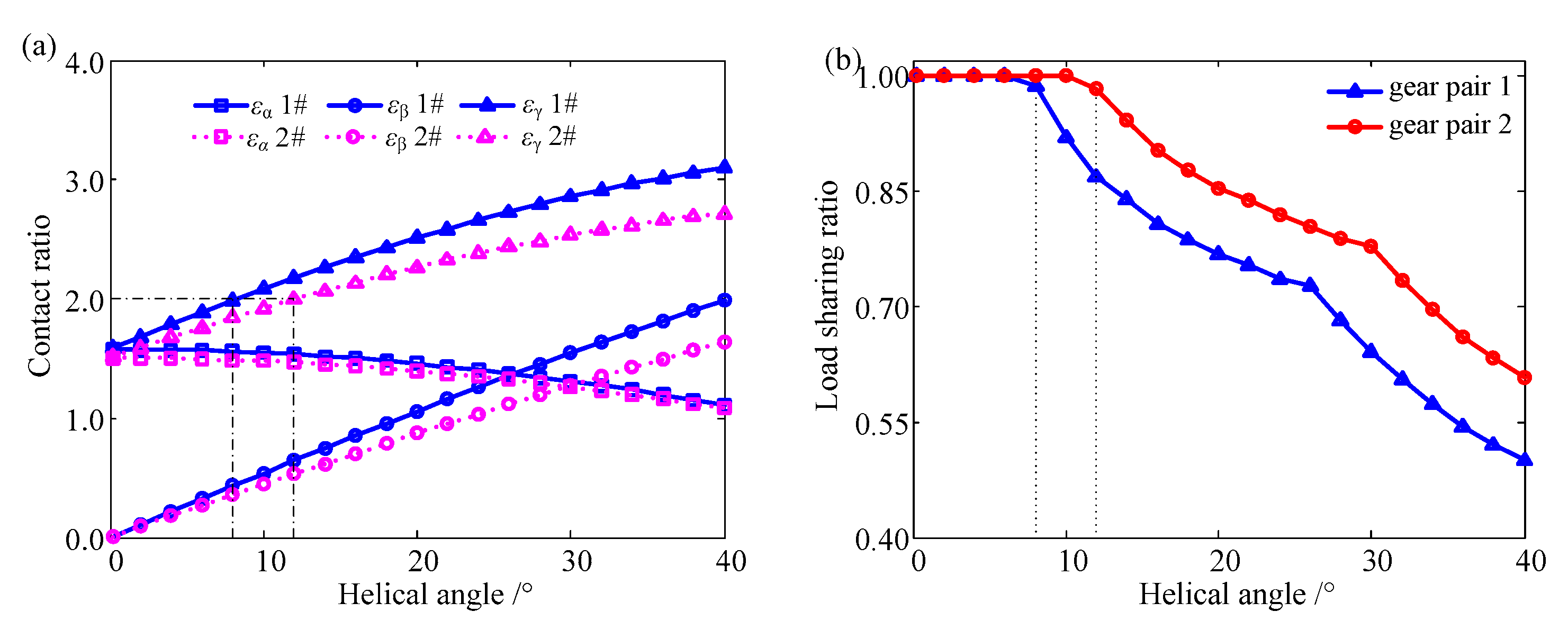
4.1.1. The Influence of Helical Angle on Mesh Stiffness
4.1.2. The Influence of Helical Angle on the Load Sharing Ratio
4.2. Addendum Modification Coefficient
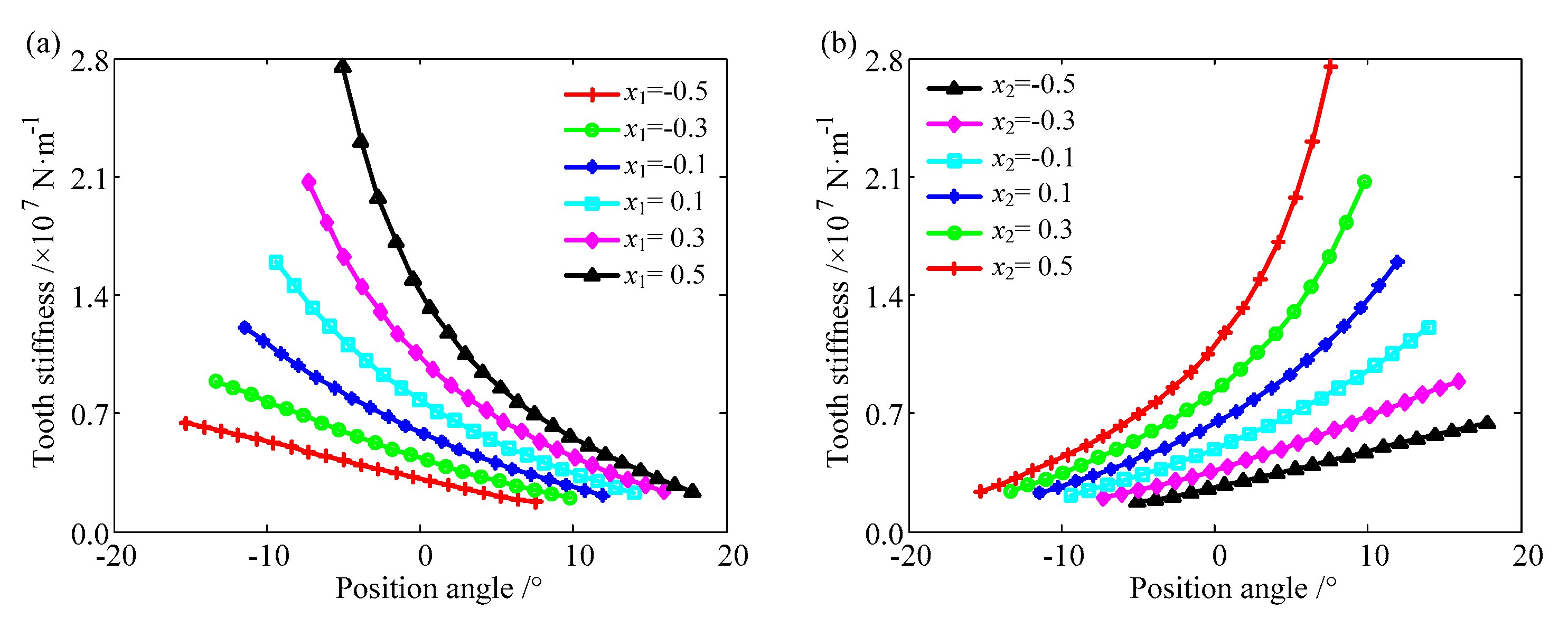
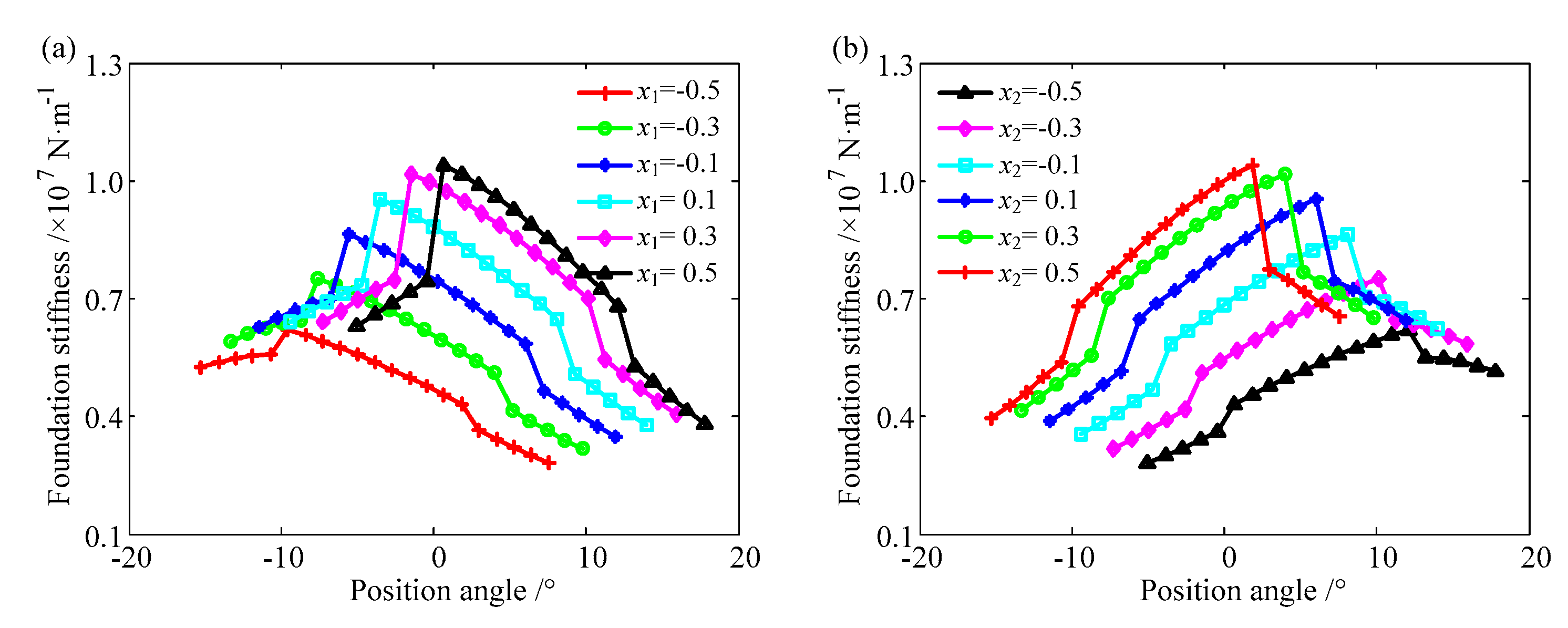
4.2.1. The Influence on Stiffness
4.2.2. The Influence on Mesh Stiffness
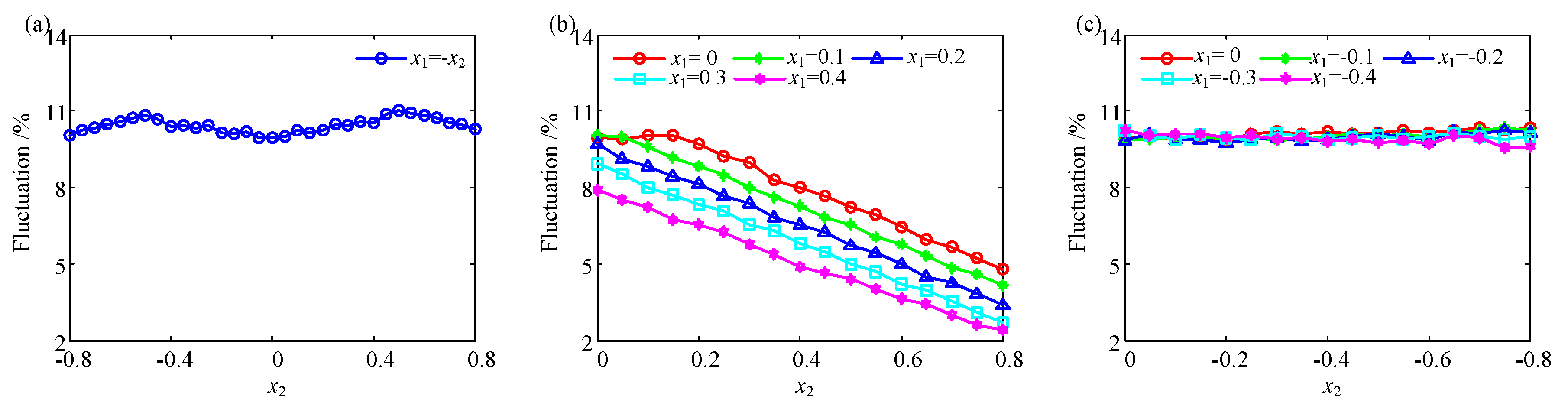
4.2.3. The Influence on the Load Sharing Ratio
5. Conclusions
- (1)
- The mesh stiffness of a helical gear will be decreased in multiteeth regions caused by the structure coupling. The more teeth involved, the greater the influence of structure coupling is.
- (2)
- The axial component of mesh force affects the mesh stiffness of the helical gear. It should not be ignored when an accurate calculation of mesh stiffness is carried out.
- (3)
- The fluctuation value of mesh stiffness decreases when a positive addendum modification coefficient is adopted. The addendum modification also changes the phase of mesh stiffness.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abousleiman, V.; Velex, P. A Hybrid 3D Finite Element/Lumped Parameter Model for Quasi-Static and Dynamic Analyses of Planetary/Epicyclic Gear Sets. Mech. Mach. Theory 2006, 41, 725–748. [Google Scholar] [CrossRef]
- Hou, S.; Wei, J.; Zhang, A.; Lim, T.C.; Zhang, C. Study of Dynamic Model of Helical/Herringbone Planetary Gear System with Friction Excitation. J. Comput. Nonlinear Dyn. 2018, 13, 121007. [Google Scholar] [CrossRef]
- Han, J.; Shin, J.; Kim, J.; Oh, S. Design 2 Speed Transmission for Compact Electric Vehicle Using Dual Brake System. Appl. Sci. 2019, 9, 1793. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Yang, S.; Liu, Y.; Mo, R. Analysis of Load-Sharing Behavior of the Multistage Planetary Gear Train Used in Wind Generators: Effects of Random Wind Load. Appl. Sci. 2019, 9, 5501. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Parker, R.G. Dynamic Modeling and Analysis of a Spur Planetary Gear Involving Tooth Wedging and Bearing Clearance Nonlinearity. Eur. J. Mech. A/Solids 2010, 29, 1022–1033. [Google Scholar] [CrossRef]
- Xiong, Y.; Huang, K.; Xu, F.; Yi, Y.; Sang, M.; Zhai, H. Research on the Influence of Backlash on Mesh Stiffness and the Nonlinear Dynamics of Spur gears. Appl. Sci. 2019, 9, 1029. [Google Scholar] [CrossRef] [Green Version]
- Yuan, B.; Liu, G.; Liu, L. Quasi-Static Characteristics and Vibration Responses Analysis of Helical Geared Rotor System with Random Cumulative Pitch Deviations. Appl. Sci. 2020, 10, 4403. [Google Scholar] [CrossRef]
- Munro, R.G.; Palmer, D.; Morrish, L. An Experimental Method to Measure Gear Tooth Stiffness throughout and Beyond the Path of Contact. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 215, 793–803. [Google Scholar] [CrossRef]
- Raghuwanshi, N.K.; Parey, A. A New Technique of Gear Mesh Stiffness Measurement Using Experimental Modal Analysis. J. Vib. Acoust. 2019, 141, 021018. [Google Scholar] [CrossRef]
- Lei, X.; Gao, Z.; Cui, J.; Wang, H.; Wang, S. The Minimum Zone Evaluation for Elliptical Profile Error Based on the Geometry Optimal Approximation Algorithm. Measurement 2015, 75, 284–288. [Google Scholar]
- Karpat, F.; Yuce, C.; Dogan, O. Experimental Measurement and Numerical Validation of Single Tooth Stiffness for Involute Spur Gears. Measurement 2020, 150, 107043. [Google Scholar] [CrossRef]
- Zhan, J.; Fard, M.; Jazar, R. A CAD-FEM-QSA Integration Technique for Determining the Time-Varying Meshing Stiffness of Gear Pairs. Measurement 2017, 100, 139–149. [Google Scholar] [CrossRef]
- Li, J.; Xu, M.; Wang, S. Finite Element Analysis of Instantaneous Mesh Stiffness of Cylindrical Gears (With and Without Flexible Gear Body). Commun. Numer. Methods Eng. 1999, 15, 579–587. [Google Scholar] [CrossRef]
- Wang, J.; Howard, I. The Torsional Stiffness of Involute Spur Gears. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 131–142. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, A.; Wang, G.; Qin, D.; Lim, T.C.; Wang, Y.; Lin, T. A Study of Nonlinear Excitation Modeling of Helical Gears with Modification: Theoretical Analysis and Experiments. Mech. Mach. Theory 2018, 128, 314–335. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Lin, J.Y. Hertzian Damping Tooth Friction and Bending Elasticity in Gear Impact Dynamics. J. Mech. Transm. Autom. Des. 1987, 109, 189–196. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, M.J.; Parey, A. Simulation of Spur Gear Dynamics and Estimation of Fault Growth. J. Sound Vib. 2008, 317, 608–624. [Google Scholar] [CrossRef]
- Liu, S.; Song, C.; Zhu, C.; Liang, C.; Yang, X. Investigation on The Influence of Work Holding Equipment Errors on Contact Characteristics of Face-Hobbed Hypoid Gear. Mech. Mach. Theory 2019, 138, 95–111. [Google Scholar] [CrossRef]
- Sainsot, P.; Velex, P.; Duverger, O. Contribution of Gear Body to Tooth Deflections-A New Bidimensional Analytical Formula. J. Mech. Des. 2004, 126, 748–752. [Google Scholar] [CrossRef]
- Chen, Z.; Shao, Y. Dynamic Simulation of Spur Gear with Tooth Root Crack Propagating Along Tooth Width and Crack Depth. Eng. Fail. Anal. 2011, 18, 2149–2164. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Feng, R.; Pang, X.; Wen, B. An Improved Analytical Method for Mesh Stiffness Calculation of Spur Gears with Tip Relief. Mech. Mach. Theory 2016, 98, 64–80. [Google Scholar] [CrossRef]
- Xie, C.; Hua, L.; Han, X.; Lan, J.; Wan, X.; Xiong, X. Analytical Formulas for Gear Body-Induced Tooth Deflections of Spur Gears Considering Structure Coupling Effect. Int. J. Mech. Sci. 2018, 148, 174–190. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, B.; Fu, Y.; Kong, X.; Ma, H. An Improved Time Varying Mesh Stiffness Model for Helical Gear Pairs Considering Axial Mesh Force Component. Mech. Syst. Signal Process. 2018, 106, 413–429. [Google Scholar] [CrossRef]
- Rezaei, M.; Poursina, M.; Jazi, S.H.; Aboutalebi, F.H. Calculation of Time Dependent Mesh Stiffness of Helical Planetary Gear System Using Analytical Approach. J. Mech. Sci. Technol. 2018, 32, 3537–3545. [Google Scholar] [CrossRef]
- Seager, D.L. Tooth Loading and Static Behavior of Helical Gears. ASLE Trans. 1970, 13, 66–77. [Google Scholar] [CrossRef]
- Yu, W.; Mechefske, C.K.; Timusk, M. Influence of the Addendum Modification on Spur Gear Back Side Mesh Stiffness and Dynamics. J. Sound Vib. 2017, 389, 183–201. [Google Scholar] [CrossRef]
- Ma, J.; Liu, T.; Zha, C.; Song, L. Simulation Research on the Time Varying Meshing Stiffness and Vibration Response of Micro-Cracks in Gears under Variable Tooth Shape Parameters. Appl. Sci. 2019, 9, 1512. [Google Scholar] [CrossRef] [Green Version]
- Hedlund, J.; Lehtovaara, A. A Parameterized Numerical Model for the Evaluation of Gear Mesh Stiffness Variation of a Helical Gear Pair. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 1321–1327. [Google Scholar] [CrossRef]






| No. | Items | 1# | 2# | ||
|---|---|---|---|---|---|
| 1 | gear | Pinion | Wheel | Pinion | Wheel |
| 2 | Normal module mn (mm) | 3.5 | 3.5 | 2 | 2 |
| 3 | Pressure angle α (°) | 20 | 20 | 20 | 20 |
| 4 | Number of teeth | 20 | 30 | 20 | 20 |
| 5 | Face width b (mm) | 34 | 34 | 16 | 16 |
| 6 | Helix angle β (°) | 5 | 5 | 30 | 30 |
| 7 | Profile shift coefficient | 0.1798 | −0.1321 | 0.0795 | 0.0795 |
| 8 | Addendum coefficient | 1 | 1 | 1 | 1 |
| 9 | Tip clearance coefficient | 0.25 | 0.25 | 0.25 | 0.25 |
| 10 | hub bore radius rint (mm) | 22 | 38 | 15 | 15 |
| 11 | Center distance (mm) | 88 | 46.5 | ||
| 12 | Contact ratio εα/εβ/εγ | 1.5684/0.2695/1.8379 | 1.2625/1.2732/2.5357 | ||
| 1# | 2# | |||||
|---|---|---|---|---|---|---|
| Max Value | Min Value | Mean Value | Max Value | Min Value | Mean Value | |
| Analytical method in this paper | 8.0745 | 5.2916 | 6.9367 | 3.7393 | 3.3846 | 3.4810 |
| Finite element method | 8.1798 | 5.2314 | 6.9553 | 3.6043 | 3.3564 | 3.4357 |
| Error (%) | 1.29 | 1.15 | 0.27 | 3.75 | 0.84 | 1.32 |
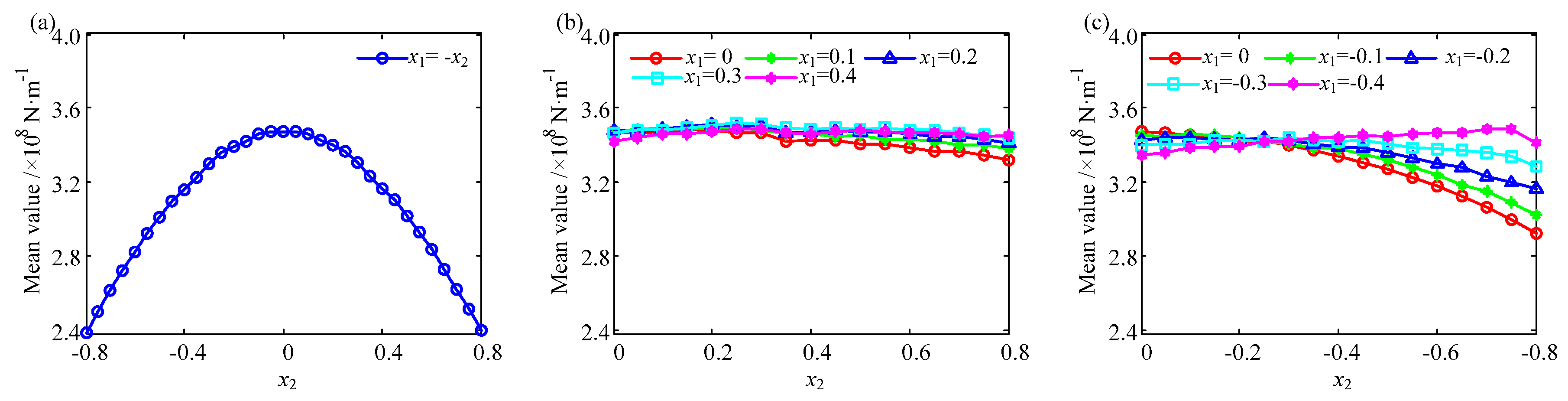
| Case 1 (x1 + x2 = 0) | Case 2 (x1 + x2 > 0) | Case 3 (x1 + x2 < 0) | |||
|---|---|---|---|---|---|
| x1 | x2 | x1 | x2 | x1 | x2 |
| −0.8~0.8 | 0.8~−0.8 | 0.1 | 0~0.8 | −0.1 | 0~−0.8 |
| 0.2 | 0~0.8 | −0.2 | 0~−0.8 | ||
| 0.3 | 0~0.8 | −0.3 | 0~−0.8 | ||
| 0.4 | 0~0.8 | −0.4 | 0~−0.8 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, S.; Wei, J.; Zhang, A.; Zhang, C.; Yan, J.; Wang, C. A Novel Comprehensive Method for Modeling and Analysis of Mesh Stiffness of Helical Gear. Appl. Sci. 2020, 10, 6695. https://doi.org/10.3390/app10196695
Hou S, Wei J, Zhang A, Zhang C, Yan J, Wang C. A Novel Comprehensive Method for Modeling and Analysis of Mesh Stiffness of Helical Gear. Applied Sciences. 2020; 10(19):6695. https://doi.org/10.3390/app10196695
Chicago/Turabian StyleHou, Shaoshuai, Jing Wei, Aiqiang Zhang, Chunpeng Zhang, Junhui Yan, and Changlu Wang. 2020. "A Novel Comprehensive Method for Modeling and Analysis of Mesh Stiffness of Helical Gear" Applied Sciences 10, no. 19: 6695. https://doi.org/10.3390/app10196695
APA StyleHou, S., Wei, J., Zhang, A., Zhang, C., Yan, J., & Wang, C. (2020). A Novel Comprehensive Method for Modeling and Analysis of Mesh Stiffness of Helical Gear. Applied Sciences, 10(19), 6695. https://doi.org/10.3390/app10196695




