Safety Issues Referred to Induced Sheath Voltages in High-Voltage Power Cables—Case Study
Abstract
:1. Introduction
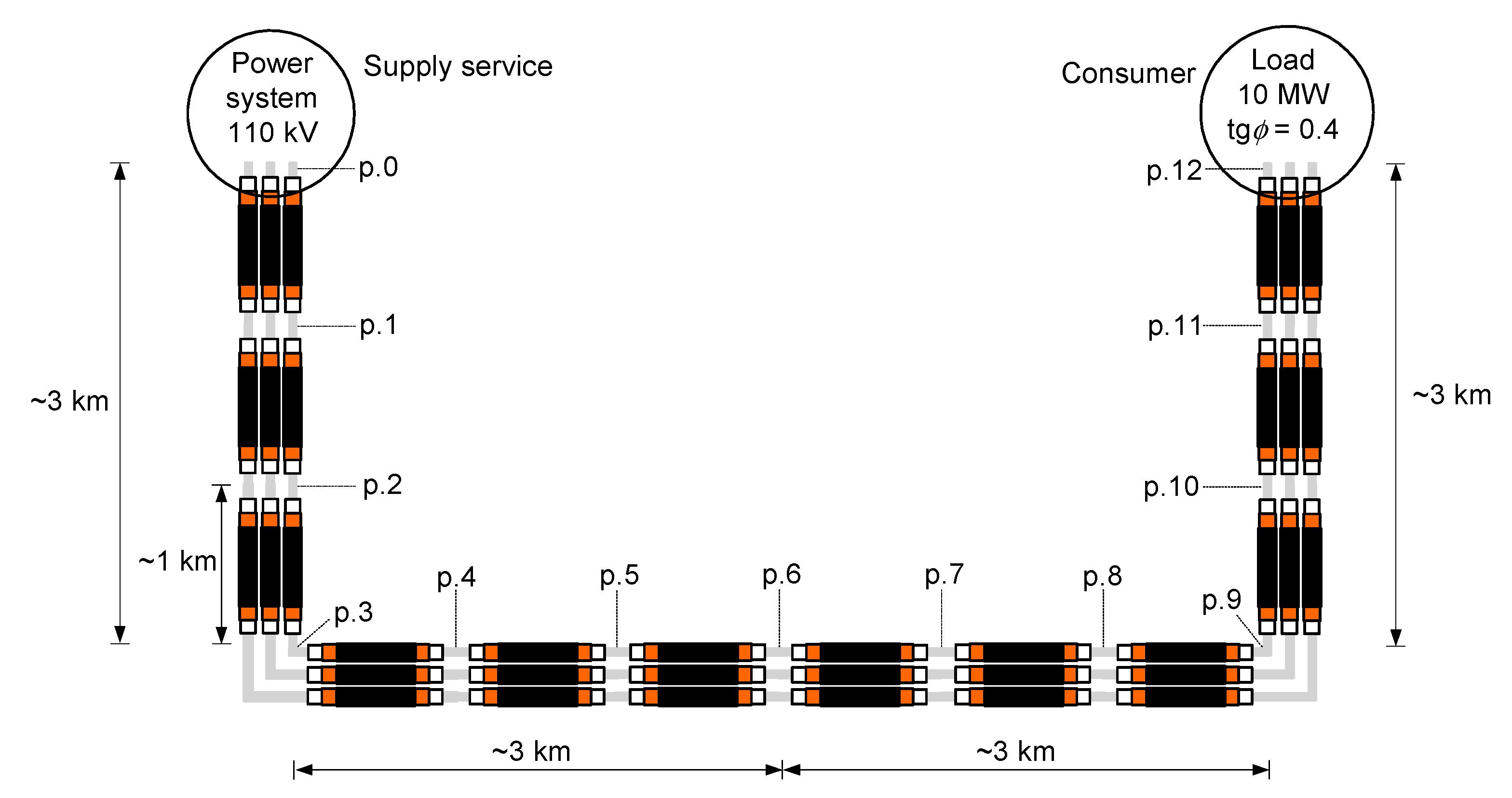
2. Description of the Analyzed 110 kV Cable Line
- nominal voltage of the cable: 110 kV (line-to-line), 64 kV (line-to-earth);
- nominal cross-sectional area of the aluminium conductor (core): 240 mm2; (external diameter DAl = 17.9 mm);
- resistance of the aluminum conductor (core): 0.125 Ω/km (DC in 20 °C), 0.161 Ω/km (AC in max temp. 90 °C);
- nominal cross-sectional area of the copper sheath: 95 mm2 (mean diameter DCu = 58.5 mm);
- resistance of the copper sheath: 0.192 Ω/km (DC in 20 °C);
- inductive reactance of the cable line in the trefoil formation: 0.143 Ω/km;
- XLPE insulation external diameter: DXLPE = 52.9 mm;
- PE outer sheath external diameter (the outer diameter of the cable): DPE = 66.6 mm;
- the current-carrying capacity in the trefoil formation: 421 A (single-point bonding), 409 A (both-ends bonding);
- short-circuit power at the supply service point: 1120 MVA.
3. Results of the Induced Voltages Computer Simulations
3.1. Induced Voltages for Single-Point Bonding
- the transferred power equal to 1 MW (an example very low power), 10 MW (contracted/declared consumed power), 80 MW (maximal permissible power in terms of the current-carrying capacity of the cables; a theoretical value, used for the comparison purposes);
- the reactive-to-active power ratio: tgϕ = Q/P = 0 or tgϕ = Q/P = 0.4 (contracted).
3.2. Induced Voltages for Both-Ends Bonding or Cross Bonding
- p.3: a quarter of the line length;
- p.6: half of the line length;
- p.9: three-quarters of the line length;
- p.12: the consumer substation.
4. Power Losses for the Analyzed Types of Bonding
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jaworski, M. Safety of staying and running field crops under overhead power lines. Prz. Elektrotechniczny 2019, 95, 17–21. [Google Scholar]
- IEEE. 575-2014 IEEE Guide for Bonding Shields and Sheaths of Single-Conductor Power Cables Rated 5 kV through 500 kV; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2014. [Google Scholar]
- IEEE. 80-2013/Cor 1-2015 IEEE Guide for Safety in AC Substation Grounding; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2015. [Google Scholar]
- CIGRE. Special Bonding of High Voltage Power Cables; Working group B1.18, Report Oct; CIGRE: Paris, France, 2005. [Google Scholar]
- Yi, Z.; Cao, X.; Wu, G.; He, F.; Zhang, X. Analysis of the sheath voltage in high-speed railway feeder cable grounding in single-ended mode. In Proceedings of the 2014 International Conference on Lightning Protection (ICLP), Shanghai, China, 11–18 October 2014. [Google Scholar]
- Akbal, B. Determination of the sheath current of high voltage underground cable line by using statistical methods. Int. J. Eng. Sci. Comput. 2016, 6, 2188–2192. [Google Scholar]
- Czapp, S.; Dobrzynski, K.; Klucznik, J.; Lubosny, Z. Computer-aided analysis of induced sheath voltages in high voltage power cable system. In Proceedings of the 10th International Conference on Digital Technologies, Zilina, Slovakia, 9–11 July 2014. [Google Scholar]
- Santos, M.; Calafat, M.A. Dynamic simulation of induced voltages in high voltage cable sheaths: Steady state approach. Int. J. Elect. Power Energy Syst. 2019, 105, 1–16. [Google Scholar] [CrossRef]
- Shaban, M.; Salam, M.A.; Ang, S.P.; Sidik, M.A.B. Assessing induced sheath voltage in multi-circuit cables: Revising the methodology. In Proceedings of the 2015 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015. [Google Scholar]
- CENELEC. EN 50522:2010. Earthing of Power Installations Exceeding 1 kV a.c.; European Committee for Electrotechnical Standardization: Brussels, Belgium, 2010. [Google Scholar]
- Czapp, S.; Dobrzynski, K.; Klucznik, J.; Lubosny, Z. Impact of configuration of earth continuity conductor on induced sheath voltages in power cables. In Proceedings of the 2016 International Conference on Information and Digital Technologies (IDT), Rzeszow, Poland, 5–7 July 2016; pp. 59–63. [Google Scholar]
- Lee, B.; Jung, C.K. Technical review on parallel ground continuity conductor of underground cable systems. J. Int. Council Elect. Eng. 2012, 2, 250–256. [Google Scholar]
- Parol, M.; Wasilewski, J.; Jakubowski, J. Assessment of electric shock hazard coming from earth continuity conductors in 110 kV cable lines. IEEE Trans. Power Deliv. 2020, 35, 600–608. [Google Scholar] [CrossRef]
- Colella, P.; Napoli, R.; Pons, E.; Tommasini, R.; Barresi, A.; Cafaro, G.; De Simone, A.; Di Silvestre, M.L.; Martirano, L.; Montegiglio, P.; et al. Currents distribution during a fault in an MV network: Methods and measurements. IEEE Trans. Ind. Appl. 2016, 52, 4585–4593. [Google Scholar] [CrossRef]
- Di Silvestre, M.L.; Dusonchet, L.; Salvatore, F.; Mangione, S.; Mineo, L.; Mitolo, M.; Riva Sanseverino, E.; Zizzo, G. On the interconnections of HV–MV stations to global grounding systems. IEEE Trans. Ind. Appl. 2019, 55, 1126–1134. [Google Scholar] [CrossRef]
- Asif, M.; Lee, H.-Y.; Park, K.-H.; Lee, B.-W. Accurate evaluation of steady-state sheath voltage and current in HVDC cable using electromagnetic transient simulation. Energies 2019, 12, 4161. [Google Scholar]
- Akbal, B. Hybrid GSA-ANN methods to forecast sheath current of high voltage underground cable lines. J. Comput. 2018, 13, 417–425. [Google Scholar] [CrossRef]
- Riba Riuz, J.R.; Garcia, A.; Morera, X.A. Circulating sheath currents in flat formation underground power lines. Renew. Energy Power Qual. J. 2007, 1, 61–65. [Google Scholar] [CrossRef]
- Gouda, O.; Faraq, A.A. Factors affecting the sheath losses in single-core underground power cables with two-points bonding method. Int. J. Electr. Comput. Eng. 2012, 2, 7–16. [Google Scholar] [CrossRef]
- Li, Z.; Du, B.X.; Wang, L.; Yang, C.; Liu, H.J. The calculation of circulating current for the single-core cables in smart grid. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Asia, Tianjin, China, 21–24 May 2012. [Google Scholar]
- Zong, H.; Gao, Q.; Wang, R.; Wang, H.; Liu, Y. Calculation and restraining method for circulating current of single core high voltage cable. In Proceedings of the 2nd International Conference on Electrical Materials and Power Equipment (ICEMPE), Guangzhou, China, 7–10 April 2019. [Google Scholar]
- Liang, W.; Zhou, Z.; Pan, W.; Li, Y.; Zhou, Q.; Zhu, M. Study on the calculation and suppression method of metal sheath circulating current of three-phase single-core cable. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, Macao, 1–4 December 2019. [Google Scholar]
- Jung, C.K.; Lee, J.B.; Kang, J.W.; Wang, X.; Song, Y.-H. Characteristics and reduction of sheath circulating currents in underground power cable systems. Int. J. Emerg. Electr. Power Syst. 2004, 1. [Google Scholar] [CrossRef]
- Ariyasinghe, A.; Warnakulasuriya, C.; Kumara, S.; Fernando, M. Optimizing medium voltage underground distribution network with minimized sheath and armor losses. In Proceedings of the 2019 14th Conference on Industrial and Information Systems (ICIIS), Kandy, Sri Lanka, 18–20 December 2019. [Google Scholar]
- Sobral, A.; Moura, A.; Carvalho, M. Technical implementation of cross bonding on underground high voltage lines projects. In Proceedings of the 21st International Conference on Electricity Distribution, Frankfurt, Germany, 6–9 June 2011. [Google Scholar]
- Noufal, S.; Anders, G. Sheath loss factor for cross-bonded cable systems with unknown minor section lengths field verification of the IEC standard. IEEE Trans. Power Deliv. 2020. [Google Scholar] [CrossRef]
- Jung, C.K.; Lee, J.B.; Kang, J.W.; Wang, X. Sheath circulating current analysis of a crossbonded power cable systems. J. Electr. Eng. Technol. 2007, 2, 320–328. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zhou, C.; Zhou, W.; Wang, C.; Yao, L.; Su, M.; Huang, X. A novel fault location method for a cross-bonded HV cable system based on sheath current monitoring. Sensors 2018, 18, 3356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Zhou, C.; Zhou, W. A revised model for calculating HV cable sheath current under short-circuit fault condition and its application for fault location—Part 1: The revised model. IEEE Trans. Power Del. 2019, 34, 1674–1683. [Google Scholar] [CrossRef]
- Weissenberg, W.; Farid, F.; Plath, R.; Rethmeier, K.; Kalkner, W. On-site PD detection at cross-bonding links of HV cables, CIGRE, Group B1: Insulated Cables. In Cigre Session 2004; CIGRE: Paris, France, 2004. [Google Scholar]
- Power Cable XRUHAKXS 1x240/95 mm2, 64/110 kV. In Technical Specification (In Polish); TELE-FONIKA Kable: Krakow, Poland, 2017.
- PowerFactory: Integrated Power System Analysis Software; DIgSILENT GmbH: Gomaringen, Germany, 2018.
- Ametani, A. A general formulation of impedance and admittance of cables. IEEE Trans. Power Appar. Syst. 1980, PAS-99, 902–910. [Google Scholar] [CrossRef]
- DIgSILENT PowerFactory. Technical Reference Documentation, Cable System; DIgSILENT GmbH: Gomaringen, Germany, 2014. [Google Scholar]
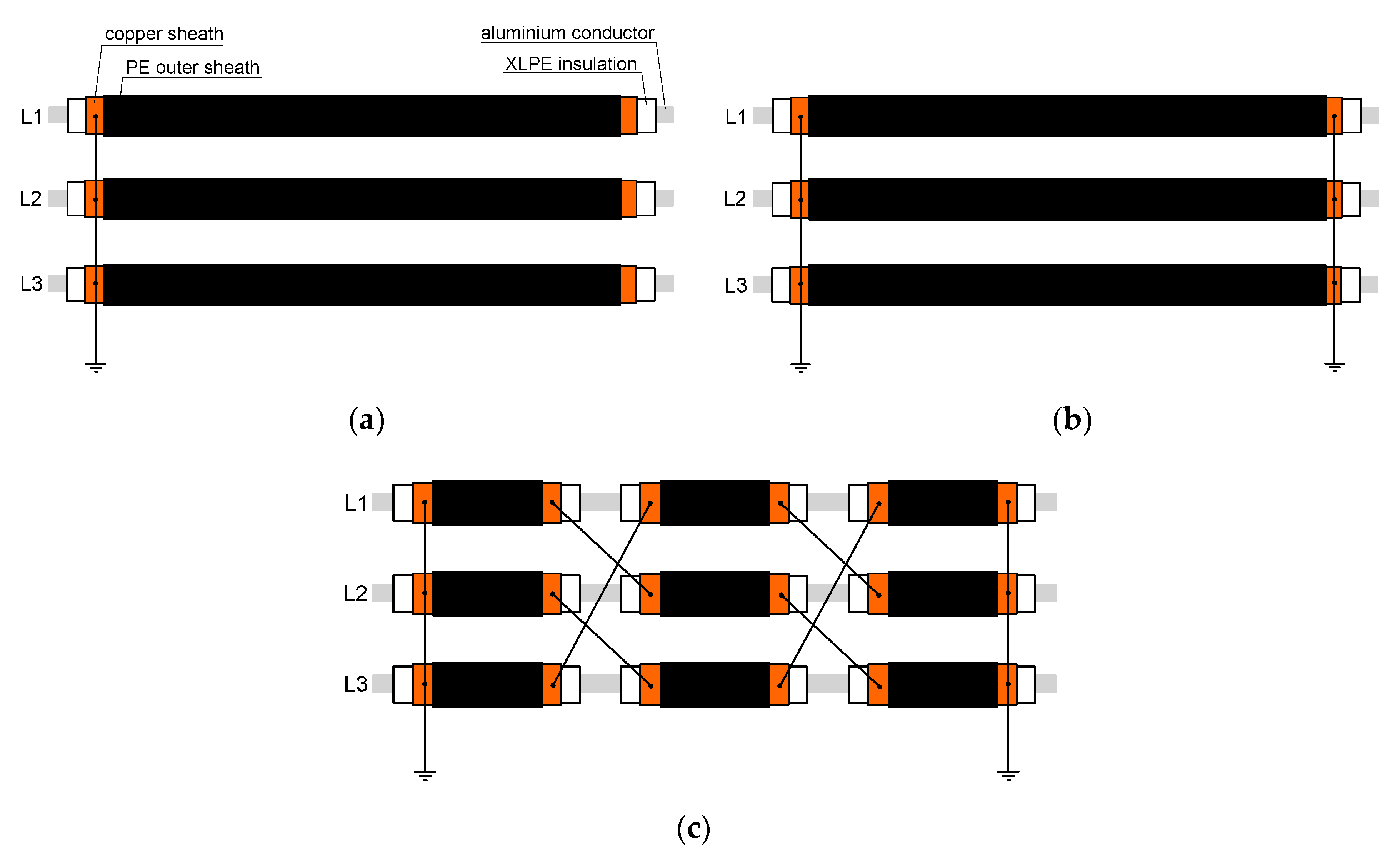











| Criterion | Single-Point Bonding | Both-Ends Bonding | Cross Bonding |
|---|---|---|---|
| Induced voltages in normal operating condition | (0) 1 | (0) | (0) |
| Induced voltages in the case of the short circuit | (-) | (+) with earthing in p.6 | (+) with earthing in p.6 |
| Power losses in the cable system | (0) | (0) | (+) |
| Simplicity of the solution and economic aspects | (+) (0) with ECC | (+) | (0) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czapp, S.; Dobrzynski, K. Safety Issues Referred to Induced Sheath Voltages in High-Voltage Power Cables—Case Study. Appl. Sci. 2020, 10, 6706. https://doi.org/10.3390/app10196706
Czapp S, Dobrzynski K. Safety Issues Referred to Induced Sheath Voltages in High-Voltage Power Cables—Case Study. Applied Sciences. 2020; 10(19):6706. https://doi.org/10.3390/app10196706
Chicago/Turabian StyleCzapp, Stanislaw, and Krzysztof Dobrzynski. 2020. "Safety Issues Referred to Induced Sheath Voltages in High-Voltage Power Cables—Case Study" Applied Sciences 10, no. 19: 6706. https://doi.org/10.3390/app10196706
APA StyleCzapp, S., & Dobrzynski, K. (2020). Safety Issues Referred to Induced Sheath Voltages in High-Voltage Power Cables—Case Study. Applied Sciences, 10(19), 6706. https://doi.org/10.3390/app10196706






