Performance Evaluation of Current Leads for a 5 Tesla Electromagnetic Properties Measurement System
Abstract
:1. Introduction
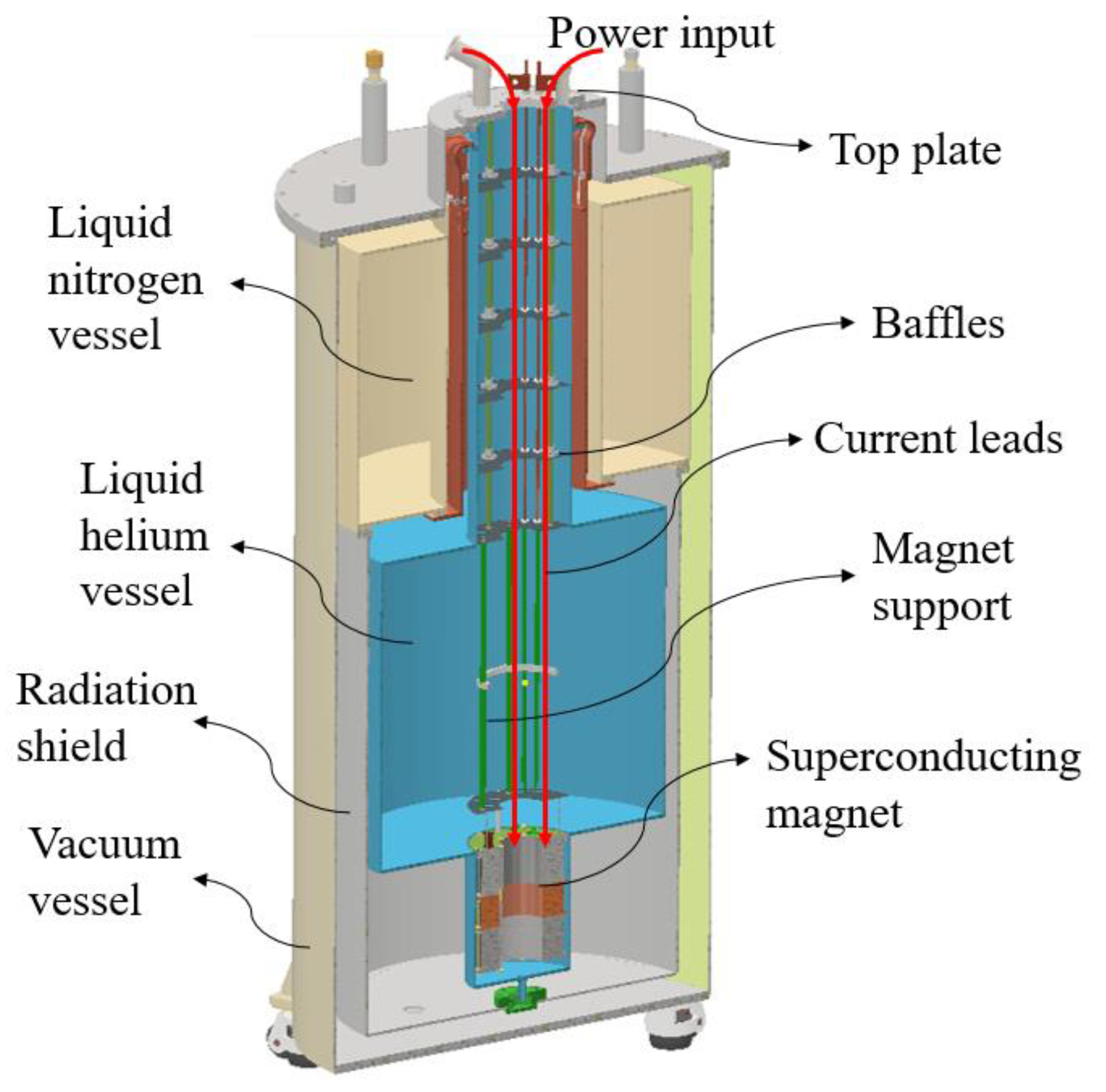
2. Design and Fabrication of the Current Leads
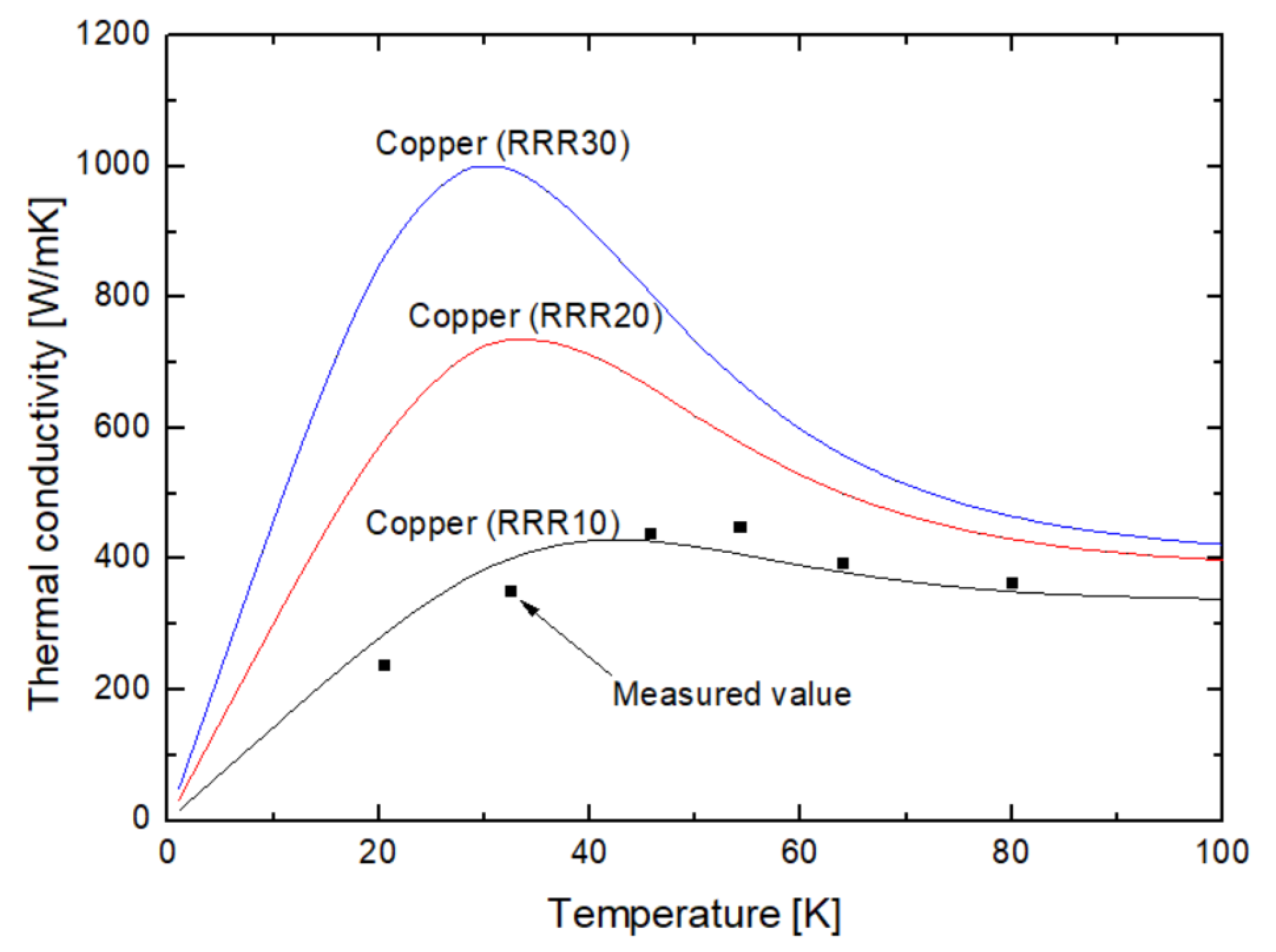
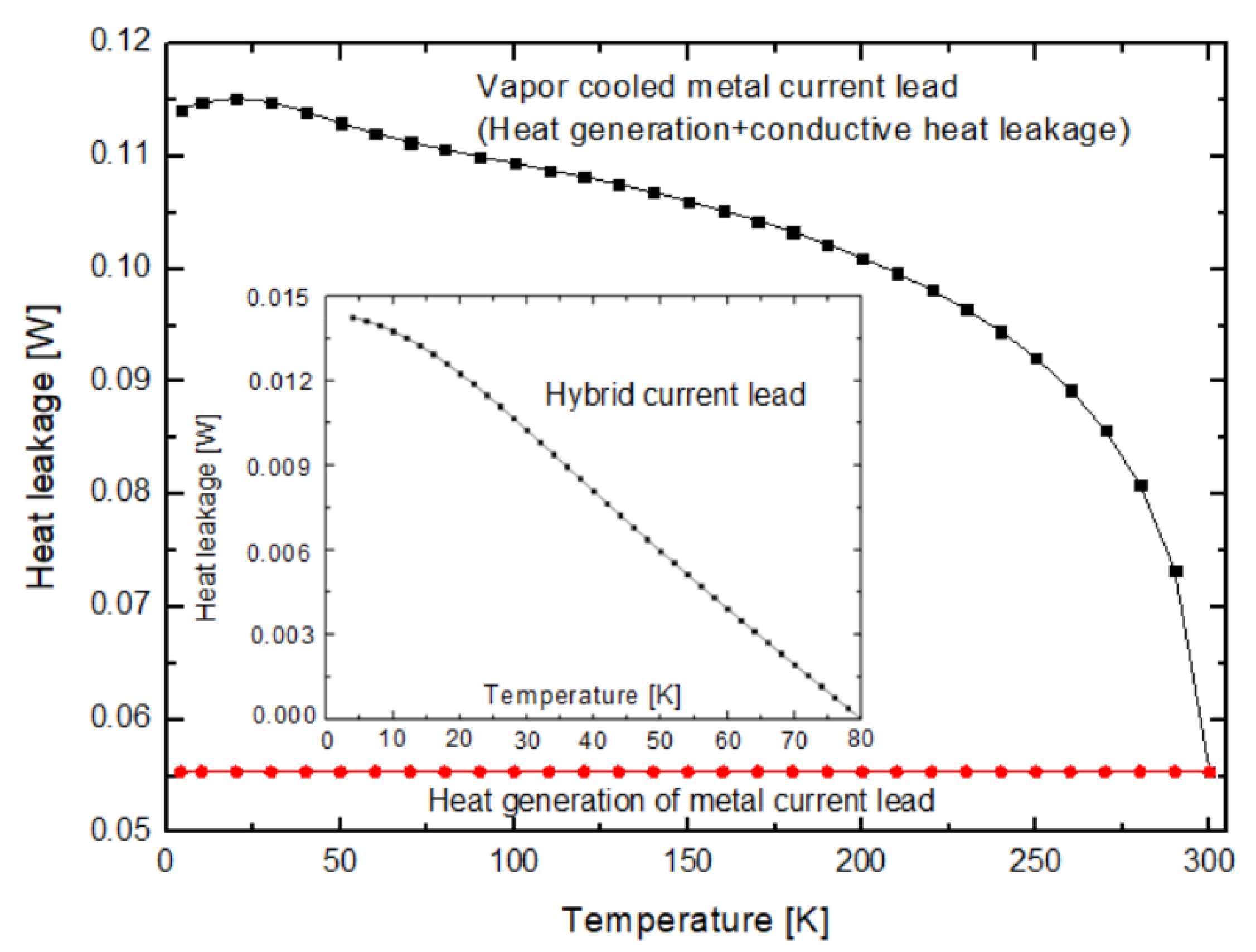
2.1. Vapor-Cooled Current Lead
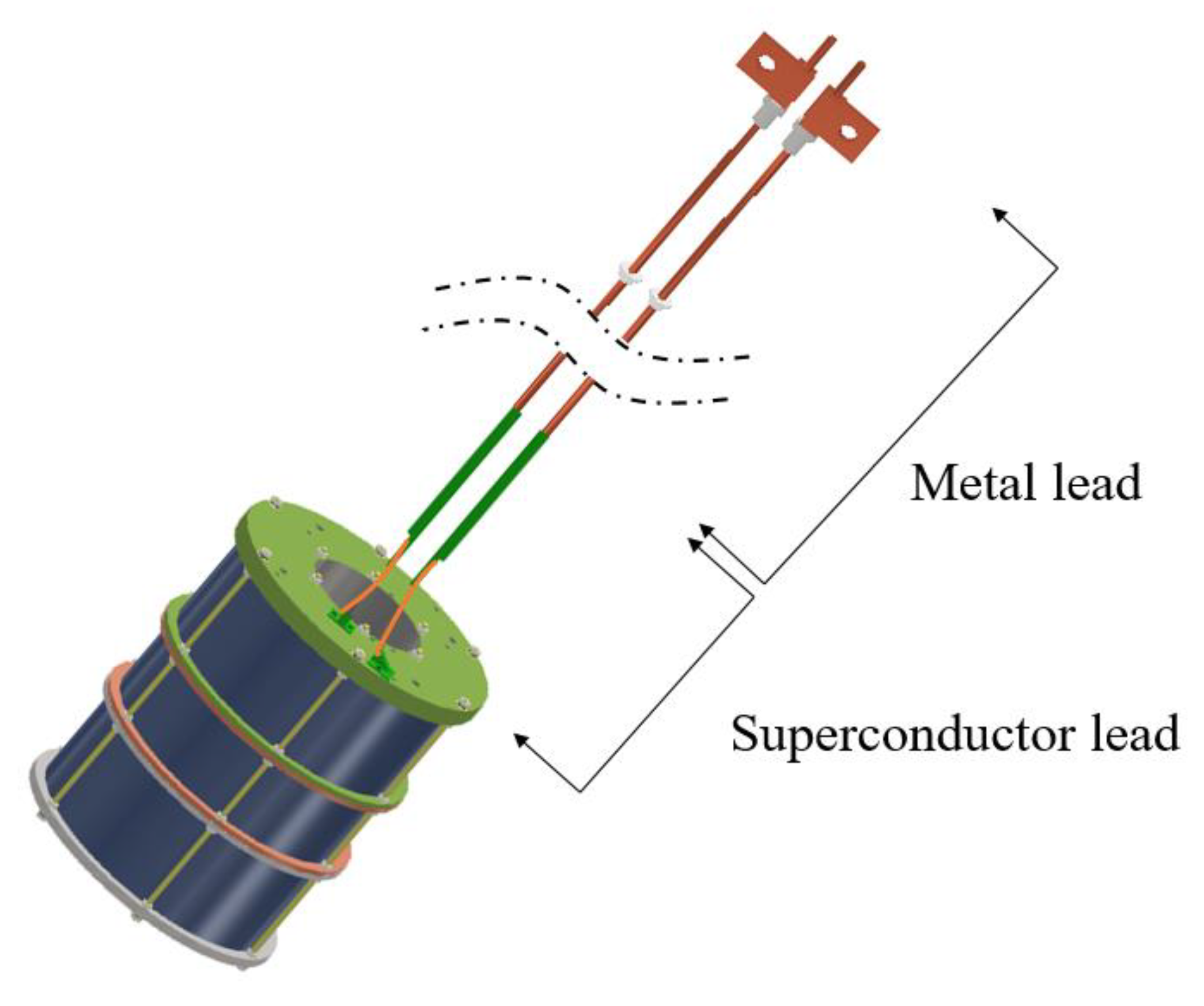
2.2. Hybrid Current Lead
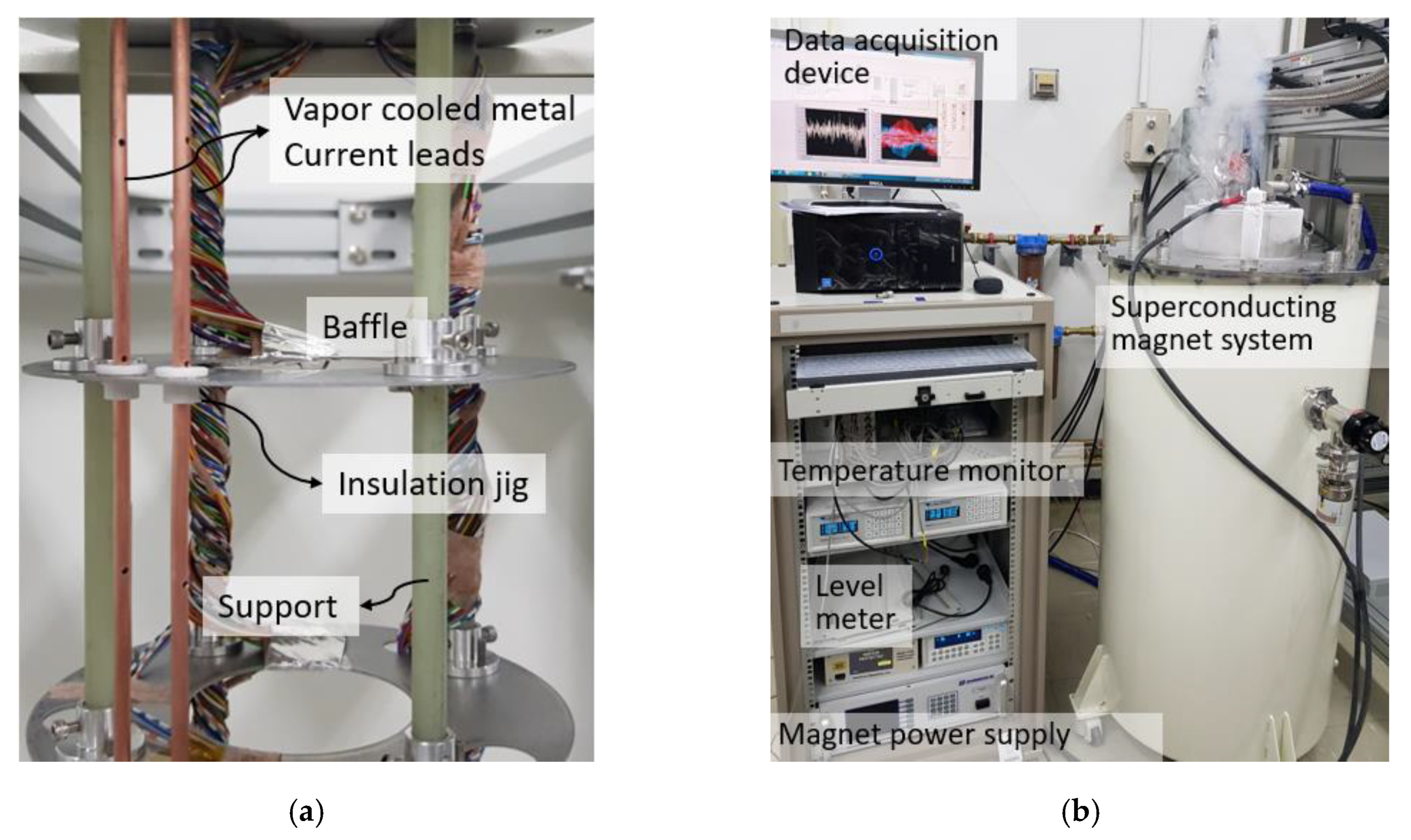
3. Experimental Setup
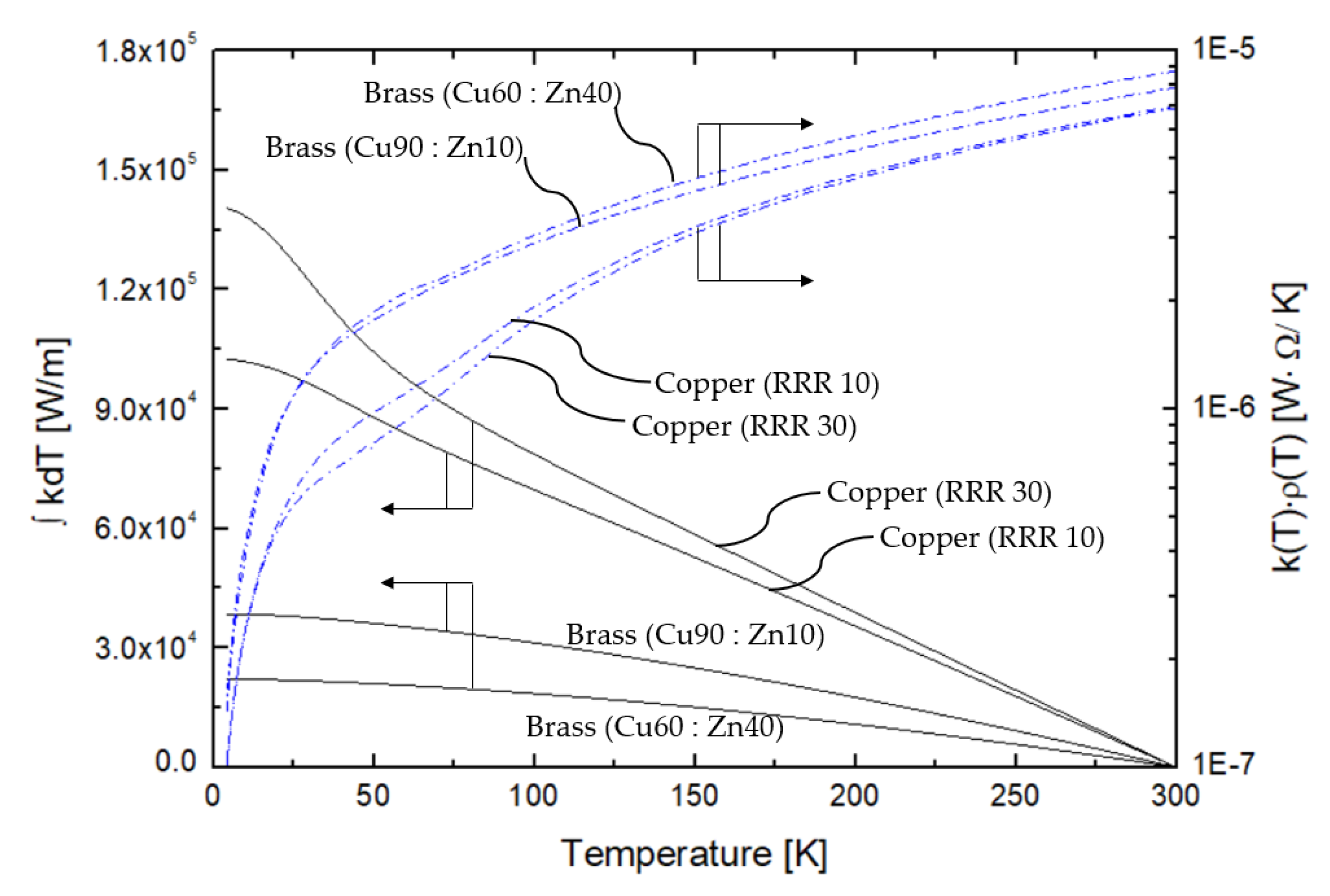
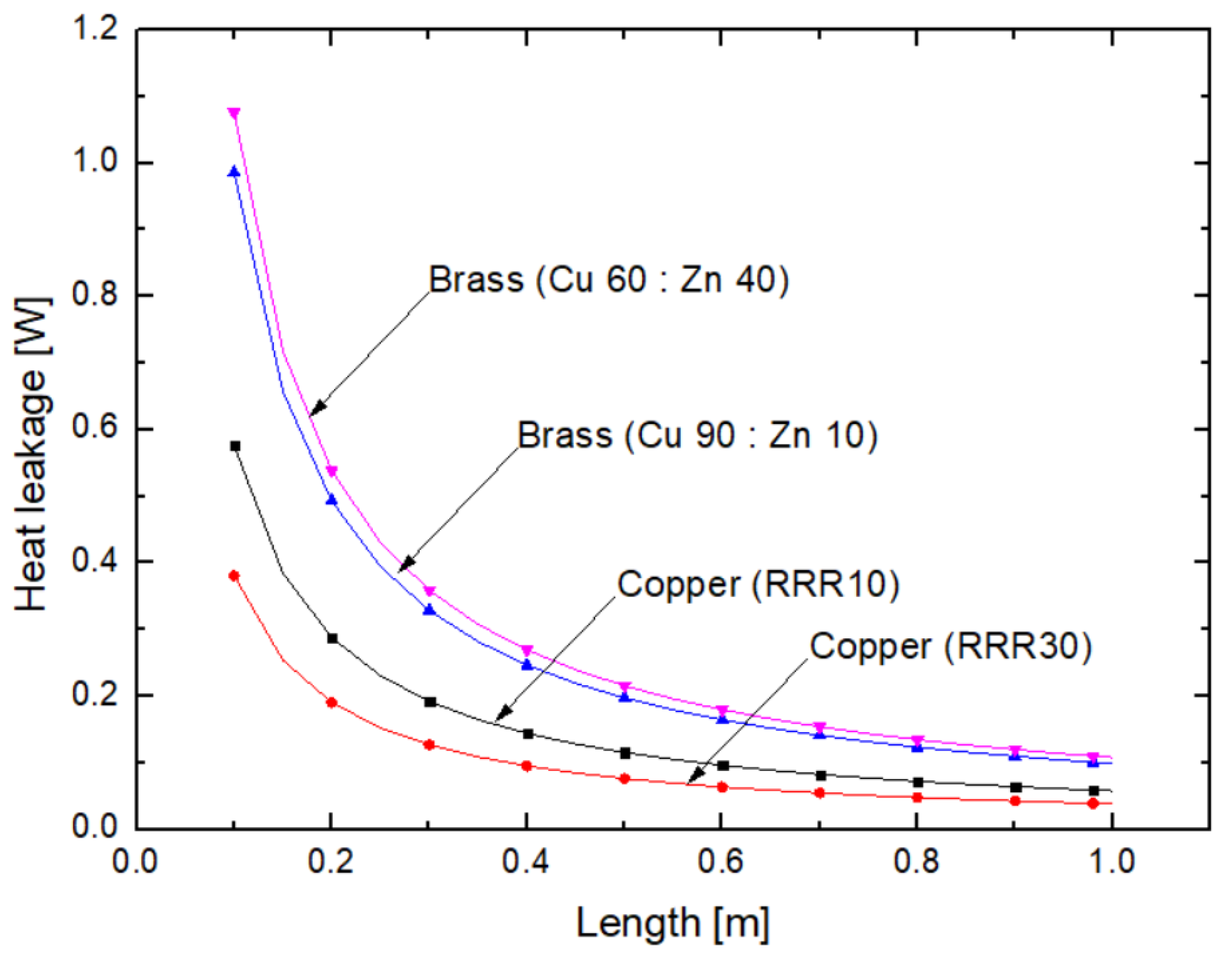
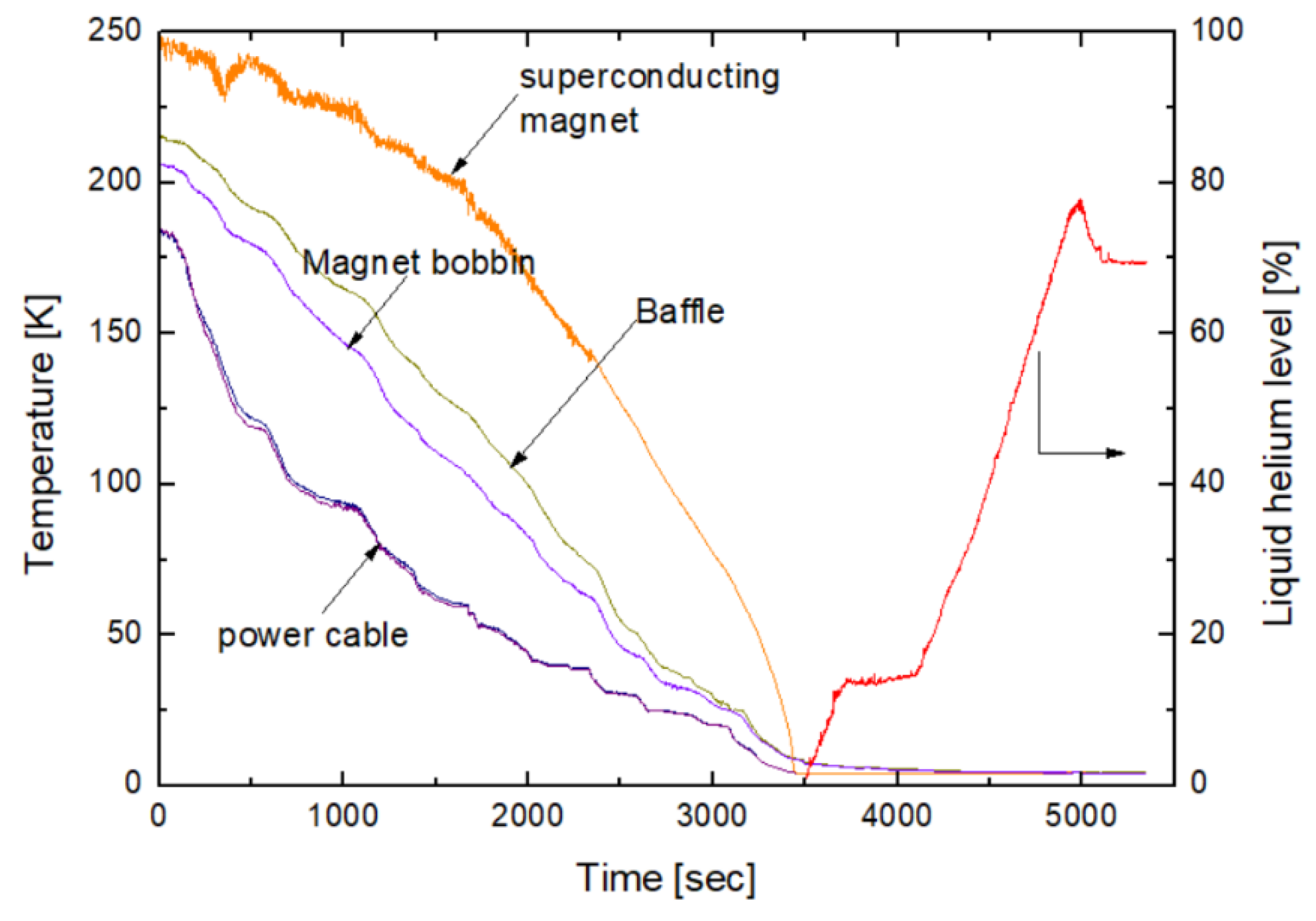
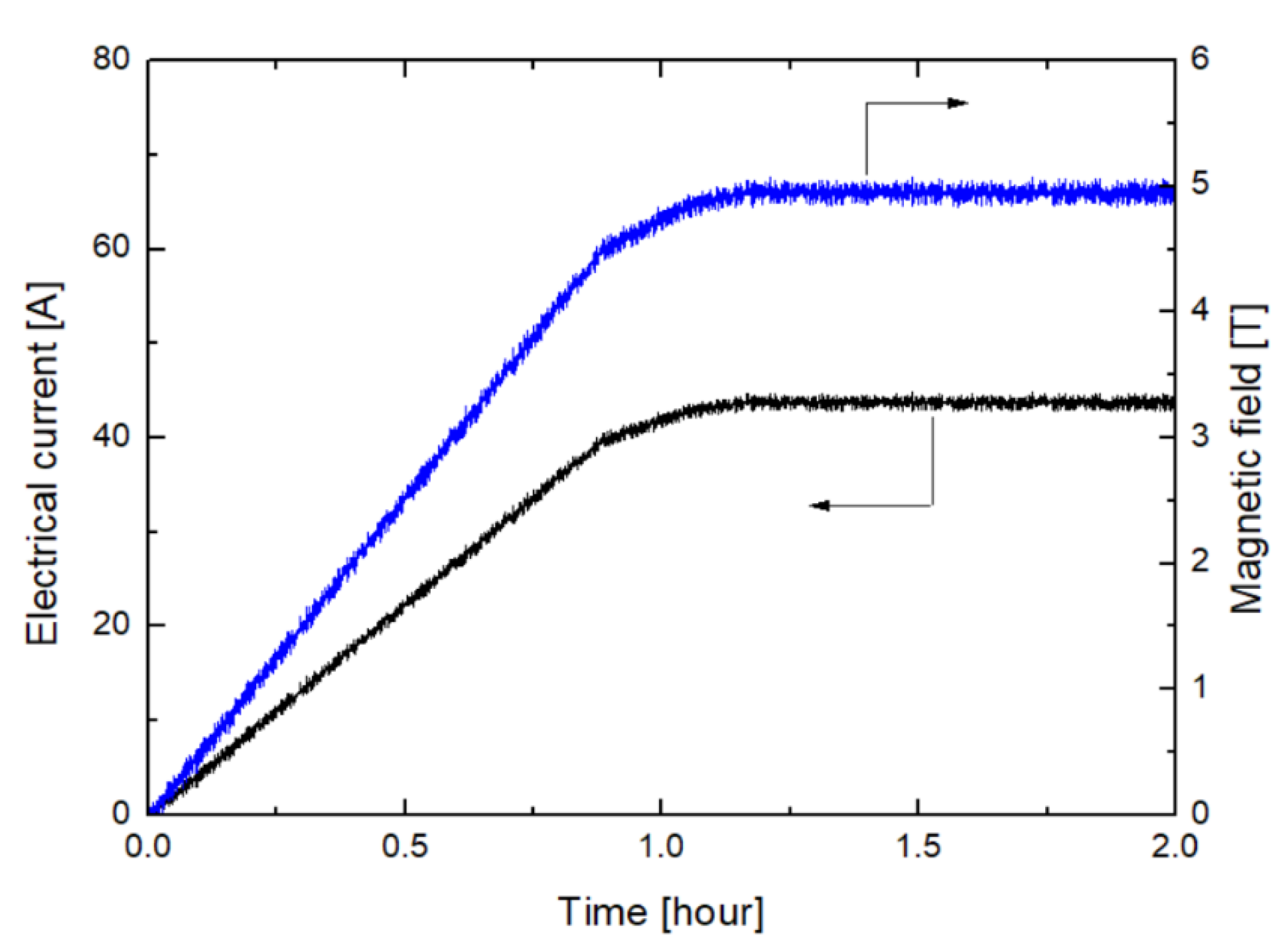
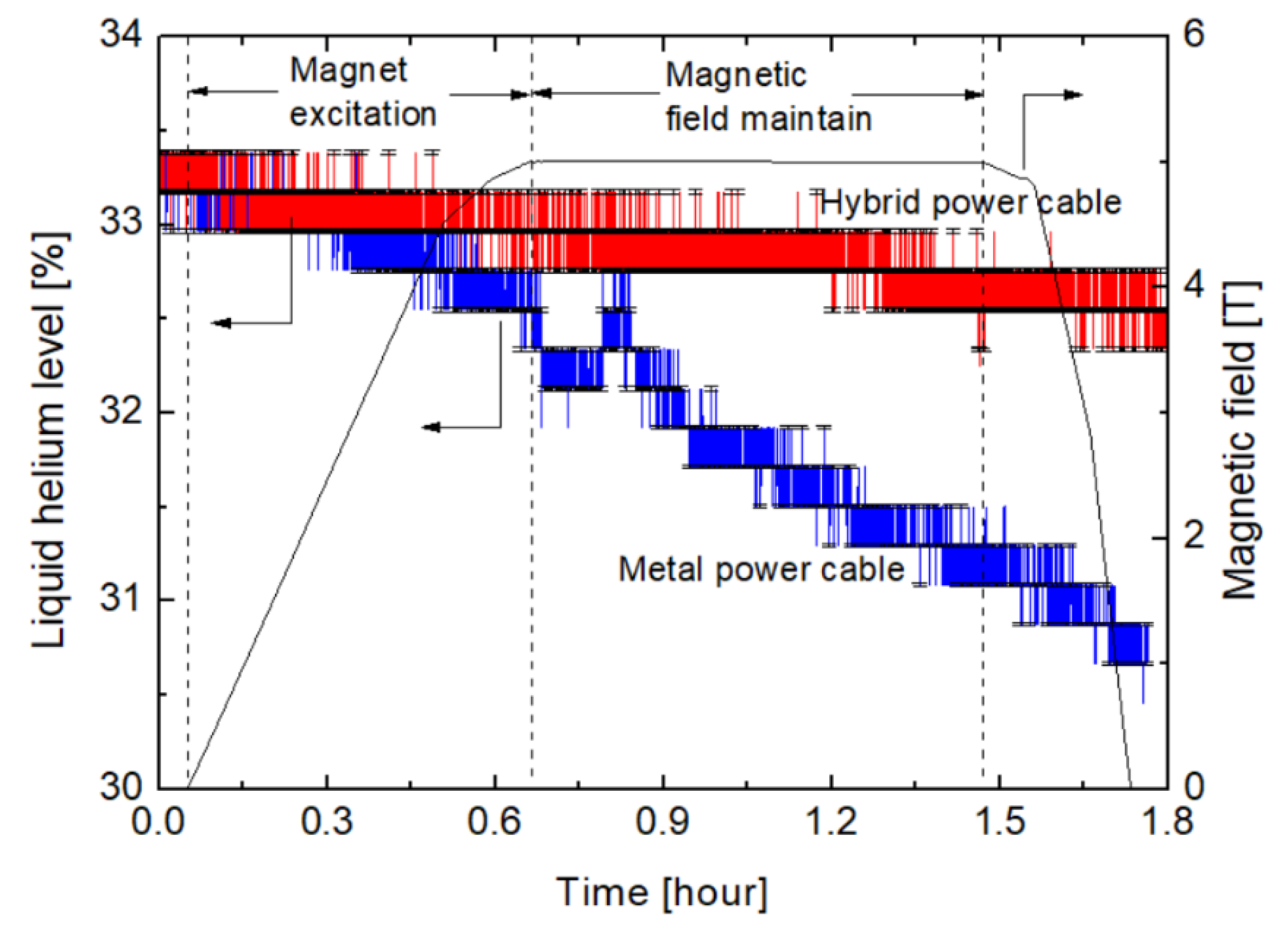
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Qin | Total heat input |
| A | Cross-sectional area |
| z | Axial distance along the current lead |
| I0 | Thermal conductivity |
| k(T) | Brood termination rate |
| ρ(T) | Electrical resistivity |
| Helium mass flow rate | |
| Cp(T) | Specific heat of liquid helium |
| hL | Latent heat of liquid helium |
| k0 | Thermal conductivity of metal current lead at cold end |
| ρ0 | Electrical resistivity at cold end |
References
- Wilson, M.N. Current Supply. In Superconducting Magnets, 1st ed.; Oxford Science Publications: New York, NY, USA, 1986; pp. 256–278. [Google Scholar]
- Lee, S.J.; Yang, H.S. Recent progress and design of three-phase coaxial HTS power cable in Korea. IEEE Trans. Appl. Supercond. 2019, 29, 5402705. [Google Scholar] [CrossRef]
- Hartikainen, T.; Mikkonen, R.; Lehtone, J. Environmental advantages of superconducting devices in distributed electricity-generation. Appl. Energy 2007, 84, 29–38. [Google Scholar] [CrossRef]
- Moon, H.J.; Kim, Y.C.; Park, H.J.; Park, M.W.; Yu, I.K. Development of a MW-Class 2G HTS ship propulsion motor. IEEE Trans. Appl. Supercond. 2016, 26, 5203805. [Google Scholar] [CrossRef]
- Lee, H.S.; Kang, H.K. Conceptual design of a resistive 154-kV/2-kA superconducting fault current limiter. IEEE Trans. Appl. Supercond. 2016, 26, 5601805. [Google Scholar] [CrossRef]
- Zhu, J.; Yuan, W.; Qiu, M.; Wei, B.; Zhang, H.; Chen, P.; Yang, Y.; Zhang, M.; Huang, X.; Li, Z. Experimental demonstration and application planning of high temperature superconducting energy storage system for renewable power girds. Appl. Energy 2015, 137, 692–698. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Xu, Y.; Liao, M.; Guo, S.; Li, Y.; Ren, L.; Su, R.; Li, S.; Zhou, X.; Tang, Y. Integrated design method for superconducting magnetic energy storage considering the high frequency pulse width modulation pulse voltage on magnet. Appl. Energy 2019, 248, 1–17. [Google Scholar] [CrossRef]
- Zhang, S.; Feng, H.; Zhuang, M.; Ding, K.; Liu, C.; Zhou, Y. Experimental Research of a 10 kA HTS Current Lead Using YBCO Tapes. IEEE Trans. Appl. Supercond. 2020, 30, 4801307. [Google Scholar] [CrossRef]
- Yamada, Y.; Ishii, Y.; Sakai, S.; Shiohara, K.; Tachikawa, K.; Aoki, Y.; Kaneko, A.; Koizumi, T.; Tamura, H.; Mito, T. HTS current leads prepared by the TFA-MOD processed YBCO tapes. IEEE Trans. Appl. Supercond. 2011, 21, 1054–1057. [Google Scholar] [CrossRef]
- Matsumura, R.; Hosono, Y.; Tanimoto, R.; Yamada, Y.; Takahashi, K.; Hironaga, R.; Hasegawa, T.; Tamura, H.; Mito, T. Transport Performance and Current Distribution of HTS Current Lead Prepared by YBCO Tapes. IEEE Trans. Appl. Supercond. 2015, 26, 4800104. [Google Scholar] [CrossRef]
- Lee, W.S.; Hwang, Y.J.; Kim, J.; Nam, S.; Park, Y.G.; Ko, T.K. Quench Protection for HTS Current Leads by Adding Connected HTS Bridges. IEEE Trans. Appl. Supercond. 2014, 24, 4801804. [Google Scholar]
- Ren, L.; Tang, Y.; Li, J.; Li, Z.; Chen, L.; Chen, J.; Shi, J.; Wen, J. Conduction-cooled YBCO HTS current lead for SMES application. IEEE Trans. Appl. Supercond. 2010, 20, 1737–1740. [Google Scholar] [CrossRef]
- Fietz, W.H.; Heller, R.; Kienzler, A.; Lietzow, R. High Temperature Superconductor Current Leads for WENDELSTEIN 7-X and JT 60SA. IEEE Trans. Appl. Supercond. 2009, 19, 2202–2205. [Google Scholar] [CrossRef]
- Saggese, A.; Iannone, G.; Gambardella, U.; Califano, N.; Ferrentino, A. 20 kA HTS Current Leads for the INFN Magnet Test Facility. IEEE Trans. Appl. Supercond. 2014, 25, 4801304. [Google Scholar] [CrossRef]
- Oshi, I.; Naoaki, K.; Misato, T.; Yusuke, Y.; Satoshi, A.; Koichi, M. Thermal expansion and magnetostriction measurement using Quantum Design Physical Property Measurement System. J. Phys. Conf. Ser. 2014, 568, 032002. [Google Scholar]
- Kim, M.S.; Choi, Y.S. Interfacial contact resistance along the thermal link in conduction-cooled low temperature superconducting magnet system. J. Supercond. Nov. Magn. 2015, 28, 681–684. [Google Scholar] [CrossRef]
- Lee, H.G.; Paul, A.; Kenneth, R.E.; Yukikazu, I. Helium vapor-cooled brass current lead: Experimental and analytical results. Cryogenics 2001, 41, 485–489. [Google Scholar] [CrossRef]
- Yukikazu, I. Case Studies in Superconducting Magnets; Plenum Press: New York, NY, USA, 1994; pp. 125–162. [Google Scholar]
- Cryogenic Technology Resources. Available online: https://trc.nist.gov/cryogenics/aboutCryogenics (accessed on 15 April 2020).
- Ekin, J. Experimental Techniques for Low-Temperature Measurements; Oxford University Press: New York, NY, USA, 2006; pp. 517–536. [Google Scholar]
- Kim, M.S.; Choi, Y.S. Characteristics of conduction-cooled binary current leads used in cryogen free probe station. IEEE Trans. Appl. Supercond. 2017, 27, 4800404. [Google Scholar]
- Kim, M.S.; Seo, Y.H.; Choi, Y.S. Thermal contact conductance of various metal interfaces at cryogenic temperature. Int. J. Nanotechnol. 2019, 16, 213–219. [Google Scholar] [CrossRef]
- Miao, W.; Wan-min, Y.; Jia-wei, L.; Zhong-Ling, F.; Peng-Tao, Y. F Comparison of the superconducting properties in GdBCO bulk superconductors fabricated with two different solid phases. Supercond. Sci. Technol. 2015, 28, 035004. [Google Scholar]
- Park, S.; Cho, B.; Park, H.; Ri, H.-C. Analysis of the local current in GdBCO coated conductors using low-temperature scanning laser and hall probe microscopy. Cryogenics 2012, 52, 744–748. [Google Scholar] [CrossRef]
- Lee, S.; Sung, H.; Park, M.; Won, D.; Yoo, J.; Yang, H.S. Analysis of the temperature characteristics of three-phase coaxial superconducting power cable according to a liquid nitrogen circulation method for real-grid application in Korea. Energies 2019, 12, 1740. [Google Scholar] [CrossRef] [Green Version]
- SuNAM Co., Ltd. Homepage. Available online: https://www.i-sunam.com (accessed on 20 June 2020).
- Ibi, A.; Fukushima, H.; Yamada, Y.; Miyata, S.; Kuriki, R.; Takahashi, K.; Shiohara, Y. Development of long GdBCO coated conductor using the IBAD/MPMT-PLD method. Supercond. Sci. Technol. 2006, 19, 1229–1232. [Google Scholar] [CrossRef]
- Fesmire, J.E.; Johnson, W.L. Cylindrical cryogenic calorimeter testing of six types of multilayer insulation systems. Cryogenics 2018, 89, 58–75. [Google Scholar] [CrossRef]
- American Magnetics Inc. Homepage. Available online: https://www.americanmagnetics.com (accessed on 11 September 2020).

| Parameter | Value | Unit |
|---|---|---|
| Conductor | NbTi | − |
| Conductor length | 6.06 | km |
| Central magnetic field | 5.01 | tesla (T) |
| Operating current | 45 | A |
| Inductance | 15 | H |
| Magnetic field energy | 15.2 | kJ |
| Material | A (mm2) (L = 0.98 m) | Conductive Heat Leakage | Heat Generation | Total Heat Leakage (W) |
|---|---|---|---|---|
| Brass (Cu 90: Zn 10) | 22.52 | 0.1005 | 0.06598 | 0.1665 |
| Brass (Cu 60: Zn 40) | 42.56 | 0.1098 | 0.06804 | 0.1778 |
| Copper (RRR30) | 2.38 | 0.0380 | 0.0554 | 0.0934 |
| Copper (RRR10) | 4.90 | 0.0588 | 0.0552 | 0.1140 |
| Vapor-Cooled Metal Current Lead (Copper RRR10) | Hybrid Current Lead | |||
|---|---|---|---|---|
| Design value | Test value | Design value | Test value | |
| Heat leakage | 0.4322 W | 0.4599 W | 0.3396 W | 0.3486 W |
| Boil-off rate | 14.31 L/day | 15.21 L/day | 11.23 L/day | 11.53 L/day |
| Decreasing rate | − | − | 21.53% | 24.19% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.S.; Jang, J.Y.; Hwang, Y.J.; Choi, Y.S. Performance Evaluation of Current Leads for a 5 Tesla Electromagnetic Properties Measurement System. Appl. Sci. 2020, 10, 6712. https://doi.org/10.3390/app10196712
Kim MS, Jang JY, Hwang YJ, Choi YS. Performance Evaluation of Current Leads for a 5 Tesla Electromagnetic Properties Measurement System. Applied Sciences. 2020; 10(19):6712. https://doi.org/10.3390/app10196712
Chicago/Turabian StyleKim, Myung Su, Jae Young Jang, Young Jin Hwang, and Yeon Suk Choi. 2020. "Performance Evaluation of Current Leads for a 5 Tesla Electromagnetic Properties Measurement System" Applied Sciences 10, no. 19: 6712. https://doi.org/10.3390/app10196712
APA StyleKim, M. S., Jang, J. Y., Hwang, Y. J., & Choi, Y. S. (2020). Performance Evaluation of Current Leads for a 5 Tesla Electromagnetic Properties Measurement System. Applied Sciences, 10(19), 6712. https://doi.org/10.3390/app10196712





