1. Introduction
The wing-in-ground (WIG) craft [
1] is a kind of aircraft that makes full use of ground effect at low altitudes to improve flight efficiency. It is mainly used for high-speed water transportation. Compared with ships, it has the advantages of fast speed and low resistance; compared with aircrafts, it has the advantages of a high lift-to-drag ratio and a high energy utilization efficiency. However, the WIG craft has unique aerodynamic characteristics when flying near to the ground which are significantly different from those of conventional aircraft. Therefore, many scholars have carried out research on the unique aerodynamic characteristics of the WIG craft [
2,
3,
4,
5,
6,
7,
8].
The WIG craft is designed to fly at a low altitude, but there are various obstacles such as buildings, trees, hills, and other obstacles on the land. The vast ocean is flat, which provides a good application scenario for the WIG craft flying at a low altitude. Therefore, most WIG crafts are used for water transportation. Up to present, most of the researchers focusing on the ground effect assume that the ground is flat. However, there are often waves on the water surface. Therefore, it is necessary to study the ground effect under wavy ground conditions.
Hsiun [
3] studied the aerodynamic characteristics of the airfoil in ground effect by solving the steady Reynolds Averaged Navier–Stokes equations (RANS). He found that ground clearance had a significant impact on the lift coefficient, and when the ground clearance was less than a specific value, the lift would be lost. Ocken [
8] applied the numerical method to study the aerodynamic characteristics of the airfoil with a deflection flap in ground effect. Yang [
9] carried out numerical simulations on WIG craft with a power-augmented ram (PAR) engine. Jamei [
4] numerically investigated the aerodynamic characteristics of compound wings with the ground effect. He concluded that, compared with the rectangular wing, the compound wing had greater lift, less drag, and better aerodynamic characteristics, especially in the case of small ground clearance. Qu [
10] investigated the aerodynamics and flow physics of a NACA4412 airfoil with ground effect for a wide range of angles of attack; his research showed that the angle of attack (AOA) versus ride height plane could be divided into three regions based on the sign of the lift increment value. Besides this, Qu [
11] also studied the aerodynamic properties of the dynamic ground effect (DGE), supposing that the distance between an aircraft and the ground keeps constantly changing during takeoff and landing. These studies all assume that the ground is a rigid flat ground, and preliminary studies of the ground effect are carried out on this basis.
Different from the ground covered with obstacles, such as trees, buildings, hills, and so on, the flatness of the sea surface provides a good flying environment for WIG crafts, therefore this kind of aircraft is mainly used for high-speed transportation along the water surface. However, the actual sea surface is a free surface. To get closer to reality, some scholars begin to employ free surface instead of rigid ground to study the ground effect. Barber [
12] studied the water surface deformation when the wing moved over a free surface at a small ride height; her results showed that any deformation occurring on the water surface was likely to be caused by the wingtip vortices rather than an increased pressure distribution beneath the wing. With the increase in velocity, the deformation of the water surface became less significant. Jung [
6] numerically investigated the effect of an endplate on the 3-D WIG problem using the assumptions of steady incompressible viscous flow. He found that endplate could effectively increase lift and reduce drag with the ground effect, and the wingtip vortex will cause a small deformation of the water surface. Zong and Liang [
13,
14] applied the lifting line theory to study the ground effect of a three-dimensional wing near the free surface. Their results showed that the deformation of the free surface was significant at a low velocity, and that the lift coefficient fluctuates dramatically; at a high velocity, the deformation of the free surface could be neglected so that the free surface could be represented by a rigid wall. Bal [
15] developed the iterative boundary element method to investigate the effects of free surface both on 2-D airfoils and 3-D wings moving over a free surface. He concluded that the free surface would affect the aerodynamic characteristics of the airfoil and wing, and the Kelvin wave would also be generated on the surface. These researchers applied free surface boundary conditions in the study of ground effect, which is closer to the real scene, and made an important contribution to research into the ground effect.
The sea is not calm most of the time, and there are always waves on the surface. The waves make the ground effect of WIG crafts more complicated. Therefore, some scholars have recently conducted research on the ground effect under wavy ground conditions. Im [
16] studied the aerodynamics of the airfoil NACA 6409 moving over wavy ground by numerically solving the Euler equations; his results indicated that the aerodynamics of the airfoil became sensitive if the wave number or amplitude of the wavy ground was increased or if the proximity of the airfoil to the ground was lowered. Qu [
17] simulated a WIG craft flying at α = 3deg and α = 9deg over wavy ground employing compressible RANS equations and the Spalart–Allmaras turbulence model. Gao [
18] investigated the aerodynamics of a transonic airfoil above wavy ground and analyzed the change in aerodynamic characteristics caused by the interaction between shock waves and wavy ground. Liang [
19] employed a potential flow-based discrete vortex method to investigate heaving airfoils for a wing in ground effect over a rigid wavy surface and over progressive water waves, considering that a WIG craft may experience a periodic heaving motion induced by the presence of water waves. Lee [
20] conducted an experimental investigation on the aerodynamics and flow field of a NACA 0015 airfoil over a wavy ground. On this basis, Tremblay [
21] extended the airfoil experiment over a sinusoidal wavy ground to the investigation of the effect of a trailing-edge flap on the aerodynamics and flow field of a NACA 0015 airfoil. Most of the above scholars used rigid wavy ground instead of water waves to study the airfoil moving over waves. Zhi [
22] applied the volume of fluid (VOF) method to numerically simulate the water wave to study the aerodynamics of the airfoil moving over waves.
It should be noted that there is a strong coupling effect between the surface waves and the air near the water–air surface. Besides this, the spumes and bubbles generated as a result of wave breaking may affect the aerodynamics of the airfoil. Yousefi [
23] performed experiments to investigate the details of the momentum flux partitioning between turbulent, wave-coherent, and viscous stresses, and he [
24] also developed vorticity equations to interpret the experimental data of fluid flow over wind-generated surface waves. Buckley [
25] studied two-dimensional airflow velocity fields above the air–water interface and found a reversed, upwind sheltering effect near the water surface. Sullivan [
26] investigated the coupling processes between surface gravity waves and adjacent winds and currents in turbulent boundary layers. Husain [
27] tried to reproduce the observed airflow dynamics induced by strongly forced wind waves through large-eddy simulation. Due to the strong coupling effect between the wave surface and the air, there are certain limitations in using wavy ground to simulate waves.
Up to now, studies on the aerodynamic characteristics of airfoils moving over wavy surfaces are still limited, and the understanding of this unique problem is not thorough. Previous studies have focused on the aerodynamics of an airfoil moving over wavy ground at a specific angle of attack. The aerodynamics of an airfoil moving over wavy ground for a wide range of angles of attack has not been studied. Therefore, unsteady RANS equations are used to simulate an airfoil moving over wavy ground for a wide range of angles of attack ranging from 0° to 18°, which covers the angle of attack that a WIG craft may encounter in actual flight.
The structure of this paper is as follows. Firstly, the numerical calculation model is defined, and the numerical calculation method is verified. Subsequently, the numerical simulation of the airfoil moving over the wavy ground is conducted. The aerodynamic coefficients under a series of angles of attack are analyzed, including the fluctuation amplitude and time-averaged value. The time-averaged value is compared with that of free stream, flat ground, and wavy ground. Finally, the structure of the flow field is analyzed.
In this study, it is found that when the airfoil moves over wavy ground, the variation in aerodynamic coefficients at a small angle of attack is different from that of other angles of attack, and the fluctuation amplitude of aerodynamic coefficients is significantly greater than that of other angles of attack. The mechanism for the difference is interpreted through an analysis of the structure of the flow field. The range of angles of attack suitable for the flight of WIG craft is given. By comparing the time-averaged aerodynamics under flat-ground and wavy-ground conditions, it is found that the wavy ground only causes fluctuation in the aerodynamic coefficient, but does not change the time-averaged value. All this is of practical significance for the design and safe flight of WIG crafts.
2. Numerical Method and Validation
In this paper, the airfoil NACA 4412 is selected. The chord length of the airfoil is 0.5 m, the incoming velocity is 30 m/s, and the corresponding Reynolds number is 1.0 × 10
6. The ride height
h between the airfoil and the ground is described by the distance between the trailing edge point of the airfoil and the ground. The selection of the reference points at the trailing edge point refers to the relevant papers in this field [
3,
16,
20,
21,
22], so that this study can be compared with the existing study.
In this study, the ride height is set to
h = 0.1
c, where
c is the chord length. The range of angles of attack is 0~18°. The shape of the wavy ground is represented by a sine function, where the wave amplitude
a is 0.05
c and the wavelength
λ is 5
c. The selection of the wave parameters refers to the studies mentioned in the introduction, thus this study can be compared with other research. The surface equation of wavy ground is shown in Equation (1), where
x0 is the initial phase.
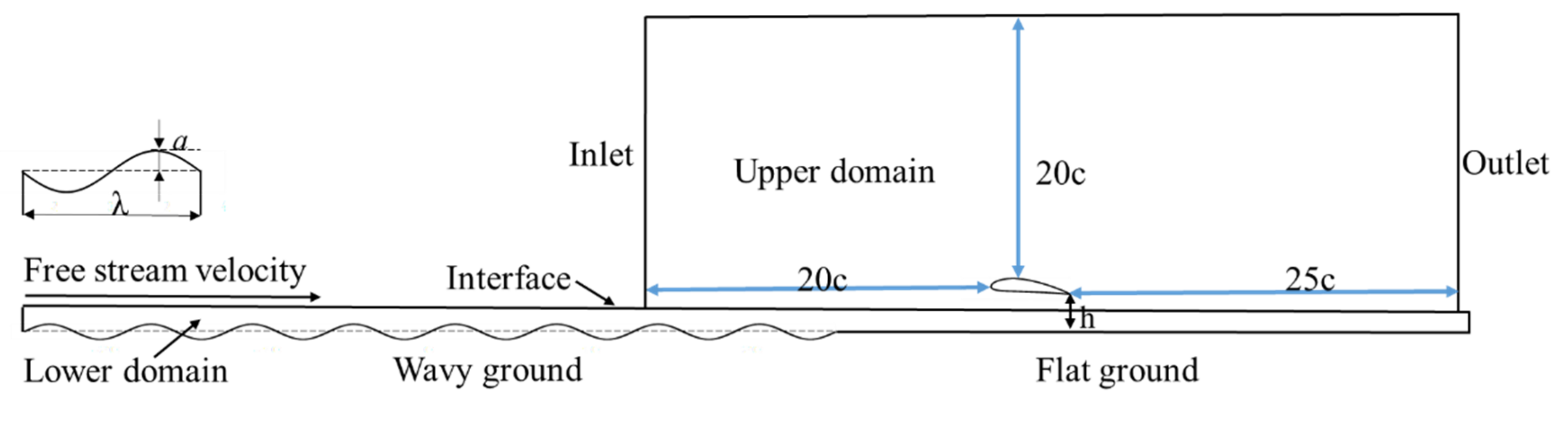
The computational domain is shown in
Figure 1. The sliding grid technology is adopted, and the whole calculation domain is divided into upper and lower parts. During the calculation, the upper domain remains static, the lower part of the domain moves to the right at a velocity equal to the incoming flow velocity, and the upper and lower domain exchange data through their contact surface. The inlet boundary and the upper boundary is 20
c away from the airfoil, and the outlet boundary is 25
c. The inlet boundary condition is set as the velocity inlet, the upper boundary and the outlet boundary as the pressure outlet, the contact surface of the upper and lower domains as the interface, and the wavy ground as the non-slip wall. In order to avoid calculation divergence at the initial time, a section of flat ground is located in front of the wavy ground. The lengths of the wavy ground and the flat ground are 75
c and 35
c, respectively. The grid of the computational domain is shown in
Figure 2. The structural grid is employed, and the grid near the airfoil and the ground is refined. The numerical simulation is carried out by solving the RANS equations coupled with the turbulence model
k-e. The second-order implicit scheme and second-order upwind scheme are employed for time discretization and spatial discretization, respectively. The time step Δ
t is 0.00015 s, considering the stability of unsteady calculation. Equation (2) is usually satisfied.
where Δ
x is the minimum grid size and
u is the incoming velocity. The convergence standard is the momentum residual and the periodicity of the aerodynamic coefficient. The residuals of the momentum, turbulent kinetic energy, and continuity are less than 1 × 10
−6. At the same time, the lift coefficient and drag coefficient change periodically. If these two conditions are satisfied simultaneously, the convergence of the numerical calculation is judged to be reached.
The validation of the computational fluid dynamics (CFD) calculation is performed before numerical calculation. Many scholars have conducted a lot of studies on the NACA 4412 airfoil with numerical calculations or experiments. Ahmed [
28] conducted an experiment to study the aerodynamic characteristics of the NACA 4412 airfoil with the ground effect. The study here also investigates the problem of the ground effect. Therefore, the experimental data in Ahmed’s paper are used for CFD validation. The angle of attack of the airfoil is taken as 4°, the ride height of the airfoil is
h/c = 0.15, and the Reynolds number is 3.0 × 10
5. These conditions are consistent with Ahmed’s experimental conditions [
28]. The ground in the calculation domain is set as a moving wall with the velocity of airflow, and the other boundary conditions are the same as those mentioned above. Grid independence verification is carried out in order to ensure that the calculation results are independent of the grid. The number of grids increases or decreases according to the same principle. Three groups of grid numbers are set—namely, coarse grid, medium grid, and fine grid. The number of nodes in the horizontal and vertical directions is adjusted according to the consistent principle to increase or decrease the number of grids. The calculation results in
Table 1 show that the calculation results are almost unchanged when the number of grids exceeds the medium grid. Hence, the medium grid is selected in this study. After convergence, the fluctuation amplitude of the lift coefficient and drag coefficient is less than 1 × 10
−6, which is far less than the lift coefficient and drag coefficient themselves. This indicates that the unphysical oscillation caused by numerical dispersion can be ignored.
Figure 3 shows the pressure coefficient of the airfoil. The calculation results are in good agreement with the experimental results.
This study involves unsteady calculations, so the unsteady calculation results need to be verified. Some scholars have studied the unsteady calculation of CFD [
29,
30,
31]. In this paper, the unsteady numerical simulation of an NACA0015 airfoil oscillating in the pitching direction is carried out and compared with the experiment results [
32]. The calculated parameters are consistent with those in the experiment. The incoming Mach number is 0.29, the Reynolds number is 1.95 × 10
6, the airfoil angle of attack is 4°, the oscillation amplitude is 4.2°, and the oscillation frequency is 10 Hz. The calculation results are shown in
Figure 4, and the airfoil lift coefficient is in good agreement with the experimental results.
There are numerical calculations of the airfoil at high angles of attack in this study. The airfoil will undergo flow separation at high angles of attack. Therefore, it is necessary to verify the accuracy of the numerical results at high angles of attack. The NASA experimental data [
33] are selected for numerical verification, and the results are also compared with the numerical results of Qu [
10]. The airfoil is NACA 4412, the Reynolds number is 6 × 10
6, and the free stream velocity is 88 m/s. The calculation results of the shear stress transport (SST) for two turbulence models
k-e and
k-ω are shown in
Figure 5.
Since a negative angle of attack is not involved in this study, the calculation of a negative angle of attack is not considered. It can be seen from
Figure 5 that the results of the two turbulence models are both in good agreement with the experimental results, as the angle of attack is less than 12°. As the angle of attack is greater than 12°, the calculation results of the
k-e turbulence model are closer to the experimental results than the
k-ω SST and also better than Qu, which is the reason for the selection of the
k-e turbulence model. However, after the stall angle of attack of 15°, the calculated results do not agree well with the experimental results. At a high angle of attack, especially for angles greater than the stall angle of attack, the airfoil is faced with flow separation, and the separation region is often accompanied by a shedding vortex. Therefore, the flow field around the airfoil is more complex than that at a low angle of attack. Flow separation occurs when the airfoil angle of attack is essentially a complicated turbulent flow. The turbulence model in RANS is an empirical model that is established on simplified assumptions. Hence, the RANS cannot fully simulate the details of the real flow [
34]. It is fair to say that the simulation of separated flow at a high angle of attack is still a challenge for CFD.