New Design Concept for Bridge Restrainers with Rubber Cushion Considering Dynamic Action: A Preliminary Study
Abstract
:1. Introduction
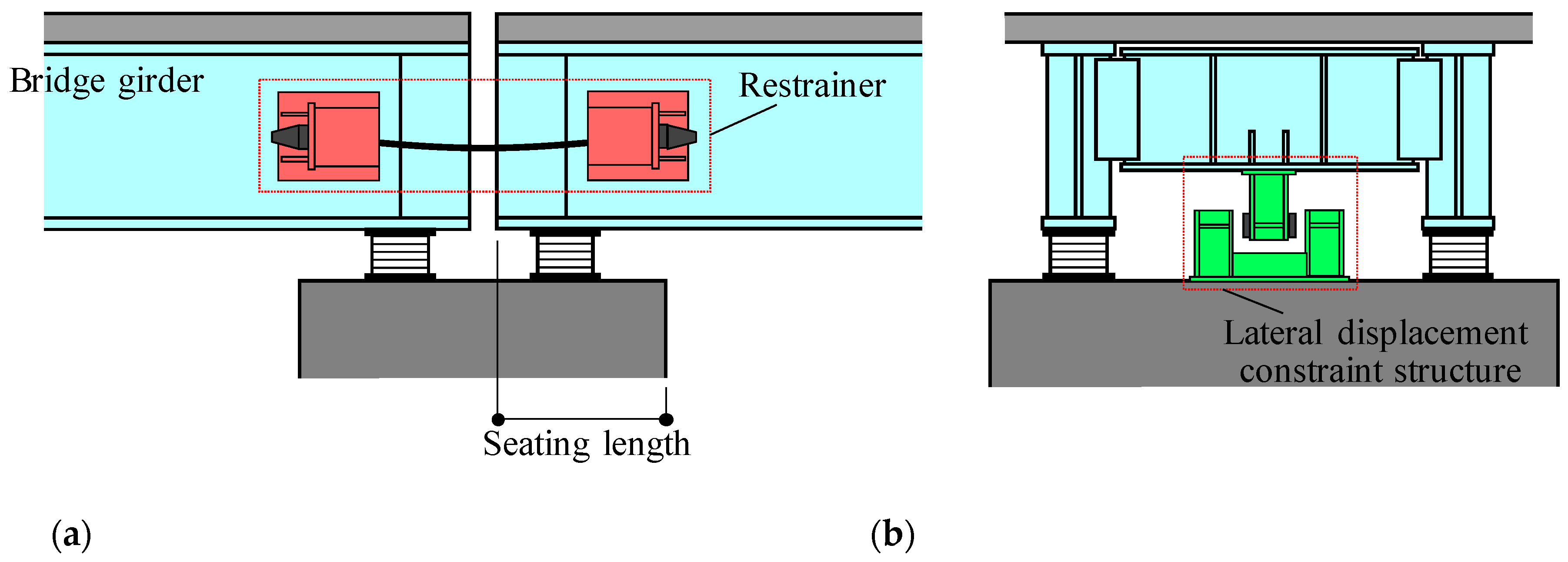
2. Discussion on the Working Conditions of a Bridge Restrainer
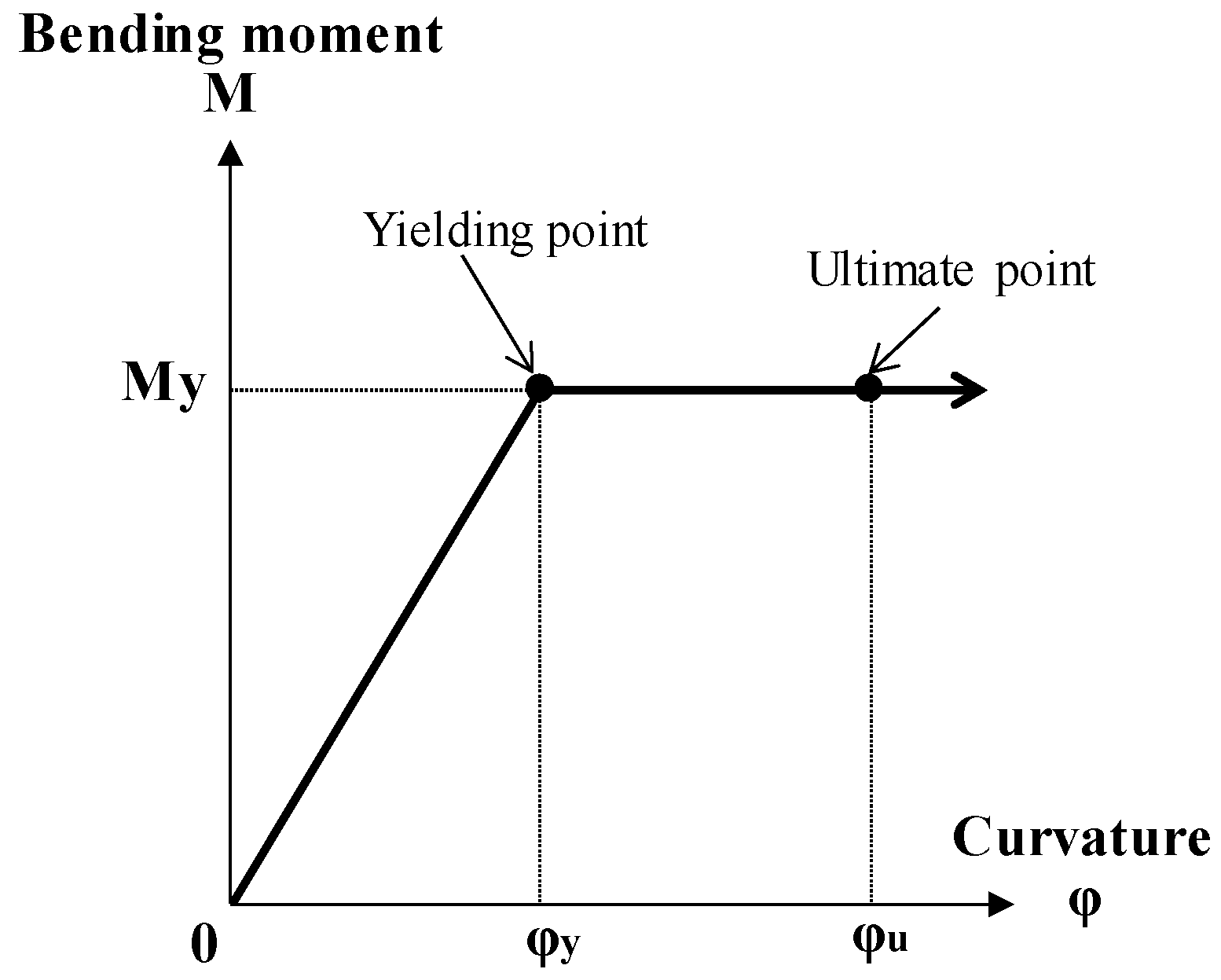
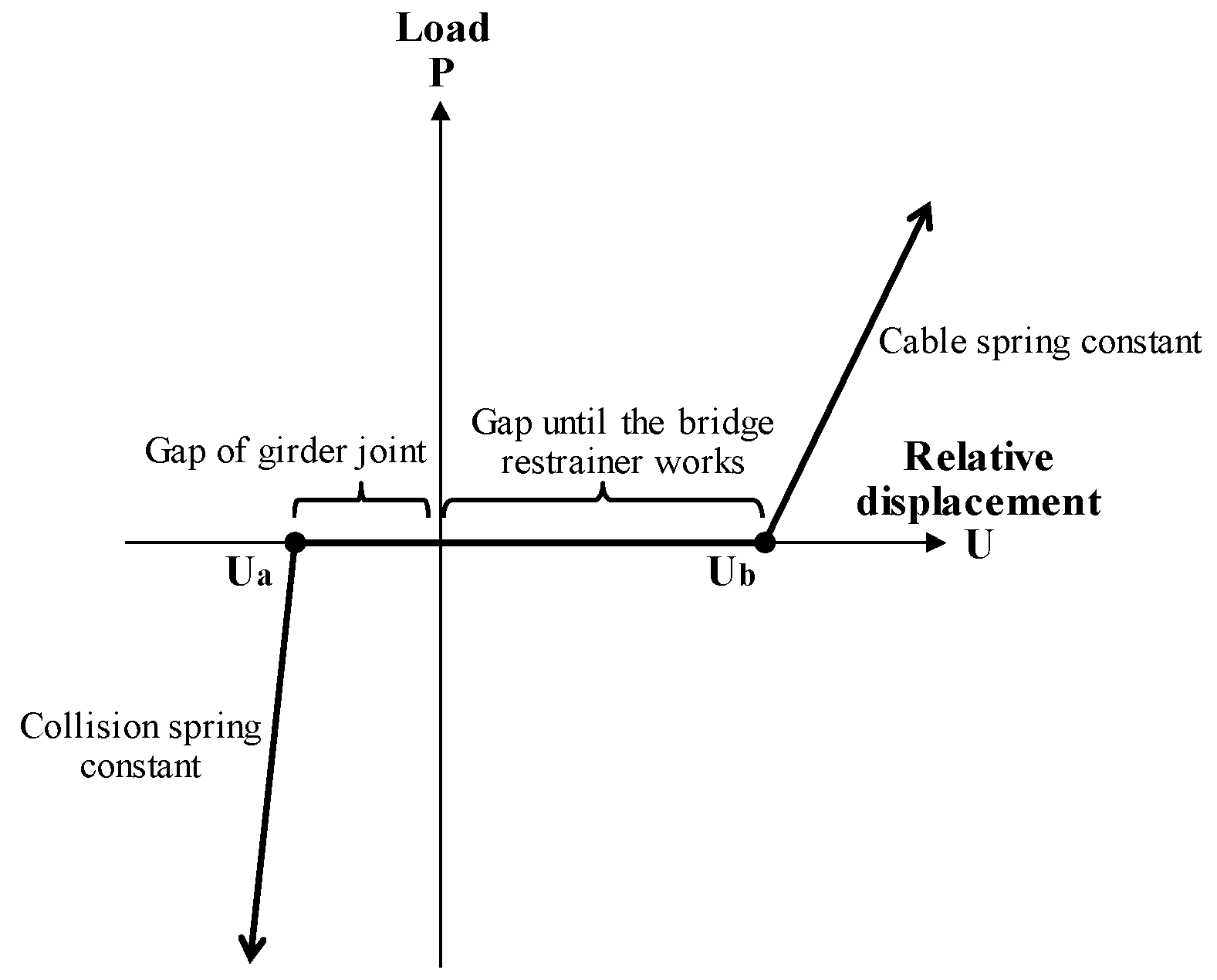
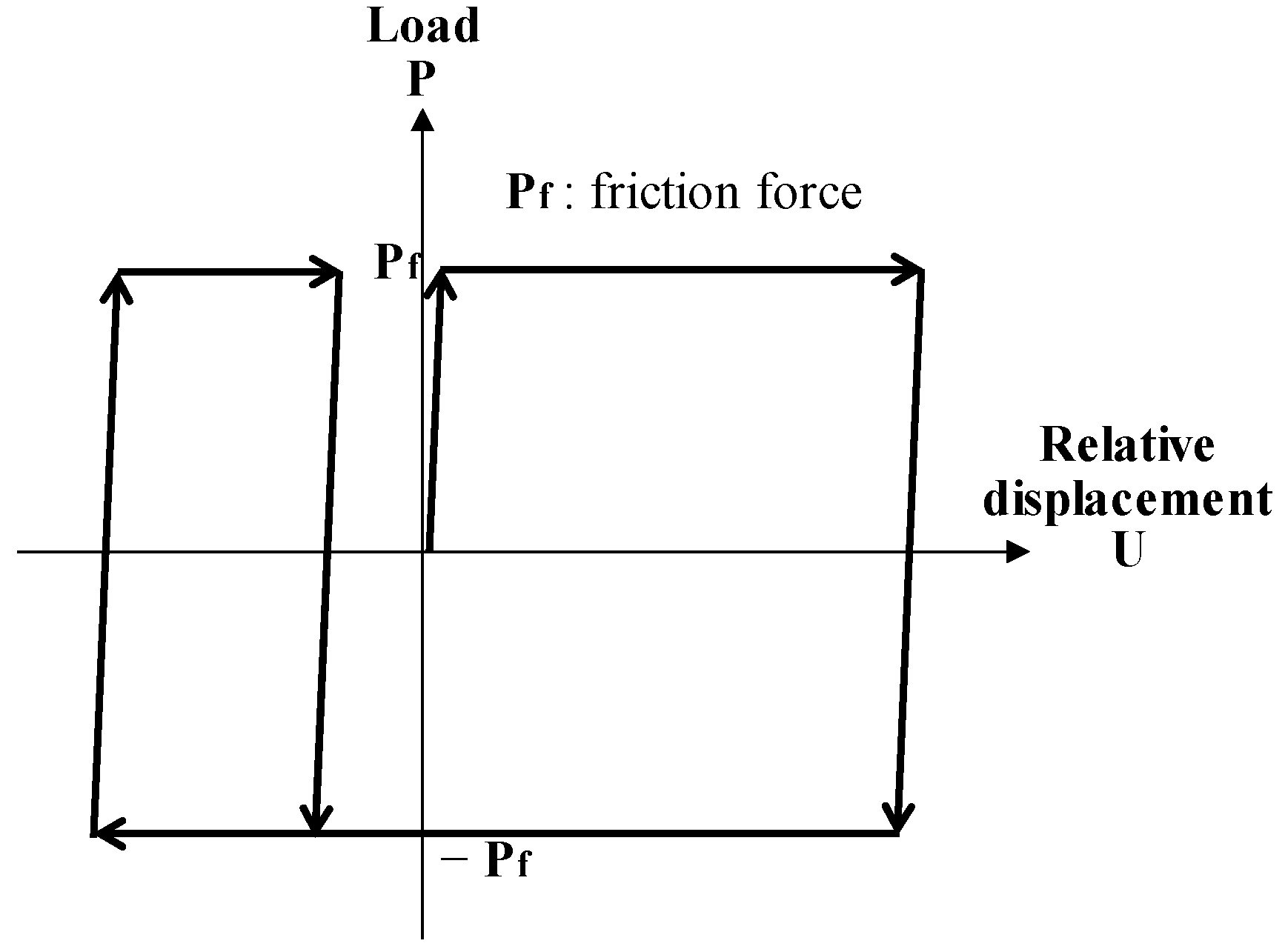
2.1. Outline of Dynamic Response Analysis
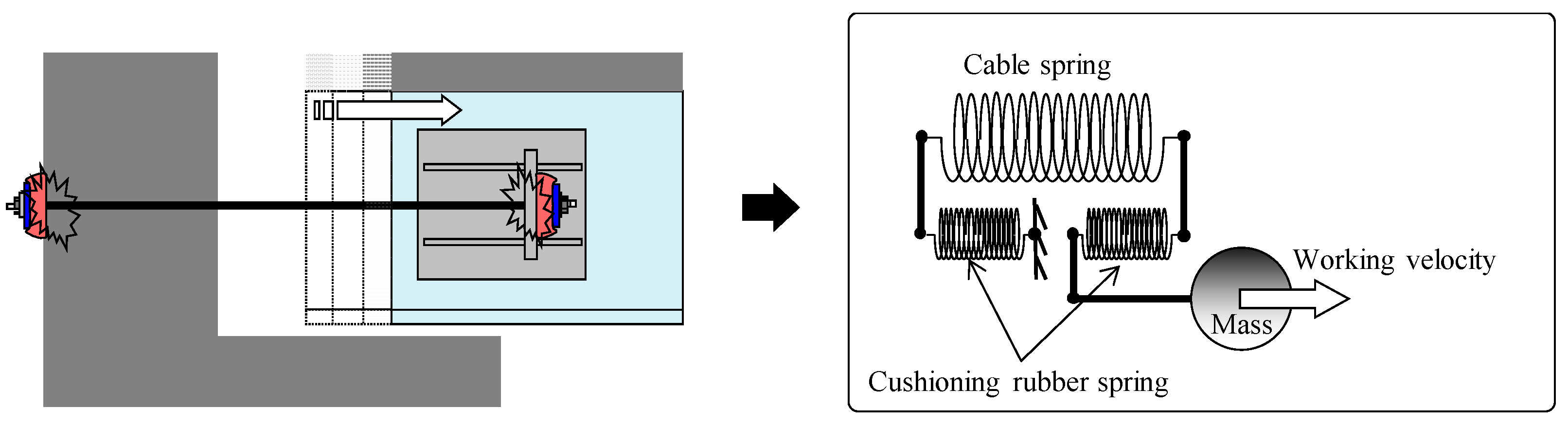
2.1.1. Analysis Model
2.1.2. Analysis Parameter
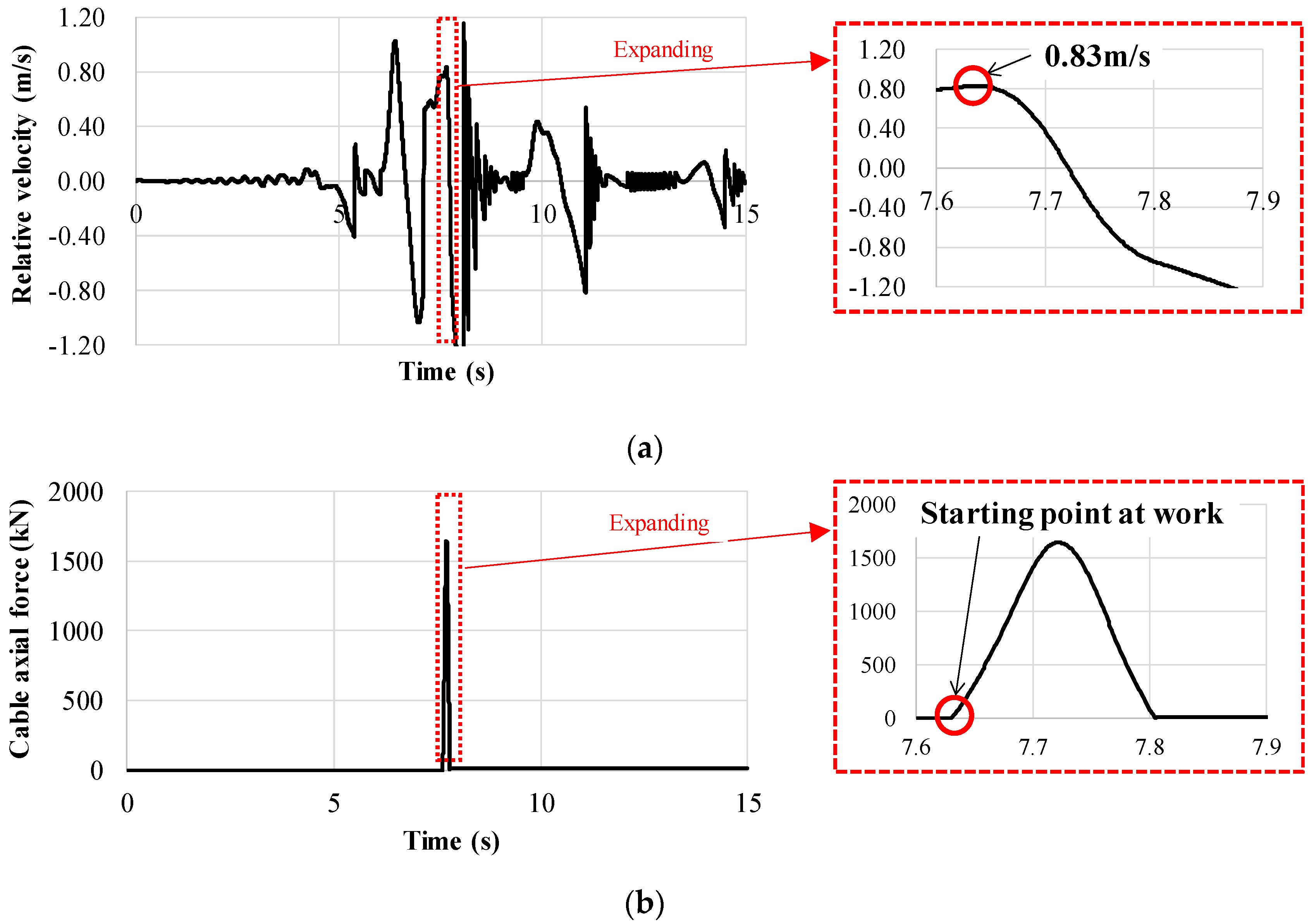
2.2. Results and Discussion
3. Suggestion on New Design Concept for Bridge Restrainers
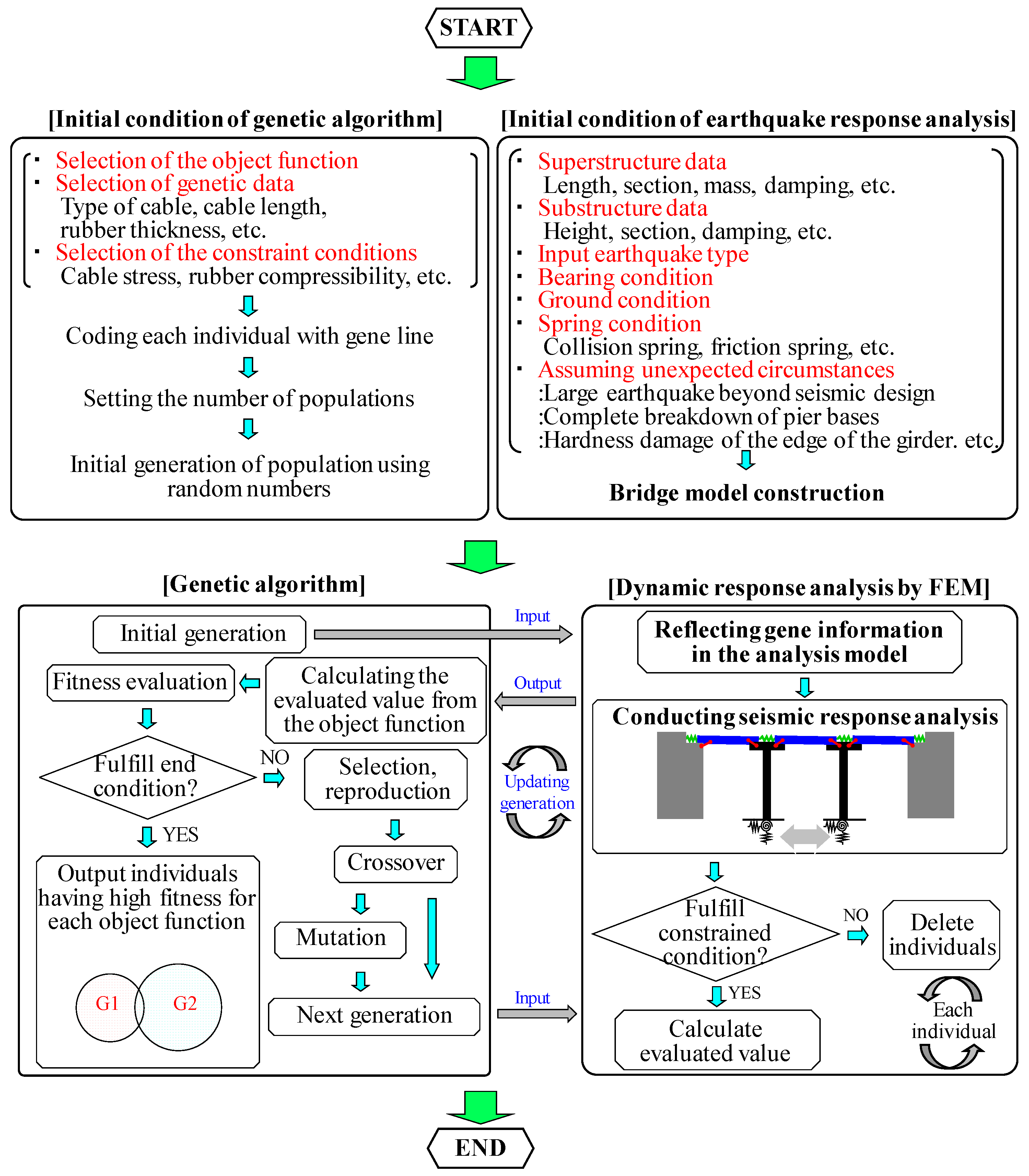
3.1. Basics of SGA
3.2. Outline of New Design Concept by Using Coupled Analysis
4. Trial Design by Using the Proposed Concept
4.1. Design Condition and Analysis Model
4.2. Analysis Cases
4.3. Results and Discussion
4.4. Verification of the Optimized Solution
5. Conclusions
- In the existing Japanese design of bridge restrainers, the design load is determined only by using the uniform dead reaction load of the bridge, regardless of the setting location. However, in view of the dynamic influence of a massive earthquake, there is the potential for a large cable reaction force that exceeds the design load, and the actual load changes significantly in each setting position. Therefore, it is believed that the design of the bridge restrainer plays a central role in the fail-safe system.
- This paper proposes a reasonable design method for bridge restrainers that employ seismic response analysis to determine the design load and the SGA for obtaining the optimal construction member. The results of a trial design using the proposed method indicate that the combination of members selected as the quasi-optimal solution differed according to the assumed unexpected situation and the applicable object function. Therefore, the designer should thoroughly examine the assumed condition of the target bridge.
- The validity of the quasi-optimal solution obtained from the results of the trial design was proven because the obtained quasi-optimal solution agreed with the optimal solution obtained by a round-robin simulation employing the single-mass model.
Author Contributions
Funding
Conflicts of Interest
References
- Japan Road Association. Specifications for Highway Bridges, 1996; Volume V.
- Japan Road Association. Specifications for Highway Bridges, 2012; Volume V.
- Wright, T.; DesRoches, R.; Padgett, J.E. Bridge seismic retrofitting practices in the central and southeastern United States. J. Bridge Eng. 2011, 16, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Sakai, J.; Unjoh, S.; Hoshikuma, J.I. Analytical Investigation on ME Chanism of Deck Unseating under Extreme Earthquake and Effects of Unseating Prevention Devices on Seis MIC Behavior of Bridges. JSCSE 2011, 67, 55–71. [Google Scholar] [CrossRef]
- Moriyama, T.; Yoda, T. Experimental study on the effect of pounding between the adjacent girders on the falling girders. Doboku Gakkai Ronbunshu 2000, 2000, 223–232. [Google Scholar] [CrossRef] [Green Version]
- Nakao, H.; Izuno, K. Design and installation method of unseating prevention cable with shock absorber. J. JSCE 2015, 28, 64. [Google Scholar]
- Padgett, J.E.; DesRoches, R. Three-dimensional nonlinear seismic performance evaluation of retrofit measures for typical steel girder bridges. Eng. Struct. 2008, 30, 1869–1878. [Google Scholar] [CrossRef]
- Julian, F.D.R.; Hayashikawa, T.; Obata, T. Seismic performance of isolated curved steel viaducts equipped with deck unseating prevention cable restrainers. J. Constr. Steel Res. 2007, 63, 237–253. [Google Scholar] [CrossRef]
- Won, J.H.; Mha, H.S.; Cho, K.I.; Kim, S.H. Effects of the restrainer upon bridge motions under seismic excitations. Eng. Struct. 2008, 30, 3532–3544. [Google Scholar] [CrossRef]
- DesRoches, R.; Fenves, G.L. Design of seismic cable hinge restrainers for bridges. J. Struct. Eng. 2000, 126, 500–509. [Google Scholar] [CrossRef]
- Yuki, Y.; Tamai, H.; Wada, N.; Sonoda, Y.; Kasugai, T. Fundamental Study on the Shock Cushioning Characteristics of a Novel pin-Fixed Aseismatic Connector for Bridges. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2014; pp. 637–642. [Google Scholar]
- Tamai, H.; Uno, M.; Yuki, Y.; Sonoda, Y.; Kasugai, T. A Study on the Effectiveness of Energy Absorbing Rubber in Pin-Fixed Cable Restrainer of a Bridge. Int. J. Prot. Struct. 2014, 5, 219–238. [Google Scholar] [CrossRef]
- Yuki, Y.; Tamai, H.; Wada, N.; Sonoda, Y.; Kasugai, T. Fundamental experiment of shape and confining effect on rubber pieces’ cushioning characteristics. Struct. Eng. 2015, 61A, 313–321. [Google Scholar]
- Yuki, Y.; Tamai, H.; Wada, N.; Sonoda, Y.; Kasugai, T. Analytical Study for Evaluation of Dynamic Response of Rubber Cushion in Bridge Restrainers. Struct. Eng. 2016, 62A, 341–350. [Google Scholar]
- Yuki, Y.; Tamai, H. Estimation of maximum load on bridge restrainers by weight-drop tests with large size weight. Steel Constr. Eng. 2016, 23, 105–115. [Google Scholar]
- Whitley, D.A. Genetic Algorithm Tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Arimura, M.; Tamura, T. Genetic algorithms in the infrastructure planning: Optimization and adaptive learning. Proc. JSCE D 2015, 62, 505–518. [Google Scholar] [CrossRef] [Green Version]
- Katsuki, S.; Nagaya, H.; Satoh, H.; Suwa, M. An Application of Genetic Algorithm Using Sub-Objective Optimal Elite Operation for Interactive Structural Optimal Design. Doboku Gakkai Ronbunshu 2001, 2001, 143–161. [Google Scholar] [CrossRef] [Green Version]
- Katsuki, S.; Fukawa, G.; Nagadori, N. An application of genetic algorithm for interactive optimal design method of truss structure. Struct. Saf. Reliab. Icossar’01 2001, 154. [Google Scholar]
- Tei, K.; Nakamura, H.; Miyamoto, A.; Fujiwara, M. Application Of Genetic Algorithm-Based Relay Search Method For Structure Design-Strengthening Problem. Doboku Gakkai Ronbunshu 1999, 1999, 149–164. [Google Scholar] [CrossRef] [Green Version]
- Emoto, H.; Nakamura, H.; Miyamoto, A. Development of impact resistance design support system for RC slabs by genetic algorithms. J. Struct. Eng. A 1999, 45, 453–464. [Google Scholar]
- ARK Information Systems Inc. TDAP III (Time Domain 3-Dimensional Dynamic Analysis Program), Version 3.01 Theoretical Manual; ARK Information Systems Inc.: Tokyo, Japan, 2008. [Google Scholar]
- Sadjadi, F. Comparison of fitness scaling functions in genetic algorithms with applications to optical processing. In Optical Information Systems II; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; pp. 356–364. [Google Scholar]
- Lin, W.Y.; Lee, W.Y.; Hong, T.P. Adapting crossover and mutation rates in genetic algorithms. J. Inf. Sci. Eng. 2003, 19, 889–903. [Google Scholar]



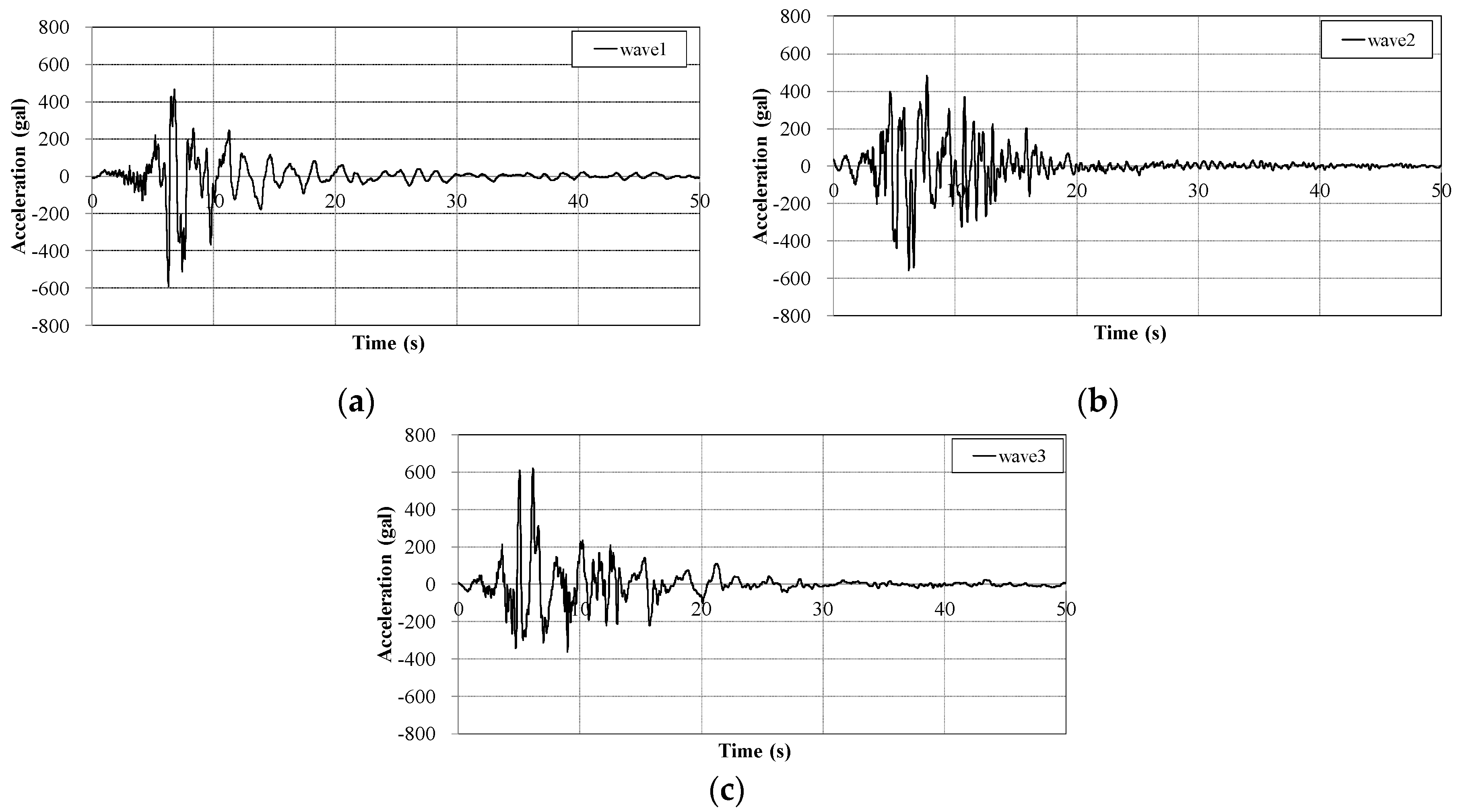
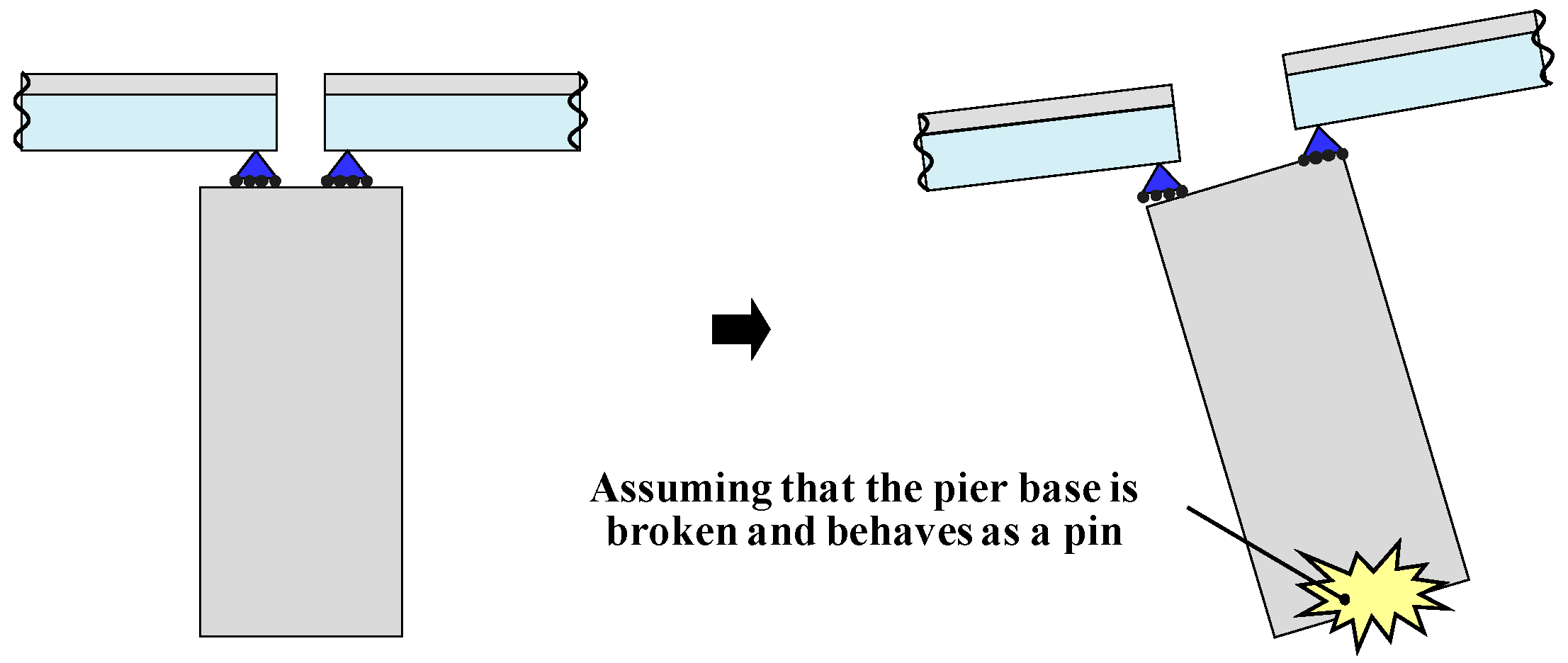
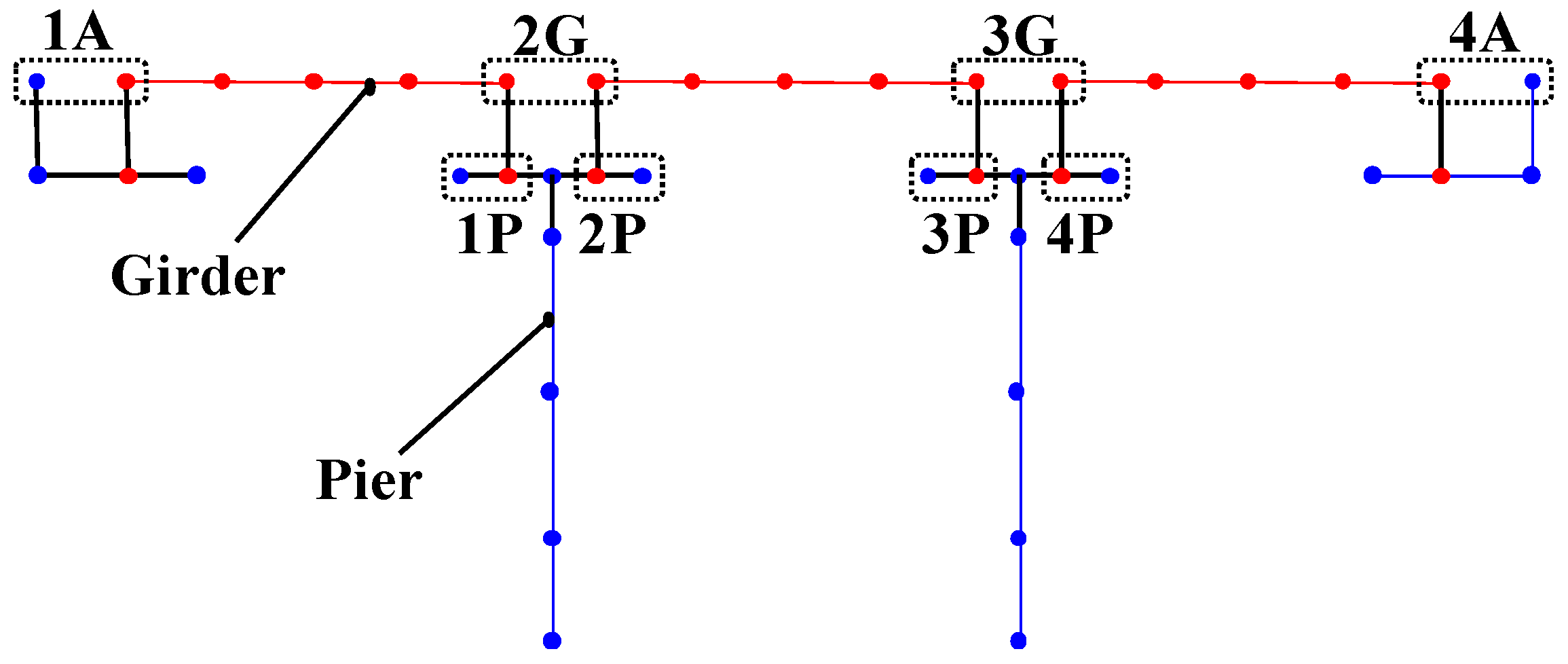


| Part | Cross-Section A (m2) | Sectional Secondary Moment Iy (m4) | Weight (kN) | Elastic Coefficient (N/mm2) | Elastic Shear Modulus (N/mm2) | |
|---|---|---|---|---|---|---|
| Girder | 0.60 | 0.121 | 4600 | 200,000 | 77,000 | |
| Pier | Upper | 8.55 | 2.005 | 2000 | 26,500 | 11,500 |
| Middle | 8.55 | 2.420 | ||||
| Low | 8.55 | 2.977 | ||||
| Rigid Member | 1000 | 1000 | - | - | - | |
| Ground | Girder-Collision Spring Constant (kN/m) | Friction Force Pf (kN) | |
|---|---|---|---|
| Horizontal-Direction Spring Constant (kN/m) | Rotation-Direction Spring Constant (kN·m/rad) | ||
| 3,300,000 | 75,000,000 | 13,714,286 | 115 |
| Superstructure | Substructure | Ground | |
|---|---|---|---|
| Steel Girder (Linear) | Pier (Linear) | Pier (Non-linear) | |
| 0.02 | 0.05 | 0.02 | 0.02 |
| Cable Type | Yield Load (kN) | Length (m) | Spring Constant (kN/m) |
|---|---|---|---|
| 1000-kN-type | 888 | 2 | 277,400 |
| Girder Gap (mm) | Working Gap of the Bridge Restrainer (m) | Friction Coefficient between the Superstructure and Substructure | Pounding of Bridge Girders and Abutment |
|---|---|---|---|
| 80 | 0.75 × Se (=0.654) | 0.05 | Existence |
| No. | Bridge Type | Bridge Length (m) | Span Length L (m) | Minimum Seat Length Se = 0.7 + 0.005L (mm) | Actual Working Gap (mm) | Actual Design Displacement Coefficient Cf |
|---|---|---|---|---|---|---|
| 1 | Single-Span Non-compositional Box Girder | 68.5 | 69 | 1043 | 350 | 0.34 |
| 2 | Single-Span Box Girder with a Steel Plate Deck | 67.0 | 67 | 1035 | 300 | 0.29 |
| 3 | 2-Span Continuous Rationalized Plate Girder | 78.5 | 47 | 934 | 300 | 0.32 |
| 78.5 | 53 | 966 | 300 | 0.31 | ||
| 4 | 2-Span Continuous Box Girder | 71.0 | 41 | 905 | 300 | 0.33 |
| 71.0 | 30 | 850 | 300 | 0.35 | ||
| 5 | 6-Span Continuous Rationalized Plate Girder | 222.0 | 36 | 881 | 301 | 0.34 |
| 6 | 3-Span Continuous Narrow Box Girder | 185.7 | 57 | 985 | 250 | 0.25 |
| 7 | 3-Span Continuous Rationalized Plate Girder | 128.2 | 32 | 861 | 200 | 0.23 |
| 8 | 8-Span Continuous Non-compositional Narrow Box Girder | 392.6 | 34 | 869 | 300 | 0.35 |
| 392.6 | 43 | 914 | 300 | 0.33 | ||
| 9 | 3-Span Continuous Non-compositional Plate Girder | 94.9 | 25 | 825 | 320 | 0.39 |
| 94.9 | 35 | 875 | 320 | 0.37 | ||
| 10 | 2-Span Continuous Plate Girder with Steel Plate Deck | 48.1 | 24 | 820 | 150 | 0.18 |
| 11 | 12-Span Continuous Rationalized Plate Girder | 534.5 | 43 | 916 | 300 | 0.33 |
| 534.5 | 46 | 931 | 300 | 0.32 | ||
| 12 | 2-Span Continuous Rationalized Plate Girder | 62.0 | 31 | 855 | 300 | 0.35 |
| 13 | Through-Type Trussed Langer Girder | 116.4 | 116 | 1282 | 300 | 0.23 |
| 14 | 2-Span Continuous Non-compositional Box Girder | 64.4 | 41 | 906 | 300 | 0.33 |
| 64.4 | 23 | 816 | 300 | 0.37 | ||
| 15 | 3-Span Continuous Plate Girder | 154.0 | 54 | 970 | 190 | 0.20 |
| Case No. | Location of Bridge Restrainer Setting | Wave Type | Assuming the Breaking of the Pier Base? | Working Gap | Assuming the Breaking of the Fixed Support? | Upper Line: Maximum Load/Yield Load Lower Line: Maximum Displacement in Working Direction (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1A | 2G | 3G | 4A | 1P | 2P | 3P | 4P | ||||||
| 1 | Girder To Girder | 1 | No | 0.75 × Se | No | - 0.032 | - 0.101 | - 0.046 | - 0.087 | - 0.046 | - 0 | - 0.114 | - 0 |
| 2 | - 0.037 | - 0.092 | - 0.057 | - 0.096 | - 0.054 | - 0 | - 0.124 | - 0 | |||||
| 3 | - 0.044 | - 0.060 | - 0.015 | - 0.105 | - 0.056 | - 0 | - 0.084 | - 0 | |||||
| Girder to Pier | 1 | - 0.032 | - | - 0.087 | - 0.046 | - 0 | - 0.114 | - 0 | |||||
| 2 | - 0.037 | - 0.096 | - 0.054 | - 0 | - 0.124 | - 0 | |||||||
| 3 | - 0.044 | - 0.105 | - 0.056 | - 0 | - 0.084 | - 0 | |||||||
| 2 | Girder to Girder | 1 | No | 0.75 × Se | Yes | - 0.260 | - 0.068 | - 0.068 | - 0.252 | - 0.086 | - 0.174 | - 0.165 | - 0.087 |
| 2 | - 0.262 | - 0.067 | - 0.009 | - 0.259 | - 0.089 | - 0.182 | - 0.174 | - 0.091 | |||||
| 3 | - 0.255 | - 0.072 | - 0.002 | - 0.280 | - 0.093 | - 0.169 | - 0.186 | - 0.087 | |||||
| Girder to Pier | 1 | - 0.260 | - | - 0.252 | - 0.086 | - 0.174 | - 0.165 | - 0.087 | |||||
| 2 | - 0.262 | - 0.259 | - 0.089 | - 0.182 | - 0.174 | - 0.091 | |||||||
| 3 | - 0.255 | - 0.280 | - 0.093 | - 0.169 | - 0.186 | - 0.087 | |||||||
| 3 | Girder to Girder | 1 | Yes | 0.75 × Se | Yes | - 0.263 | - 0.112 | - 0.074 | - 0.250 | - 0.620 | - 0.381 | - 0.886 | - 0.337 |
| 2 | - 0.255 | - 0.063 | - 0.007 | - 0.269 | - 0.646 | - 0.201 | - 0.727 | - 0.193 | |||||
| 3 | - 0.276 | - 0.038 | - 0.156 | - 0.244 | - 0.200 | - 0.760 | - 0.199 | - 0.598 | |||||
| Girder to Pier | 1 | - 0.263 | - | - 0.250 | - 0.294 | - 0.381 | - 0.375 | - 0.337 | |||||
| 2 | - 0.255 | - 0.269 | - 0.236 | - 0.201 | - 0.255 | - 0.193 | |||||||
| 3 | - 0.262 | - 0.244 | 0.420.690 | - 0.619 | 0.140.667 | - 0.587 | |||||||
| 4 | Girder to Girder | 1 | No | 0.3 × Se | Yes | - 0.256 | - 0.076 | - 0.066 | - 0.253 | - 0.088 | - 0.174 | - 0.165 | - 0.088 |
| 2 | 0.25 0.266 | - 0.065 | - 0.092 | - 0.255 | - 0.089 | - 0.183 | - 0.171 | - 0.093 | |||||
| 3 | - 0.255 | - 0.072 | - 0.022 | 0.24 0.266 | - 0.090 | - 0.171 | - 0.179 | - 0.086 | |||||
| Girder to Pier | 1 | - 0.256 | - | - 0.253 | - 0.088 | - 0.174 | - 0.165 | - 0.088 | |||||
| 2 | 0.25 0.266 | - 0.255 | - 0.089 | - 0.183 | - 0.171 | - 0.093 | |||||||
| 3 | - 0.255 | 0.24 0.266 | - 0.090 | - 0.171 | - 0.179 | - 0.086 | |||||||
| 5 | Girder to Girder | 1 | Yes | 0.3 × Se | Yes | 0.06 0.263 | - 0.034 | - 0.055 | - 0.254 | - 0.670 | - 0.338 | - 0.642 | - 0.304 |
| 2 | - 0.261 | - 0.060 | - 0.035 | 0.42 0.269 | - 0.638 | - 0.225 | - 0.764 | - 0.163 | |||||
| 3 | 0.10 0.264 | - 0.041 | - 0.083 | - 0.248 | - 0.138 | - 0.815 | - 0.210 | - 0.691 | |||||
| Girder to Pier | 1 | 0.68 0.273 | - | - 0.255 | 1.5 0.286 | 0.50 0.270 | 1.27 0.282 | 0.36 0.268 | |||||
| 2 | - 0.261 | - 0.252 | 1.08 0.279 | 1.13 0.280 | 1.38 0.284 | 0.87 0.276 | |||||||
| 3 | 0.31 0.267 | - 0.251 | 0.86 0.276 | 1.08 0.279 | 1.06 0.279 | 1.33 0.283 | |||||||
| Yellow cells indicate the collapse of a bridge. | |||||||||||||
| Blue cells show working bridge restrainers. | |||||||||||||
| N. | Red values indicate a load that exceeds the design load. | ||||||||||||
| Cable | Strength Type | Code | Rubber Cushion | Cross-Section Area (mm × mm) | Code |
| 180 kN | 0000 | 100 × 100 | 0000 | ||
| 260 kN | 0001 | 150 × 150 | 0001 | ||
| 390 kN | 0010 | 200 × 200 | 0010 | ||
| 570 kN | 0011 | 250 × 250 | 0011 | ||
| 730 kN | 0100 | 300 × 300 | 0100 | ||
| 1000 kN | 0101 | 350 × 350 | 0101 | ||
| 1300 kN | 0110 | 400 × 400 | 0110 | ||
| 1500 kN | 0111 | 450 × 450 | 0111 | ||
| 1800 kN | 1000 | 500 × 500 | 1000 | ||
| 1900 kN | 1001 | 550 × 550 | 1001 | ||
| 2300 kN | 1010 | Thickness (mm) | Code | ||
| 2700 kN | 1011 | 20 | 00 | ||
| 3200 kN | 1100 | 30 | 01 | ||
| 3400 kN | 1101 | 40 | 10 | ||
| 4000 kN | 1110 | 50 | 11 | ||
| 4600 kN | 1111 | Hardness (°) | Code | ||
| 45 | 00 | ||||
| 55 | 01 | ||||
| 65 | 10 |
| Cable | Rubber Cushion | ||
| Type (Including Yield Strength and Cross-Sectional Area) | Thickness | Cross-Sectional Area | Hardness |
| 0 0 0 0 | 0 0 | 0 0 0 0 | 0 0 |
| Stress Range | Weight Coefficient, ω |
|---|---|
| 0.0 ≦ σ/σy < 0.1 | 0.1 |
| 0.1 ≦ σ/σy < 0.3 | 0.3 |
| 0.3 ≦ σ/σy < 0.5 | 0.5 |
| 0.5 ≦ σ/σy < 0.7 | 0.7 |
| 0.7 ≦ σ/σy < 0.9 | 0.9 |
| 0.9 ≤ σ/σy < 1.0 | 1.0 |
| Characteristics of Spring Element | |||
| Basic Characteristics of Spring Element in Each Thickness(Load-Displacement Relationship) | |||
| Coefficient about Hardeness | Hardness 45 (degree) | Hardness 55 (degree) | Hardness 65 (degree) |
| 0.502 | 1.000 | 1.410 | |
| Coefficient about Cross-Section Area | |||
| Case | Input Earthquake Wave | Assumued Situation | Object Function | ||
|---|---|---|---|---|---|
| Fixed-Support Condition | Pier Base Condition | Pounding of Bridge Girders | |||
| Case 1 | wave1 | Breaking | Breaking | Exists | G1, G2 |
| Case 2 | Good | Ignore | G2 | ||
| Rank | Cable | X-Group | Cable | Y-Group | Evaluated Value by G1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cushioning Rubber | Cushioning Rubber | ||||||||||
| Type | σ/σy | Hardness (º) | Thickness (mm) | Cross-Sectional Area (mm × mm) | Type | σ/σy | Hardness (º) | Thickness (mm) | Cross-Sectional Area (mm × mm) | ||
| 1 | - | - | - | - | - | 1800 kN | 0.92 | 45 | 50 | 400 × 400 | 0.033 |
| 2 | - | - | - | - | - | 1800 kN | 0.99 | 55 | 50 | 400 × 400 | 0.033 |
| 3 | - | - | - | - | - | 2700 kN | 0.86 | 55 | 50 | 500 × 500 | 0.030 |
| 4 | - | - | - | - | - | 1900 kN | 0.86 | 55 | 50 | 300 × 300 | 0.032 |
| 5 | - | - | - | - | - | 2700 kN | 0.93 | 55 | 40 | 500 × 500 | 0.037 |
| 6 | - | - | - | - | - | 2300 kN | 0.91 | 55 | 50 | 450 × 450 | 0.037 |
| 7 | - | - | - | - | - | 2300 kN | 0.99 | 55 | 50 | 500 × 500 | 0.038 |
| 8 | - | - | - | - | - | 2700 kN | 0.92 | 65 | 50 | 500 × 500 | 0.038 |
| 9 | - | - | - | - | - | 1800 kN | 0.96 | 45 | 50 | 450 × 450 | 0.038 |
| 10 | - | - | - | - | - | 1900 kN | 0.95 | 55 | 50 | 400 × 400 | 0.038 |
| Rank | Cable | X-Group | Cable | Y-Group | Evaluated Value by G2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cushioning Rubber | Cushioning Rubber | ||||||||||
| Type | σ/σy | Hardness (º) | Thickness (mm) | Cross-Sectional Area (mm × mm) | Type | σ/σy | Hardness (º) | Thickness (mm) | Cross-Sectional Area (mm × mm) | ||
| 1 | - | - | - | - | - | 1800 kN | 0.85 | 45 | 50 | 300 × 300 | 1316 |
| 2 | - | - | - | - | - | 1800 kN | 0.90 | 55 | 50 | 300 × 300 | 1389 |
| 3 | - | - | - | - | - | 1800 kN | 0.92 | 65 | 50 | 300 × 300 | 1419 |
| 4 | - | - | - | - | - | 1900 kN | 0.86 | 55 | 50 | 300 × 300 | 1425 |
| 5 | - | - | - | - | - | 1800 kN | 0.93 | 55 | 50 | 350 × 350 | 1444 |
| 6 | - | - | - | - | - | 1900 kN | 0.89 | 55 | 50 | 350 × 350 | 1474 |
| 7 | - | - | - | - | - | 2300 kN | 0.76 | 55 | 50 | 300 × 300 | 1474 |
| 8 | - | - | - | - | - | 2700 kN | 0.66 | 55 | 50 | 300 × 300 | 1356 |
| 9 | - | - | - | - | - | 1800 kN | 0.99 | 55 | 50 | 400 × 400 | 1359 |
| 10 | - | - | - | - | - | 3200 kN | 0.57 | 65 | 50 | 250 × 250 | 1544 |
| Rank | Cable | X-Group | Cable | Y-Group | Evaluated Value by G2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cushioning Rubber | Cushioning Rubber | ||||||||||
| Type | σ/σy | Hardness (º) | Thickness (mm) | Cross-Sectional Area (mm × mm) | Type | σ/σy | Hardness (º) | Thickness (mm) | Cross-Sectional Area (mm × mm) | ||
| 1 | 1900 kN | 0.72 | 65 | 50 | 300 × 300 | 2700 kN | 0.71 | 65 | 50 | 300 × 300 | 1662 |
| 2 | 2300 kN | 0.73 | 65 | 50 | 300 × 300 | 2700 kN | 0.66 | 65 | 50 | 300 × 300 | 1766 |
| 3 | 3200 kN | 0.68 | 65 | 50 | 300 × 300 | 2700 kN | 0.70 | 65 | 50 | 300 × 300 | 1903 |
| 4 | 2300 kN | 0.74 | 65 | 50 | 300 × 300 | 4600 kN | 0.58 | 65 | 50 | 300 × 300 | 1913 |
| 5 | 2700 kN | 0.68 | 65 | 50 | 300 × 300 | 2300 kN | 0.66 | 65 | 50 | 350 × 350 | 1955 |
| 6 | 3400 kN | 0.75 | 65 | 50 | 300 × 300 | 2700 kN | 0.66 | 65 | 50 | 350 × 350 | 1959 |
| 7 | 2700 kN | 0.60 | 65 | 50 | 300 × 300 | 2700 kN | 0.66 | 65 | 50 | 300 × 300 | 1988 |
| 8 | 4000 kN | 0.77 | 65 | 50 | 300 × 300 | 2700 kN | 0.71 | 65 | 50 | 300 × 300 | 2034 |
| 9 | 2700 kN | 0.78 | 65 | 50 | 300 × 300 | 2700 kN | 0.71 | 55 | 50 | 400 × 400 | 2055 |
| 10 | 4000 kN | 0.78 | 65 | 50 | 300 × 300 | 1900 kN | 0.65 | 65 | 50 | 250 × 250 | 2123 |
| Initial Velocity (m/s) | Cable Type | Rubber Cushion | ||
|---|---|---|---|---|
| Hardness (°) | Thickness (mm) | Cross-Sectional Area (mm × mm) | ||
| 0.80 | 1800 kN-type | 55 | 50 | 250 × 250 |
| 0.85 | 1900 kN-type | 55 | 50 | 250 × 250 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamai, H.; Lu, C.; Yuki, Y. New Design Concept for Bridge Restrainers with Rubber Cushion Considering Dynamic Action: A Preliminary Study. Appl. Sci. 2020, 10, 6847. https://doi.org/10.3390/app10196847
Tamai H, Lu C, Yuki Y. New Design Concept for Bridge Restrainers with Rubber Cushion Considering Dynamic Action: A Preliminary Study. Applied Sciences. 2020; 10(19):6847. https://doi.org/10.3390/app10196847
Chicago/Turabian StyleTamai, Hiroki, Chi Lu, and Yoichi Yuki. 2020. "New Design Concept for Bridge Restrainers with Rubber Cushion Considering Dynamic Action: A Preliminary Study" Applied Sciences 10, no. 19: 6847. https://doi.org/10.3390/app10196847
APA StyleTamai, H., Lu, C., & Yuki, Y. (2020). New Design Concept for Bridge Restrainers with Rubber Cushion Considering Dynamic Action: A Preliminary Study. Applied Sciences, 10(19), 6847. https://doi.org/10.3390/app10196847





