Effect of Parameters on Vapor Generation in Ship-to-Ship Liquefied Natural Gas Bunkering
Abstract
:1. Introduction
2. Description of Liquefied Natural Gas (LNG) Bunkering System
3. Simulation and Input Preparation
4. Results and Discussions
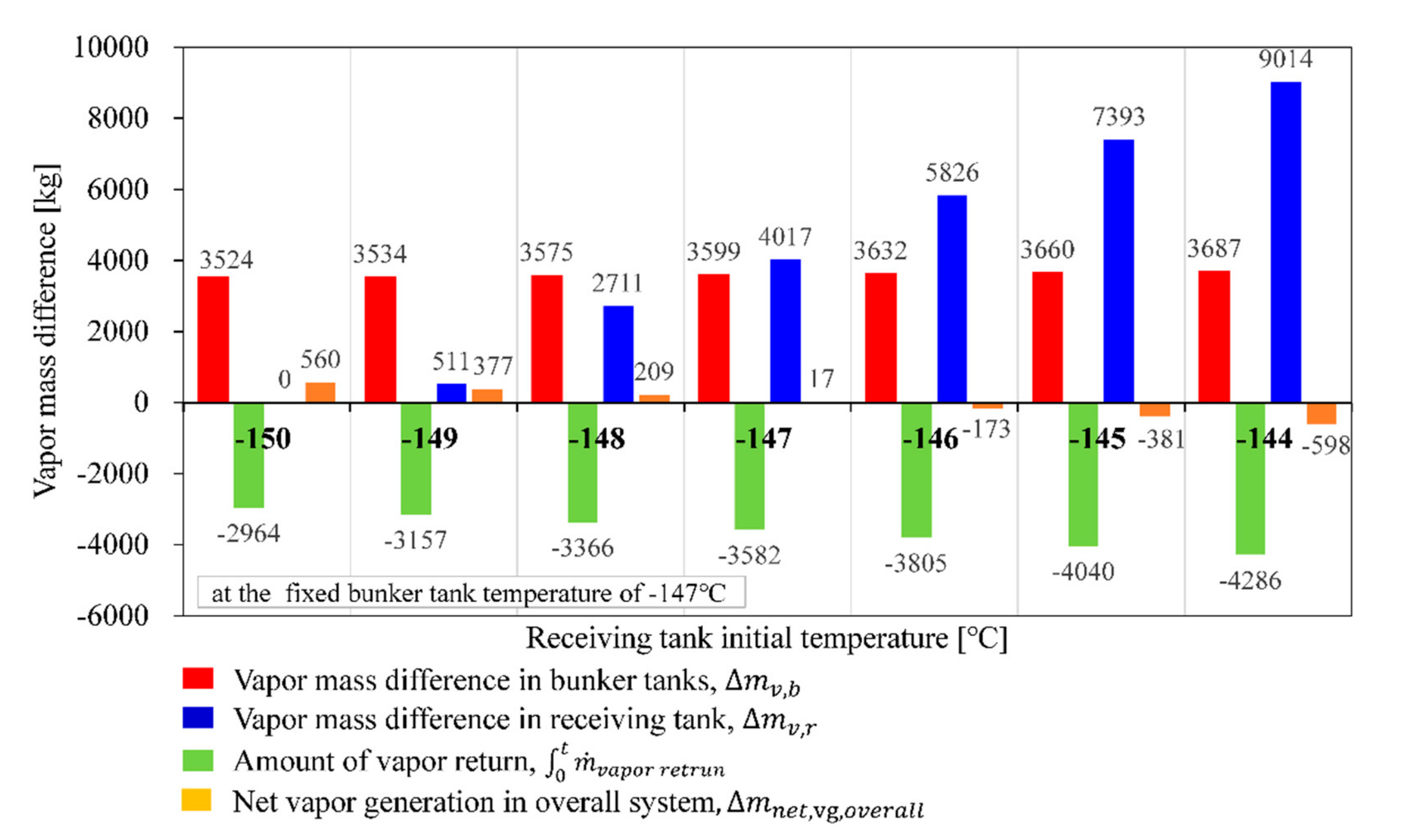
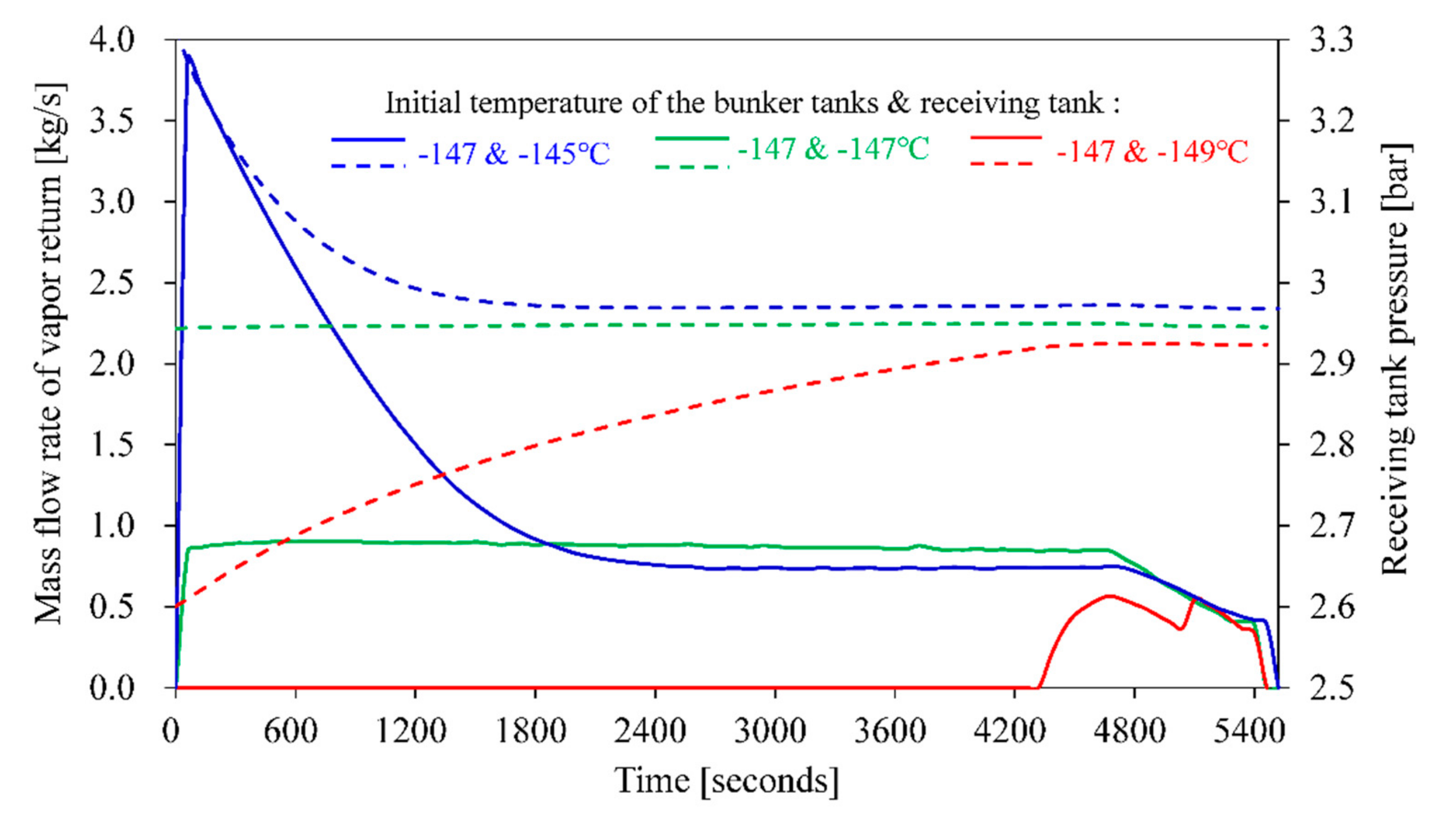
4.1. Effect of Initial Temperature of Receiving Tank
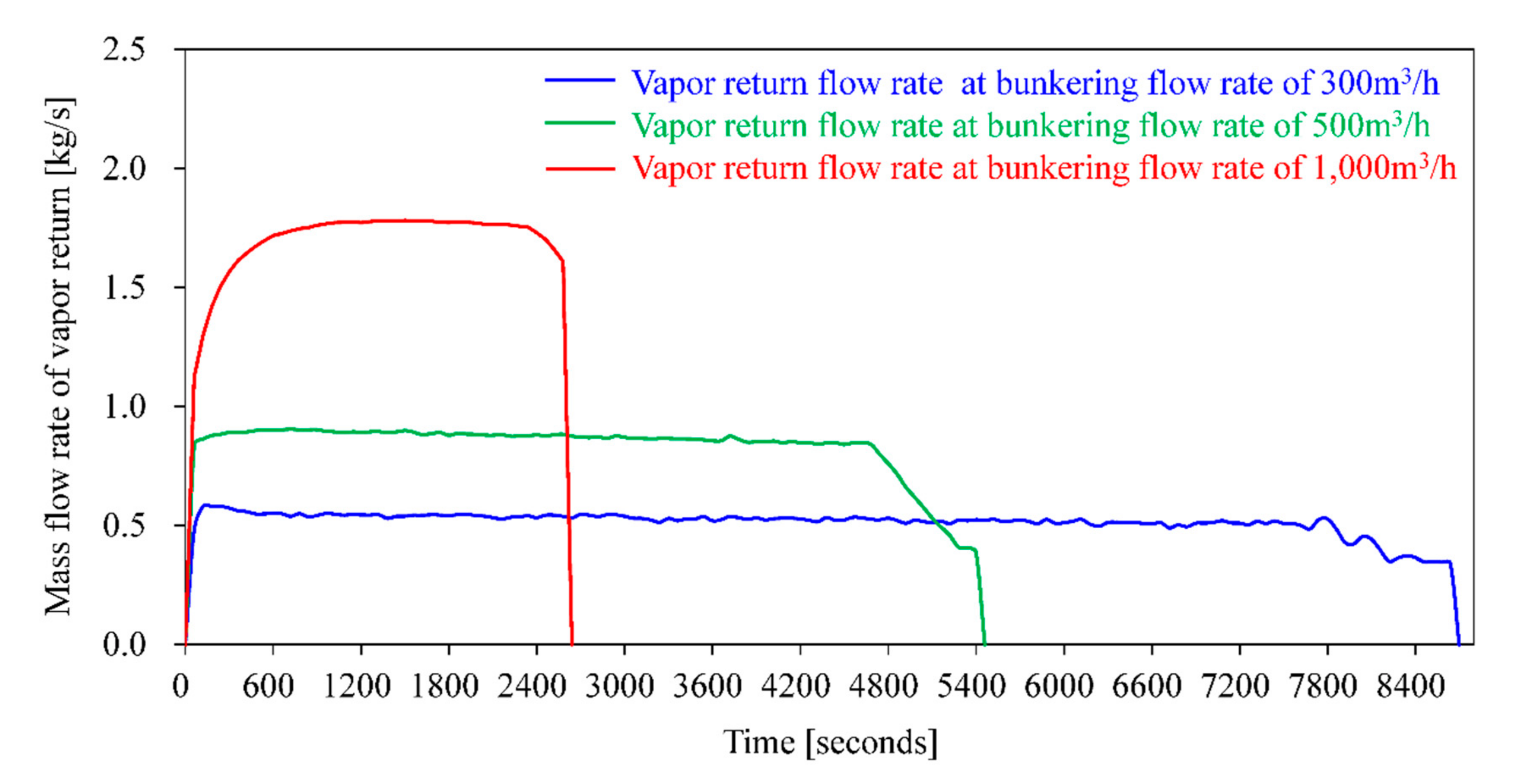
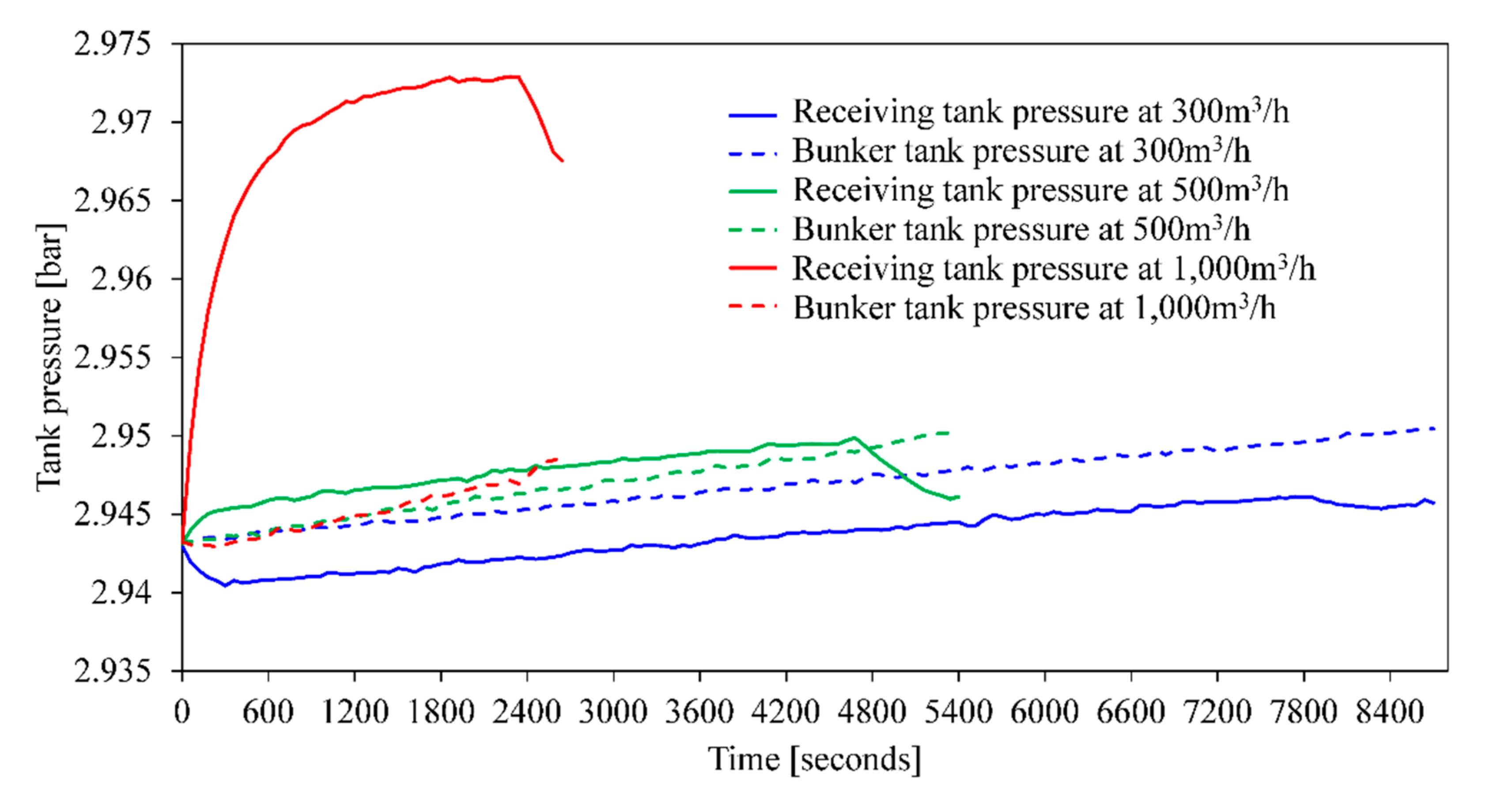
4.2. Effect of Bunkering Flow Rate
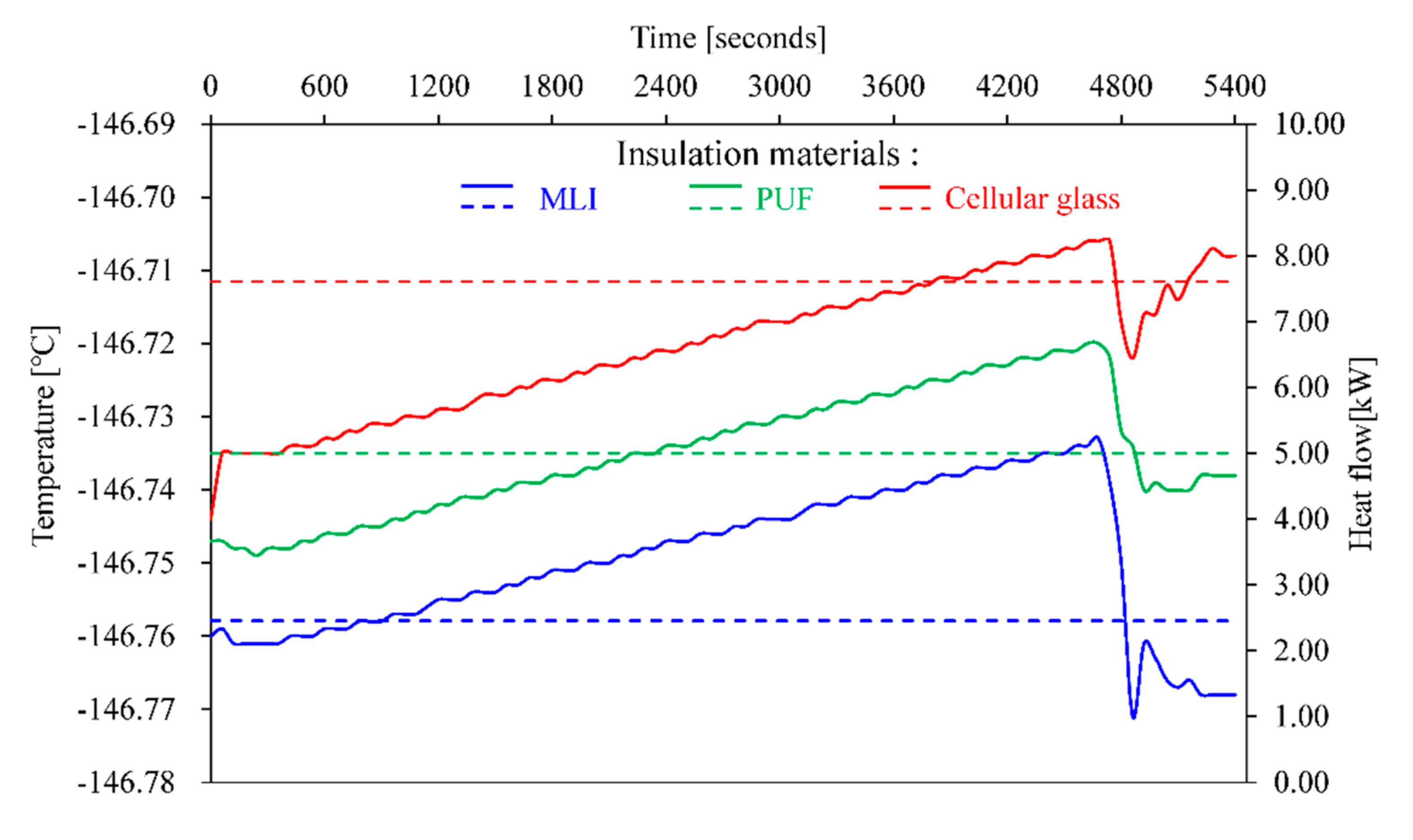
4.3. Effects of Insulation Performance of LNG Bunkering Lines
4.4. Effects of LNG Composition
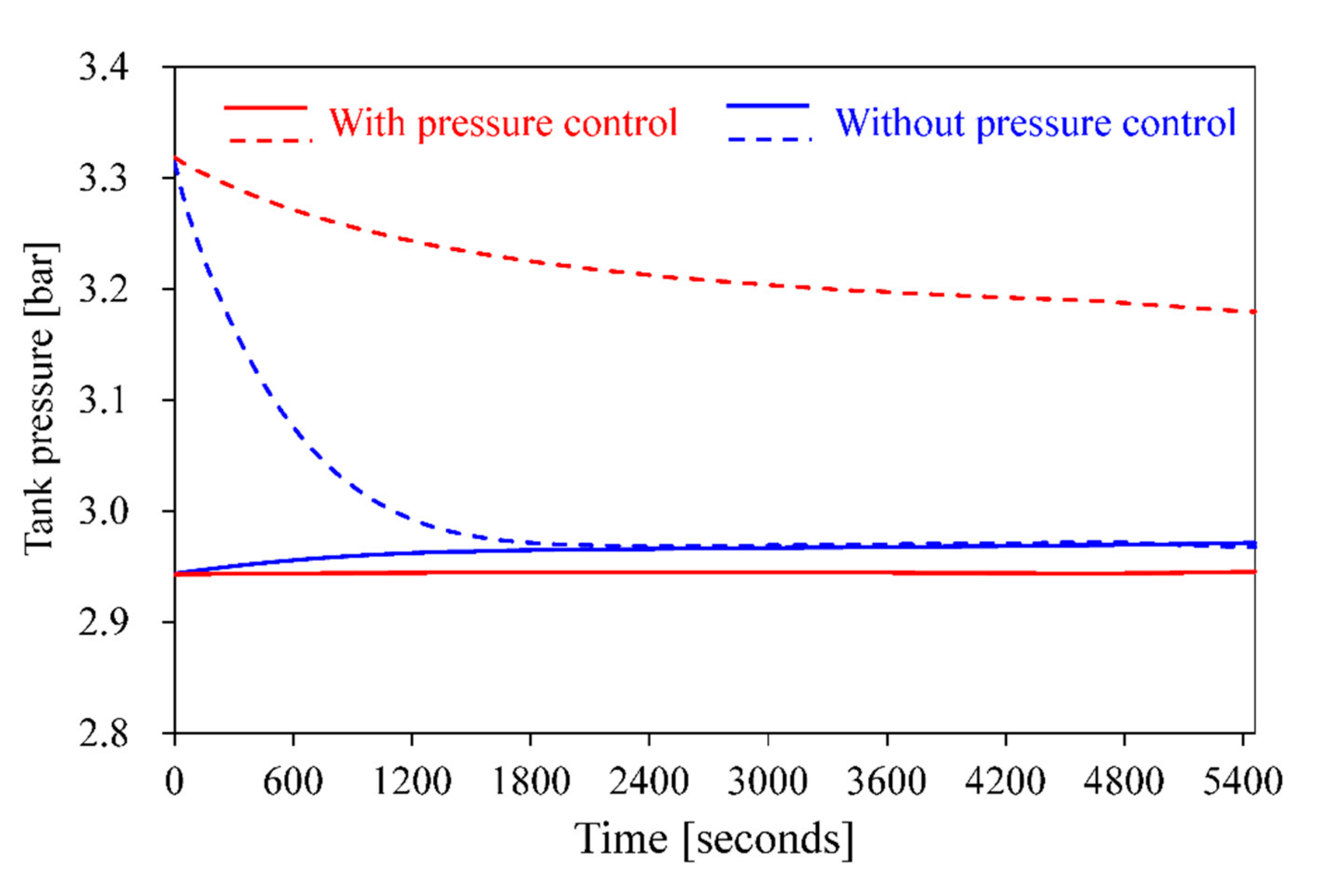
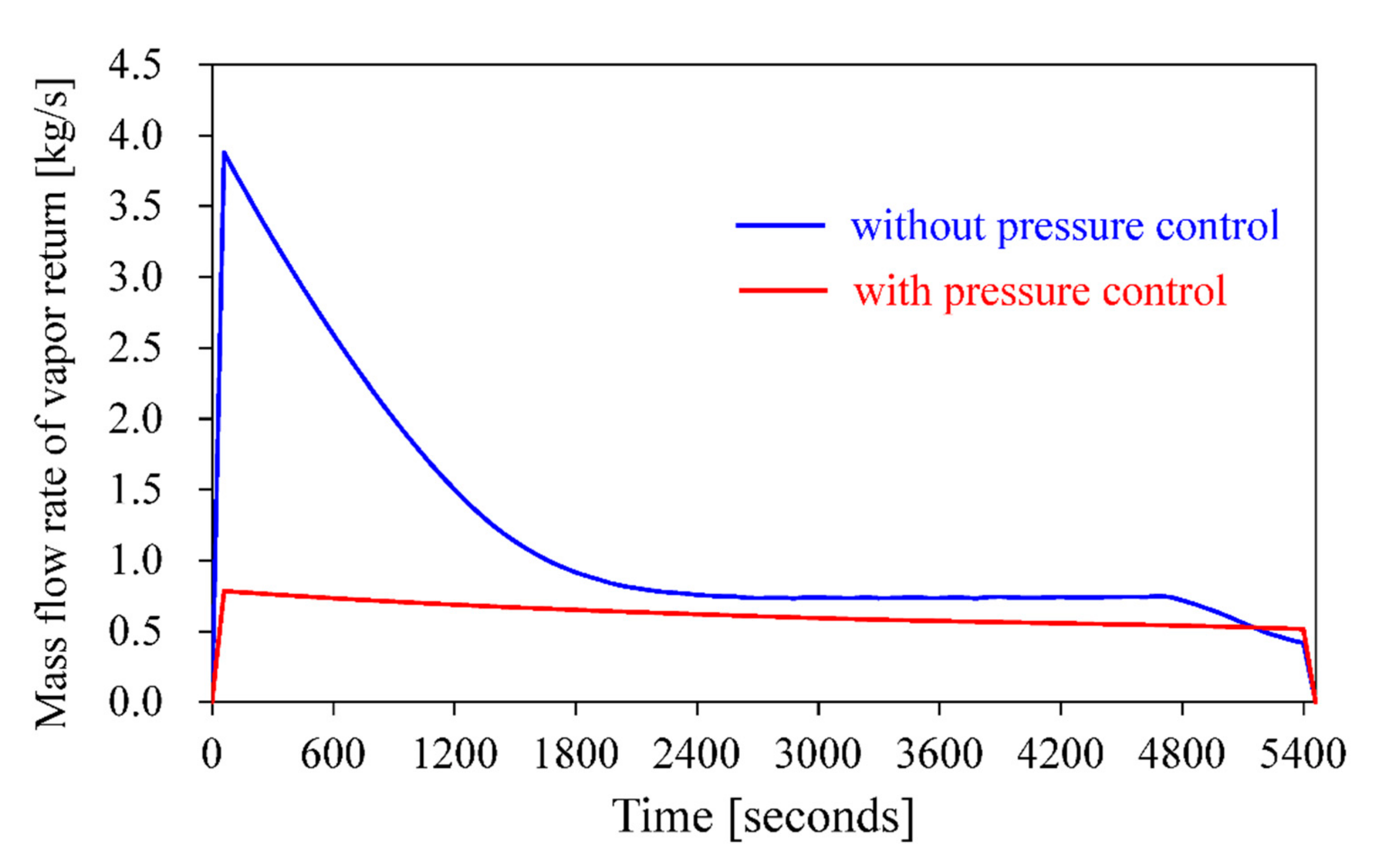
5. Method of Pressure Control in the Bunker Tanks and Receiving Tank
6. Conclusions
- When the initial temperature of the receiving tank increases from −150 to −145 °C at a fixed temperature of the bunkering tank (−147 °C), the amount of vapor return is proportionally increased. The optimum temperature difference (and pressure difference) should be determined in consideration of tank pressure management.
- The net vapor generation in the overall system has a positive value when the receiving tank temperature is colder than the bunkering LNG temperature. In contrast, it has a negative value when the receiving tank temperature is warmer than the bunkering LNG temperature.
- Increasing the bunkering flow rate decreases the amount of heat ingress through the pipes and tanks, although the heat dissipated by the pump shaft power increases. In addition to the heat ingress effect, the pressure increase in the receiving tank from pumping is also an important factor. The optimum flow rate must be determined while considering the vapor return and bunkering time limit.
- The influences of different insulation materials on the vapor return and vapor generation are minor; however, the influence of the insulation depends on the layout of the bunkering system (i.e., the results may be different for longer pipe lengths).
- The composition of the LNG affects the vapor return and vapor generation. Different LNG compositions in the bunker tank lead to changes in the initial pressure of the bunker tank, influencing the vapor return and vapor generation in the receiving tank. When the nitrogen content is varied, the pressure and vapor return are significantly affected.
Author Contributions
Funding
Conflicts of Interest
References
- Kim, K.; Park, K.; Roh, G.; Chun, K. Case study on boil-off gas (BOG) minimization for lng bunkering vessel using energy storage system (ESS). J. Mar. Sci. Eng. 2019, 7, 130. [Google Scholar] [CrossRef] [Green Version]
- Hwang, S.; Jeong, B.; Jung, K.; Kim, M.; Zhou, P. Life cycle assessment of lng fueled vessel in domestic services. J. Mar. Sci. Eng. 2019, 7, 359. [Google Scholar] [CrossRef] [Green Version]
- EMSA (European Maritime Safety Agency). Guidance on LNG Bunkering to Port Authorities and Administration; EMSA (European Maritime Safety Agency): Lisbon, Portugal, 2018. [Google Scholar]
- Vandebroek, L. Risk assessment Study Supplying Flemish ports with LNG as a marine fuel. LNG Fuelling 2017. [Google Scholar] [CrossRef]
- IMO. Studies on the fessibility and use of as a fuel for shipping. Air Pollut. Energy Effic. Stud. 2016. Available online: http://www.imo.org/en/OurWork/Environment/PollutionPrevention/AirPollution/Documents/LNG%20Study.pdf (accessed on 30 August 2020).
- TGE. 5100 cbm LNG Bunker-Vessel ’Engie Zeebrugge’. Available online: https://www.tge-marine.com/wp-content/uploads/Datasheet-2735-engie_Zeebrugge-bunkervessel.pdf (accessed on 17 August 2020).
- Choi, W.J.; Navarro, J.M.; Tustin, R.D. Purpose designed LNG bunkering vessels (1). SWZ Marit. Marit. Tech. Vakbl. 2018, 139, 36–40. [Google Scholar]
- TGE. 5800 cbm LNG Bunker-Vessel ’Coralius’. Available online: https://www.tge-marine.com/wp-content/uploads/Datasheet-2826-coralius-bunkervessel.pdf (accessed on 17 August 2020).
- TGE. 6500 cbm LNG Bunker-Vessel ’Cardissa’. Available online: https://www.tge-marine.com/wp-content/uploads/Datasheet-2960-cardissa-bunkervessel.pdf (accessed on 17 August 2020).
- TGE. 7500 cbm LNG/LPG/Ethylene-Carrier/Bunker Vessel, ’Coral Methane’. Available online: https://www.tge-marine.com/wp-content/uploads/Datasheet-2021-CoralMethane-LNG-LPG-Ethylene-Ammonia-VCMcarrier-7500cbm.pdf (accessed on 17 August 2020).
- Dobrota, Đ.; Lalić, B.; Komar, I. Problem of Boil-off in LNG Supply Chain. Trans. Marit. Sci. 2013, 2, 91–100. [Google Scholar] [CrossRef] [Green Version]
- Yan, G.; Gu, Y. Effect of parameters on performance of LNG-FPSO offloading system in offshore associated gas fields. Appl. Energy 2010, 87, 3393–3400. [Google Scholar] [CrossRef]
- Benito, A. Accurate determination of LNG quality unloaded in Receiving Terminals: An Innovative Approach. Int. Gas. Union World Gas. Conf. Pap. 2009, 6, 4627–4646. [Google Scholar]
- IACS. LNG Bunkering Guidelines. IACS Rec. No. 142. 2016. Available online: http://www.iacs.org.uk/download/1962 (accessed on 30 August 2020).
- Sharafian, A.; Herrera, O.E.; Mérida, W. Performance analysis of liquefied natural gas storage tanks in refueling stations. J. Nat. Gas. Sci. Eng. 2016, 36, 496–509. [Google Scholar] [CrossRef]
- Shao, Y.; Lee, Y.-H.; Kim, Y.-T.; Kang, H.-K. Parametric Investigation of BOG Generation for Ship-to-Ship LNG Bunkering. J. Korean Soc. Mar. Environ. Saf. 2018, 24, 352–359. [Google Scholar] [CrossRef]
- Shao, Y.; Lee, Y.; Kang, H. Dynamic optimization of boil-off gas generation for different time limits in liquid natural gas bunkering. Energies 2019, 12, 1130. [Google Scholar] [CrossRef] [Green Version]
- Querol, E.; Gonzalez-Regueral, B.; García-Torrent, J.; García-Martínez, M.J. Boil off gas (BOG) management in Spanish liquid natural gas (LNG) terminals. Appl. Energy 2010, 87, 3384–3392. [Google Scholar] [CrossRef]
- Sharafian, A.; Blomerus, P.; Mérida, W. Liquefied natural gas tanker truck-to-tank transfer for on-road transportation. Appl. Therm. Eng. 2019, 162. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y. Dynamic optimization of the Boil-Off Gas (BOG) fluctuations at an LNG receiving terminal. J. Nat. Gas. Sci. Eng. 2016, 30, 322–330. [Google Scholar] [CrossRef]
- Kurle, Y.M.; Wang, S.; Xu, Q. Dynamic simulation of LNG loading, BOG generation, and BOG recovery at LNG exporting terminals. Comput. Chem. Eng. 2017, 97, 47–58. [Google Scholar] [CrossRef]
- Zargham, M.; Pahwa, A.; Dwarkanath, P.S. Concept Design of LNG Bunkering Ship. 2012, pp. 1–32. Available online: http://name2-engineering.sites.olt.ubc.ca/files/2015/08/UBC-LNG-Bunker-Supply-Vessel-Final-Report.pdf (accessed on 30 August 2020).
- Linde Cryo, A.B. LNG ship to ship bunkering procedure. Uddevalla: Swedish Marine Technology Forum. 2010. Available online: https://smtf.se/fileadmin/documents/LNG02_projektrapport_appendix_www.pdf (accessed on 17 August 2020).
- Park, C.; Song, K.; Lee, S.; Lim, Y.; Han, C. Retrofit design of a boil-off gas handling process in liquefied natural gas receiving terminals. Energy 2012, 44, 69–78. [Google Scholar] [CrossRef]
- GUTTELING Product Catalog, Multi-LNG White STS Composite Hose. Available online: http://www.gutteling.com (accessed on 30 August 2020).
- IMO. International Code of Safety for Ship Using Gases or Other Low-Flashpoint Fuels. 2016. Available online: https://mdnautical.com/marine-safety/21370-imo-i109e-igf-code-2016-edition.html (accessed on 29 September 2020).
- American Bereau of Shipping. LNG Bunkering: Technical and Operational Advisory. LNG Bunkering 2014, 1, 25. [Google Scholar]
- Lu, M.; Connell, L.D. Transient, thermal wellbore flow of multispecies carbon dioxide mixtures with phase transition during geological storage. Int. J. Multiph. Flow 2014, 63, 82–92. [Google Scholar] [CrossRef]
- Marie, N.; Arnet, L. LNG Bunkering Operations. 2014. Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/bitstream/handle/11250/235731/748638_FULLTEXT01.pdf?sequence=2 (accessed on 17 August 2020).
- Fesmire, J.E.; Augustynowicz, S.D. Cryogenic thermal insulation systems. In Proceedings of the 16th Thermal and Fluids Analysis Workshop, Orlando, FL, USA, 8–12 August 2005. [Google Scholar]
- Hasan, M.M.F.; Zheng, A.M.; Karimi, I.A. Minimizing boil-off losses in liquefied natural gas transportation. Ind. Eng. Chem. Res. 2009, 48, 9571–9580. [Google Scholar] [CrossRef]
- Kurle, Y.M.; Wang, S.; Xu, Q. Simulation study on boil-off gas minimization and recovery strategies at LNG exporting terminals. Appl. Energy 2015, 156, 628–641. [Google Scholar] [CrossRef]

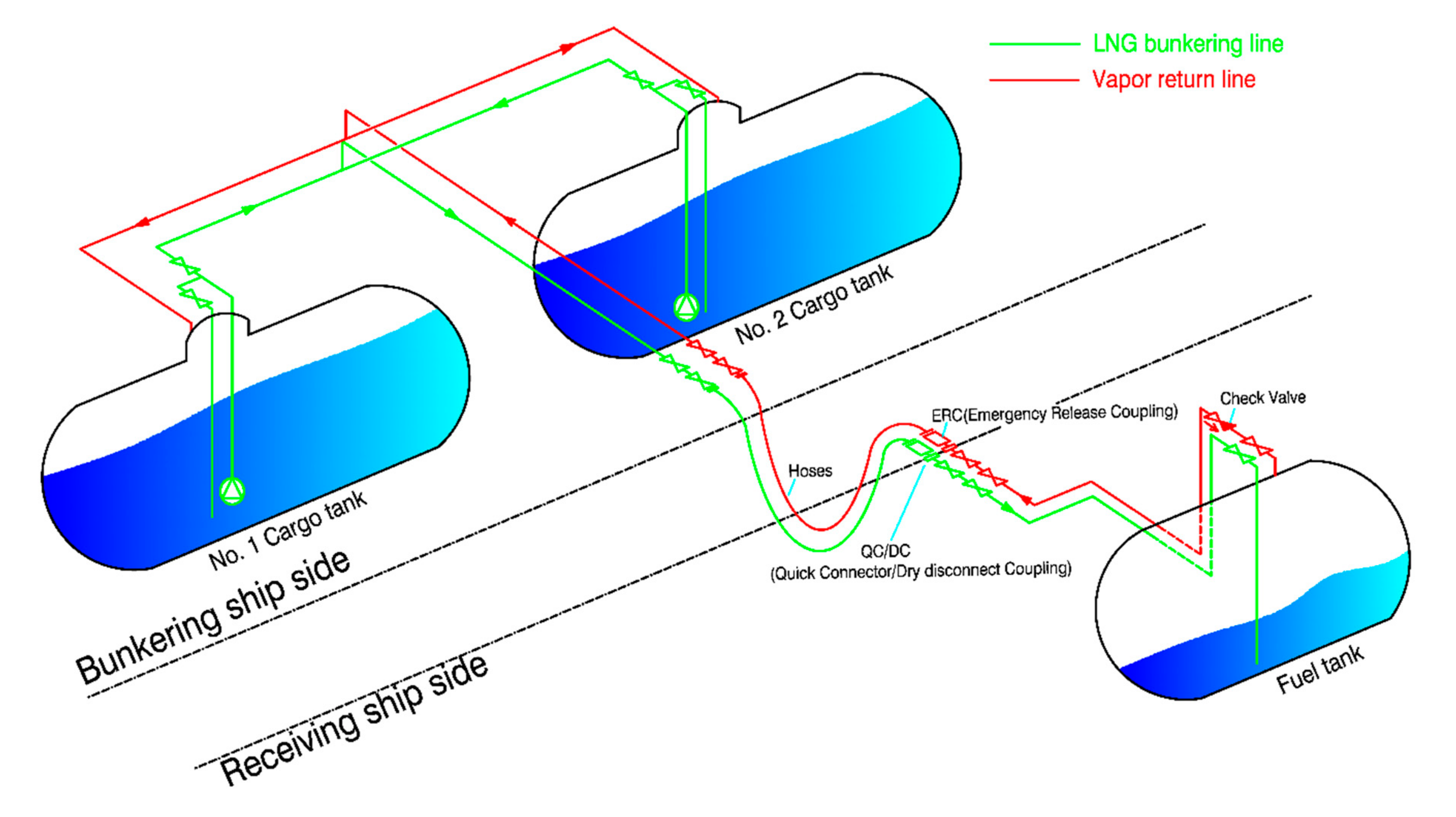



| Vessel Name | Cargo Tank (Bunker Tank) | Bunkering Rate (m3/h) | Boil-Off Gas Handling | Reference | ||||
|---|---|---|---|---|---|---|---|---|
| Tank Type | Cargo Capacity (m3) | Design Pressure (Barg) | As fuel | Burning | Re-Liquefaction | |||
| Engie Zeebrugge | Type C | 5100 | 4 | 600 | Yes | Yes | No | [6,7] |
| Coralius | Bi-lobe | 5800 | 4.5 | 840 | Yes | Yes | No | [7,8] |
| Cardissa | Type C | 6500 | 3.5 | 1100 | Yes | Yes | Yes | [7,9] |
| Karios | Type C | 7500 | 3.75 | 1150 | Yes | No | No | [7] |
| Coral Methane | Type C | 7500 | 3.2 | 900 | Yes | - | Not for LNG | [10] |
| Parameter | Value | Unit | Notes |
|---|---|---|---|
| Quantity of bunker tank | 2 | ea | Bunkering ship has two independent International Maritime Organization (IMO) type C tanks |
| Net capacity of bunker tank, Vnet, bt | 3250 | m3 | Total cargo capacity of bunkering ship is 6500 m3 in two bunker tanks |
| Overall length of each bunker tank | 30.74 | m | 2:1 ellipsoidal head, D/2h = 2, head height 3 m |
| Diameter of each bunker tank | 12 | m | Assumed based on Reference [22] |
| Surface area of each bunker tank, Abt | 932.5 | m2 | Calculated from length and diameter |
| Maximum allowable relief valve setting, Pbt, MARVS | 4 | bar | Assumed |
| Boil-off rate (Normal) | 0.25 | % | Assumed |
| Thermal conductance of bunker tank, (UA)bt | 107.36 | W/K | Calculated from Equations (2) and (3) |
| Overall heat transfer coefficient of bunker tank, Ubt | 0.414 | kJ/h·m2·K | Calculated from Equations (2)–(4) |
| Quantity of cargo pump | 2 | ea | There is a submerged electrical driven cargo pump in each bunker tank |
| Cargo pump performance curves | - | - | Three performance curves generated in Aspen HYSYS at efficiency of 70%, 210 mlc and volumetric flow rate of 400 m3/h |
| Ambient Temperature | 25 | °C | |
| Base case conditions at bunkering | |||
| LNG Volume % | 80 | % | |
| LNG temperature in bunker tank | −147 | °C | |
| Pressure in bunker tank | 2.94 | bar | |
| Parameter | Value | Unit | Notes |
|---|---|---|---|
| Quantity of receiving tank | 1 | ea | Receiving ship has an independent IMO type C tank |
| Net capacity of receiving tank, Vnet, rt | 1000 | m3 | |
| Overall length of receiving tank | 27.15 | m | 2:1 ellipsoidal head, D/2h = 2, head height 1.75 m |
| Diameter of receiving tank | 7 | m | Assumed |
| Surface area of receiving tank, Art | 520.1 | m2 | Calculated from length and diameter |
| Maximum allowable relief valve setting, Prt, MARVS | 6 | bar | Assumed |
| Boil-off rate (Normal) | 0.35 | % | Assumed |
| Thermal conductance of tank, (UA)rt | 46.25 | W/K | Calculated from Equations (2) and (3) |
| Overall heat transfer coefficient of tank, Urt | 0.320 | kJ/h·m2·K | Calculated from Equations (2)–(4) |
| Ambient Temperature | 25 | °C | |
| Base case conditions at bunkering | |||
| LNG Volume % (Heel) | 20 | % | |
| LNG temperature | −147 | °C | |
| Pressure in receiving tank | 2.94 | bar | |
| Loading limit | 90 | % | |
| It was assumed that a dual fuel engine generator was installed on the receiving ship, and that the receiving ship did not use the LNG as fuel during bunkering. | |||
| Parameter | Value | Unit | Notes |
|---|---|---|---|
| Bunkering line diameter (Nominal) | 8 | inch | Sch10S (3.76 mm), Inner diameter 211.58 mm |
| Total length of LNG bunkering pipe, Lpipe | 112 | m | Sch10S (3.40 mm), Inner diameter 161.5 mm |
| Hose length, Lhose | 10 | m | Reference [29] |
| Hose pressure drop, | 0.1 | bar/m | Hose pressure drop of 0.1 bar/m is applied for liquid line only |
| Pipe insulation thermal conductivity, kinsulation | 0.021 | W/m·K | PUF (Polyurethane foam) at −162 °C, 1 atm and density of 32 kg/m3 [30] |
| Pipe Insulation thickness, tinsulation | 50 | mm | Assumed |
| Overall heat transfer coefficient of liquid line, Upipe | 1.730 | kJ/h·m2·K | Calculated |
| Total bunkering flow rate | 500 | m3/h | Bunkering duration of about 2 h assumed |
| Topping up flow rate | 200 | m3/h | When the volume % of fuel tank reaches 85%, flow rate is adjusted from 500 to 200 m3/h |
| Ambient Temperature | 25 | °C |
| Category | 300 m3/h | 500 m3/h | 1000 m3/h |
|---|---|---|---|
| Heat ingress through pump (kJ) | 59,866 | 76,805 | 151,431 |
| Heat ingress through pipe (kJ) | 43,658 | 27,150 | 13,338 |
| Heat ingress through tanks (kJ) | 69,411 | 43,169 | 21,213 |
| Total heat ingress (kJ) | 172,935 | 147,124 | 185,982 |
| Parameter | Cellular Glass | Polyurethane Foam (PUF) | Multi-Layer Insulation (MLI) |
|---|---|---|---|
| Thermal conductivity (W/m·K) | 0.033 | 0.021 | 0.010 (at 133.3 Pa) |
| Overall heat transfer coefficient of pipe insulation (kJ/h·m2·K) | 2.632 | 1.730 | 0.849 (at 133.3 Pa) |
| Category | Cellular Glass | Polyurethane Foam (PUF) | Multi-Layer Insulation (MLI) |
|---|---|---|---|
| Total amount of vapor return (kg) | 3991.22 | 4016.52 | 4036.62 |
| Receiving tank net vapor generation, (kg) | 409.15 | 434.83 | 459.35 |
| Net vapor generation (overall system), (kg) | 14.39 | 17.01 | 20.01 |
| Conditions | LNG Lean | LNG Medium (Base Case) | LNG Rich-1 | LNG Rich-2 |
|---|---|---|---|---|
| Composition (mole %) | ||||
| Methane | 0.985 | 0.923 | 0.860 | 0.860 |
| Ethane | 0.013 | 0.050 | 0.094 | 0.099 |
| Propane | 0.001 | 0.015 | 0.025 | 0.025 |
| Nitrogen | 0.001 | 0.005 | 0.010 | 0.005 |
| n-Pentane | 0.000 | 0.001 | 0.001 | 0.001 |
| n-Butane | 0.001 | 0.006 | 0.010 | 0.010 |
| Temperature (°C) | −147 | −147 | −147 | −147 |
| Pressure (bar) | 2.916 | 2.941 | 3.077 | 2.803 |
| Total amount of vapor return (kg) | 4224.51 | 4016.52 | 3230.68 | 5296.50 |
| Receiving tank net vapor generation, (kg) | 626.14 | 434.83 | −314.20 | 1696.62 |
| Net vapor generation (overall system), (kg) | −167.18 | 17.01 | 386.24 | −134.93 |
| Category | Without Pressure Control | With Pressure Control |
|---|---|---|
| Total amount of vapor return (kg) | 7392.55 | 3317.15 |
| Receiving tank net vapor generation, (kg) | 3352.41 | −695.32 |
| Net vapor generation (Overall system), (kg) | −380.61 | −442.49 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Choi, J.; Jung, I.; Lee, S.; Yoon, S.; Ryu, B.; Kang, H. Effect of Parameters on Vapor Generation in Ship-to-Ship Liquefied Natural Gas Bunkering. Appl. Sci. 2020, 10, 6861. https://doi.org/10.3390/app10196861
Lee H, Choi J, Jung I, Lee S, Yoon S, Ryu B, Kang H. Effect of Parameters on Vapor Generation in Ship-to-Ship Liquefied Natural Gas Bunkering. Applied Sciences. 2020; 10(19):6861. https://doi.org/10.3390/app10196861
Chicago/Turabian StyleLee, Hyunyong, Jungho Choi, Inchul Jung, Sangick Lee, Sangdeuk Yoon, Borim Ryu, and Hokeun Kang. 2020. "Effect of Parameters on Vapor Generation in Ship-to-Ship Liquefied Natural Gas Bunkering" Applied Sciences 10, no. 19: 6861. https://doi.org/10.3390/app10196861
APA StyleLee, H., Choi, J., Jung, I., Lee, S., Yoon, S., Ryu, B., & Kang, H. (2020). Effect of Parameters on Vapor Generation in Ship-to-Ship Liquefied Natural Gas Bunkering. Applied Sciences, 10(19), 6861. https://doi.org/10.3390/app10196861






