Shear Failure Mode and Concrete Edge Breakout Resistance of Cast-In-Place Anchors in Steel Fiber-Reinforced Normal Strength Concrete
Abstract
:1. Introduction
2. Experiments
2.1. SFRC Material
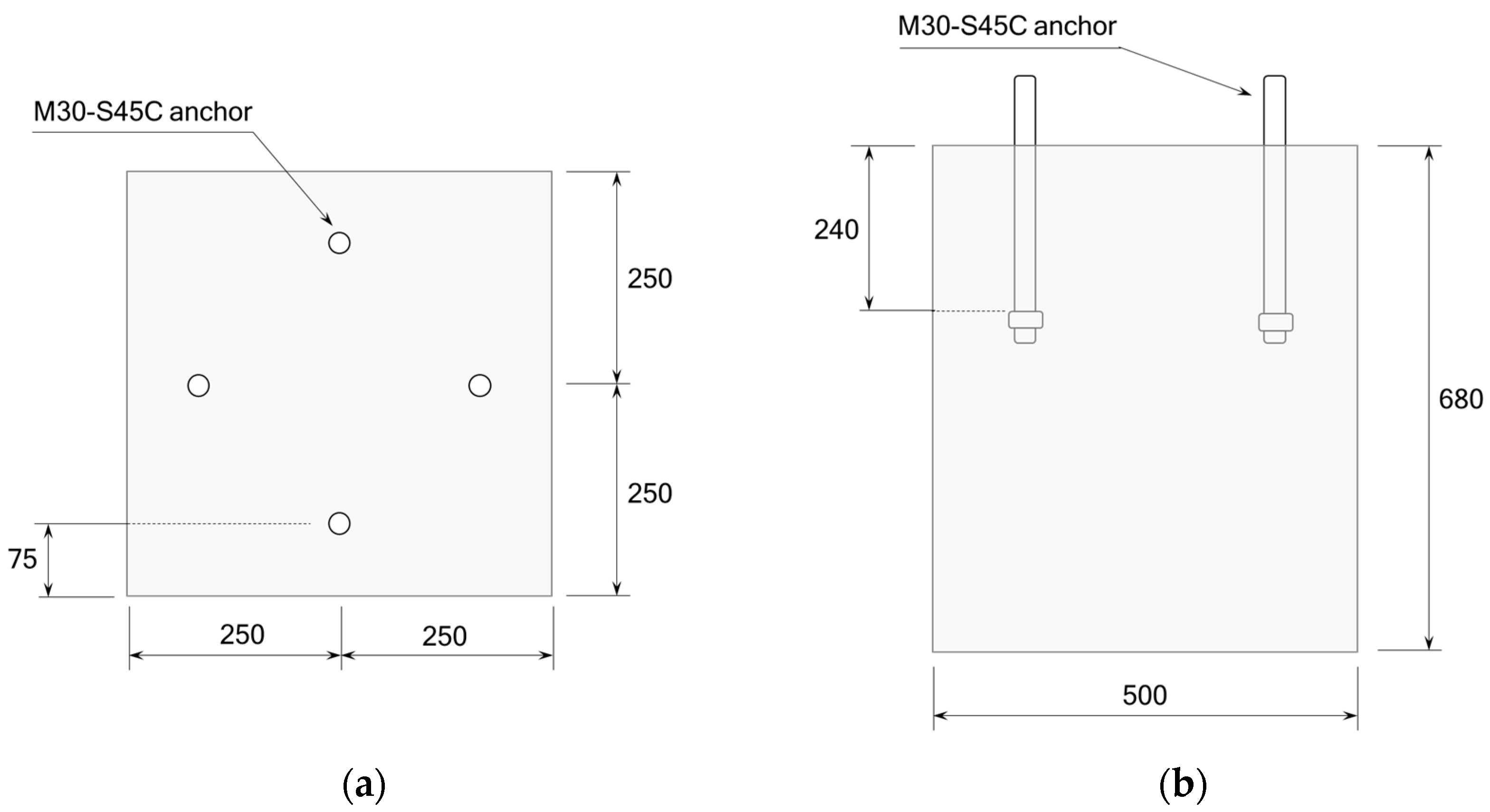
2.2. Preparation of the Anchor and Beam Specimens
2.3. Installation and Measurement of the Specimens
3. Bending Test Results and Discussion
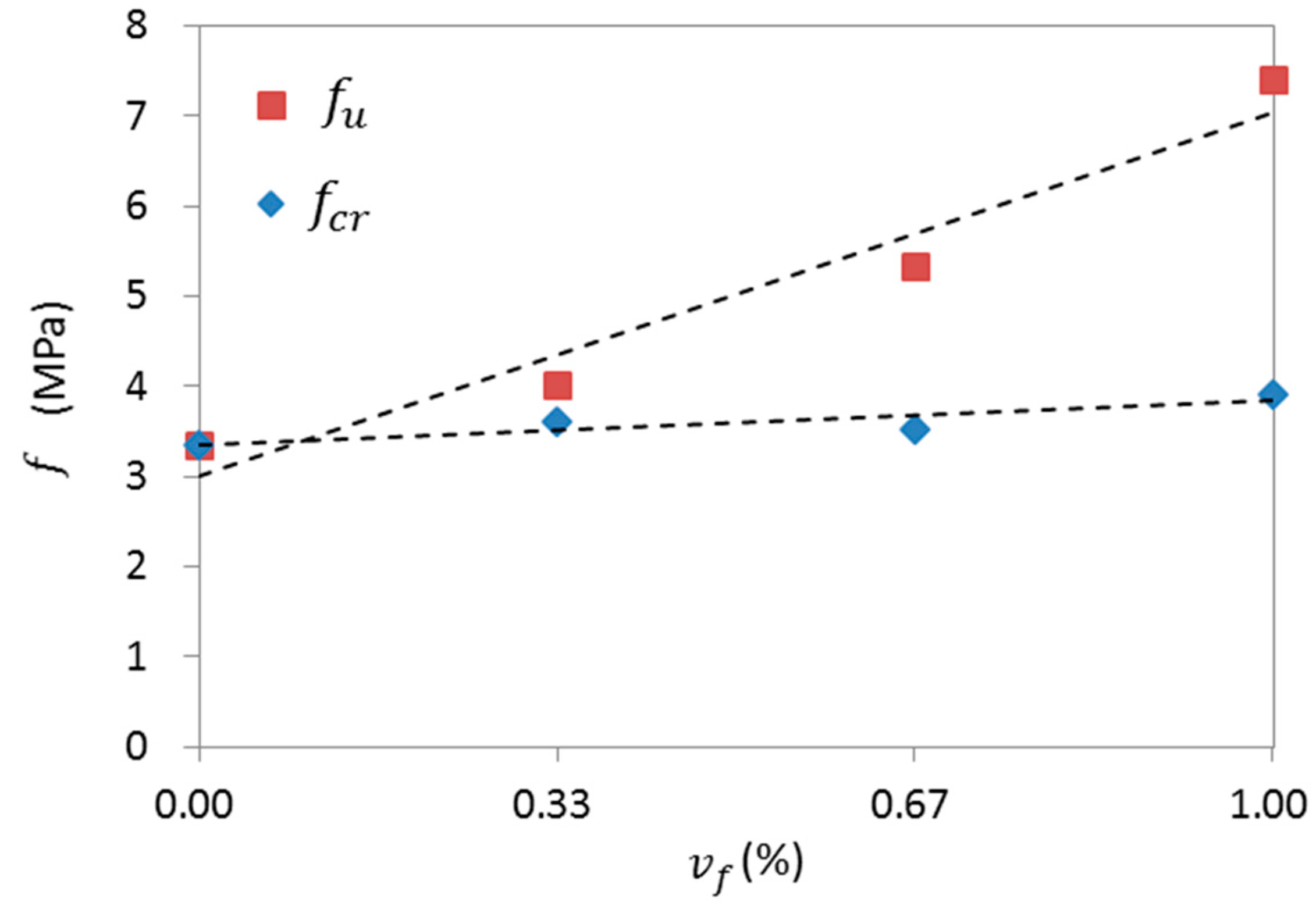
3.1. Tensile Strength before and after Cracking
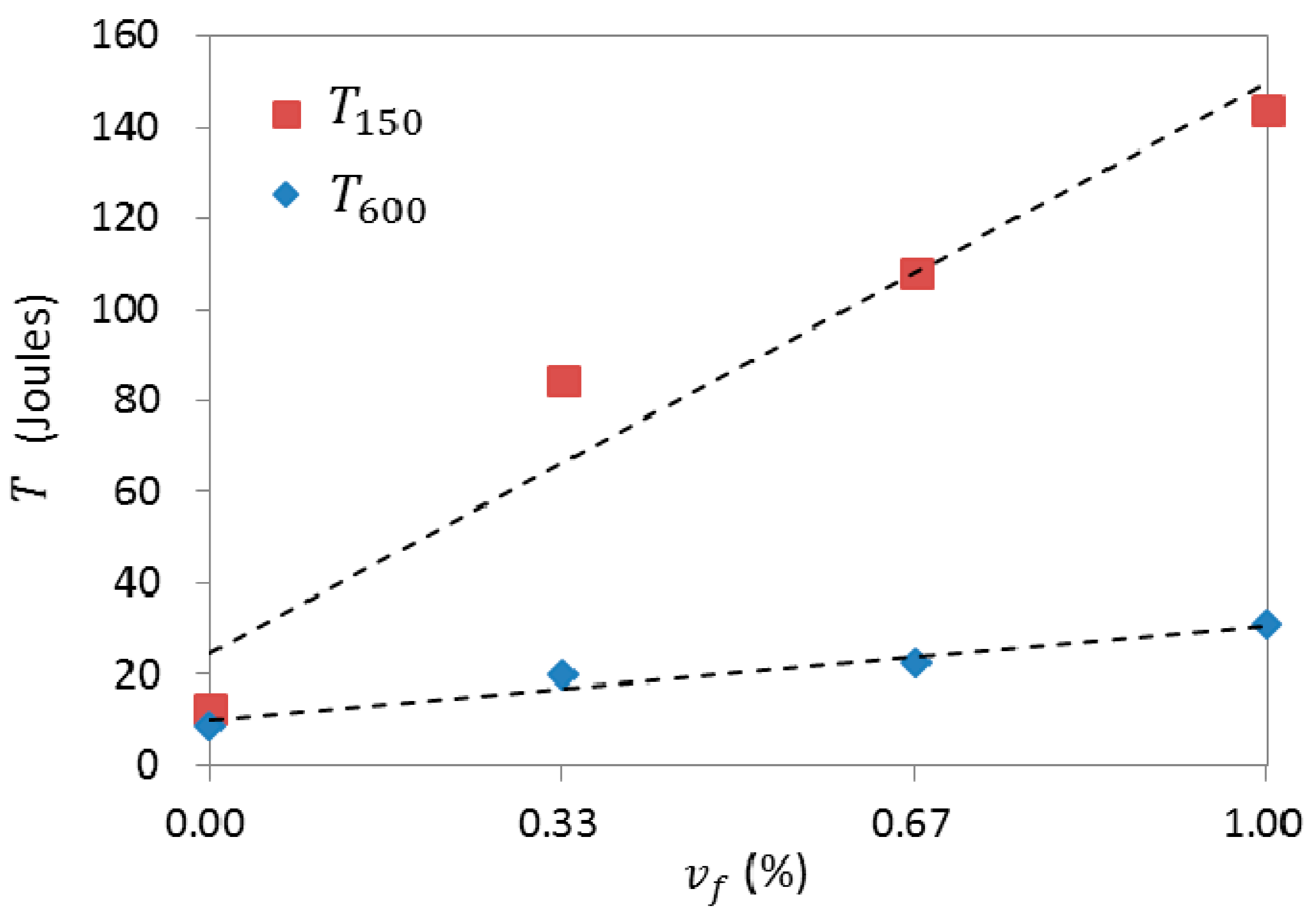
3.2. Energy Absorption Capacity
4. Shear Test Results and Discussion
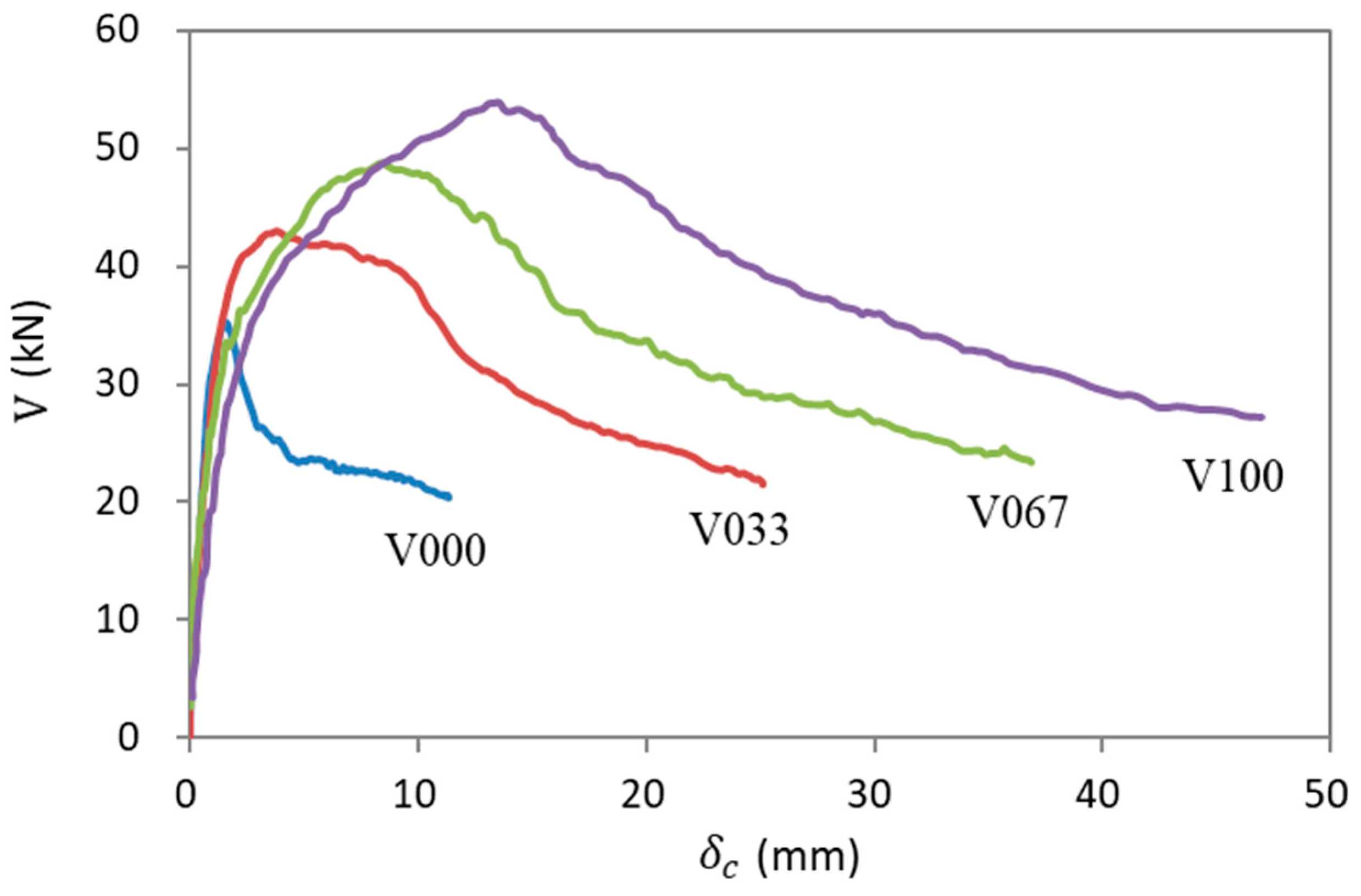
4.1. Test Results and Failure Mode
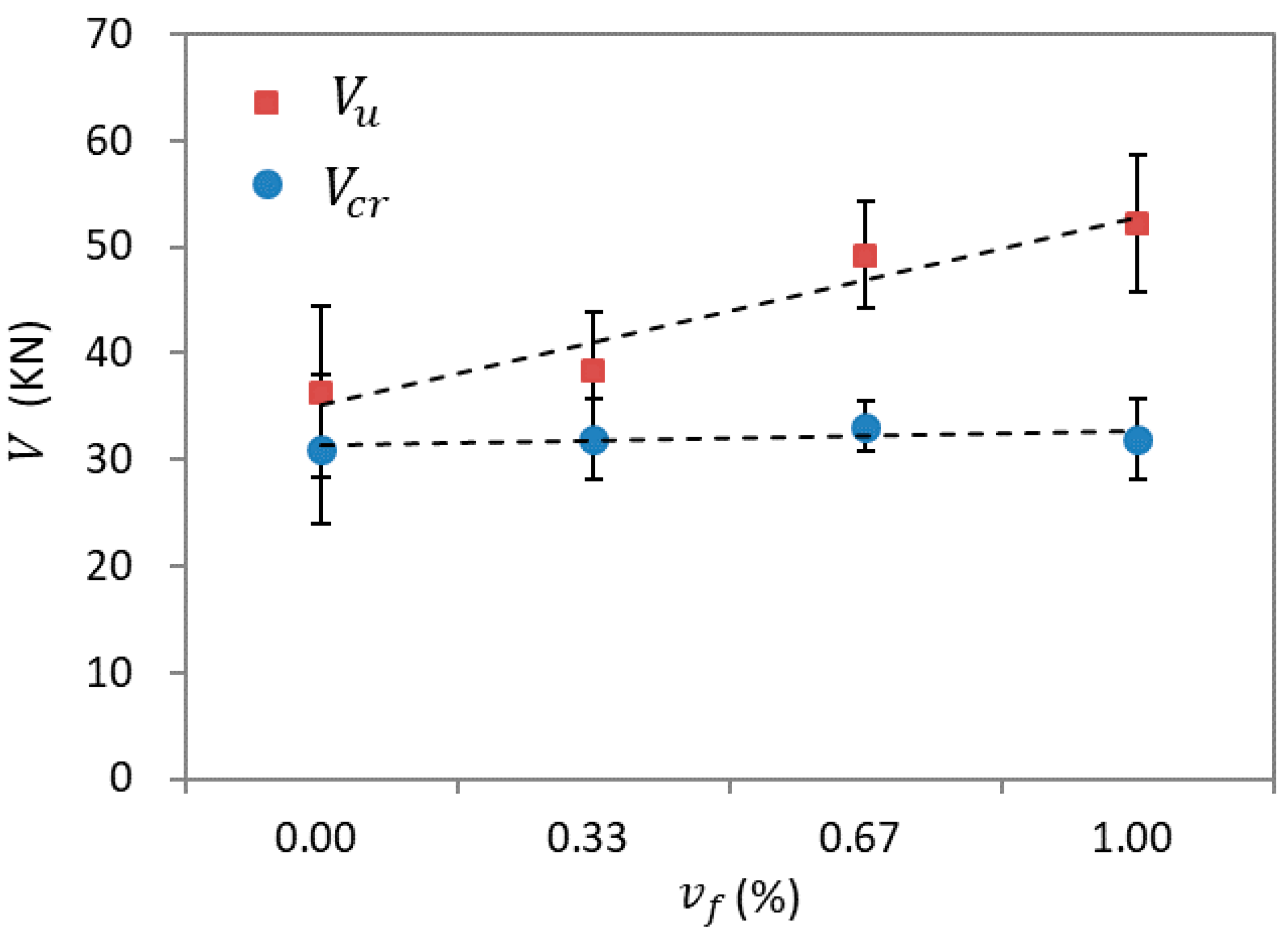
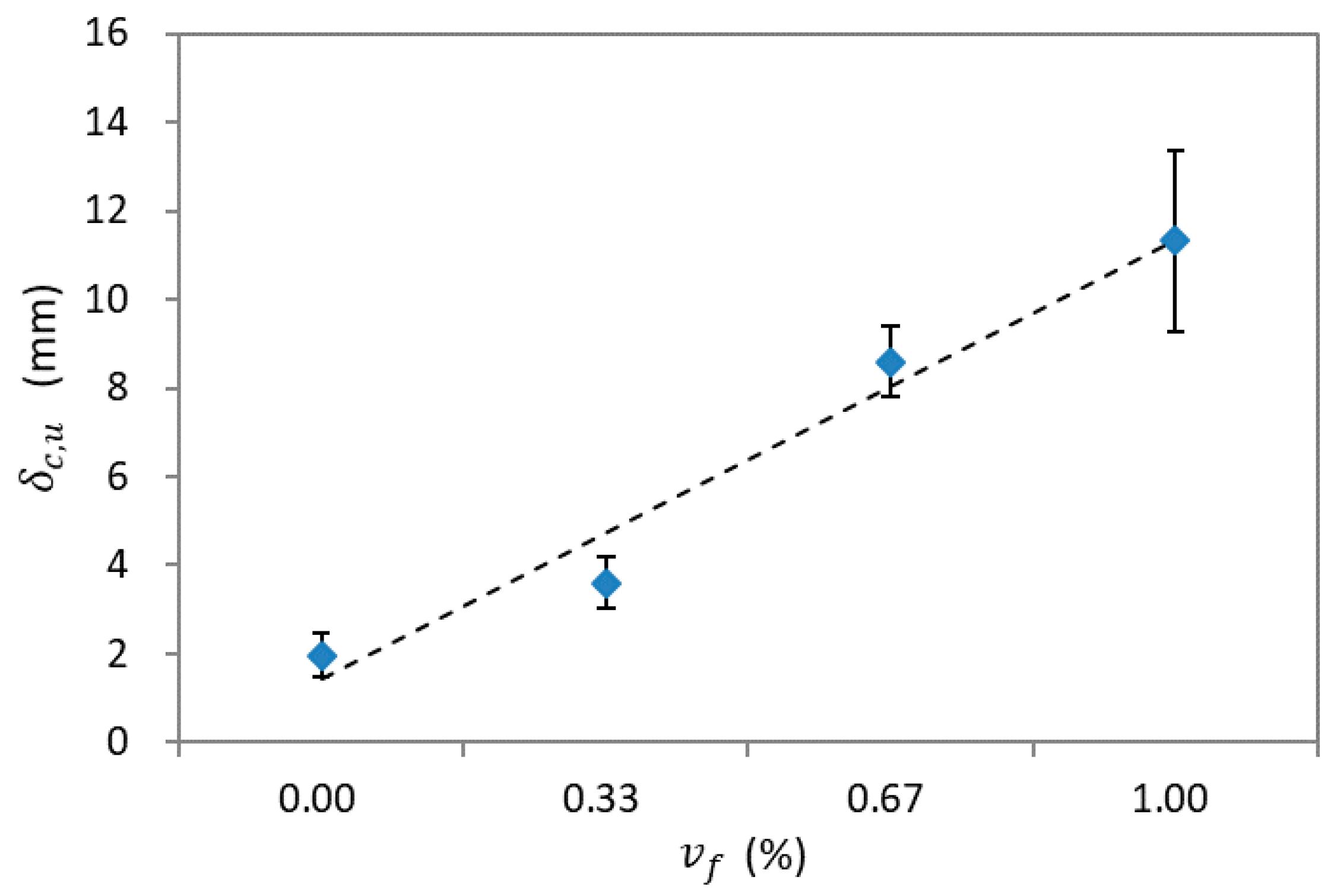
4.2. Load and Displacement Resistance
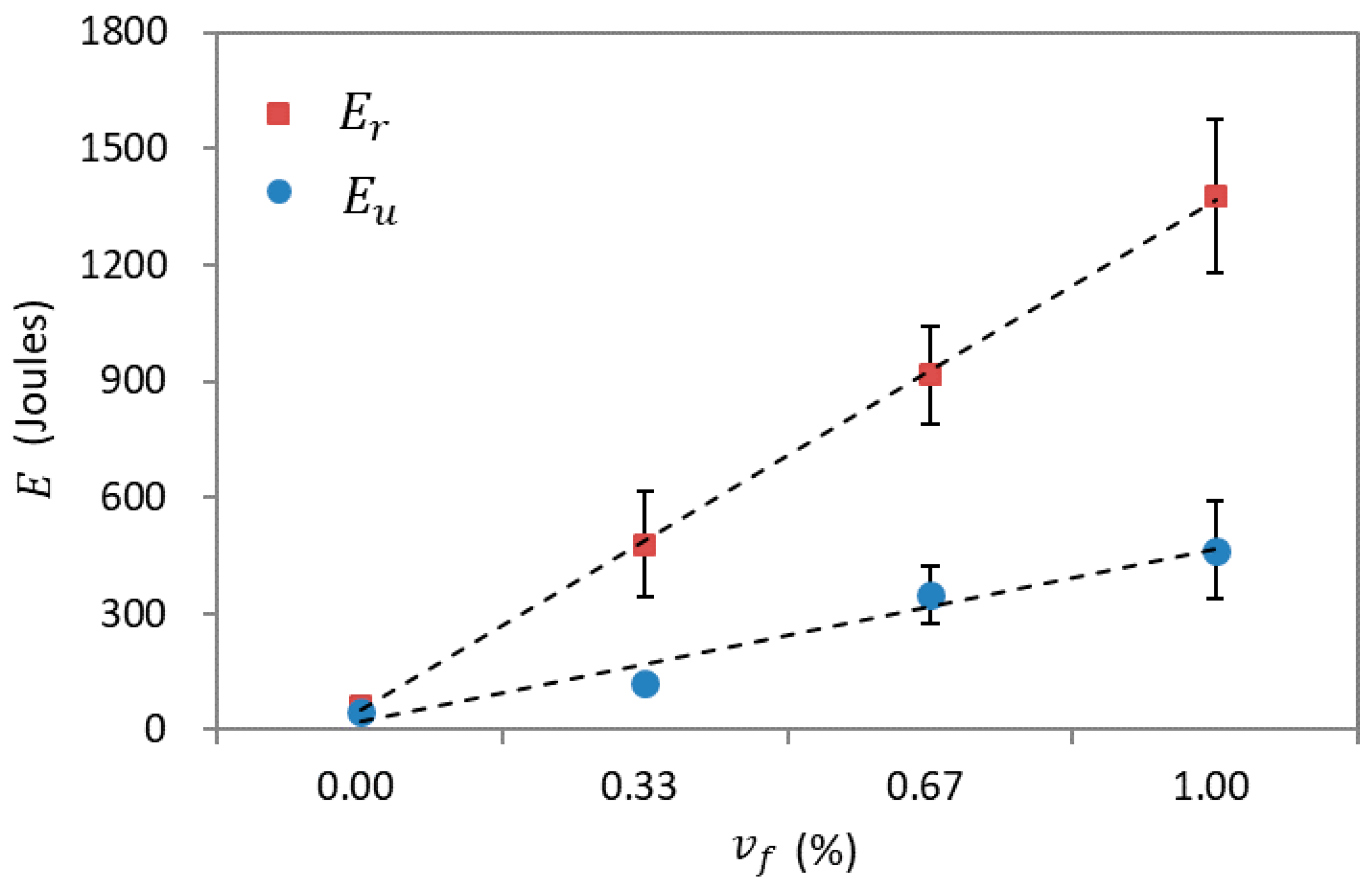
4.3. Energy Absorption Capacity
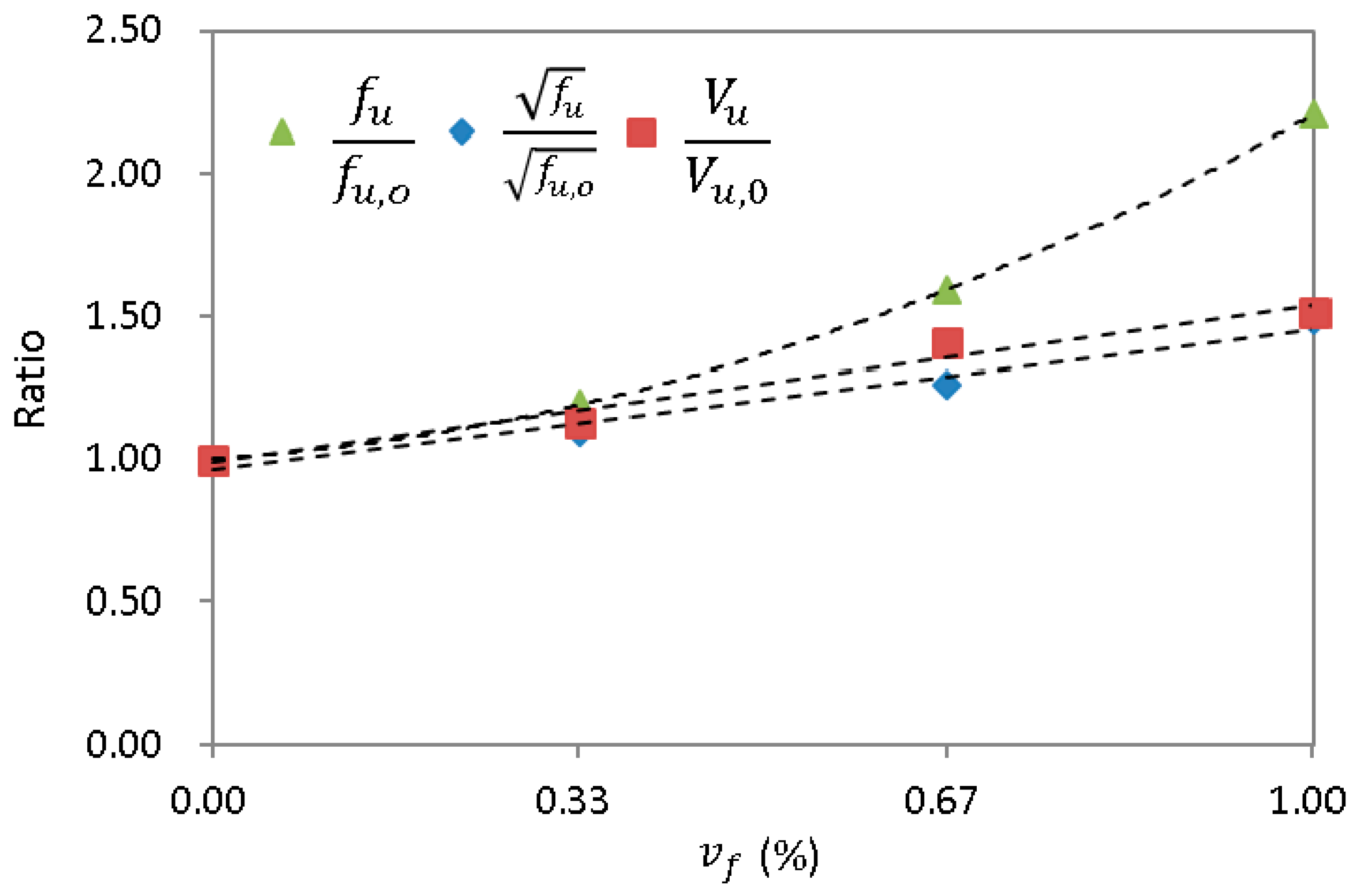
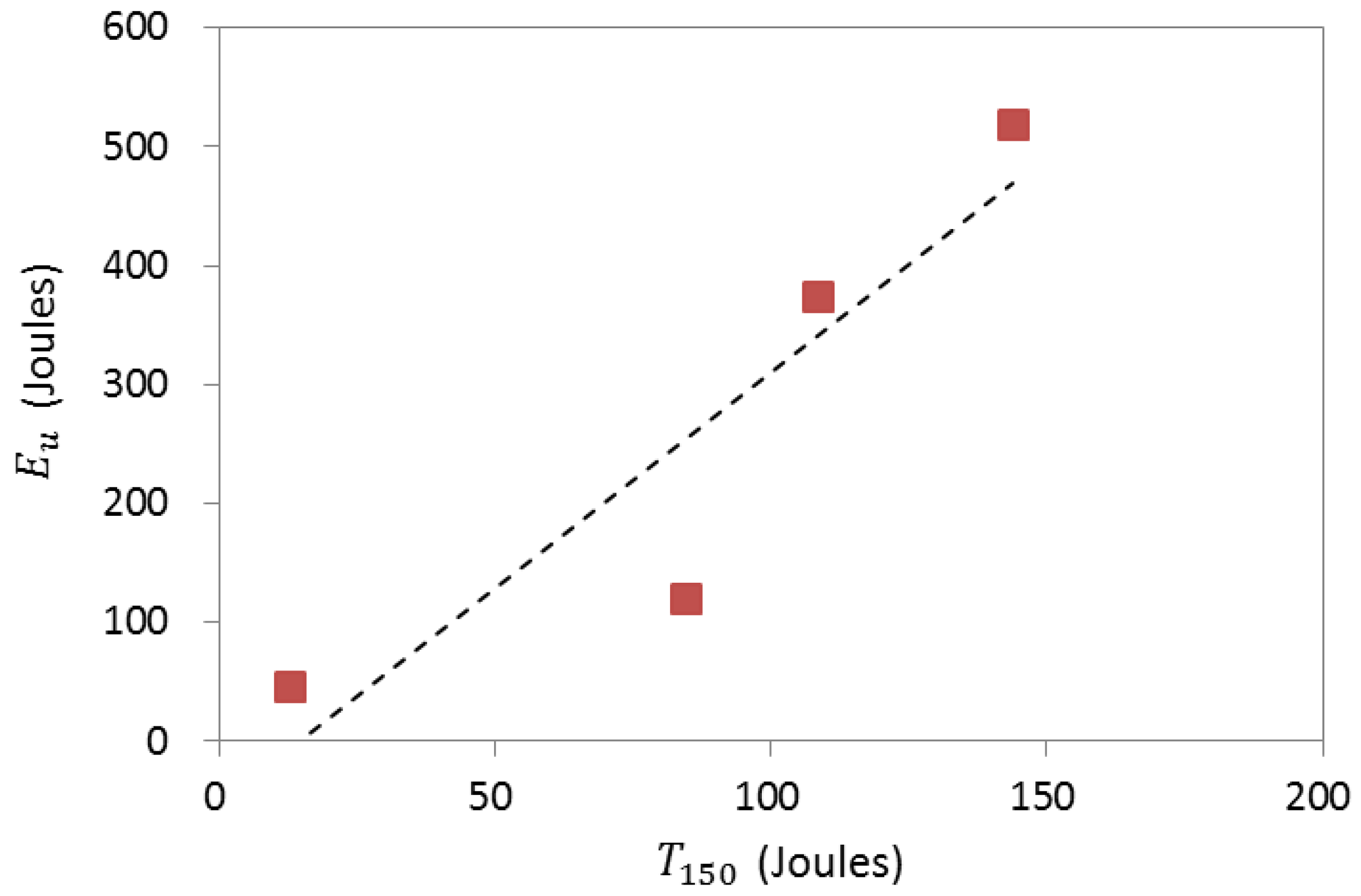
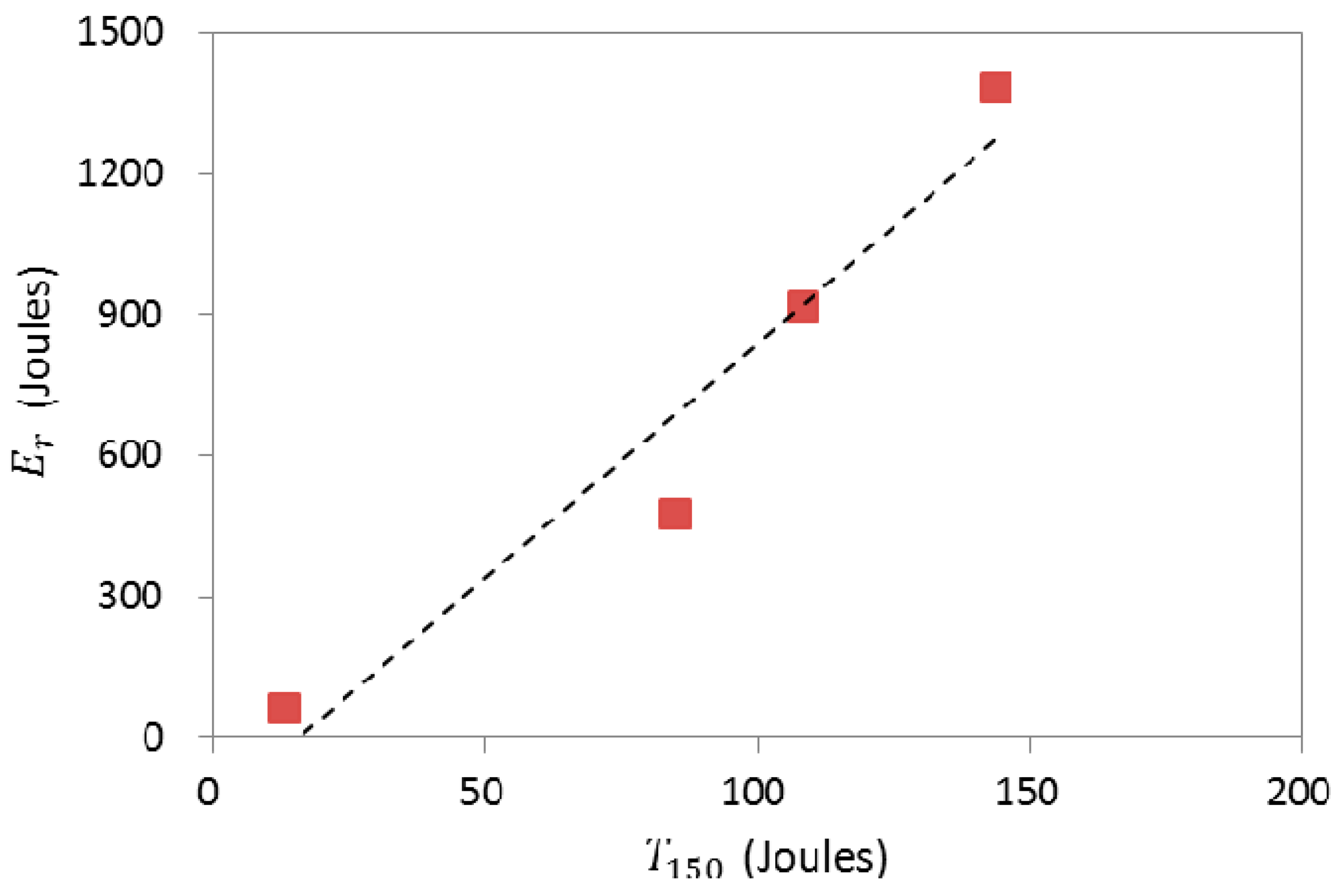
5. Relationship between Shear Behavior of Anchors and Tensile Performance of SFRC
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, D.; Wu, D.; He, S.; Zhou, J.; Ouyang, C. Behavior of post-installed large-diameter anchors in concrete foundations. Constr. Build. Mater. 2015, 95, 124–132. [Google Scholar] [CrossRef]
- Park, Y.M.; Kim, T.H.; Kim, D.H.; Kang, C.H.; Lee, J.H. Breakout shear strength of cast-in-place anchors using shaking table tests. Proc. Inst. Civ. Eng. Struct. Build. 2017, 170, 939–950. [Google Scholar] [CrossRef]
- Fuchs, W.; Eligehausen, R.; Breen, J.E. Concrete capacity design (CCD) approach for fastenings to concrete. ACI Struct. J. 1995, 92, 794–802. [Google Scholar]
- Eligehausen, R.; Balogh, T. Behavior of fasteners loaded in tension in cracked reinforced concrete. ACI Struct. J. 1995, 92, 365–379. [Google Scholar]
- Muratli, H.; Klingner, R.E.; Graves, H.L., III. Breakout capacity of anchors in concrete-Part 2: Shear. ACI Struct. J. 2004, 101, 821–829. [Google Scholar]
- ACI 349-01. Code Requirements for Nuclear Safety Related Concrete Structures, Appendix B: Anchoring to Concrete; ACI (American Concrete Institute): Farmington Hills, MI, USA, 2001. [Google Scholar]
- ACI 318M-02. Building Code Requirements for Structural Concrete and Commentary, Appendix D Anchoring to Concrete; 3rd Amendment; ACI (American Concrete Institute): Farmington Hills, MI, USA, 2002. [Google Scholar]
- ACI 318M-08. Building Code Requirements for Structural Concrete and Commentary, Appendix D: Anchoring to Concrete; 3rd Amendment; ACI (American Concrete Institute): Farmington Hills, MI, USA, 2008. [Google Scholar]
- ACI 318M-11. Building Code Requirements for Structural Concrete and Commentary, Appendix D: Anchoring to Concrete; 3rd Amendment; ACI (American Concrete Institute): Farmington Hills, MI, USA, 2011. [Google Scholar]
- Olalusi, O.B.; Spyridis, P. Uncertainty modelling and analysis of the concrete edge breakout resistance of single anchors in shear. Eng. Struct. 2020, 222, 111112. [Google Scholar] [CrossRef]
- Bokor, B.; Sharma, A.; Hofmann, J. Experimental investigations on concrete cone failure of rectangular and non-rectangular anchor groups. Eng. Struct. 2019, 188, 200–217. [Google Scholar] [CrossRef]
- Pürgstaller, A.; Gallo, P.Q.; Pampanin, S.; Bergmeister, K. Seismic demands on nonstructural components anchored to concrete accounting for structure-fastener-nonstructural interaction (SFNI). Earthq. Eng. Struct. Dyn. 2020, 49, 589–606. [Google Scholar] [CrossRef] [Green Version]
- Dengg, F.; Zeman, O.; Voit, K.; Bergmeister, K. Fastening application in concrete using recycled tunnel excavation material. Struct. Concr. 2018, 19, 374–386. [Google Scholar] [CrossRef]
- Lee, J.H.; Cho, B.; Choi, E.; Kim, Y.H. Experimental study of the reinforcement effect of macro-type high strength polypropylene on the flexural capacity of concrete. Constr. Build. Mater. 2016, 126, 967–975. [Google Scholar] [CrossRef]
- Lee, J.H.; Kighuta, K. Twin-twist effect of fibers on the pullout resistance in cementitious materials. Constr. Build. Mater. 2017, 146, 555–562. [Google Scholar] [CrossRef]
- Naaman, A.E.; Najm, H. Bond-slip mechanisms of steel fibres in concrete. ACI Mater. J. 1991, 88, 135–145. [Google Scholar]
- Alwan, J.M.; Naaman, A.E.; Hansen, W. Analytical investigation on pullout work of steel fibers from cementitious composites. Cem. Concr. Compos. 1991, 13, 247–255. [Google Scholar] [CrossRef] [Green Version]
- Gopalaratnam, V.S.; Gettu, R. On the characterization of flexural toughness in fiber reinforced concrete. Cem. Concr. Compos. 1995, 17, 239–254. [Google Scholar] [CrossRef]
- Lee, J.H.; Cho, B.; Choi, E. Flexural capacity of fiber reinforced concrete with a consideration of concrete strength and fiber content. Constr. Build. Mater. 2017, 138, 222–231. [Google Scholar] [CrossRef]
- Narayanan, R.; Darwish, I.Y.S. Use of steel fibers as shear reinforcement. ACI Struct. J. 1987, 84, 216–227. [Google Scholar]
- Sharma, A.K. Shear strength of steel fiber reinforced concrete beams. ACI J. Proc. 1986, 83, 624–628. [Google Scholar]
- Amin, A.; Foster, S.J. Shear strength of steel fibre reinforced concrete beams with stirrups. Eng. Struct. 2016, 111, 323–332. [Google Scholar] [CrossRef]
- Khuntia, M.; Stojadinovic, B.; Goel, S.C. Shear strength of normal and high strength fiber reinforced concrete beams without stirrups. ACI Struct. J. 1999, 96, 282–289. [Google Scholar]
- Mansur, M.A.; Chin, M.S.; Wee, T.H. Stress-strain relationship of high-strength fiber concrete in compression. J. Mater. Civ. Eng. 1999, 11, 21–29. [Google Scholar] [CrossRef]
- Holschemacher, K.; Mueller, T.; Ribakov, Y. Effect of steel fibers on mechanical properties of high strength concrete. Mater. Des. 2010, 31, 2604–2615. [Google Scholar] [CrossRef]
- Lee, J.H. Influence of concrete strength combined with fiber content in the residual flexural strengths of fiber reinforced concrete. Compos. Struct. 2017, 168, 216–225. [Google Scholar] [CrossRef]
- Jeng, F.; Lin, M.L.; Yuan, S.C. Performance of toughness indices for steel fiber reinforced shotcrete. Tunn. Undergr. Space Technol. 2002, 17, 69–82. [Google Scholar] [CrossRef]
- Sorelli, L.G.; Meda, A.; Plizzari, G.A. Steel fiber concrete slabs on ground: A structural matter. ACI Struct. J. 2006, 103, 551–558. [Google Scholar]
- Altoubat, S.A.; Roesler, J.R.; Lange, D.A.; Rieder, K.A. Simplified method for concrete pavement design with discrete structural fibers. Constr. Build. Mater. 2008, 22, 384–393. [Google Scholar] [CrossRef]
- Roesler, J.R.; Altoubat, S.A.; Lange, D.A.; Rieder, K.A.; Ulreich, G.R. Effect of synthetic fibers on structural behavior of concrete slabs-on-ground. ACI Mater. J. 2016, 103, 3–10. [Google Scholar]
- Nilforouch, R.; Nilsson, M.; Elfgren, L. Experimental evaluation of tensile behaviour of single cast-in-place anchor bolts in plain and steel fibre-reinforced normal- and high-strength concrete. Eng. Struct. 2017, 147, 195–206. [Google Scholar] [CrossRef]
- Tóth, M.; Bokor, B.; Sharma, A. Anchorage in steel fiber reinforced concrete–concept, experimental evidence and design recommendations for concrete cone and concrete edge breakout failure modes. Eng. Struct. 2019, 181, 60–75. [Google Scholar] [CrossRef]
- Mahrenholtz, C.; Ayoubi, M.; Müller, S.; Bachschmid, S. Tension and shear performance of anchor channels with channel bolts cast in Fibre Reinforced Concrete (FRC). IOP Conf. Ser. Mater. Sci. Eng. 2019, 615, 012089. [Google Scholar] [CrossRef]
- Lee, J.H.; Cho, B.; Kim, J.B.; Lee, K.J.; Jung, C.Y. Shear capacity of cast-in headed anchors in steel fiber-reinforced concrete. Eng. Struct. 2018, 171, 421–432. [Google Scholar] [CrossRef]
- ASTM C 1609. Standard Test Method for Flexural Performance of Fiber Reinforced Concrete; ASTM (American Society of Testing Material): West Conshonocken, PA, USA, 2007. [Google Scholar]
- Gopalaratnam, V.S.; Shah, S.P.; Batson, G.B.; Criswell, M.E.; Ramakrishnam, V.; Wicharatana, M. Fracture toughness of fiber reinforced concrete. ACI Mater. J. 1991, 88, 339–353. [Google Scholar]
- BS EN 14651. Test Method for Metallic Fibered Concrete–Measuring the Flexural Tensile Strength (Limit of Proportionality (LOP), Residual); European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- JSCE SF-4. Method of Tests for Flexural Strength and Flexural Toughness of SFRC.; The Japanese Society of Civil Engineers (JSCE): Tokyo, Japan, 1985; pp. 45–74. [Google Scholar]
- ASTM C 1550. Standard Test Method for Flexural Toughness of Fiber Reinforced Concrete (Using centrally Loaded Round Panel); ASTM (American Society of Testing Material): West Conshonocken, PA, USA, 2010. [Google Scholar]
- ASTM C 1608. Standard Test Method for Flexural Toughness and First-Crack Strength of Fiber Reinforced Concrete; ASTM (American Society of Testing Material): West Conshonocken, PA, USA, 1987. [Google Scholar]







| Cement | Fine Aggregate | Coarse Aggregate | Fly Ash | Superplasticizer |
|---|---|---|---|---|
| 279 | 931 | 929 | 31 | 1.17 |
| Name of Specimens | Number of Concrete Blocks | Number ofAnchor Specimens | |
|---|---|---|---|
| V000 | 1 | 4 | 0.00 |
| V033 | 0.33 | ||
| V067 | 0.67 | ||
| V100 | 1.00 |
| Name of Specimen | ||||
|---|---|---|---|---|
| V000 | 29.6 | 38.0 | 2.55 | |
| 30.3 | 35.2 | 2.17 | ||
| 40.5 | 45.8 | 1.52 | ||
| 23.6 | 26.4 | 1.66 | ||
| Mean | 31.0 | 36.3 | 1.98 | |
| (Std.) | (7.01) | (8.01) | (0.48) | |
| V033 | 35.2 | 42.9 | 3.78 | |
| 29.5 | 38.2 | 3.81 | ||
| 35.3 | 41.8 | 4.06 | ||
| 28.1 | 30.5 | 2.76 | ||
| Mean | 32.0 | 38.3 | 3.60 | |
| (Std.) | (3.78) | (5.63) | (0.58) | |
| V067 | 34.8 | 48.7 | 8.58 | |
| 34.6 | 55.9 | 9.56 | ||
| 33.4 | 48.7 | 8.64 | ||
| 29.8 | 43.6 | 7.59 | ||
| Mean | 33.1 | 49.2 | 8.59 | |
| (Std.) | (2.31) | (5.05) | (0.80) | |
| V100 | 37.4 | 52.1 | 12.27 | |
| 30.7 | 59.4 | 9.72 | ||
| 28.8 | 53.8 | 13.76 | ||
| 30.7 | 43.7 | 9.56 | ||
| Mean | 31.9 | 52.2 | 11.33 | |
| (Std.) | (3.77) | (6.48) | (2.04) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Choi, E.; Cho, B.-S. Shear Failure Mode and Concrete Edge Breakout Resistance of Cast-In-Place Anchors in Steel Fiber-Reinforced Normal Strength Concrete. Appl. Sci. 2020, 10, 6883. https://doi.org/10.3390/app10196883
Lee J-H, Choi E, Cho B-S. Shear Failure Mode and Concrete Edge Breakout Resistance of Cast-In-Place Anchors in Steel Fiber-Reinforced Normal Strength Concrete. Applied Sciences. 2020; 10(19):6883. https://doi.org/10.3390/app10196883
Chicago/Turabian StyleLee, Jong-Han, Eunsoo Choi, and Baik-Soon Cho. 2020. "Shear Failure Mode and Concrete Edge Breakout Resistance of Cast-In-Place Anchors in Steel Fiber-Reinforced Normal Strength Concrete" Applied Sciences 10, no. 19: 6883. https://doi.org/10.3390/app10196883







