A Quantitative Study on the Void Defects Evolving into Damage in Wind Turbine Blade Based on Internal Energy Storage

Abstract

As manufacturing defects, voids in wind turbine blades may cause damage under fatigue loads. In this paper, the internal energy storage is used as an indicator to identify the critical moment when a defect evolves into damage. The heat transfer equation of composites material containing void defects is derived based upon the theory of the thermodynamics of irreversible processes. In order to obtain the numerical calculation model of the internal energy storage of the evolving process, the thermal conductivity along the transverse direction is homogenized as the temperature date along this direction is acquired by a thermal camera. Specimens with different void fractions are tested with infrared thermal imaging under fatigue load, during which the stress, strain and temperature data are acquired to establish the curve of internal energy storage against the fatigue cycle. This relationship curve can be used to identify the critical moment when void defects evolve into damage. The feasibility of this method is proven by microscopic observation.

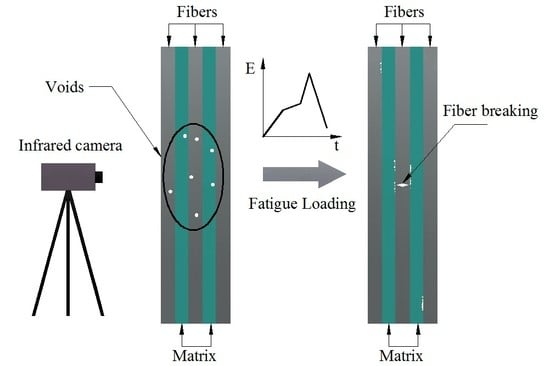
1. Introduction

As a new type of clean energy, wind energy can be exploited and utilized by producing electricity with wind turbines [1]. Comparing to other parts of the wind turbine, its blade is the most important part of the wind turbine to capture wind energy. The blade is easy to damage in the terrible working environment [2,3]. The maintaining and replacement of the blade is hard to carry out because of its heavy weights [4]. Thus, it is essential to develop the health monitoring technology of the blade to adapt the development of the wind power industry. However, it is difficult to detect the early damage of a particular blade. The manufacturing defects may reduce the strength of the blade especially in the defect region. However, the defective blade can still be sold even though it contains voids, because the overall strength can meet the requirements of the ex-factory inspection standards. The fibers around the defect area will break under loads, leading to the interlayer cracking and the actual damage. The corresponding time point can be detected as the critical moment when damage occurs.

At present, resin-based, glass-fiber-reinforced plastic (GFRP) is commonly used as the material of the blade [5]. As a high-quality substitute material for metal materials, the GFRP composite has the advantages on light weight, corrosion resistance, excellent strength and fatigue resistance [6]. The girder is the main load-bearing structure of the blade, which also causes blade fracture mainly [7]. The main structure of the girder is laminate, in which unidirectional glass-fiber fabric cloth is used. During the process of vacuum, the pressure of the volatile gas would increase as the temperature rises during solidification if the air bubbles are not excluded totally. Voids are formed and grown, and then remain in the laminate when the voids’ pressure exceeds the internal pressure of the resin fluid [8]. Therefore, a method to study the evolution of void defects in unidirectional GFRP laminate is proposed, which can provide a basis reference for the technological inspection in the production of blades.

Void is a common defect which may occur during the process of blade manufacturing. A lot of researches make the effort to understand the effect of void defect on the mechanical properties of composites. Chambers et al. studied the damage propagation of unidirectional carbon fiber composites under bending fatigue loading, and found that the fatigue life decreased from 10⁶ times to 2000 times at the same stress level, when the void fraction changes from 1.6% to 3.1% [9]. A large number of studies have shown that the fatigue resistance and corrosion resistance of composites decreases as the void fraction increases, and then the shear strength, compressive strength and flexural strength are correspondingly greatly reduced [10,11]. Based on the influence of the void on the mechanical properties of composites, the effect of different void fractions on the damage identification of composites has been conducted.

Fatigue damage in the process of defect evolution is irreversible, which deteriorates that the material properties grow progressively toward a critical condition when damage occurs [12,13,14,15]. Take fiber–matrix debonding as an example, in the case of the fatigue loading of matrix-dominated composites, fiber pull-out and matrix cracking generate a significant amount of heat, which causes temperature increments even when the stresses are well below the high cycle fatigue strength of the material [16]. According to a number of authors, different forms of energy are regarded as fatigue damage state indicators. During the fatigue test, internal energy storage within the material dissipates as heat [17,18,19,20,21]. Gamstedt et al. used heat dissipation as a damage parameter when analyzing the fatigue behavior of angle-ply and unidirectional hybrid laminates [22]. Kaleta et al. assumed that the internal energy storage within the material can be used as a fatigue damage indicator [23]. Risitano and co-workers proposed the use of a parameter derived from the experimental measurement of the surface temperature, which has been correlated to the internal energy storage after the failure of composites. Moreover, such a parameter has been assumed as a material constant at fatigue failure [24]. These studies show that the damage evolution of the internal defects of materials under fatigue is an irreversible thermodynamic process, during which the internal energy storage of the plastic deformation zone of defects can be used as the indicator of defect evolution.

Of particular interest in this paper is to investigate the void defects of the main girder in wind turbine blades. The heat transfer equation of the blade is derived based on the theory of irreversible thermodynamics. The thermal conductivity in the transverse direction of fibers is homogenized, and the internal energy storage calculation model of the void defect evolution process is obtained. Through the fatigue infrared thermal imaging tests, the relationship curve between internal energy storage and the number of cycles is established. The critical moment of damage evolution is identified according to the internal energy storage threshold. Finally, the internal energy storage criterion that the void defects evolve into actual damage is verified by microscopic observation.

2. Internal Energy Storage Calculation Model of Defect Evolution Process

Energy cannot be absorbed by large plastic deformations, because the residual strain of the blade material with defects under fatigue load is small. Part of the mechanical energy is stored in the material in the form of internal energy storage, and most of the remaining energy is dissipated as heat [25]. According to the law of the conservation of energy, with the mechanical energy $W$, the heat dissipation $Q$ and the internal energy storage $E$ that is generated during the material loading, we can express the energy balance equation as follows [26]:

$$W=E+Q,$$

(1)

where $E$ is the internal energy storage, and $Q$ is the heat source intensity caused by the internal friction, that is, the heat dissipation.

The accumulation of the internal energy storage during defects evolution causes irreversible changes in the microstructure of the material. The mechanical energy W at the continuous and uniform position can be expressed as follows:

$$W=\sigma \epsilon V,$$

(2)

where $\sigma$ is the stress in a cycle, $\epsilon$ is the strain in a cycle and $V$ is the volume of material within the measurement range.

According to Fourier’s law of heat conduction [27]:

$$Q+\lambda {\nabla }^{2}T=\rho c\frac{\partial T}{\partial t},$$

(3)

where $\nabla$ represents the Laplace operator, $\rho$ represents the density of the material (kg/m³), λ represents the thermal conductivity (W/(m·°C)), and c represents the specific heat capacity (J/(kg·°C)).

According to the law of energy and the Gauss theorem, Equation (3) can be transformed as follows [28]:

$$Q-\nabla ·\overrightarrow{q}=\rho c\frac{\partial T}{\partial t},$$

(4)

As the GFRP composite is anisotropic, its thermal conductivity is also anisotropic. The thermal conductivity is no longer a constant, but a second-order tensor consisting of nine components ${\lambda }_{ij}$, i, j = 1, 2, 3. Therefore, the linear combination of the temperature gradients of the heat fluxes in the Cartesian coordinate system along the three coordinate axes is as follows [29]:

$$\{\begin{array}{c}-q_x{=\lambda }_{11}\frac{\partial T}{\partial x}{+\lambda }_{12}\frac{\partial T}{\partial y}{+\lambda }_{13}\frac{\partial T}{\partial z},\\ -q_y{=\lambda }_{21}\frac{\partial T}{\partial x}{+\lambda }_{22}\frac{\partial T}{\partial y}{+\lambda }_{23}\frac{\partial T}{\partial z}\\ -q_y{=\lambda }_{21}\frac{\partial T}{\partial x}{+\lambda }_{22}\frac{\partial T}{\partial y}{+\lambda }_{23}\frac{\partial T}{\partial z},\end{array},$$

(5)

By substituting (5) into (4), we obtain the following:

$${Q+\lambda }_{11}\frac{{\partial }^{2}T}{\partial x^2}{+\lambda }_{22}\frac{{\partial }^{2}T}{\partial y^2}{+\lambda }_{33}\frac{{\partial }^{2}T}{\partial z^2}+\left({\lambda }_{12}{+\lambda }_{21}\right)\frac{{\partial }^{2}T}{\partial x\partial y}+\left({\lambda }_{13}{+\lambda }_{31}\right)\frac{{\partial }^{2}T}{\partial x\partial z}+\left({\lambda }_{23}{+\lambda }_{32}\right)\frac{{\partial }^{2}T}{\partial y\partial z}=\rho c\frac{\partial T}{\partial t},$$

(6)

According to the Onsager principle of the thermodynamics of irreversible processes, the phenomenological coefficients in Equation (5) have the following reciprocal relationship:

$${\lambda }_{ij}{=\lambda }_{ji}i,j=1,2,3,i\ne j,{\lambda }_{ii}{\lambda }_{jj}>0,$$

(7)

The axes are x, y and z as the coordinate system shown in Figure 1. Axis x is in the longitude direction of the fibers, axis y is in the transverse direction and axis z is the thickness direction of the laminate. The corresponding dominant thermal coefficients are denoted as ${\lambda }_x{,\lambda }_y$ and ${\lambda }_z$, respectively, and the differential equation of Equation (6) can be simplified to:

$${Q+\lambda }_x\frac{{\partial }^{2}T}{\partial x^2}{+\lambda }_y\frac{{\partial }^{2}T}{\partial y^2}{+\lambda }_z\frac{{\partial }^{2}T}{\partial z^2}=\rho c\frac{\partial T}{\partial t},$$

(8)

when the thickness of the GFRP composite is tiny, the heat conduction effect in the thickness direction can be ignored in the calculation, so the thermal conductivity in the x direction and y direction on the coordinate axis are considered. Therefore, the Formula (8) is simplified as follows:

$${Q+\lambda }_x\frac{{\partial }^{2}T}{\partial x^2}{+\lambda }_y\frac{{\partial }^{2}T}{\partial y^2}=\rho c\frac{\partial T}{\partial t},$$

(9)

The heat dissipation $Q$ obtained by Equation (9) is:

$$Q=\rho c\frac{\partial T}{\partial t}-{\lambda }_x\frac{{\partial }^{2}T}{\partial x^2} -{\lambda }_y\frac{{\partial }^{2}T}{\partial y^2},$$

(10)

The calculation model of the internal energy storage $E$ in the process of the defect evolution derived from Equations (1), (2) and (10) is:

$$E=\sigma \epsilon V-\rho c\frac{\partial T}{\partial t}{+\lambda }_x\frac{{\partial }^{2}T}{\partial x^2}{+\lambda }_y\frac{{\partial }^{2}T}{\partial y^2},$$

(11)

where ${\lambda }_x$ represents the thermal conductivity in the longitude direction of the fibers of the experimental material and ${\lambda }_y$ represents the thermal conductivity in the transverse direction of the fibers of the experimental material.

3. Simplification of Physical Property Parameters of Materials with Void Defects

The void-defect affects the thermal properties of the glass fiber and the epoxy resin in composites laminate. According to the characteristics of the unidirectional composite laminate, the parameters are homogenized and the following hypotheses are Formulated [30]:

• Glass fibers are evenly distributed in the resin matrix, void defects only exist in the resin matrix, and the material is assumed to have no other manufacturing defects. In the calculations, the GFRP laminate with void defects is regarded as a structure having a mixed volume of air and the GFRP.
• The glass fiber and the resin matrix are in firm contact, and the contact resistance is negligible.
• The performance parameters of the material in a transient temperature field remain to be constant, which do not change as the temperature changes. In the x-axis direction, the phases of the fiber and the resin are all continuous during the heat conduction. In the y-axis direction, the resin is in the continuous phase, and the fiber is in the discrete phase.

The properties of the experimental material with different void fractions were homogenized, and the thermal performance parameters $\rho$, $c$, ${\lambda }_h$ are calculated as follows:

$${\rho =\rho }_g·V_g{+\rho }_a·(1-V_g),$$

(12)

$${c=c}_g·V_g{+c}_a·(1-V_g),$$

(13)

$${\lambda }_h{=\lambda }_{gx}·V_g{+\lambda }_a·(1-V_g),$$

(14)

where ${\rho }_g$ and ${\rho }_a$ represent the density of GFRP and the air respectively. $c_g$ and $c_a$ represent the specific heat capacity of GFRP and the air, respectively. ${\lambda }_{gx}$ represents the thermal conductivity in the longitudinal direction of the fibers of GFRP. ${\lambda }_a$ represents the thermal conductivity of the air. $V_g$ represents the volume fractions of the experimental material except the voids. $\rho$ represents the density of the experimental material. $c$ represents the specific heat capacity of the experimental material. ${\lambda }_h$ represents the thermal conductivity in the longitude direction of the fibers of the experimental material.

The thermal conductivity in the transverse direction has a greatest influence on the surface temperature of the specimen, which can be acquired by an infrared camera. Therefore, the thermal conductivity in the transverse direction of the fibers is simplified, and the thermal conductivity ${\lambda }_l$ in this direction can be represented as follows:

$${\lambda }_l=(\frac{V_g}{{\lambda }_{gy}}+\frac{1-V_g}{{\lambda }_a}{)}^{-1},$$

(15)

where ${\lambda }_{gy}$ is the thermal conductivity in the vertical direction of the fibers of GFRP.

After using Equations (12)−(15) to calculate the performance parameters of $\rho$, $c$,${\lambda }_h$,${\lambda }_l$, we substituted these parameters into (11) to obtain the calculation model of the internal energy storage $E$ in the process of defect evolution:

$$E=\sigma \epsilon V-\rho c\frac{\partial T}{\partial t}{+\lambda }_h\frac{{\partial }^{2}T}{\partial x^2}{+\lambda }_l\frac{{\partial }^{2}T}{\partial y^2},$$

(16)

where ${\lambda }_h$ is the thermal conductivity in the longitudinal direction of the fibers, ${\lambda }_l$ is the thermal conductivity in the vertical direction of the fibers.

According to Formula (16), if the $\sigma$, $\epsilon$, $V$, $c$, $\rho$, ${\lambda }_h$ and ${\lambda }_l$ in the process of defect evolution are already known, the internal energy storage value can be obtained.

4. Fatigue Infrared Thermal Imaging Test

4.1. Test Methods

For this study, the GFRP materials which are widely used in the 1.5 MW wind turbine blade are chosen to fabricate the specimen. ECW600-1270 unidirectional glass fiber and 920W epoxy resin provided by Taishan Fiberglass Inc. (Taishan, China). were used to produce specimens. The fiber cloth used in the experiment was unidirectional prepreg glass cloth, and the ratio of epoxy resin was 42%. The laminates were hand-laid and the fiber layup angle was 0° [20]. The vacuum bag–autoclave process was used to cure the GFRP composite. The pressure of the vacuum bag is 0.06 MPa. The void fractions can be varied by applying different autoclave pressures [31]. In order to obtain different void fractions, specimens were prepared respectively under three different autoclave curing pressures of 0.1 MPa, 0.3 MPa and 0.4 MPa. According to the ASTM D3039 standard, the specimens were cut with a diamond cutting machine. Ten specimens were produced under each of the three curing pressures with the size of 250 mm × 25 mm × 10 mm. Then the cutting surfaces of the specimens were polished and the allowable parallelism error of the edges should be less than 0.25 mm. It is necessary to bond the bracing sheets at both ends of each specimen to prevent it from slipping off the test machine during the loading process, which may reduce the reliability of data. The material of the tab was a continuous E glass fiber-reinforced polymer with the length of 55 mm and the thickness of 2 mm. The schematic of the specimen is shown in Figure 2.

The cured laminates were separately ultrasonically scanned to evaluate the different void fractions under each curing pressure. The regions with uniformed distributed void defects were chosen to be observed by a microscope according to the scanning results.

Then a micrograph was obtained, the void fraction of which was analyzed by an image analysis software. Then the void defects area was marked on the surface of each specimen. The analysis results showed that when curing pressures were 0.4 MPa, 0.3 MPa and 0.1 MPa, the average void fractions of each group were 0.5%, 2.8% and 5.7%, correspondingly. The three groups of specimens were marked as A, B, C.

The specimens A, B and C were tested in a static tensile test and the pull–pull fatigue test under the condition of room temperature and air medium. An infrared camera NEC R300 was used to measure the surface temperature accurately. As shown in Figure 3, an electro-hydraulic servo universal fatigue testing machine MTS810 was used in these tests. The maximum static load was 333 kN, the maximum dynamic load was 250 kN and the frequency range was 0–30 Hz. The operating wavelength of NEC R300 thermal imaging camera was 8–12 μm, the measurement accuracy was ±0.1 °C and the frame frequency range was from 8.5 Hz to 60 Hz.

In order to obtain a high and uniform surface emissivity of the specimen, a thin oxide layer on the surface of the specimen was previously removed with fine-grained sandpaper. Then a thin layer of black paint with a high emissivity was applied to the surface of the specimen. The specimen in the same environment was placed with the experiment equipment 24 h before the test. The specimen was clamped tightly, and a strain gauge was attached to the center of the back of the specimen, then an external strain meter was attached to the strain gauge. The temperature and humidity of the environment should be constant during the entire experimental process to avoid the influence of changing temperature in the infrared thermograph. The infrared camera was calibrated and automatically focused before being used. During the test, it was necessary to ensure that the infrared camera was on the same horizontal line with the specimen, so as to ensure that the infrared thermograph was clearly displayed at the center of the screen. The infrared camera was set to take a photo in every 3 s.

The static strength tensile test was loaded using displacement control at a loading rate of 2 mm/min. The fatigue test adopted force-controlled loading in which the loading frequency was 10 Hz, the waveform was sinusoidal, and the stress ratio was R = 0.1. The changes of stress, strain and average temperature could be simultaneously observed and recorded by the experimental system during the evolution process of the void defects.

4.2. Experimental Results

Three specimens are selected from each group for the static strength tensile test. The experimental results are shown in

Table 1. Static strength tensile experimental results.

Test Number	Void Fraction (%)	Static Strength/MPa
		Experimental Results			Average Value
A	0.5	488.44	470.90	478.09	479.14
B	2.8	382.97	343.81	403.37	376.72
C	5.7	253.82	264.24	277.20	265.09

.

From Table 1, the larger the void fraction of the specimen is, the lower the static tensile strength is, indicating that the existence of void defects reduces the bearing capacity of the composite structure to a certain degree. The average static strengths of the three groups A, B, C are obtained as 479.14 MPa, 376.72 MPa and 265.09 MPa from the test, respectively.

The load-number of cycles curve and stress–strain curve during the pull–pull fatigue test of the three groups A, B and C are shown in Figure 4.

As shown in Figure 4a, during the loading process, the load-number of cycles curves of the three groups of specimens follow the same trend, that is, they all increase first and then decrease. Additionally, the larger the void fraction is, the lower the fatigue load value is, because the local stress concentration is generated in a field where the void defects are densely distributed, resulting in a decrease in the strength. The stress at this field quickly falls to the limit stress, which is the corresponding stress when each group of specimens is subjected to fracture or failure. The limit stress can be sustained by nearby fibers at best, and then damage is formed. Figure 4b illustrates the stress $\sigma$ and strain $\epsilon$ of the three groups of specimens at any time during the fatigue loading. The value of the internal energy storage E can be calculated by substituting the stress $\sigma$ and strain $\epsilon$ into Equation (16). However, there is no determination in previous studies of the critical moment at which the defect evolves into actual damage. The defect evolution causes the interior of the material to be irreversibly deformed, and the energy is released in the form of heat dissipation, which is reflected as the temperature change on the infrared thermograph. The surface temperature of the specimen is measured by an infrared camera and formation of actual damage is studied from the perspective of energy dissipation. Taking group C as an example, the infrared thermographs of the defect evolution process monitored in the specimen are shown in Figure 5, and the voids area is marked.

It can be seen from Figure 5 that in the marked defect area, the surface temperature distribution is not uniform, and as the heat dissipation increases during the defect evolution process, the surface temperature rises, and an obvious regional temperature field appears. Later, this defect evolution area continues to expand and be enhanced until the number of cycles is up to 8076, indicating that the defect would not evolve any longer, which means that the material has undergone tremendous damage. When the defect evolution areas of the infrared thermograph of group A and group B are no longer expanded, the corresponding numbers of cycles are 9501 and 8784, respectively. However, the criterion for the critical moment of damage still needs to be clarified from the theoretical variation of internal energy storage.

4.3. Calculated Results of Internal Energy Storage

In order to obtain the internal energy storage values of the defect evolution process of the three groups of A, B and C, several steps are adopted as follows. Firstly, the void fractions of the three groups are 0.5%, 2.8% and 5.7%, then the performance parameters of GFRP composites in

Table 2. Performance parameters of the glass-fiber-reinforced plastic (GFRP) composites.

Name	Model	ρg/kg·m−3	Cg/KJ·(kg·k)−1	${\mathit{\lambda }}_{\mathit{x}}/\mathbf{W}·{(\mathbf{m}·\mathbf{k})}^{-1}$	${\mathit{\lambda }}_{\mathit{y}}/\mathbf{W}·{(\mathbf{m}·\mathbf{k})}^{-1}$
epoxy resin	920 W	0.920	1	0.98	0.87
glass fiber	ECW600-1270	2780	0.76	1.46	1.22
GFRP		2550	0.8	1.3	0.97

and the air performance parameters in

Table 3. Performance parameters of air [32].

$\mathit{\rho }$a/kg·m−3	Ca/KJ·(kg·k)−1	${\mathit{\lambda }}_{\mathit{a}}/\mathbf{W}·{(\mathbf{m}·\mathbf{k})}^{-1}$
1.293	1.004	2.57

are substituted into Formulas (12)–(15), and the values of $c$, $\rho$, ${\lambda }_h$, ${\lambda }_l$ of A, B and could be obtained, respectively. V represents the valid measurement volume, which is the difference between the volume of a specimen with dimensions of 250 × 25 × 10 mm and that of the part covered by two tabs, and the dimension of each part is 55 × 25 × 10 mm. $\sigma$, $\epsilon$, $V$ and T of A, B and C at each moment in the test are substituted into the Formula (16), and three internal energy storage values can be obtained.

The calculated internal energy storage $E$- number of cycles curve is shown in Figure 6.

As shown in Figure 6, the internal energy storage values of the three groups all show a trend of rising first and then decreasing, and each group has a maximum peak of internal energy storage. During the evolution of void defects, the plastic deformation energy increases gradually, leading to a gradual rise of the internal energy storage. The accumulated internal energy storage value reaches the critical threshold, when the material actually damages, and the internal storage energy reaches a maximum peak. At the critical moment, the sound of internal fiber breakage can be heard, the material properties deteriorates rapidly, and the heat dissipation energy is quickly released, causing the surface temperature of the specimen rise rapidly in a short time. After that, the deformation becomes severe. The plastic strain energy is released rapidly, which leads to the internal energy storage significantly reduced. By comparing to the internal energy storage peaks of the three curves, the larger the void fraction is, the smaller the peak of internal energy storage is, because the plastic strain energy is tiny in the process of larger defects evolving into actual damage.

It can be seen from Figure 6 that when the internal energy storage in three groups A, B and C reaches peak, respectively, the number of cycles is 9450, 8820 and 8160. It can be assumed that these three moments are the critical moments of the actual damage of the specimens. Figure 5 shows that when the defect area would not evolve any longer, the corresponding numbers of cycles are 9501, 8784 and 8076. This shows that at the critical moment of the assumption, the defect area of the material is almost no longer evolved.

4.4. Microscopic Observation

In order to verify the accuracy of the critical moments obtained by the peak of internal energy storage, the specimens of three groups were stopped twice during the test. The test of group A halted when N = 5567, and ceased when N = 9450 at the critical moment when the actual damage might occur. In this way, the test of group B halted when N = 5385, and ceased when N = 8820, at the suspected critical moment. The test of group C halted when N = 5034, and ceased when N = 8160 at the suspected critical moment. The microscopic images of the defect area marked during the preparation of the specimens were observed under a microscope. The microscope images of group A, group B and group C are shown in Figure 7, Figure 8 and Figure 9, respectively.

As shown in Figure 7a, Figure 8a and Figure 9a, the void defects dispersed in the material matrix, which reduced the strength of the material, and a slight matrix cracking damage emerges in the material. With the defect evolving, the voids gradually deformed and propagated, and the area of the plastic deformation cumulative area became larger and the deformation was also irregular. When the internal fibers of the material were continuously destroyed, the friction between the layers was increased to release more heat dissipation energy, causing the temperature to rise sharply. Then, the structure near the internal defects of the material has undergone an irreversible deformation and the actual damage occurred. At this moment, the internal stored energy value went up to its maximum, and the corresponding internal microstructures are shown in Figure 7b, Figure 8b and Figure 9b. It can be seen that the fibers were completely withdrawn from the matrix, and the bearing capacity was no longer available, indicating that the actual damage began to form. The tests of three groups with the same phenomenon also verified the correctness of the method that the actual damage moments can be identified by the internal energy storage maximum.

5. Conclusions and Outlook

In this paper, the quantitative identification method is developed to detect the local damage of a defect in the wind blade so that the accurate state parameters can be provided for the initial damage state during the fatigue test.

As shown by the experimental results, the theoretical calculation of the simplified formula is consistent with the experimental result, indicating that it is feasible to obtain the value of internal energy storage with this method. During the fatigue test, the internal storage energy will first move up to the maximum value at some point before it starts to decline. The maximum value is the critical threshold, and the corresponding time point is regarded as the critical moment when the defect evolves into damage. Thus, the method proposed in this paper can provide a solution to identify the state of initial damage for the experimental study of damage.

The environmental load during the operation of a wind turbine blade is very complicated, thus the consistency issue between the actual load and the test load will be an important research subject for us in the future. In addition, a method to halt the test process automatically when the fatigue cycles arrive at the setting value is also our research interest in the future, which can ensure that the micrograph can be captured at the most appropriate moment to illustrate the critical state of defect evolution.