In Silico-Enhanced Treatment and Rehabilitation Planning for Patients with Musculoskeletal Disorders: Can Musculoskeletal Modelling and Dynamic Simulations Really Impact Current Clinical Practice?
Abstract
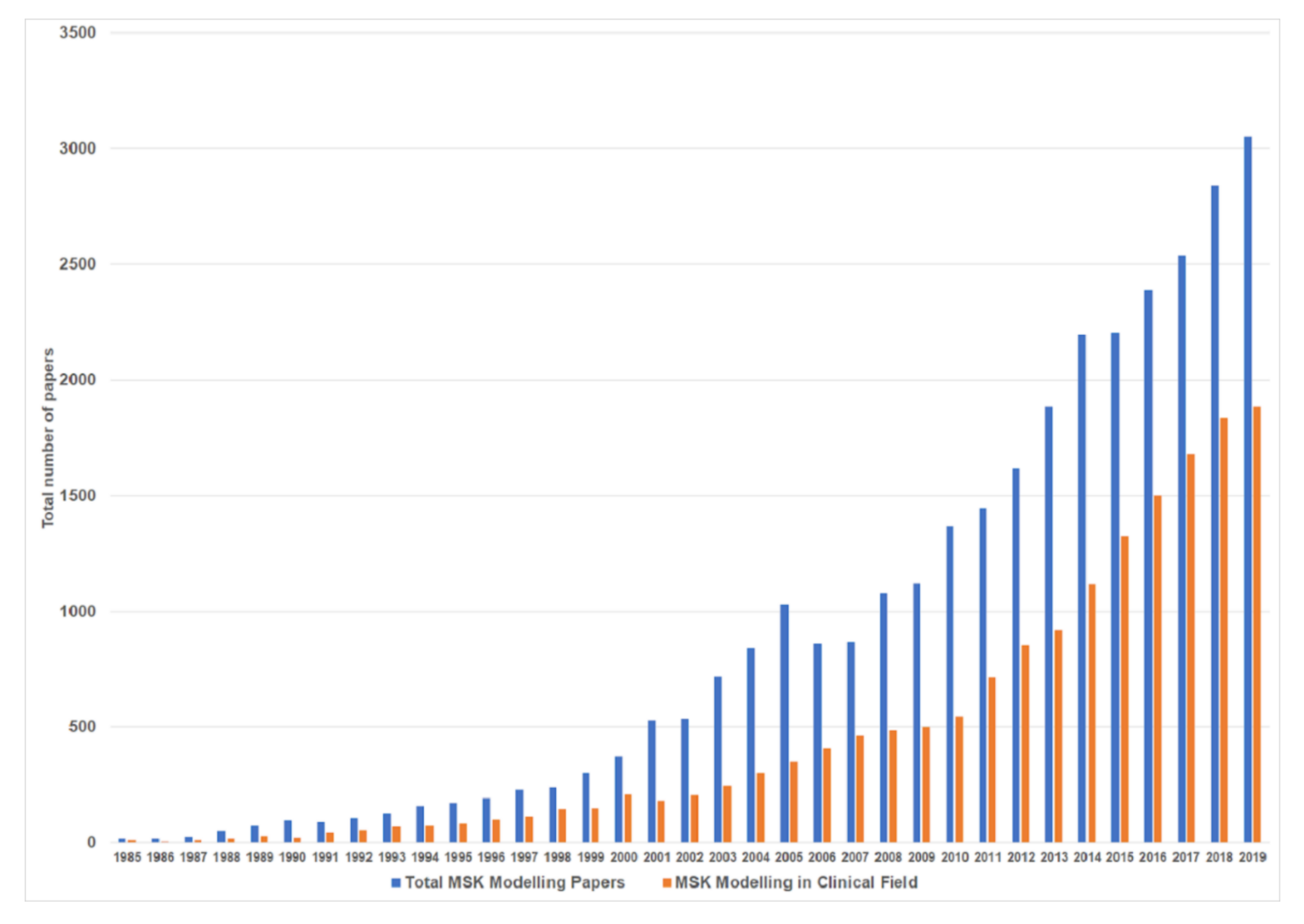
:1. Introduction
2. Model-Based Analysis of MSK Function
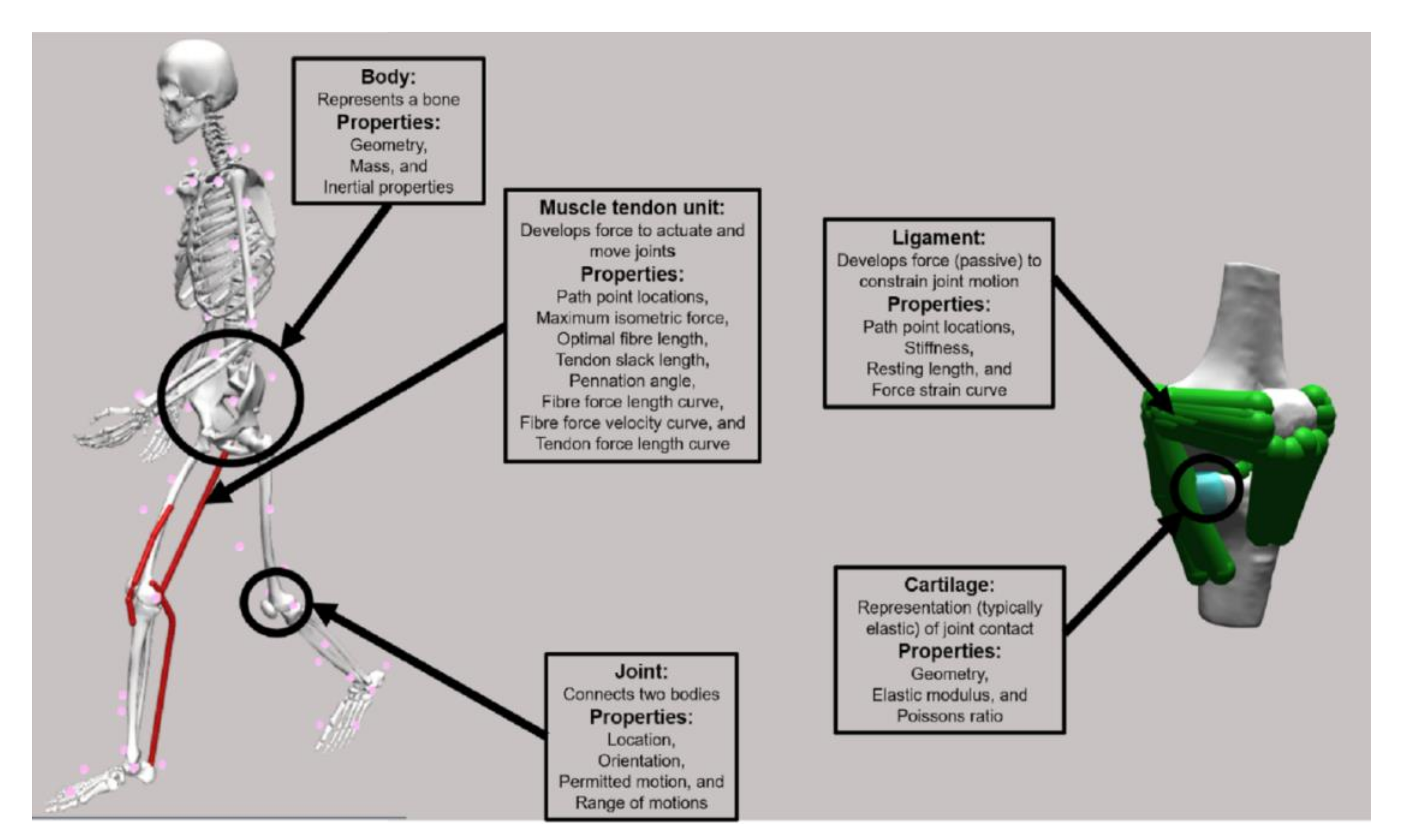
2.1. Model Structure
2.2. Model Customisation
2.3. Inverse Kinematics
2.4. Inverse Dynamics
2.5. Muscle Activation and Force Estimation
2.6. Joint Contact Force Estimation
2.7. Complex Models and Modelling Approaches
2.8. Forward Simulations
3. Role of Musculoskeletal Models in Disease Prevention and Patient Stratification
4. Role of Musculoskeletal Models in Rehabilitation
5. Role of Musculoskeletal Models in Pre-Surgical Planning, and Implant and Assistive Device Design
6. Model Validity
7. Modelling and Simulation Assumptions
8. Barriers for Clinical Implementation
9. Roadmap for Future Transfer of MSK Modelling and Simulations into Clinics
Author Contributions
Funding
Conflicts of Interest
References
- Rajagopal, A.; Dembia, C.L.; Demers, M.S.; Delp, D.D.; Hicks, J.L.; Delp, S.L. Full-Body Musculoskeletal Model for Muscle-Driven Simulation of Human Gait. IEEE Trans. Biomed. Eng. 2016, 63, 2068–2079. [Google Scholar] [CrossRef]
- Lenaerts, G.; De Groote, F.; Demeulenaere, B.; Mulier, M.; Van der Perre, G.; Spaepen, A.; Jonkers, I. Subject-specific hip geometry affects predicted hip joint contact forces during gait. J. Biomech. 2008, 41, 1243–1252. [Google Scholar] [CrossRef]
- Smith, C.R.; Vignos, M.F.; Lenhart, R.L.; Kaiser, J.; Thelen, D.G. The Influence of Component Alignment and Ligament Properties on Tibiofemoral Contact Forces in Total Knee Replacement. J. Biomech. Eng. 2016, 138, 21017. [Google Scholar] [CrossRef]
- Arnold, E.M.; Ward, S.R.; Lieber, R.L.; Delp, S.L. A Model of the Lower Limb of Analysis of Human Movement. Ann. Biomed. Eng. 2010, 38, 269–279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garner, B.A.; Pandy, M.G. The Obstacle Set Method for Representing Muslce Paths in Musculoskeletal Models. Comput. Methods Bioemchan. Biomed. Eng. 2000, 3, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Sherman, M.A.; Seth, A.; Delp, S.L. What is a moment arm? Calculating muscle effectiveness in biomechanical models using generalized coordinates. Proc. ASME Des. Eng. Tech. Conf. 2013, 2013, V07BT10A052. [Google Scholar] [CrossRef] [Green Version]
- Hill, A. V The Heat of Shortening and the Dynamic Constants of Muscle. Proc. R. Soc. B Biol. Sci. 1938, 126, 136–195. [Google Scholar]
- Ziegler, J.; Reiter, A.; Gattringer, H.; Müller, A. Simultaneous identification of human body model parameters and gait trajectory from 3D motion capture data. Med. Eng. Phys. 2020, 84, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Lund, M.E.; Andersen, M.S.; de Zee, M.; Rasmussen, J. Scaling of musculoskeletal models from static and dynamic trials. Int. Biomech. 2015, 2, 1–11. [Google Scholar] [CrossRef]
- Ayusawa, K.; Ikegami, Y.; Nakamura, Y. Simultaneous global inverse kinematics and geometric parameter identification of human skeletal model from motion capture data. Mech. Mach. Theory 2014, 74, 274–284. [Google Scholar] [CrossRef]
- Scheys, L.; Loeckx, D.; Spaepen, A.; Suetens, P.; Jonkers, I. Atlas-based non-rigid image registration to automatically define line-of-action muscle models: a validation study. J. Biomech. 2009, 42, 565–572. [Google Scholar] [CrossRef]
- Modenese, L.; Kohout, J. Automated Generation of Three-Dimensional Complex Muscle Geometries for Use in Personalised Musculoskeletal Models. Ann. Biomed. Eng. 2020, 48, 1793–1804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Sorby, H.; Clement, J.; Thomas, D.L.C.; Hunter, P.; Nielson, P.; Lloyd, D.G.; Taylor, M.; Besier, T.F. The MAP Client: User-Friendly Musculoskeletal Modelling Workflows. In Proceedings of the International Symposium on Biomedical Simulation, Strasbourg, France, 16–17 October 2016; pp. 182–192. [Google Scholar]
- Marra, M.A.; Vanheule, V.; Fluit, R.; Koopman, B.H.F.J.M.; Rasmussen, J.; Verdonschot, N.; Andersen, M.S. A subject-specific musculoskeletal modeling framework to predict in vivo mechanics of total knee arthroplasty. J. Biomech. Eng. 2015, 137, 20904. [Google Scholar] [CrossRef]
- Valente, G.; Crimi, G.; Vanella, N.; Schileo, E.; Taddei, F. nmsBuilder: Freeware to create subject-specific musculoskeletal models for OpenSim. Comput. Methods Programs Biomed. 2017, 152, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Nolte, D.; Tsang, C.K.; Zhang, K.Y.; Ding, Z.; Kedgley, A.E.; Bull, A.M.J. Non-linear scaling of a musculoskeletal model of the lower limb using statistical shape models. J. Biomech. 2016, 49, 3576–3581. [Google Scholar] [CrossRef] [Green Version]
- Modenese, L.; Kohout, J. Automated Generation of Three-Dimensional Complex Muscle Geometries for Use in Personalised Musculoskeletal Models. Ann. Biomed. Eng. 2020, 48, 1793–1804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davico, G.; Pizzolato, C.; Killen, B.A.; Barzan, M.; Suwarganda, E.; Lloyd, D.G.; Carty, C.P. Reconstruction of paediatric lower limb bones using statistical shape modelling for musculoskeletal modelling. Biomech. Model. Mechanobiol. 2019. [Google Scholar] [CrossRef]
- Suwarganda, E.K.; Diamond, L.E.; Lloyd, D.G.; Besier, T.F.; Zhang, J.; Killen, B.A.; Savage, T.N.; Saxby, D.J. Minimal medical imaging can accurately reconstruct geometric bone models for musculoskeletal models. PLoS ONE 2019. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Hislop-Jambrish, J.; Besier, T.F. Predictive statistical models of baseline variations in 3-D femoral cortex morphology. Med. Eng. Phys. 2016, 38, 450–457. [Google Scholar] [CrossRef]
- Torres, P.M.B.; Sanches, J.M.; Gonçalves, P.J.S.; Martins, J.M.M. 3D femur reconstruction using a robotized ultrasound probe. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 884–888. [Google Scholar]
- Barratt, D.C.; Chan, C.S.K.; Edwards, P.J.; Penney, G.P.; Slomczykowski, M.; Carter, T.J.; Hawkes, D.J. Instantiation and registration of statistical shape models of the femur and pelvis using 3D ultrasound imaging. Med. Image Anal. 2008, 12, 358–374. [Google Scholar] [CrossRef]
- Devaprakash, D.; Lloyd, D.G.; Barrett, R.S.; Obst, S.J.; Kennedy, B.; Adams, K.L.; Hunter, A.; Vlahovich, N.; Pease, D.L.; Pizzolato, C. Magnetic Resonance Imaging and Freehand 3-D Ultrasound Provide Similar Estimates of Free Achilles Tendon Shape and 3-D Geometry. Ultrasound Med. Biol. 2019, 45, 2898–2905. [Google Scholar] [CrossRef] [PubMed]
- Obst, S.J.; Newsham-West, R.; Barrett, R.S. In vivo measurement of human achilles tendon morphology using freehand 3-D ultrasound. Ultrasound Med. Biol. 2014, 40, 62–70. [Google Scholar] [CrossRef] [PubMed]
- Barber, L.; Barrett, R.; Lichtwark, G. Validation of a freehand 3D ultrasound system for morphological measures of the medial gastrocnemius muscle. J. Biomech. 2009, 42, 1313–1319. [Google Scholar] [CrossRef]
- Maganaris, C.N. Force-length characteristics of in vivo human skeletal muscle. Acta Physiol. Scand. 2001, 172, 279–285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carbone, V.; Van der Krogt, M.M.; Koopman, B.F.J.M.; Verdonschot, N. Subject-specific musculo-tendon parameters based on MRI and dynamometer tests. Gait Posture 2013, 38, S4. [Google Scholar] [CrossRef]
- Van Campen, A.; Pipeleers, G.; De Groote, F.; Jonkers, I.; De Schutter, J. A new method for estimating subject-specific muscle-tendon parameters of the knee joint actuators: a simulation study. Int. J. Numer. Method. Biomed. Eng. 2014, 30, 969–987. [Google Scholar] [CrossRef] [PubMed]
- Delabastita, T.; Afschrift, M.; Vanwanseele, B.; De Groote, F. Ultrasound-Based Optimal Parameter Estimation Improves Assessment of Calf Muscle–Tendon Interaction During Walking. Ann. Biomed. Eng. 2020, 48, 722–733. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.W.; O’Connor, J.J. Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J. Biomech. 1999, 32, 129–134. [Google Scholar] [CrossRef]
- De Groote, F.; De Laet, T.; Jonkers, I.; De Schutter, J. Kalman smoothing improves the estimation of joint kinematics and kinetics in marker-based human gait analysis. J. Biomech. 2008, 41, 3390–3398. [Google Scholar] [CrossRef]
- Kuo, A.D. A least-squares estimation approach to improving the precision of inverse dynamics computations. J. Biomech. Eng. 1998, 120, 148–159. [Google Scholar] [CrossRef] [Green Version]
- An, K.N.; Kaufman, K.R.; Chao, E.Y. Physiological considerations of muscle force through the elbow joint. J. Biomech. 1989, 22, 1249–1256. [Google Scholar] [CrossRef]
- Anderson, F.C.; Pandy, M.G. Static and dynamic optimization solutions for gait are practically equivalent. J. Biomech. 2001, 34, 153–161. [Google Scholar] [CrossRef]
- Erdemir, A.; McLean, S.; Herzog, W.; van den Bogert, A.J. Model-based estimation of muscle forces exerted during movements. Clin. Biomech. 2007, 22, 131–154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersen, M.S.; Damsgaard, M.; MacWilliams, B.; Rasmussen, J. A computationally efficient optimisation-based method for parameter identification of kinematically determinate and over-determinate biomechanical systems. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 171–183. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.; Pandy, M.G. A neuromusculoskeletal tracking method for estimating individual muscle forces in human movement. J. Biomech. 2007, 40, 356–366. [Google Scholar] [CrossRef] [Green Version]
- De Groote, F.; Van Campen, A.; Jonkers, I.; De Schutter, J. Sensitivity of dynamic simulations of gait and dynamometer experiments to hill muscle model parameters of knee flexors and extensors. J. Biomech. 2010, 43, 1876–1883. [Google Scholar] [CrossRef]
- Thelen, D.G.; Anderson, F.C. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. J. Biomech. 2006, 39, 1107–1115. [Google Scholar] [CrossRef]
- Thelen, D.G.; Anderson, F.C.; Delp, S.L. Generating dynamic simulations of movement using computed muscle control. J. Biomech. 2003, 36, 321–328. [Google Scholar] [CrossRef]
- Pizzolato, C.; Lloyd, D.G.; Sartori, M.; Ceseracciu, E.; Besier, T.F.; Fregly, B.J.; Reggiani, M. CEINMS: A toolbox to investigate the influence of different neural control solutions on the prediction of muscle excitation and joint moments during dynamic motor tasks. J. Biomech. 2015, 48, 3929–3936. [Google Scholar] [CrossRef]
- Lloyd, D.G.; Besier, T.F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomech. 2003, 36, 765–776. [Google Scholar] [CrossRef]
- Steele, K.M.; Demers, M.S.; Schwartz, M.H.; Delp, S.L. Compressive tibiofemoral force during crouch gait. Gait Posture 2012, 35, 556–560. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, H.; Bloswick, D.; Merryweather, A. An improved OpenSim gait model with multiple degrees of freedom knee joint and knee ligaments. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1217–1224. [Google Scholar] [CrossRef] [PubMed]
- Eskinazi, I.; Fregly, B.J. An Open-Source Toolbox for Surrogate Modeling of Joint Contact Mechanics. IEEE Trans. Biomed. Eng. 2016, 63, 269–277. [Google Scholar] [CrossRef] [Green Version]
- Falisse, A.; Serrancoli, G.; Dembia, C.L.; Gillis, J.; Jonkers, I.; De Groote, F. Rapid predictive simulations with complex musculoskeletal models suggest that diverse healthy and pathological human gaits can emerge from similar control strategies. J. R. Soc. Interface 2019, 16, 20190402. [Google Scholar] [CrossRef] [Green Version]
- Dembia, C.; Bianco, N.; Falisse, A.; Hicks, J.; Delp, S. OpenSim Moco: Musculoskeletal optimal control. bioRxiv 2019. [Google Scholar] [CrossRef]
- Geijtenbeek, T. SCONE: Open Source Software for Predictive Simulation of Biological Motion’. J. Open Source Softw. 2019, 4. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Wang, D.; De Groote, F.; Scheys, L.; Jonkers, I. Implementation of physiological functional spinal units in a rigid-body model of the thoracolumbar spine. J. Biomech. 2020, 98, 109437. [Google Scholar] [CrossRef]
- Ackland, D.C.; Roshan-Zamir, S.; Richardson, M.; Pandy, M.G. Muscle and joint-contact loading at the glenohumeral joint after reverse total shoulder arthroplasty. J. Orthop. Res. 2011, 29, 1850–1858. [Google Scholar] [CrossRef] [PubMed]
- Vasavada, A.N.; Li, S.; Delp, S.L. Influence of muscle morphometry and moment arms on the moment-generating capacity of human neck muscles. Spine 1998, 23, 412–422. [Google Scholar] [CrossRef]
- Damsgaard, M.; Rasmussen, J.; Christensen, S.T.; Surma, E.; de Zee, M. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul. Model. Pr. Theory 2006, 14, 1100–1111. [Google Scholar] [CrossRef]
- Delp, S.L.; Loan, J.P.; Hoy, M.G.; Zajac, F.E.; Topp, E.L.; Rosen, J.M. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans. Biomed. Eng. 1990, 37, 757–767. [Google Scholar] [CrossRef]
- Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef] [PubMed]
- Saxby, D.J.; Bryant, A.L.; Modenese, L.; Gerus, P.; Killen, B.A.; Konrath, J.; Fortin, K.; Wrigley, T.V.; Bennell, K.L.; Cicuttini, F.M.; et al. Tibiofemoral Contact Forces in the Anterior Cruciate Ligament-Reconstructed Knee. Med. Sci. Sports Exerc. 2016, 48, 2195–2206. [Google Scholar] [CrossRef] [Green Version]
- Van Rossom, S.; Khatib, N.; Holt, C.; Van Assche, D.; Jonkers, I. Subjects with medial and lateral tibiofemoral articular cartilage defects do not alter compartmental loading during walking. Clin. Biomech. (BristolAvon) 2018, 60, 149–156. [Google Scholar] [CrossRef]
- Meireles, S.; Wesseling, M.; Smith, C.R.; Thelen, D.G.; Verschueren, S.; Jonkers, I. Medial knee loading is altered in subjects with early osteoarthritis during gait but not during step-up-and-over task. PLoS ONE 2017, 12, e0187583. [Google Scholar] [CrossRef] [Green Version]
- Meyer, C.A.G.; Wesseling, M.; Corten, K.; Nieuwenhuys, A.; Monari, D.; Simon, J.-P.; Jonkers, I.; Desloovere, K. Hip movement pathomechanics of patients with hip osteoarthritis aim at reducing hip joint loading on the osteoarthritic side. Gait Posture 2018, 59, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Wesseling, M.; de Groote, F.; Meyer, C.; Corten, K.; Simon, J.-P.; Desloovere, K.; Jonkers, I. Gait alterations to effectively reduce hip contact forces. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 2015, 33, 1094–1102. [Google Scholar] [CrossRef]
- Wesseling, M.; Meyer, C.; Corten, K.; Desloovere, K.; Jonkers, I. Longitudinal joint loading in patients before and up to one year after unilateral total hip arthroplasty. Gait Posture 2018, 61, 117–124. [Google Scholar] [CrossRef]
- Mobasheri, A.; Batt, M. An update on the pathophysiology of osteoarthritis. Ann. Phys. Rehabil. Med. 2016, 59, 333–339. [Google Scholar] [CrossRef]
- Karsdal, M.A.; Christiansen, C.; Ladel, C.; Henriksen, K.; Kraus, V.B.; Bay-Jensen, A.C. Osteoarthritis—A case for personalized health care? Osteoarthr. Cart. 2014, 22, 7–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
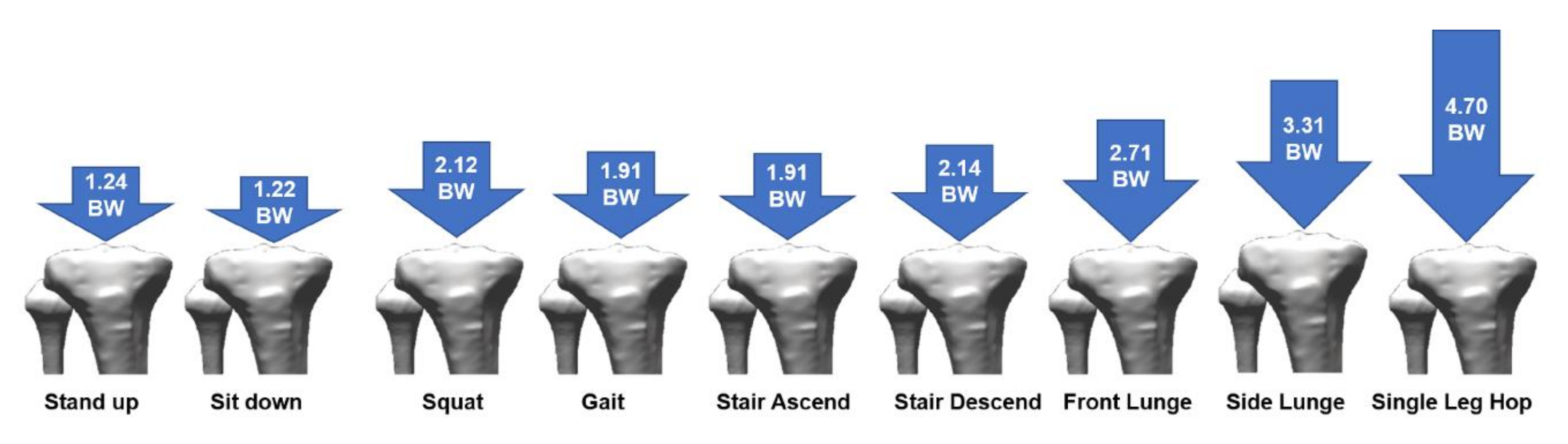
- Van Rossom, S.; Smith, C.R.; Thelen, D.G.; Vanwanseele, B.; Van Assche, D.; Jonkers, I. Knee Joint Loading in Healthy Adults During Functional Exercises: Implications for Rehabilitation Guidelines. J. Orthop. Sports Phys. 2018, 48, 162–173. [Google Scholar] [CrossRef] [Green Version]
- Pellikaan, P.; Giarmatzis, G.; Vander Sloten, J.; Verschueren, S.; Jonkers, I. Ranking of osteogenic potential of physical exercises in postmenopausal women based on femoral neck strains. PLoS ONE 2018, 13, e0195463. [Google Scholar] [CrossRef] [Green Version]
- Giarmatzis, G.; Jonkers, I.; Baggen, R.; Verschueren, S. Less hip joint loading only during running rather than walking in elderly compared to young adults. Gait Posture 2017, 53, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Favre, J.; Erhart-Hledik, J.C.; Chehab, E.F.; Andriacchi, T.P. General scheme to reduce the knee adduction moment by modifying a combination of gait variables. J. Orthop. Res. 2016, 34, 1547–1556. [Google Scholar] [CrossRef]
- Gerbrands, T.A.; Pisters, M.F.; Vanwanseele, B. Individual selection of gait retraining strategies is essential to optimally reduce medial knee load during gait. Clin. Biomech. 2014, 29, 828–834. [Google Scholar] [CrossRef] [PubMed]
- Gerbrands, T.A.; Pisters, M.F.; Theeven, P.J.R.; Verschueren, S.; Vanwanseele, B. Lateral trunk lean and medializing the knee as gait strategies for knee osteoarthritis. Gait Posture 2017, 51, 247–253. [Google Scholar] [CrossRef]
- Shull, P.B.; Silder, A.; Shultz, R.; Dragoo, J.L.; Besier, T.F.; Delp, S.L.; Cutkosky, M.R. Six-week gait retraining program reduces knee adduction moment, reduces pain, and improves function for individuals with medial compartment knee osteoarthritis. J. Orthop. Res. 2013, 31, 1020–1025. [Google Scholar] [CrossRef]
- Shull, P.B.; Lurie, K.L.; Cutkosky, M.R.; Besier, T.F. Training multi-parameter gaits to reduce the knee adduction moment with data-driven models and haptic feedback. J. Biomech. 2011, 44, 1605–1609. [Google Scholar] [CrossRef] [PubMed]
- Uhlrich, S.D.; Silder, A.; Beaupre, G.S.; Shull, P.B.; Delp, S.L. Subject-specific toe-in or toe-out gait modifications reduce the larger knee adduction moment peak more than a non-personalized approach. J. Biomech. 2018, 66, 103–110. [Google Scholar] [CrossRef]
- Wesseling, M.; Meyer, C.; De Groote, F.; Corten, K.; Simon, J.-P.; Desloovere, K.; Jonkers, I. Gait alterations can reduce the risk of edge loading. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 2016, 34, 1069–1076. [Google Scholar] [CrossRef]
- Van Den Noort, J.C.; Steenbrink, F.; Roeles, S.; Harlaar, J. Real-time visual feedback for gait retraining: toward application in knee osteoarthritis. Med. Biol. Eng. Comput. 2015, 53, 275–286. [Google Scholar] [CrossRef]
- Pizzolato, C.; Reggiani, M.; Saxby, D.J.; Ceseracciu, E.; Modenese, L.; Lloyd, D.G. Biofeedback for Gait Retraining Based on Real-Time Estimation of Tibiofemoral Joint Contact Forces. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1612–1621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pizzolato, C.; Reggiani, M.; Modenese, L.; Lloyd, D.G. Real-time inverse kinematics and inverse dynamics for lower limb applications using OpenSim. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 436–445. [Google Scholar] [CrossRef]
- Fregly, B.J.; Reinbolt, J.A.; Rooney, K.L.; Mitchell, K.H.; Chmielewski, T.L. Design of patient-specific gait modifications for knee osteoarthritis rehabilitation. IEEE Trans. Biomed. Eng. 2007, 54, 1687–1695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lombardi, A.V.J.; Berend, K.R.; Adams, J.B. Patient-specific approach in total knee arthroplasty. Orthopedics 2008, 31, 927–930. [Google Scholar] [CrossRef] [PubMed]
- Fitz, W. Unicompartmental Knee Arthroplasty with Use of Novel Patient-Specific Resurfacing Implants and Personalized Jigs. JBJS 2009, 91, 69–76. [Google Scholar] [CrossRef]
- Jun, Y.; Choi, K. Design of patient-specific hip implants based on the 3D geometry of the human femur. Adv. Eng. Softw. 2010, 41, 537–547. [Google Scholar] [CrossRef]
- Dérand, P.; Rännar, L.-E.; Hirsch, J.-M. Imaging, Virtual Planning, Design, and Production of Patient-Specific Implants and Clinical Validation in Craniomaxillofacial Surgery. Craniomaxillofac. Trauma Reconstr. 2012, 5, 137–143. [Google Scholar] [CrossRef] [Green Version]
- Demange, M.K.; Von Keudell, A.; Probst, C.; Yoshioka, H.; Gomoll, A.H. Patient-specific implants for lateral unicompartmental knee arthroplasty. Int. Orthop. 2015, 39, 1519–1526. [Google Scholar] [CrossRef]
- Ackland, D.C.; Robinson, D.; Redhead, M.; Lee, P.V.S.; Moskaljuk, A.; Dimitroulis, G. A personalized 3D-printed prosthetic joint replacement for the human temporomandibular joint: From implant design to implantation. J. Mech. Behav. Biomed. Mater. 2017, 69, 404–411. [Google Scholar] [CrossRef]
- Jonkers, I.; Sauwen, N.; Lenaerts, G.; Mulier, M.; Van der Perre, G.; Jaecques, S. Relation between subject-specific hip joint loading, stress distribution in the proximal femur and bone mineral density changes after total hip replacement. J. Biomech. 2008, 41, 3405–3413. [Google Scholar] [CrossRef]
- Van Rossom, S.; Wesseling, M.; Smith, C.R.; Thelen, D.G.; Vanwanseele, B.; Dieter, V.A.; Jonkers, I. The influence of knee joint geometry and alignment on the tibiofemoral load distribution: A computational study. Knee 2019, 26, 813–823. [Google Scholar] [CrossRef] [PubMed]
- Gromov, K.; Korchi, M.; Thomsen, M.G.; Husted, H.; Troelsen, A. What is the optimal alignment of the tibial and femoral components in knee arthroplasty? Acta Orthop. 2014, 85, 480–487. [Google Scholar] [CrossRef] [PubMed]
- Innocenti, B.; Bellemans, J.; Catani, F. Deviations From Optimal Alignment in TKA: Is There a Biomechanical Difference Between Femoral or Tibial Component Alignment? J. Arthroplast. 2016, 31, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Vanheule, V.; Delport, H.P.; Andersen, M.S.; Scheys, L.; Wirix-Speetjens, R.; Jonkers, I.; Victor, J.; Vander Sloten, J. Evaluation of predicted knee function for component malrotation in total knee arthroplasty. Med. Eng. Phys. 2017, 40, 56–64. [Google Scholar] [CrossRef] [Green Version]
- Wesseling, M.; Meyer, C.; Corten, K.; Simon, J.-P.; Desloovere, K.; Jonkers, I. Does surgical approach or prosthesis type affect hip joint loading one year after surgery? Gait Posture 2016, 44, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Aerts, W.; Scarton, A.; De Groote, F.; Guiotto, A.; Sawacha, Z.; Cobelli, C.; Vander Sloten, J.; Jonkers, I. Validation of plantar pressure simulations using finite and discrete element modelling in healthy and diabetic subjects. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1442–1452. [Google Scholar] [CrossRef] [PubMed]
- Guldemond, N.A.; Leffers, P.; Schaper, N.C.; Sanders, A.P.; Nieman, F.; Willems, P.; Walenkamp, G.H.I.M. The effects of insole configurations on forefoot plantar pressure and walking convenience in diabetic patients with neuropathic feet. Clin. Biomech. 2007, 22, 81–87. [Google Scholar] [CrossRef]
- Lemmon, D.; Shiang, T.Y.; Hashmi, A.; Ulbrecht, J.S.; Cavanagh, P.R. The effect of insoles in therapeutic footwear—A finite element approach. J. Diabetes Complicat. 1997, 30, 615–620. [Google Scholar] [CrossRef]
- Nigg, B.M.; Stergiou, P.; Cole, G.; Stefanyshyn, D.; Mündermann, A.; Humble, N. Effect of shoe inserts on kinematics, center of pressure, and leg joint moments during running. Med. Sci. Sports Exerc. 2003, 35, 314–319. [Google Scholar] [CrossRef] [Green Version]
- Uccioli, L.; Faglia, E.; Monticone, G.; Favales, F.; Durola, L.; Aldeghi, A.; Quarantiello, A.; Calia, P.; Menzinger, G. Manufactured Shoes in the Prevention of Diabetic Foot Ulcers. Diabetes Care 1995, 18, 1376LP–1378LP. [Google Scholar] [CrossRef]
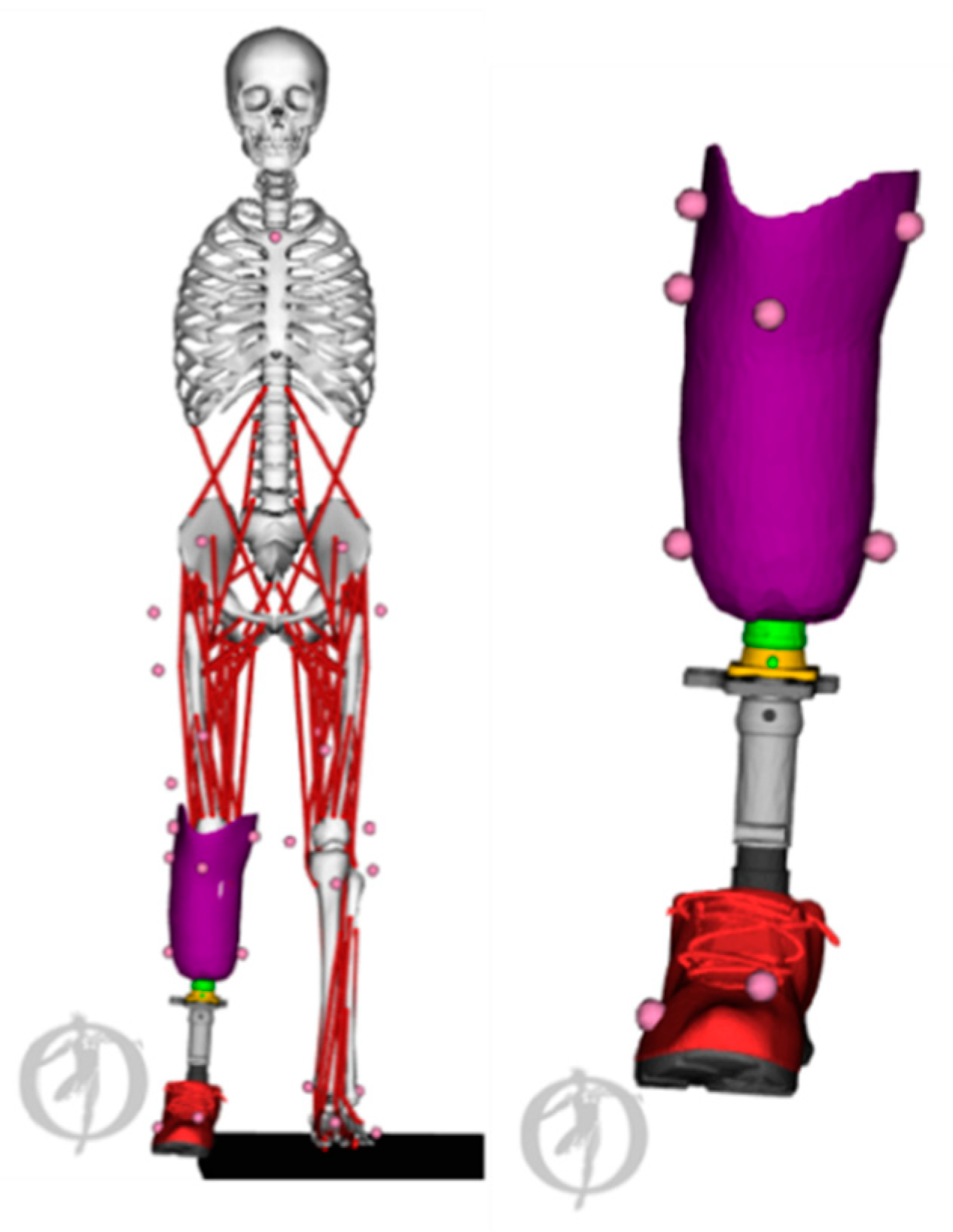
- Rohani, F.; Richter, H.; van den Bogert, A.J. Optimal design and control of an electromechanical transfemoral prosthesis with energy regeneration. PLoS ONE 2017, 12, e0188266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scarton, A.; Guiotto, A.; Malaquias, T.; Spolaor, F.; Sinigaglia, G.; Cobelli, C.; Jonkers, I.; Sawacha, Z. A methodological framework for detecting ulcers’ risk in diabetic foot subjects by combining gait analysis, a new musculoskeletal foot model and a foot finite element model. Gait Posture 2018, 60, 279–285. [Google Scholar] [CrossRef]
- Eilenberg, M.F.; Geyer, H.; Herr, H. Control of a powered ankle-foot prosthesis based on a neuromuscular model. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 164–173. [Google Scholar] [CrossRef] [PubMed]
- Handford, M.L.; Srinivasan, M. Robotic lower limb prosthesis design through simultaneous computer optimizations of human and prosthesis costs. Sci. Rep. 2016, 6, 19983. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thatte, N.; Geyer, H. Toward Balance Recovery With Leg Prostheses Using Neuromuscular Model Control. IEEE Trans. Biomed. Eng. 2016, 63, 904–913. [Google Scholar] [CrossRef]
- Wu, A.R.; Dzeladini, F.; Brug, T.J.H.; Tamburella, F.; Tagliamonte, N.L.; van Asseldonk, E.H.F.; van der Kooij, H.; Ijspeert, A.J. An Adaptive Neuromuscular Controller for Assistive Lower-Limb Exoskeletons: A Preliminary Study on Subjects with Spinal Cord Injury. Front. Neurorobot. 2017, 11, 30. [Google Scholar] [CrossRef]
- Vantilt, J.; Tanghe, K.; Afschrift, M.; Bruijnes, A.K.B.D.; Junius, K.; Geeroms, J.; Aertbeliën, E.; De Groote, F.; Lefeber, D.; Jonkers, I.; et al. Model-based control for exoskeletons with series elastic actuators evaluated on sit-to-stand movements. J. Neuroeng. Rehabil. 2019, 16, 65. [Google Scholar] [CrossRef]
- Serrancoli, G.; Falisse, A.; Dembia, C.; Vantilt, J.; Tanghe, K.; Lefeber, D.; Jonkers, I.; De Schutter, J.; De Groote, F. Subject-Exoskeleton Contact Model Calibration Leads to Accurate Interaction Force Predictions. IEEE Trans. Neural Syst. Rehabil. Eng. Publ. IEEE Eng. Med. Biol. Soc. 2019, 27, 1597–1605. [Google Scholar] [CrossRef]
- Aerts, W.; Creylman, V.; Vander Sloten, J.; Jonkers, I. Extension and anterior alignment of the prosthetic foot normalizes hip and knee loading symmetry in unilateral trans-tibial amputees. GaitPosture 2016, 49, 127. [Google Scholar]
- Hicks, J.L.; Uchida, T.K.; Seth, A.; Rajagopal, A.; Delp, S.L. Is my model good enough? Best practices for verification and validation of musculoskeletal models and simulations of movement. J. Biomech. Eng. 2015, 137, 20905. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Dorn, T.W.; Schache, A.G.; Pandy, M.G. Comparison of different methods for estimating muscle forces in human movement. Proc. Inst. Mech. Eng. Part. H J. Eng. Med. 2011, 226, 103–112. [Google Scholar] [CrossRef]
- Bergmann, G.; Graichen, F.; Rohlmann, A. Hip joint contact forces during stumbling. Langenbeck’s Arch. Surg. 2004, 389, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, G.; Graichen, F.; Rohlmann, A.; Bender, A.; Heinlein, B.; Duda, G.N.; Heller, M.O.; Morlock, M.M. Realistic loads for testing hip implants. Biomed. Mater. Eng. 2010, 20, 65–75. [Google Scholar] [CrossRef] [PubMed]
- Fregly, B.J.; Besier, T.F.; Lloyd, D.G.; Delp, S.L.; Banks, S.A.; Pandy, M.G.; D’Lima, D.D. Grand challenge competition to predict in vivo knee loads. J. Orthop. Res. 2012, 30, 503–513. [Google Scholar] [CrossRef] [Green Version]
- Taylor, W.R.; Schütz, P.; Bergmann, G.; List, R.; Postolka, B.; Hitz, M.; Dymke, J.; Damm, P.; Duda, G.; Gerber, H.; et al. A comprehensive assessment of the musculoskeletal system: The CAMS-Knee data set. J. Biomech. 2017, 65, 32–39. [Google Scholar] [CrossRef]
- Gerus, P.; Sartori, M.; Besier, T.F.; Fregly, B.J.; Delp, S.L.; Banks, S.A.; Pandy, M.G.; D’Lima, D.D.; Lloyd, D.G. Subject-specific knee joint geometry improves predictions of medial tibiofemoral contact forces. J. Biomech. 2013, 9, 2–9. [Google Scholar] [CrossRef] [Green Version]
- Weinhandl, J.T.; Bennett, H.J. Musculoskeletal model choice influences hip joint load estimations during gait. J. Biomech. 2019, 91, 124–132. [Google Scholar] [CrossRef]
- Hoang, H.X.; Pizzolato, C.; Diamond, L.E.; Lloyd, D.G. Subject-specific calibration of neuromuscular parameters enables neuromusculoskeletal models to estimate physiologically plausible hip joint contact forces in healthy adults. J. Biomech. 2018, 80, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Zargham, A.; Afschrift, M.; De Schutter, J.; Jonkers, I.; De Groote, F. Inverse dynamic estimates of muscle recruitment and joint contact forces are more realistic when minimizing muscle activity rather than metabolic energy or contact forces. Gait Posture 2019, 74, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Hoang, H.X.; Diamond, L.E.; Lloyd, D.G.; Pizzolato, C. A calibrated EMG-informed neuromusculoskeletal model can appropriately account for muscle co-contraction in the estimation of hip joint contact forces in people with hip osteoarthritis. J. Biomech. 2019, 83, 134–142. [Google Scholar] [CrossRef] [Green Version]
- Hainisch, R.; Gfoehler, M.; Zubayer-Ul-Karim, M.; Pandy, M.G. Method for determining musculotendon parameters in subject-specific musculoskeletal models of children developed from MRI data. Multibody Syst. Dyn. 2012, 28, 143–156. [Google Scholar] [CrossRef] [Green Version]
- Modenese, L.; Ceseracciu, E.; Reggiani, M.; Lloyd, D.G. Estimation of musculotendon parameters for scaled and subject specific musculoskeletal models using an optimization technique. J. Biomech. 2016, 49, 141–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serrancolí, G.; Kinney, A.L.; Fregly, B.J.; Font-Llagunes, J.M. Neuromusculoskeletal Model Calibration Significantly Affects Predicted Knee Contact Forces for Walking. J. Biomech. Eng. 2016, 138, 810011–8100111. [Google Scholar] [CrossRef] [Green Version]
- Winby, C.R.; Lloyd, D.G.; Kirk, T.B. Evaluation of different analytical methods for subject-specific scaling of musculotendon parameters. J. Biomech. 2008, 41, 1682–1688. [Google Scholar] [CrossRef] [PubMed]
- Falisse, A.; Bar-On, L.; Desloovere, K.; Jonkers, I.; De Groote, F. A spasticity model based on feedback from muscle force explains muscle activity during passive stretches and gait in children with cerebral palsy. PLoS ONE 2018, 13, e0208811. [Google Scholar] [CrossRef] [Green Version]
- Falisse, A.; Van Rossom, S.; Jonkers, I.; De Groote, F. EMG-Driven Optimal Estimation of Subject-SPECIFIC Hill Model Muscle-Tendon Parameters of the Knee Joint Actuators. IEEE Trans. Biomed. Eng. 2017, 64, 2253–2262. [Google Scholar] [CrossRef]
- Zelik, K.E.; Honert, E.C. Ankle and foot power in gait analysis: Implications for science, technology and clinical assessment. J. Biomech. 2018, 75, 1–12. [Google Scholar] [CrossRef]
- Malaguias, T.M.; Silveira, C.; Aerts, W.; De Groote, F.; Dereymaeker, G.; Vander Sloten, J.; Jonkers, J. Extended foot-ankle musculoskeletal models for application in movement analysis. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 153–159. [Google Scholar] [CrossRef] [Green Version]
- Montefiori, E.; Modenese, L.; Di Marco, R.; Magni-Manzoni, S.; Malattia, C.; Petrarca, M.; Ronchetti, A.; de Horatio, L.T.; van Dijkhuizen, P.; Wang, A.; et al. An image-based kinematic model of the tibiotalar and subtalar joints and its application to gait analysis in children with Juvenile Idiopathic Arthritis. J. Biomech. 2019, 85, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Kainz, H.; Carty, C.P.; Maine, S.; Walsh, H.P.J.; Lloyd, D.G.; Modenese, L. Effects of hip joint centre mislocation on gait kinematics of children with cerebral palsy calculated using patient-specific direct and inverse kinematic models. Gait Posture 2017, 57, 154–160. [Google Scholar] [CrossRef] [Green Version]
- Dzialo, C.M.; Pedersen, P.H.; Simonsen, C.W.; Jensen, K.K.; de Zee, M.; Andersen, M.S. Development and validation of a subject-specific moving-axis tibiofemoral joint model using MRI and EOS imaging during a quasi-static lunge. J. Biomech. 2018, 72, 71–80. [Google Scholar] [CrossRef] [Green Version]
- Modenese, L.; Montefiori, E.; Wang, A.; Wesarg, S.; Viceconti, M.; Mazzà, C. Investigation of the dependence of joint contact forces on musculotendon parameters using a codified workflow for image-based modelling. J. Biomech. 2018, 73, 108–118. [Google Scholar] [CrossRef] [PubMed]
- Barzan, M.; Modenese, L.; Carty, C.P.; Maine, S.; Stockton, C.A.; Sancisi, N.; Lewis, A.; Grant, J.; Lloyd, D.G.; Brito da Luz, S. Development and validation of subject-specific pediatric multibody knee kinematic models with ligamentous constraints. J. Biomech. 2019, 93, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Stewart, C.; Jonkers, I.; Roberts, A. Estimation of hamstring length at initial contact based on kinematic gait data. Gait Posture 2004, 20, 61–66. [Google Scholar] [CrossRef]
- Rajagopal, A.; Kidziński, Ł.; McGlaughlin, A.S.; Hicks, J.L.; Delp, S.L.; Schwartz, M.H. Pre-operative gastrocnemius lengths in gait predict outcomes following gastrocnemius lengthening surgery in children with cerebral palsy. PLoS ONE 2020, 15, e0233706. [Google Scholar] [CrossRef]
- van den Bogert, A.J.; Geijtenbeek, T.; Even-Zohar, O.; Steenbrink, F.; Hardin, E.C. A real-time system for biomechanical analysis of human movement and muscle function. Med. Biol. Eng. Comput. 2013, 51, 1069–1077. [Google Scholar] [CrossRef] [Green Version]
- Falisse, A.; Van Rossom, S.; Gijsbers, J.; Steenbrink, F.; van Basten, B.J.H.; Jonkers, I.; van den Bogert, A.J.; De Groote, F. OpenSim Versus Human Body Model: A Comparison Study for the Lower Limbs During Gait. J. Appl. Biomech. 2018, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Pitto, L.; Kainz, H.; Falisse, A.; Wesseling, M.; Van Rossom, S.; Hoang, H.; Papageorgiou, E.; Hallemans, A.; Desloovere, K.; Molenaers, G.; et al. SimCP: A Simulation Platform to Predict Gait Performance Following Orthopedic Intervention in Children With Cerebral Palsy. Front. Neurorobot. 2019, 13, 54. [Google Scholar] [CrossRef] [Green Version]
- Bahl, J.S.; Zhang, J.; Killen, B.A.; Taylor, M.; Soloman, L.B.; Arnold, J.B.; Lloyd, D.G.; Besier, T.F.; Thewlis, D. Statistical shape modelling versus linear scaling: effects on predictions of hip joint centre location and muscle moment arms in people with hip osteoarthritis. J. Biomech. 2019, 85, 164–172. [Google Scholar] [CrossRef] [Green Version]
- Bakke, D.; Besier, T. Shape model constrained scaling improves repeatability of gait data. J. Biomech. 2020, 107, 109838. [Google Scholar] [CrossRef]
- Zhang, J.; Fernandez, J.; Hislop-Jambrish, J.; Besier, T.F. Lower limb estimation from sparse landmarks using an articulated shape model. J. Biomech. 2016, 49, 3875–3881. [Google Scholar] [CrossRef]
- Valente, G.; Taddei, F.; Jonkers, I. Influence of weak hip abductor muscles on joint contact forces during normal walking: probabilistic modeling analysis. J. Biomech. 2013, 46, 2186–2193. [Google Scholar] [CrossRef]
- Bosmans, L.; Valente, G.; Wesseling, M.; Van Campen, A.; De Groote, F.; De Schutter, J.; Jonkers, I. Sensitivity of predicted muscle forces during gait to anatomical variability in musculotendon geometry. J. Biomech. 2015, 48, 2116–2123. [Google Scholar] [CrossRef] [PubMed]
- Karatsidis, A.; Bellusci, G.; Schepers, H.M.; de Zee, M.; Andersen, M.S.; Veltink, P.H. Estimation of Ground Reaction Forces and Moments During Gait Using Only Inertial Motion Capture. Sensors 2016, 17, 75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnson, W.R.; Mian, A.; Donnelly, C.J.; Lloyd, D.; Alderson, J. Predicting athlete ground reaction forces and moments from motion capture. Med. Biol. Eng. Comput. 2018, 56, 1781–1792. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnson, W.R.; Alderson, J.; Lloyd, D.; Mian, A. Predicting Athlete Ground Reaction Forces and Moments From Spatio-Temporal Driven CNN Models. IEEE Trans. Biomed. Eng. 2019, 66, 689–694. [Google Scholar] [CrossRef] [Green Version]
- Tagliapietra, L.; Modenese, L.; Ceseracciu, E.; Mazzà, C.; Reggiani, M. Validation of a model-based inverse kinematics approach based on wearable inertial sensors. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 834–844. [Google Scholar] [CrossRef] [PubMed]
- Konrath, J.; Karatsidis, A.; Schepers, H.; Bellusci, G.; de Zee, M.; Andersen, M. Estimation of the Knee Adduction Moment and Joint Contact Force during Daily Living Activities Using Inertial Motion Capture. Sensors 2019, 19, 1681. [Google Scholar] [CrossRef] [Green Version]
- De Brabandere, A.; Emmerzaal, J.; Timmermans, A.; Jonkers, I.; Vanwanseele, B.; Davis, J. A Machine Learning Approach to Estimate Hip and Knee Joint Loading Using a Mobile Phone-Embedded IMU. Front. Bioeng. Biotechnol. 2020, 8, 320. [Google Scholar] [CrossRef] [Green Version]
- Stetter, B.J.; Krafft, F.C.; Ringhof, S.; Stein, T.; Sell, S. A Machine Learning and Wearable Sensor Based Approach to Estimate External Knee Flexion and Adduction Moments During Various Locomotion Tasks. Front. Bioeng. Biotechnol. 2020, 8, 9. [Google Scholar] [CrossRef]
- Kidziński, Ł.; Yang, B.; Hicks, J.L.; Rajagopal, A.; Delp, S.L.; Schwartz, M.H. Deep neural networks enable quantitative movement analysis using single-camera videos. Nat. Commun. 2020, 11, 4054. [Google Scholar] [CrossRef] [PubMed]
- Pitto, L.; van Rossom, S.; Desloovere, K.; Molenaers, G.; Huenaerts, C.; De Groote, F.; Jonkers, I. Pre-treatment EMG can be used to model post-treatment muscle coordination during walking in children with cerebral palsy. PLoS ONE 2020, 15, e0228851. [Google Scholar] [CrossRef] [Green Version]
- Rabbi, M.F.; Pizzolato, C.; Lloyd, D.G.; Carty, C.P.; Devaprakash, D.; Diamond, L.E. Non-negative matrix factorisation is the most appropriate method for extraction of muscle synergies in walking and running. Sci. Rep. 2020, 10, 8266. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Five basic muscle activation patterns account for muscle activity during human locomotion. J. Physiol. 2004, 556, 267–282. [Google Scholar] [CrossRef] [PubMed]
- Clark, D.J.; Ting, L.H.; Zajac, F.E.; Neptune, R.R.; Kautz, S.A. Merging of healthy motor modules predicts reduced locomotor performance and muscle coordination complexity post-stroke. J. Neurophysiol. 2010, 103, 844–857. [Google Scholar] [CrossRef] [Green Version]
- Torres-Oviedo, G.; Ting, L.H. Muscle Synergies Characterizing Human Postural Responses. J. Neurophysiol. 2007, 98, 2144–2156. [Google Scholar] [CrossRef] [Green Version]
- Reinbolt, J.A.; Haftka, R.T.; Chmielewski, T.L.; Fregly, B.J. Are patient-specific joint and inertial parameters necessary for accurate inverse dynamics analyses of gait? IEEE Trans. Biomed. Eng. 2007, 54, 782–793. [Google Scholar] [CrossRef] [Green Version]
- Lerner, Z.F.; Demers, M.S.; Delp, S.L.; Browning, R.C. How tibiofemoral alignment and contact locations affect predictions of medial and lateral tibiofemoral contact forces. J. Biomech. 2015, 48, 644–650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ackland, D.C.; Lin, Y.-C.; Pandy, M.G. Sensitivity of model predictions of muscle function to changes in moment arms and muscle–tendon properties: A Monte-Carlo analysis. J. Biomech. 2012, 45, 1463–1471. [Google Scholar] [CrossRef] [PubMed]
- Cleather, D.J.; Bull, A.M.J. Knee and hip joint forces—Sensitivity to the degrees of freedom classification at the knee. Proc. Inst. Mech. Eng. Part. H J. Eng. Med. 2011, 225, 621–626. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Killen, B.A.; Falisse, A.; De Groote, F.; Jonkers, I. In Silico-Enhanced Treatment and Rehabilitation Planning for Patients with Musculoskeletal Disorders: Can Musculoskeletal Modelling and Dynamic Simulations Really Impact Current Clinical Practice? Appl. Sci. 2020, 10, 7255. https://doi.org/10.3390/app10207255
Killen BA, Falisse A, De Groote F, Jonkers I. In Silico-Enhanced Treatment and Rehabilitation Planning for Patients with Musculoskeletal Disorders: Can Musculoskeletal Modelling and Dynamic Simulations Really Impact Current Clinical Practice? Applied Sciences. 2020; 10(20):7255. https://doi.org/10.3390/app10207255
Chicago/Turabian StyleKillen, Bryce A, Antoine Falisse, Friedl De Groote, and Ilse Jonkers. 2020. "In Silico-Enhanced Treatment and Rehabilitation Planning for Patients with Musculoskeletal Disorders: Can Musculoskeletal Modelling and Dynamic Simulations Really Impact Current Clinical Practice?" Applied Sciences 10, no. 20: 7255. https://doi.org/10.3390/app10207255
APA StyleKillen, B. A., Falisse, A., De Groote, F., & Jonkers, I. (2020). In Silico-Enhanced Treatment and Rehabilitation Planning for Patients with Musculoskeletal Disorders: Can Musculoskeletal Modelling and Dynamic Simulations Really Impact Current Clinical Practice? Applied Sciences, 10(20), 7255. https://doi.org/10.3390/app10207255





