Tide-Surge-Wave Interaction in the Taiwan Strait during Typhoons Soudelor (2015) and Dujuan (2015)
Abstract
1. Introduction
2. Materials and Methods
2.1. FETSWCM
- ζ = the rise of the water level above the undisturbed sea level;
- t = time;
- x, y = longitude (east) and latitude (north), respectively;
- U, V = the east and north components, respectively, of depth averaged velocity;
- H = the total water depth, where H = h + ζ;
- h = the depth of the undisturbed water;
- f = the Coriolis parameter;
- g = acceleration due to gravity;
- Ps = sea surface atmospheric pressure;
- ρa = the density of air;
- ρ0 = the density of sea water;
- W = the wind velocity vector at the height of 10 m above sea surface;
- τsx, τsy = the east and north components, respectively, of wind stress friction;where Cs is the wind stress coefficient, which varies with wind velocity as follows:τbx, τby = the east and north components, respectively, of bottom friction.where Cd is the bottom friction coefficient, which was taken as 0.0015 in this study.
- τwx, τwy = the east and north components, respectively of wave force (gradient of the wave radiation stress) which are calculated through SWAN model (Section 2.2) as follows:where Sxx, Sxy, Syx, Syy = the radiation stress tensor (m/s).
2.2. SWAN
- N = wave action density (Joule/m2/Hz);
- t = time (s);
- σ = frequency (Hz);
- θ = wave propagation direction;
- Cx, Cy = the propagation velocities of wave energy in spatial x-, y-space;where U, V = the east and north components, respectively, of depth averaged velocity;
- d = water depth (m);
- k = wave number;
- Cσ, Cθ = the propagation velocities in spectral space σ-, θ-space;
- S = physical processes of generation, dissipation and non-linear wave-wave interactions, the options of these terms are list in Table 1.
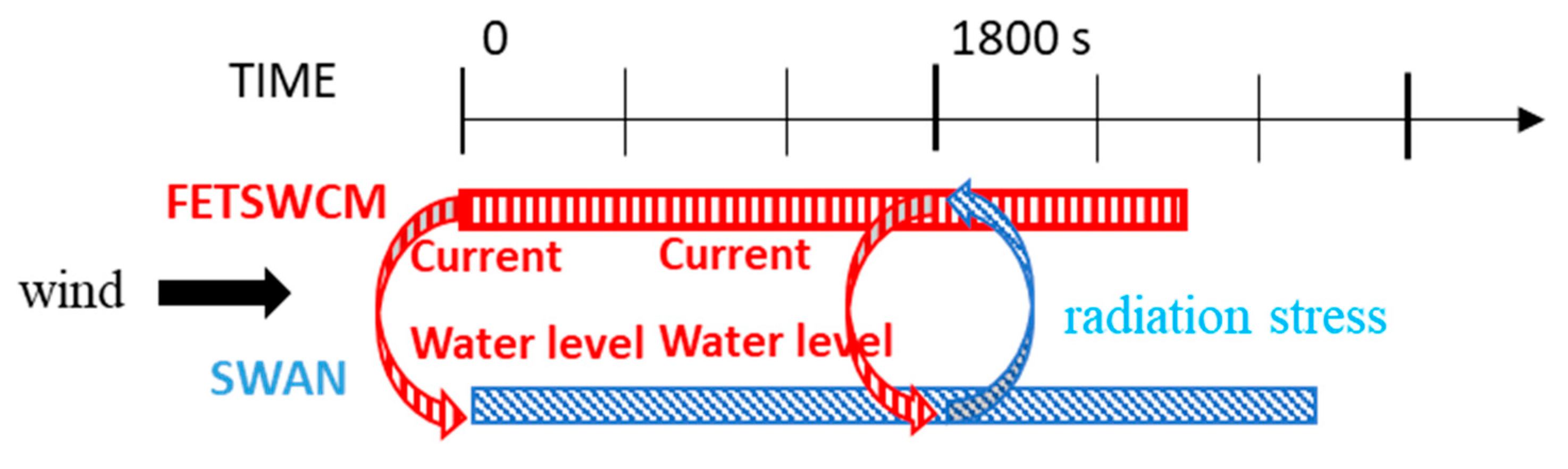
2.3. FETSWCM-SWAN Model
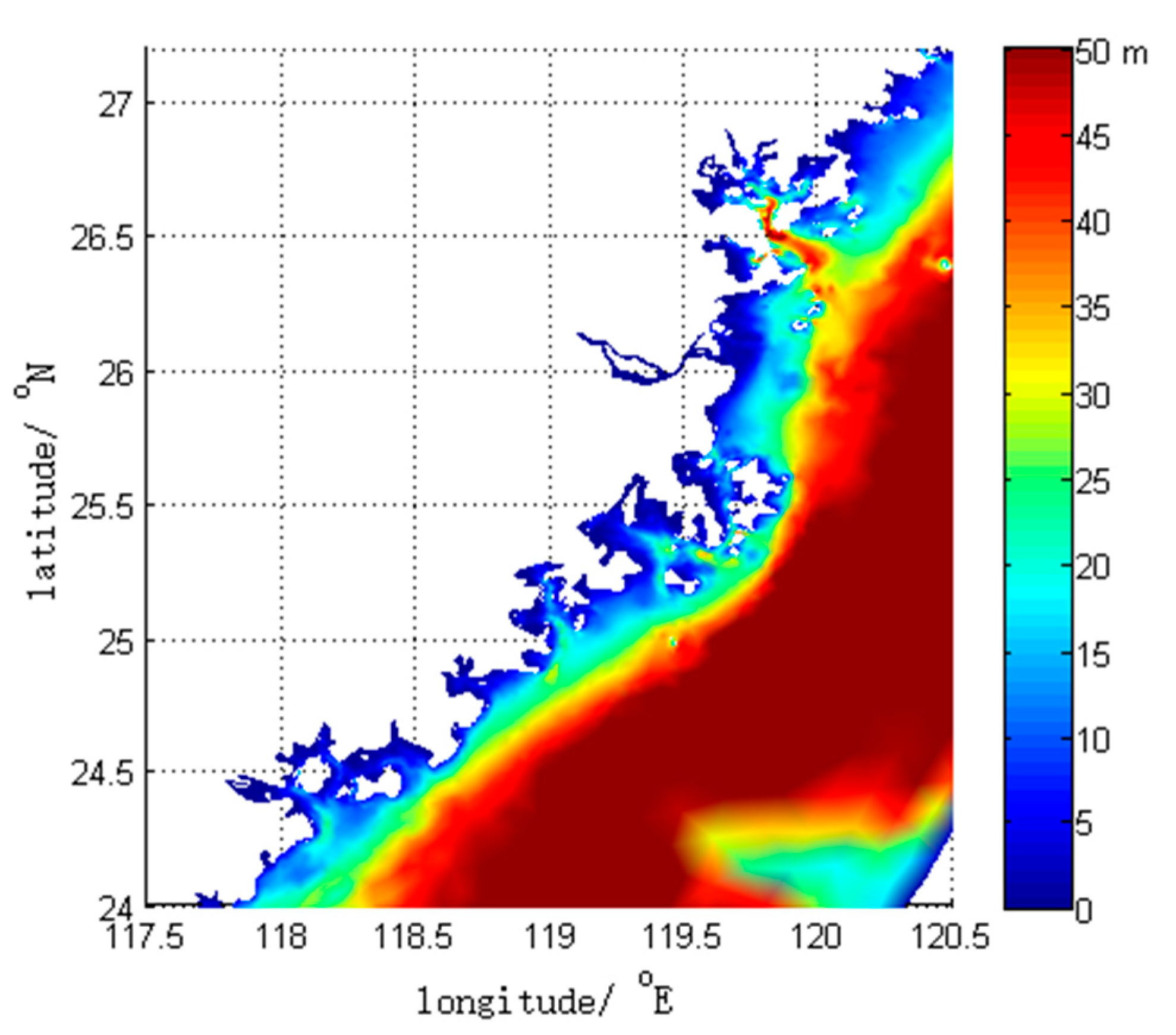
2.4. Model Configuration
2.4.1. Atmospheric forcing functions
- P = the pressure at radius r;
- Pe = the ambient pressure;
- Pc = the central pressure of storm;
- ΔP = Pe − Pc;
- ΔV is the additional velocity caused by topography,
- AT is the attenuation factor of landing typhoon,
2.4.2. Tidal forcing functions
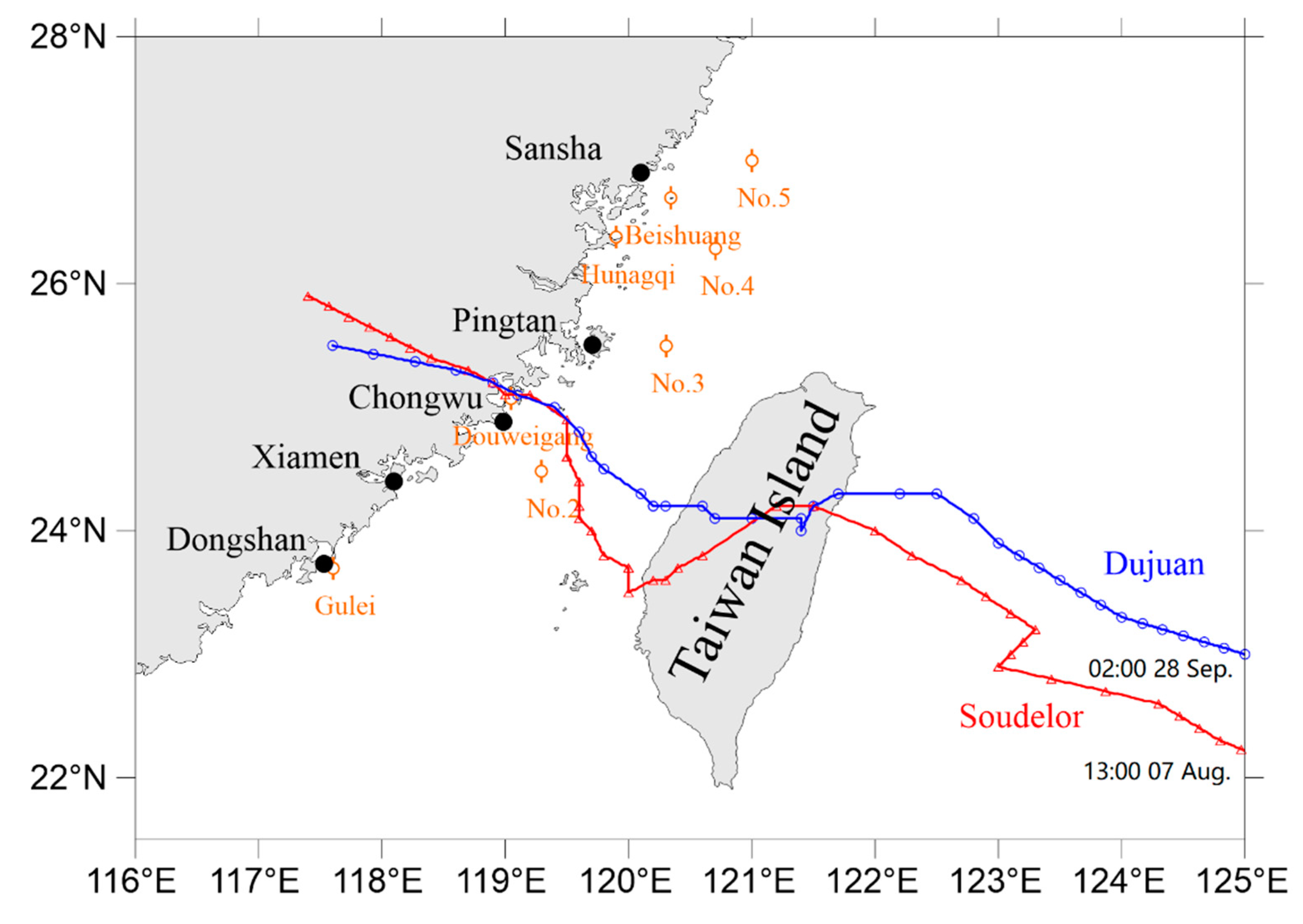
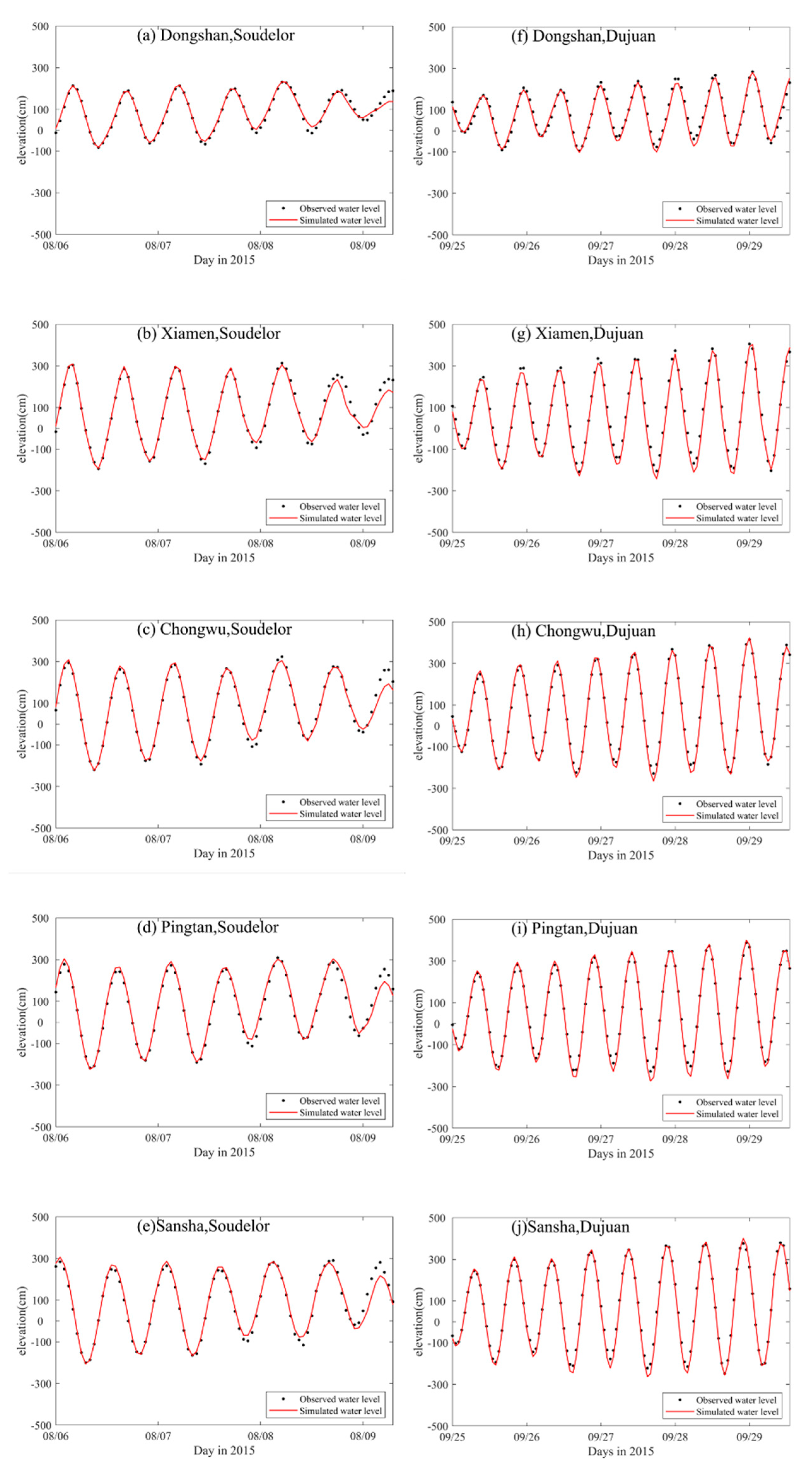
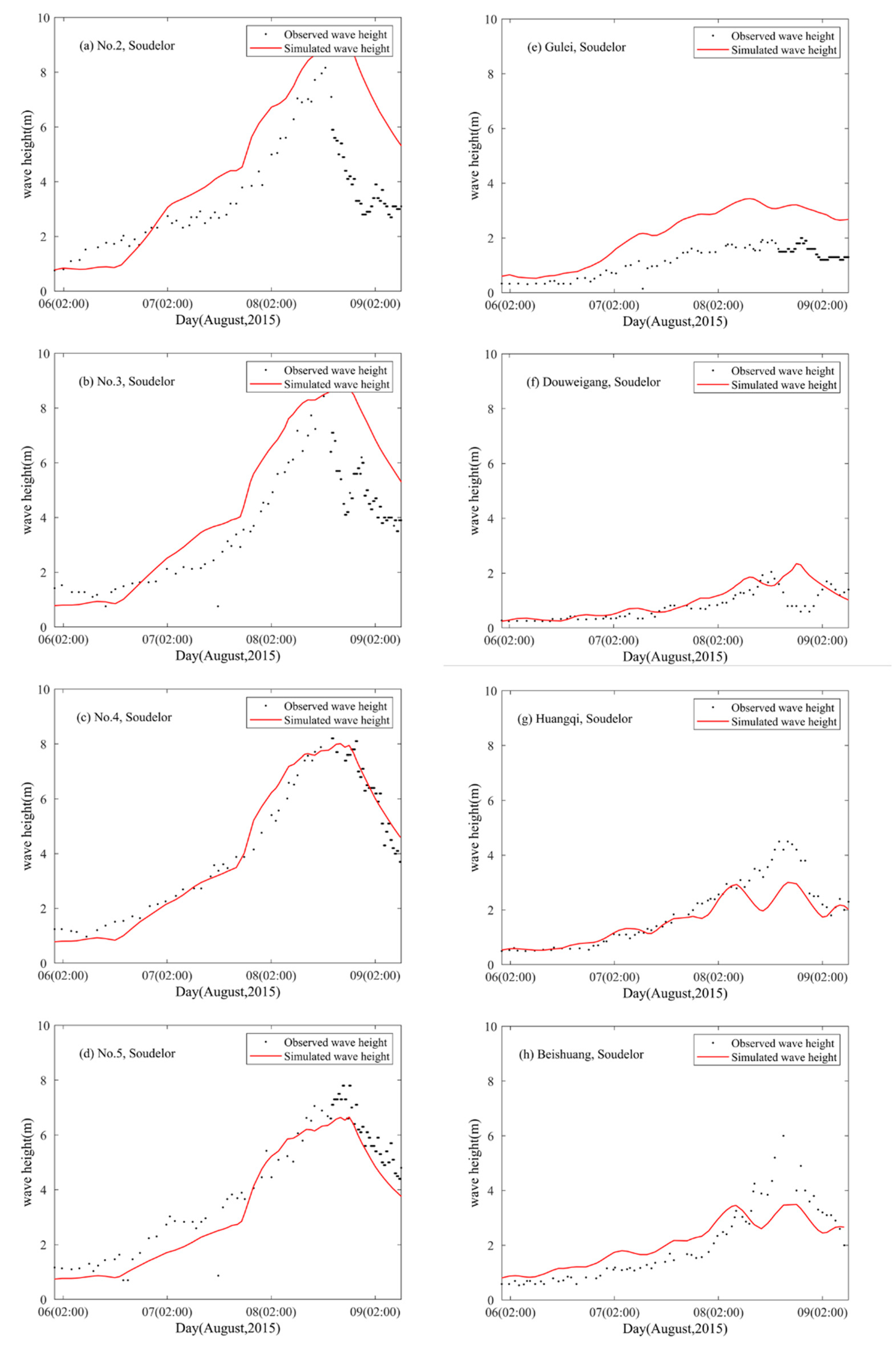
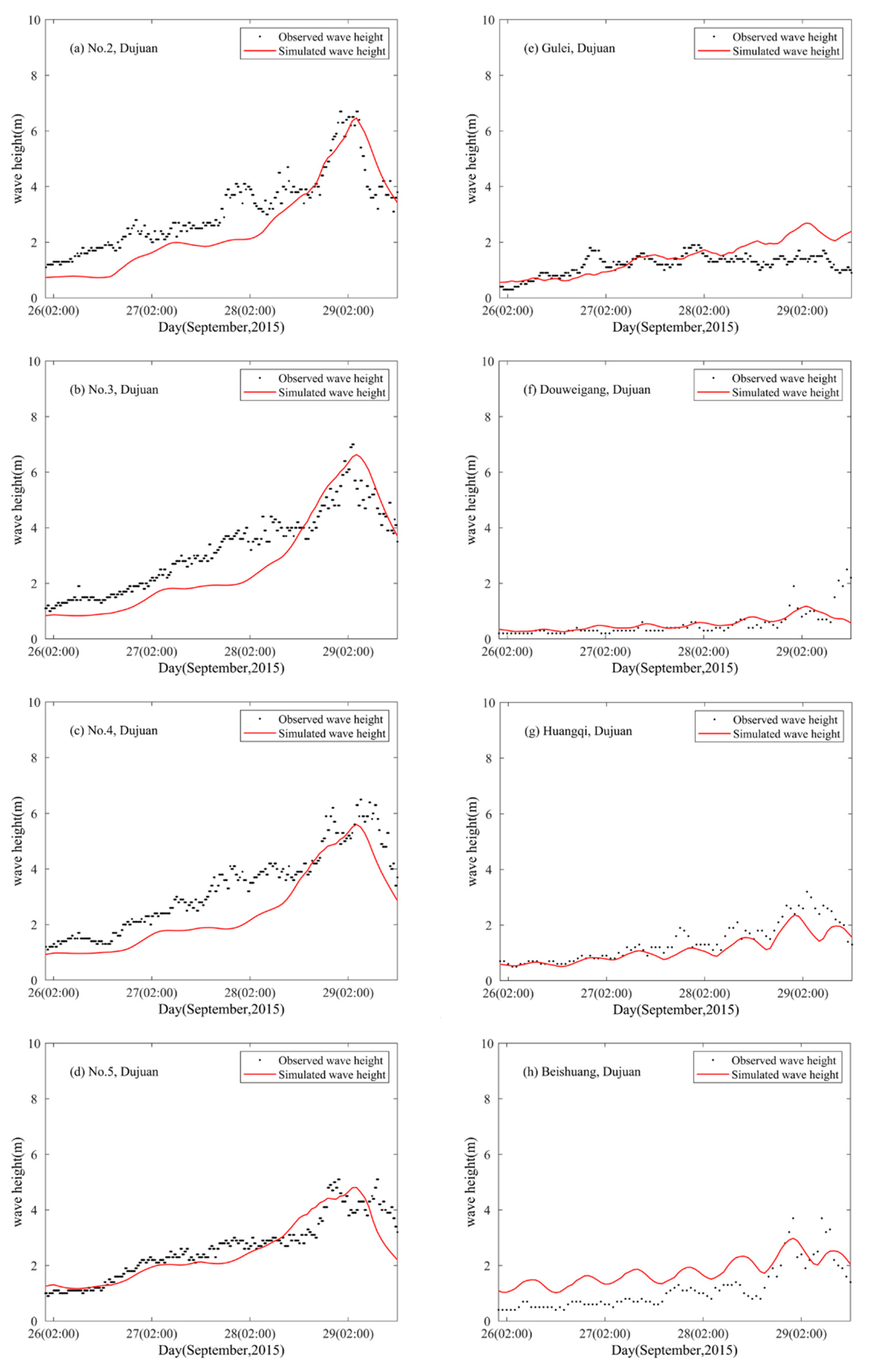
3. Validation
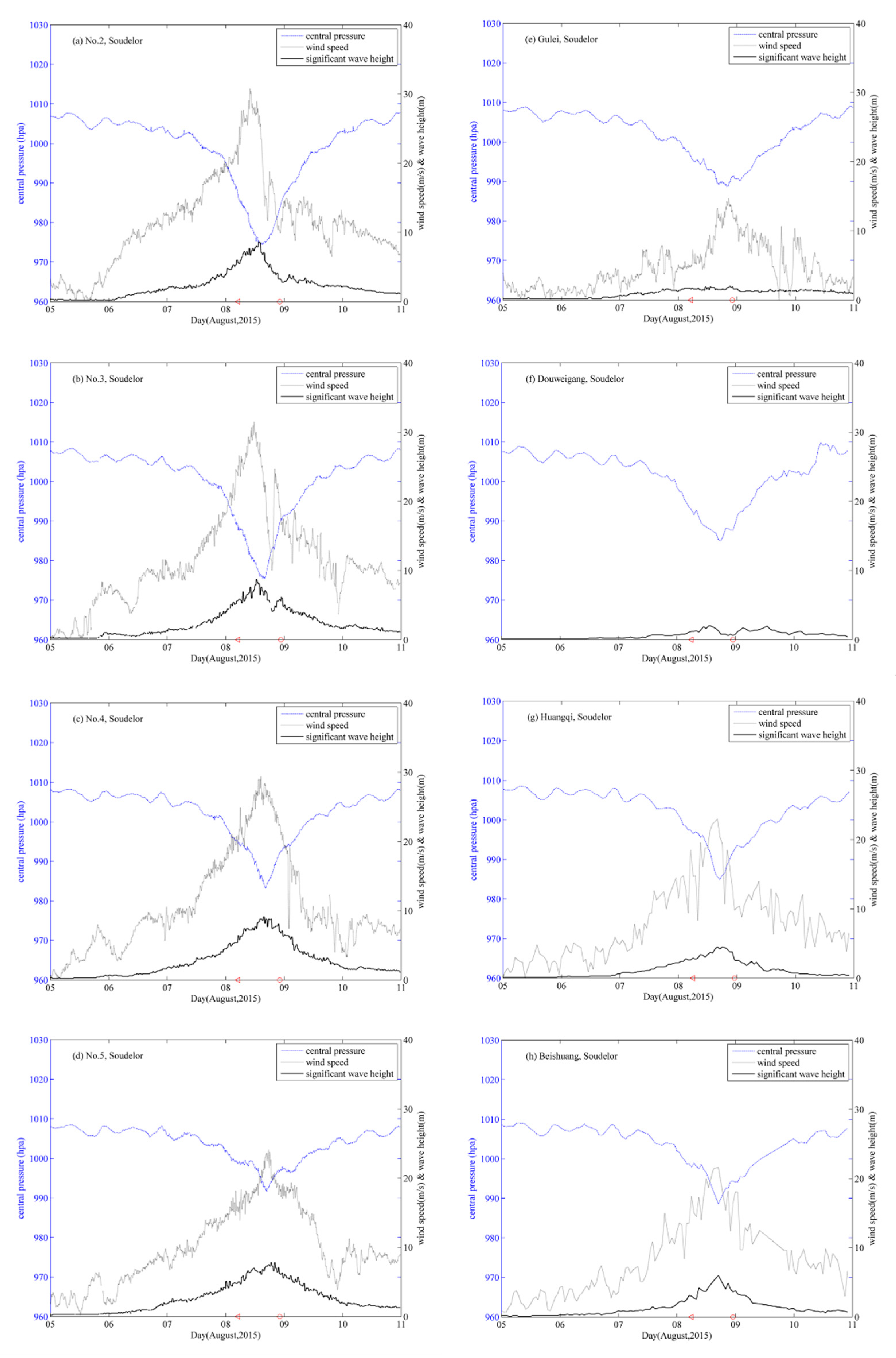
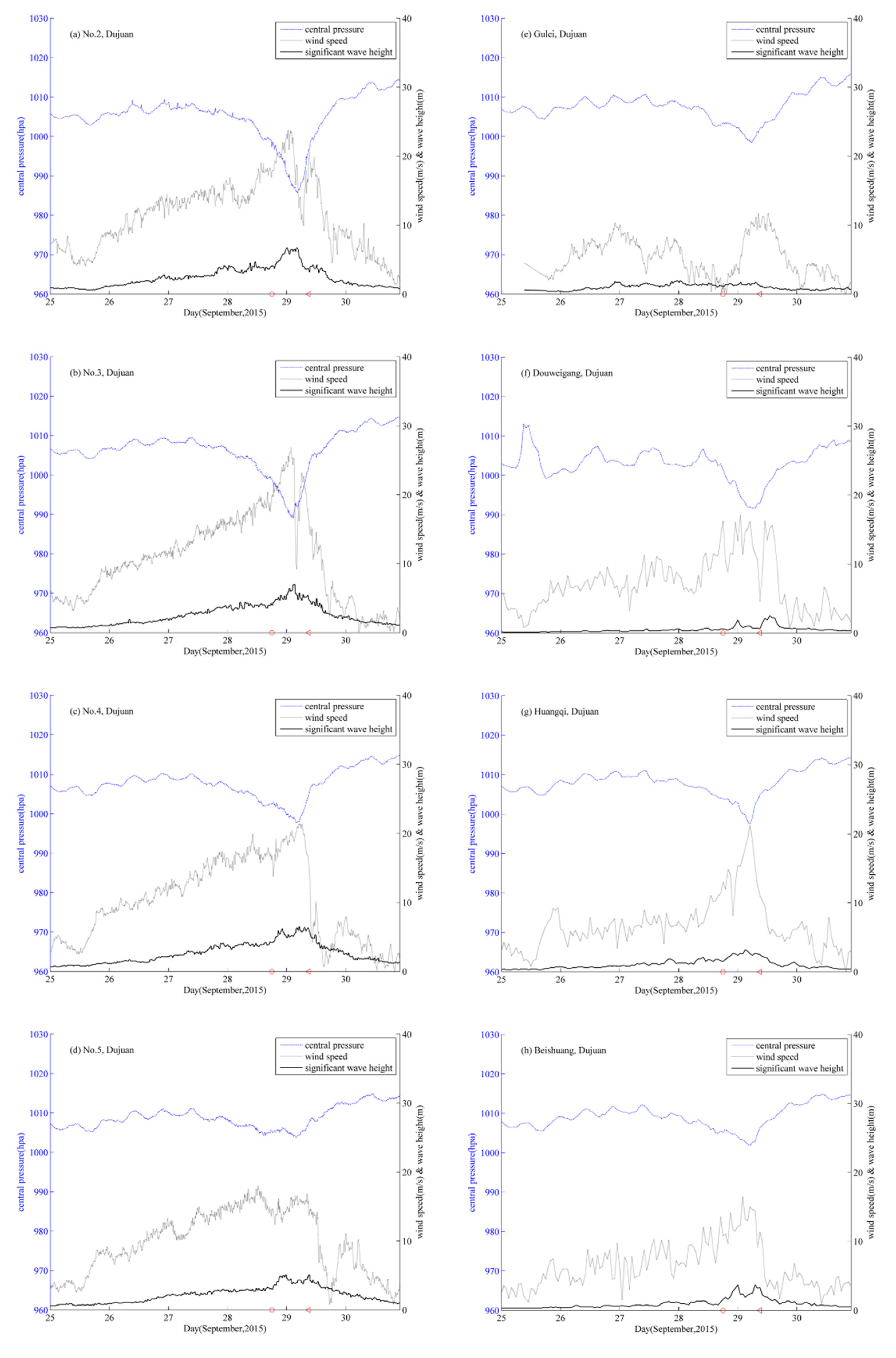
3.1. Tidal Water Level Validation
3.2. Significant Wave Height Validation
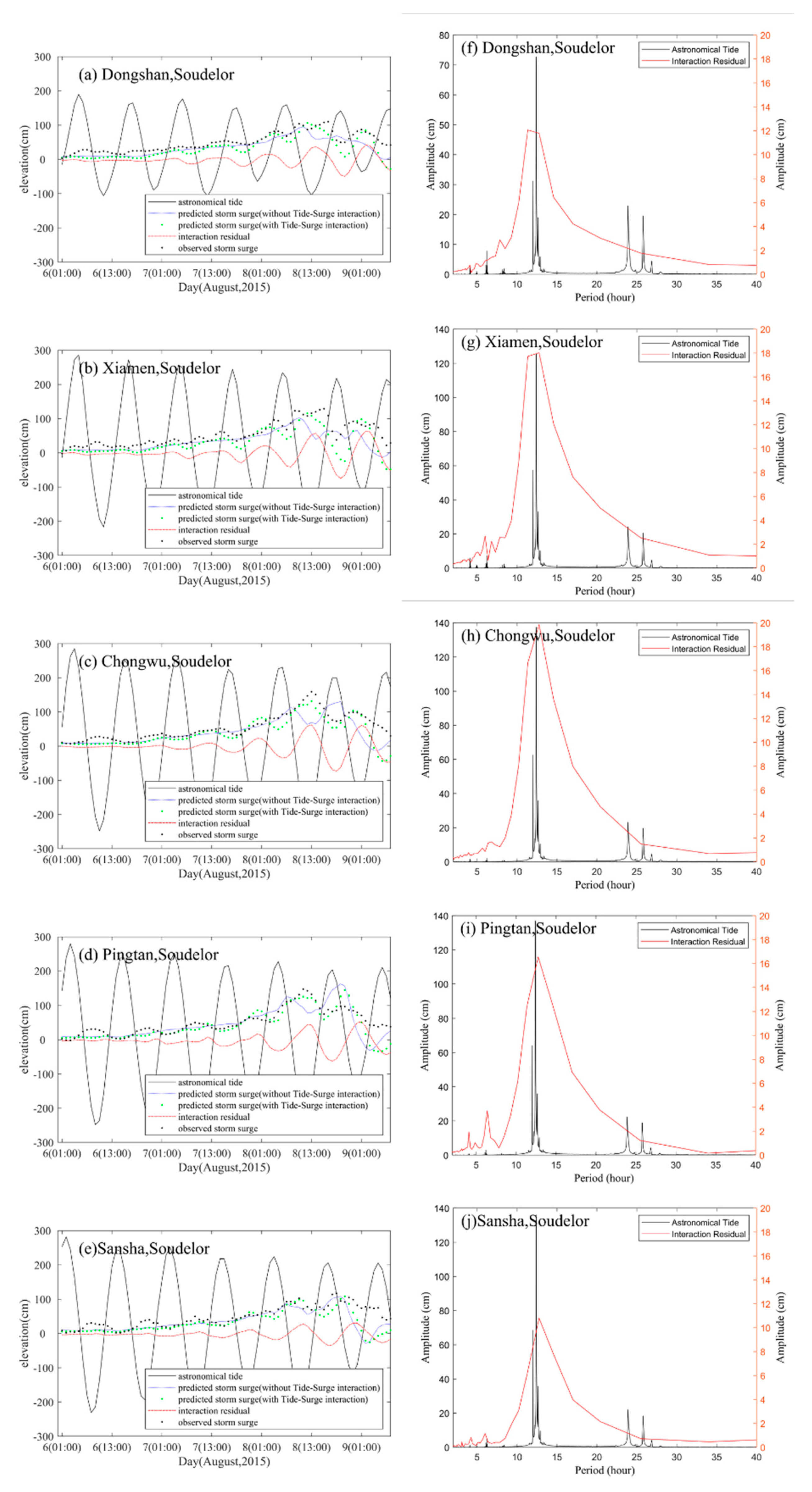
4. Discussion
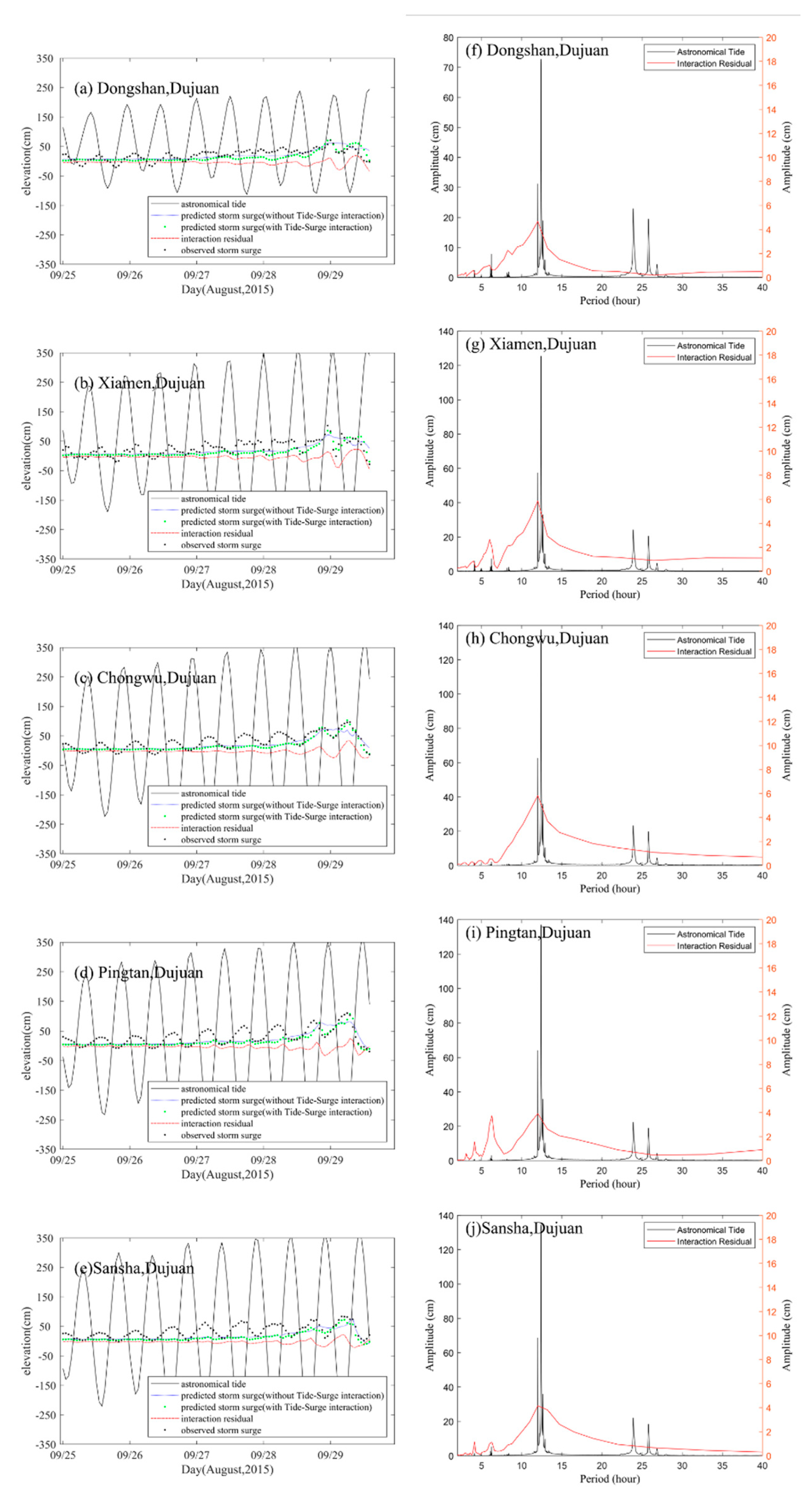
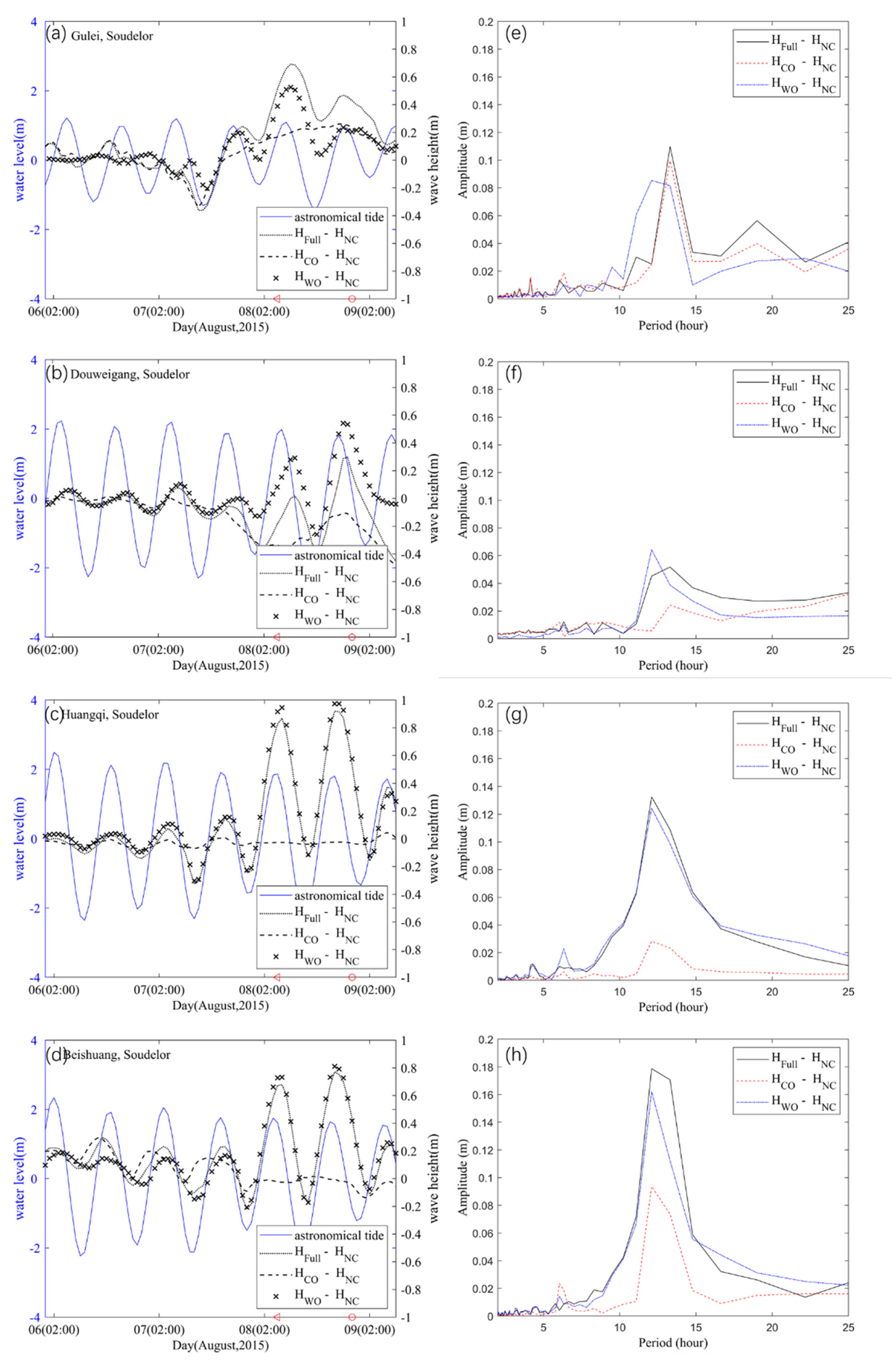
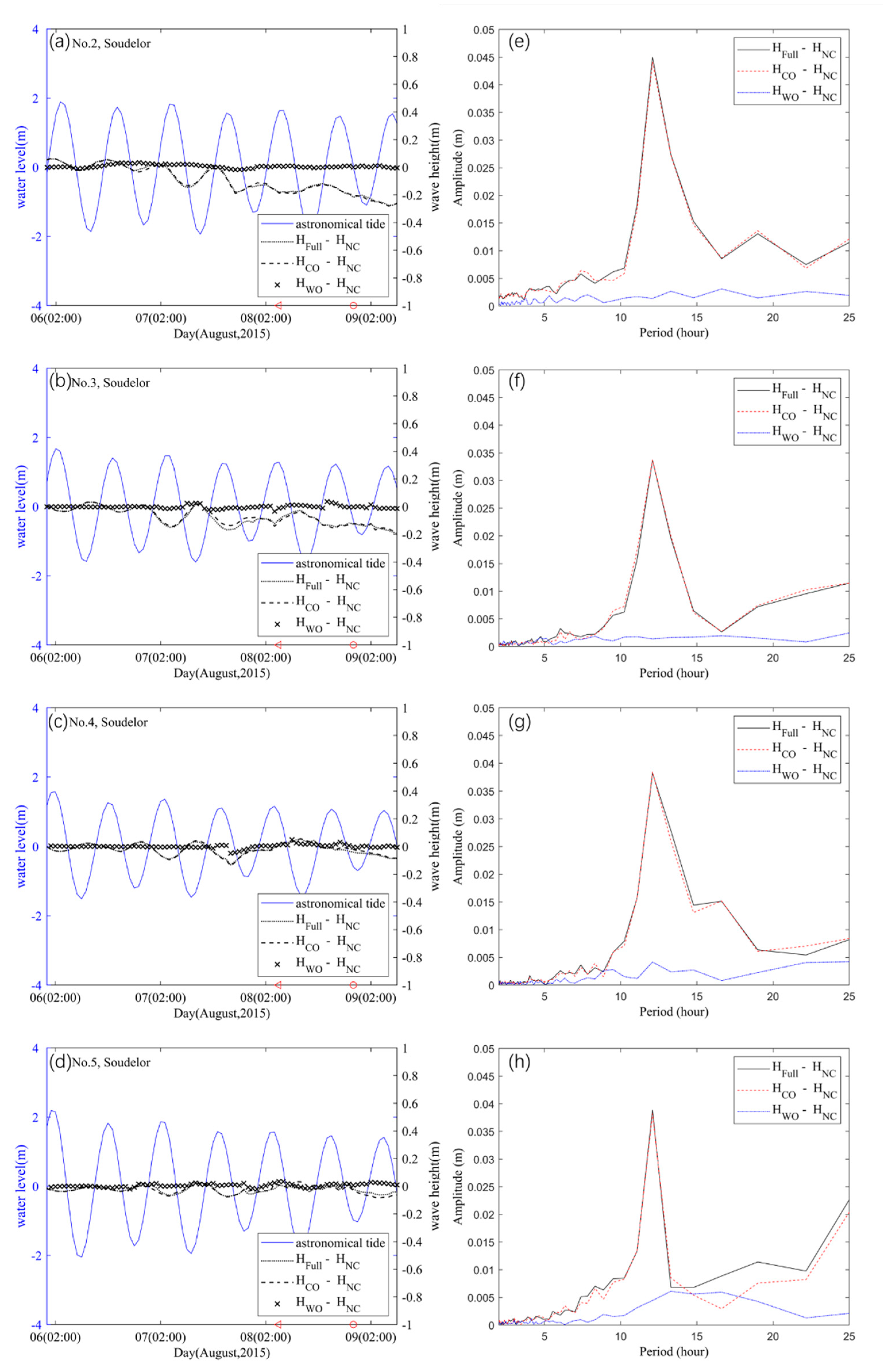
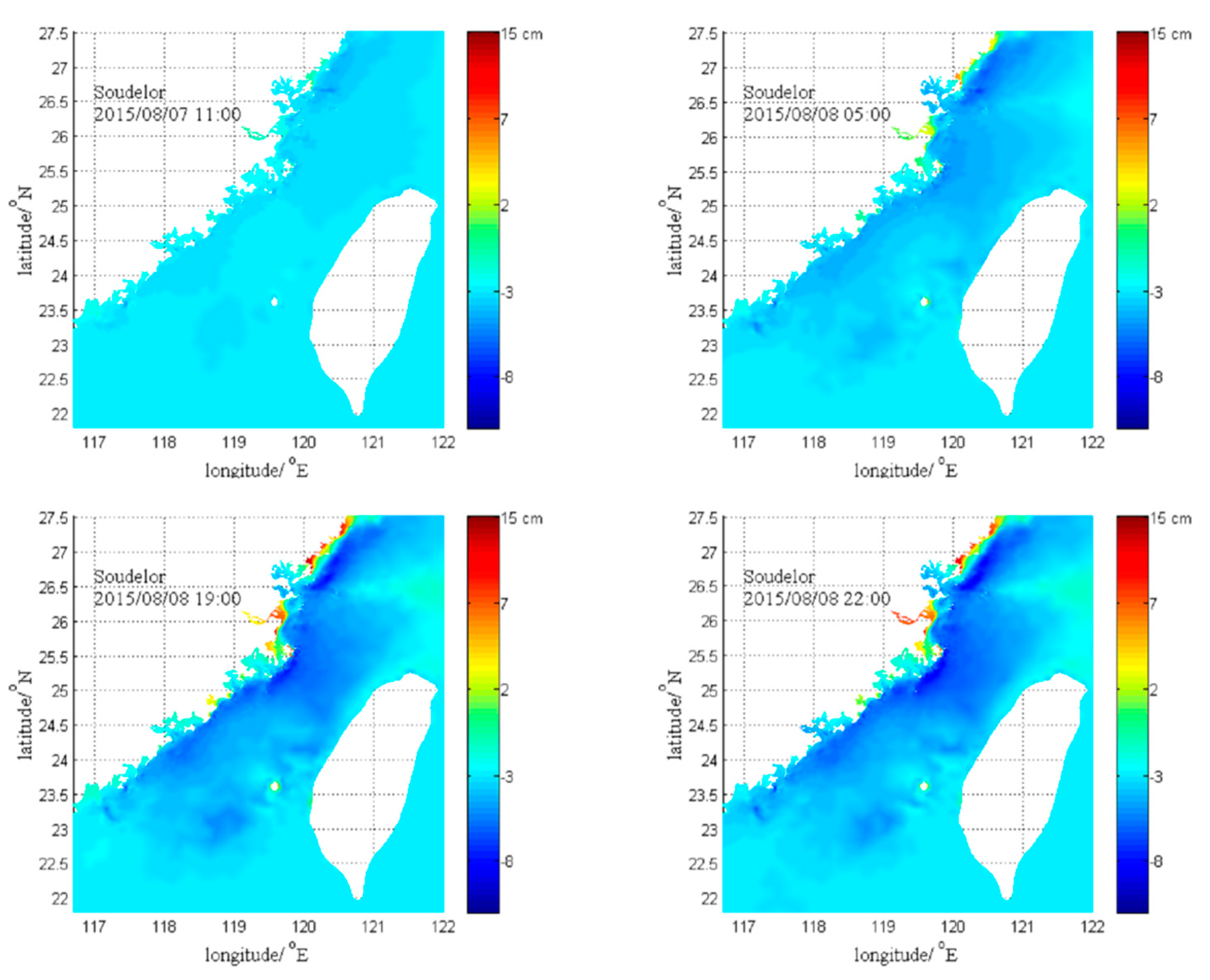
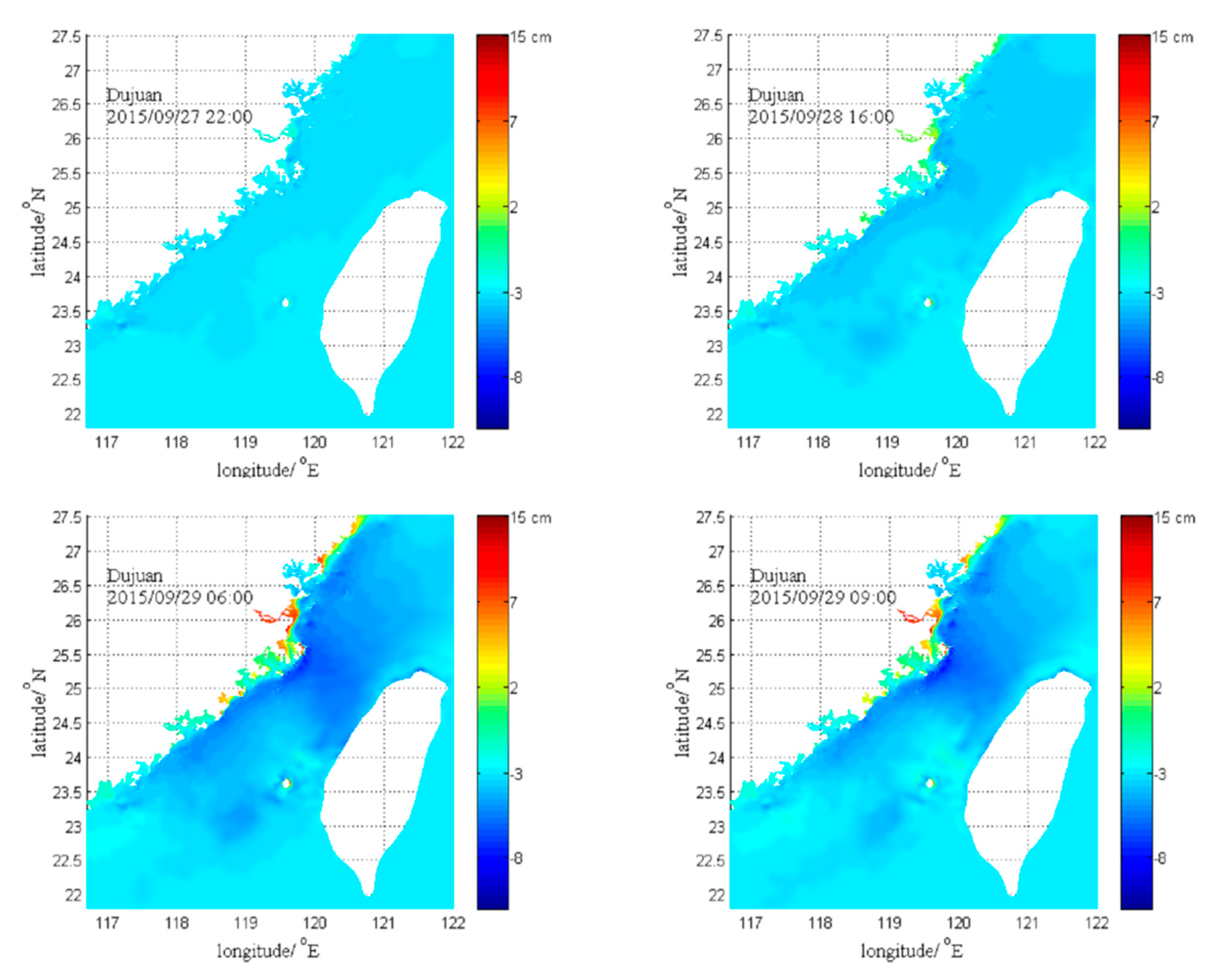
4.1. Tide and Storm Surge Interaction
4.2. Wave and Tide Surge Interaction
4.3. Wave Setup in the Taiwan Strait during Soudelor and Dujuan
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fang, G.H.; Yang, J.F.; Zhao, X.C. A numerical model for the tides and tidal currents in the Taiwan Strait. Acta Oceanol. Sin. 1985, 2, 23–24. [Google Scholar]
- Wolf, J. Coastal flooding: Impacts of coupled wave–surge–tide models. Nat. Hazards 2009, 49, 241–260. [Google Scholar] [CrossRef]
- Horsburgh, K.J.; Wilson, C. Tide-surge interaction and its role in the distribution of surge residuals in the North Sea. J. Geophys. Res. 2007, 112, 207–220. [Google Scholar] [CrossRef]
- Park, Y.H.; Suh, K.D. Variations of storm surge caused by shallow water depths and extreme tidal ranges. Ocean. Eng. 2012, 55, 44–51. [Google Scholar] [CrossRef]
- Bernier, N.B.; Thompson, K.R. Tide-surge interaction off the east coast of Canada and northeastern United States. J. Geophys. Res. Atmos. 2007, 112, 137–154. [Google Scholar] [CrossRef]
- Zhang, W.Z.; Shi, F.; Hong, H.S.; Shang, S.P.; Kirby, J.T. Tide-surge Interaction Intensified by the Taiwan Strait. J. Geophys. Res. Ocean. 2010, 115, 187–194. [Google Scholar] [CrossRef]
- Moon, I.J. Impact of a coupled ocean wave–tide–circulation system on coastal modeling. Ocean. Model. 2005, 8, 203–236. [Google Scholar] [CrossRef]
- Chen, W.B.; Lin, L.Y.; Jang, J.H.; Chang, C.H. Simulation of Typhoon-Induced Storm Tides and Wind Waves for the Northeastern Coast of Taiwan Using a Tide–Surge–Wave Coupled Model. Water 2017, 9, 549. [Google Scholar] [CrossRef]
- Huang, Y.; Weisberg, R.H.; Zheng, L. Coupling of surge and waves for an Ivan-like hurricane impacting the Tampa Bay, Florida region. J. Geophys. Res. Ocean. 2010, 115, 93–102. [Google Scholar] [CrossRef]
- Bertin, X.; Li, K.; Roland, A.; Bidlot, J.R. The contribution of short-waves in storm surges: Two case studies in the Bay of Biscay. Cont. Shelf Res. 2015, 96, 1–15. [Google Scholar] [CrossRef]
- Zhang, L.; Shang, S.P.; Xie, Y.S.; Zhang, F. A tide-storm surge coupled model based on finite element method for Fujian coast. J. Appl. Oceanogr. 2016, 35, 264–273. [Google Scholar]
- Zhang, L.; Shang, S.P.; Zhang, F.; Xie, Y.S. A Tide-Storm Surge-Wave Over-Seawall Warning System for Fujian Coast. Mar. Forecast. 2016, 33, 1–9. [Google Scholar]
- Chen, D.W.; Shang, S.P.; Shang, S.L.; University, X. Remote Sensing Study of Sea Surface Wind Field Around Taiwan Island During Typhoon Periods. J. Xiamen Univ. 2011, 46, 141–145. [Google Scholar]
- Lynch, D.R.; Gray, W.G. A wave equation model for finite element tidal computations. Comput. Fluids 1979, 7, 207–228. [Google Scholar] [CrossRef]
- Westerink, J.J.; Luettich, R.A. Tide and Storm Surge Predictions in the Gulf of Mexico Using Model ADCIRC-2D; Report to the US Army Engineer Waterways Experiment Station; US Army Corps of Engineers: Washington, DC, USA, 1991. [Google Scholar]
- Ji, H.D.; Lan, Y.Y.; Zhao, D.B. Application of SWAN in Taiwan Strait typhoon waves numerical simulation. J. Waterw. Harb. 2013, 34, 113–117. [Google Scholar]
- Ou, S.H.; Liau, J.M.; Hsu, T.W.; Tzang, S.Y. Simulating typhoon waves by SWAN wave model in coastal waters of Taiwan. Ocean. Eng. 2002, 29, 947–971. [Google Scholar] [CrossRef]
- Yuan, K.R.; Shang, S.P.; Xie, Y.S.; Zhang, L.; Zhang, Y.D.; Zhang, F. The Simulation of Typhoon Waves in Taiwan Strait. J. Xiamen Univ. 1985, 4, 53. [Google Scholar]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deut. Hydrogr. Z. 1973, 8, 1–95. [Google Scholar]
- Cavaleri, L.; Malanotte-Rizzoli, P. Wind wave prediction in shallow water theory and applications. J. Geophys. Res. 1981, 86, 10961–10973. [Google Scholar] [CrossRef]
- Komen, G.J.; Hasselmann, S.; Hasselmann, K. On the existence of a fully developed wind-sea spetrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Eldeberky, Y. Nonlinear Transformation of Wave Spectra in the Nearshore Zone. Ph.D. Thesis, Department of Civil Engineering. Delft University of Technology, Delft, The Netherlands, 1996. [Google Scholar]
- Hasselmann, S.; Hasselmann, K.; Allender, J.H.; Bamett, T.P. Computations and parameter zations of the linear energy transfer in a gravity wave spectrum. Part II: Parameterizations of the nonlinear transfer for application in wave models. J. Phys. Oceanogr. 1985, 15, 1378–1391. [Google Scholar] [CrossRef]
- Battjes, J.A.; Stive, M.J.F. Calibration and verification of a dissipation model for random breaking waves. J. Geophys. Res. 1985, 90, 9159–9167. [Google Scholar] [CrossRef]
- Gerg, J. Holland. An analytic model of wind and pressure profiles in hurricanes. Mon. Weather. Rev. 1980, 108, 1212–1218. [Google Scholar]
- Willoughby, H.E.; Rahn, M.E. Parametric representation of the primary hurricane vortex. Part I: Observations and evaluation of the holland (1980) model. Mon. Weather. Rev. 2004, 132, 3033. [Google Scholar] [CrossRef]
- Jelesnianski, C.; Chen, J.; Shaffer, W.; Gilad, A. Slosh—A hurricane storm surge forecast model. In Proceedings of the OCEANS, Washington, DC, USA, 10–12 September 1984; IEEE: Piscataway Township, NJ, USA, 1984. [Google Scholar]
- Matsumoto, K.; Takanezawa, T.; Ooe, M. Ocean Tide Models Developed by Assimilating TOPEX/POSEIDON Altimeter Data into Hydrodynamical Model: A Global Model and a Regional Model around Japan. J. Oceanogr. 2000, 56, 567–581. [Google Scholar] [CrossRef]
- Wang, X.N.; Liu, F.S. Preliminary study on typhoon surges along the Fujian and Guangdong coastal areas. Stud. Mar. Sin. 1987, 27, 33–43. [Google Scholar]
- Guérin, T.; Bertin, X.; Coulombier, T.; De Bakker, A. Impacts of wave-induced circulation in the surf zone on wave setup. Ocean. Model. 2018, 123, 86–97. [Google Scholar] [CrossRef]
- Ardhuin, F.; Roland, A.; Dumas, F.; Bennis, A.-C.; Sentchev, A.; Forget, P.; Wolf, J.; Girard, F.; Osuna, P.; Benoit, M. Numerical wave modeling in conditions with strong currents: Dissipation, refraction, and relative wind. J. Phys. Oceanogr. 2012, 42, 2101–2120. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.; Stewart, R. Radiation stresses in water waves; a physical discussion, with applications. Deep. Sea Res. Oceanogr. Abstr. 1964, 11, 529–562. [Google Scholar] [CrossRef]



| Source Term | Scheme |
|---|---|
| Linear wind growth | Cavaleri and Malanotte-Rizzoli (1981) [20] |
| Exponential wind growth | Komen et al. (1984) [21] |
| White capping | Komen et al. (1984) [21] |
| Triad interaction | Eldeberky (1996) [22] |
| Quadruplet interaction | Hasselmann et al. (1985) [23] |
| Depth induced breaking | Battjes and Stive (1985) [24] |
| Bottom friction | Hasselmann et al. (JONSWAP) (1973) [19] |
| Name of Typhoon | Soudelor (2015) | Dujuan (2015) | |
|---|---|---|---|
| First landfall | location | 121.5° E, 24.2° N | 121.7° E, 24.3° N |
| time | 05:00, 8 August | 18:00, 28 September | |
| Max Wind Speed (m/s) | 45 | 48 | |
| Central Pressure (hPa) | 950 | 945 | |
| Second landfall | location | 119.2° E, 25.1° N | 119.1° E, 25.1° N |
| time | 22:00, 8 August | 09:00, 29 September | |
| Max Wind Speed (m/s) | 38 | 33 | |
| Central Pressure (hPa) | 970 | 975 | |
| Typhon Soudelor | Typhon Dujuan | |||||
|---|---|---|---|---|---|---|
| M2(cm) | Interaction Residual (cm) | % | M2 (cm) | Interaction Residual (cm) | % | |
| Sansha | 134.7 | 10.8 | 8.0 | 134.7 | 4.2 | 3.1 |
| Pingtan | 137.1 | 16.6 | 12.1 | 137.1 | 3.9 | 2.9 |
| Chongwu | 137.6 | 19.9 | 14.4 | 5.8 | 4.2 | |
| Xiamen | 124.5 | 18.0 | 14.5 | 125.5 | 5.9 | 4.7 |
| Dongshan | 72.7 | 11.8 | 16.2 | 72.7 | 4.6 | 6.3 |
| average | 13.0 | 4.2 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Shang, S.; Zhang, F.; Xie, Y. Tide-Surge-Wave Interaction in the Taiwan Strait during Typhoons Soudelor (2015) and Dujuan (2015). Appl. Sci. 2020, 10, 7382. https://doi.org/10.3390/app10207382
Zhang L, Shang S, Zhang F, Xie Y. Tide-Surge-Wave Interaction in the Taiwan Strait during Typhoons Soudelor (2015) and Dujuan (2015). Applied Sciences. 2020; 10(20):7382. https://doi.org/10.3390/app10207382
Chicago/Turabian StyleZhang, Li, Shaoping Shang, Feng Zhang, and Yanshuang Xie. 2020. "Tide-Surge-Wave Interaction in the Taiwan Strait during Typhoons Soudelor (2015) and Dujuan (2015)" Applied Sciences 10, no. 20: 7382. https://doi.org/10.3390/app10207382
APA StyleZhang, L., Shang, S., Zhang, F., & Xie, Y. (2020). Tide-Surge-Wave Interaction in the Taiwan Strait during Typhoons Soudelor (2015) and Dujuan (2015). Applied Sciences, 10(20), 7382. https://doi.org/10.3390/app10207382





