The Development of the Temporal Measurements for Ultrashort Laser Pulses
Abstract
:1. Introduction
2. The Basics
3. Correlation Measurement
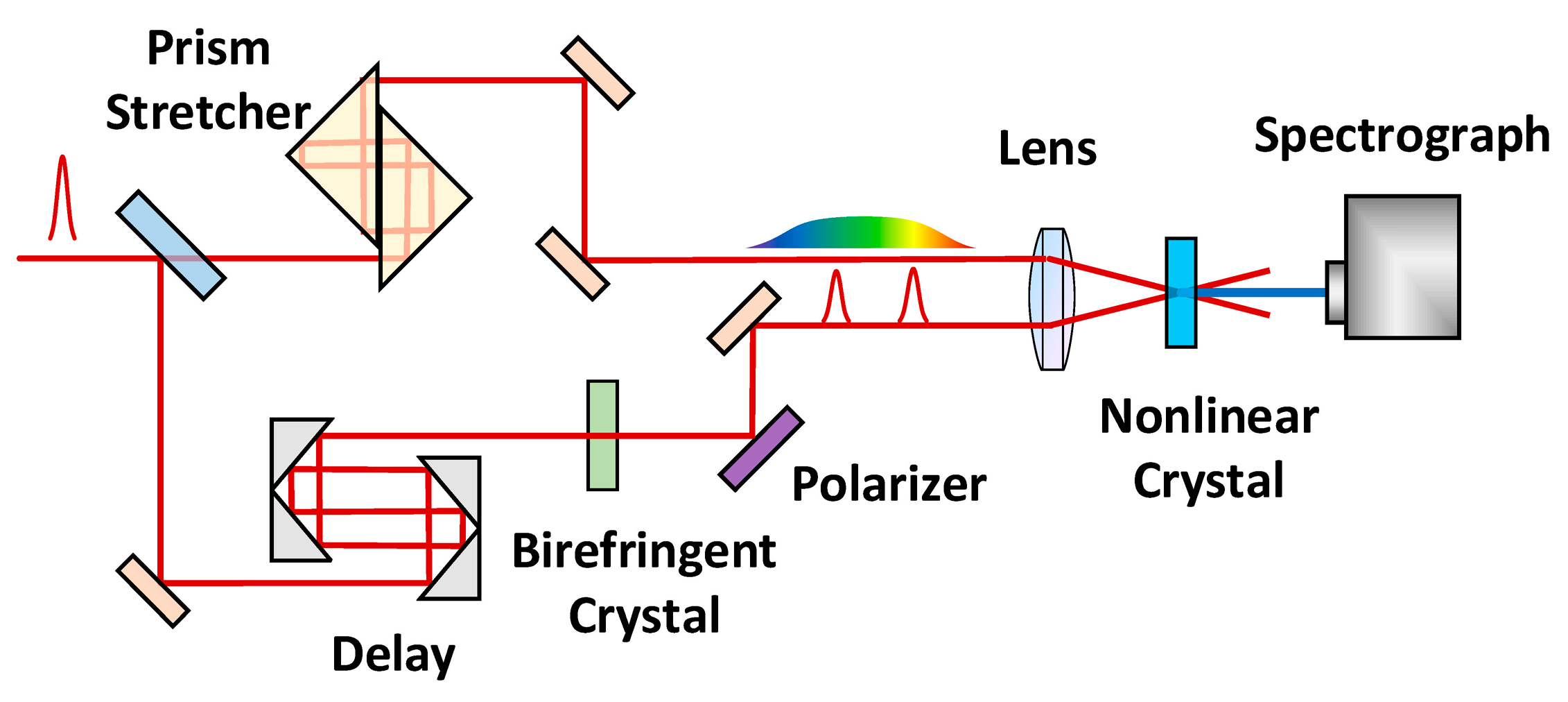
4. Spectrogram
5. Spectral Interferometry
| SPIDER Geometry | Traditional | TSPS/CTP [65,68] | CP [71] | 2DSI [13] |
|---|---|---|---|---|
| Operating Mode | Single-shot | Single-shot | Single-shot | Multi-shot Scanning |
| Acquire data | 1D | 1D × 21 | 1D/1D × 2 | 2D |
| Spectral resolution 2 | 5~10 Δωres | ~2 Δωres | ~2 Δωres | ~ Δωres |
| Shear 3 | 0.1~0.2 ΔωBW | ~0.015 ΔωBW | ~0.03 ΔωBW | ~0.05 ΔωBW |
| Phase error (3dB bandwidth) | ~44 mrad [74] | 74.2 mrad (TSPS) 19.3 mrad (CTP) | 2.6 mrad | Unspecified |
6. Conclusions and Prospect
Author Contributions
Funding
Conflicts of Interest
References
- Li, W.Q.; Gan, Z.B.; Yu, L.H.; Wang, C.; Liu, Y.Q.; Guo, Z.; Xu, L.; Xu, M.; Hang, Y.; Xu, Y.; et al. 339 j high-energy ti:Sapphire chirped-pulse amplifier for 10 pw laser facility. Opt. Lett. 2018, 43, 5681–5684. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Yu, L.H.; Wang, J.Y.; Wang, C.; Liu, Y.Q.; Gan, Z.B.; Li, W.Q.; Leng, Y.X.; Liang, X.Y.; Li, R.X. Improvement of the focusing ability by double deformable mirrors for 10-pw-level ti: Sapphire chirped pulse amplification laser system. Opt. Express 2018, 26, 26776–26786. [Google Scholar] [CrossRef]
- Yoon, J.W.; Jeon, C.; Shin, J.; Lee, S.K.; Lee, H.W.; Choi, I.W.; Kim, H.T.; Sung, J.H.; Nam, C.H. Achieving the laser intensity of 5.5×10^22 w/cm2 with a wavefront-corrected multi-pw laser. Opt. Express 2019, 27, 20412–20420. [Google Scholar] [CrossRef] [PubMed]
- Wirth, A.; Hassan, M.T.; Grguras, I.; Gagnon, J.; Moulet, A.; Luu, T.T.; Pabst, S.; Santra, R.; Alahmed, Z.A.; Azzeer, A.M.; et al. Synthesized light transients. Science 2011, 334, 195–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bradley, D.J.; Liddy, B.; Sleat, W.E. Direct linear measurement of ultrashort light pulses with a picosecond streak camera. Opt. Commun. 1971, 2, 391–395. [Google Scholar] [CrossRef]
- Etchepare, J.; Grillon, G.; Orszag, A. Third order autocorrelation study of amplified subpicosecond laser pulses. IEEE J. Quantum Electron. 1983, 19, 775–778. [Google Scholar] [CrossRef]
- Iaconis, C.; Walmsley, I.A. Spectral phase interferometry for direct electric-field reconstruction of ultrashort optical pulses. Opt. Lett. 1998, 23, 792–794. [Google Scholar] [CrossRef]
- Iaconis, C.; Walmsley, I.A. Self-referencing spectral interferometry for measuring ultrashort optical pulses. IEEE J. Quantum Electron. 1999, 35, 501–509. [Google Scholar] [CrossRef] [Green Version]
- O’Shea, P.; Kimmel, M.; Gu, X.; Trebino, R. Highly simplified device for ultrashort-pulse measurement. Opt. Lett. 2001, 26, 932–934. [Google Scholar] [CrossRef]
- Janszky, J.; Corradi, G. Full intensity profile analysis of ultrashort laser pulses using four-wave mixing or third harmonic generation. Opt. Commun. 1986, 60, 251–256. [Google Scholar] [CrossRef]
- Kane, D.J.; Trebino, R. Single-shot measurement of the intensity and phase of an arbitrary ultrashort pulse by using frequency-resolved optical gating. Opt. Lett. 1993, 18, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Trebino, R.; DeLong, K.W.; Fittinghoff, D.N.; Sweetser, J.N.; Krumbugel, M.A.; Richman, B.A.; Kane, D.J. Measuring ultrashort laser pulses in the time-frequency domain using frequency-resolved optical gating. Rev. Sci. Instrum. 1997, 68, 3277–3295. [Google Scholar] [CrossRef]
- Oksenhendler, T.; Coudreau, S.; Forget, N.; Crozatier, V.; Grabielle, S.; Herzog, R.; Gobert, O.; Kaplan, D. Self-referenced spectral interferometry. Appl. Phys. B 2010, 99, 7–12. [Google Scholar] [CrossRef]
- Hu, Y.; Tehranchi, A.; Wabnitz, S.; Kashyap, R.; Chen, Z.; Morandotti, R. Improved intrapulse Raman scattering control via asymmetric airy pulses. Phys. Rev. Lett. 2015, 114, 073901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Husakou, A.V.; Herrmann, J. Supercontinuum generation of higher-order solitons by fission in photonic crystal fibers. Phys. Rev. Lett. 2001, 87, 203901. [Google Scholar] [CrossRef] [Green Version]
- Trebino, R. Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses; Kluwer Academic Publishers: Boston, MA, USA, 2002; pp. 16–17. [Google Scholar]
- Oriana, A.; Réhault, J.; Preda, F.; Polli, D.; Cerullo, G. Scanning Fourier transform spectrometer in the visible range based on birefringent wedges. J. Opt. Soc. Am. A 2016, 33, 1415–1420. [Google Scholar] [CrossRef] [Green Version]
- Adler, F.; Maslowski, P.; Foltynowicz, A.; Cossel, K.C.; Briles, T.C.; Hartl, I.; Ye, J. Mid-infrared fourier transform spectroscopy with a broadband frequency comb. Opt. Express 2010, 18, 21861–21872. [Google Scholar] [CrossRef]
- Diels, J.-C.M.; Fontaine, J.J.; McMichael, I.C.; Simoni, F. Control and measurement of ultrashort pulse shapes (in amplitude and phase) with femtosecond accuracy. Appl. Opt. 1985, 24, 1270–1282. [Google Scholar] [CrossRef]
- Diels, J.-C.; Van Stryland, E.; Benedict, G. Generation and measurement of 200 femtosecond optical pulses. J. Opt. Soc. Am. 1978, 68, 666. [Google Scholar] [CrossRef]
- Diels, J.-C.; Rudolph, W. Ultrashort Laser Pulse Phenomena, 2nd ed.; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Available online: https://www.ape-berlin.de/en/autocorrelator/ (accessed on 22 October 2020).
- Available online: http://www.lightcon.com/Products/autocorrelators.html (accessed on 22 October 2020).
- Available online: https://www.edmundoptics.com/f/edmund-optics-ultrafast-autocorrelator-by-ape/39533/ (accessed on 22 October 2020).
- Wang, Y.; Ma, J.; Wang, J.; Yuan, P.; Xie, G.; Ge, X.; Liu, F.; Yuan, X.; Zhu, H.; Qian, L. Single-shot measurement of >1010 pulse contrast for ultra-high peak-power lasers. Sci. Rep. 2014, 4, 3818. [Google Scholar] [CrossRef]
- Luan, S.; Hutchinson, M.H.R.; Smith, R.A.; Zhou, F. High dynamic range third-order correlation measurement of picosecond laser pulse shapes. Meas. Sci. Technol. 1993, 4, 1426–1429. [Google Scholar] [CrossRef]
- Divall, E.J.; Ross, I.N. High dynamic range contrast measurements by use of an optical parametric amplifier correlator. Opt. Lett. 2004, 29, 2273–2275. [Google Scholar] [CrossRef] [PubMed]
- Dorrer, C.; Bromage, J.; Zuegel, J.D. High-dynamic-range single-shot cross-correlator based on an optical pulse replicator. Opt. Express 2008, 16, 13534–13544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shah, R.C.; Johnson, R.P.; Shimada, T.; Hegelich, B.M. Large temporal window contrast measurement using optical parametric amplification and low-sensitivity detectors. Eur. Phys. J. D 2009, 55, 305–309. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Yuan, P.; Ma, J.G.; Qian, L.J. Scattering noise and measurement artifacts in a single-shot cross-correlator and their suppression. Appl. Phys. B 2013, 111, 501–508. [Google Scholar] [CrossRef]
- Wang, P.; Shen, X.; Liu, J.; Li, R. Single-shot fourth-order autocorrelator. Adv. Photonics 2019, 1, 056001. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis: Theory and Applications; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Stark, H. Image Recovery: Theory and Application; Academic Press: Orlando, FL, USA, 1987. [Google Scholar]
- Clement, T.S.; Taylor, A.J.; Kane, D.J. Single-shot measurement of the amplitude and phase of ultrashort laser pulses in the violet. Opt. Lett. 1995, 20, 70–72. [Google Scholar] [CrossRef]
- Sweetser, J.N.; Fittinghoff, D.N.; Trebino, R. Transient-grating frequency-resolved optical gating. Opt. Lett. 1997, 22, 519–521. [Google Scholar] [CrossRef]
- Trebino, R. Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses; Kluwer Academic Publishers: Boston, MA, USA, 2000; pp. 117–137. [Google Scholar]
- Available online: http://www.swampoptics.com/index.html (accessed on 22 October 2020).
- Stibenz, G.; Steinmeyer, G. Interferometric frequency-resolved optical gating. Opt. Express 2005, 13, 2617–2626. [Google Scholar] [CrossRef]
- Linden, S.; Kuhl, J.; Giessen, H. Amplitude and phase characterization of weak blue ultrashort pulses by downconversion. Opt. Lett. 1999, 24, 569–571. [Google Scholar] [CrossRef]
- Available online: http://www.swampoptics.com/ (accessed on 22 October 2020).
- Rhodes, M.; Steinmeyer, G.; Ratner, J.; Trebino, R. Pulse-shape instabilities and their measurement. Laser Photonics Rev. 2013, 7, 557–565. [Google Scholar] [CrossRef]
- Rhodes, M.; Mukhopadhyay, M.; Birge, J.; Trebino, R. Coherent artifact study of two-dimensional spectral shearing interferometry. J. Opt. Soc. Am. B 2015, 32, 1881–1888. [Google Scholar] [CrossRef] [Green Version]
- Lozovoy, V.V.; Pastirk, I.; Dantus, M. Multiphoton intrapulse interference. Iv. Ultrashort laser pulse spectral phase characterization and compensation. Opt. Lett. 2004, 29, 775–777. [Google Scholar] [CrossRef] [Green Version]
- Lozovoy, V.V.; Xu, B.; Coello, Y.; Dantus, M. Direct measurement of spectral phase for ultrashort laser pulses. Opt. Express 2008, 16, 592–597. [Google Scholar] [CrossRef]
- Xu, B.W.; Gunn, J.M.; Dela Cruz, J.M.; Lozovoy, V.V.; Dantus, M. Quantitative investigation of the multiphoton intrapulse interference phase scan method for simultaneous phase measurement and compensation of femtosecond laser pulses. J. Opt. Soc. Am. B 2006, 23, 750–759. [Google Scholar] [CrossRef]
- Comin, A.; Ciesielski, R.; Piredda, G.; Donkers, K.; Hartschuh, A. Compression of ultrashort laser pulses via gated multiphoton intrapulse interference phase scans. J. Opt. Soc. Am. B 2014, 31, 1118–1125. [Google Scholar] [CrossRef] [Green Version]
- Miranda, M.; Fordell, T.; Arnold, C.; L’Huillier, A.; Crespo, H. Simultaneous compression and characterization of ultrashort laser pulses using chirped mirrors and glass wedges. Opt. Express 2012, 20, 688–697. [Google Scholar] [CrossRef] [Green Version]
- Miranda, M.; Arnold, C.L.; Fordell, T.; Silva, F.; Alonso, B.; Weigand, R.; L’Huillier, A.; Crespo, H. Characterization of broadband few-cycle laser pulses with the d-scan technique. Opt. Express 2012, 20, 18732–18743. [Google Scholar] [CrossRef]
- Canhota, M.; Silva, F.A.D.; Weigand, R.; Crespo, H. Inline self-diffraction dispersion-scan of over octave-spanning pulses in the single-cycle regime. Opt. Lett. 2017, 42, 3048–3051. [Google Scholar] [CrossRef] [PubMed]
- Tajalli, A.; Kalousdian, T.K.; Kretschmar, M.; Kleinert, S.; Morgner, U.; Nagy, T. Full characterization of 8 fs deep uv pulses via a dispersion scan. Opt. Lett. 2019, 44, 2498–2501. [Google Scholar] [CrossRef]
- Tajalli, A.; Ouille, M.; Vernier, A.; Bohle, F.; Escoto, E.; Kleinert, S.; Romero, R.; Csontos, J.; Morgner, U.; Steinmeyer, G. Propagation effects in the characterization of 1.5-cycle pulses by xpw dispersion scan. IEEE J. Sel. Top. Quant. 2019, 25, 1–7. [Google Scholar] [CrossRef]
- Spangenberg, D.; Rohwer, E.G.; Brugmann, M.; Feurer, T. Ptychographic ultrafast pulse reconstruction. Opt. Lett. 2015, 40, 1002–1005. [Google Scholar] [CrossRef] [PubMed]
- Witting, T.; Greening, D.; Walke, D.; Matia-Hernando, P.; Barillot, T.; Marangos, J.P.; Tisch, J.W.G. Time-domain ptychography of over-octave-spanning laser pulses in the single-cycle regime. Opt. Lett. 2016, 41, 4218. [Google Scholar] [CrossRef] [PubMed]
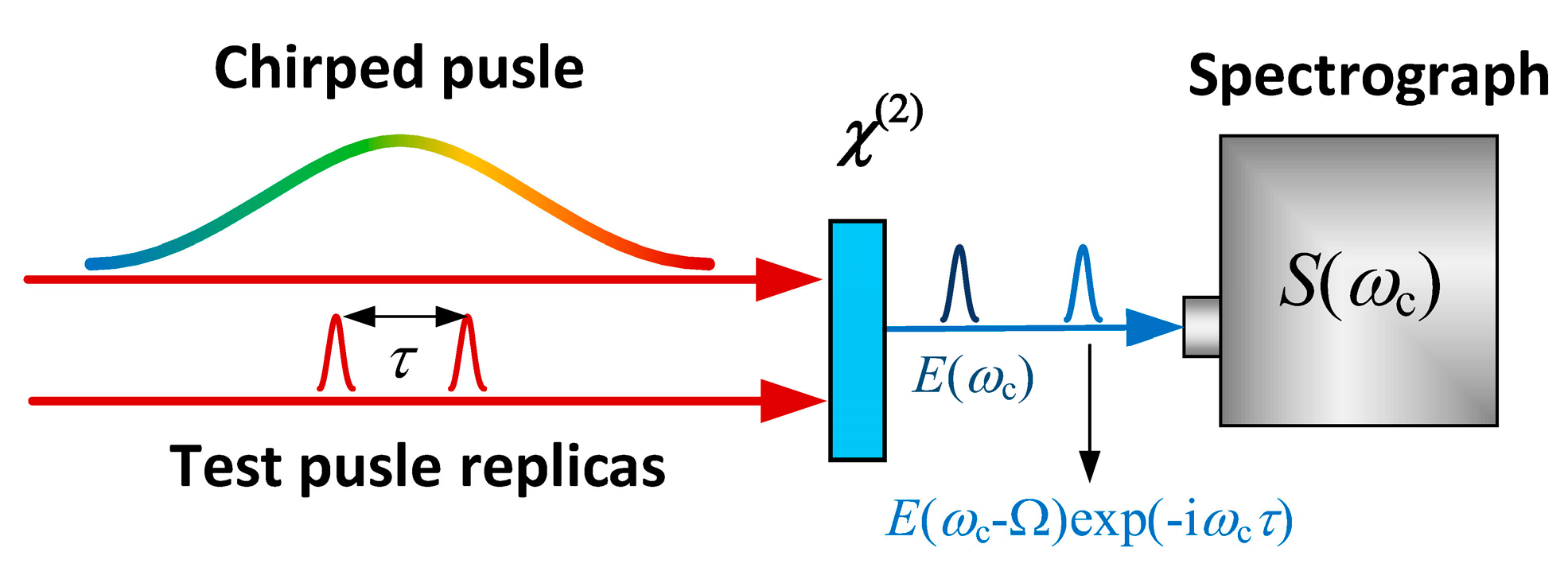
- Loriot, V.; Gitzinger, G.; Forget, N. Self-referenced characterization of femtosecond laser pulses by chirp scan. Opt. Express 2013, 21, 24879. [Google Scholar] [CrossRef] [PubMed]
- Meshulach, D.; Silberberg, Y. Coherent quantum control of two-photon transitions by a femtosecond laser pulse. Nature 1998, 396, 239–242. [Google Scholar] [CrossRef]
- Geib, N.C.; Zilk, M.; Pertsch, T.; Eilenberger, F. Common pulse retrieval algorithm: A fast and universal method to retrieve ultrashort pulses. Optica 2019, 6, 495–505. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Baum, P.; Lochbrunner, S.; Riedle, E. Zero-additional-phase spider: Full characterization of visible and sub-20-fs ultraviolet pulses. Opt. Lett. 2004, 29, 210–212. [Google Scholar] [CrossRef]
- Kosik, E.M.; Radunsky, A.S.; Walmsley, I.A.; Dorrer, C. Interferometric technique for measuring broadband ultrashort pulses at the sampling limit. Opt. Lett. 2005, 30, 326–328. [Google Scholar] [CrossRef]
- Bethge, J.; Grebing, C.; Steinmeyer, G. A fast gabor wavelet transform for high-precision phase retrieval in spectral interferometry. Opt. Express 2007, 15, 14313–14321. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, C.; Chai, L.; Zhang, Z. Determination of gabor wavelet shaping factor for accurate phase retrieval with wavelet-transform. Appl. Phys. B 2005, 81, 1107–1111. [Google Scholar] [CrossRef]
- Wyatt, A.S.; Walmsley, I.A.; Stibenz, G.; Steinmeyer, G. Sub-10 fs pulse characterization using spatially encoded arrangement for spectral phase interferometry for direct electric field reconstruction. Opt. Lett. 2006, 31, 1914–1916. [Google Scholar] [CrossRef] [PubMed]
- Birge, J.R.; Ell, R.; Kärtner, F.X. Two-dimensional spectral shearing interferometry for few-cycle pulse characterization. Opt. Lett. 2006, 31, 2063–2065. [Google Scholar] [CrossRef] [PubMed]
- Birge, J.R.; Kärtner, F.X. Analysis and mitigation of systematic errors in spectral shearing interferometry of pulses approaching the single-cycle limit [invited]. J. Opt. Soc. Am. B 2008, 25, A111–A119. [Google Scholar] [CrossRef]
- Zheng, S.; Cai, Y.; Pan, X.; Zeng, X.; Li, J.; Li, Y.; Zhu, T.; Lin, Q.; Xu, S. Two-step phase-shifting SPIDER. Sci. Rep. 2016, 6, 33837. [Google Scholar] [CrossRef] [Green Version]
- Gero Stibenz, G.S. Optimizing spectral phase interferometry for direct electric-field reconstruction. Rev. Sci. Instrum. 2006, 77, 073105. [Google Scholar] [CrossRef]
- Austin, D.R.; Witting, T.; Walmsley, I.A. High precision self-referenced phase retrieval of complex pulses with multiple-shearing spectral interferometry. J. Opt. Soc. Am. B 2009, 26, 1818–1830. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Z.K.; Zheng, S.Q.; Lin, Q.G.; Zeng, X.K.; Li, Y.; Li, J.Z.; Xu, S.X. Accurate reconstruction of electric field of ultrashort laser pulse with complete two-step phase-shifting. High. Power Laser Sci. 2019, 7, e13. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.E.; Witting, T.; Walmsley, I.A. Gold-spider: Spectral phase interferometry for direct electric field reconstruction utilizing sum-frequency generation from a gold surface. J. Opt. Soc. Am. B 2008, 25, A13–A16. [Google Scholar] [CrossRef] [Green Version]
- Gorza, S.P.; Radunsky, A.S.; Wasylczyk, P.; Walmsley, I.A. Tailoring the phase-matching function for ultrashort pulse characterization by spectral shearing interferometry. J. Opt. Soc. Am. B 2007, 24, 2064–2074. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Chen, Z.; Zheng, S.; Shangguan, H.; Zeng, X.; Lu, X.; Wang, H.; Xu, S. A compact, highly stable spectral shearing interferometer to accurately reconstruct ultrafast laser fields. Opt. Lasers Eng. 2020, 130, 106081. [Google Scholar] [CrossRef]
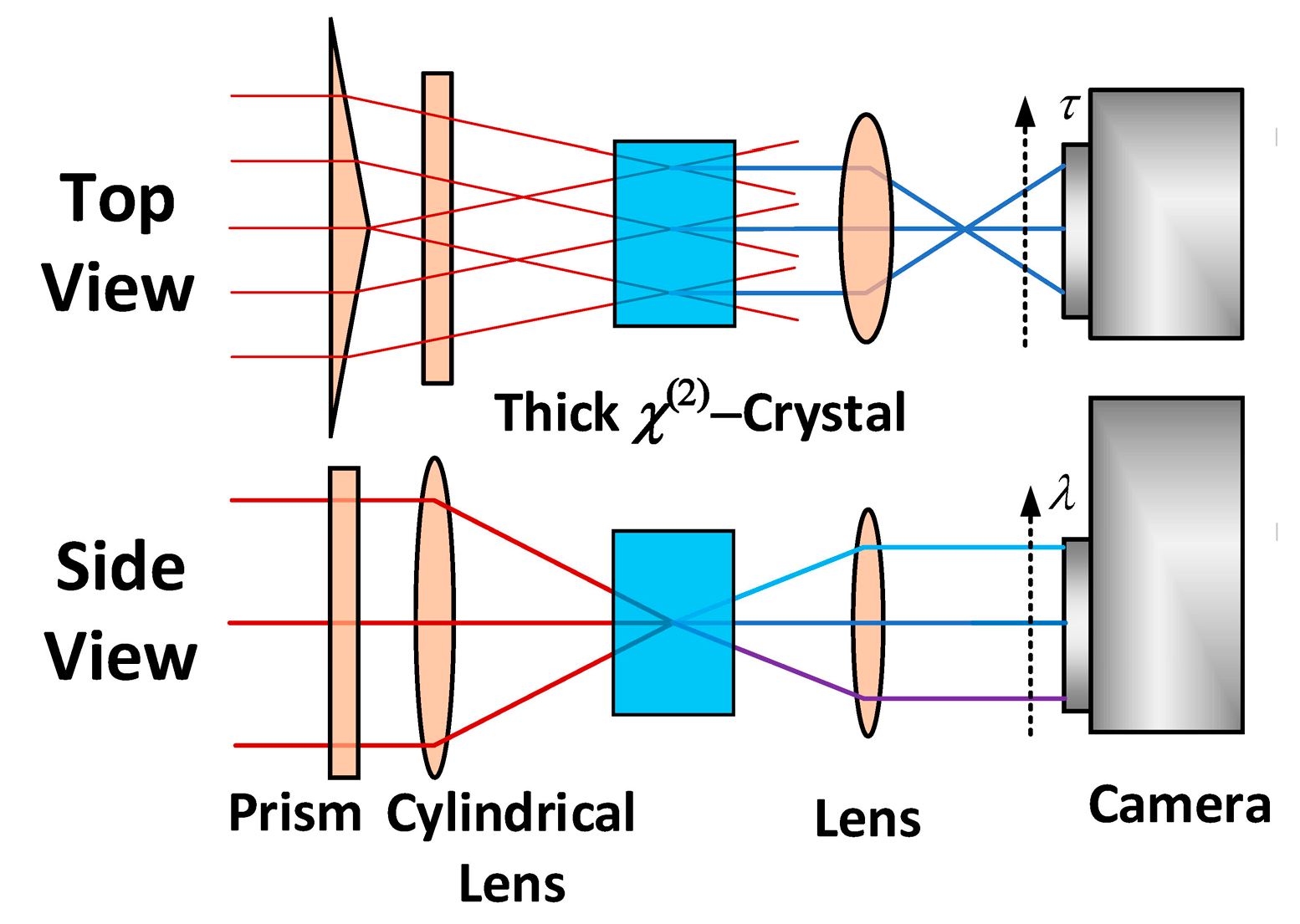
- Radunsky, A.S.; Kosik Williams, E.M.; Walmsley, I.A.; Wasylczyk, P.; Wasilewski, W.; U’Ren, A.B.; Anderson, M.E. Simplified spectral phase interferometry for direct electric-field reconstruction by using a thick nonlinear crystal. Opt. Lett. 2006, 31, 1008–1010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radunsky, A.S.; Walmsley, I.A.; Gorza, S.-P.; Wasylczyk, P. Compact spectral shearing interferometer for ultrashort pulse characterization. Opt. Lett. 2007, 32, 181–183. [Google Scholar] [CrossRef]
- Gallmann, L.; Sutter, D.H.; Matuschek, N.; Steinmeyer, G.; Keller, U. Techniques for the characterization of sub-10-fs optical pulses: A comparison. Appl. Phys. B 2000, 70, S67–S75. [Google Scholar] [CrossRef]
- Oksenhendler, T. Self-referenced spectral interferometry theory. arXiv 2012, arXiv:1204.4949. [Google Scholar]
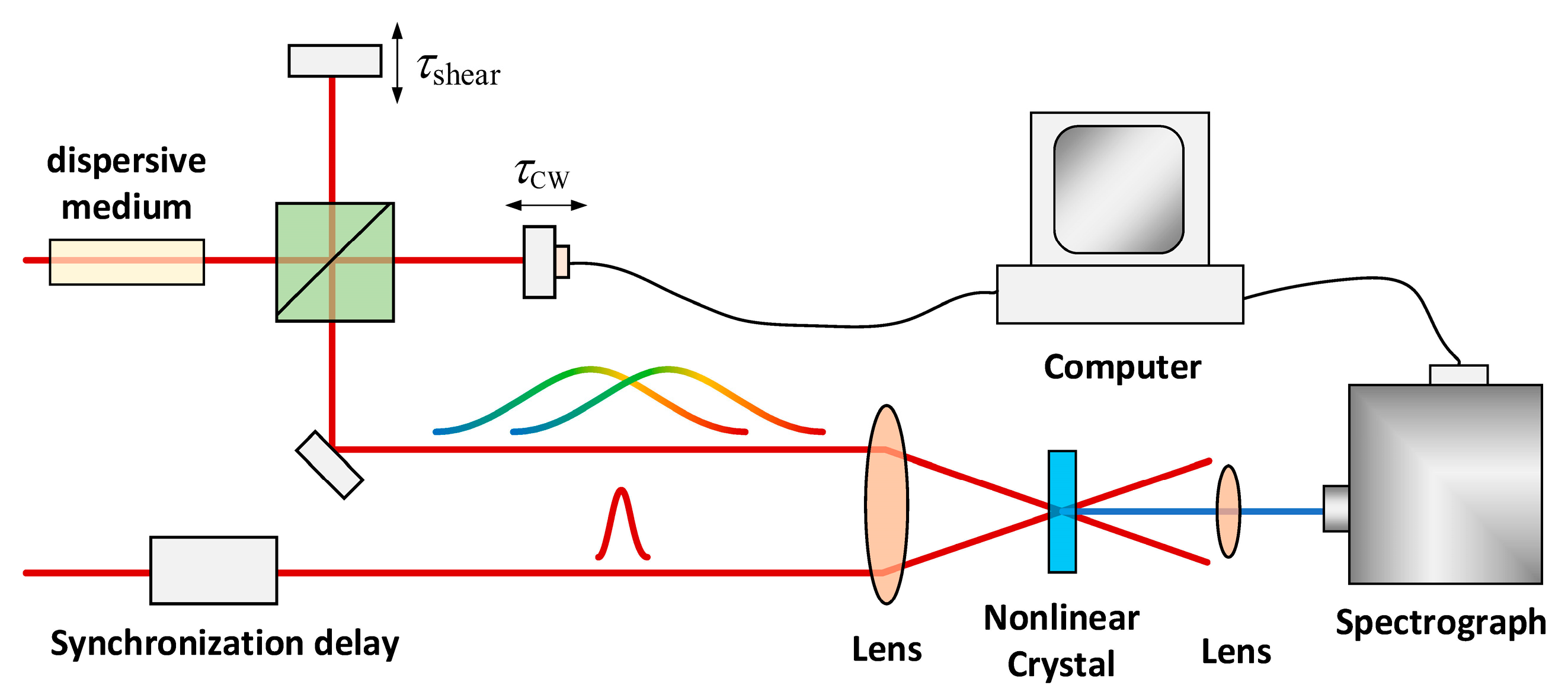
- Liu, J.; Jiang, Y.; Kobayashi, T.; Li, R.; Xu, Z. Self-referenced spectral interferometry based on self-diffraction effect. J. Opt. Soc. Am. B 2012, 29, 29–34. [Google Scholar] [CrossRef]
- Birkholz, S.; Steinmeyer, G.; Koke, S.; Gerth, D.; Bürger, S.; Hofmann, B. Phase retrieval via regularization in self-diffraction-based spectral interferometry. J. Opt. Soc. Am. B 2015, 32, 983–992. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Li, F.J.; Jiang, Y.L.; Li, C.; Leng, Y.X.; Kobayashi, T.; Li, R.X.; Xu, Z.Z. Transient-grating self-referenced spectral interferometry for infrared femtosecond pulse characterization. Opt. Lett. 2012, 37, 4829–4831. [Google Scholar] [CrossRef]
- Shen, X.; Wang, P.; Liu, J.; Li, R.X. Compact transient-grating self-referenced spectral interferometry for sub-nanojoule femtosecond pulse characterization. Appl. Opt. 2017, 56, 582–586. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Yuan, P.; Wang, J.; Wang, Y.; Xie, G.; Zhu, H.; Qian, L. Spatiotemporal noise characterization for chirped-pulse amplification systems. Nat. Commun. 2015, 6, 6192. [Google Scholar] [CrossRef]
- Pires, H.; Baudisch, M.; Sanchez, D.; Hemmer, M.; Biegert, J. Ultrashort pulse generation in the mid-ir. Prog. Quantum Electron. 2015, 43, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Shumakova, V.; Malevich, P.; Ališauskas, S.; Voronin, A.; Zheltikov, A.M.; Faccio, D.; Kartashov, D.; Baltuška, A.; Pugžlys, A. Multi-millijoule few-cycle mid-infrared pulses through nonlinear self-compression in bulk. Nat. Commun. 2016, 7, 12877. [Google Scholar] [CrossRef] [PubMed] [Green Version]
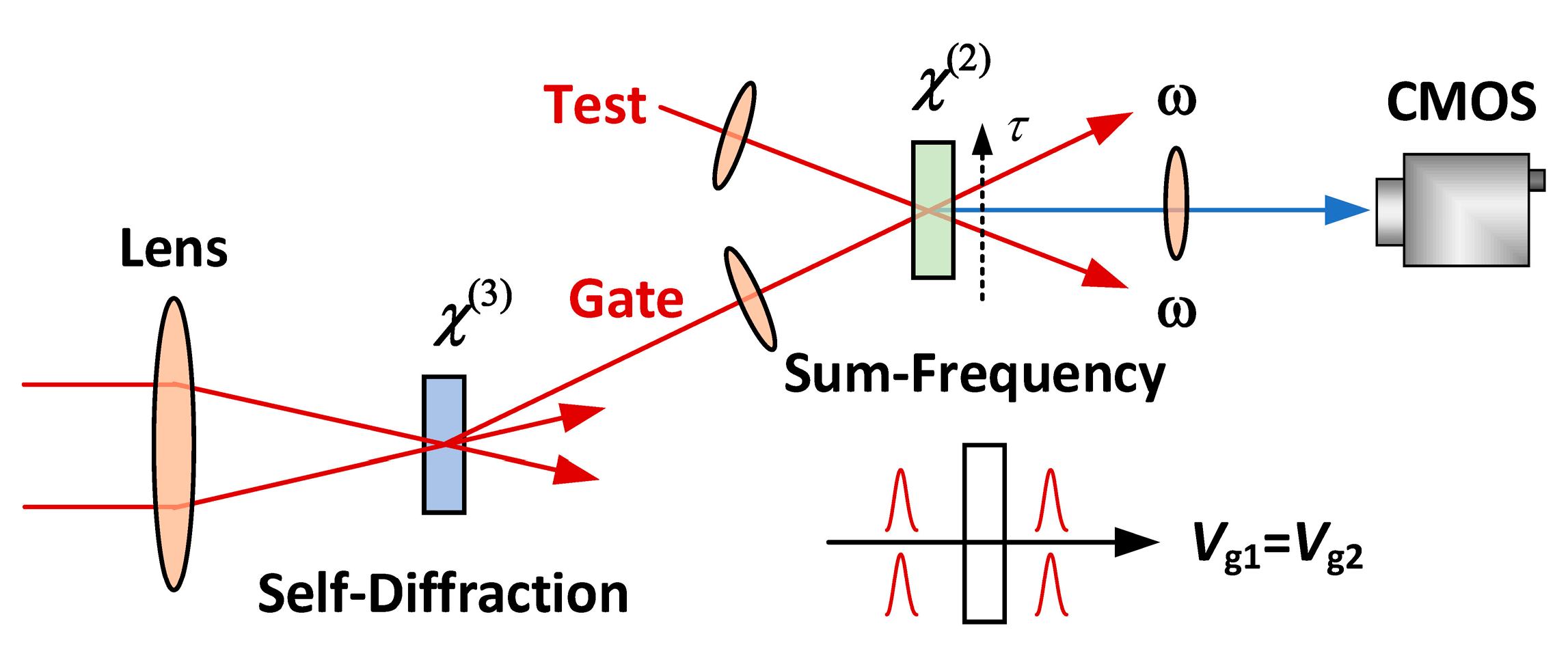

| Nonlinearity | XPW | SD | TG | SHG |
|---|---|---|---|---|
| Sensitivity (Single-shot) | ~1 μJ | ~10 μJ | ~0.1 μJ | ~10 nJ |
| Sensitivity (Multi-shot) | ~0.1 μJ | ~1 μJ | ~10 nJ | ~1 pJ |
| Advantage | Auto phase-matching | UV capability | Sensitive; deep UV capability | Very sensitive; High SNR |
| Disadvantage | Require polarizers | Require phase-matching | Three beams | Phase-matching; Unintuitive traces |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Chen, Z.; Zeng, X.; Shangguan, H.; Lu, X.; Song, Q.; Ai, Y.; Xu, S.; Li, J. The Development of the Temporal Measurements for Ultrashort Laser Pulses. Appl. Sci. 2020, 10, 7401. https://doi.org/10.3390/app10217401
Cai Y, Chen Z, Zeng X, Shangguan H, Lu X, Song Q, Ai Y, Xu S, Li J. The Development of the Temporal Measurements for Ultrashort Laser Pulses. Applied Sciences. 2020; 10(21):7401. https://doi.org/10.3390/app10217401
Chicago/Turabian StyleCai, Yi, Zhenkuan Chen, Xuanke Zeng, Huangcheng Shangguan, Xiaowei Lu, Qiying Song, Yuexia Ai, Shixiang Xu, and Jingzhen Li. 2020. "The Development of the Temporal Measurements for Ultrashort Laser Pulses" Applied Sciences 10, no. 21: 7401. https://doi.org/10.3390/app10217401
APA StyleCai, Y., Chen, Z., Zeng, X., Shangguan, H., Lu, X., Song, Q., Ai, Y., Xu, S., & Li, J. (2020). The Development of the Temporal Measurements for Ultrashort Laser Pulses. Applied Sciences, 10(21), 7401. https://doi.org/10.3390/app10217401





