On Effective Bending Stiffness of a Laminate Nanoplate Considering Steigmann–Ogden Surface Elasticity
Abstract
1. Introduction
2. On the Steigmann–Ogden Surface Elasticity
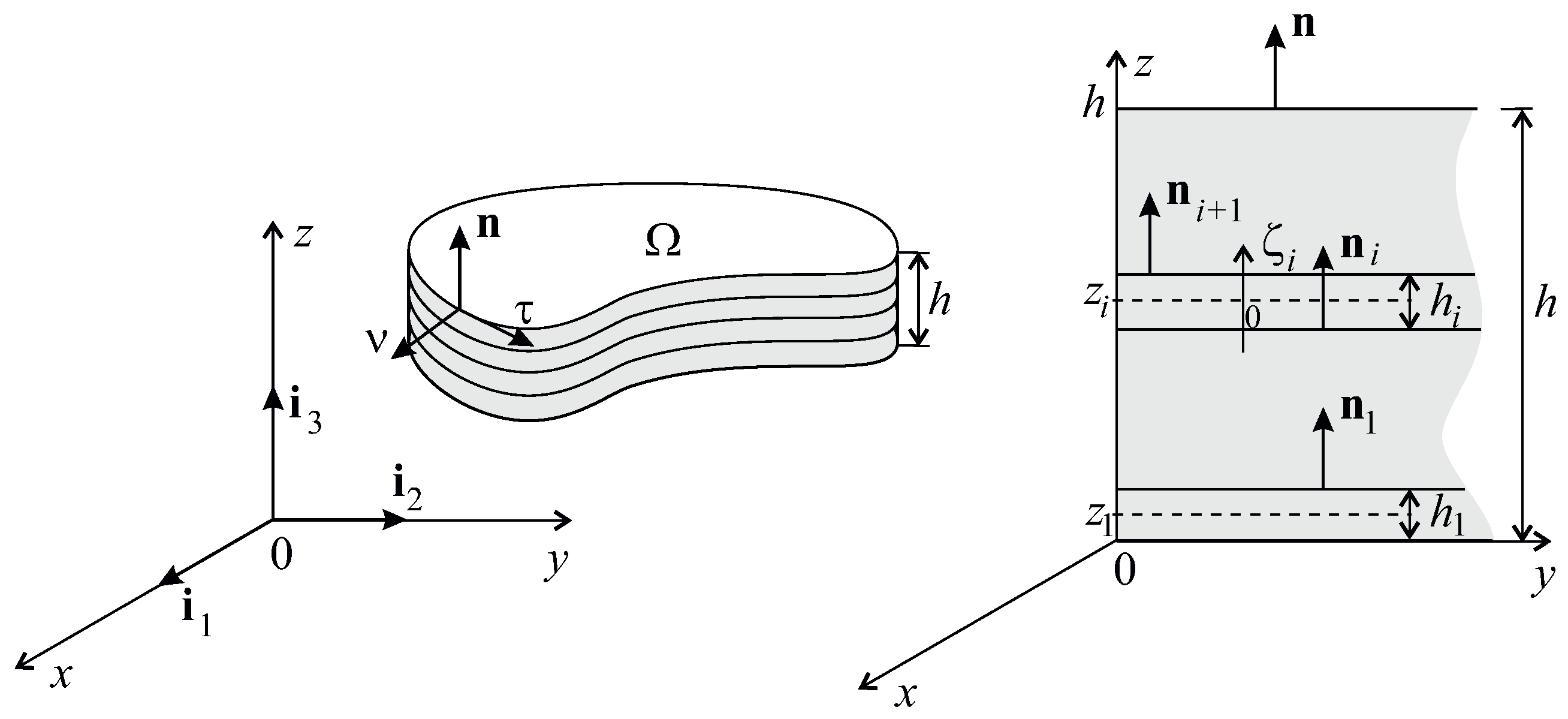
3. Laminate Plate
4. Effective Bending Stiffness
4.1. One-Layered Plate with Surface Stresses
4.2. Three-Layered Plate with Surface Stresses
4.3. N-Layered Plate with Surface Stresses
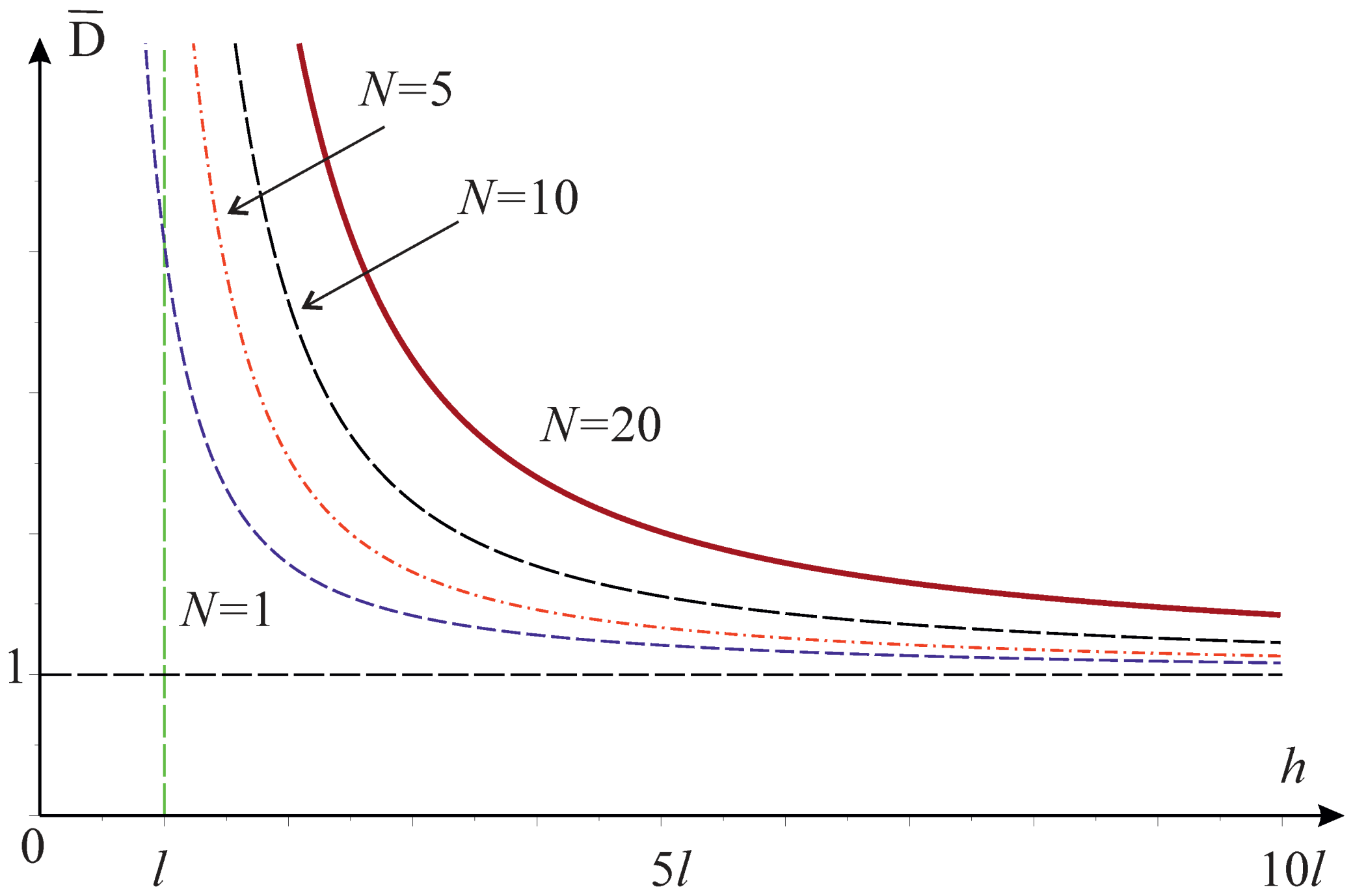
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miller, R.E.; Shenoy, V.B. Size-dependent elastic properties of nanosized structural elements. Nanotechnology 2000, 11, 139–147. [Google Scholar] [CrossRef]
- Wang, J.; Duan, H.L.; Huang, Z.P.; Karihaloo, B.L. A scaling law for properties of nano-structured materials. Proc. R. Soc. Lond. A 2006, 462, 1355–1363. [Google Scholar] [CrossRef]
- Duan, H.L.; Wang, J.; Karihaloo, B.L. Theory of Elasticity at the Nanoscale. In Advances in Applied Mechanic; Elsevier: Amsterdam, The Netherlands, 2008; Volume 42, pp. 1–68. [Google Scholar]
- Kis, A.; Kasas, S.; Babic, B.; Kulik, A.J.; Benoit, W.; Briggs, G.; Schonenberger, C.; Catsicas, S.; Forro, L. Nanomechanics of microtubules. Phys. Rev. Lett. 2002, 89, 248101. [Google Scholar] [CrossRef] [PubMed]
- Jing, G.Y.; Duan, H.L.; Sun, X.M.; Zhang, Z.S.; Xu, J.; Li, Y.D.; Wang, J.X.; Yu, D.P. Surface effects on elastic properties of silver nanowires: Contact atomic-force microscopy. Phys. Rev. B 2006, 73, 235409–235416. [Google Scholar] [CrossRef]
- Pustan, M.; Birleanu, C.; Dudescu, C. Nanocharacterization of the adhesion effect and bending stiffness in optical MEMS. Appl. Surf. Sci. 2017, 421, 191–199. [Google Scholar] [CrossRef]
- Kirchhoff, G.R. Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. Crelles J. Für Die Reine Und Angew. Math. 1850, 40, 51–88. [Google Scholar]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw Hill: New York, NY, USA, 1985. [Google Scholar]
- Steigmann, D.J.; Ogden, R.W. Plane deformations of elastic solids with intrinsic boundary elasticity. Proc. R. Soc. A 1997, 453, 853–877. [Google Scholar] [CrossRef]
- Steigmann, D.J.; Ogden, R.W. Elastic surface-substrate interactions. Proc. R. Soc. A 1999, 455, 437–474. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. Surface stress in solids. Int. J. Solids Struct. 1978, 14, 431–440. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Z.; Duan, H.; Yu, S.; Feng, X.; Wang, G.; Zhang, W.; Wang, T. Surface stress effect in mechanics of nanostructured materials. Acta Mech. Solida Sin. 2011, 24, 52–82. [Google Scholar] [CrossRef]
- Zemlyanova, A.Y.; Mogilevskaya, S.G. Circular inhomogeneity with Steigmann–Ogden interface: Local fields, neutrality, and Maxwell’s type approximation formula. Int. J. Solids Struct. 2018, 135, 85–98. [Google Scholar] [CrossRef]
- Han, Z.; Mogilevskaya, S.G.; Schillinger, D. Local fields and overall transverse properties of unidirectional composite materials with multiple nanofibers and Steigmann–Ogden interfaces. Int. J. Solids Struct. 2018, 147, 166–182. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Rosi, G.; Naili, S. Comparison of anti-plane surface waves in strain-gradient materials and materials with surface stresses. Math. Mech. Solids 2019, 24, 2526–2535. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Rosi, G.; Naili, S. Transverse surface waves on a cylindrical surface with coating. Int. J. Eng. Sci. 2020, 147, 103188. [Google Scholar] [CrossRef]
- Rahali, Y.; Eremeyev, V.A.; Ganghoffer, J.F. Surface effects of network materials based on strain gradient homogenized media. Math. Mech. Solids 2020, 25, 389–406. [Google Scholar] [CrossRef]
- Gorbushin, N.; Eremeyev, V.A.; Mishuris, G. On stress singularity near the tip of a crack with surface stresses. Int. J. Eng. Sci. 2020, 146, 103183. [Google Scholar] [CrossRef]
- Chebakov, R.; Kaplunov, J.; Rogerson, G.A. A non-local asymptotic theory for thin elastic plates. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170249. [Google Scholar] [CrossRef]
- Sajadi, B.; Goosen, H.; van Keulen, F. Capturing the effect of thickness on size-dependent behavior of plates with nonlocal theory. Int. J. Solids Struct. 2017, 115-116, 140–148. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Sharma, B.L. Anti-plane surface waves in media with surface structure: Discrete vs. continuum model. Int. J. Eng. Sci. 2019, 143, 33–38. [Google Scholar] [CrossRef]
- Simmonds, J.G. A Brief on Tensor Analysis, 2nd ed.; Springer: New York, NY, USA, 1994. [Google Scholar]
- Eremeyev, V.A.; Cloud, M.J.; Lebedev, L.P. Applications of Tensor Analysis in Continuum Mechanics; World Scientific: Singapore, 2018. [Google Scholar]
- Eremeyev, V.A.; Lebedev, L.P. Mathematical study of boundary-value problems within the framework of Steigmann–Ogden model of surface elasticity. Contin. Mech. Thermodyn. 2016, 28, 407–422. [Google Scholar] [CrossRef]
- Benveniste, Y.; Miloh, T. Imperfect soft and stiff interfaces in two-dimensional elasticity. Mech. Mater. 2001, 33, 309–323. [Google Scholar] [CrossRef]
- Mishuris, G.S.; Movchan, N.V.; Movchan, A.B. Steady-state motion of a mode-III crack on imperfect interfaces. Q. J. Mech. Appl. Math. 2006, 59, 487–516. [Google Scholar] [CrossRef]
- Berdichevsky, V.L. Nonlinear theory of hard-skin plates and shells. Int. J. Eng. Sci. 2010, 48, 357–369. [Google Scholar] [CrossRef]
- Eremeyev, V.A. On dynamic boundary conditions within the linear Steigmann-Ogden model of surface elasticity and strain gradient elasticity. In Dynamical Processes in Generalized Continua and Structures; Altenbach, H., Belyaev, A., Eremeyev, V.A., Krivtsov, A., Porubov, A.V., Eds.; Springer: Cham, Switzerland, 2019; pp. 195–207. [Google Scholar]
- Abali, B.E.; Müller, W.H.; dell’Isola, F. Theory and computation of higher gradient elasticity theories based on action principles. Arch. Appl. Mech. 2017, 87, 1495–1510. [Google Scholar] [CrossRef]
- Altenbach, H.; Eremeyev, V. Thin-Walled Structural Elements: Classification, Classical and Advanced Theories, New Applications. In Shell-like Structures: Advanced Theories and Applications; Altenbach, H., Eremeyev, V., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–62. [Google Scholar]
- Altenbach, H.; Eremeyev, V.A. On the shell theory on the nanoscale with surface stresses. Int. J. Eng. Sci. 2011, 49, 1294–1301. [Google Scholar] [CrossRef]
- Altenbach, H.; Eremeyev, V.A. Direct approach-based analysis of plates composed of functionally graded materials. Arch. Appl. Mech. 2008, 78, 775–794. [Google Scholar] [CrossRef]
- Naumenko, K.; Eremeyev, V.A. A layer-wise theory for laminated glass and photovoltaic panels. Compos. Struct. 2014, 112, 283–291. [Google Scholar] [CrossRef]
- Naumenko, K.; Eremeyev, V.A. A layer-wise theory of shallow shells with thin soft core for laminated glass and photovoltaic applications. Compos. Struct. 2017, 178, 434–446. [Google Scholar] [CrossRef]
- dell’Isola, F.; Guarascio, M.; Hutter, K. A variational approach for the deformation of a saturated porous solid. A second-gradient theory extending Terzaghi’s effective stress principle. Arch. Appl. Mech. 2000, 70, 323–337. [Google Scholar] [CrossRef]
- Casalotti, A.; D’Annibale, F.; Rosi, G. Multi-scale design of an architected composite structure with optimized graded properties. Compos. Struct. 2020, 252, 112608. [Google Scholar] [CrossRef]
- dell’Isola, F.; Giorgio, I.; Pawlikowski, M.; Rizzi, N.L. Large deformations of planar extensible beams and pantographic lattices: Heuristic homogenization, experimental and numerical examples of equilibrium. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150790. [Google Scholar] [CrossRef]
- Turco, E.; Golaszewski, M.; Giorgio, I.; D’Annibale, F. Pantographic lattices with non-orthogonal fibres: Experiments and their numerical simulations. Compos. Part B Eng. 2017, 118, 1–14. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Seppecher, P.; Alibert, J.J.; Lekszycki, T.; Grygoruk, R.; Pawlikowski, M.; Steigmann, D.; Giorgio, I.; Andreaus, U.; Turco, E.; et al. Pantographic metamaterials: An example of mathematically driven design and of its technological challenges. Contin. Mech. Thermodyn. 2019, 31, 851–884. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Seppecher, P.; Spagnuolo, M.; Barchiesi, E.; Hild, F.; Lekszycki, T.; Giorgio, I.; Placidi, L.; Andreaus, U.; Cuomo, M.; et al. Advances in pantographic structures: Design, manufacturing, models, experiments and image analyses. Contin. Mech. Thermodyn. 2019, 31, 1231–1282. [Google Scholar] [CrossRef]
- Alibert, J.J.; Seppecher, P.; dell’Isola, F. Truss modular beams with deformation energy depending on higher displacement gradients. Math. Mech. Solids 2003, 8, 51–73. [Google Scholar] [CrossRef]
- Turco, E.; Barchiesi, E. Equilibrium paths of Hencky pantographic beams in three-point bending problem. Math. Mech. Complex Syst. 2019, 7, 287–310. [Google Scholar] [CrossRef]
- Barchiesi, E.; Eugster, S.R.; Placidi, L.; dell’Isola, F. Pantographic beam: A complete second gradient 1D-continuum in plane. Z. Für Angew. Math. Und Phys. 2019, 70, 135. [Google Scholar] [CrossRef]
- Eremeyev, V.A.; Ganghoffer, J.F.; Konopińska-Zmysłowska, V.; Uglov, N.S. Flexoelectricity and apparent piezoelectricity of a pantographic micro-bar. Int. J. Eng. Sci. 2020, 149, 103213. [Google Scholar] [CrossRef]
- Scerrato, D.; Giorgio, I.; Rizzi, N.L. Three-dimensional instabilities of pantographic sheets with parabolic lattices: Numerical investigations. Z. Für Angew. Math. Und Phys. 2016, 67, 53. [Google Scholar] [CrossRef]
- Giorgio, I.; Rizzi, N.; Turco, E. Continuum modelling of pantographic sheets for out-of-plane bifurcation and vibrational analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170636. [Google Scholar] [CrossRef]
- Giorgio, I.; Rizzi, N.L.; Andreaus, U.; Steigmann, D.J. A two-dimensional continuum model of pantographic sheets moving in a 3D space and accounting for the offset and relative rotations of the fibers. Math. Mech. Complex Syst. 2019, 7, 311–325. [Google Scholar] [CrossRef]
- dell’Isola, F.; Turco, E.; Misra, A.; Vangelatos, Z.; Grigoropoulos, C.; Melissinaki, V.; Farsari, M. Force–displacement relationship in micro-metric pantographs: Experiments and numerical simulations. Comptes Rendus Mécanique 2019, 347, 397–405. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eremeyev, V.A.; Wiczenbach, T. On Effective Bending Stiffness of a Laminate Nanoplate Considering Steigmann–Ogden Surface Elasticity. Appl. Sci. 2020, 10, 7402. https://doi.org/10.3390/app10217402
Eremeyev VA, Wiczenbach T. On Effective Bending Stiffness of a Laminate Nanoplate Considering Steigmann–Ogden Surface Elasticity. Applied Sciences. 2020; 10(21):7402. https://doi.org/10.3390/app10217402
Chicago/Turabian StyleEremeyev, Victor A., and Tomasz Wiczenbach. 2020. "On Effective Bending Stiffness of a Laminate Nanoplate Considering Steigmann–Ogden Surface Elasticity" Applied Sciences 10, no. 21: 7402. https://doi.org/10.3390/app10217402
APA StyleEremeyev, V. A., & Wiczenbach, T. (2020). On Effective Bending Stiffness of a Laminate Nanoplate Considering Steigmann–Ogden Surface Elasticity. Applied Sciences, 10(21), 7402. https://doi.org/10.3390/app10217402





