A Study on the Evaluation of Effective Properties of Randomly Distributed Gas Diffusion Layer (GDL) Tissues with Different Compression Ratios

Abstract

The gas diffusion layer (GDL) typically consists of a thin layer of carbon fiber paper, carbon cloth or nonwoven and has numerous pores. The GDL plays an important role that determines the performance of the fuel cell. It is a medium through which hydrogen and oxygen are transferred and serves as a passage through which water, generated by the electrochemical reaction, is discharged. The GDL tissue undergoes a compressive loading during the stacking process. This leads to changes in fiber content, porosity and resin content due to compressive load, which affects the mechanical, chemical and electrical properties of the GDL and ultimately determines fuel cell performance. In this study, the geometry of a GDL was modeled according to the compression ratios (10%, 20%, 30%, 40% and 50%), which simulated the compression during the stacking process and predicted the equivalent properties according to the change of GDL carbon fiber content, matrix content and pore porosity, etc. The proposed method to predict the equivalent material properties can not only consider the stacking direction of the material during stack assembling process, but can also provide a manufacturing standard for fastening compressive load for GDL.

1. Introduction

Fuel cells are electrochemical devices that convert chemical energy directly into electrical energy. There are various types such as proton-exchange membrane fuel cells (PEMFCs), solid oxide fuel cells (SOFCs) and molten carbonate fuel cell (MCFCs) depending on fuel and substances. Among them, PEMFCs are the most attractive fuel cells due to their low operating temperature, compact structure and fast startup and shutdown facilities [1,2,3,4]. In terms of structural and functional aspects, the fuel cell can be divided into a separation plate, a gas diffusion layer (GDL), a membrane electrode assembly (MEA) and a gasket. The porous structure of a GDL transfers the reactant gas (hydrogen and oxygen) supplied through the separator to the MEA where the electrochemical reaction occurs and discharges the water generated by the electrochemical reaction to the separator in the catalyst layer of the MEA. There are many pores in the GDL that are the passages of the reaction gas and the generated water. Through these numerous pores, the gases (hydrogen and oxygen) are transported, and the water produced by the electrochemical reaction is discharged [5,6].

The porous structure of the GDL typically consists of a thin layer of carbon fiber paper, carbon cloth or nonwoven. The GDL plays an important role that determines the performance of the fuel cell. Recently, in order to improve the efficiency of the flow characteristics inside the GDL, various studies have been carried out from the viewpoint of the design such as the clamping pressure that is produced in the stack assembly process, the assembling method and the optimum structural design method [7,8]. These studies aim to control the material characteristics and the design variables of fuel cells, such as hydrophobic polymer content [9,10], pore-size distribution [11,12], temperature distribution [13], humidity, differential pressure effects and compressive force effects of GDLs [14,15,16,17,18,19,20,21,22,23]. The amount of compression ratio of the GDL affects the porosity, directionality and the fraction of the pore space occupied by liquid water and affects the performance of a fuel cell. For example, Cheema et al. [24] studied porosity characteristics of the composite porous GDLs due to manufacturing variations in the manufacturing process. Hwang et al. [25] studied alternative methods to control the compression ratio according to the design of the stack structure and thickness of the gasket. Jeong et al. [26] predicted the pore structure according to the direction and geometrical changes of GDL structure by compression load and then investigated the change of internal flow characteristics. Chippar et al. [27] performed computational fluid dynamics (CFD) analysis on the intrusion effect of the gas diffusion layer pushing into the channel, due to the compressive force of the separator and the deterioration of the cell performance due to the thickness reduction of the GDL itself. Most of the above studies are mostly for predicting the changes in GDL flow characteristics and fuel cell performance due to the compressive force. Especially in order to analyze the performance of the fuel cell, it is essential to identify the physical properties of the GDL. Since these properties vary greatly depending on the compression ratio, it is necessary to study the prediction of GDL properties depending on the compression ratio. For GDL tissues, both chemical and mechanical stability should be satisfied [28]; the prediction of effective mechanical properties of the GDL can give us the ability to consider the orientation of the material stacking during the stack assembling process and manufacturing standard for the compressive clamping load.

Several types of homogenization methods have been studied to predict the equivalent material properties of composite materials on the information for microstructure, such as mean field and full field approaches. Within the mean field approach, bounding and estimating methods can be distinguished [29]. The former specifies the allowable range of the available equivalent properties. For instance, Voigt et al. [30] assumed that strain fields or stress fields, respectively, are uniform throughout the heterogeneous materials. Hashin [31] and Willis et al. [32] provided more extended and specific bounds for anisotropic materials. Unlike the bounding method, the estimating methods approximate the effective behavior. According to Mori-Tanaka [33], the generalized self-consistent (SC) [34] and the interaction direct derivative (IDD) are representatives of mean field methods [35,36,37]. They have been applied to homogenize the multiphase composites, such as thermoelastic and elastoplastic materials [38]. For full field approaches [39,40,41,42], several researchers introduced the concept of a unit-cell called a representative volume element (RVE). After determining the local domains in the RVE, the equivalent properties can be estimated by the volume average method of the full field simulation [43]. Muller et al. [44] calculated linear elastic properties which predicted the properties of randomly distributed GDL tissues without considering compression.

In this paper, the equivalent mechanical properties of the GDL were calculated by considering the deformation due to compression ratio through the Fourier series-based, full field homogenization method. For the nonwoven GDL structure, it was modeled before compression and implemented the deformed geometry by compression ratio. The compression ratio was set to 10%, 20%, 30%, 40% and 50%, respectively. The deformed shape of the GDL structure with the compression ratio was implemented using the commercial program GeoDict. The porosity, fiber volume fraction (FVF) and fiber anisotropy in the GDL were calculated with the compression ratio. In order to evaluate the equivalent properties, the Fourier series-based homogenization technique was applied based on the same fiber volume ratio and orientation tensor in previous study [44]. A subroutine script for the Fourier series-based homogenization method was created through a Python input file in Abaqus.

2. Fourier Series-Based Homogenization Method Materials

The actual stress tensor σ in the linear elastic unit-cell can be expressed as the strain tensors ε* and ε, as follows [45,46,47,48,49]:

σ = C(ε − ε*) in D

(1)

where C is elasticity tensor of the matrix, ε* is eigenstrain and ε is actual strain. Assume that the body force is to zero, and the tensor σ should satisfy the following equilibrium conditions:

divσ = 0 in D

(2)

Additionally, the Fourier series representation of u, ε and ε* can be considered, since the solid and boundary condition displacements are periodic.

$$u(x)={\displaystyle \sum _{\xi }^{\pm \infty }\overline{u}(}\xi )\exp (i\xi x)$$

(3)

$$\epsilon (x)=sym(\nabla u(x))={\displaystyle \sum _{\xi }^{\pm \infty }\overline{\epsilon }(}\xi )\exp (i\xi x)$$

(4)

$${\epsilon }^{\ast }(x)={\displaystyle \sum _{\xi }^{\pm \infty }{\overline{\epsilon }}^{\ast }(}\xi )\exp (i\xi x)$$

(5)

where $\xi =({\xi }_1,{\xi }_2,{\xi }_3)$, ${\xi }_j=2\pi n_j/a_j(n_j=0,\pm 1,\pm 2,\dots ,j)$, $(j=1,2,3)$.

$$\overline{u}(\xi )={\displaystyle {\int }_{D}u(x)\exp (-i\xi x)dx}$$

(6)

$$\overline{\epsilon }(\xi )=\frac{i}{2}[\xi \otimes \overline{u}(\xi )+\overline{u}(\xi )\otimes \xi ]$$

(7)

$${\overline{\epsilon }}^{\ast }(\xi )={\displaystyle {\int }_D{\epsilon }^{\ast }}(x)\exp (-i\xi x)dx$$

(8)

Combining Equations (1) and (2) provides

div C(ε − ε^∗) = 0 in D

(9)

Then, by using Equations (4), (5) and (7) in (9), the following expressions are obtained:

$$-\xi \cdot C(\xi \otimes \overline{u}(\xi ))=i\xi \cdot C{\overline{\epsilon }}^{\ast }(\xi )\mathrm{for}\mathrm{every}\xi \ne 0$$

(10)

where $\otimes$ and $\cdot$ represent the outer and inner products, respectively [46]; C is the elastic tensor of the matrix, and the coefficients $\overline{u}(\xi )$ are represented by ${\overline{\epsilon }}^{\ast }(\xi )$ as follows:

$$\overline{u}(\xi )=-i{(\xi \cdot C\cdot \xi )}^{-1}\cdot \xi \cdot C{\overline{\epsilon }}^{\ast }(\xi )\mathrm{for}\mathrm{every}\xi \ne 0$$

(11)

and the Fourier coefficient of the strain from Equation (7) is

$$\overline{\epsilon }(\xi )=sym(\xi \otimes {(\xi \cdot C\cdot \xi )}^{-1}\otimes \xi ):C{\overline{\epsilon }}^{\ast }(\xi )\mathrm{for}\mathrm{every}\xi \ne 0$$

(12)

finally denoting

$$P^{\prime }(\xi )=sym(\xi \otimes {(\xi \cdot C\cdot \xi )}^{-1}\otimes \xi )$$

(13)

Using Equations (4) and (8) to find the actual strain inside the inclusion from Equation (12):

$$\epsilon (x)=\frac{1}{V}{\displaystyle \sum _{\zeta }^{\pm {\infty }^{\prime }}{P}^{\prime }(\xi ):}C{\displaystyle {\int }_D{\epsilon }^{\ast }}(x)\exp (-i\xi (x^{\prime }-x)d{x}^{\prime }$$

(14)

The exact representation of strain tensor $\epsilon \left(x\right)$ is not essential for obtaining the overall elastic tensor C*, but its volume averages on Ω are denoted by

$$\overline{\epsilon }(x)=\frac{1}{V}{\displaystyle \sum _{\zeta }^{\pm {\infty }^{\prime }}{P}^{\prime }(\xi ):}C\left(\frac{g_o(\xi )}{V_{\mathrm{\Omega }}}\right){\displaystyle {\int }_D{\epsilon }^{\ast }}(x)\exp (-i\xi x^{\prime })d{x}^{\prime }$$

(15)

V_Ω is the volume of the inclusion, and ε* is considered in Ω.

$$g_0(\xi )={\displaystyle {\int }_{\mathrm{\Omega }}\exp (i\xi x)dx}$$

(16)

Then, replacing ε* with its volume average ${\overline{\epsilon }}^{*}$

$$\overline{\epsilon }(x)=\frac{1}{V}{\displaystyle \sum _{\xi }^{\pm {\infty }^{\prime }}{P}^{\prime }(\xi ):}C\left(\frac{g_o(\xi )g_o(-\xi )}{V_{\mathrm{\Omega }}}\right){\overline{\epsilon }}^{*}$$

(17)

The denotation and combination of equations gives:

$$t(\xi )=f\left(\frac{g_o(\xi )}{V_{\mathrm{\Omega }}}\right)\left(\frac{g_o(-\xi )}{V_{\mathrm{\Omega }}}\right)$$

(18)

$$P={\displaystyle \sum _{\xi }^{\pm {\infty }^{\prime }}t(\xi )P^{\prime }(\xi )}$$

(19)

$$\overline{\epsilon }=P:C:{\overline{\epsilon }}^{*}in\mathrm{\Omega }$$

(20)

To obtain the homogenization eigenstrain that simulates the presence of the periodic inclusion in the body, an average strain tensor ${\overline{\epsilon }}_0$ should be considered in the unit-cell [46,47,48,49,50,51].

$$C^{\prime }:({\overline{\epsilon }}_o+P:C:{\overline{\epsilon }}^{*})=C:({\overline{\epsilon }}_o+(P:C-I^{(4)}):{\overline{\epsilon }}^{*})$$

(21)

where C represents the elastic tensor of the matrix, C′ represents the elastic tensor of the inclusion and $I^{\left(4\right)}$ represents the identity fourth-order tensor. Note that ${\overline{\epsilon }}_0$ is arbitrary, and the following equation for the overall stiffness tensor of the composite material can be obtained:

$$C^{*}=C-f{({(C-C^{\prime })}^{-1}-P)}^{-1}$$

(22)

Since P, C and C′ are all symmetric to evaluate C* in Equation (22), an averaging process [45] is used to obtain the average isotropic stiffness tensor including the reversal of the symmetric tensor. For unidirectional fibers aligned in the x₁-direction or x₂-direction, the following equations are obtained by the coefficients of the tensor C* [45,46,47,48,52,53].

$$E_A=C_{11}^{\ast }-\frac{C_{12}^{*}{}^2}{C_{22}^{*}+C_{23}^{*}}$$

(23)

$$E_T=\frac{(2C_{11}^{*}{C}_{22}^{*}+2C_{11}^{*}{C}_{23}^{*}-4C_{12}^{*}{}^2)(C_{22}^{*}-C_{23}^{*}+2C_{44}^{*})}{3C_{11}^{*}{C}_{22}^{*}+C_{11}^{*}{C}_{23}^{*}+2C_{11}^{*}{C}_{44}^{*}-4C_{12}^{*}{}^2}$$

(24)

$$G_A=C_{66}^{*}$$

(25)

$$G_T=\frac{C_{22}^{*}}{4}-\frac{C_{23}^{*}}{4}+\frac{C_{44}^{*}}{2}=\frac{E_T}{2(1+{\upsilon }_T)}$$

(26)

$${\upsilon }_A=\frac{C_{12}^{*}}{C_{22}^{*}+C_{23}^{*}}$$

(27)

$${\upsilon }_T=\frac{C_{11}^{*}{C}_{22}^{*}+3C_{11}^{*}{C}_{23}^{*}-2C_{11}^{*}{C}_{44}^{*}-4C_{12}^{*}{}^2}{3C_{11}^{*}{C}_{22}^{*}+C_{11}^{*}{C}_{23}^{*}+2C_{11}^{*}{C}_{44}^{*}-4C_{12}^{*}{}^2}$$

(28)

3. Modeling and Analysis Method

3.1. Generating a Fiber Network for Verification of the Proposed Homogenization Technique

To verify the Fourier series theory, the modeling and verification for microstructure were firstly performed based on the proposed fiber orientation tensors [44]. The overall fiber orientation tensor is defined as [50]:

$$N=\frac{1}{N}{\displaystyle \sum _{\alpha =1}^N{n}_{\alpha }\otimes n_{\alpha }}$$

(29)

Since the fiber axis direction n is normalized, the trajectory of the fiber orientation tensor is always a unity. It is defined as the operator, $\otimes$, which is the dyadic product. For all microstructures, the fibers were modeled as circular rods with a length of l = 200 μm and a diameter of d = 10 μm. The resolution is 100, corresponding to a voxel length of 2 μm. Fiber volume fraction was 13%. The domain size was 125 × 125 × 125 voxels (250 μm × 250 μm × 250 μm), and the aspect ratio is 20. In addition, the mechanical properties of the matrix and fibers were set to E_m = 1.665 GPa, υm = 0.36, E_f = 73 GPa and υ_f = 0.36, respectively. Based on the above information, fiber network modeling and overall fiber orientation tensors are shown in Figure 1 and

Table 1. Components of orientation tensors used for the generation of microstructures for verification of Fourier series.

Orientation Tensor	1	2	3
1	0.61	-	-
2	-	0.36	-
3	-	-	0.03

.

3.2. Generating Fiber Network of Unit-Cell for Different Compression Ratios

The fiber network was generated by the commercial software GeoDict’s Fiber-guess module through the random modeling process. The randomly distributed GDL fiber network was generated using the voxel mesh technique. The star length distribution (SLD) method was used to obtain the overall fiber orientation tensor for the unit-cell. The SLD approach analyzes a voxel’s length for predefined directions. The components of the fiber orientation unit vector n = (n_x, n_y, n_z) are calculated by SLD [54,55,56,57]. The tensor was averaged over all voxels contained in the unit-cell. The overall average tensor is derived to overcome the difficulty of considering the direction for each distributed discontinuous carbon fiber. The fibers were modeled as circular rods with a length of l = 200 μm and a diameter of d = 10 μm. The resolution is 100, corresponding to a voxel length of 2 μm. Initial fiber volume fraction is 17.89%. The domain size is 100 × 100 × 100 (200 μm × 200 μm × 200 μm). Additionally, the Young’s moduli and Poisson’s ratios of the matrix and of the fibers are set to E_m = 3.12 GPa, υ_m = 0.38, E_f = 230 GPa and υ_f = 0.2, respectively. The phase contrast of this combination amounts to ς = 73.7.

When a fiber network was created with various compression ratios under the above conditions, the carbon fibers were drained out of the unit-cell domain during the compression process. As a result, a procedure was performed to exclude fibers and resin that deviated from the domain area. Figure 2 shows the variation of fiber volume fraction along the x-direction and y-direction according to the GDL compression ratio. There are rapid changes in the fiber content at the two opposite parallel sides, which are the boundaries of the domains, and this is due to the out-of-domain fibers and matrix.

Figure 3 shows the GDL fiber network according to the compression ratio, which allows visual identification of changes in porosity, carbon fiber and epoxy content.

Table 2. Components of orientation tensors used for the generation of the model microstructures

	Orientation Tensor	1	2	3
Original GDL model	1	0.464	-	-
	2	-	0.464	-
	3	-	-	0.072
10% compressed GDL model	1	0.464	-	-
	2	-	0.467	-
	3	-	-	0.069
20% compressed GDL model	1	0.461	-	-
	2	-	0.471	-
	3	-	-	0.068
30% compressed GDL model	1	0.459	-	-
	2	-	0.461	-
	3	-	-	0.080
40% compressed GDL model	1	0.454	-	-
	2	-	0.454	-
	3	-	-	0.092
50% compressed GDL model	1	0.448	-	-
	2	-	0.451	-
	3	-	-	0.101

and

Table 3. Components of fiber volume fraction for the generation of the model microstructures.

	Original	10%	20%	30%	40%	50%
Porosity	70.16	70.05 (∇0.11)	65.85 (∇4.2)	61.43 (∇4.42)	55.59 (∇5.84)	47.74 (∇7.85)
Fiber volume fraction	17.89	19.79 (∆1.9)	22.06 (∆2.27)	24.94 (∆2.88)	29.14 (∆4.2)	35.04 (∆5.9)
Resin volume fraction	11.95	10.16 (∇1.79)	12.09 (∆0.17)	13.63 (∆1.68)	15.26 (∆3.31)	17.22 (∆5.27)

indicate the results for the overall orientation tensor for carbon fiber as reinforcement, and geometric properties with the compression ratios, respectively. Figure 3 and Table 2 are the input values for calculating the equivalent properties in the commercial program ABAQUS.

3.3. Boundary Conditions in the Finite Element Model

As shown in Figure 4, the homogeneous boundary conditions applied to the surface of a homogeneous object create a uniform field in the commercial software ABAQUS. These boundary conditions are obtained by imposing displacements at the boundary as follows [45,52,53]:

$$u_i(S)={\epsilon }_{ij}^0{x}_j$$

(30)

where ${\epsilon }_{ij}$ are constant strains.

Meshing constitutes a challenge for microstructural simulations of composite materials. To avoid these difficulties with automated meshing, the simulations are usually performed on regular voxel grids.

4. Results and Discussion

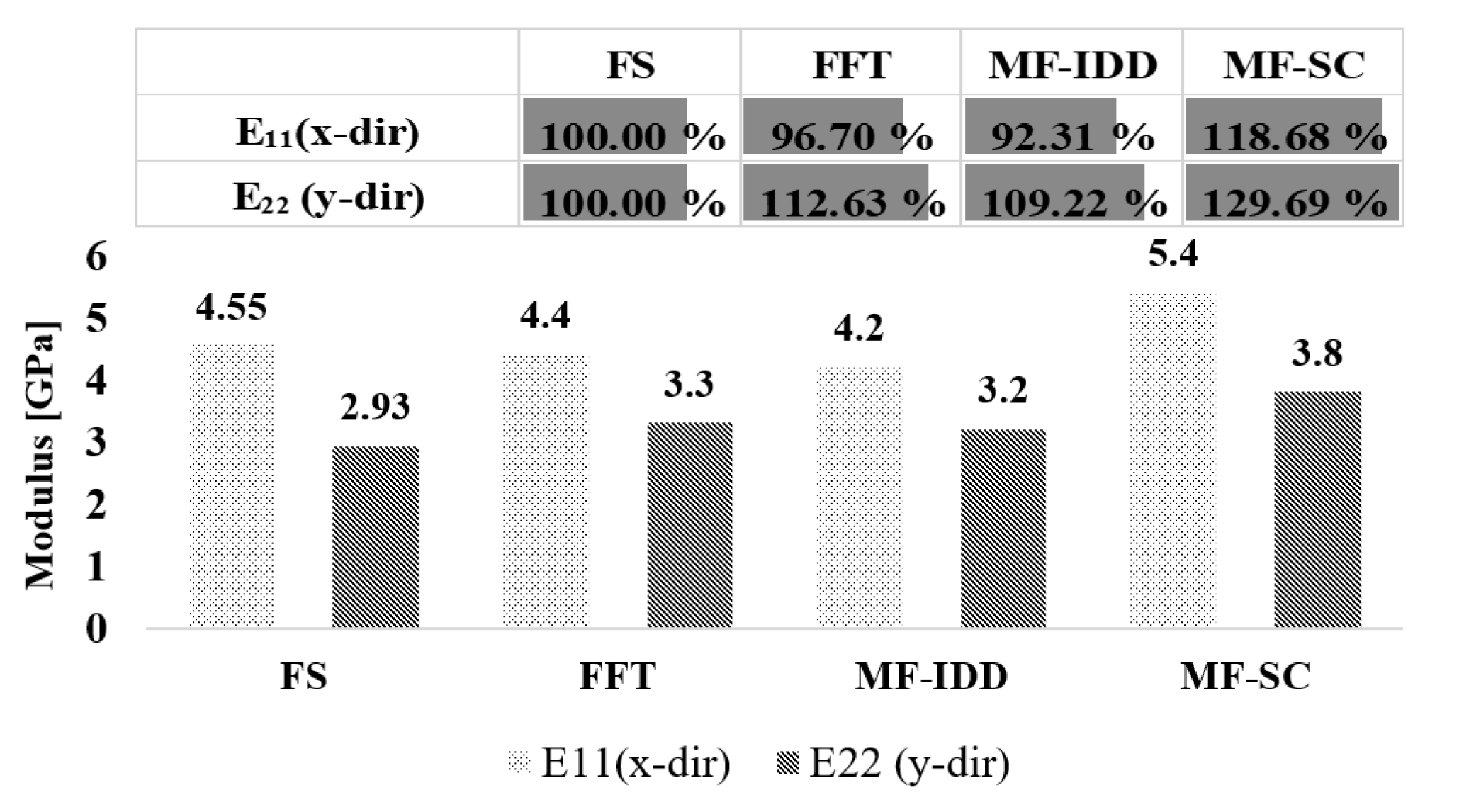
4.1. Verification Results for Fourier Series-Based Homogenization Theory

To verify the proposed the Fourier series (FS)-based homogenization theory, the numerical analysis was performed for the unit-cell established in Section 3.1. Here, the fiber volume fraction, phase contrast combination amount and resolution were 13%, ς = 44 and 125, respectively. Muller et al. [44] confirmed that the higher the resolution, the smaller the phase contrast ratio and the smaller the deviation range of the result. For the GDL fiber network of this paper, the phase contrast combination amount satisfies the condition that the reliability is secured with ς = 73.7 and resolution = 100.

Numerical analysis was performed based on FS theory for the unit-cells using the commercial software ABAQUS. The user run-script was developed using a homogenization technique based on the FS to compute equivalence properties. Figure 5 compares the equivalent properties obtained from the Fourier series-based homogenization method developed in this paper, with the results from the conventional homogenization methods which have been already verified by several studies [44] such as the fast Fourier transformation (FFT), the mean field generalized self-consistent (MF-SC) and mean field interaction direct derivative (MF-IDD). Assuming that the result obtained by the FS-based homogenization theory is 100%, the degree error of the results from the conventional methods can be identified by comparing the referenced results [44] with the longitudinal elastic moduli (E₁₁ and E₂₂). The results of the FS-based homogenization theory are relatively intermediate of the properties obtained from the FFT, MF-IDD and MF-SC theories.

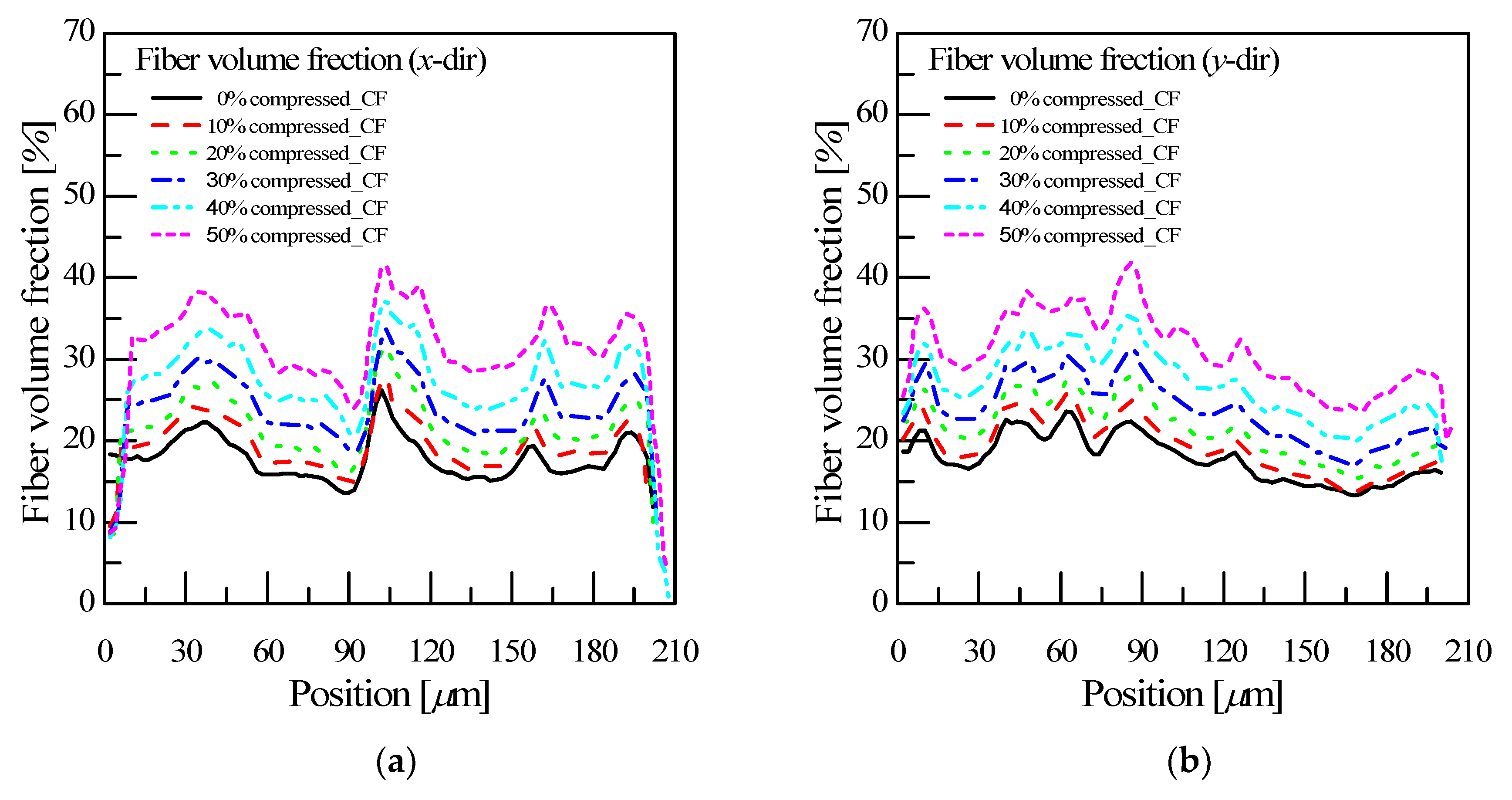
4.2. Evaluation of Equivalent Properties of GDL for Different Compression Ratios

The homogenization analysis for the GDL unit-cell was performed to identify the equivalent mechanical properties with the compression ratios based on FS-based homogenization theory verified in previous section. Figure 6 indicates the stress distributions for the GDL unit-cell at compression ratios of 30% and 50%, respectively, under the compression load of 100 N. In the figure, the 50% compressed GDL shows a denser fiber distribution and much higher stress distribution than the 30% compressed GDL, as expected. As the stress distribution is identified to be affected compression ratios, the effective physical properties are also considered to be influenced by the compression ratios. Figure 7 shows the resulting effective mechanical properties with compression ratios. From Figure 7a, it can be seen that the effective physical properties of the GDL increase in proportion to the compression ratios. The E₁₁ and E₂₂ are increasing rapidly at a compression ratio of 30% or more, and the E₃₃ is remarkably small at a noncompression state but is greatly increased with increasing compression ratio. This is because the FVF of Table 3, which has the greatest effect on the longitudinal elastic modulus, increases sharply at a compression ratio of 30% or more. On the other hand, the shear moduli have different behavior with the compression ratio. Further understating the effect of the compression ratio on the mechanical properties, each mechanical property is summarized with the compression ratios and shown in Figure 7b. In the figure, the longitudinal elastic moduli (E₁₁, E₂₂ and E₃₃) show a rapid increase according to the compression ratio, and the shear moduli have a relatively small effect. From these results, it can be stated that the change of fiber volume fraction according to the compression ratio has a great effect on the longitudinal elastic moduli but relatively little effect on the shear elastic moduli.

5. Conclusions

In this study, we developed a technique using the FS method to predict the effective mechanical properties for discontinuous nonwoven GDLs under compressive loading conditions. The following conclusions were obtained.

• A user run-script was developed using a homogenization technique based on the Fourier series to compute effective mechanical properties of GDLs with various compress ratios;
• Among the several homogenization theories, the homogenization theory with the Fourier series method is suitable to predict the effective mechanical properties of GDLs;
• The change of fiber volume fraction according to the compression ratio has a great effect on the longitudinal elastic moduli but relatively little effect on the shear elastic moduli;
• The fiber volume fraction increases sharply at the compression ratios of more than 30%, and then the effective mechanical properties and the stress/force behaviors rapidly change.