Minimization of the Energy Consumption in Industrial Robots through Regenerative Drives and Optimally Designed Compliant Elements
Abstract
:1. Introduction
2. Electromechanical Model
- and denote the first and second time derivative of vector , i.e., the vectors of the actuated joint velocities and accelerations, respectively;
- is the diagonal matrix of the motor inertia;
- is the diagonal matrix of the gear transmission ratios;
- is the mass matrix;
- is the torque vector due to centrifugal and Coriolis effects;
- is the diagonal matrix of viscous friction coefficients;
- is the vector of the static friction torques, that may be represented by means of the Coulomb friction model. In this case , where is a diagonal matrix of the static friction coefficients;
- is the torque vector due to the effects of gravity;
- is the torque vector due to the interaction of the end-effector with the environment.
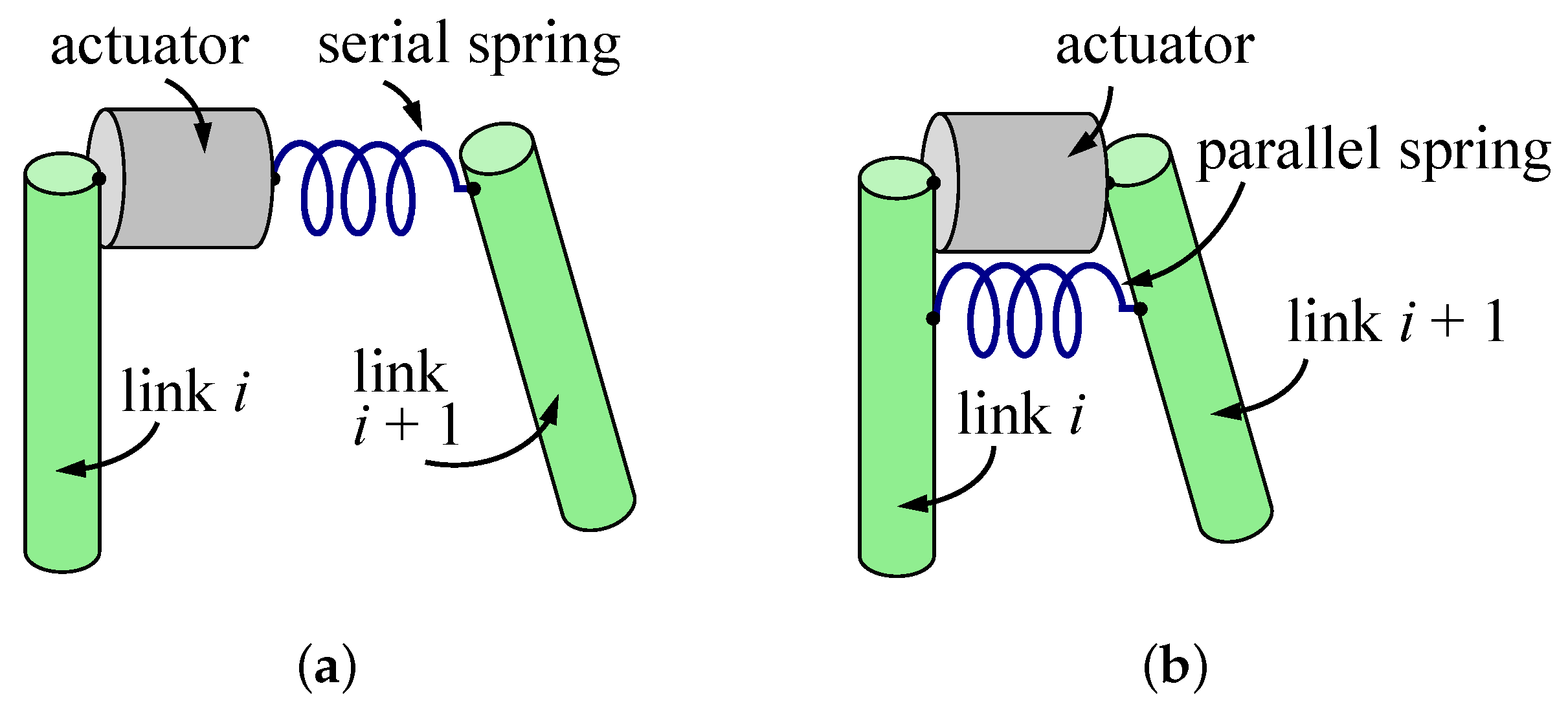
3. Optimal Design of Compliant Elements
- Stationary condition:
- Complementary slackness:
- Primal feasibility:
- Dual feasibility:
- 5.
- Positive definite matrix:
3.1. Inactive Constraint ()
3.2. Active Constraint ()
Determination of the Lower Bounds
4. Results
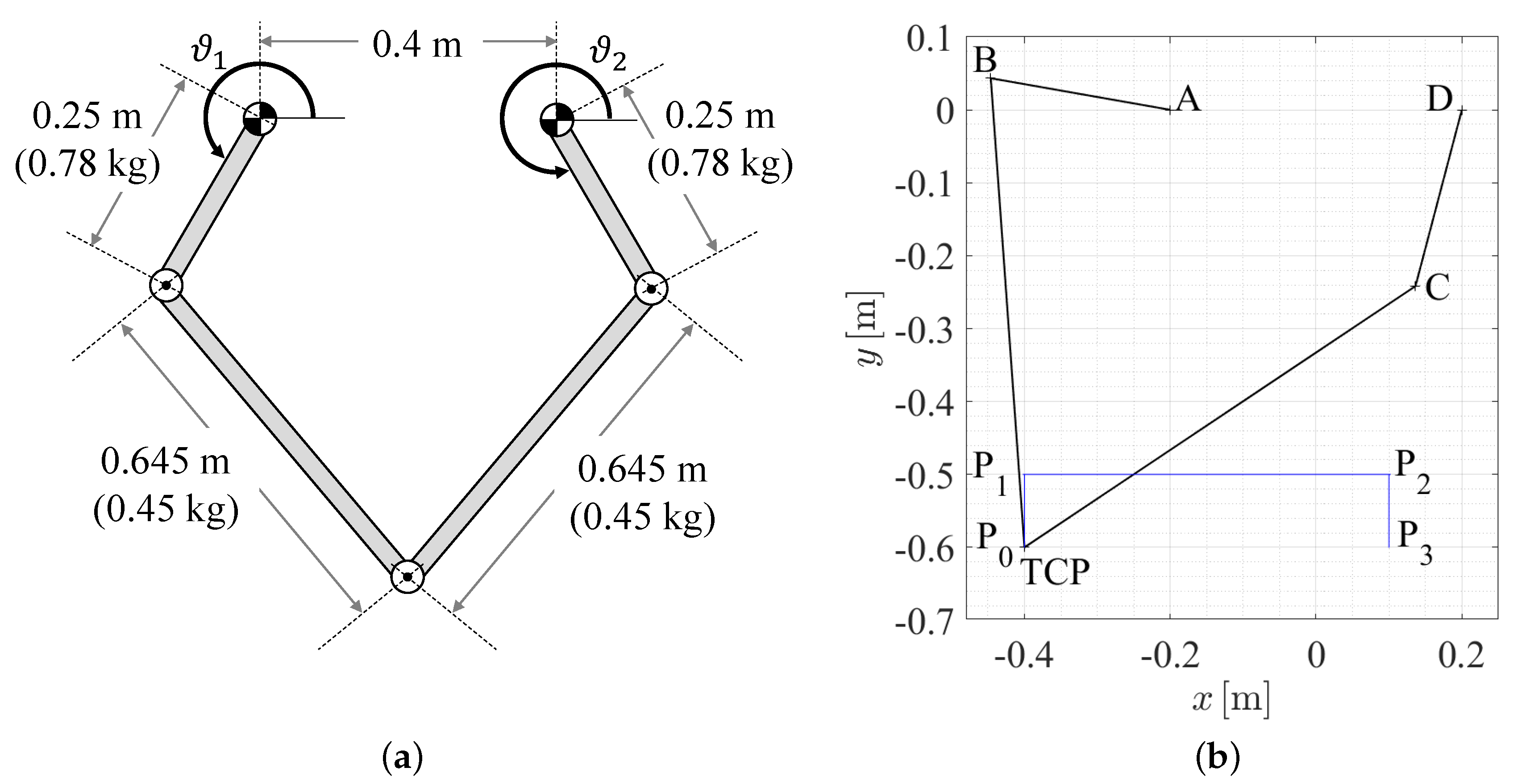
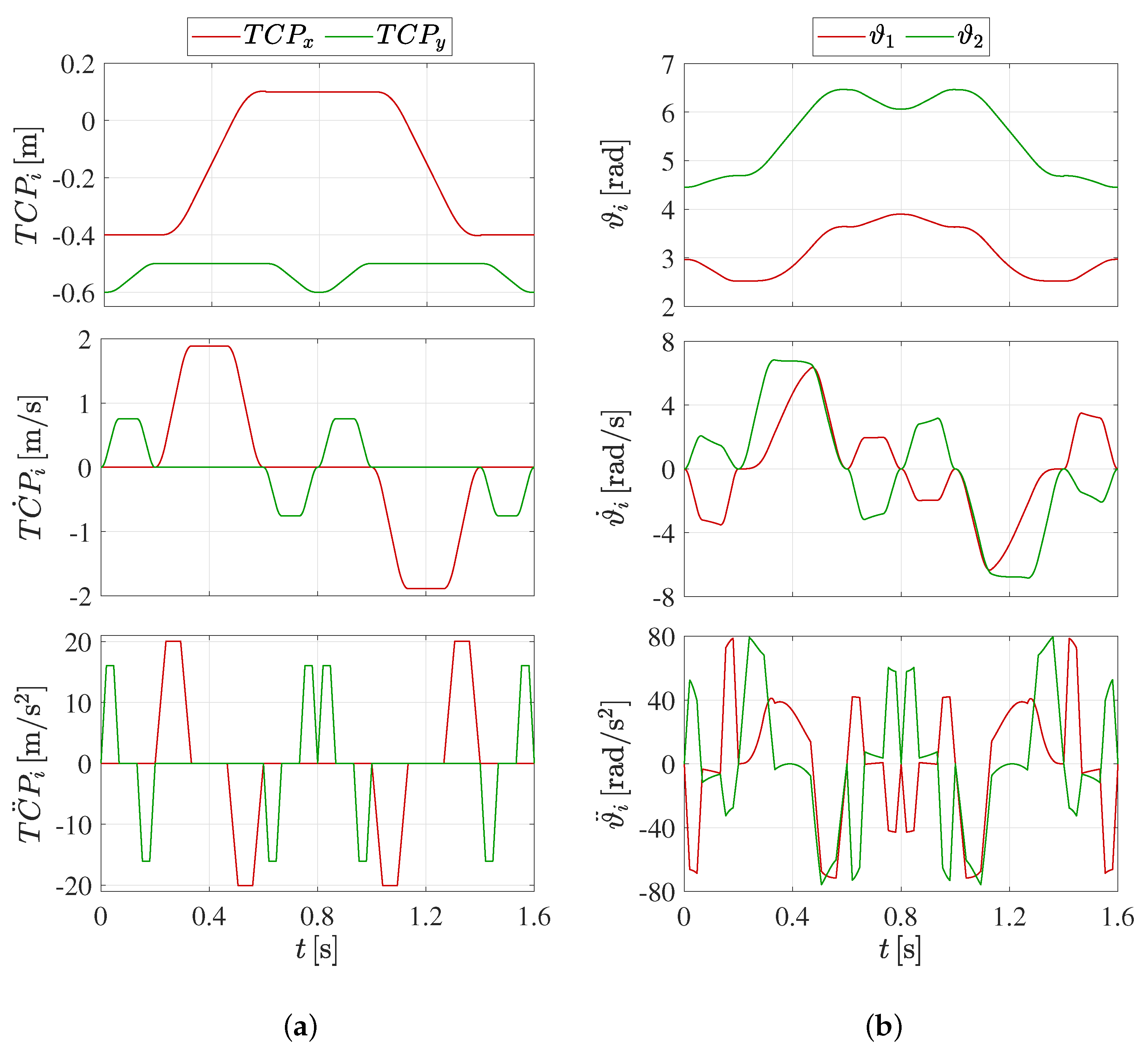
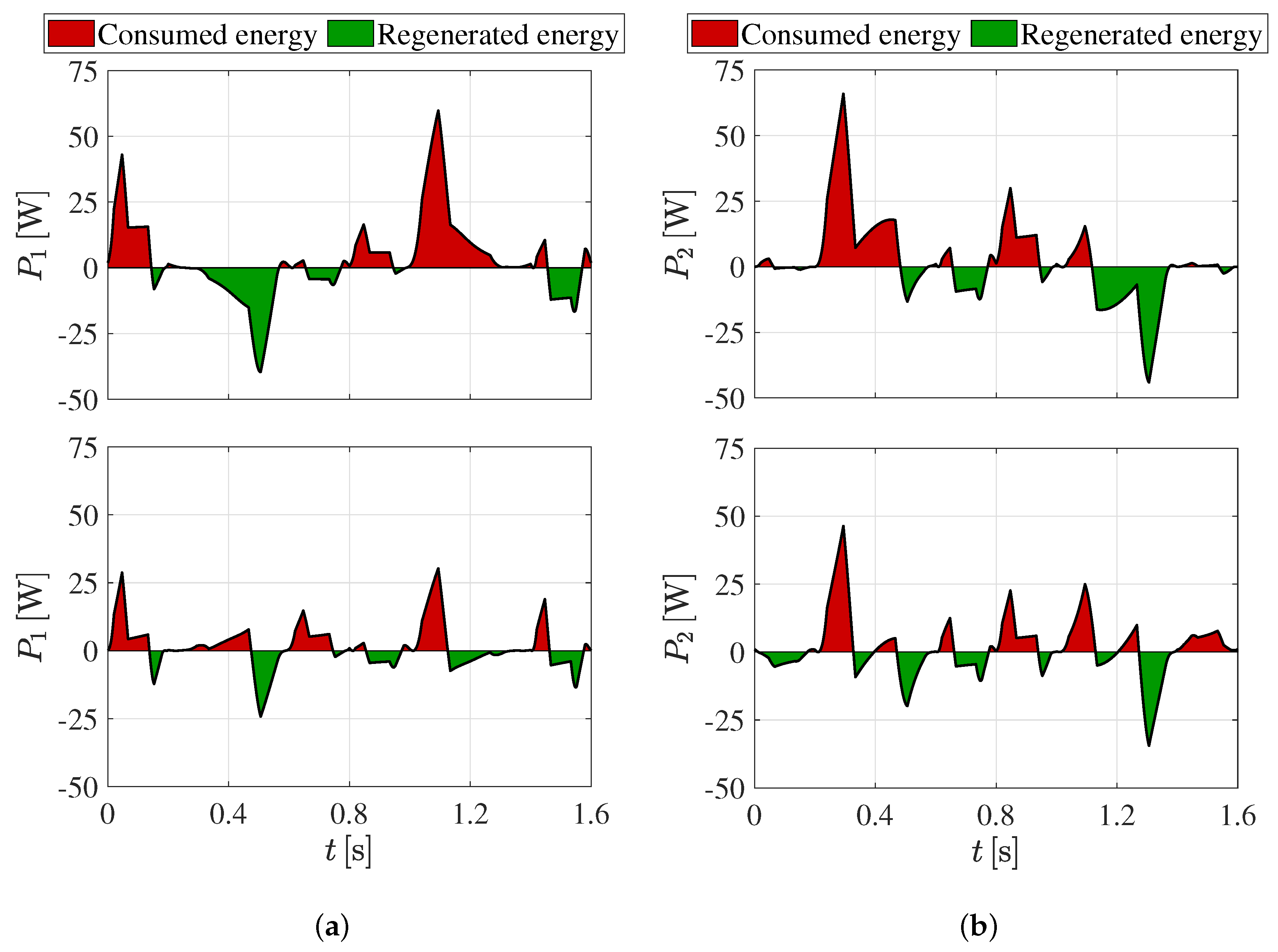
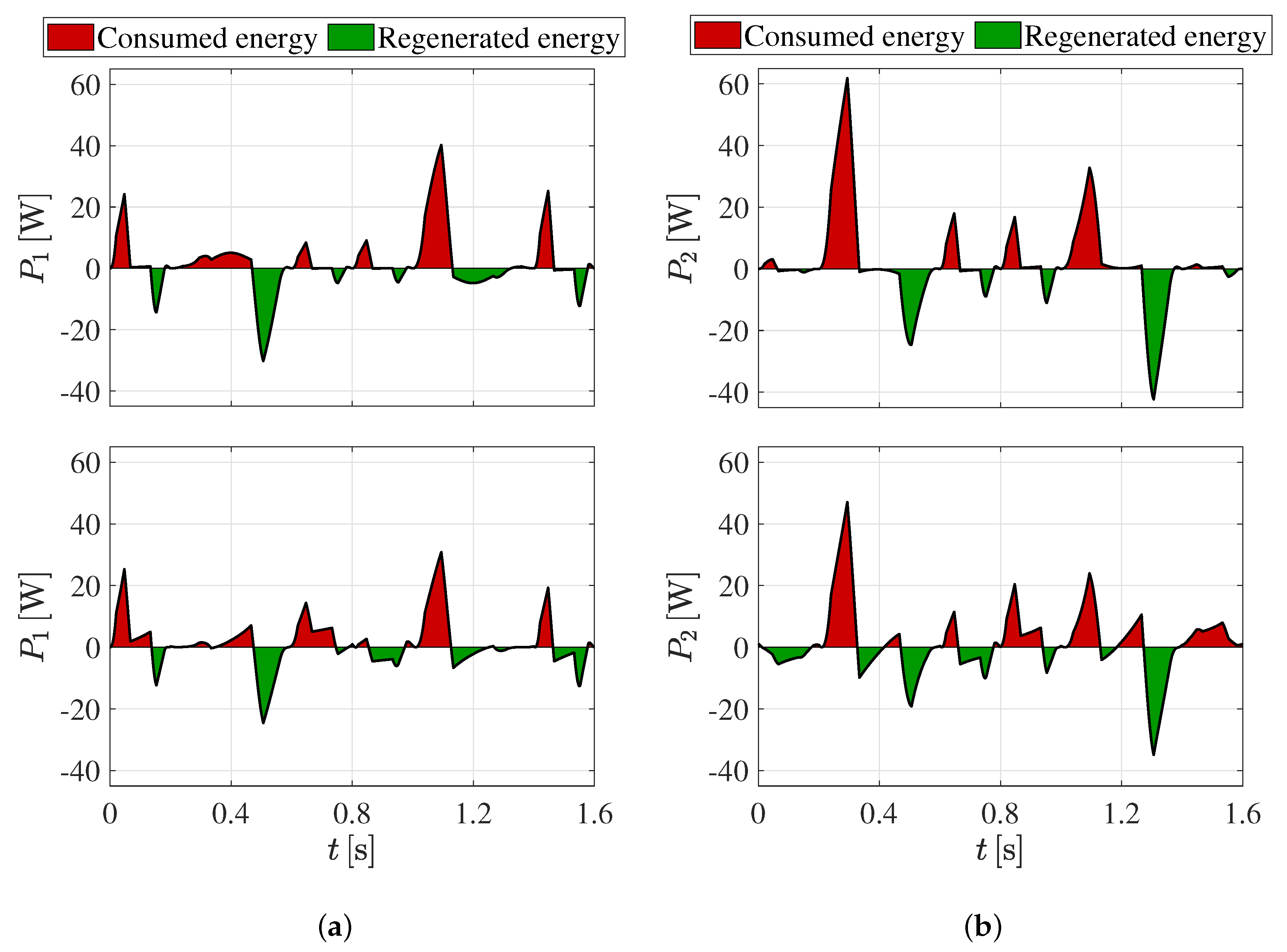
4.1. Five-Bar Mechanism
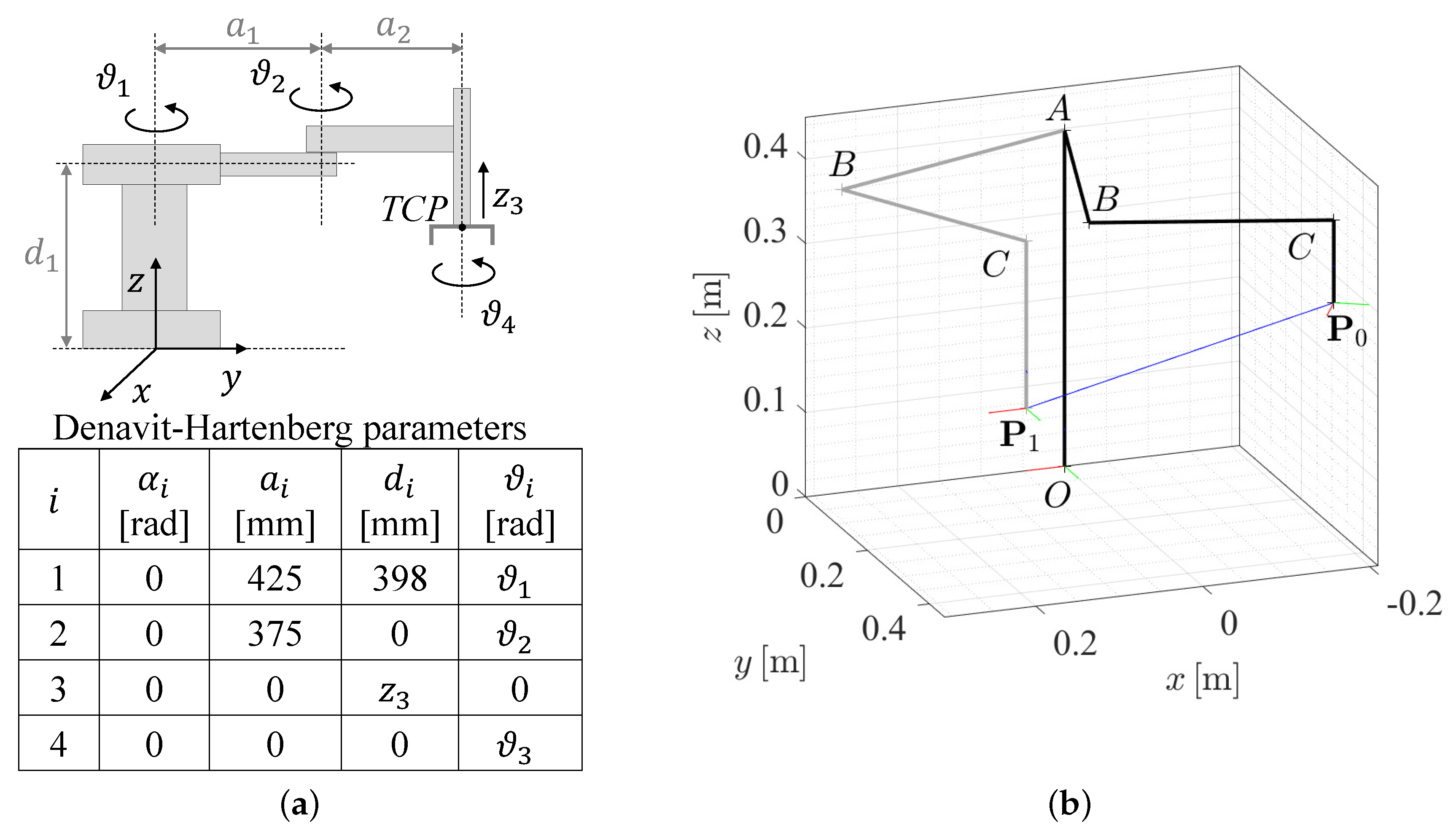
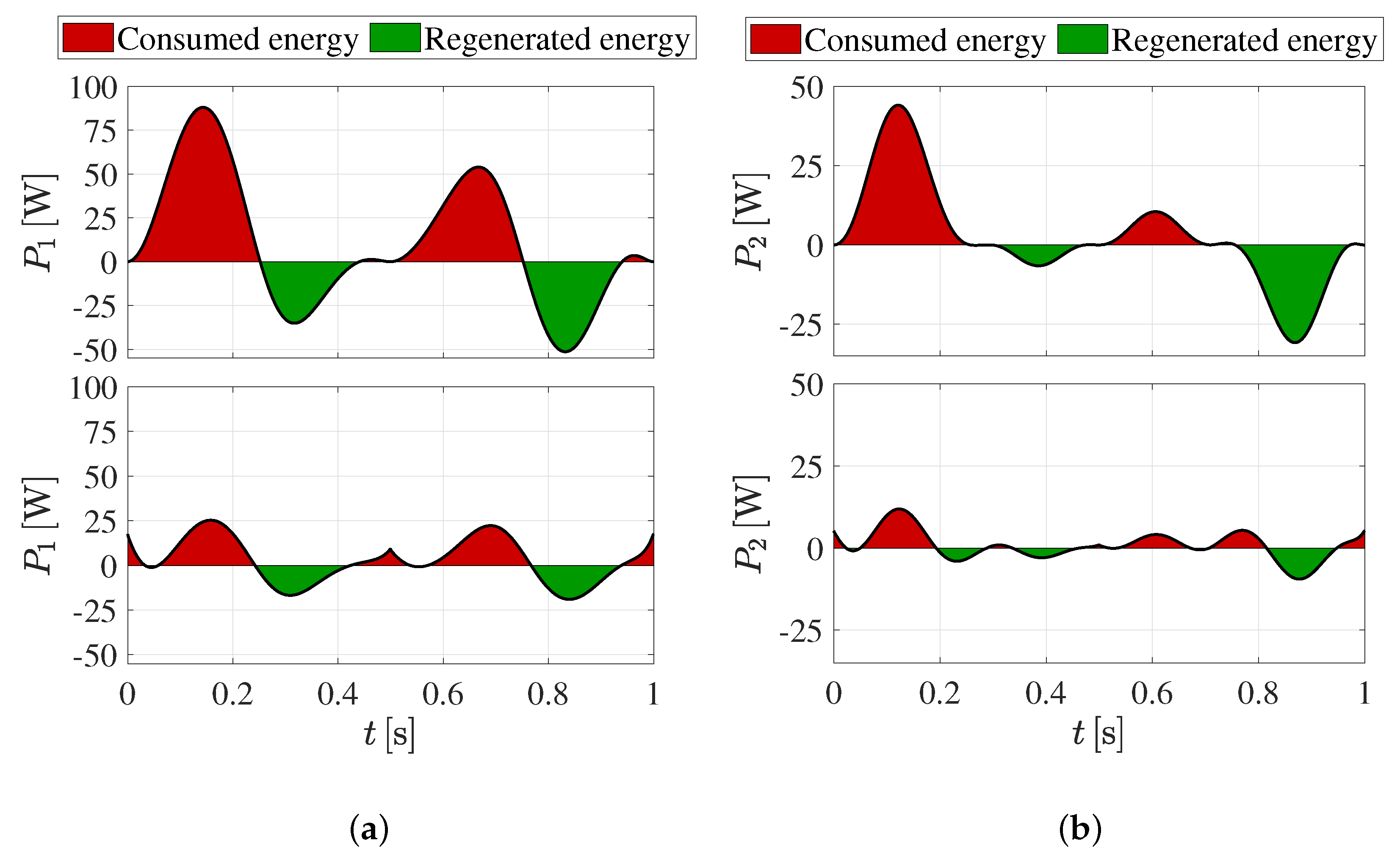
4.2. SCARA Robot
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Paryanto; Brossog, M.; Bornschlegl, M.; Franke, J. Reducing the energy consumption of industrial robots in manufacturing systems. Int. J. Adv. Manuf. Technol. 2015, 78, 1315–1328. [Google Scholar] [CrossRef]
- Carabin, G.; Wehrle, E.; Vidoni, R. A review on energy-saving optimization methods for robotic and automatic systems. Robotics 2017, 6, 39. [Google Scholar] [CrossRef] [Green Version]
- Scalera, L.; Boscariol, P.; Carabin, G.; Vidoni, R.; Gasparetto, A. Enhancing energy efficiency of a 4-DOF parallel robot through task-related analysis. Machines 2020, 8, 10. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, A.; Fontes, J.; Da Silva, M. The influence of kinematic redundancies in the energy efficiency of planar parallel manipulators. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition (IMECE), Houston, TA, USA, 13–19 November 2015; Volume 4A-2015. [Google Scholar] [CrossRef]
- Boscariol, P.; Richiedei, D. Trajectory design for energy savings in redundant robotic cells. Robotics 2019, 8, 15. [Google Scholar] [CrossRef] [Green Version]
- Boscariol, P.; Caracciolo, R.; Richiedei, D.; Trevisani, A. Energy optimization of functionally redundant robots through motion design. Appl. Sci. 2020, 10, 22. [Google Scholar] [CrossRef]
- Carabin, G.; Vidoni, R.; Wehrle, E. Energy saving in mechatronic systems through optimal point-to-point trajectory generation via standard primitives. Mech. Mach. Sci. 2019, 68, 20–28. [Google Scholar] [CrossRef]
- Boscariol, P.; Richiedei, D. Energy-efficient design of multipoint trajectories for Cartesian robots. Int. J. Adv. Manuf. Technol. 2019, 102, 1853–1870. [Google Scholar] [CrossRef]
- Hansen, C.; Kotlarski, J.; Ortmaier, T. Optimal motion planning for energy efficient multi-axis applications. Int. J. Mechatronics Autom. 2014, 4, 147–160. [Google Scholar] [CrossRef]
- Khalaf, P.; Richter, H. Parametric optimization of stored energy in robots with regenerative drive systems. In Proceedings of the 2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; pp. 1424–1429. [Google Scholar]
- Kim, Y.J. Design of low inertia manipulator with high stiffness and strength using tension amplifying mechanisms. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; Volume 2015-December, pp. 5850–5856. [Google Scholar] [CrossRef]
- Yin, H.; Liu, J.; Yang, F. Hybrid Structure Design of Lightweight Robotic Arms Based on Carbon Fiber Reinforced Plastic and Aluminum Alloy. IEEE Access 2019, 7, 64932–64945. [Google Scholar] [CrossRef]
- Meike, D.; Ribickis, L. Recuperated energy savings potential and approaches in industrial robotics. In Proceedings of the 2011 IEEE International Conference on Automation Science and Engineering, Trieste, Italy, 24–27 August 2011; pp. 299–303. [Google Scholar]
- Sayed-Ahmed, A.; Wei, L.; Seibel, B. Industrial regenerative motor-drive systems. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 1555–1561. [Google Scholar]
- Kapoor, R.; Parveen, C. Comparative study on various KERS. In Proceedings of the Lecture Notes in Engineering and Computer Science, London, UK, 3–5 July 2013; Volume 3 LNECS, pp. 1969–1973. [Google Scholar]
- Rankis, I.; Meike, D.; Senfelds, A. Utilization of Regeneration Energy in Industrial Robots System. In Proceedings of the International Conference on Renewable Energy and Environmental Technology (REET 2013), Jilin, China, 21–22 September 2013; pp. 448–453. [Google Scholar]
- Gale, S.; Eielsen, A.; Gravdahl, J. Modelling and simulation of a flywheel based energy storage system for an industrial manipulator. In Proceedings of the IEEE International Conference on Industrial Technology, Seville, Spain, 17–19 March 2015; Volume 2015-June, pp. 332–337. [Google Scholar] [CrossRef]
- Verstraten, T.; Beckerle, P.; Furnémont, R.; Mathijssen, G.; Vanderborght, B.; Lefeber, D. Series and parallel elastic actuation: Impact of natural dynamics on power and energy consumption. Mech. Mach. Theory 2016, 102, 232–246. [Google Scholar] [CrossRef]
- Scalera, L.; Palomba, I.; Wehrle, E.; Gasparetto, A.; Vidoni, R. Natural motion for energy saving in robotic and mechatronic systems. Appl. Sci. 2019, 9, 3516. [Google Scholar] [CrossRef] [Green Version]
- Veer, S.; Sujatha, S. Approximate spring balancing of linkages to reduce actuator requirements. Mech. Mach. Theory 2015, 86, 108–124. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Algorithm for the static balancing of serial and parallel mechanisms combining counterweights and springs: Generation, assessment and ranking of effective design variants. Mech. Mach. Theory 2019, 137, 336–354. [Google Scholar] [CrossRef]
- Barreto, J.; Schöler, F.F.; Corves, B. The concept of natural motion for pick and place operations. Mech. Mach. Sci. 2017, 46, 89–98. [Google Scholar] [CrossRef]
- Barreto, J.P.; Corves, B. Matching the Free-Vibration Response of a Delta Robot with Pick-and-Place Tasks Using Multi-Body Simulation. In Proceedings of the 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE), Munich, Germany, 20–24 August 2018; pp. 1487–1492. [Google Scholar]
- Kashiri, N.; Spyrakos-Papastavridis, E.; Caldwell, D.; Tsagarakis, N. Exploiting the natural dynamics of compliant joint robots for cyclic motions. In Proceedings of the 2017 22nd International Conference on Methods and Models in Automation and Robotics, (MMAR 2017), Miedzyzdroje, Poland, 28–31 August 2017; pp. 676–681. [Google Scholar] [CrossRef]
- Schiehlen, W.; Iwamura, M. Minimum energy control of multibody systems utilizing storage elements. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009; American Society of Mechanical Engineers: New York, NY, USA, 2009; pp. 1919–1926. [Google Scholar]
- Iwamura, M.; Imafuku, S.; Kawamoto, T.; Schiehlen, W. Design and Control of an Energy-Saving Robot Using Storage Elements and Reaction Wheels. In Multibody Dynamics; Springer: Cham, Switzerland, 2016; pp. 277–297. [Google Scholar]
- Schmit, N.; Okada, M. Simultaneous optimization of robot trajectory and nonlinear springs to minimize actuator torque. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 2806–2811. [Google Scholar]
- Bidgoly, H.J.; Parsa, A.; Yazdanpanah, M.J.; Ahmadabadi, M.N. Benefiting From Kinematic Redundancy Alongside Mono-and Biarticular Parallel Compliances for Energy Efficiency in Cyclic Tasks. IEEE Trans. Robot. 2017, 33, 1088–1102. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, M.Y. Minimum time path planning of robotic manipulator in drilling/spot welding tasks. J. Comput. Des. Eng. 2016, 3, 132–139. [Google Scholar] [CrossRef] [Green Version]
- Rojas, R.; Garcia, M.; Wehrle, E.; Vidoni, R. A Variational Approach to Minimum-Jerk Trajectories for Psychological Safety in Collaborative Assembly Stations. IEEE Robot. Autom. Lett. 2019, 4, 823–829. [Google Scholar] [CrossRef]
- Boscariol, P.; Boschetti, G.; Gallina, P.; Passarini, C. Spring design for motor torque reduction in articulated mechanisms. Mech. Mach. Sci. 2018, 49, 557–564. [Google Scholar] [CrossRef]
- Scalera, L.; Carabin, G.; Vidoni, R.; Wongratanaphisan, T. Energy efficiency in a 4-dof parallel robot featuring compliant elements. Int. J. Mech. Control 2019, 20, 1–9. [Google Scholar]
- Richiedei, D.; Trevisani, A. Optimization of the Energy Consumption Through Spring Balancing of Servo-Actuated Mechanisms. J. Mech. Des. 2019, 142. [Google Scholar] [CrossRef]
- Carabin, G.; Palomba, I.; Wehrle, E.; Vidoni, R. Energy Expenditure Minimization for a Delta-2 Robot Through a Mixed Approach. Comput. Methods Appl. Sci. 2020, 53, 383–390. [Google Scholar] [CrossRef]
- Richiedei, D.; Trevisani, A. Analytical computation of the energy-efficient optimal planning in rest-to-rest motion of constant inertia systems. Mechatronics 2016, 39, 147–159. [Google Scholar] [CrossRef]
- Karush, W. Minima of Functions of Several Variables with Inequalities as Side Constraints. Master’s Thesis, Department of Mathematics, University of Chicago, Chicago, IL, USA, 1939. [Google Scholar]
- Kuhn, H.W.; Tucker, A.W. Nonlinear Programming, Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, Department of Mathematics, University of California, CA, USA, 31 July–12 August 1950; University of California Press: Berkeley, CA, USA, 1951; pp. 481–492. [Google Scholar] [CrossRef]

| Parameters | Joint 1 and Joint 2 | |
|---|---|---|
| Gear ratio | ||
| Motor inertia | ||
| Motor winding resistance | ||
| Motor velocity constant | ||
| Motor torque constant | ||
| Efficiency | 1 | |
| Vertical Plane | Horizontal Plane | |||||
|---|---|---|---|---|---|---|
| Motor | Energy (J) | Energy | Energy (J) | Energy | ||
| ∘ | • | Reduction (%) | ∘ | • | Reduction (%) | |
| 1 | 10.15 | 2.06 | 79.70 | 5.62 | 1.88 | 66.59 |
| 2 | 9.43 | 2.29 | 75.69 | 7.31 | 2.14 | 70.63 |
| Total | 19.58 | 4.35 | 77.78 | 12.93 | 4.02 | 68.90 |
| Parameters | Joint 1 | Joint 2 | Joint 3 | Joint 4 |
|---|---|---|---|---|
| 12 | 15 | − | 2 | |
| 1 | 1 | 1 | 1 |
| Motor | Energy (J) | Energy | |
|---|---|---|---|
| ∘ | • | Reduction (%) | |
| 1 | 19.69 | 2.50 | 87.28 |
| 2 | 6.38 | 0.6689 | 89.53 |
| 3 | 19.68 | 14.30 | 27.35 |
| 4 | 1.97 | 1.50 | 24.03 |
| Total | 47.72 | 18.96 | 60.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palomba, I.; Wehrle, E.; Carabin, G.; Vidoni, R. Minimization of the Energy Consumption in Industrial Robots through Regenerative Drives and Optimally Designed Compliant Elements. Appl. Sci. 2020, 10, 7475. https://doi.org/10.3390/app10217475
Palomba I, Wehrle E, Carabin G, Vidoni R. Minimization of the Energy Consumption in Industrial Robots through Regenerative Drives and Optimally Designed Compliant Elements. Applied Sciences. 2020; 10(21):7475. https://doi.org/10.3390/app10217475
Chicago/Turabian StylePalomba, Ilaria, Erich Wehrle, Giovanni Carabin, and Renato Vidoni. 2020. "Minimization of the Energy Consumption in Industrial Robots through Regenerative Drives and Optimally Designed Compliant Elements" Applied Sciences 10, no. 21: 7475. https://doi.org/10.3390/app10217475
APA StylePalomba, I., Wehrle, E., Carabin, G., & Vidoni, R. (2020). Minimization of the Energy Consumption in Industrial Robots through Regenerative Drives and Optimally Designed Compliant Elements. Applied Sciences, 10(21), 7475. https://doi.org/10.3390/app10217475








