Research on Dynamic Mechanical Properties and Constitutive Model of Basalt Fiber Reinforced Concrete after Exposure to Elevated Temperatures under Impact Loading
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Materials and Specimen Preparation
2.2. Heating and Cooling
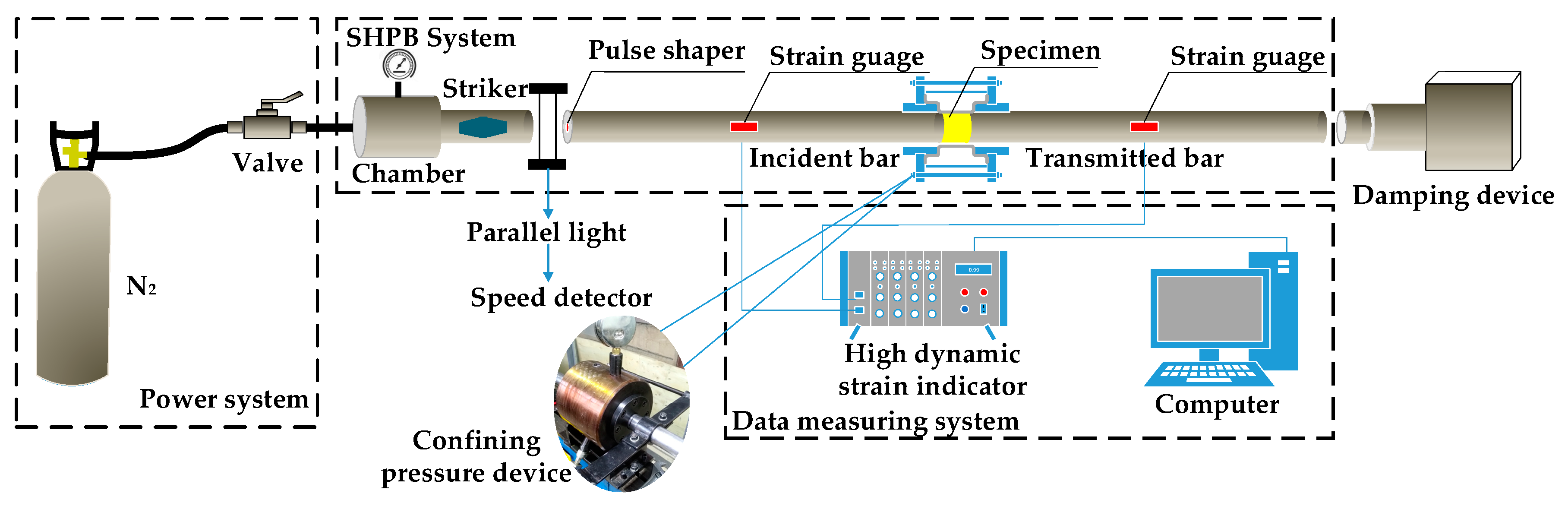
2.3. SHPB System
3. Test Results and Analysis
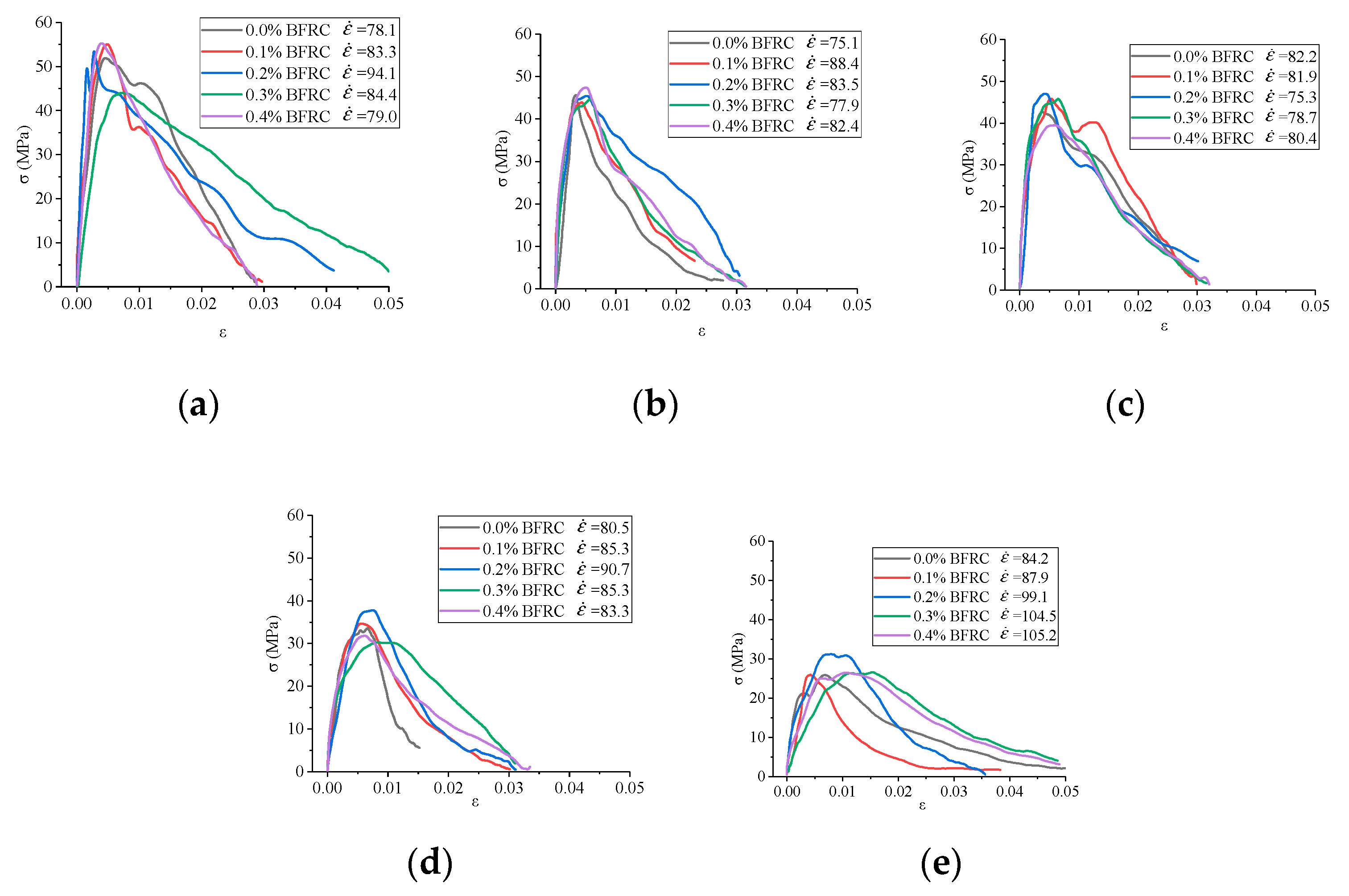
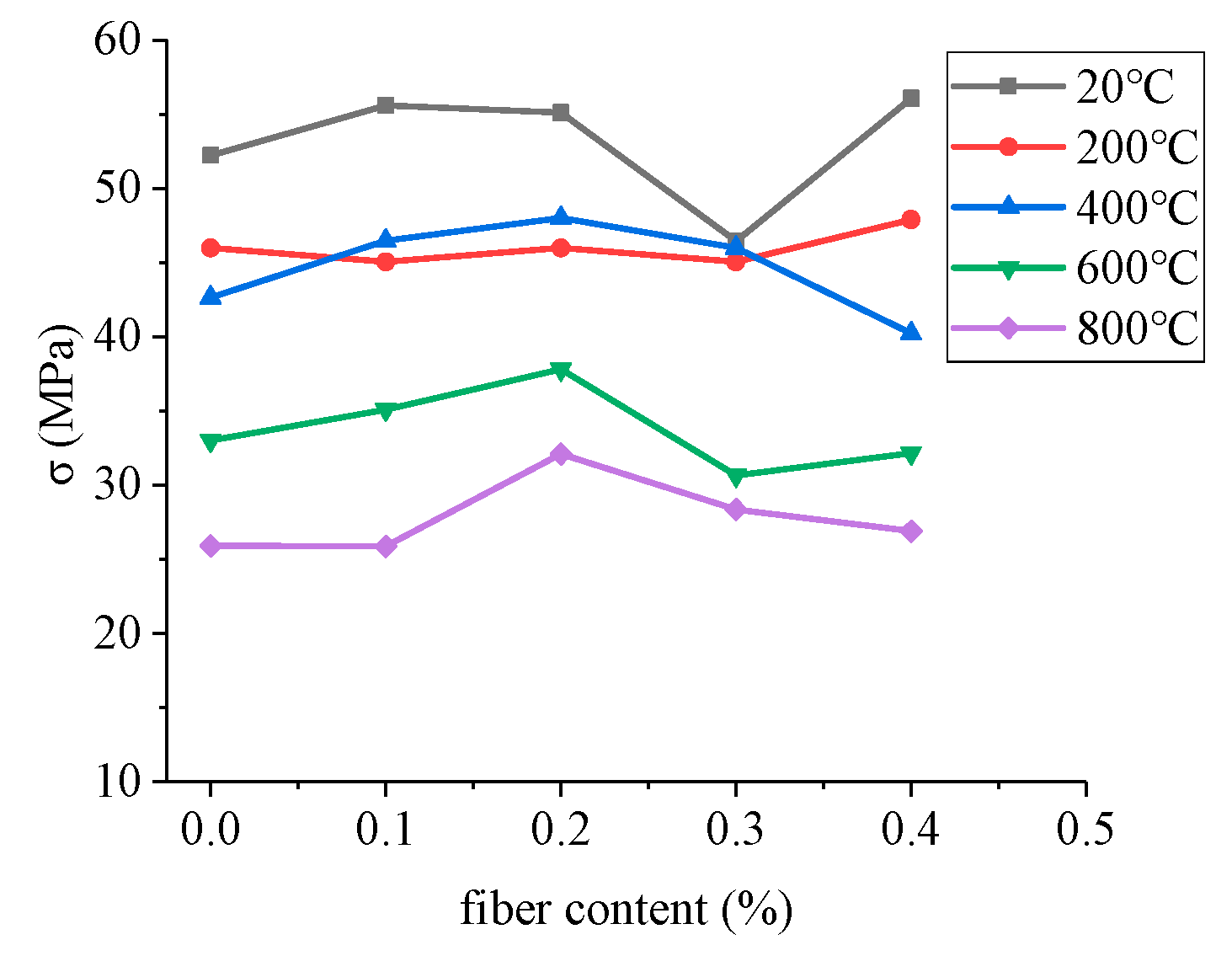
3.1. Influence Analysis of Fiber Content
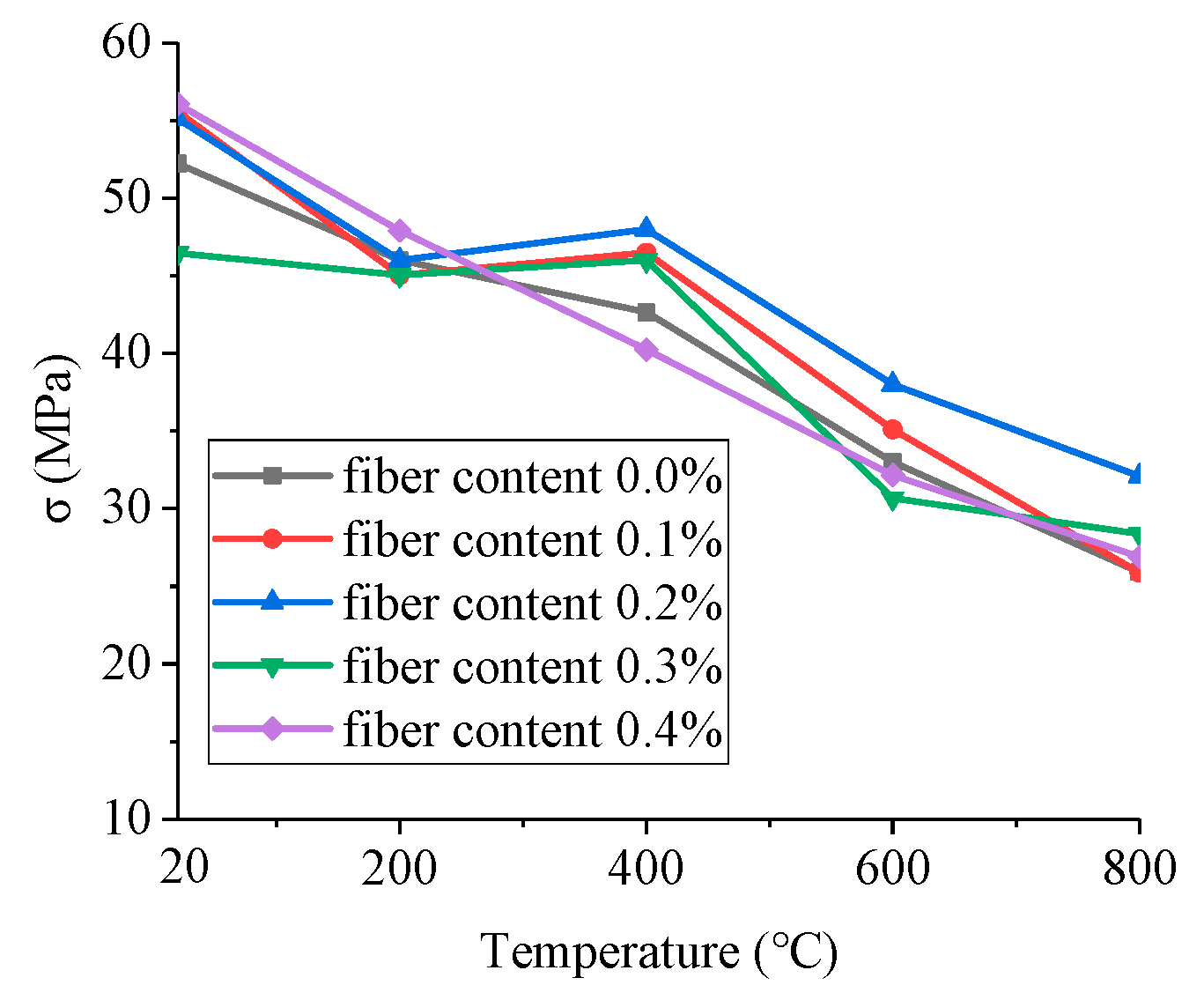
3.2. Influence Analysis of Temperature
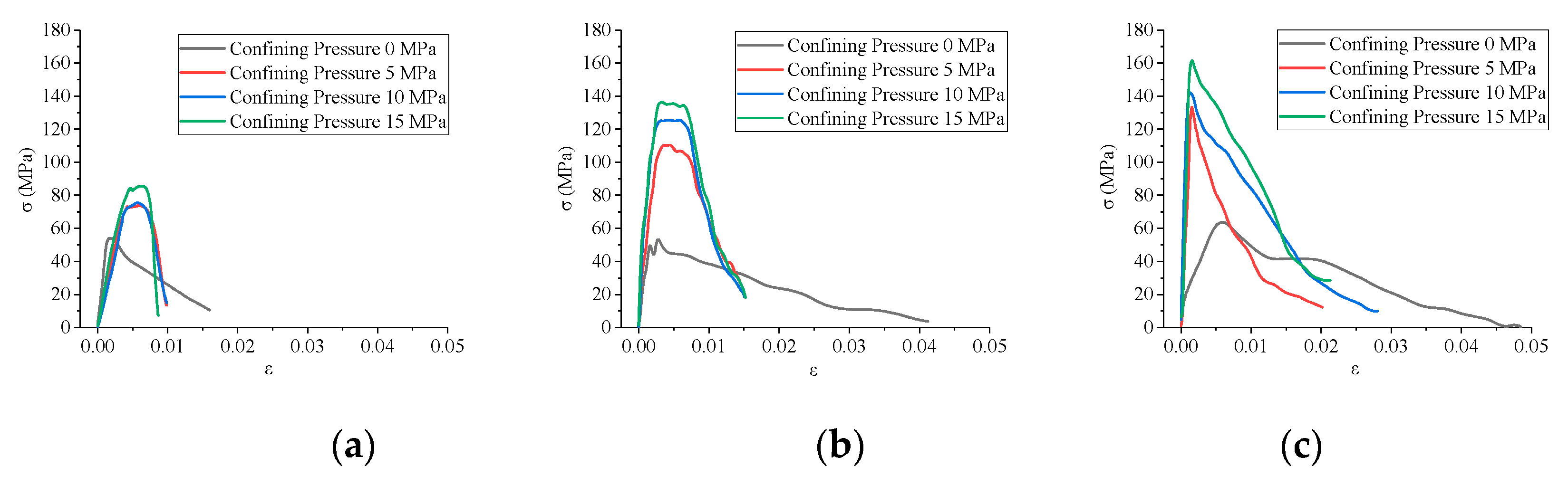
3.3. Influence Analysis of Confining Pressure
4. Dynamic Damage Constitutive Model
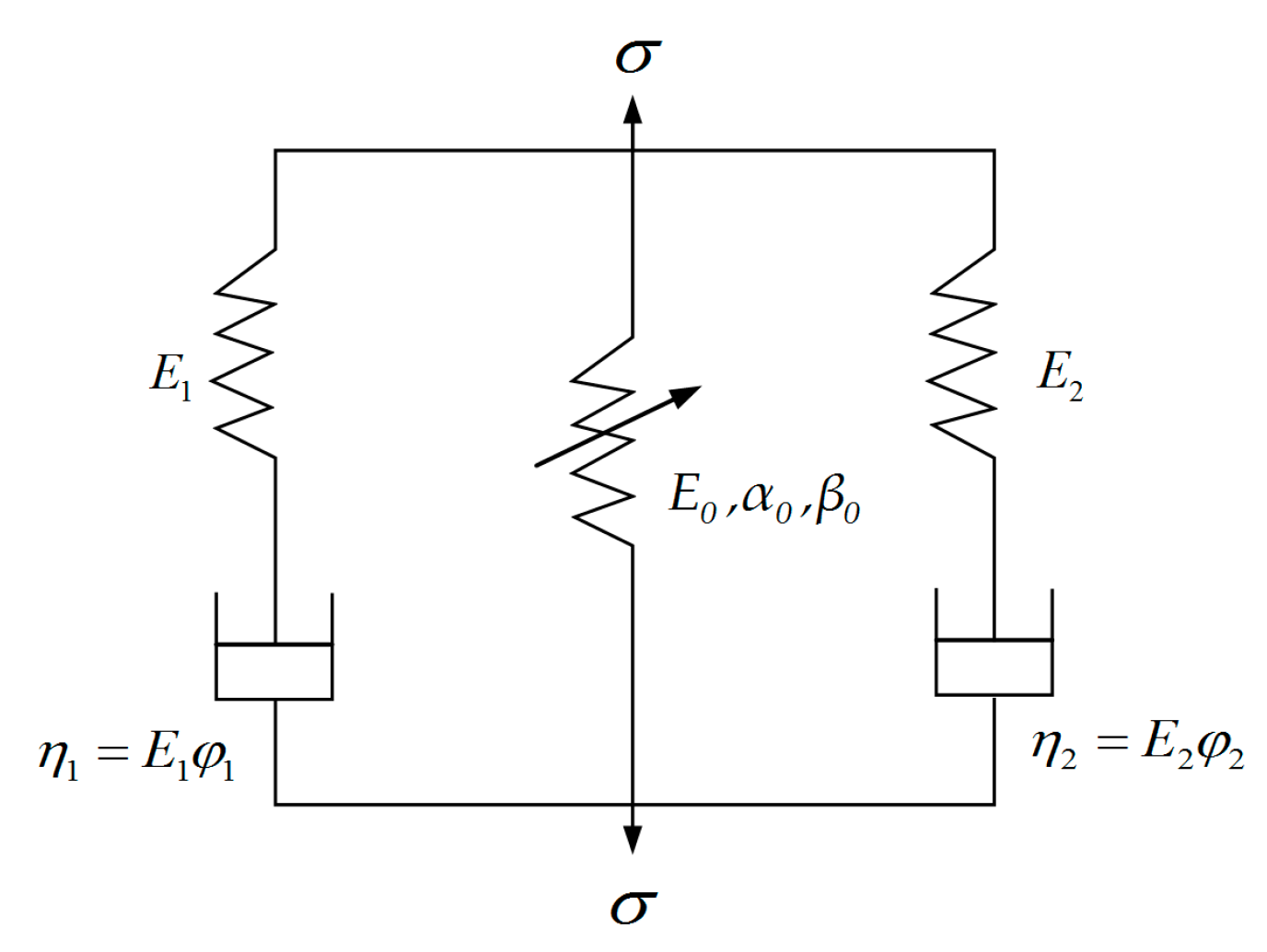
4.1. Visco-Elastic Damage Constitutive Model (V-E Model)
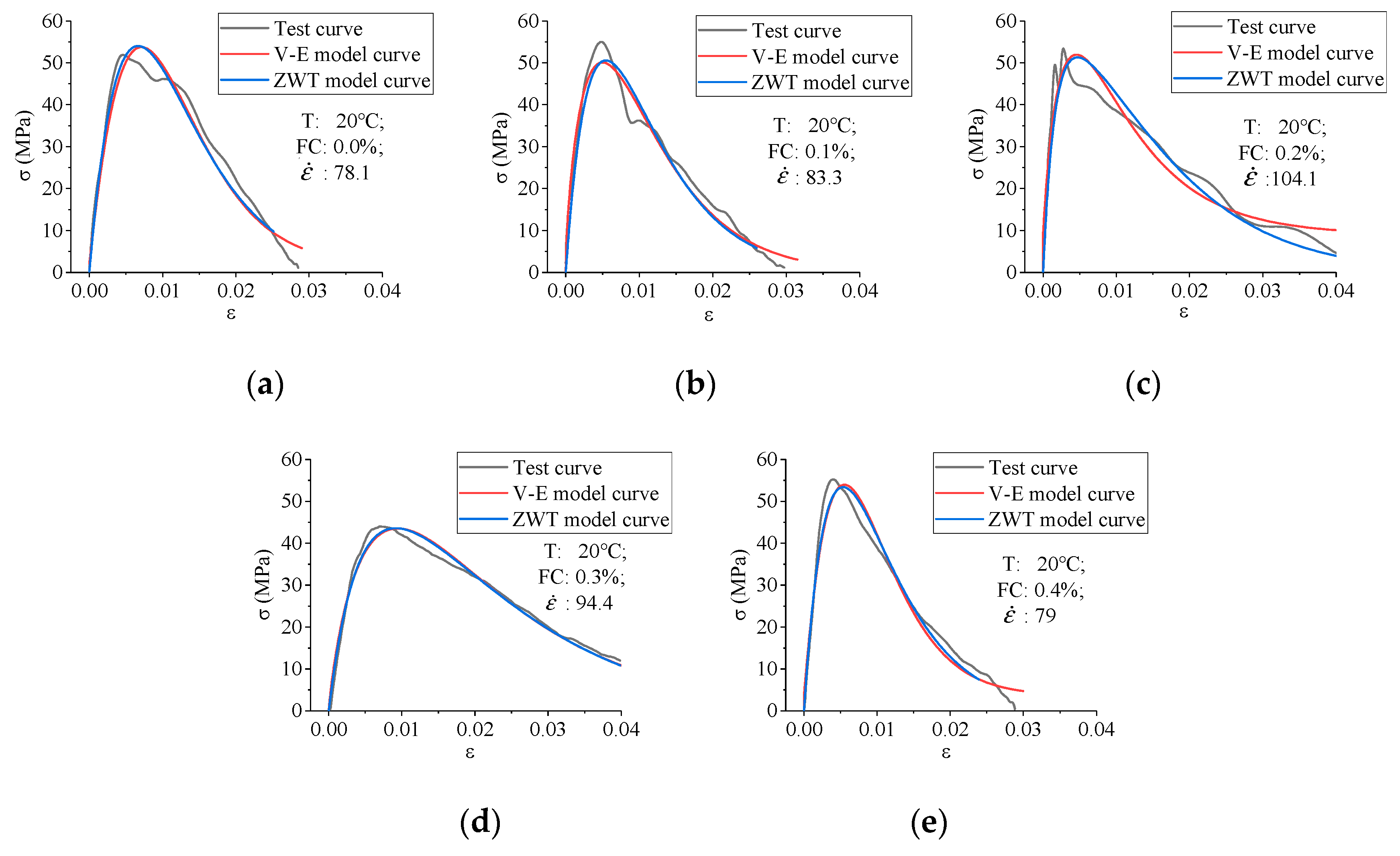
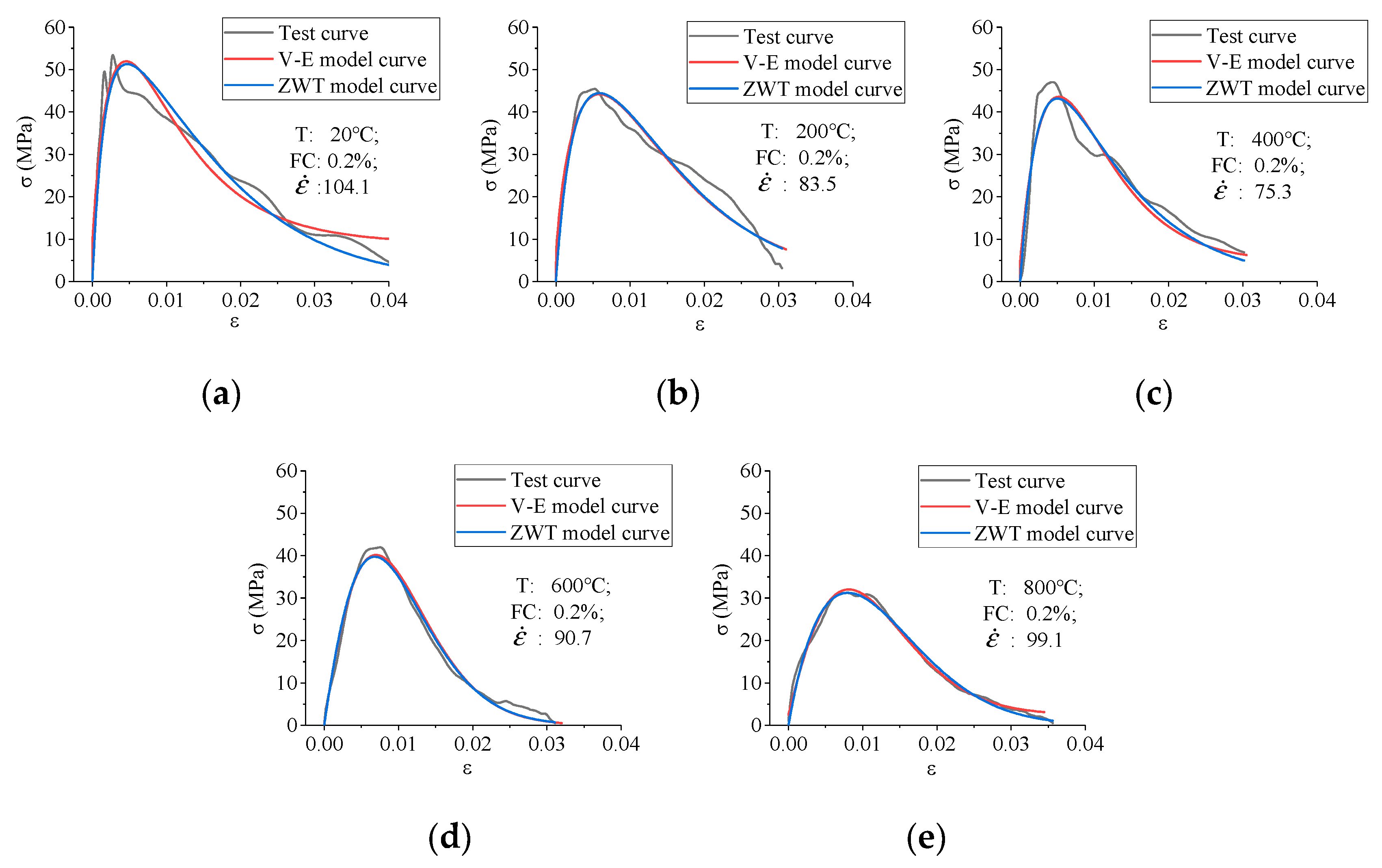
4.2. The Fitting of Parameters
4.3. Comparative Analysis with ZWT Model
- (1)
- The V-E model needs fewer parameters to fit the test curve well.
- (2)
- The expression of the V-E model is simpler, so it has better practicability.
- (3)
- The deficiency of the V-E model is the need for strain rate data, while the ZWT model only needs average strain rate (), except for stress and strain data.
5. Conclusions
- At different temperatures, the optimum fiber content of BFRC is different. When the fiber content is between 0.1% and 0.3%, BFRC has higher dynamic strength and ductility. The mechanical properties of BFRC can’t reach the optimal level whether the fiber content is too low or too high.
- The dynamic peak stresses of BFRC specimens gradually reduce and the crush degree increases as the temperature rises. High temperature has a remarkable damage effect on the dynamic mechanical properties of concrete, especially when the temperature is above 400 °C, the peak stress will be greatly reduced. However, the peak strength decreased less than 20% when the temperatures ranged from 20 °C to 400 °C.
- The confining pressure has a noticeable effect on the dynamic mechanic properties of BFRC. It can improve the dynamic peak stress, ductility and dynamic elastic modulus, change the crushing morphology and reduce the degree of crushing fragment.
- Compared with the ZWT model, the visco-elastic damage constitutive model was established in this paper can fit with test curves very well with fewer parameters, so the V-E model has better practicability.
Author Contributions
Funding
Conflicts of Interest
References
- Sim, J.; Park, C.; Moon, D.Y. Characteristics of basalt fiber as a strengthening material for concrete structures. Compos. Part B Eng. 2005, 36, 504–512. [Google Scholar] [CrossRef]
- Jiang, C.H.; Fan, K.; Wu, F.; Chen, D. Experimental study on the mechanical properties and microstructure of chopped basalt fiber reinforced concrete. Mater. Des. 2014, 58, 187–193. [Google Scholar] [CrossRef]
- Wei, B.; Cao, H.L.; Song, S.H. Tensile behavior contrast of basalt and glass fibers after chemical treatment. Mater. Des. 2010, 31, 4244–4250. [Google Scholar] [CrossRef]
- Fiore, V.; Scalici, T.; Bella, G.D.; Valenza, A. A review on basalt fibre and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Padmanabhan, L.; Sara, Y.K.; Sreekanta, D. Mechanical properties of fiber-reinforced concrete made with basalt filament fibers. J. Mater. Civ. Eng. 2015, 27, 04015015. [Google Scholar]
- John, B.; Sreekanta, D.; Sara, Y.K.; Craig, T. Mechanical behaviour of basalt fibre reinforced concrete. Constr. Build. Mater. 2016, 124, 878–886. [Google Scholar]
- Wang, Y.G.; Li, S.P.; Peter, H.; Fan, Y.H. Mechanical properties and microstructure of basalt fibre and nano-silica reinforced recycle concrete after exposure to elevated temperatures. Constr. Build. Mater. 2020, 247, 118561. [Google Scholar]
- Wang, Z.L.; Shi, Z.M.; Wang, J.G. On the strength and toughness properties of SFRC under static-dynamic compression. Compos. Part B Eng. 2011, 42, 1285–1290. [Google Scholar] [CrossRef]
- Xu, J.Y.; Liu, J.; Li, Z.W.; Bai, E.L.; Ren, W.B. Impact mechanical properties of concrete at and after exposure to high temperature. J. Build. Mater. 2013, 16, 1–5. [Google Scholar]
- Wang, Z.H.; Xu, J.Y.; Wang, T.J.; Meng, B.X.; Liu, G.J. Research on biaxial dynamic mechanical properties of concrete after high temperature under combined static and dynamic loads. J. Civ. Environ. Eng. 2020, 42, 1–8. [Google Scholar]
- Dias, D.P.; Thaumaturgo, C. Fracture toughness of geopolymeric concretes reinforced with basalt fibers. Cem. Concr. Compos. 2005, 27, 49–54. [Google Scholar] [CrossRef]
- Muazzam, G.S.; Wael, A.; Alaa, T.; Khaled, A. Sustainable alternative aggregates: Characterization and influence on mechanical behavior of basalt fiber reinforced concrete. Constr. Build. Mater. 2020, 255, 119365. [Google Scholar]
- Ayub, T.; Shafiq, N.; Nuruddin, M.F. Mechanical properties of high-performance concrete reinforced with basalt fibers. Procedia Eng. 2014, 77, 131–139. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.Y.; Fan, F.L.; Bai, E.L.; Liu, J.Z. Study on dynamic mechanical properties of basalt fibre reinforced concrete. Chin. J. Undergr. Space Eng. 2010, 6, 1665–1671. [Google Scholar]
- Li, W.M.; Xu, J.Y. Mechanical properties of basalt fiber reinforced geopolymeric concrete under impact loading. Mater. Sci. Eng. A 2009, 505, 178–186. [Google Scholar] [CrossRef]
- Li, W.M.; Xu, J.Y. Impact characterization of basalt fiber reinforced geopolymeric concrete using a 100-mm-diameter split Hopkinson pressure bar. Mater. Sci. Eng. A 2009, 513–514, 145–153. [Google Scholar] [CrossRef]
- Fan, F.L.; Ye, X.H.; Xu, J.Y.; Li, W.M.; Chen, Y. Dynamic constitutive relation of basalt fiber reinforced concrete under impact loading. J. Vib. Shock 2010, 29, 110–114. [Google Scholar]
- Zhang, H.; Wang, B.; Xie, A.Y.; Qi, Y.Z. Experimental study on dynamic mechanical properties and constitutive model of basalt fiber reinforced concrete. Constr. Build. Mater. 2017, 152, 154–167. [Google Scholar] [CrossRef]
- Ren, W.B.; Xu, J.Y.; Su, H.Y. Dynamic compressive behavior of basalt fiber reinforced concrete after exposure to elevated temperature. Fire Mater. 2016, 40, 738–755. [Google Scholar] [CrossRef]
- Ren, W.B.; Xu, J.Y.; Bai, E.L.; Fan, J.S. Dynamic mechanical properties of basalt fiber reinforced concrete after elevated temperature. Explos. Shock Waves 2015, 35, 36–42. [Google Scholar]
- Li, Y.; Zhai, Y.; Liu, X.Y.; Liang, W.B. Research on fractal characteristics and energy dissipation of concrete suffered freeze-thaw cycle action and impact loading. Materials 2019, 12, 2585. [Google Scholar] [CrossRef] [Green Version]
- Liang, W.B.; Zhao, J.H.; Li, Y.; Zhai, Y. Research on fractal characteristics and energy dissipation of basalt fiber reinforced concrete after exposure to elevated temperatures under impact loading. Materials 2020, 13, 1902. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.Y.; Li, W.M.; Huang, X.M.; Li, P. Dynamic constitutive model of basalt fiber reinforced geopolymeric concrete. Eng. Mech. 2010, 27, 111–116. [Google Scholar]
- Luo, X.; Sun, W.; Chan, S.Y.S.N. Effect of heating and cooling regimes on residual strength and microstructure of normal strength and high-performance concrete. Cem. Concr. Res. 2000, 30, 379–383. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Chen, W. Pulse shaping techniques for testing brittle materials with a split Hopkinson pressure bar. Exp. Mech. 2002, 42, 93–106. [Google Scholar] [CrossRef]
- Poon, C.S.; Azhar, S.; Anson, M.; Wong, Y.L. Comparison of the strength and durability performance of normal—and high—strength pozzolanic concretes at elevated temperatures. Cem. Concr. Res. 2001, 31, 1291–1300. [Google Scholar] [CrossRef]
- Khoury, G.A. Effect of fire on concrete and concrete structures. Prog. Struct. Eng. Mater. 2000, 2, 429–447. [Google Scholar] [CrossRef]
- Arioz, O. Effects of elevated temperatures on properties of concrete. Fire Saf. 2007, 42, 516–522. [Google Scholar] [CrossRef]
- Li, N.B.; Shi, X.D.; Xiao, M.H. Experimental investigation on compressive strength decaying behaviors of concrete after elevated temperature. Build. Sci. 2007, 23, 58–61. [Google Scholar]
- Borhan, T.M. Properties of glass concrete reinforced with short basalt fibre. Mater. Des. 2012, 42, 265–271. [Google Scholar] [CrossRef]
- Eibl, J.; Schmidt-Hurtienne, B. Strain-rate-sensitive constitutive law for concrete. J. Eng. Mech. 1999, 125, 1411–1420. [Google Scholar] [CrossRef]
- Rossi, P. A physical phenomenon which can explain the mechanical behavior of concrete under high strain rates. Mater. Struct. 1991, 24, 422–424. [Google Scholar] [CrossRef]
- Liu, J.Z.; Xu, J.Y.; Lv, X.C.; Wang, Z.D.; Zhang, L. Study on dynamic behavior and damage constitutive model of rock under impact loading with confining pressure. Eng. Mech. 2012, 29, 55–63. [Google Scholar]
- Chen, J.Y.; Wang, L.L. Rate-dependent constitutive equation of cement mortar. J. Ningbo Univ. (NSEE) 2000, 2, 1–5. [Google Scholar]
- Zhu, Z.X.; Xu, D.B.; Wang, L.L. Thermoviscoelastic constitutive equation and time-temperature equivalence of epoxy resin at high strain rates. J. Ningbo Univ. 1988, 1, 58–68. [Google Scholar]




| Item | Water | Cement | Fine Aggregate | Coarse Aggregate | Fly Ash | Water Reducer |
|---|---|---|---|---|---|---|
| Proportion | 0.56 | 1 | 2.03 | 3.80 | 0.40 | 0.02 |
| Diameter (μm) | Length (mm) | Tensile Strength (MPa) | Elasticity Modulus (GPa) | Fracture Elongation (%) | Density (kg/m3) |
|---|---|---|---|---|---|
| 17.4 | 12 | ≥2000 | ≥85 | 2.5 | 2699 |
| Item | Density (kg/m3) | Elasticity Modulus (GPa) | Longitudinal Sound Velocity (m/s) | Yield Strength (MPa) |
|---|---|---|---|---|
| Bars | 7800 | 210 | 5124 | ≥1200 |
| Temperature (°C) | Fiber Content | Strain Rate (s−1) | E (GPa) | R2 | |||
|---|---|---|---|---|---|---|---|
| 20 | 0.0% | 78.1 | 15.7 | 1.30 | 0.0021 | 0.025 | 0.96 |
| 0.1% | 83.3 | 18.7 | 1.22 | 0.0021 | 0.072 | 0.96 | |
| 0.2% | 104.1 | 30.0 | 0.80 | 0.0108 | 0.086 | 0.92 | |
| 0.3% | 94.4 | 10.5 | 1.05 | 0.0082 | 0.042 | 0.96 | |
| 0.4% | 79.0 | 20.7 | 1.21 | 0.0022 | 0.046 | 0.97 | |
| 200 | 0.0% | 75.1 | 46.0 | 0.90 | 0.0033 | 0.085 | 0.86 |
| 0.1% | 98.4 | 21.3 | 1.09 | 0.0029 | 0.072 | 0.96 | |
| 0.2% | 83.5 | 16.1 | 1.04 | 0.0053 | 0.071 | 0.93 | |
| 0.3% | 77.9 | 26.0 | 1.01 | 0.0065 | 0.052 | 0.97 | |
| 0.4% | 82.4 | 27.8 | 0.95 | 0.0075 | 0.068 | 0.95 | |
| 400 | 0.0% | 82.2 | 20.5 | 0.95 | 0.0067 | 0.055 | 0.95 |
| 0.1% | 81.9 | 16.3 | 1.10 | 0.0045 | 0.041 | 0.94 | |
| 0.2% | 75.3 | 20.0 | 1.02 | 0.0048 | 0.062 | 0.88 | |
| 0.3% | 78.7 | 25.0 | 0.94 | 0.0054 | 0.056 | 0.97 | |
| 0.4% | 80.4 | 21.4 | 0.97 | 0.0086 | 0.043 | 0.96 | |
| 600 | 0.0% | 60.5 | 11.0 | 1.25 | 0.0030 | 0.026 | 0.96 |
| 0.1% | 85.3 | 10.7 | 1.45 | 0.0008 | 0.030 | 0.99 | |
| 0.2% | 90.7 | 9.0 | 1.87 | 0.0002 | 0.029 | 0.99 | |
| 0.3% | 85.3 | 8.8 | 1.17 | 0.0040 | 0.033 | 0.95 | |
| 0.4% | 83.3 | 15.0 | 0.99 | 0.0043 | 0.040 | 0.96 | |
| 800 | 0.0% | 104.2 | 10.2 | 0.70 | 0.0163 | 0.021 | 0.96 |
| 0.1% | 87.9 | 7.5 | 1.44 | 0.0009 | 0.027 | 0.93 | |
| 0.2% | 99.1 | 7.0 | 1.53 | 0.0010 | 0.025 | 0.98 | |
| 0.3% | 114.5 | 3.5 | 1.58 | 0.0018 | 0.018 | 0.97 | |
| 0.4% | 115.2 | 4.8 | 1.30 | 0.0036 | 0.024 | 0.99 |
| Temperature (°C) | Fiber Content (%) | Impact Velocity (m/s) | R2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 0 | 8.8 | 1.120 | 0.00425 | 1.97 | 2.26 | 44.93 | 15.7 | 871.9 | 0.97 |
| 0.1 | 8.8 | 1.185 | 0.00359 | 2.05 | 3.55 | 5.04 | 18.6 | 56.13 | 0.95 | |
| 0.2 | 8.8 | 1.100 | 0.00699 | 1.40 | 3.41 | 59.61 | 30.0 | 16.70 | 0.91 | |
| 0.3 | 8.8 | 1.130 | 0.00902 | 1.50 | 2.33 | 21.90 | 10.5 | 47.07 | 0.98 | |
| 0.4 | 8.8 | 1.150 | 0.00394 | 1.60 | 3.50 | 19.64 | 20.7 | 72.26 | 0.98 | |
| 200 | 0.2 | 8.8 | 1.03 | 0.0074 | 3.70 | 5.50 | 26.86 | 16.1 | 26.81 | 0.94 |
| 400 | 0.2 | 8.8 | 1.02 | 0.0073 | 2.29 | 3.30 | 53.03 | 20.0 | 44.80 | 0.90 |
| 600 | 0.2 | 8.8 | 1.60 | 0.0007 | 1.10 | 2.10 | 66.67 | 9.0 | 100.0 | 0.98 |
| 800 | 0.2 | 8.8 | 1.71 | 0.0007 | 1.18 | 1.71 | 78.86 | 7.0 | 35.89 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, W.; Zhao, J.; Li, Y.; Zhai, Y.; Wang, Z.; Yang, Y. Research on Dynamic Mechanical Properties and Constitutive Model of Basalt Fiber Reinforced Concrete after Exposure to Elevated Temperatures under Impact Loading. Appl. Sci. 2020, 10, 7684. https://doi.org/10.3390/app10217684
Liang W, Zhao J, Li Y, Zhai Y, Wang Z, Yang Y. Research on Dynamic Mechanical Properties and Constitutive Model of Basalt Fiber Reinforced Concrete after Exposure to Elevated Temperatures under Impact Loading. Applied Sciences. 2020; 10(21):7684. https://doi.org/10.3390/app10217684
Chicago/Turabian StyleLiang, Wenbiao, Junhai Zhao, Yan Li, Yue Zhai, Zhou Wang, and Yubing Yang. 2020. "Research on Dynamic Mechanical Properties and Constitutive Model of Basalt Fiber Reinforced Concrete after Exposure to Elevated Temperatures under Impact Loading" Applied Sciences 10, no. 21: 7684. https://doi.org/10.3390/app10217684





