Feature Extraction for Bearing Fault Detection Using Wavelet Packet Energy and Fast Kurtogram Analysis
Abstract
:1. Introduction
2. Wavelet Packet Transform
2.1. WPT
2.2. Frequency Band Energy Feature Extraction
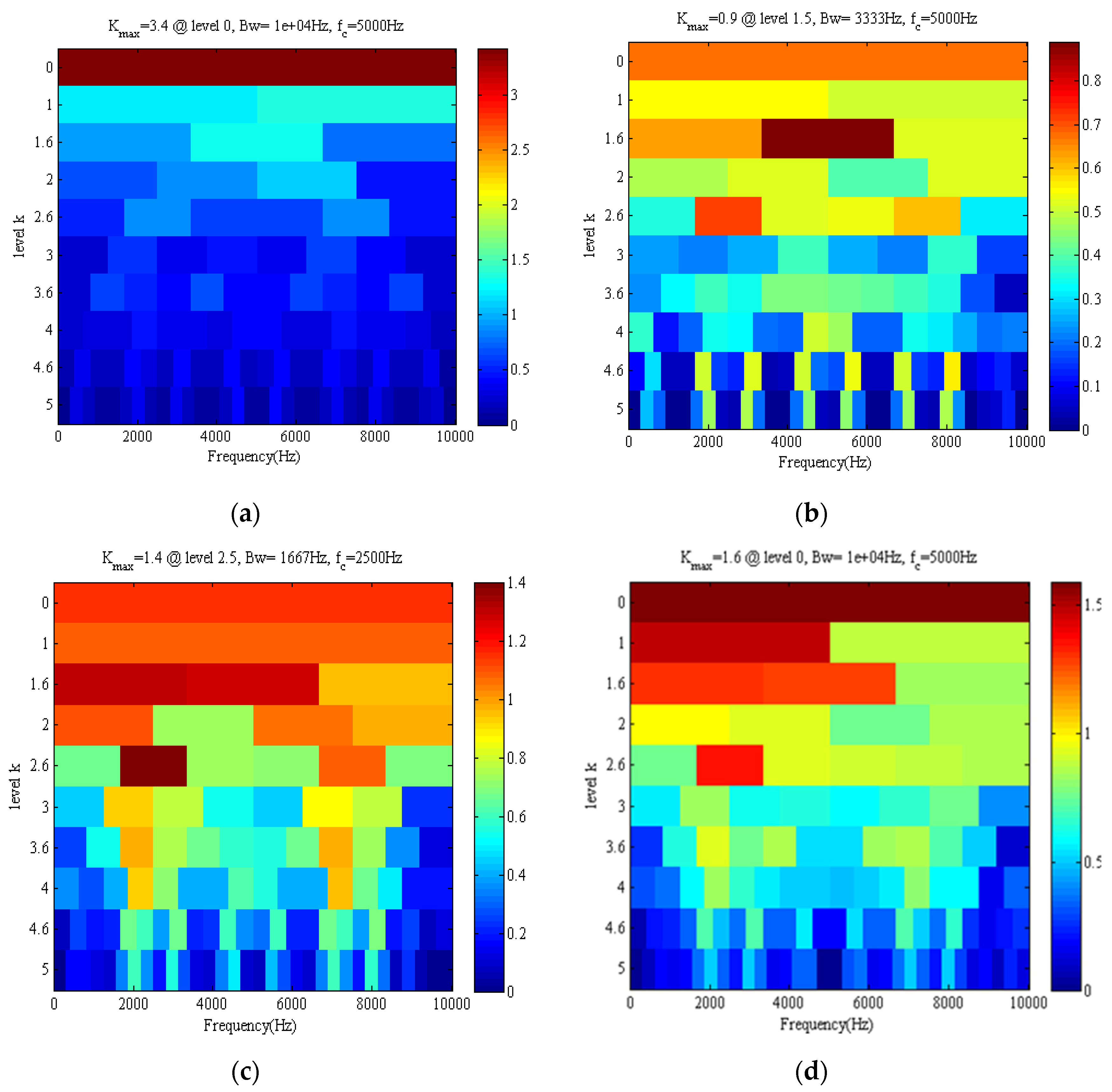
3. Kurtogram Calculation
4. Simulation Analysis
4.1. Data Acquisition
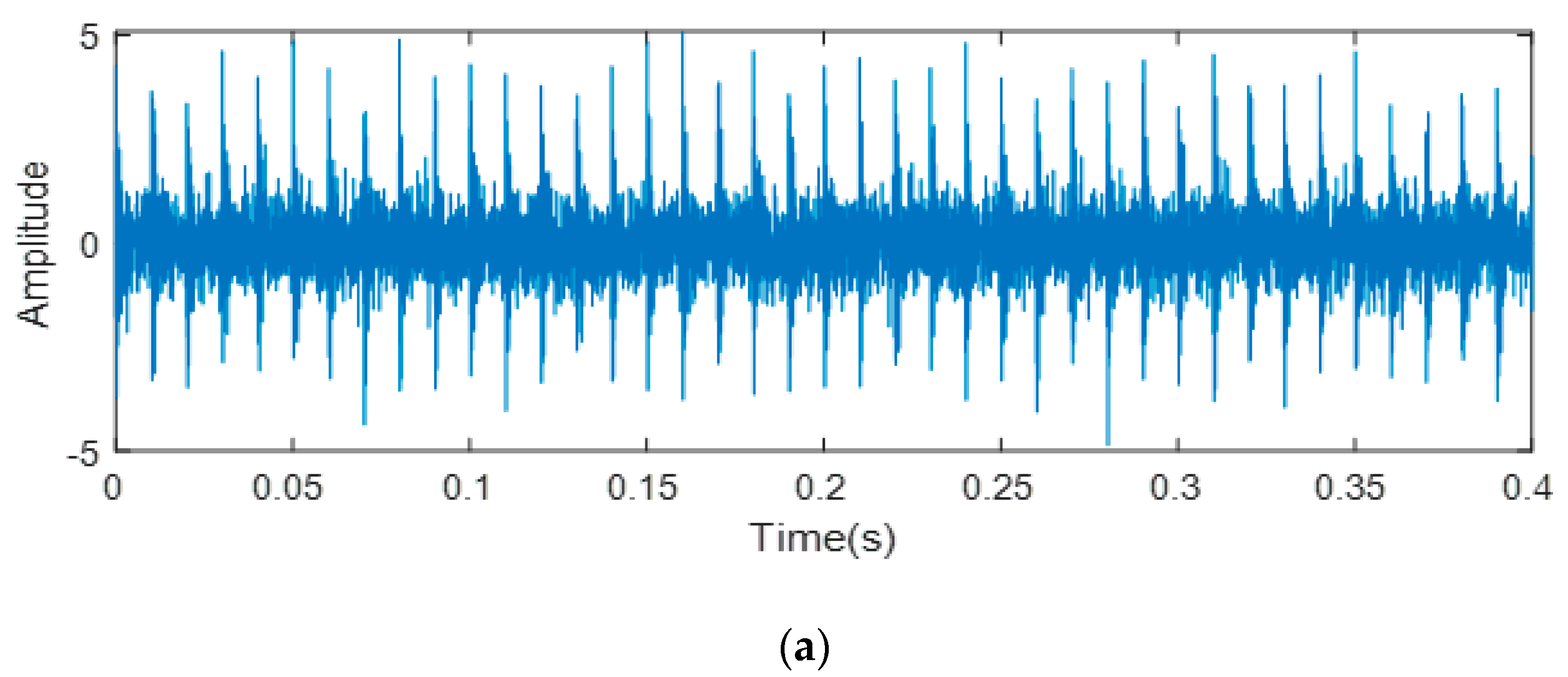
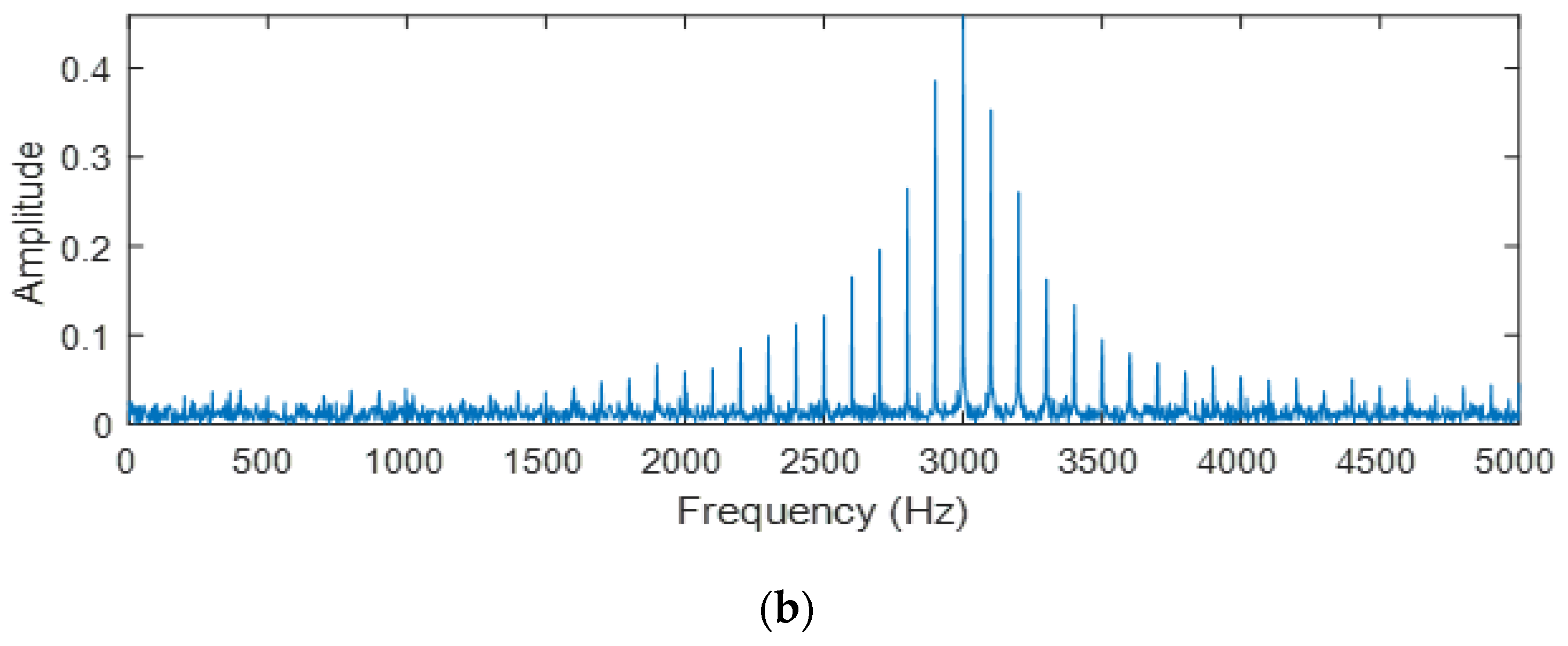
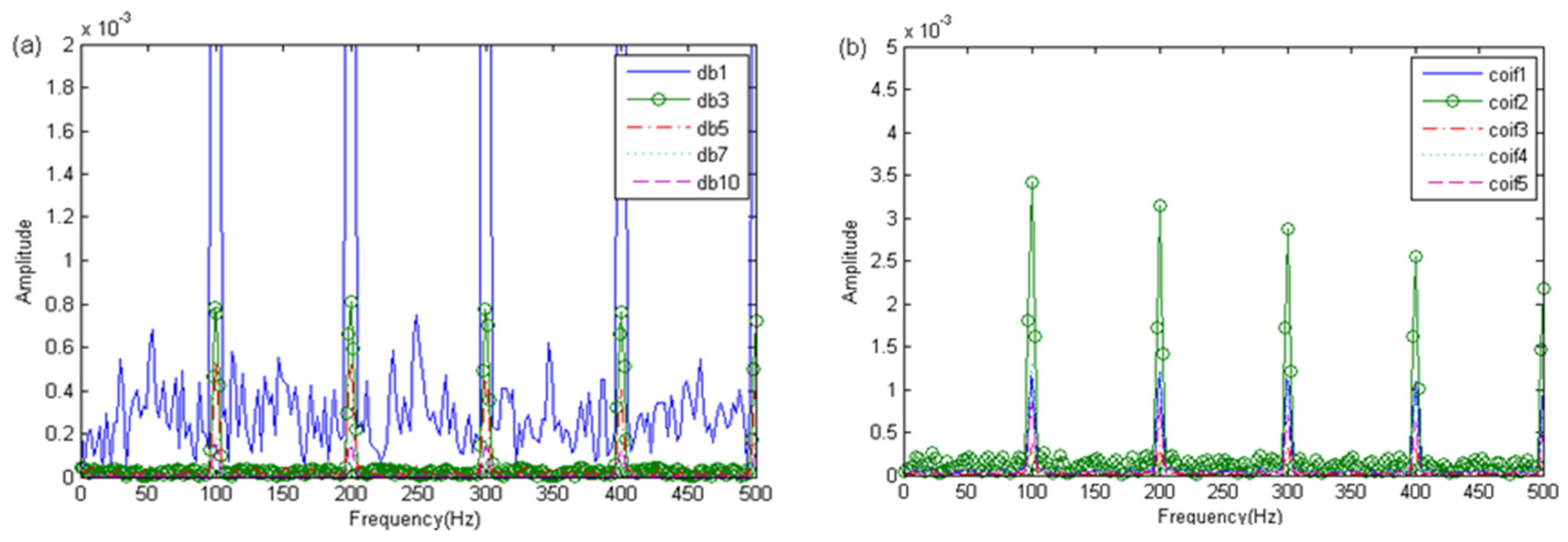
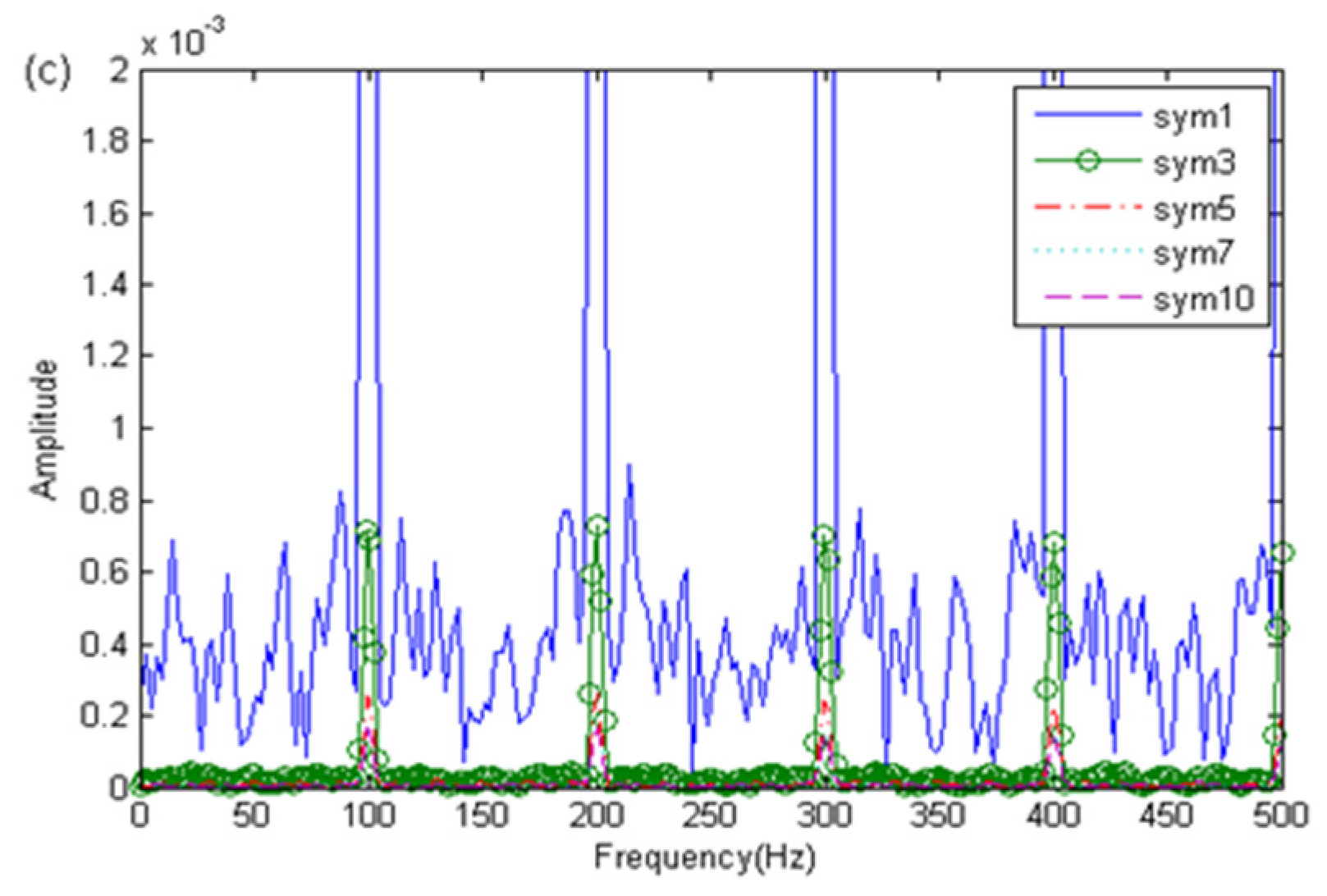
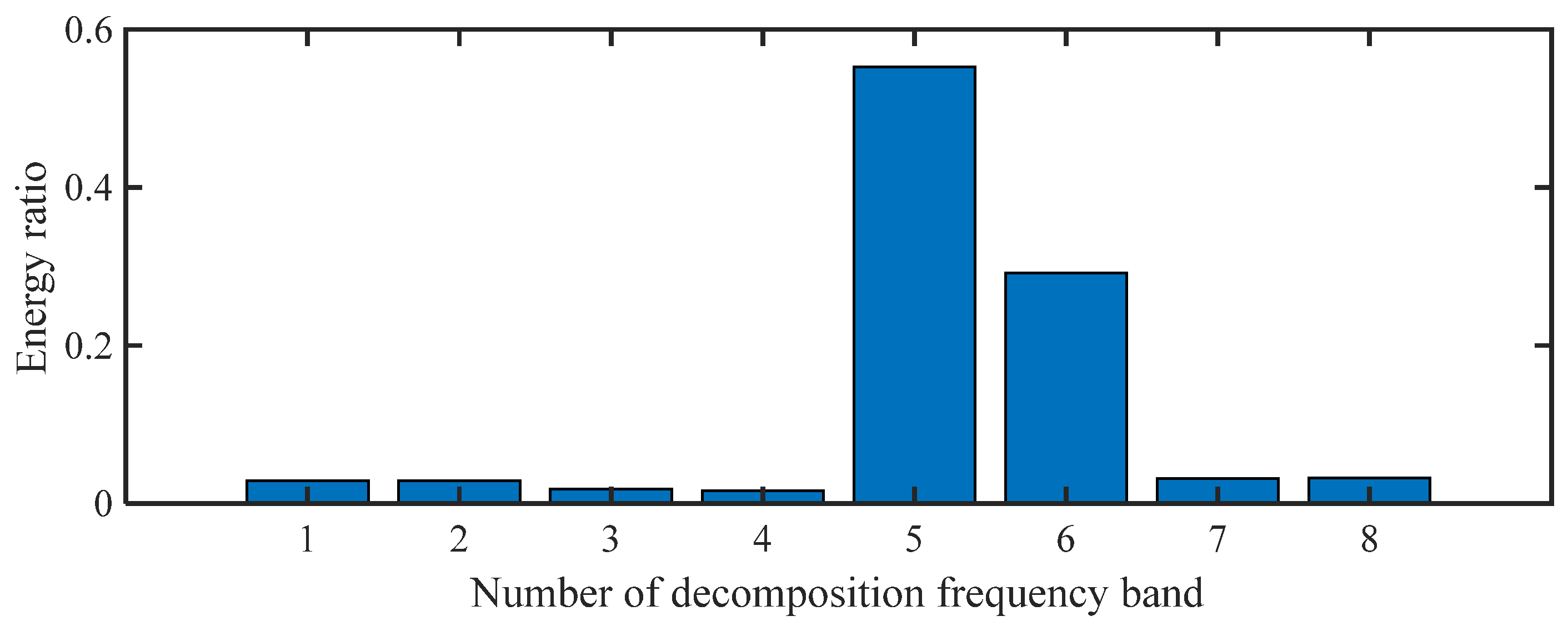
4.2. Optimization of the WPE Parameters
4.3. Results and Analysis
5. The Flowchart of the Fault Diagnosis Method
- (1)
- By selecting the appropriate wavelet function and the number of decomposition layers, the measurement signal is decomposed by WPT and passed to obtain the WPT coefficient of each node;
- (2)
- Calculate the WPT energy value of each node;
- (3)
- Select the decomposed signal with the concentrated energy for reconstruction;
- (4)
- Calculate the SK map of the acquired reconstructed signal and select the center frequency and bandwidth corresponding to the maximum kurtosis value;
- (5)
- Filter the reconstructed signal using the optimized center frequency and bandwidth as the band-pass filter parameters;
- (6)
- Perform square envelope demodulation on the filtered signal to obtain the envelope spectrum of the signal;
- (7)
- Analyze the envelope spectrum to obtain the fault diagnosis result.
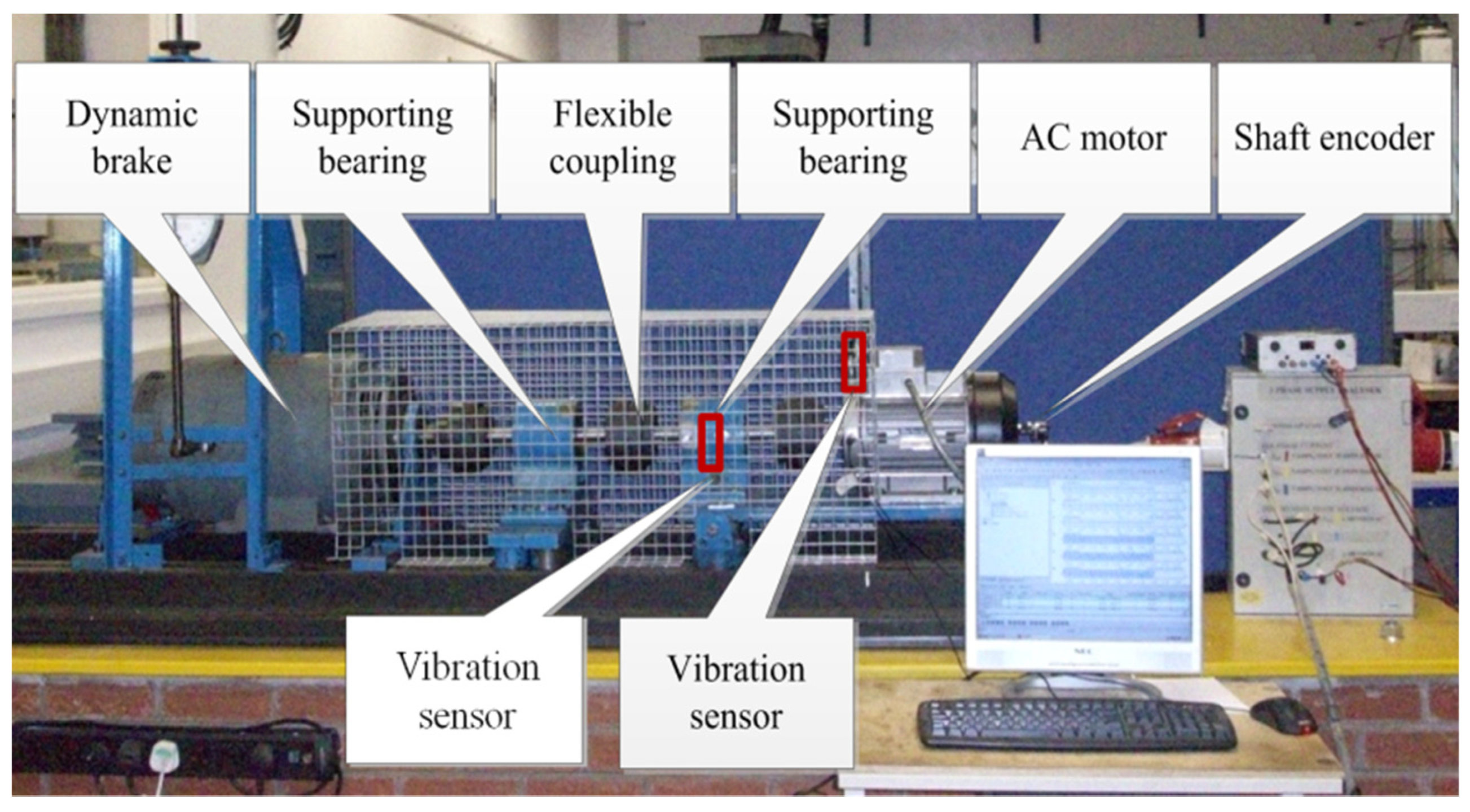
6. Experiments Validation
6.1. Data Acquisition
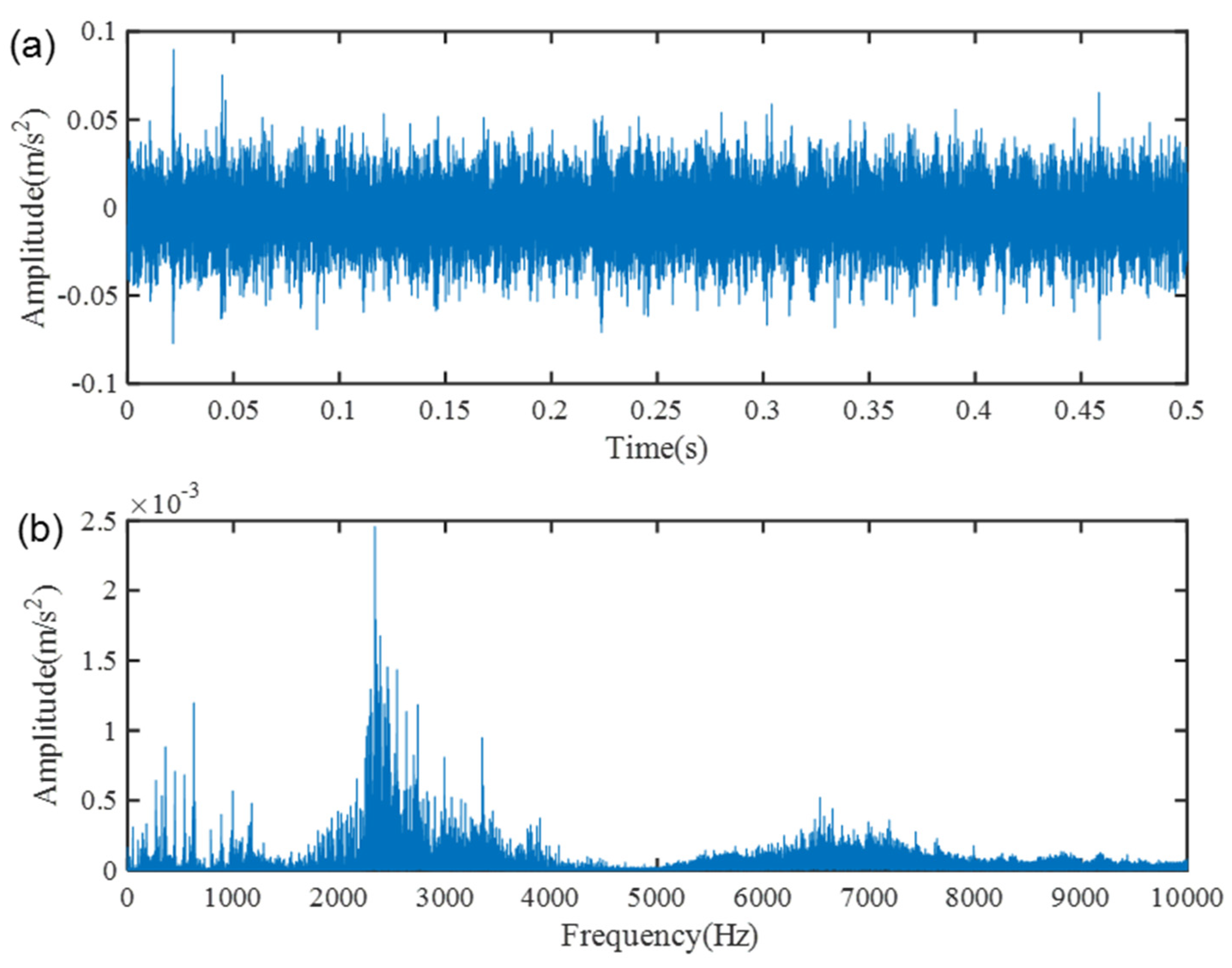
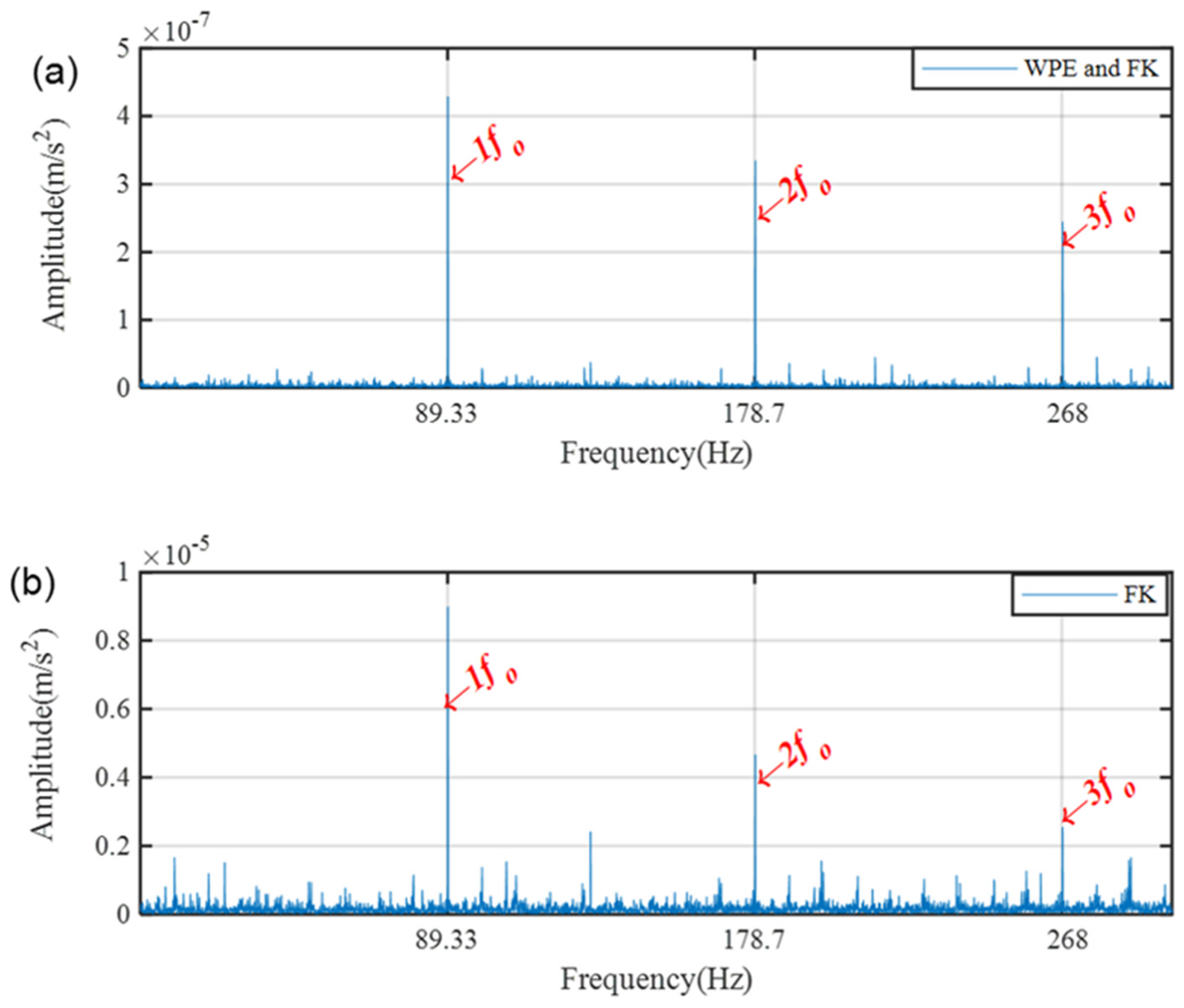
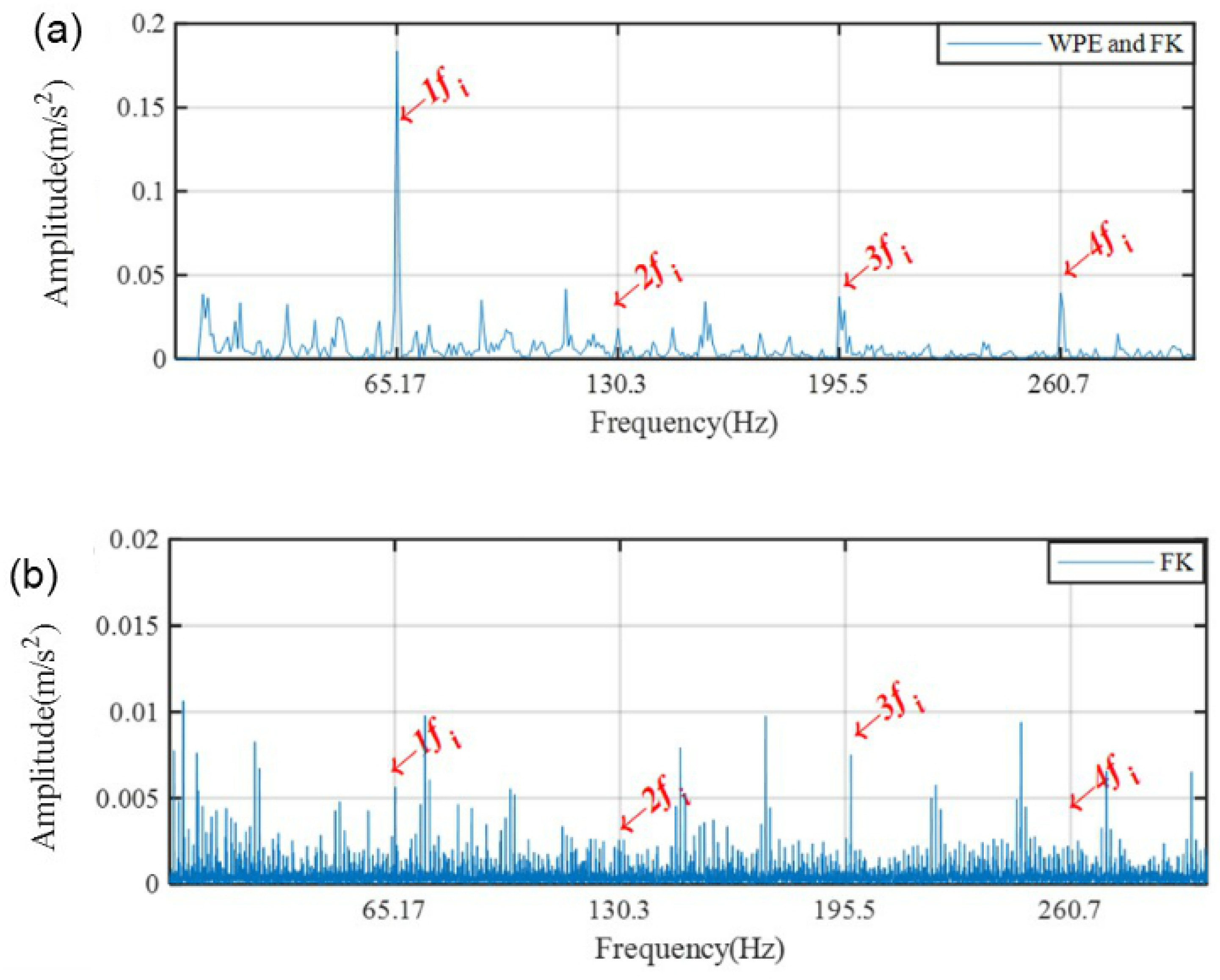
6.2. Motor Bearing Fault Detection
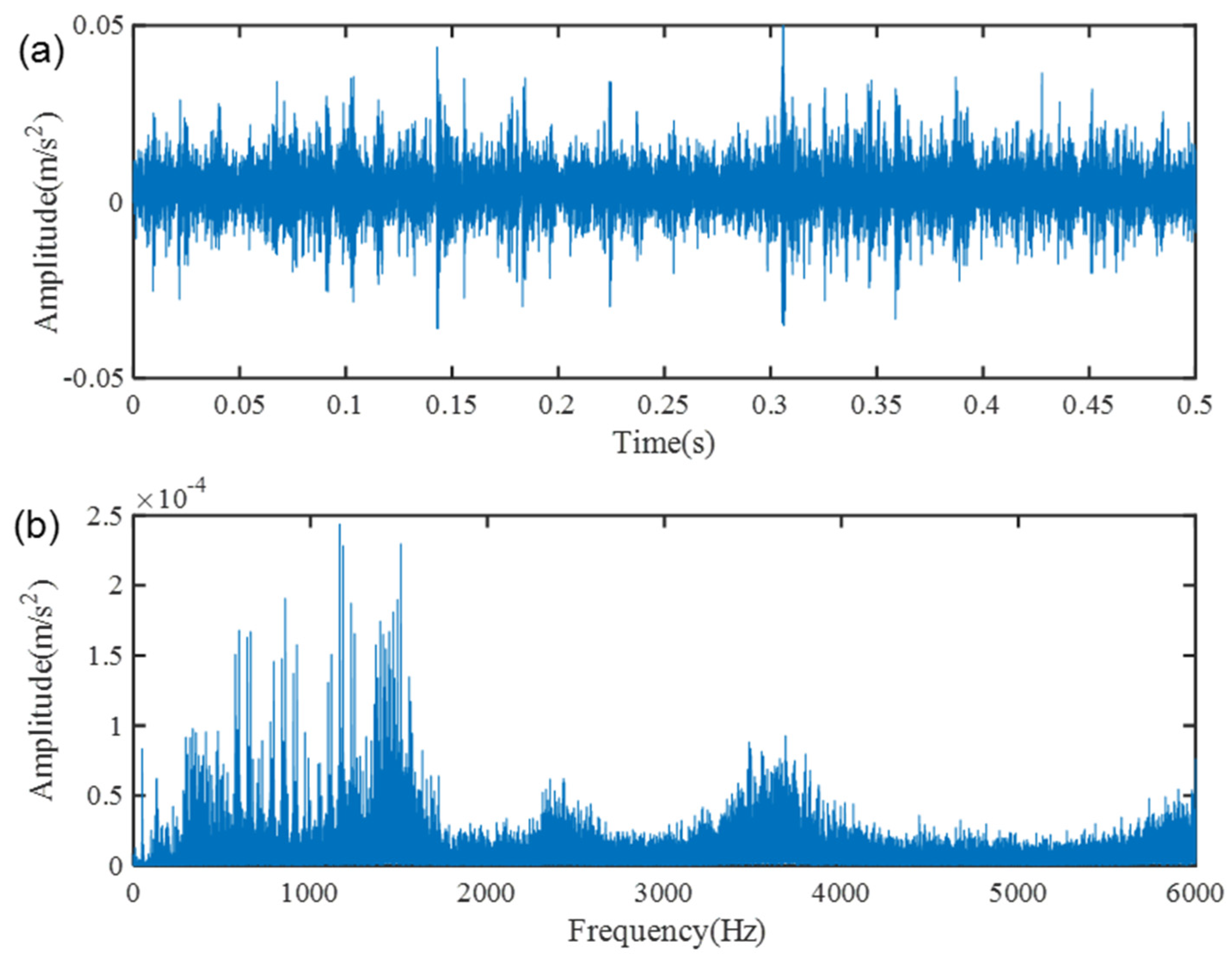
6.3. Supporting Bearing Fault Detection
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, Z.; Ming, A.; Zhang, W.; Liu, T.; Chu, F.; Li, Y. Fault feature extraction and enhancement of rolling element bearings based on maximum correlated kurtosis deconvolution and improved empirical wavelet transform. Appl. Sci. 2019, 9, 1876. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Wang, J.; Liu, Z.; Wang, J. Weak feature enhancement in machinery fault diagnosis using empirical wavelet transform and an improved adaptive bistable stochastic resonance. ISA Trans. 2019, 84, 283–295. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Wang, X.; Wang, H.; Jiang, H. Remaining useful life prediction of rolling element bearings based on simulated performance degradation dictionary. Mech. Mach. Theory 2020, 153, 103967. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, Z.; Lin, J.; Lu, F. Phenomenological models of vibration signals for condition monitoring and fault diagnosis of epicyclic gearboxes. J. Sound Vib. 2016, 369, 266–281. [Google Scholar] [CrossRef]
- Zhou, R.; Bao, W.; Li, N.; Huang, X.; Yu, D. Mechanical equipment fault diagnosis based on redundant second generation wavelet packet transform. Digit. Signal Process. 2010, 20, 276–288. [Google Scholar] [CrossRef]
- Guo, J.; Zhen, D.; Li, H.; Shi, Z.; Gu, F.; Ball, A. Fault detection for planetary gearbox based on an enhanced average filter and modulation signal bispectrum analysis. ISA Trans. 2020, 101, 408–420. [Google Scholar] [CrossRef]
- Cui, L.; Wang, X.; Wang, H.; Ma, J. Research on remaining useful life prediction of rolling element bearings based on time-varying Kalman filter. IEEE Trans. Instrum. Meas. 2020, 69, 2858–2867. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, Y.; Shi, L.; Guo, H.; Chen, H. Sound quality recognition using optimal wavelet-packet transform and artificial neural network methods. Mech. Syst. Signal Process. 2015, 66. [Google Scholar] [CrossRef]
- Mavaddaty, S.; Ahadi, S.M.; Seyedin, S. Speech enhancement using sparse dictionary learning in wavelet packet transform domain. Comput. Speech Lang. 2017, 44, 22–47. [Google Scholar] [CrossRef]
- Xu, X.; Luo, M.; Tan, Z.; Pei, R. Echo signal extraction method of laser radar based on improved singular value decomposition and wavelet threshold denoising. Infrared. Phys. Tech. 2018, 92, 327–335. [Google Scholar] [CrossRef]
- Bianchi, D.; Mayrhofer, E.; Gröschl, M.; Betz, G.; Vernes, A. Wavelet packet transform for detection of single events in acoustic emission signals. Mech. Syst. Signal. Process. 2015, 64, 441–451. [Google Scholar] [CrossRef]
- He, Q. Vibration signal classification by wavelet packet energy flow manifold learning. J. Sound Vib. 2013, 332, 1881–1894. [Google Scholar] [CrossRef]
- Han, L.; Li, C.; Guo, S.; Su, X. Feature extraction method of bearing AE signal based on improved FAST-ICA and wavelet packet energy. Mech. Syst. Signal Process. 2015, 62, 91–99. [Google Scholar] [CrossRef]
- Hoseinzadeh, M.S.; Khadem, S.E.; Sadooghi, M.S. Quantitative diagnosis for bearing faults by improving ensemble empirical mode decomposition. ISA Trans. 2018, 83, 261–275. [Google Scholar] [CrossRef]
- Dwyer, R. Detection of non-gaussian signals by frequency domain kurtosis estimation. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Boston, MA, USA, 14–16 April 1983; Volume 8, pp. 607–610. [Google Scholar]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal. Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Smith, W.A.; Fan, Z.; Peng, Z.; Li, H.; Randall, R.B. Optimised spectral kurtosis for bearing diagnostics under electromagnetic interference. Mech. Syst. Signal Process. 2016, 75, 371–394. [Google Scholar] [CrossRef] [Green Version]
- He, D.; Wang, X.; Li, S.; Lin, J.; Zhao, M. Identification of multiple faults in rotating machinery based on minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal Process. 2016, 81, 235–249. [Google Scholar] [CrossRef]
- Zhang, Y.; Randall, R.B. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram. Mech. Syst. Signal Process. 2009, 23, 1509–1517. [Google Scholar] [CrossRef]
- Guo, J.; Zhen, D.; Li, H.; Shi, Z.; Gu, F.; Ball, A. Fault feature extraction for rolling element bearing diagnosis based on a multi-stage noise reduction method. Measurement 2019, 139, 226–235. [Google Scholar] [CrossRef] [Green Version]
- Mishra, C.; Samantaray, A.K.; Chakraborty, G. Rolling element bearing fault diagnosis under slow speed operation using wavelet de-noising. Measurement 2017, 103, 77–86. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 1–14. [Google Scholar] [CrossRef]
- Ren, Y.; Li, W.; Zhang, B.; Zhu, Z.; Jiang, F. Fault diagnosis of rolling bearings based on improved kurtogram in varying speed conditions. Appl. Sci. 2019, 9, 1157. [Google Scholar] [CrossRef] [Green Version]
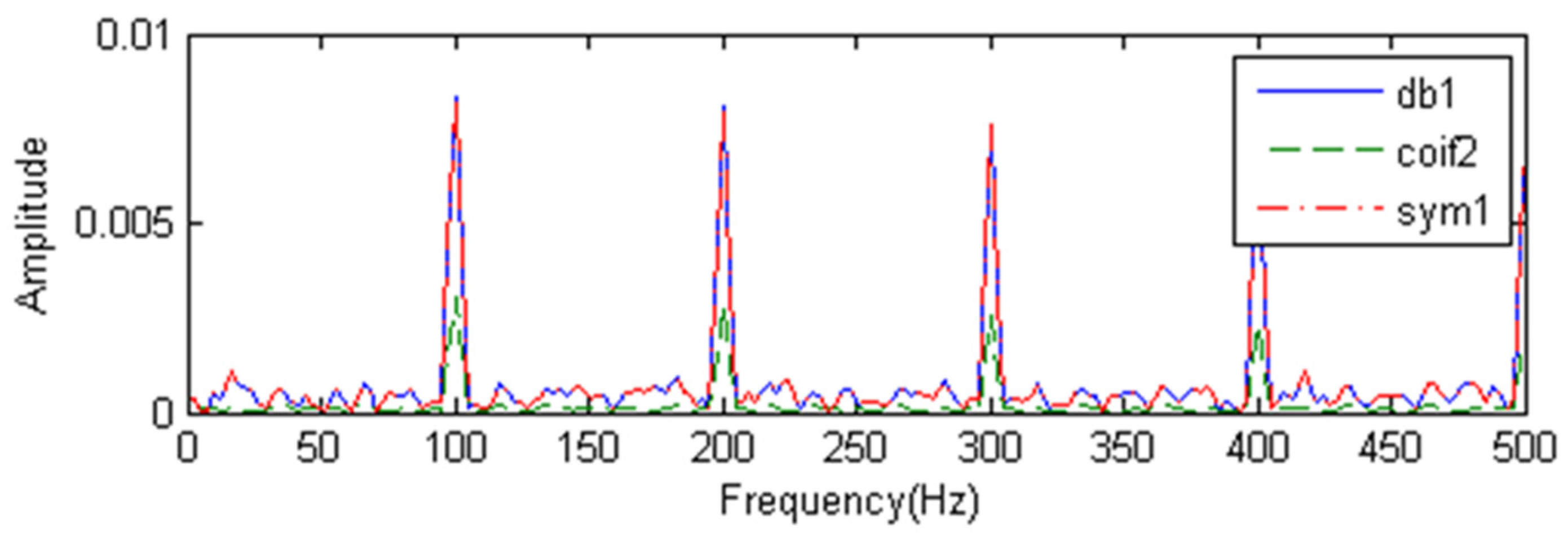
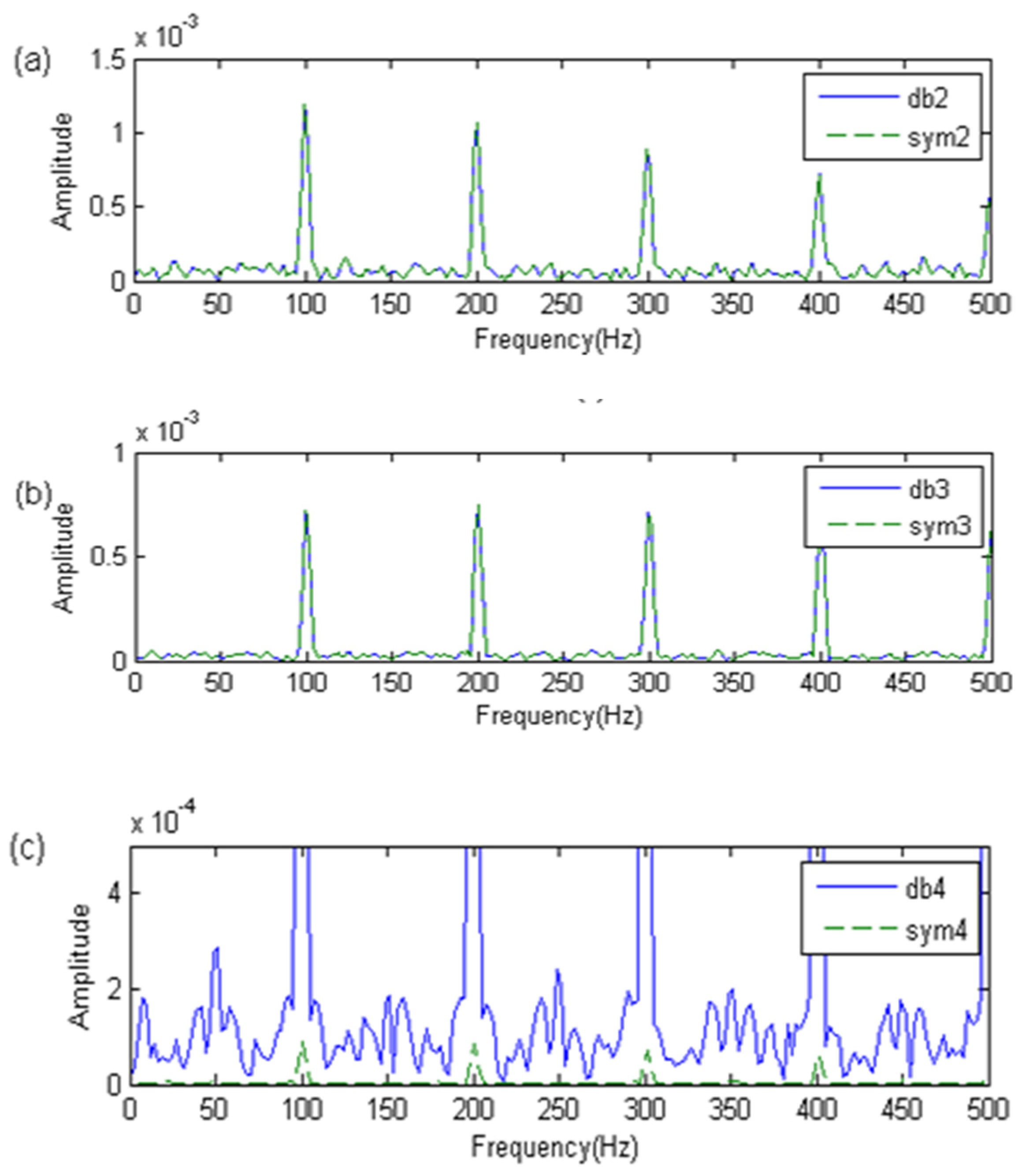
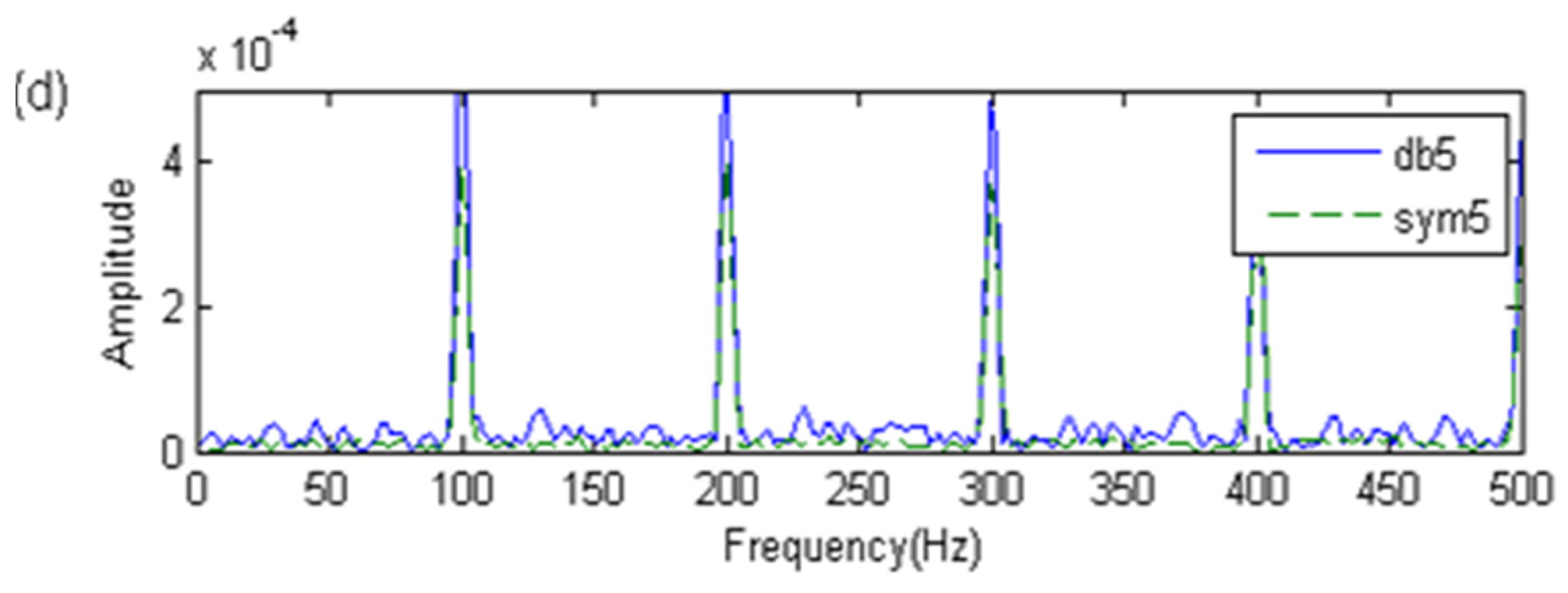





| Wavelet Function | Order Range |
|---|---|
| dbN | 1–45 |
| coifN | 1–5 |
| symN | 1–45 |
| Serial Number | Node Situation | Frequency/Hz |
|---|---|---|
| 1st | node[3,0] | 0–1250 Hz |
| 2nd | node[3,1] | 1250–2500 Hz |
| 3rd | node[3,2] | 2500–3750 Hz |
| 4th | node[3,3] | 3750–5000 Hz |
| 5th | node[3,4] | 5000–6250 Hz |
| 6th | node[3,5] | 6250–7500 Hz |
| 7th | node[3,6] | 7500–8750 Hz |
| 8th | node[3,7] | 8750–10,000 Hz |
| Bearing Designation | Pitch Diameter | Ball Diameter d (mm) | Ball Numbers z |
|---|---|---|---|
| 6206ZZ | 46.4 | 9.53 | 9 |
| 89.33 | 130.99 | 62.42 | 9.93 |
| Bearing Designation | Pitch Diameter | Ball Diameter d (mm) | Ball Numbers z |
|---|---|---|---|
| 6008 | 54 | 7.9 | 12 |
| 49.25 | 65.17 | 33.60 | 4.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhu, J.; Wu, Y.; Zhen, D.; Zhang, M. Feature Extraction for Bearing Fault Detection Using Wavelet Packet Energy and Fast Kurtogram Analysis. Appl. Sci. 2020, 10, 7715. https://doi.org/10.3390/app10217715
Zhang X, Zhu J, Wu Y, Zhen D, Zhang M. Feature Extraction for Bearing Fault Detection Using Wavelet Packet Energy and Fast Kurtogram Analysis. Applied Sciences. 2020; 10(21):7715. https://doi.org/10.3390/app10217715
Chicago/Turabian StyleZhang, Xiaojun, Jirui Zhu, Yaqi Wu, Dong Zhen, and Minglu Zhang. 2020. "Feature Extraction for Bearing Fault Detection Using Wavelet Packet Energy and Fast Kurtogram Analysis" Applied Sciences 10, no. 21: 7715. https://doi.org/10.3390/app10217715
APA StyleZhang, X., Zhu, J., Wu, Y., Zhen, D., & Zhang, M. (2020). Feature Extraction for Bearing Fault Detection Using Wavelet Packet Energy and Fast Kurtogram Analysis. Applied Sciences, 10(21), 7715. https://doi.org/10.3390/app10217715





