A Review of Modular Multilevel Converters for Stationary Applications
Abstract
:1. Introduction
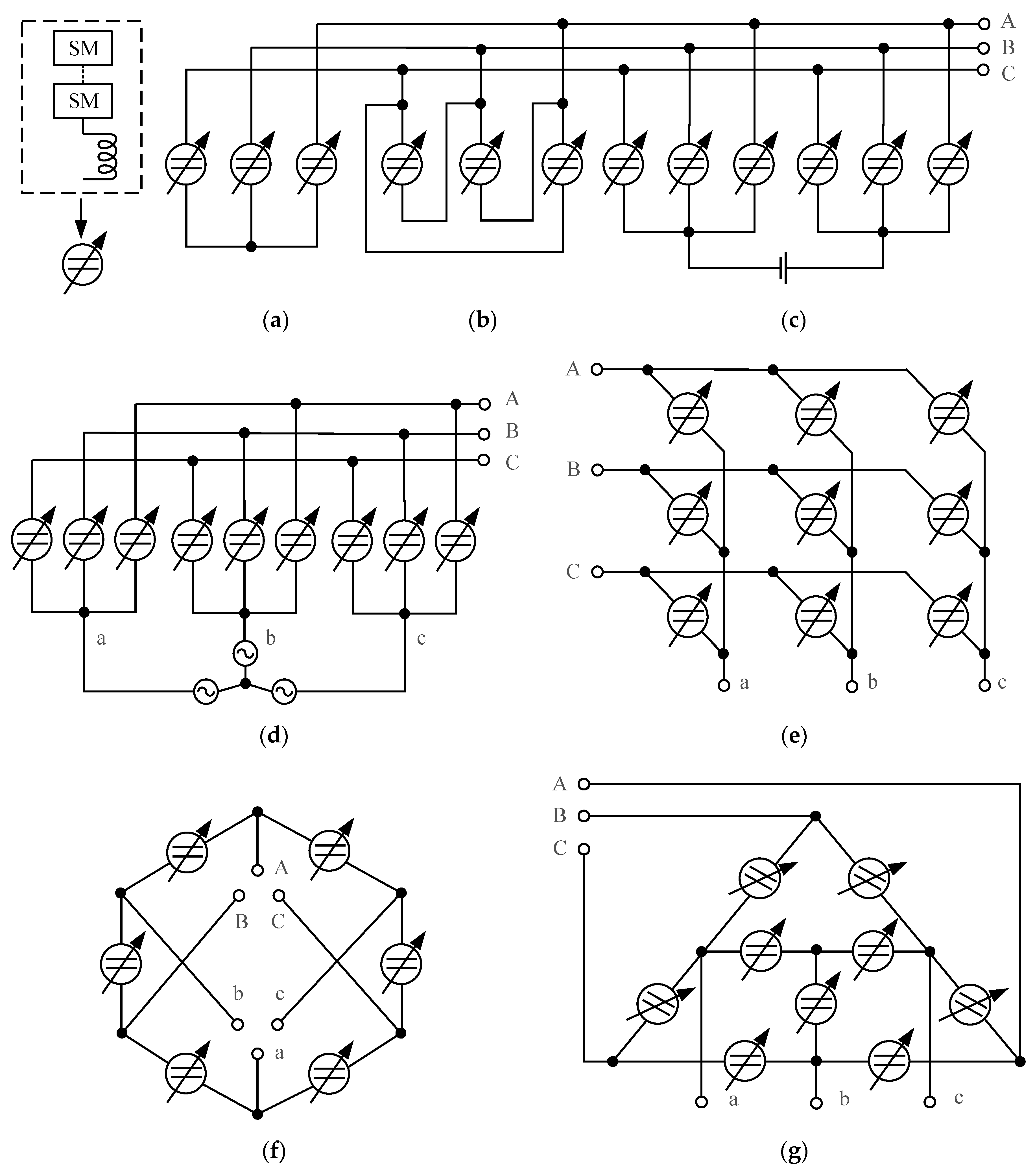
2. MMC Topologies
2.1. Submodule Topologies
2.1.1. Two-Level Submodule Topologies
2.1.2. Multilevel Submodule Topologies
2.2. Overall Topologies
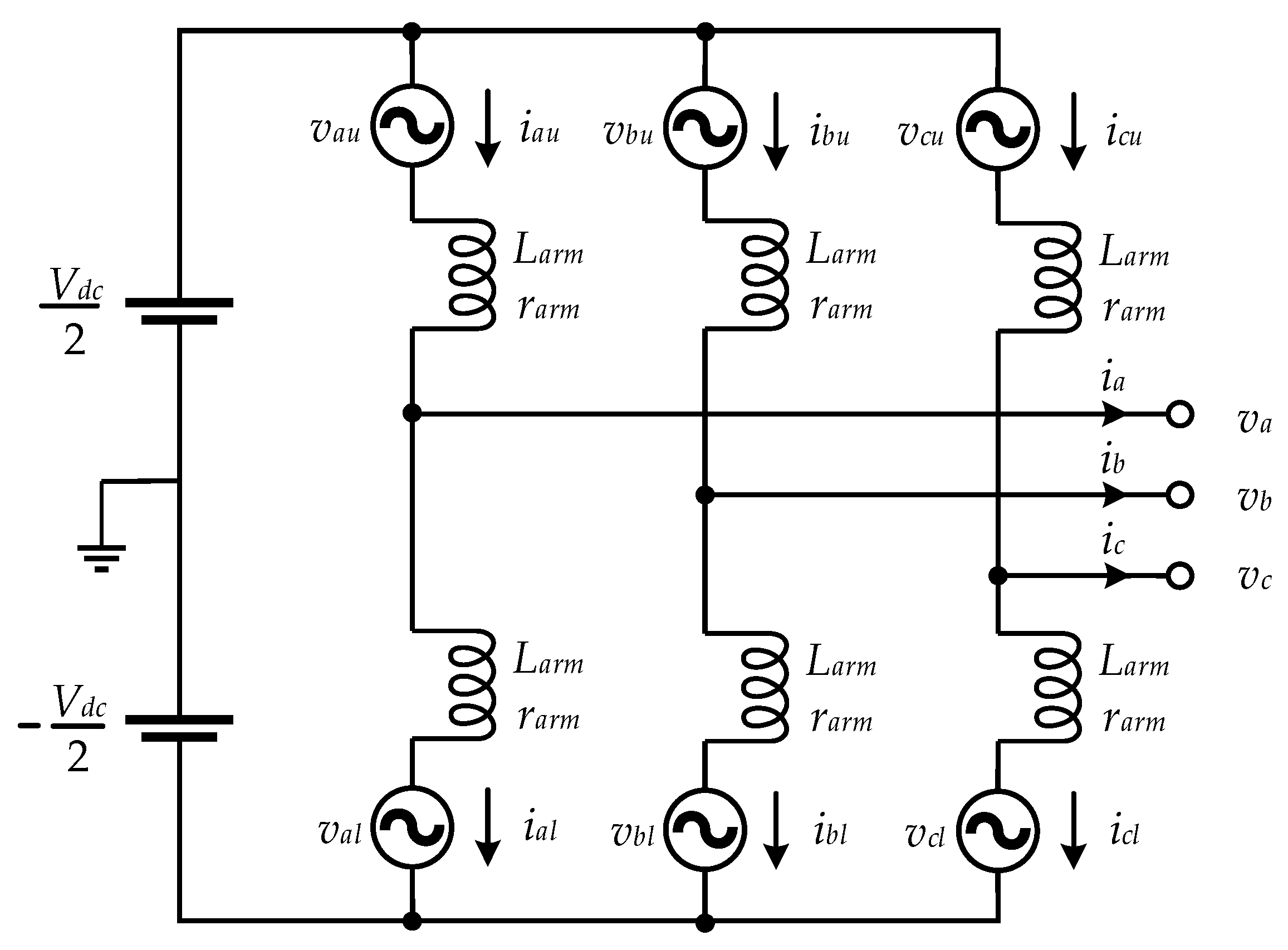
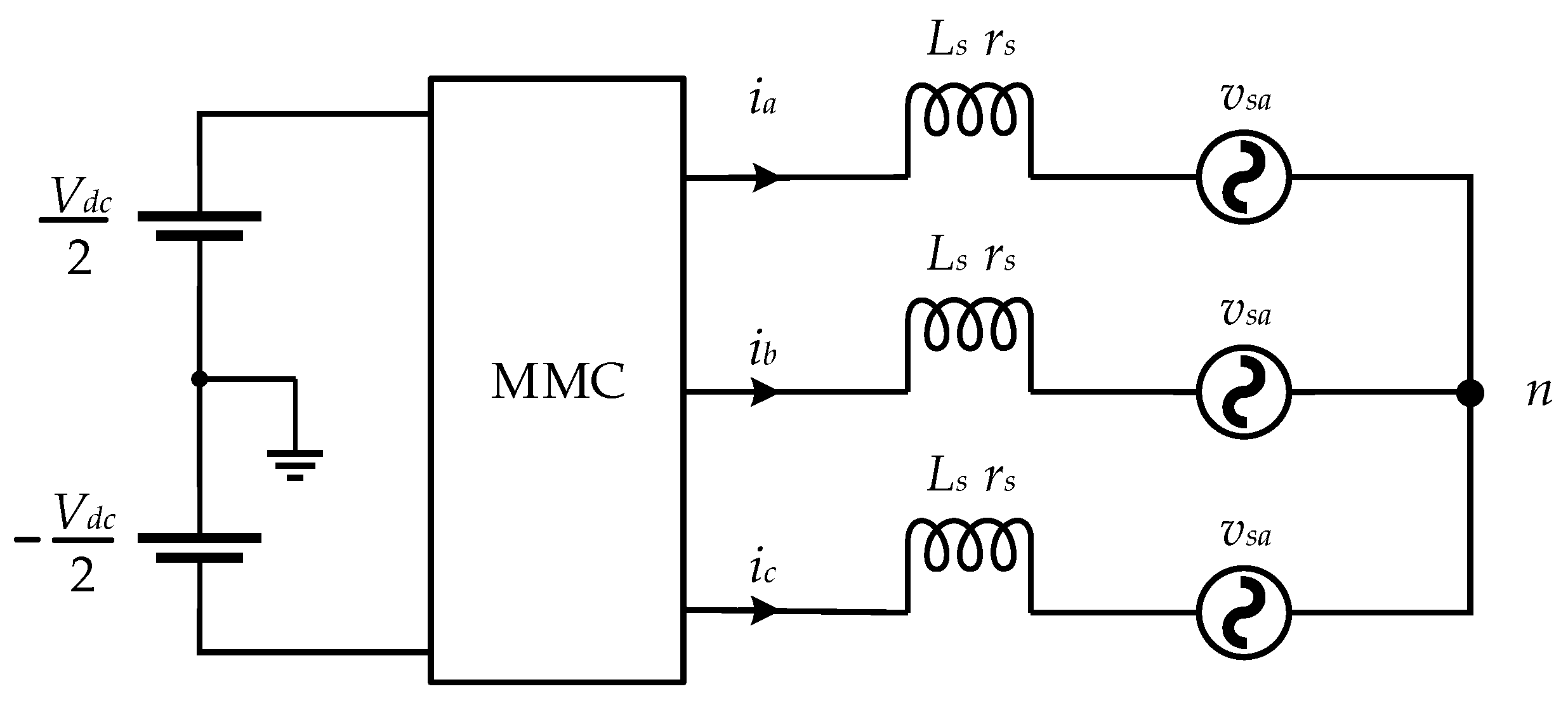
3. Mathematical Modeling and Control of Three-Phase MMC
3.1. Mathematical Modeling
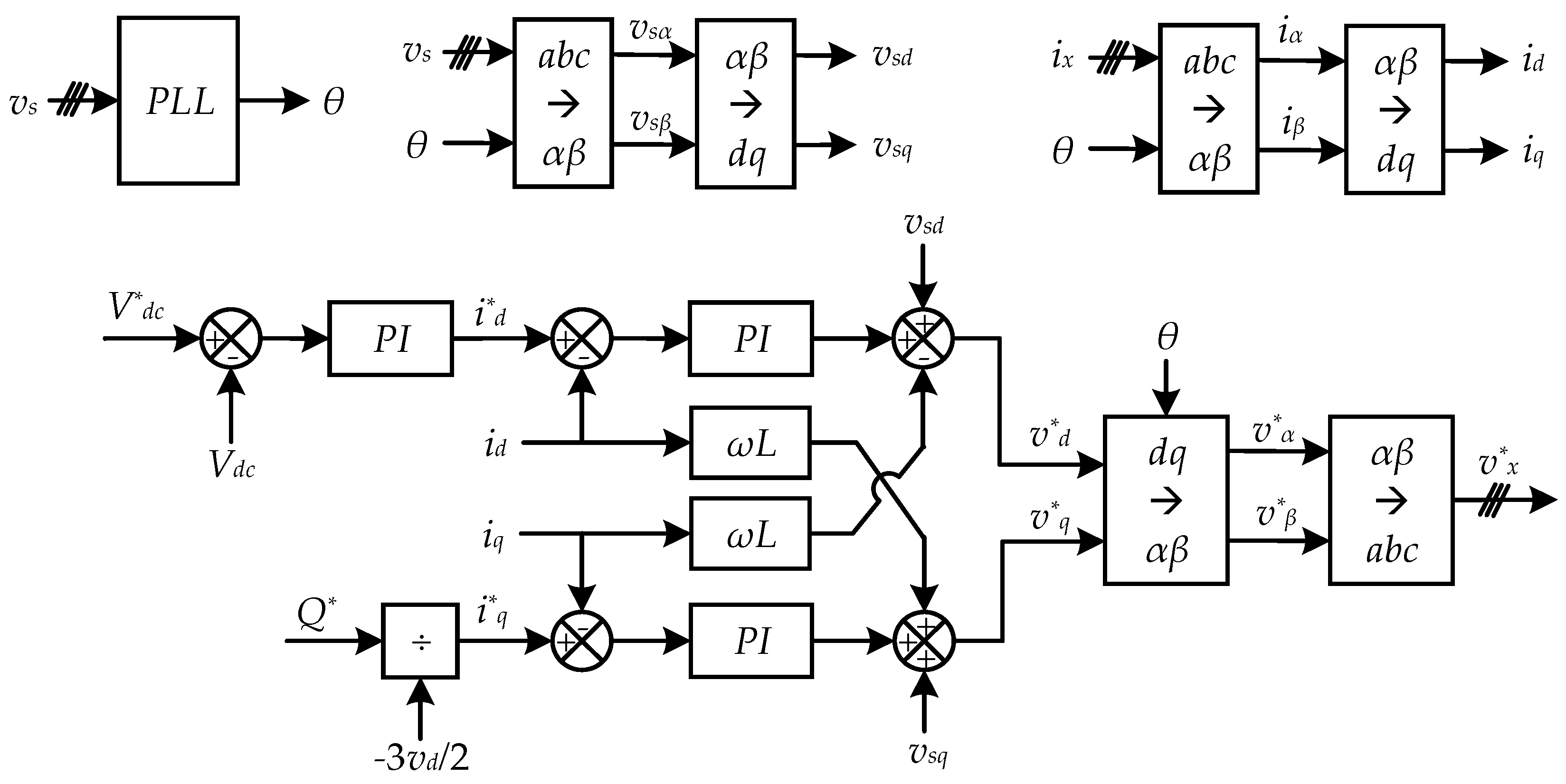
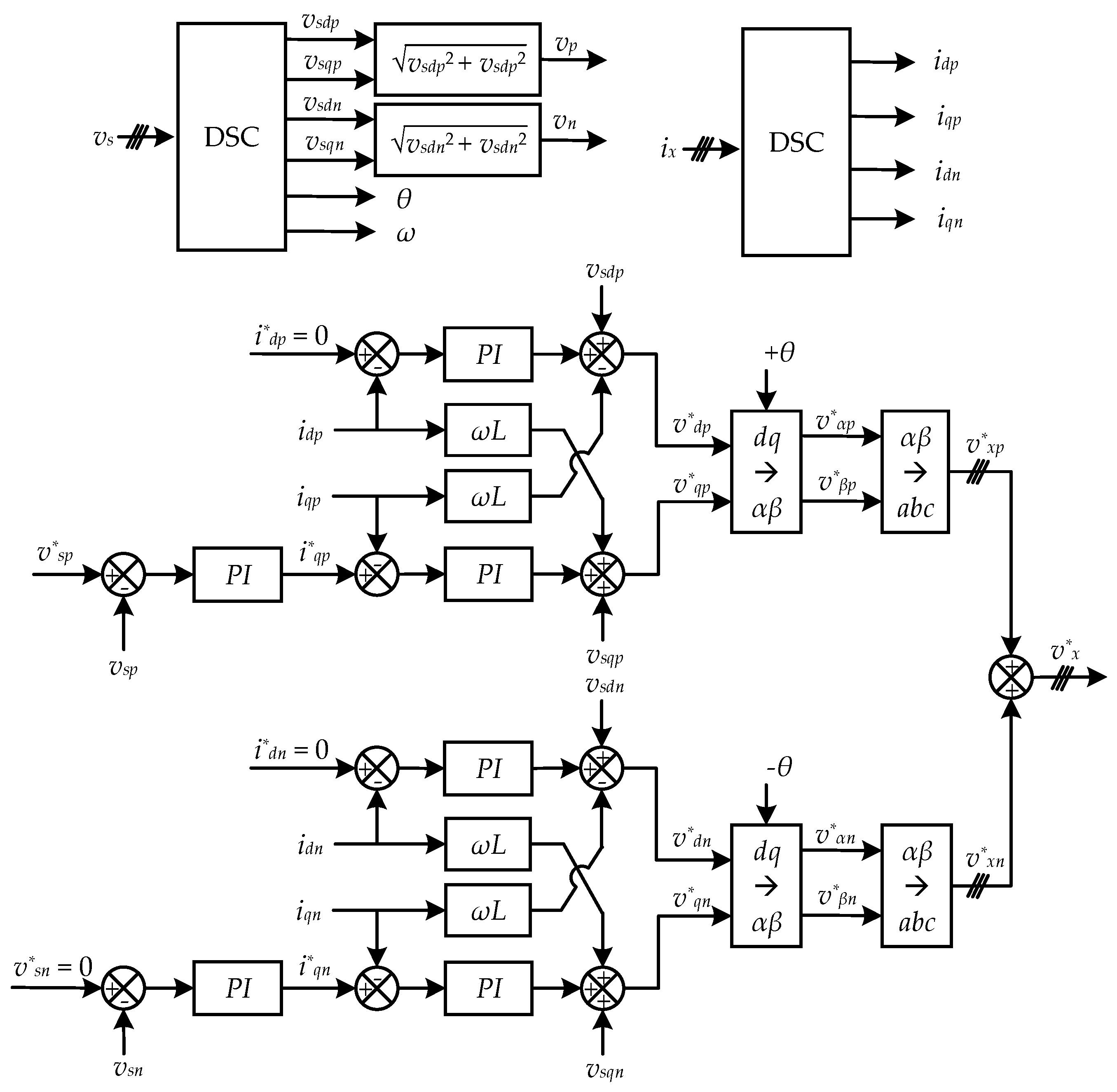
3.2. Output Voltage and Current Control
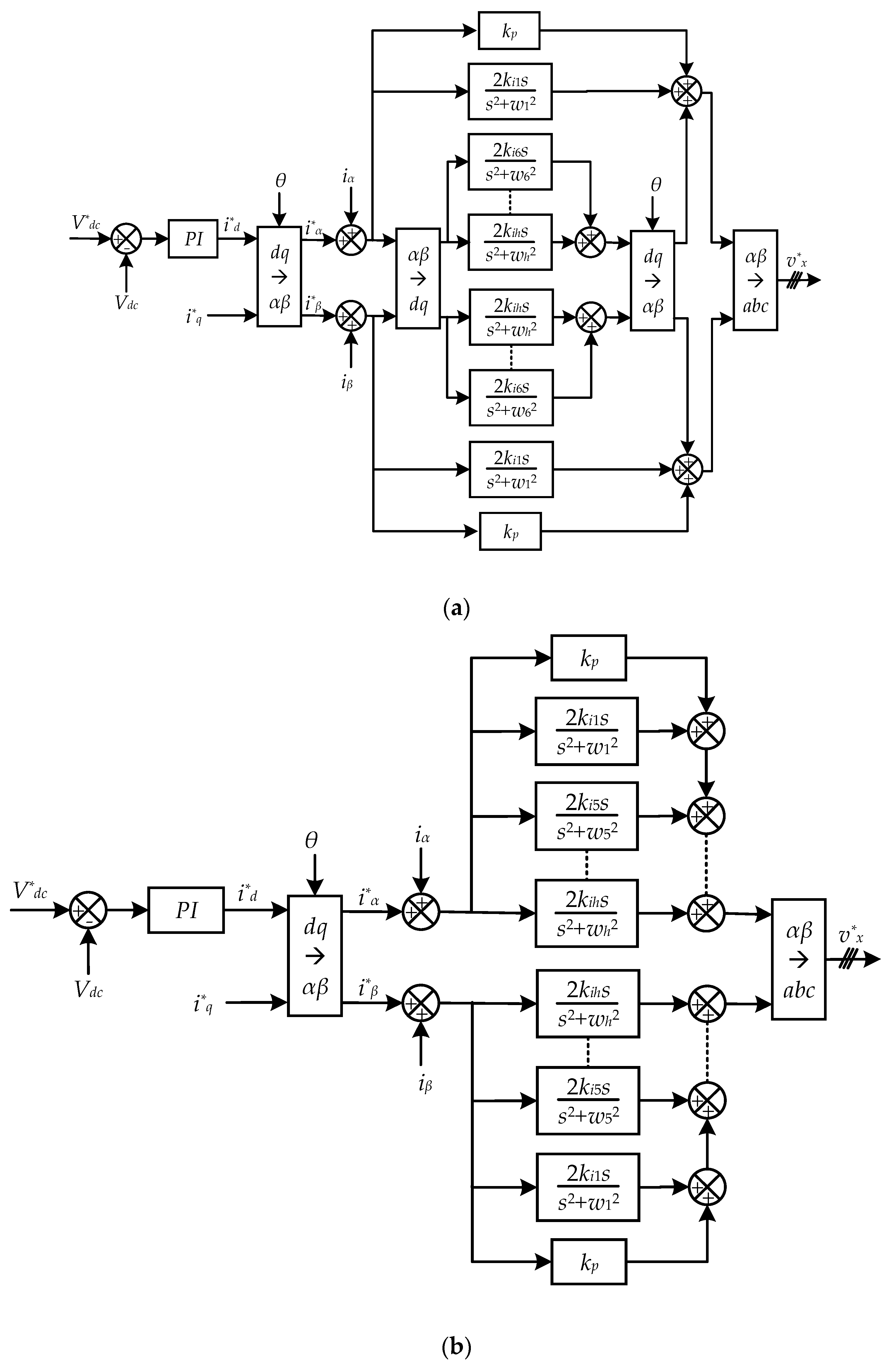
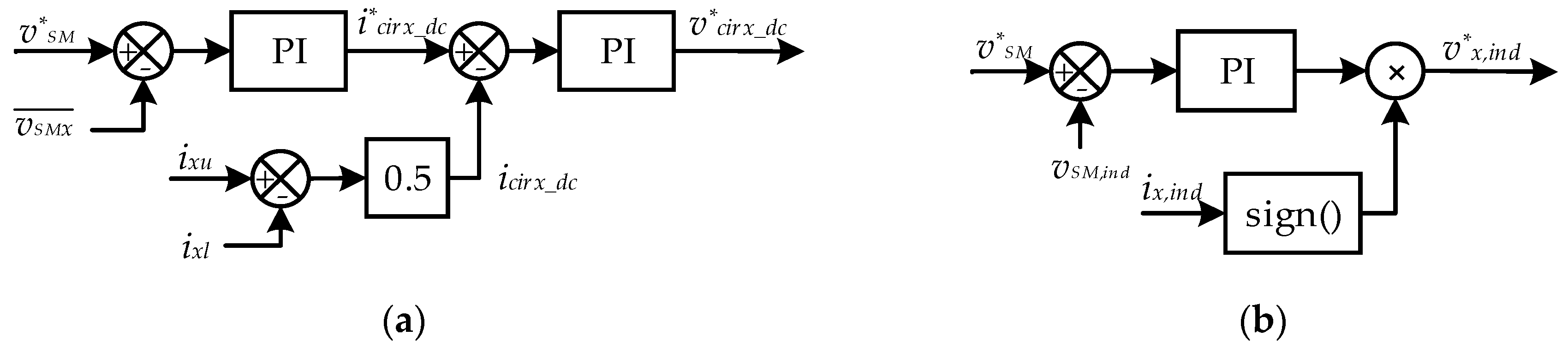
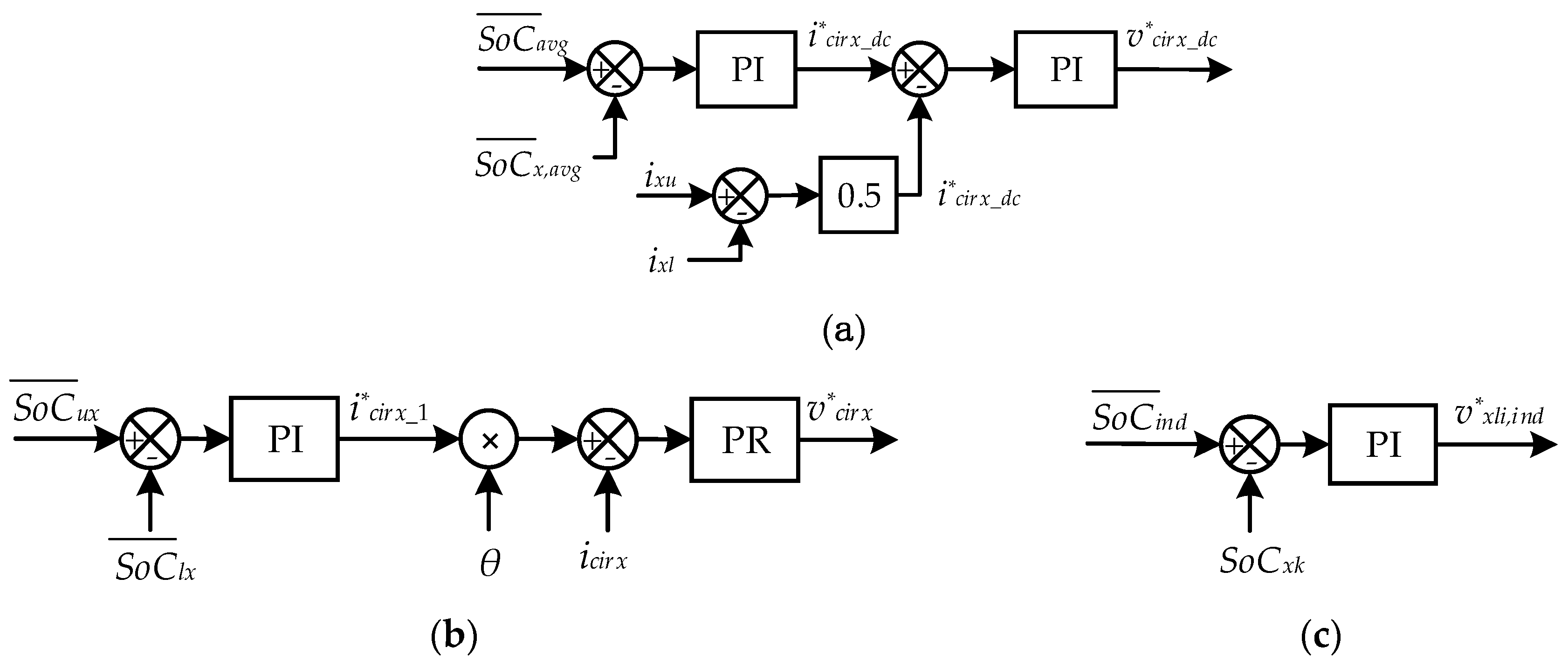
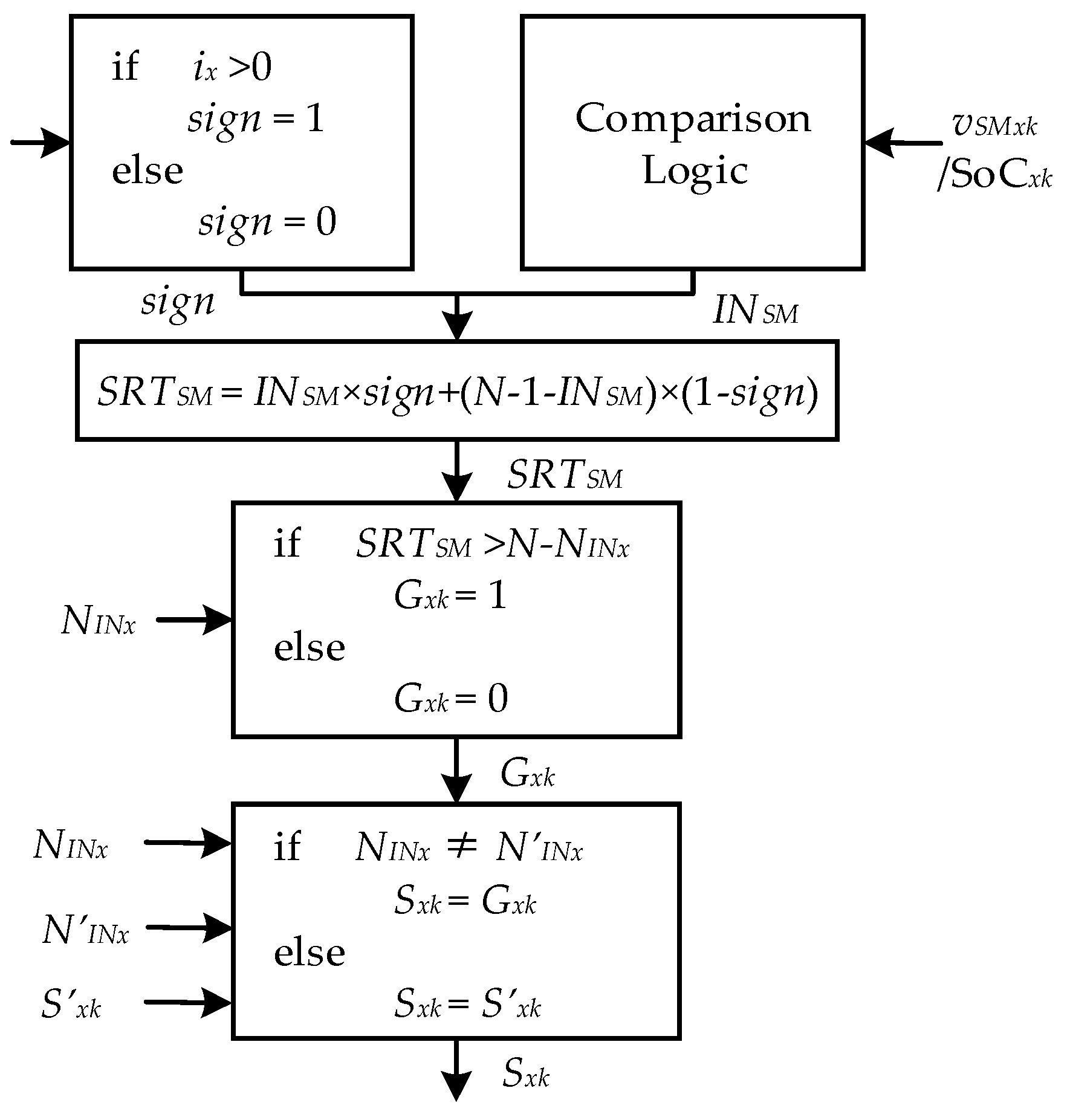
3.3. Submodule Balancing Control
3.4. Circulating Current Control
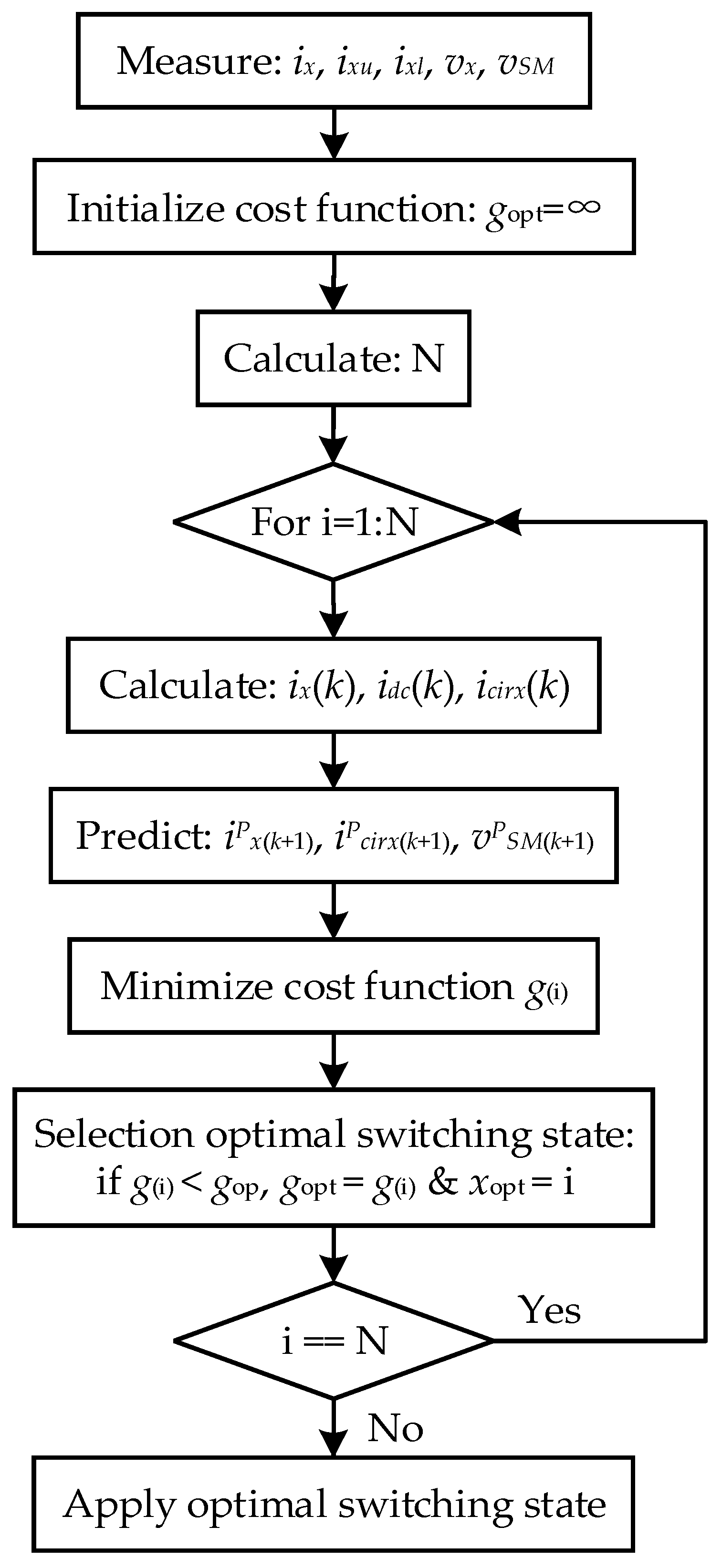
3.5. Nonlinear and Predictive Control
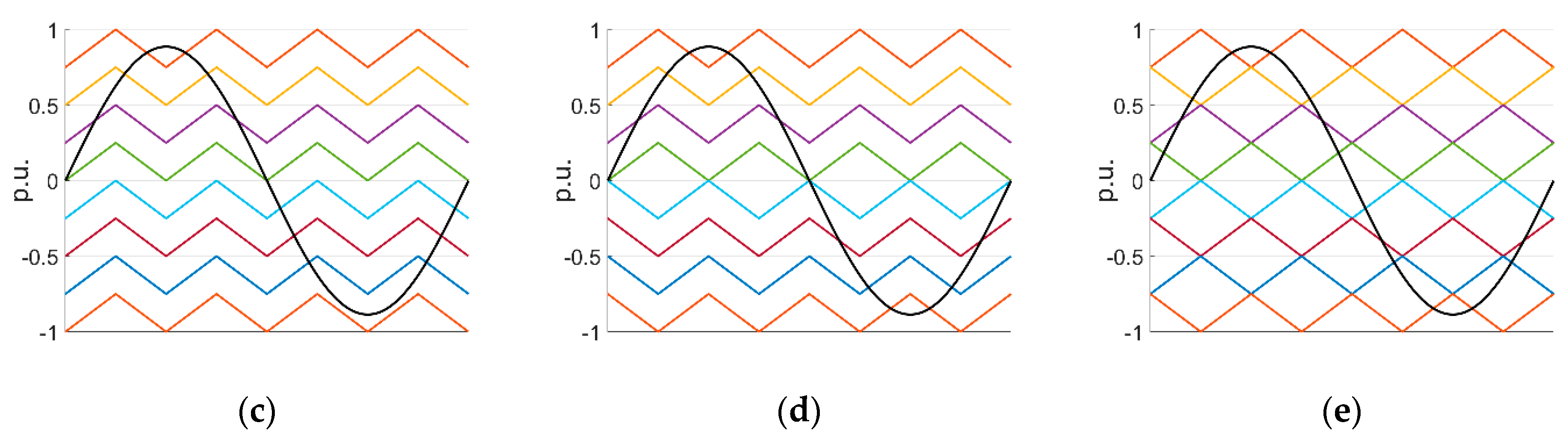
4. MMC Modulation Techniques
5. Power Losses and WBG Technology
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; Volume 3, pp. 272–277. [Google Scholar]
- Friedrich, K. Modern HVDC PLUS application of VSC in Modular Multilevel Converter topology. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 3807–3810. [Google Scholar]
- Du, S.; Dekka, A.; Wu, B.; Zargari, N. Modular Multilevel Converters: Analysis, Control, and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; ISBN 9781119367291. [Google Scholar]
- Martinez-Rodrigo, F.; Ramirez, D.; Rey-Boue, A.B.; De Pablo, S.; Herrero-De Lucas, L.C. Modular multilevel converters: Control and applications. Energies 2017, 10, 1709. [Google Scholar] [CrossRef] [Green Version]
- Raju, M.N.; Sreedevi, J.; Mandi, R.P.; Meera, K.S. Modular multilevel converters technology: A comprehensive study on its topologies, modelling, control and applications. IET Power Electron. 2019, 12, 149–169. [Google Scholar] [CrossRef]
- Lyu, D.; Sun, Y.; Teixeira, C.A.; Holmes, D.G.; McGrath, B.P.; Wang, Q. A Novel Modular Multilevel Converter with Coupled-inductor Semi-bridge Submodules. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; Volume 40, pp. 6860–6867. [Google Scholar]
- Alyami, H.; Mohamed, Y. Review and development of MMC employed in VSC-HVDC systems. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–6. [Google Scholar]
- Li, Y.; Guo, J.; Zhang, X.; Wang, S.; Ma, S.; Zhao, B.; Wu, G.; Wang, T. Over-Voltage Suppression Methods for the MMC-VSC-HVDC Wind Farm Integration System. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 355–359. [Google Scholar] [CrossRef]
- Chakraborty, S.; Vu, H.-N.; Hasan, M.M.; Tran, D.-D.; El Baghdadi, M.; Hegazy, O. DC-DC Converter Topologies for Electric Vehicles, Plug-in Hybrid Electric Vehicles and Fast Charging Stations: State of the Art and Future Trends. Energies 2019, 12, 1569. [Google Scholar] [CrossRef] [Green Version]
- Du, S.; Wu, B.; Zargari, N.R.; Cheng, Z. A Flying-Capacitor Modular Multilevel Converter for Medium-Voltage Motor Drive. IEEE Trans. Power Electron. 2017, 32, 2081–2089. [Google Scholar] [CrossRef]
- Du, S.; Wu, B.; Tian, K.; Zargari, N.; Cheng, Z. An Active Cross-Connected Modular Multilevel Converter (AC-MMC) for Medium-voltage Motor Drive. IEEE Trans. Ind. Electron. 2016, 63, 1. [Google Scholar] [CrossRef]
- Chakraborty, S.; Maiti, S. A Novel Modular Multilevel Converter for Medium Voltage Variable Speed Induction Motor Drives. In Proceedings of the 45th Annual Conference of the IEEE Industrial Electronics Society (IECON 2019), Lisbon, Portugal, 14–17 October 2019; pp. 6049–6054. [Google Scholar]
- Verdugo, C.; Candela, J.I.; Blaabjerg, F.; Rodriguez, P. Three-Phase Isolated Multimodular Converter in Renewable Energy Distribution Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 854–865. [Google Scholar] [CrossRef]
- Bayat, H.; Yazdani, A. A Hybrid MMC-Based Photovoltaic and Battery Energy Storage System. IEEE Power Energy Technol. Syst. J. 2019, 6, 32–40. [Google Scholar] [CrossRef]
- Cao, S.; Lin, N.; Dinavahi, V. Faster-Than-Real-Time Dynamic Simulation of AC/DC Grids on Reconfigurable Hardware. IEEE Trans. Power Syst. 2020, 35, 1539–1548. [Google Scholar] [CrossRef]
- Hillers, A.; Biela, J. Fault-tolerant operation of the modular multilevel converter in an energy storage system based on split batteries. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–8. [Google Scholar]
- Sangiri, J.B.; Raiesh, V.; Chattopadhyay, S.K.; Chakraborty, C. Modular Multilevel Converter for Multifunctional Battery Management System of Electric Vehicle. In Proceedings of the 44th Annual Conference of the IEEE Industrial Electronics Society (IECON 2018), Washington, DC, USA, 21–23 October 2018; pp. 1333–1338. [Google Scholar]
- Li, N.; Gao, F. Linearized operation of MMC battery energy storage system. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–5. [Google Scholar]
- Tianqi, L.; Youyin, W.; Zhanjun, L.; Meijun, L.; Weimao, X.; Yunche, S.; Zhijian, C.; Na, Z. Reactive Power Compensation and Control Strategy for MMC-STATCOM Doubly-Fed Wind Farm. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3537–3542. [Google Scholar]
- Zhang, Y.; Chen, X.; Sun, J. Sequence Impedance Modeling and Analysis of MMC in Single-Star Configuration. IEEE Trans. Power Electron. 2020, 35, 334–346. [Google Scholar] [CrossRef]
- Mao, M.; Ding, Y.; Chang, L.; Hatziargyriou, N.D.; Chen, Q.; Tao, T.; Li, Y. Multi-Objective Power Management for EV Fleet With MMC-Based Integration Into Smart Grid. IEEE Trans. Smart Grid 2019, 10, 1428–1439. [Google Scholar] [CrossRef]
- Del Pizzo, A.; Coppola, M.; Spina, I. Current waveforms distribution among electrochemical cells of Modular Multilevel Converters in Battery Electric Vehicles. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018; pp. 1–4. [Google Scholar]
- Ashourloo, M.; Zaman, M.S.; Nasr, M.; Trescases, O. Opportunities for Leveraging Low-Voltage GaN Devices in Modular Multi-level Converters for Electric-Vehicle Charging Applications. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018—ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 2380–2385. [Google Scholar]
- Nademi, H.; Zadeh, M.; Undeland, T. Interfacing an Electric Vehicle to the Grid with Modular Conversion Unit: A Case Study of a Charging Station and its Control Framework. In Proceedings of the 44th Annual Conference of the IEEE Industrial Electronics Society (IECON 2018), Washington, DC, USA, 21–23 October 2018; pp. 5171–5176. [Google Scholar]
- Mahmoud, A.A.; Hafez, A.A.; Yousef, A.M. Modular Multilevel Converters for Renewable Energies Interfacing: Comparative review. In Proceedings of the 2019 IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019; pp. 397–406. [Google Scholar]
- Wang, S.; Ahmed, K.H.; Adam, G.P.; Massoud, A.M.; Williams, B.W. A Novel Converter Station Structure for Improving Multiterminal HVDC System Resiliency Against AC and DC Faults. IEEE Trans. Ind. Electron. 2020, 67, 4270–4280. [Google Scholar] [CrossRef]
- Li, X.; Song, Q.; Liu, W.; Rao, H.; Xu, S.; Li, L. Protection of Nonpermanent Faults on DC Overhead Lines in MMC-Based HVDC Systems. IEEE Trans. Power Deliv. 2013, 28, 483–490. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, P.; Zhao, C. Reliability Analysis and Redundancy Configuration of MMC With Hybrid Submodule Topologies. IEEE Trans. Power Electron. 2016, 31, 2720–2729. [Google Scholar] [CrossRef]
- Wei, J. Review of Current Control Strategies in Modular Multilevel Converter. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2016. [Google Scholar]
- Kumar, Y.S.; Poddar, G. Balanced Submodule Operation of Modular Multilevel Converter-Based Induction Motor Drive for Wide-Speed Range. IEEE Trans. Power Electron. 2020, 35, 3918–3927. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Z.; Zhang, Z.; Xiao, H. A Novel Circulating Current Controller for MMC Capacitor Voltage Fluctuation Suppression. IEEE Access 2019, 7, 120141–120151. [Google Scholar] [CrossRef]
- Li, B.; Xu, Z.; Shi, S.; Xu, D.; Wang, W. Comparative Study of the Active and Passive Circulating Current Suppression Methods for Modular Multilevel Converters. IEEE Trans. Power Electron. 2018, 33, 1878–1883. [Google Scholar] [CrossRef]
- Perez, M.A.; Rodriguez, J.; Fuentes, E.J.; Kammerer, F. Predictive Control of AC–AC Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2012, 59, 2832–2839. [Google Scholar] [CrossRef]
- Marquez, A.; Leon, J.I.; Vazquez, S.; Franquelo, L.G.; Perez, M. A comprehensive comparison of modulation methods for MMC converters. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society (IECON 2017), Beijing, China, 29 October–1 November 2017; pp. 4459–4464. [Google Scholar]
- Shenai, K. Future Prospects of Widebandgap (WBG) Semiconductor Power Switching Devices. IEEE Trans. Electron Devices 2015, 62, 248–257. [Google Scholar] [CrossRef]
- Bhesaniya, M.M.; Shukla, A. Norton Equivalent Modeling of Current Source MMC and Its Use for Dynamic Studies of Back-to-Back Converter System. IEEE Trans. Power Deliv. 2017, 32, 1935–1945. [Google Scholar] [CrossRef]
- Adam, G.P.; Davidson, I.E. Robust and Generic Control of Full-Bridge Modular Multilevel Converter High-Voltage DC Transmission Systems. IEEE Trans. Power Deliv. 2015, 30, 2468–2476. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Song, Q.; Xu, S.; Rao, H.; Liu, W. An MMC Topology Based on Unidirectional Current H-Bridge Submodule With Active Circulating Current Injection. IEEE Trans. Power Electron. 2018, 33, 3870–3883. [Google Scholar] [CrossRef]
- Yang, W.; Song, Q.; Zhao, B. Energy Storage Requirement and Low Capacitance Operation of Unidirectional Current H-Bridge Modular Multilevel Converters. IEEE Trans. Power Electron. 2019, 34, 11748–11759. [Google Scholar] [CrossRef]
- Gao, C.; Lv, J. A New Parallel-Connected Diode-Clamped Modular Multilevel Converter With Voltage Self-Balancing. IEEE Trans. Power Deliv. 2017, 32, 1616–1625. [Google Scholar] [CrossRef]
- Shu, H.; Lei, S.; Tian, X. A New Topology of Modular Multilevel Converter With Voltage Self-Balancing Ability. IEEE Access 2019, 7, 184786–184796. [Google Scholar] [CrossRef]
- Xiang, W.; Lin, W.; An, T.; Wen, J.; Wu, Y. Equivalent Electromagnetic Transient Simulation Model and Fast Recovery Control of Overhead VSC-HVDC Based on SB-MMC. IEEE Trans. Power Deliv. 2017, 32, 778–788. [Google Scholar] [CrossRef]
- Solas, E.; Abad, G.; Barrena, J.A.; Aurtenetxea, S.; Carcar, A.; Zajac, L. Modular Multilevel Converter With Different Submodule Concepts—Part I: Capacitor Voltage Balancing Method. IEEE Trans. Ind. Electron. 2013, 60, 4525–4535. [Google Scholar] [CrossRef]
- Solas, E.; Abad, G.; Barrena, J.A.; Aurtenetxea, S.; Carcar, A.; Zajac, L. Modular Multilevel Converter With Different Submodule Concepts—Part II: Experimental Validation and Comparison for HVDC Application. IEEE Trans. Ind. Electron. 2013, 60, 4536–4545. [Google Scholar] [CrossRef]
- Adam, G.P.; Abdelsalam, I.; Fletcher, J.E.; Burt, G.M.; Holliday, D.; Finney, S.J. New Efficient Submodule for a Modular Multilevel Converter in Multiterminal HVDC Networks. IEEE Trans. Power Electron. 2017, 32, 4258–4278. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Chen, M.; Ran, L. A compact MMC submodule structure with reduced capacitor size using the stacked switched capacitor architecture. IEEE Trans. Power Electron. 2015, 31, 1. [Google Scholar] [CrossRef]
- Marquardt, R. Modular Multilevel Converter Topologies with DC-Short Circuit Current Limitation. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 29 May–2 June 2011; pp. 1425–1431. [Google Scholar]
- Zhang, Y.; Ravishankar, J.; Fletcher, J.; Li, R.; Han, M. Review of Modular Multilevel Converter Based Multi-terminal HVDC Systems for Offshore Wind Power Transmission. Renew. Sustain. Energy Rev. 2016, 61, 572–586. [Google Scholar] [CrossRef]
- Meng, X.; Han, J.; Bieber, L.M.; Wang, L.; Li, W.; Belanger, J. A Universal Blocking-Module-Based Average Value Model of Modular Multilevel Converters With Different Types of Submodules. IEEE Trans. Energy Convers. 2020, 35, 53–66. [Google Scholar] [CrossRef]
- Adam, G.P.; Ahmed, K.H.; Williams, B.W. Mixed Cells Modular Multilevel Converter. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1390–1395. [Google Scholar]
- Ji, M.; Wang, Y.; Tan, K.; Wang, C. A Voltage-balanced Hybrid MMC Topology for DC Fault Ride-through. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2282–2286. [Google Scholar]
- Nami, A.; Wang, L.; Dijkhuizen, F.; Shukla, A. Five Level Cross Connected Cell for Cascaded Converters. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 3–5 September 2013; pp. 1–9. [Google Scholar]
- Elserougi, A.A.; Massoud, A.M.; Ahmed, S. A Switched-Capacitor Submodule for Modular Multilevel HVDC Converters With DC-Fault Blocking Capability and a Reduced Number of Sensors. IEEE Trans. Power Deliv. 2016, 31, 313–322. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, C.; Han, Y. Modular Multilevel Converter Composite Submodule Topology and Control. J. Eng. 2019, 2019, 2643–2648. [Google Scholar] [CrossRef]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, Control, and Applications of the Modular Multilevel Converter: A Review. IEEE Trans. Power Electron. 2015, 30, 37–53. [Google Scholar] [CrossRef]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular Multilevel Converters for HVDC Applications: Review on Converter Cells and Functionalities. IEEE Trans. Power Electron. 2015, 30, 18–36. [Google Scholar] [CrossRef]
- Cai, Y.; Wen, M.; Chen, Y.; Shi, Y.; Qin, Y. Low DC Voltage Control Strategy of Bipolar LCC-MMC Hybrid HVDC Transmission System. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 20–23 September 2017; pp. 166–171. [Google Scholar]
- Jung, J.-J.; Cui, S.; Sul, S.-K. A New Topology of Multilevel VSC Converter for Hybrid HVDC Transmission System. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 2620–2628. [Google Scholar]
- Xia, X.; Zhou, Y.; Fu, C.; Zhou, Z.; He, Y. Research on High Voltage DC Transmission System Optimal Control Based on MMC. Int. J. Electr. Power Energy Syst. 2016, 82, 207–212. [Google Scholar] [CrossRef]
- Shi, G.; Chang, Y.; Cai, X.; Zhang, J. Bifurcate Modular Multilevel Converter for Low-modulation-ratio Applications. IET Power Electron. 2016, 9, 145–154. [Google Scholar] [CrossRef]
- Chang, Y.; Cai, X. A New Family of Modular Multilevel Converters. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–25 May 2016; Volume 1, pp. 3483–3488. [Google Scholar]
- Jin, L.; Dong, Z.; Deng, Y.; Zhou, L.; Lu, Y.; Yang, Y. Operation Range Analysis and Capacitor Voltage Regulation of A Dual-AC-Terminal MMC based on Bifurcated-Arm Topology. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6868–6874. [Google Scholar]
- Du, S.; Wu, B.; Zargari, N.R. A Star-Channel Modular Multilevel Converter for Zero/Low-Fundamental-Frequency Operation Without Injecting Common-Mode Voltage. IEEE Trans. Power Electron. 2018, 33, 2857–2865. [Google Scholar] [CrossRef]
- Du, S.; Wu, B.; Zargari, N. Delta-Channel Modular Multilevel Converter for a Variable-Speed Motor Drive Application. IEEE Trans. Ind. Electron. 2018, 65, 6131–6139. [Google Scholar] [CrossRef]
- Priya, M.; Ponnambalam, P.; Muralikumar, K. Modular-multilevel Converter Topologies and Applications—A Review. IET Power Electron. 2019, 12, 170–183. [Google Scholar] [CrossRef]
- Madichetty, S.; Abhijit, D.; Jinka, S. A Survey and Experimental Verification of Modular Multilevel Converters. Int. J. Power Electron. Drive Syst. 2014, 4, 363–375. [Google Scholar] [CrossRef]
- Kawamura, W.; Hagiwara, M.; Akagi, H. Control and Experiment of a Modular Multilevel Cascade Converter Based on Triple-Star Bridge Cells. IEEE Trans. Ind. Appl. 2014, 50, 3536–3548. [Google Scholar] [CrossRef]
- Karwatzki, D.; Mertens, A. Control Approach for a Class of Modular Multilevel Converter Topologies. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–9. [Google Scholar]
- Kammerer, F.; Kolb, J.; Braun, M. Fully Decoupled Current Control and Energy Balancing of The Modular Multilevel Matrix Converter. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. LS2a.3-1–LS2a.3-8. [Google Scholar]
- Angkititrakul, S.; Erickson, R.W. Control and Implementation of a New Modular Matrix Converter. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition (APEC ’04), Anaheim, CA, USA, 22–26 February 2004; Volume 2, pp. 813–819. [Google Scholar]
- Liu, S.; Wang, X.; Wang, B.; Sun, P.; Zhou, Q.; Cui, Y. Comparison between Back-to-back MMC and M3C as High Power AC/AC Converters. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 671–676. [Google Scholar]
- Baruschka, L.; Mertens, A. A New 3-phase AC/AC Modular Multilevel Converter with Six Branches in Hexagonal Configuration. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, Arizona, 16–21 September 2011; pp. 4005–4012. [Google Scholar]
- Blaszczyk, P. Hex-Y—A New Modular Multilevel Converter Topology for a Direct AC-AC Power Conversion. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE ’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; pp. P.1–P.10. [Google Scholar]
- Blaszczyk, P. Low Frequency Mode Operation for Direct ac-ac Modular Multilevel Converter Systems. A Comparison of M3C and Hex-Y Topology. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 2–5 September 2019; pp. P.1–P.10. [Google Scholar]
- Saeedifard, M.; Iravani, R. Dynamic Performance of a Modular Multilevel Back-to-Back HVDC System. IEEE Trans. Power Deliv. 2010, 25, 2903–2912. [Google Scholar] [CrossRef]
- Debnath, S.; Saeedifard, M. A New Hybrid Modular Multilevel Converter for Grid Connection of Large Wind Turbines. IEEE Trans. Sustain. Energy 2013, 4, 1051–1064. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Zargari, N.R.; Fuentes, R.L. Dynamic Voltage Balancing Algorithm for Modular Multilevel Converter: A Unique Solution. IEEE Trans. Power Electron. 2016, 31, 952–963. [Google Scholar] [CrossRef]
- Belhaouane, M.M.; Ayari, M.; Guillaud, X.; Braiek, N.B. Robust Control Design of MMC-HVDC Systems Using Multivariable Optimal Guaranteed Cost Approach. IEEE Trans. Ind. Appl. 2019, 55, 2952–2963. [Google Scholar] [CrossRef]
- Zhang, H.; Belhaouane, M.M.; Colas, F.; Kadri, R.; Gruson, F.; Guillaud, X. On Comprehensive Description and Analysis of MMC Control Design: Simulation and Experimental Study. IEEE Trans. Power Deliv. 2020, 8977, 1. [Google Scholar] [CrossRef]
- D’Arco, S.; Quraan, M.; Tricoli, P.; Piegari, L. Low frequency operation of Modular Multilevel Converters with embedded battery cells for traction drives. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 1375–1382. [Google Scholar]
- Soong, T.; Lehn, P.W. Evaluation of Emerging Modular Multilevel Converters for BESS Applications. IEEE Trans. Power Deliv. 2014, 29, 2086–2094. [Google Scholar] [CrossRef]
- Xie, J.; Ma, J.; Bai, K. Enhanced Coulomb Counting Method for State-of-Charge Estimation of Lithium-ion Batteries based on Peukert’s Law and Coulombic Efficiency. J. Power Electron. 2018, 18, 910–922. [Google Scholar] [CrossRef]
- Quraan, M.; Yeo, T.; Tricoli, P. Design and Control of Modular Multilevel Converters for Battery Electric Vehicles. IEEE Trans. Power Electron. 2016, 31, 507–517. [Google Scholar] [CrossRef]
- Wang, X.; Tang, G.; He, Z.; Wei, X.; Pang, H.; Xiao, X. Modeling and Control of an Isolated Module Multilevel DC/DC Converter for DC Grid. CSEE J. Power Energy Syst. 2017, 3, 150–159. [Google Scholar] [CrossRef]
- Seul-Ki Kim; Jin-Hong Jeon; Jong-Bo Ahn; Byongjun Lee; Sae-Hyuk Kwon Frequency-Shift Acceleration Control for Anti-Islanding of a Distributed-Generation Inverter. IEEE Trans. Ind. Electron. 2010, 57, 494–504. [CrossRef]
- Awad, H.; Svensson, J.; Bollen, M. Mitigation of Unbalanced Voltage Dips Using Static Series Compensator. IEEE Trans. Power Electron. 2004, 19, 837–846. [Google Scholar] [CrossRef]
- Ramirez, D.; Martinez-Rodrigo, F.; de Pablo, S.; Carlos Herrero-de Lucas, L. Assessment of a Non Linear Current Control Technique Applied to MMC-HVDC during Grid Disturbances. Renew. Energy 2017, 101, 945–963. [Google Scholar] [CrossRef]
- Guerrero-Rodríguez, N.F.; Herrero-de Lucas, L.C.; de Pablo-Gómez, S.; Rey-Boué, A.B. Performance Study of a Synchronization Algorithm for a 3-phase Photovoltaic Grid-connected System under Harmonic Distortions and Unbalances. Electr. Power Syst. Res. 2014, 116, 252–265. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons Ltd: Chichester, UK, 2011; ISBN 9780470667057. [Google Scholar]
- Lai, N.; Kim, K.-H. An Improved Current Control Strategy for a Grid-Connected Inverter under Distorted Grid Conditions. Energies 2016, 9, 190. [Google Scholar] [CrossRef] [Green Version]
- Bojoi, R.; Griva, G.; Guerriero, M.; Farina, F.; Profumo, F.; Bostan, V. Improved current control strategy for power conditioners using sinusoidal signal integrators in synchronous reference frame. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4623–4629. [Google Scholar]
- Guerrero-Rodríguez, N.F.; Rey-Boué, A.B. Modelling, simulation and experimental verification for renewable agents connected to a distorted utility grid using a Real-Time Digital Simulation Platform. Energy Convers. Manag. 2014, 84, 108–121. [Google Scholar] [CrossRef]
- Deng, F.; Lu, Y.; Liu, C.; Heng, Q.; Yu, Q.; Zhao, J. Overview on Submodule Topologies, Modeling, Modulation, Control Schemes, Fault Diagnosis, and Tolerant Control Strategies of Modular Multilevel Converters. Chin. J. Electr. Eng. 2020, 6, 1–21. [Google Scholar] [CrossRef]
- Hagiwara, M.; Akagi, H. Control and Experiment of Pulsewidth-Modulated Modular Multilevel Converters. IEEE Trans. Power Electron. 2009, 24, 1737–1746. [Google Scholar] [CrossRef]
- Xia, B.; Li, Y.; Li, Z.; Xu, F.; Wang, P. A Distributed Voltage Balancing Method for Modular Multilevel Converter. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017—ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 1944–1948. [Google Scholar]
- Wei, J.; Acharya, A.B.; Norum, L.; Bauer, P. Comparison of Current Control Strategies in Modular Multilevel Converter. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018 -ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 2630–2637. [Google Scholar]
- Li, Y.; Wang, F. Arm Inductance Selection Principle for Modular Multilevel Converters with Circulating Current Suppressing Control. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 1321–1325. [Google Scholar]
- Agelidis, V.G.; Pou, J.; Ceballos, S.; Darus, R.; Konstantinou, G. Controllers for Eliminating the ac Components in the Circulating Current of Modular Multilevel Converters. IET Power Electron. 2016, 9, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Tu, Q.; Xu, Z.; Xu, L. Reduced Switching-Frequency Modulation and Circulating Current Suppression for Modular Multilevel Converters. IEEE Trans. Power Deliv. 2011, 26, 2009–2017. [Google Scholar] [CrossRef]
- Bahrani, B.; Debnath, S.; Saeedifard, M. Circulating Current Suppression of the Modular Multilevel Converter in a Double-Frequency Rotating Reference Frame. IEEE Trans. Power Electron. 2016, 31, 783–792. [Google Scholar] [CrossRef]
- He, L.; Zhang, K.; Xiong, J.; Fan, S. A Repetitive Control Scheme for Harmonic Suppression of Circulating Current in Modular Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 471–481. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, L.; Yao, W.; Lu, Z. Circulating Harmonic Current Elimination of a CPS-PWM-Based Modular Multilevel Converter With a Plug-In Repetitive Controller. IEEE Trans. Power Electron. 2014, 29, 2083–2097. [Google Scholar] [CrossRef]
- Li, S.; Wang, X.; Yao, Z.; Li, T.; Peng, Z. Circulating Current Suppressing Strategy for MMC-HVDC Based on Nonideal Proportional Resonant Controllers Under Unbalanced Grid Conditions. IEEE Trans. Power Electron. 2015, 30, 387–397. [Google Scholar] [CrossRef]
- Ma, Y.; Fan, L. Circulating current and DC current ripple control in MMC under unbalanced grid voltage. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; pp. 1–6. [Google Scholar]
- Geng, S.; Gan, Y.; Li, Y.; Hang, L.; Li, G. Novel Method for Circulating Current Suppression in MMCs Based on Multiple Quasi-PR Controller. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; Volume 18, pp. 3560–3565. [Google Scholar]
- She, X.; Huang, A.; Ni, X.; Burgos, R. AC Circulating Currents Suppression in Modular Multilevel Converter. In Proceedings of the 38th Annual Conference of the IEEE Industrial Electronics Society (IECON 2012), Montreal, QB, Canada, 25–28 October 2012; pp. 191–196. [Google Scholar]
- Picas, R.; Pou, J.; Ceballos, S.; Agelidis, V.G.; Saeedifard, M. Minimization of the Capacitor Voltage Fluctuations of a Modular Multilevel Converter by Circulating Current Control. In Proceedings of the 38th Annual Conference of the IEEE Industrial Electronics Society (IECON 2012), Montreal, QB, Canada, 25–28 October 2012; pp. 4985–4991. [Google Scholar]
- Wang, J.; Han, X.; Ma, H.; Bai, Z. Analysis and Injection Control of Circulating Current for Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2019, 66, 2280–2290. [Google Scholar] [CrossRef]
- Leng, P.; Li, Y.; Zhou, D.; Li, J.; Zhou, S. Decoupling Control of Maglev Train Based on Feedback Linearization. IEEE Access 2019, 7, 130352–130362. [Google Scholar] [CrossRef]
- Yang, Q.; Saeedifard, M. Sliding Mode Control of the Modular Multilevel Converter. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1036–1043. [Google Scholar]
- Liu, X.; Huang, J.; Sun, Y.; Gao, S.; Tong, X. Passive Control for the MMC-HVDC System Based on the Energy Function. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 2232–2237. [Google Scholar]
- Bergna-Diaz, G.; Zonetti, D.; Sanchez, S.; Ortega, R.; Tedeschi, E. PI Passivity-Based Control and Performance Analysis of MMC Multiterminal HVDC Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2453–2466. [Google Scholar] [CrossRef] [Green Version]
- Ke, S.; Zhu, M.; Chen, Y.; Zheng, C.; Hu, C. Passive Sliding Mode Variable Structure Control For MMC-UPFC. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2184–2189. [Google Scholar]
- Ahmadijokani, M.; Mehrasa, M.; Sleiman, M.; Sharifzadeh, M.; Sheikholeslami, A.; Al-Haddad, K. A Back-Stepping Control Method for Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2020, 3, 1. [Google Scholar] [CrossRef]
- Elsheikh, M.G.; Bakeer, A.; Magdy, G.; Shabib, G.; Elbaset, A.A.; Mitani, Y. Voltage Control of Modular Multilevel Converter Employing Finite Control Set-Model Predictive Control. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 1128–1132. [Google Scholar]
- Vatani, M.; Bahrani, B.; Saeedifard, M.; Hovd, M. Indirect Finite Control Set Model Predictive Control of Modular Multilevel Converters. IEEE Trans. Smart Grid 2015, 6, 1520–1529. [Google Scholar] [CrossRef] [Green Version]
- McGrath, B.P.; Holmes, D.G. Multicarrier PWM Strategies for Multilevel Inverters. IEEE Trans. Ind. Electron. 2002, 49, 858–867. [Google Scholar] [CrossRef]
- Konstantinou, G.S.; Ciobotaru, M.; Agelidis, V.G. Analysis of Multi-carrier PWM Methods for Back-to-back HVDC Systems based on Modular Multilevel Converters. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society (IECON 2011), Melbourne, Australia, 7–10 November 2011; pp. 4391–4396. [Google Scholar]
- Deng, F.; Chen, Z. Elimination of DC-Link Current Ripple for Modular Multilevel Converters With Capacitor Voltage-Balancing Pulse-Shifted Carrier PWM. IEEE Trans. Power Electron. 2015, 30, 284–296. [Google Scholar] [CrossRef]
- Konstantinou, G.S.; Agelidis, V.G. Performance Evaluation of Half-Bridge Cascaded Multilevel Converters Operated with Multicarrier Sinusoidal PWM Techniques. In Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009; pp. 3399–3404. [Google Scholar]
- Hassanpoor, A.; Norrga, S.; Nee, H.P.; Angquist, L. Evaluation of different carrier-based PWM methods for modular multilevel converters for HVDC application. In Proceedings of the 38th Annual Conference of the IEEE Industrial Electronics Society (IECON), Montreal, QB, Canada, 25–28 October 2012; pp. 388–393. [Google Scholar]
- Kang, D.-W.; Lee, W.-K.; Hyun, D.-S. Carrier-rotation Strategy for Voltage Balancing in Flying Capacitor Multilevel Inverter. IEE Proc. Electr. Power Appl. 2004, 151, 239. [Google Scholar] [CrossRef]
- Jin, B.-S.; Lee, W.-K.; Kim, T.-J.; Kang, D.-W.; Hyun, D.-S. A Study on the Multi-Carrier PWM Methods for Voltage Balancing of Flying Capacitor in the Flying Capacitor Multi-Level Inverter. In Proceedings of the 31st Annual Conference of the IEEE Industrial Electronics Society (IECON 2005), Raleigh, NC, USA, 6–10 October 2005; p. 6. [Google Scholar]
- Mei, J.; Shen, K.; Xiao, B.; Tolbert, L.M.; Zheng, J. A New Selective Loop Bias Mapping Phase Disposition PWM With Dynamic Voltage Balance Capability for Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2014, 61, 798–807. [Google Scholar] [CrossRef]
- McGrath, B.P.; Teixeira, C.A.; Holmes, D.G. Optimized Phase Disposition (PD) Modulation of a Modular Multilevel Converter. IEEE Trans. Ind. Appl. 2017, 53, 4624–4633. [Google Scholar] [CrossRef]
- Pinheiro, H.; Botteron, F.; Rech, C.; Schuch, L.; Camargo, R.F.; Hey, H.L.; Grundling, H.A.; Pinheiro, J.R. Space Vector Modulation for Voltage-Source Inverters: A Unified Approach. In Proceedings of the IEEE 2002 28th Annual Conference of the Industrial Electronics Society.(IECON 02), Sevilla, Spain, 5–8 November 2002; Volume 1, pp. 23–29. [Google Scholar]
- Dekka, A.; Wu, B.; Zargari, N.R.; Fuentes, R.L. A Space-Vector PWM-Based Voltage-Balancing Approach With Reduced Current Sensors for Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2016, 63, 2734–2745. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Zargari, N.R. A Novel Modulation Scheme and Voltage Balancing Algorithm for Modular Multilevel Converter. IEEE Trans. Ind. Appl. 2016, 52, 432–443. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Kwak, S. Nearest-Level Control Method With Improved Output Quality for Modular Multilevel Converters. IEEE Access 2020, 8, 110237–110250. [Google Scholar] [CrossRef]
- Meshram, P.M.; Borghate, V.B. A Simplified Nearest Level Control (NLC) Voltage Balancing Method for Modular Multilevel Converter (MMC). IEEE Trans. Power Electron. 2015, 30, 450–462. [Google Scholar] [CrossRef]
- Shen, K.; Zhao, D.; Mei, J.; Tolbert, L.M.; Wang, J.; Ban, M.; Ji, Y.; Cai, X. Elimination of Harmonics in a Modular Multilevel Converter Using Particle Swarm Optimization-Based Staircase Modulation Strategy. IEEE Trans. Ind. Electron. 2014, 61, 5311–5322. [Google Scholar] [CrossRef]
- Shenai, K. Wide Bandgap (WBG) Semiconductor Power Converters for DC Microgrid Applications. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 24–27 May 2015; pp. 263–268. [Google Scholar]
- Shenai, K. Power Electronic Module: Enabling the 21st-century energy economy. IEEE Power Electron. Mag. 2014, 1, 27–32. [Google Scholar] [CrossRef]
- Millan, J.; Godignon, P.; Perpina, X.; Perez-Tomas, A.; Rebollo, J. A Survey of Wide Bandgap Power Semiconductor Devices. IEEE Trans. Power Electron. 2014, 29, 2155–2163. [Google Scholar] [CrossRef]
- Jones, E.A.; Wang, F.F.; Costinett, D. Review of Commercial GaN Power Devices and GaN-Based Converter Design Challenges. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 707–719. [Google Scholar] [CrossRef]
- Shenai, K. WBG Power Converters for Hybrid & EV Applications. Auto Tech Rev. 2016, 5, 42–47. [Google Scholar] [CrossRef]
- Bieber, L.; Pfannschmidt, J.; Wang, L.; Nami, A.; Li, W. A Hybrid Three-Level and Modular Multilevel Converter With DC Fault Blocking Capability and Reduced Semiconductor Losses. IEEE Trans. Power Deliv. 2020, 35, 1895–1908. [Google Scholar] [CrossRef]
- Xiang, M.; Hu, J.; He, Z. Loss Reduction Analysis and Control of AC-voltage-boosted FBSM MMC by Injecting Second Harmonic Circulating Current. J. Eng. 2019, 2019, 2328–2331. [Google Scholar] [CrossRef]

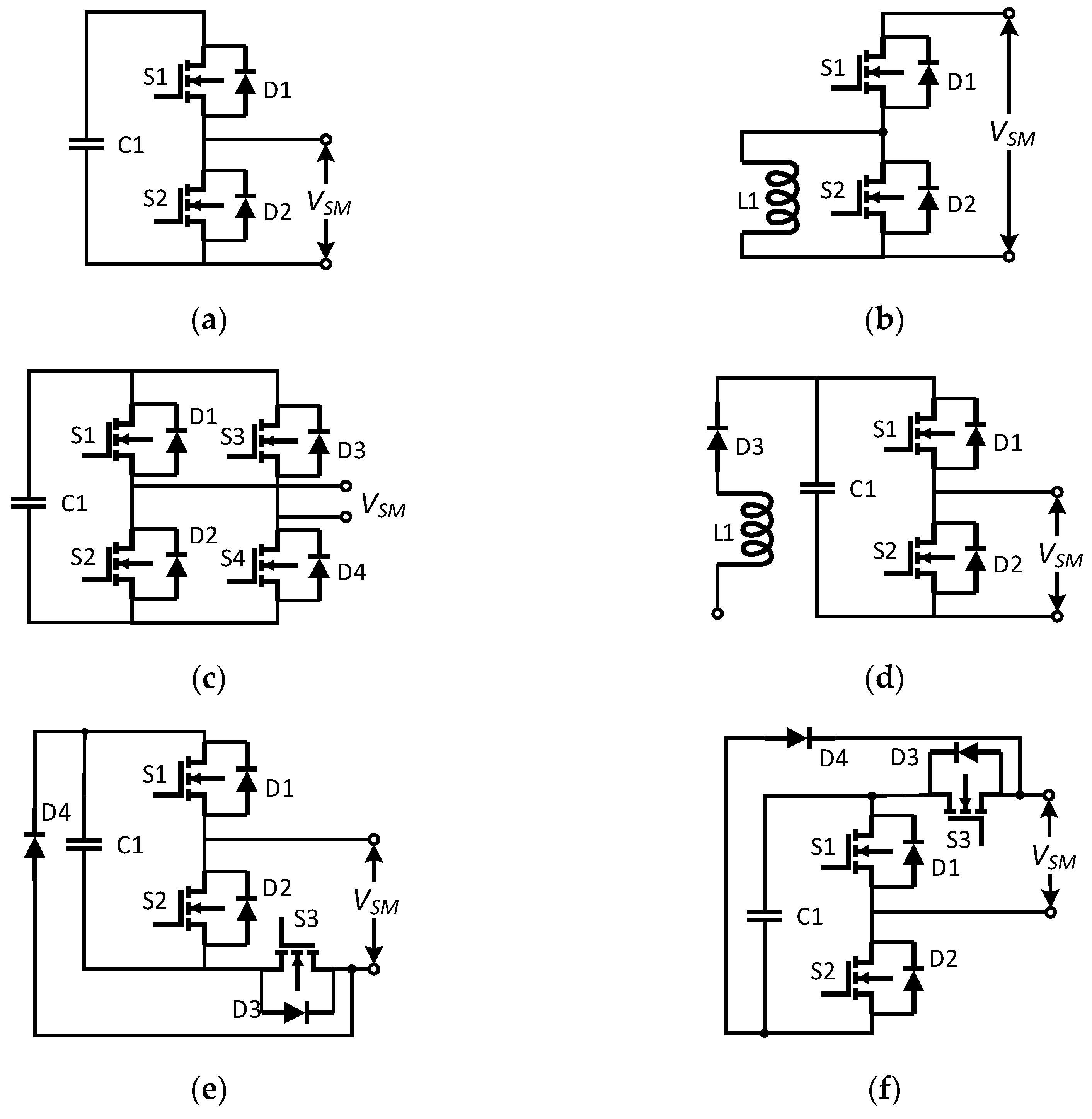
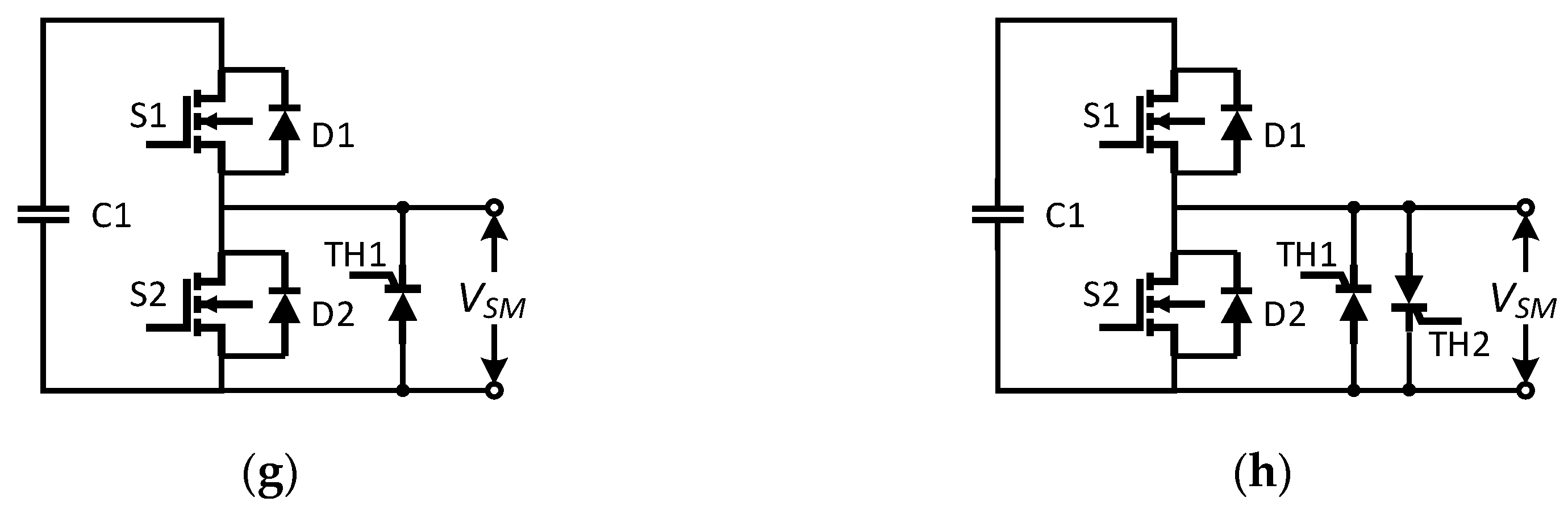
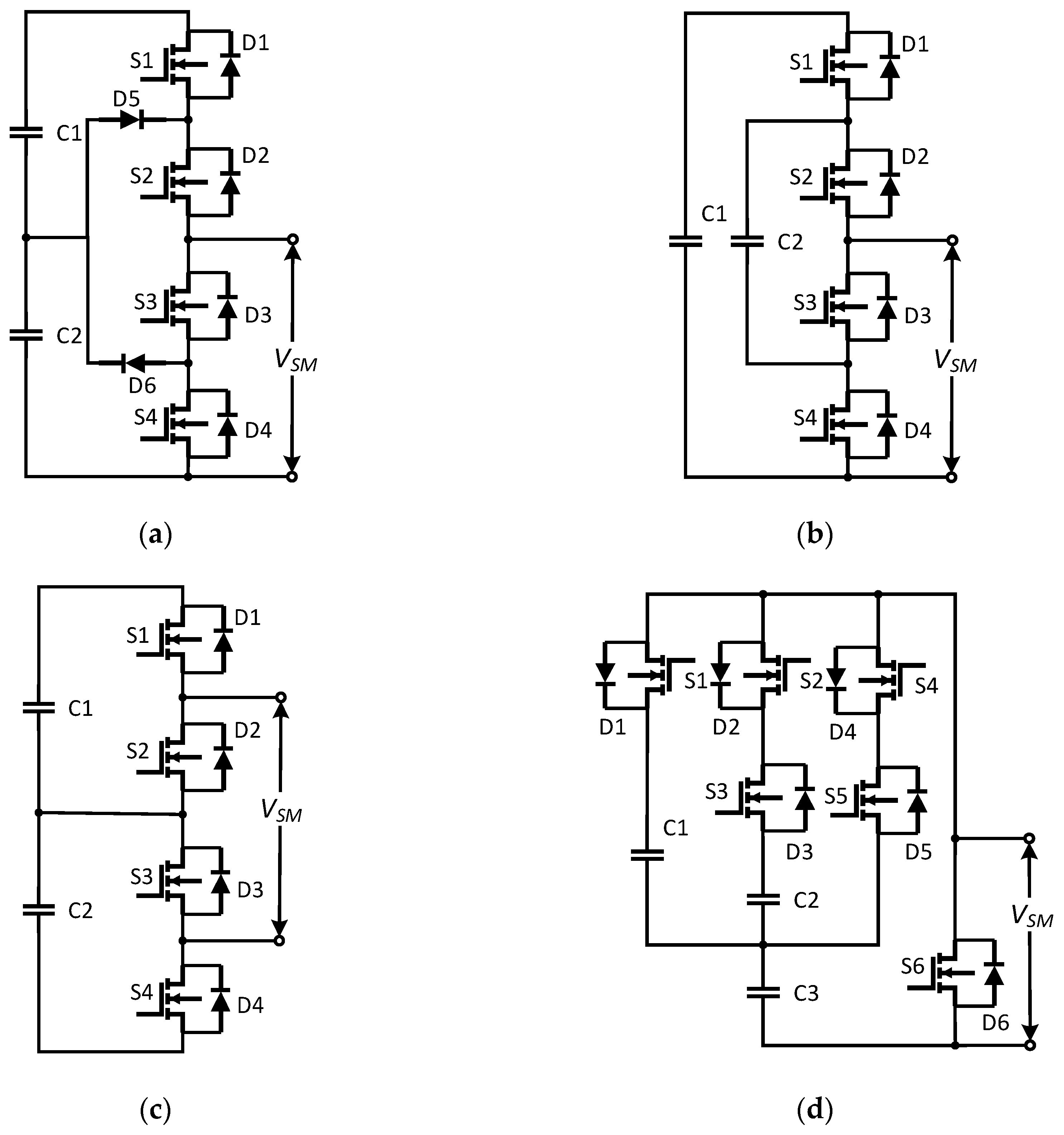

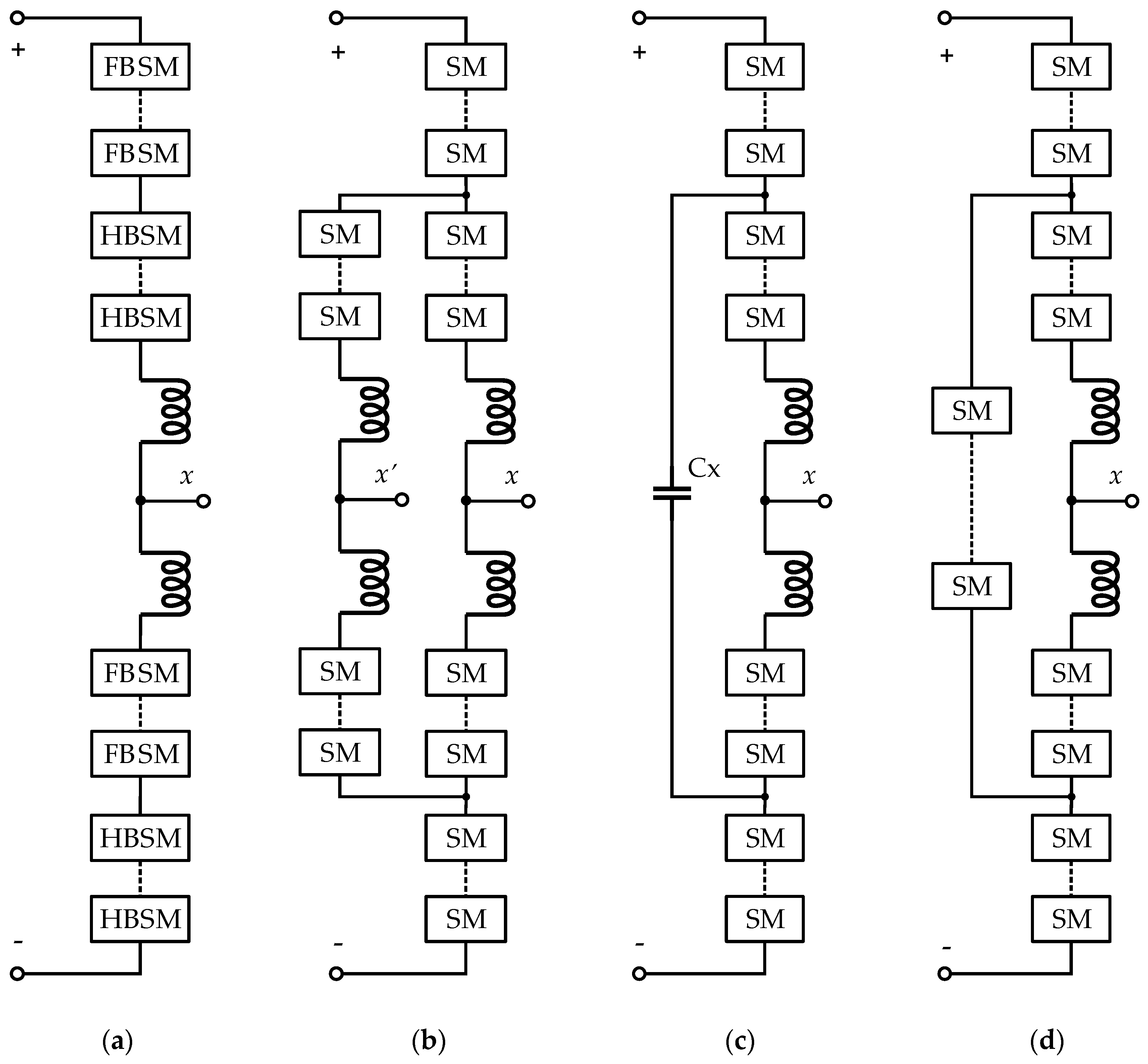

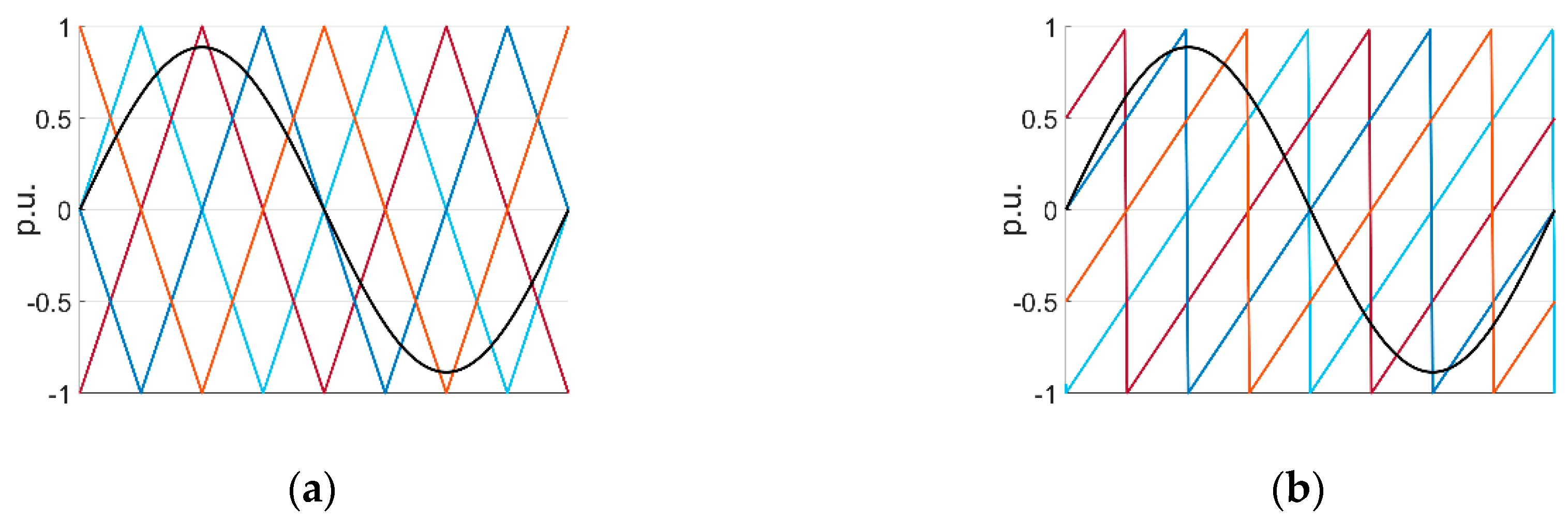
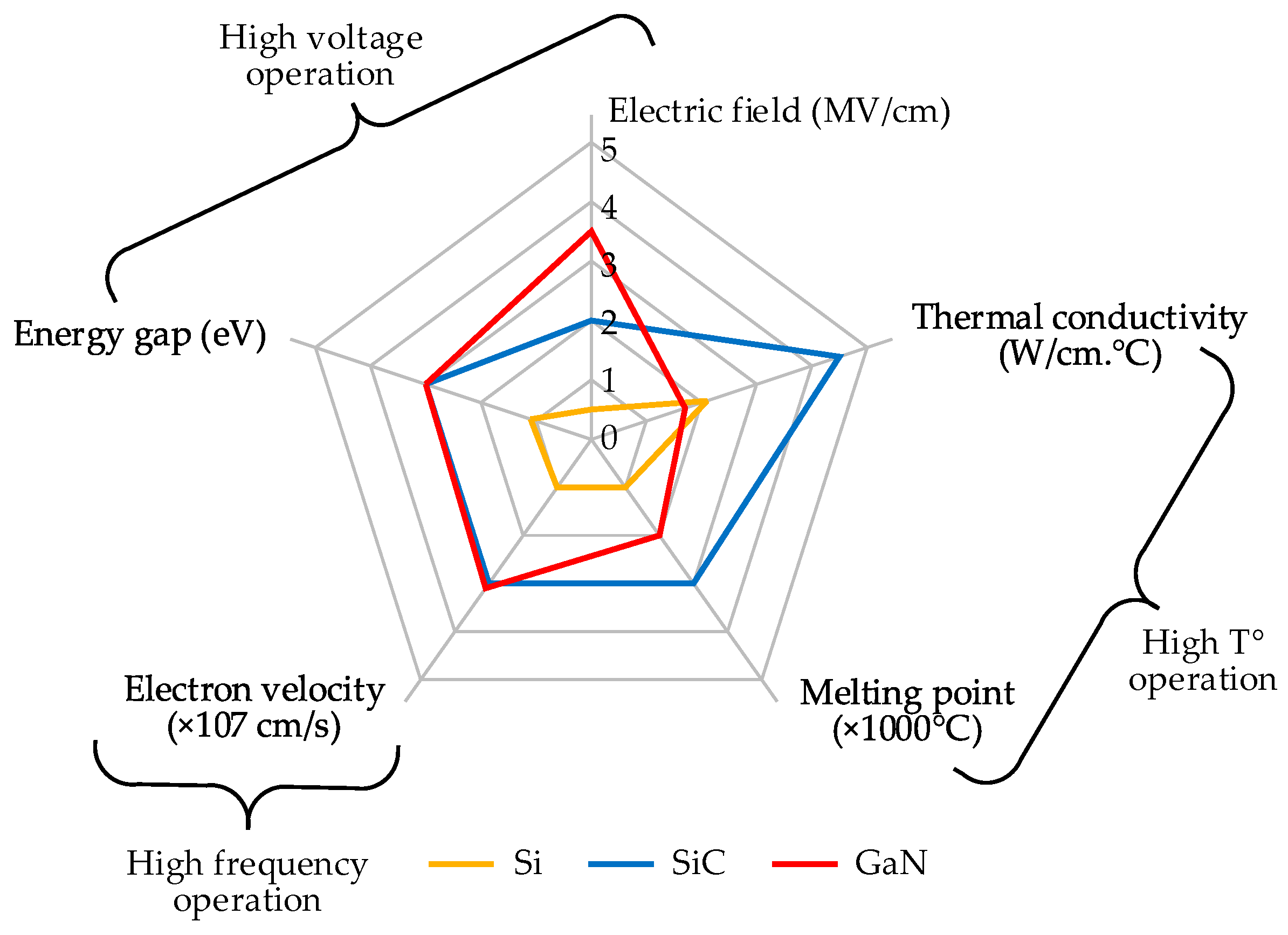
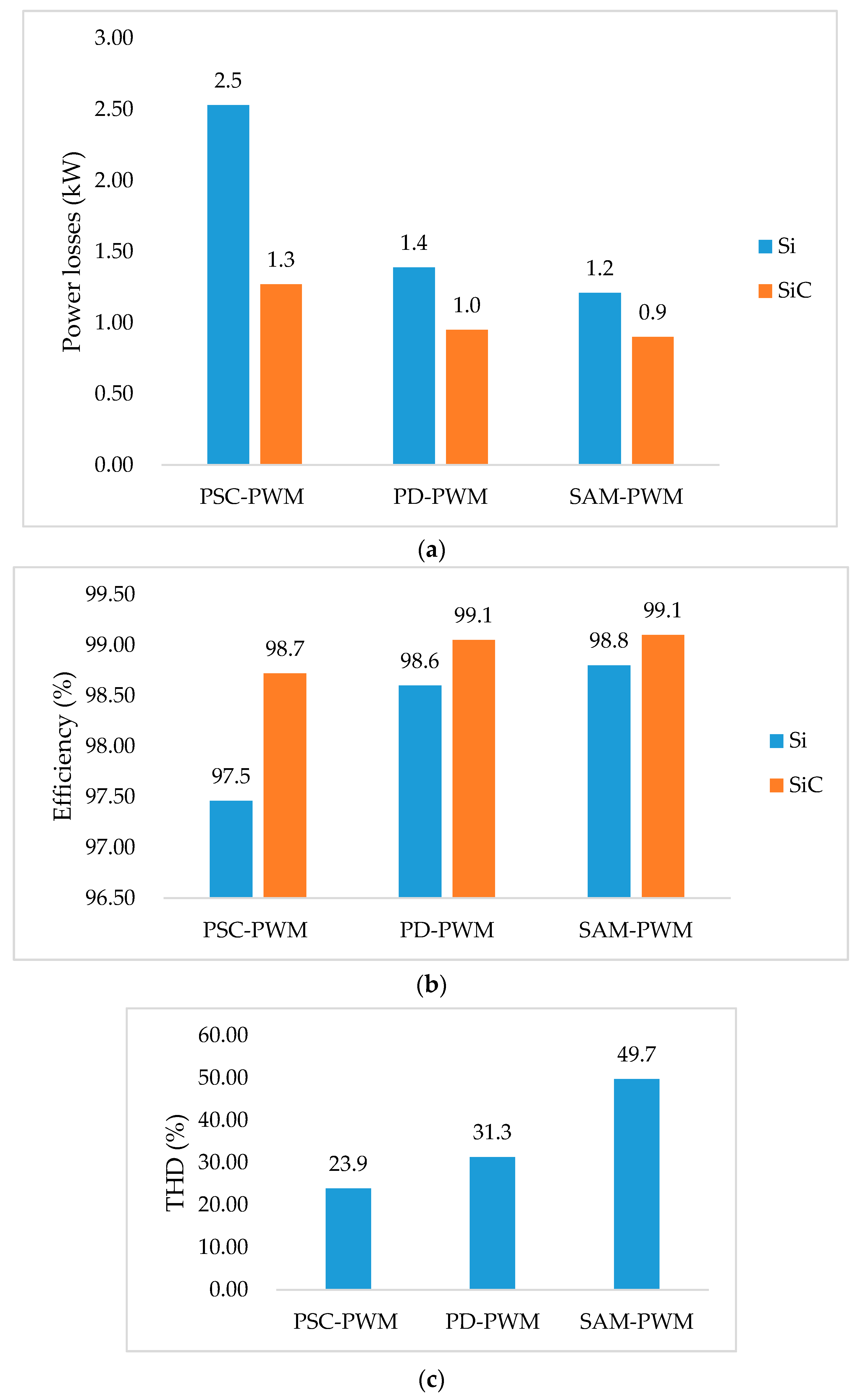
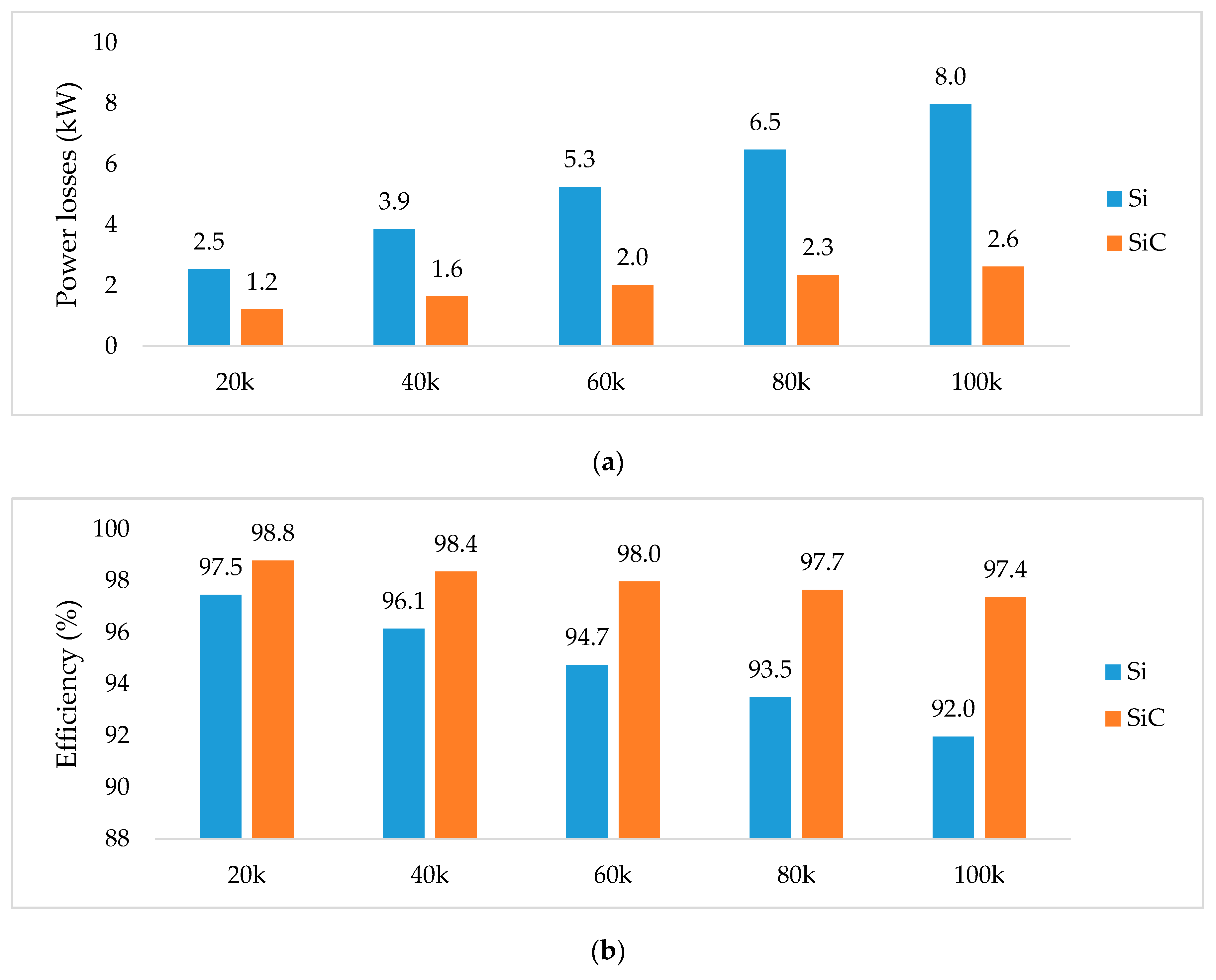
| Performance Index | HBSM | FBSM | SCSM | NPCSM | FCSM | CDSM | HSM | CCSM |
|---|---|---|---|---|---|---|---|---|
| No. of sources | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
| No. of transistors | 2 | 4 | 3 | 4 | 4 | 5 | 6 | 6 |
| No. of diodes | 2 | 4 | 4 | 6 | 4 | 7 | 6 | 6 |
| Max. voltage | 2 | 2 | 2 | 2 | 2 | |||
| Bipolar operation | No | Yes | Yes | No | No | Yes | Yes | Yes |
| DC fault blocking | No | Yes | Yes | No | No | Yes | Yes | Yes |
| Power losses | Low | High | Low | Moderate | Low | Moderate | Moderate | Moderate |
| Cost | Low | Moderate | Moderate | High | High | High | High | High |
| Control complexity | Low | Low | Low | High | High | Low | Low | High |
| PWM | Category | Switching Frequency | SM Count | Performance | Effort |
|---|---|---|---|---|---|
| PSC-PWM | HSF-PWM | 2000 Hz | Small/Large | High | Complex |
| LSC-PWM | HSF-PWM | 2000 Hz | Small/Large | Moderate | Moderate |
| SVM-PWM | LSF-PWM | 100 Hz 2000 Hz | Small | High | Complex |
| SAM-PWM | LSF-PWM | 100 Hz 2000 Hz | Small/Large | Moderate | Easy |
| NLM-PWM | LSF-PWM | 50/60 Hz | Large | Low | Easy |
| SHE-PWM | LSF-PWM | 50/60 Hz | Small | High | Complex |
| Parameters | Values |
|---|---|
| No. of submodules per leg | 5 |
| Nominal SM voltage | 300 V |
| DC-link voltage | 1500 V |
| RMS grid voltage | 380 V |
| Grid frequency | 50 Hz |
| Nominal power level | 100 kW |
| Modulation technique | PSC-PWM, PD-PWM, SAM-PWM |
| Switching frequency rang | 20 kHz; 20–100 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Aksoz, A.; Geury, T.; Ozturk, S.B.; Kivanc, O.C.; Hegazy, O. A Review of Modular Multilevel Converters for Stationary Applications. Appl. Sci. 2020, 10, 7719. https://doi.org/10.3390/app10217719
Wang Y, Aksoz A, Geury T, Ozturk SB, Kivanc OC, Hegazy O. A Review of Modular Multilevel Converters for Stationary Applications. Applied Sciences. 2020; 10(21):7719. https://doi.org/10.3390/app10217719
Chicago/Turabian StyleWang, Yang, Ahmet Aksoz, Thomas Geury, Salih Baris Ozturk, Omer Cihan Kivanc, and Omar Hegazy. 2020. "A Review of Modular Multilevel Converters for Stationary Applications" Applied Sciences 10, no. 21: 7719. https://doi.org/10.3390/app10217719
APA StyleWang, Y., Aksoz, A., Geury, T., Ozturk, S. B., Kivanc, O. C., & Hegazy, O. (2020). A Review of Modular Multilevel Converters for Stationary Applications. Applied Sciences, 10(21), 7719. https://doi.org/10.3390/app10217719









