Additive Manufacture of 3D Auxetic Structures by Laser Powder Bed Fusion—Design Influence on Manufacturing Accuracy and Mechanical Properties
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
3. Results
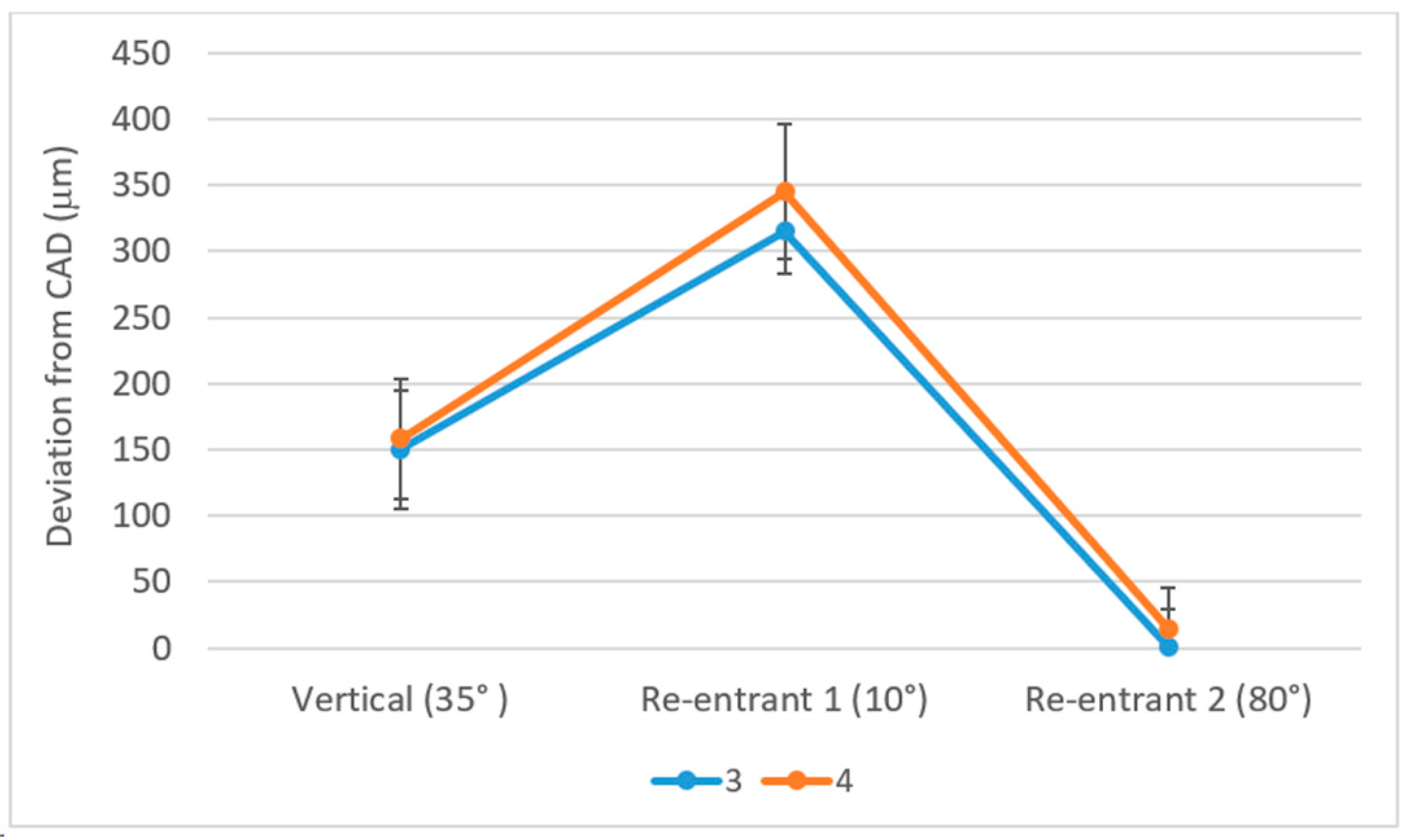
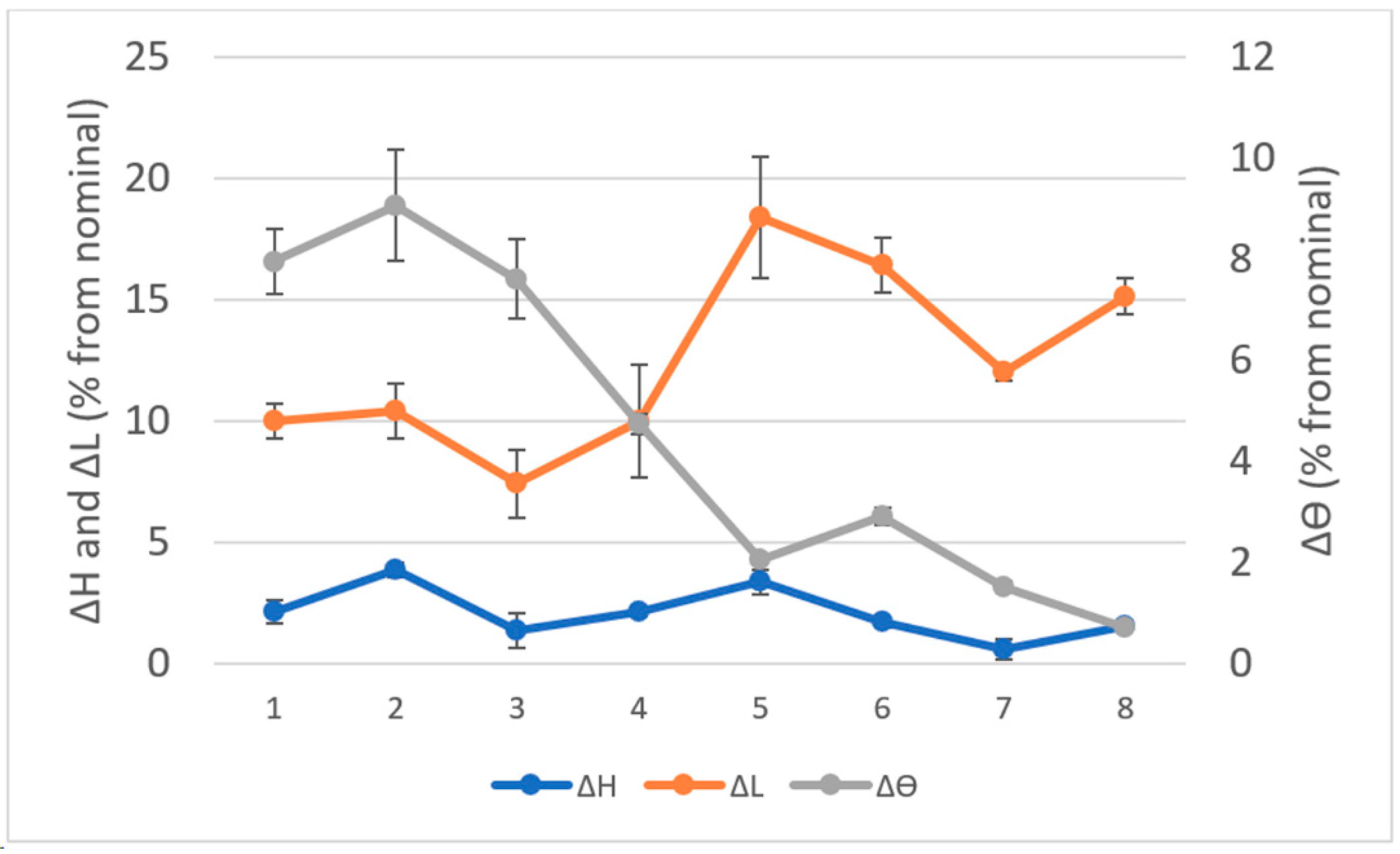
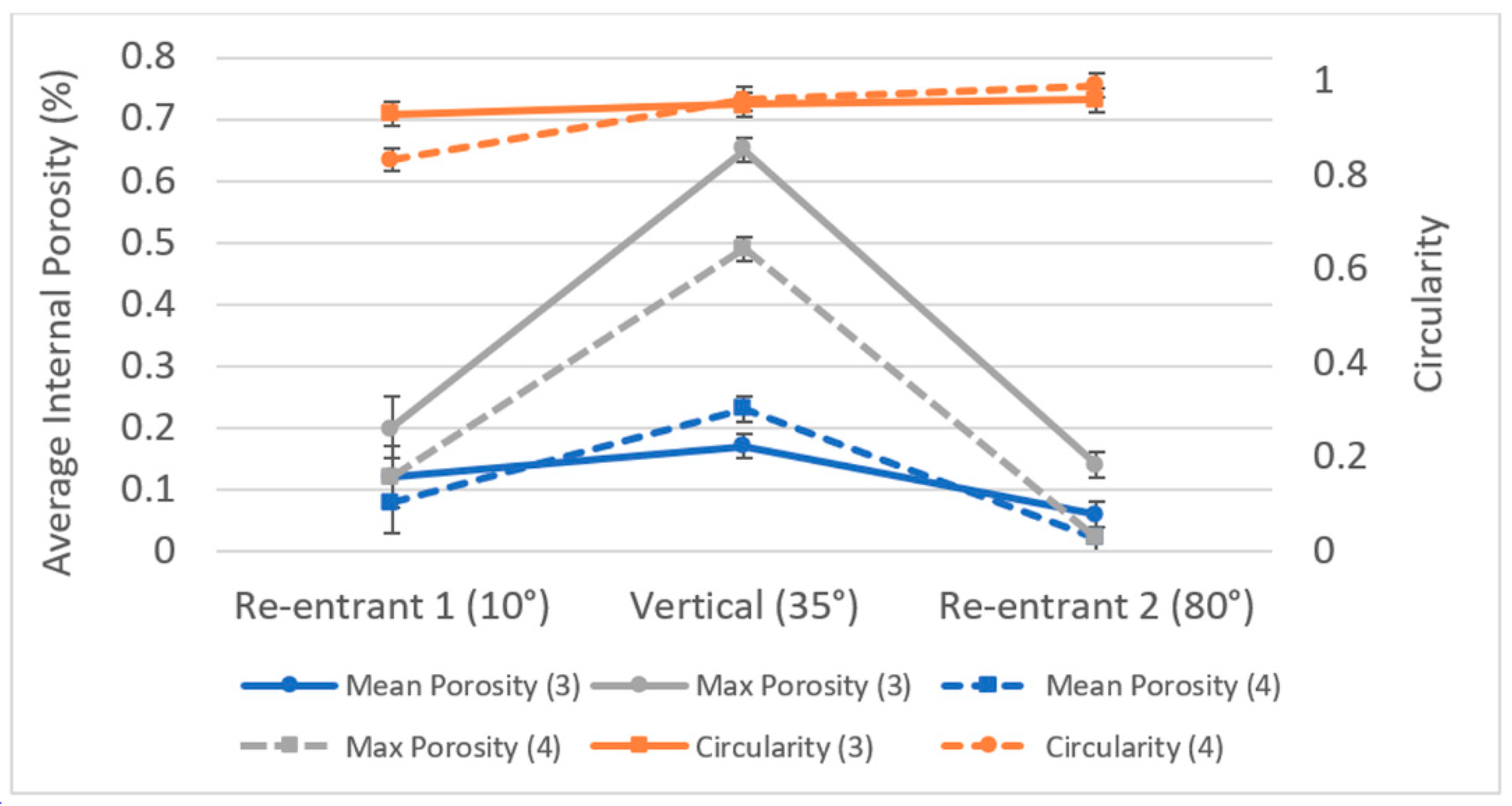
3.1. Density and Dimensional Accuracy
3.2. Compressive Behaviour
3.2.1. Elastic Modulus and Yield Strength
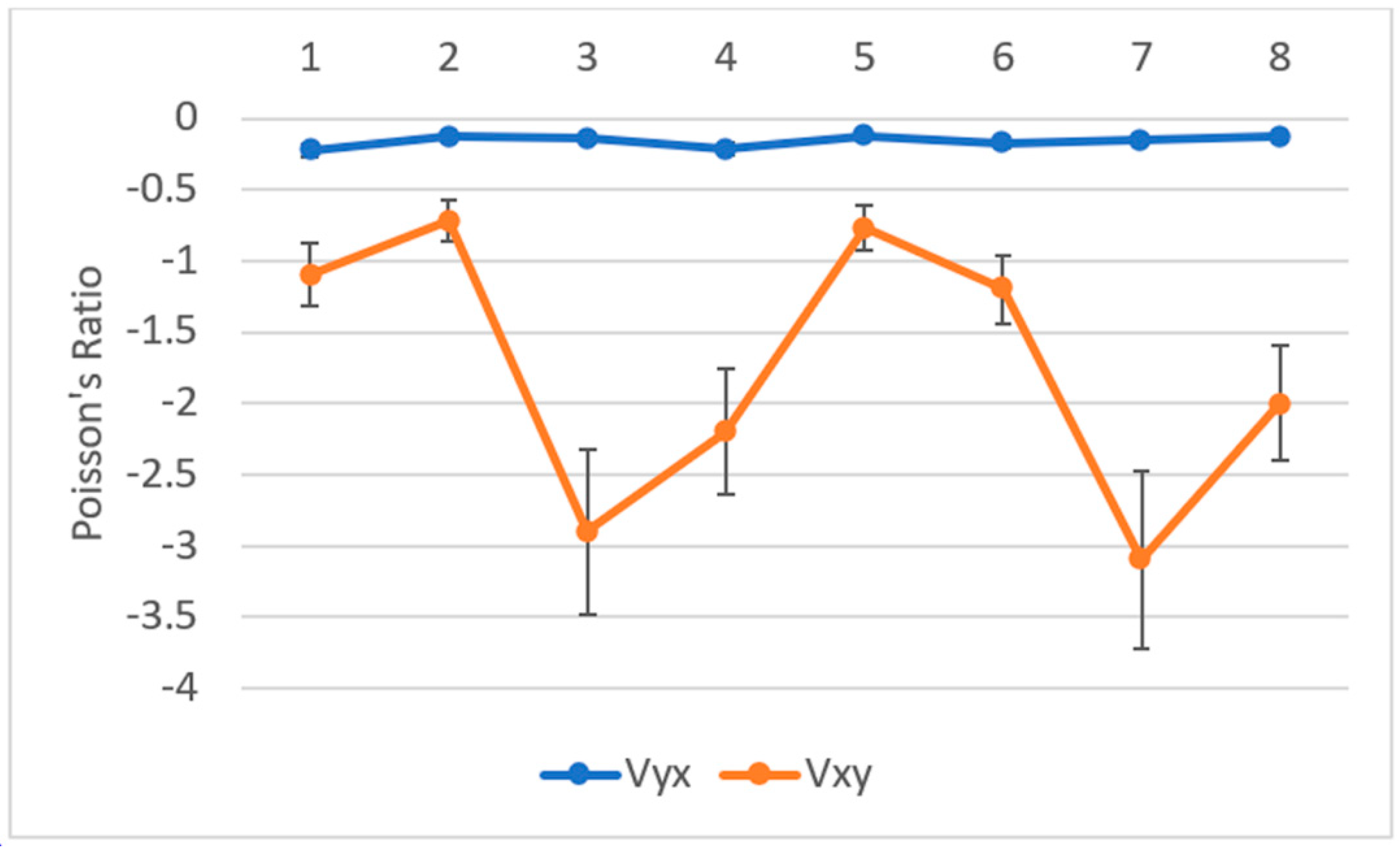
3.2.2. Poisson’s Ratio
3.3. ANOVA Investigation of Parameter Effects of E, σ and ν.
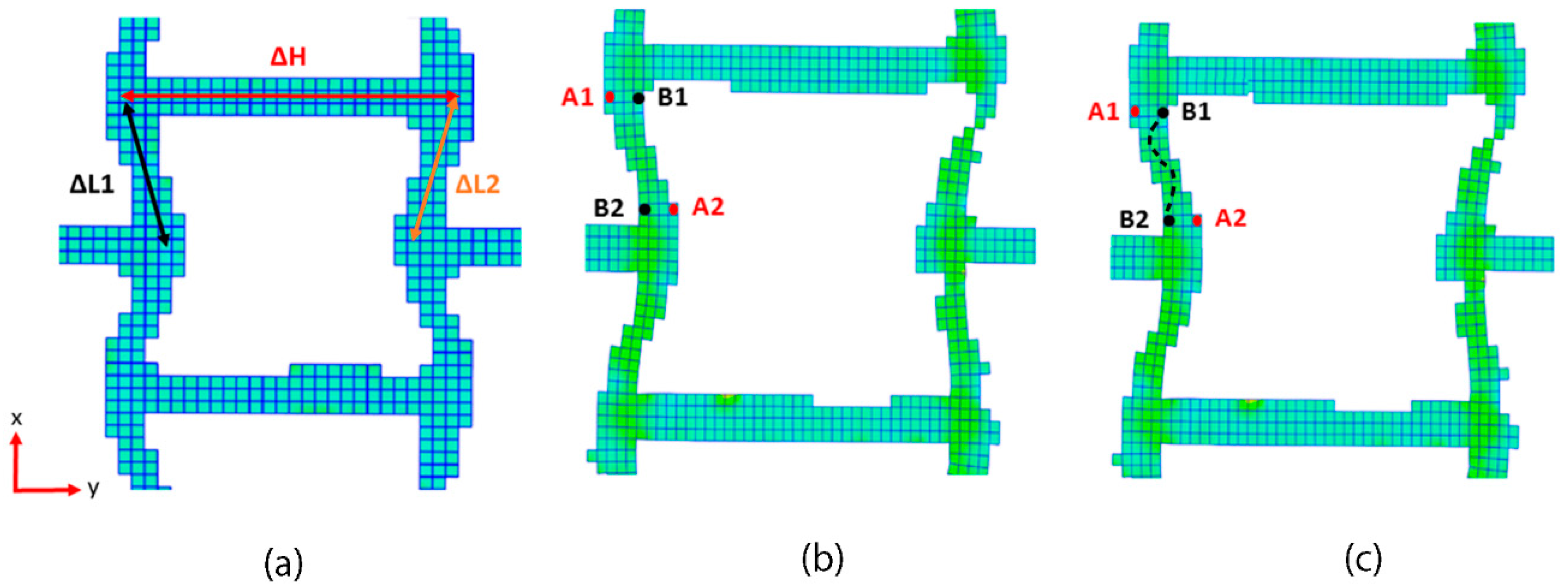
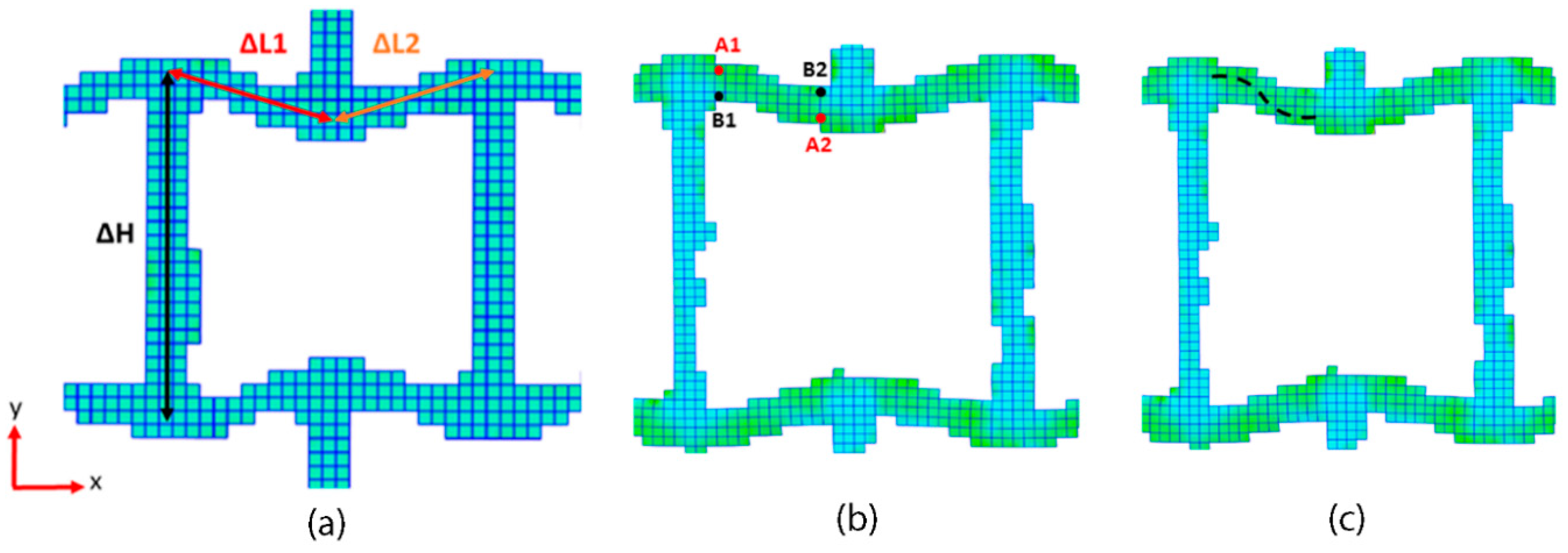
3.4. Deformation Mechanism
3.4.1. Compression in the x Direction
3.4.2. Compression in the y Direction
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Love, A. A Treatise on The Mathematical Theory of Elasticity, 1st ed.; Cambridge University Press: England, UK, 1892. [Google Scholar]
- Evans, K.E.; Nkansah, M.A. Molecular network design. Nature 1991, 353, 124–128. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: England, UK, 1997; pp. 15–50. [Google Scholar]
- Almgren, R. An isotropic three-dimensional structure with Poisson’s ratio =−1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Wojciechowski, K.W. Auxetic, Partially auxetic, and nonauxetic behaviour in 2D crystals of hard cyclic tetramers. Phys. Status Solidi Rapid Res. Lett. 2020, 14. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Alderson, A.; Evans, K. Microstructural modelling of auxetic microporous polymers. J. Mater. Sci. 1995, 30, 3319–3332. [Google Scholar] [CrossRef]
- Larsen, U.D.; Sigmund, O.; Bouwstra, S. Design and fabrication of compliant micromechanisms and structures with negative Poisson’s ratio. J. Microelectromech. Syst. 1997, 6, 365–371. [Google Scholar] [CrossRef]
- Lakes, R. Deformation mechanisms of negative Poisson’s ratio materials: Structural aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Prall, D.; Lakes, R. Properties of a chiral honeycomb with a Poisson’s ratio of -1. J. Mech. Sci. 1997, 39, 305–314. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Ishibashi, I.; Iwata, M. A microscopic model of a negative Poisson’s ratio in some crystals. J. Phys. Soc. Jpn. 2000, 69, 2702–2703. [Google Scholar] [CrossRef]
- Smith, C.; Grima, J. Novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta. Mater. 2000, 48, 4349–4365. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Howell, B.; Prendergast, P. Examination of acoustic behavior of negative Poisson’s ratio materials. Appl. Acoust. 1994, 43, 141–148. [Google Scholar] [CrossRef]
- Scarpa, F.; Burriesci, G. Mechanical and electromagnetic behaviour of auxetic honeycomb structures. Aeronaut. J. 2003, 107, 175–183. [Google Scholar]
- Yang, W.; Zhong, G. Review on auxetic materials. J. Mat. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Anurag, A.C.; Harsha, A.S. Auxetic materials. Int. J. Trends. Eng. Technol. 2015, 15, 427–430. [Google Scholar]
- Zhou, Y.Y.; Zhou, C.F.; Shu, Z.; Jia, L.J. Effect of two-dimensional re-entrant honeycomb configuration on elastoplastic performance of perforated steel plate. Appl. Sci. 2020, 10, 3067. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Schlangen, E.; Luković, M.; Šavija, B. Cementitious cellular composites with auxetic behavior. Cem. Concr. Compos. 2020, 111. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Cauchi, R.; Attard, D.; Gatt, R.; Grima, J.N. Smart honeycomb “mechanical metamaterials” with tunable poisson’s ratios. Phys. Status. Solidi 2020, 257. [Google Scholar] [CrossRef]
- Rawal, A.; Sharma, S.; Singh, D.; Jangir, N.K.; Saraswat, H.; Sebők, b.; Kukovecz, A.; Hietel, D.; Dauner, M.; Onalf, L. Out-of-plane auxetic nonwoven as a designer meta-biomaterial. J. Mech. Behav. Biomed. Mater. 2020, 112. [Google Scholar] [CrossRef]
- Choi, J.-B.; Lakes, R. Analysis of elastic modulus of conventional foams and of re-entrant foam materials with a negative Poisson’s ratio. Int. J. Mech. Sci. 1995, 37, 51–59. [Google Scholar] [CrossRef]
- Du Plessis, A.; Yadroitsava, I. Ti6Al4V lightweight lattice structures manufactured by laser powder bed fusion for load-bearing applications. Opt. Laser. Technol. 2018, 108, 521–528. [Google Scholar] [CrossRef]
- Rehme, O. Cellular Design for Laser Freeform Fabrication, 1st ed.; Cuvillier Verlag: Göttingen, Germany, 2010; pp. 143–182. [Google Scholar]
- Mckown, S.; Shen, W.K. The quasi-static and blast loading response of lattice structures. Int. J. Impact. Eng. 2008, 35, 795–810. [Google Scholar] [CrossRef]
- Hussein, A.Y. The Development of Lightweight Cellular Structures for Metal Additive Manufacting. Ph.D. Thesis, University of Exeter, Exeter, UK, November 2013. [Google Scholar]
- Hasan, R. Progressive collapse of titanium alloy micro-lattice structures manufactured using Selective Laser Melting. Ph.D. Thesis, University of Liverpool, Liverpool, UK, February 2013. [Google Scholar]
- Contuzzi, N.; Campanelli, S. Manufacturing and characterization of 18Ni Marage 300 lattice components by Selective Laser Melting. Materials 2013, 6, 3451–3468. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Hassanin, H. The development of TiNi-based negative Poisson’s ratio structure using selective laser melting. Acta. Mater. 2016, 105, 75–83. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Heinl, P. Auxetic cellular structures through selective electron-beam melting. Phys. Status. Solidi. 2010, 247, 269–272. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, D. Additive manufacturing of metal cellular structures: Designand fabrication. J. Mater. 2015, 67, 608–615. [Google Scholar] [CrossRef]
- Abdelaal, O.; Darwish, S. Analysis, fabrication and a biomedical application of auxetic cellular structures. J. Int. Eng. Innov. Technol. 2012, 2, 218–223. [Google Scholar]
- Yang, L.; Harrysson, D. Compressive properties of Ti–6Al–4V auxetic mesh structures made by electron beam melting. Acta. Mater. 2012, 60, 3370–3379. [Google Scholar] [CrossRef]
- EOS Maraging Steel MS1. Available online: https://www.eos.info/en/additive-manufacturing/3d-printing-metal/dmls-metal-materials/tool-steel (accessed on 26 May 2020).
- Casalino, R.; Campanelli, S.L. Experimental investigation and statistical optimisation of the selective laser melting process of a maraging steel. Opt. Laser. Technol. 2015, 65, 151–158. [Google Scholar] [CrossRef]
- Wauthle, R.; Vrancken, V. Effects of build orientation and heat treatment on the microstructure and mechanical properties of selective laser melted Ti6Al4 V lattice structures. Addit. Manuf. 2014, 5, 77–84. [Google Scholar]
- Kempen, K. Dimensional accuracy of internal channels in SLM produced parts. In Proceedings of the ASPE Spring Topical Meeting: Dimensional Accuracy and Surface Finish in Additive Manufacturing, San Francisco, CA, USA, 14–16 April 2014; pp. 76–79. [Google Scholar]
- Craeghs, T.; Bechmann, S. Feedback control of layerwise laser melting using optical sensors. Phys. Procedia 2010, 5, 505–514. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y. Research on the fabricating quality optimization of the overhanging surface in SLM process. Int. J. Adv. Manuf. Technol. 2012, 65, 1471–1484. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 1st ed.; Pergamon Press: England, UK, 1988; pp. 94–98. [Google Scholar]
- Wang, A.J.; Mcdowell, D.L. In-plane stiffness and yield strength of periodic metal honeycombs. J. Eng. Mater. Technol. 2004, 126, 137–156. [Google Scholar] [CrossRef]
- Fu, M.-H.; Chen, Y.; Hu, L.-L. A novel auxetic honeycomb with enhanced in-plane stiffness and buckling strength. Comp. Struct. 2017, 160, 574–585. [Google Scholar] [CrossRef]
- Yang, L. Structural design, optimization and application of 3D re-entrant auxetic structures. Ph.D. Thesis, NC State University, Raleigh, NC, USA, 24 October 2011. [Google Scholar]
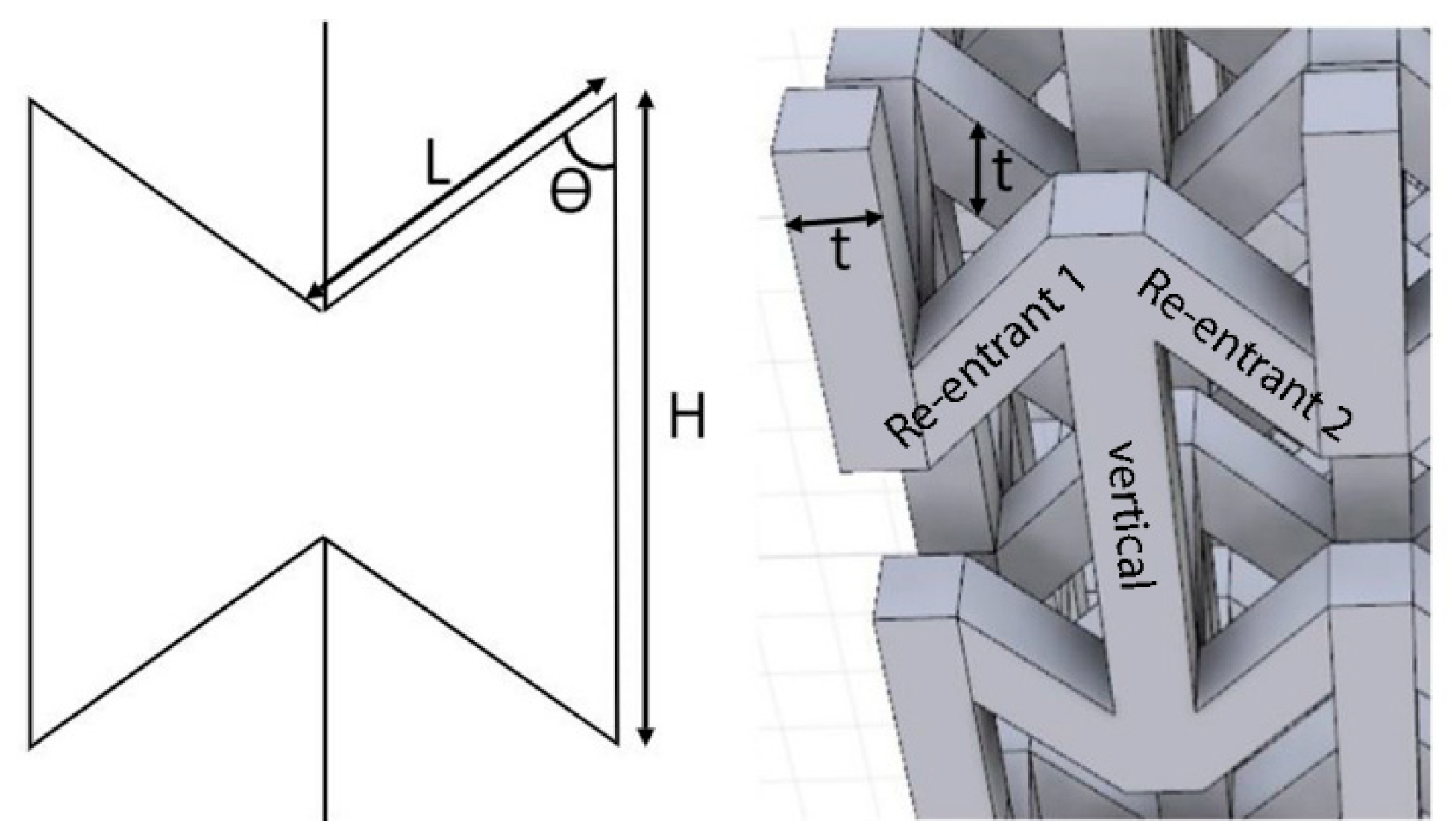

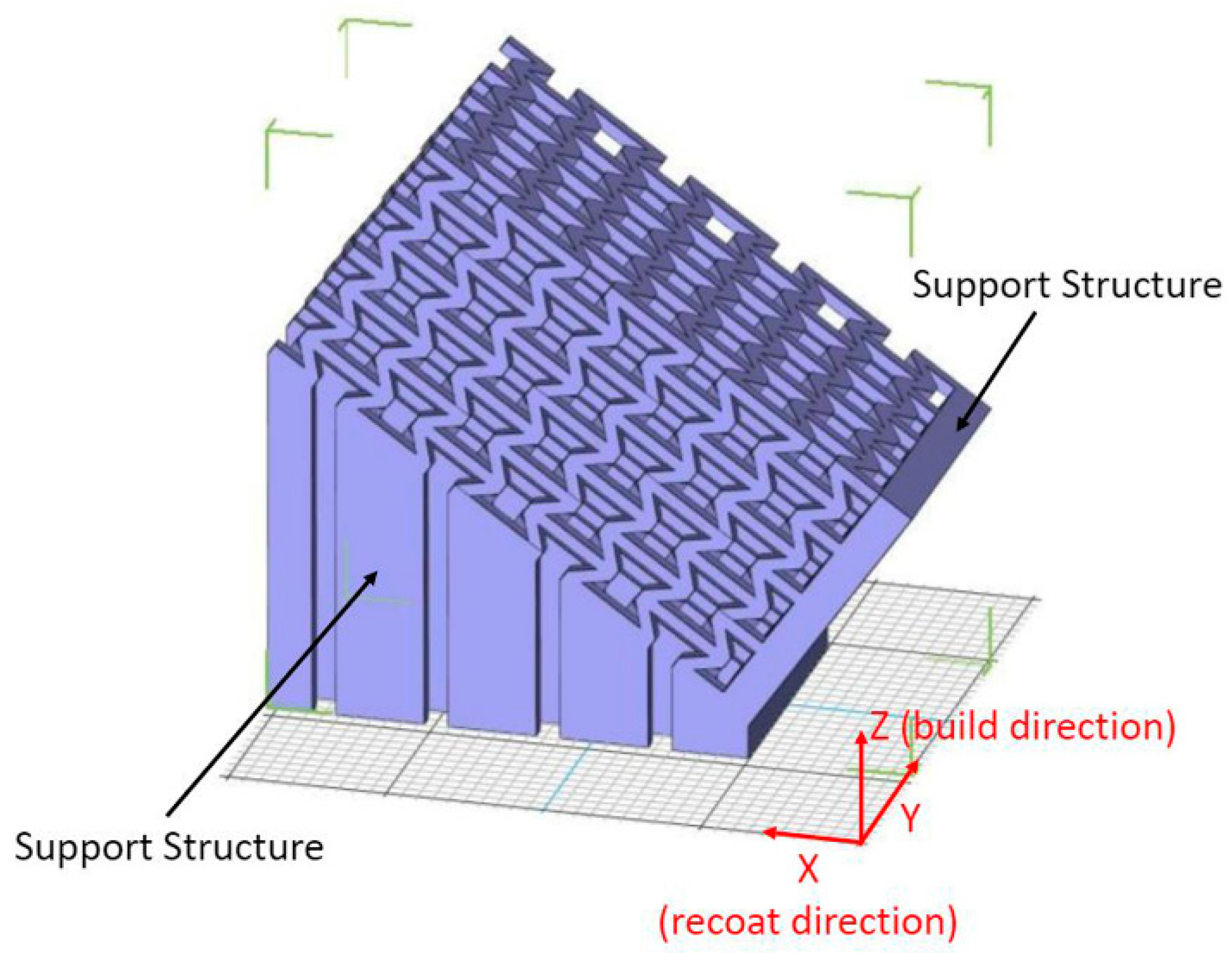


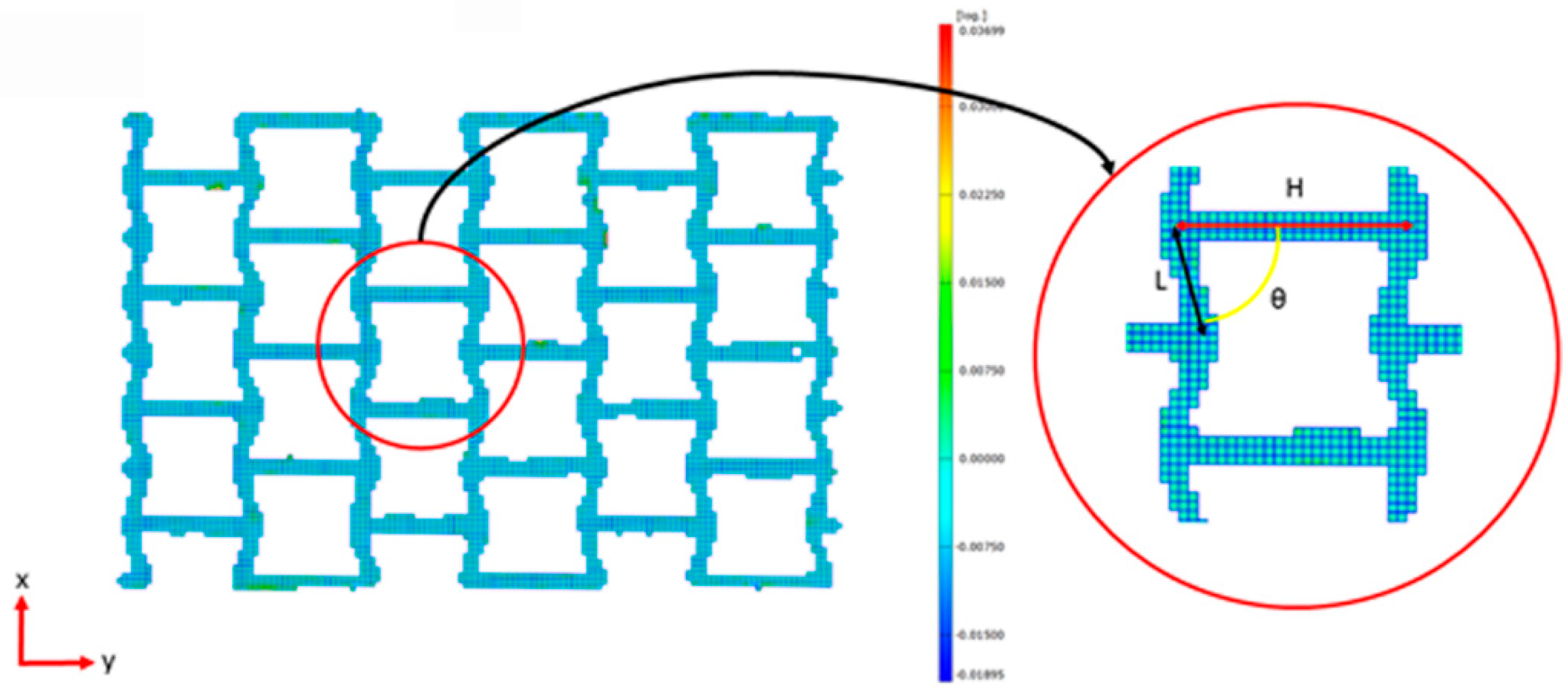

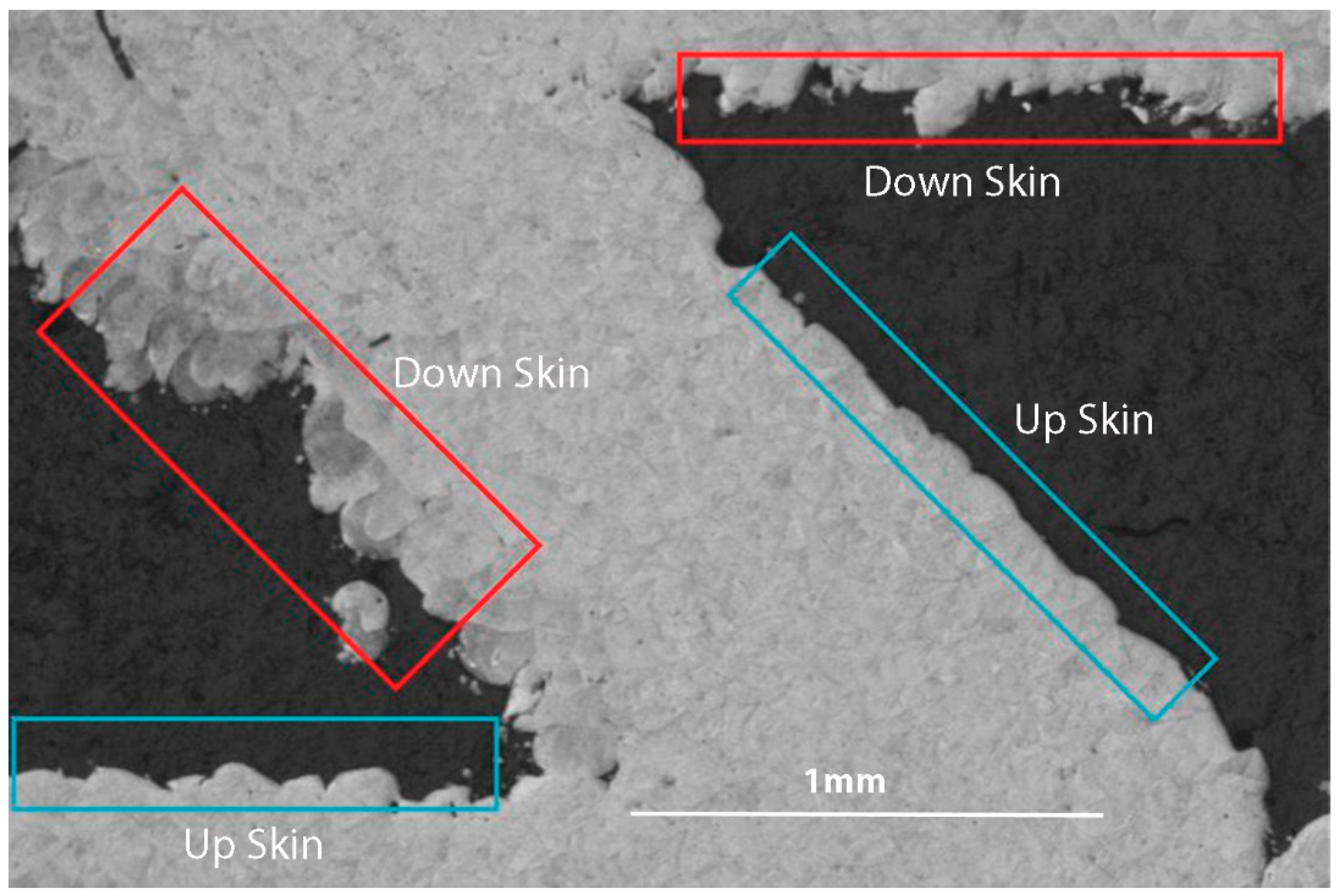
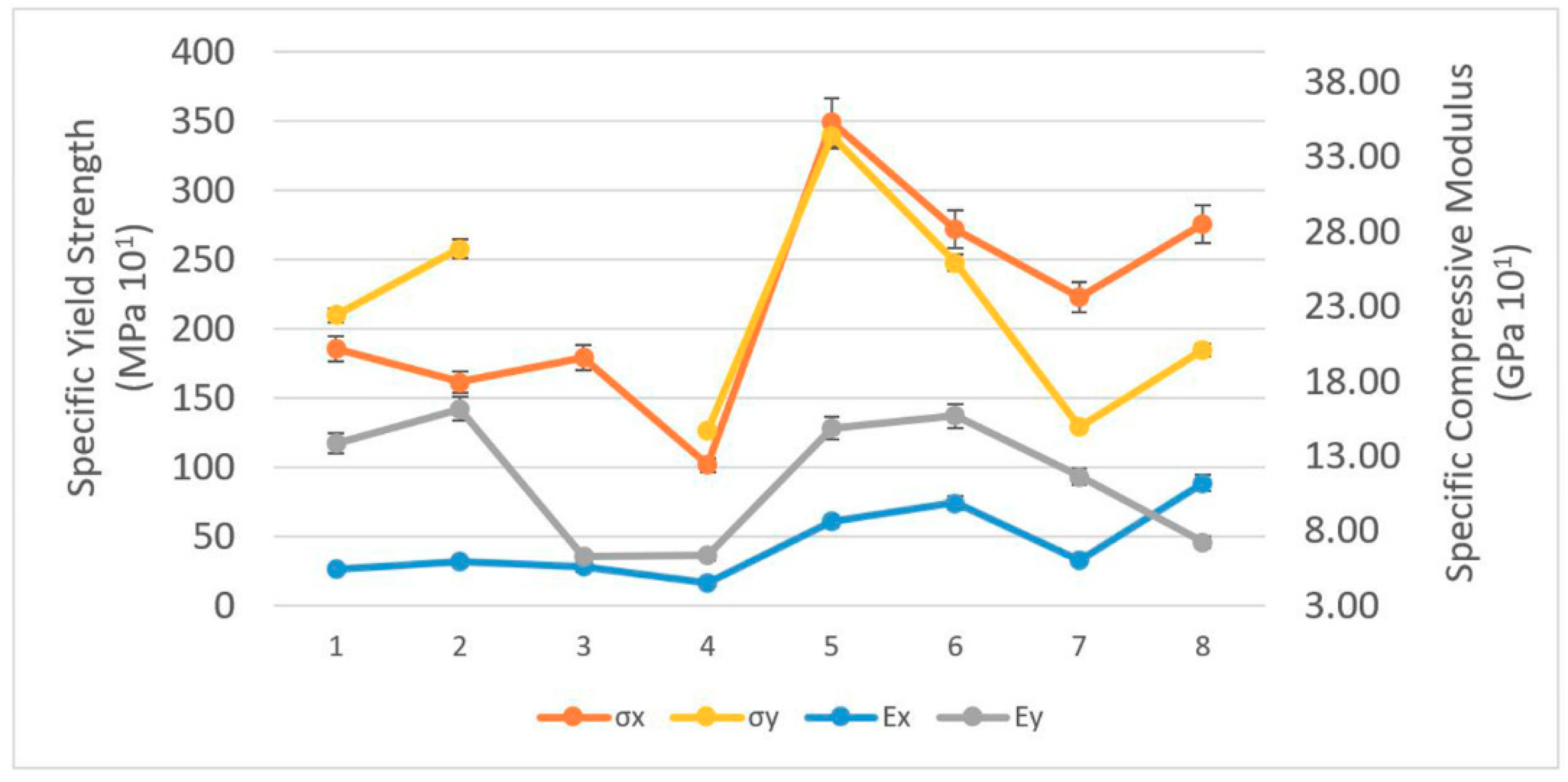

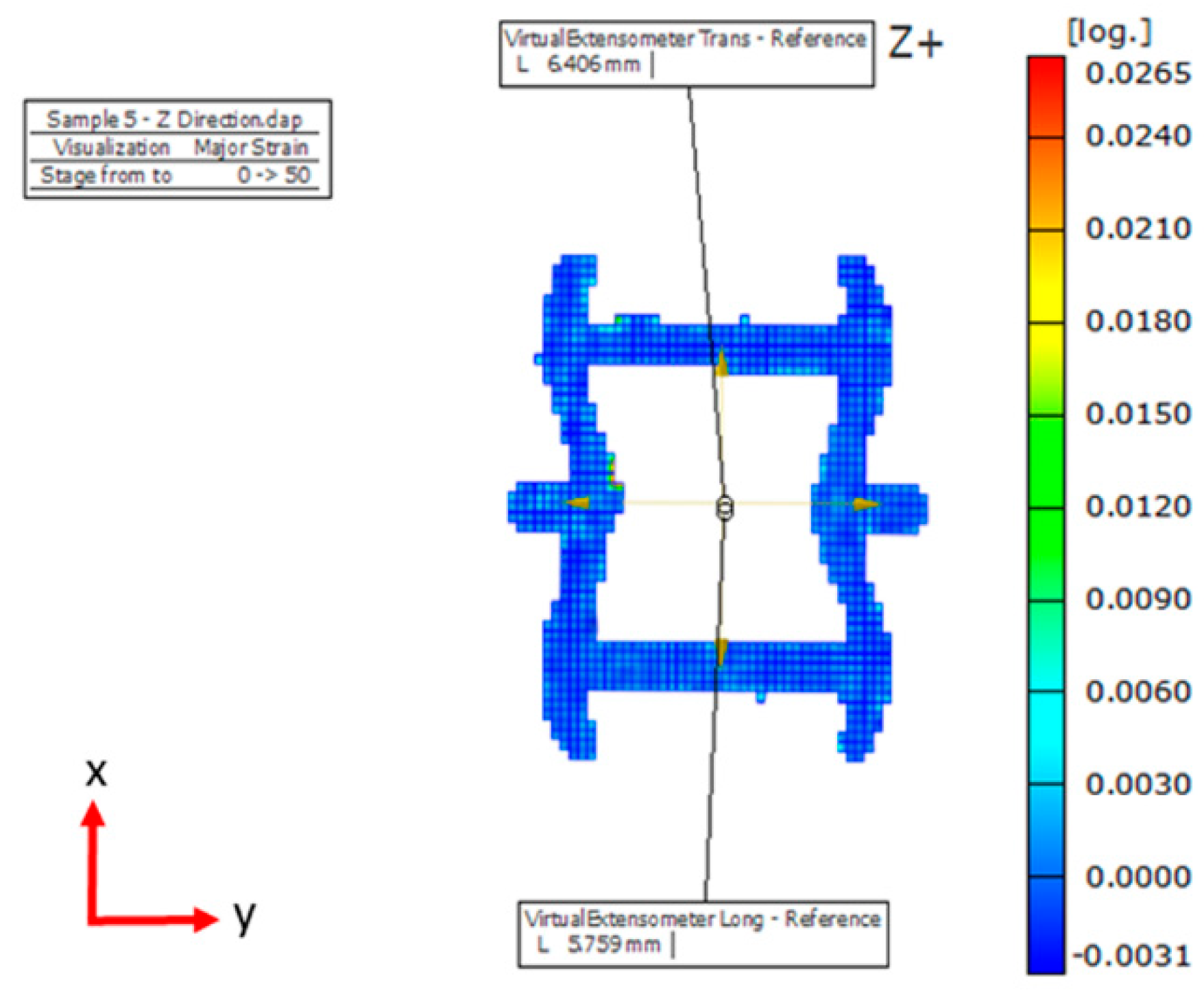
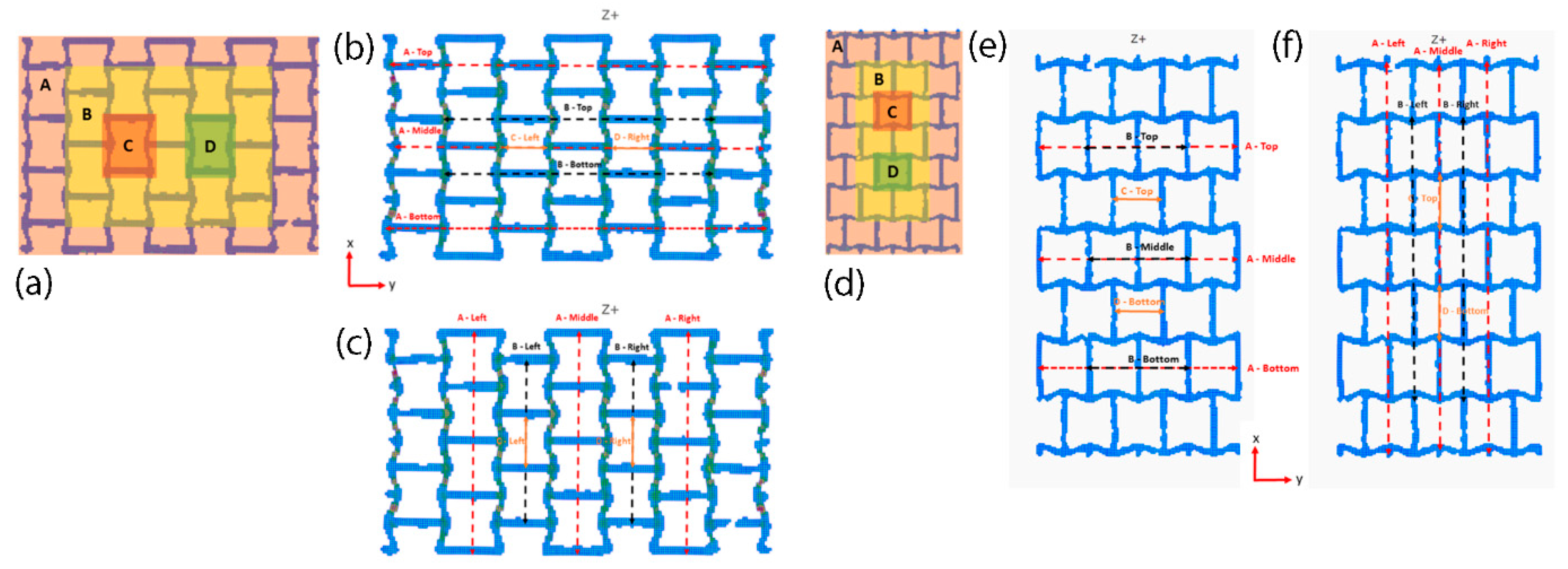
| Sample | H (mm) | L (mm) | Ɵ (⁰) | t (mm) |
|---|---|---|---|---|
| 1 | 6.5 | 2.5 | 45 | 0.8 |
| 2 | 7 | 2.5 | 45 | 1 |
| 3 | 6.5 | 3.5 | 45 | 1 |
| 4 | 7 | 3.5 | 45 | 0.8 |
| 5 | 6.5 | 2.5 | 70 | 1 |
| 6 | 7 | 2.5 | 70 | 0.8 |
| 7 | 6.5 | 3.5 | 70 | 0.8 |
| 8 | 7 | 3.5 | 70 | 1 |
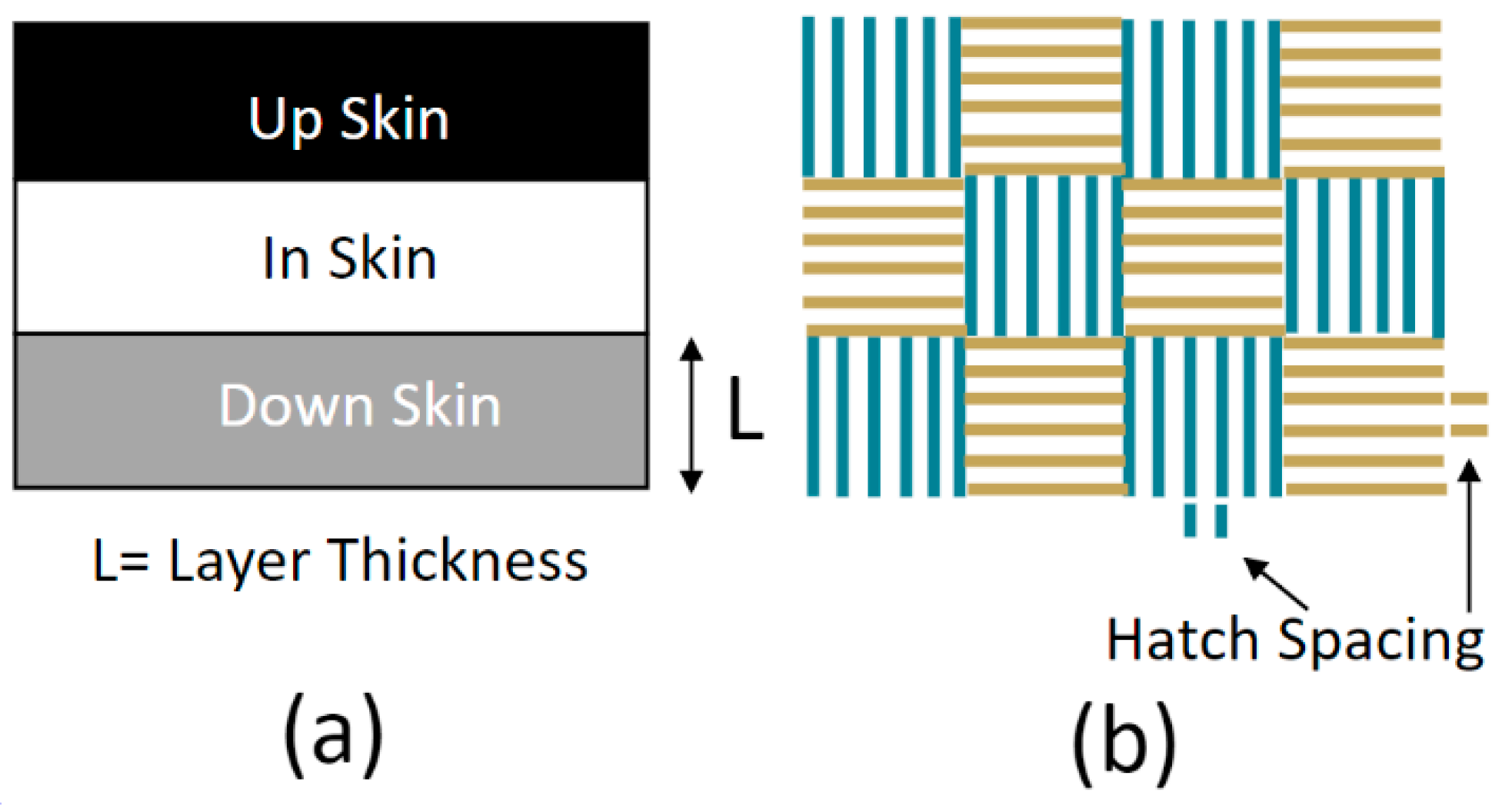
| Layer | Laser Power (W) | Scan Speed (mm/s) | Hatch Spacing (μm) |
|---|---|---|---|
| Up Skin | 165 | 600 | 110 |
| In Skin | 305 | 1010 | 90 |
| Down Skin | 150 | 2000 | 60 |
| Region | Poisson’s Ratio (ν) Compression in x Direction | Poisson’s Ratio (ν) Compression in y Direction |
|---|---|---|
| A | −0.6 ± 0.5 | 0.0 ± 0.1 |
| B | −0.7 ± 0.6 | −0.1 ± 0.1 |
| C | −1.2 ± 0.8 | −0.2 ± 0.1 |
| D | −1.3 ± 0.7 | −0.2 ± 0.1 |
| Average | −0.9 ± 0.7 | −0.1 ± 0.1 |
| SD | 0.34 | 0.09 |
| Error | 18% | 43% |
| Young’s Modulus (Ex) x Direction | Young’s Modulus (Ey) y-Direction | |||
|---|---|---|---|---|
| Parameter | F-Value | p-Value | F-Value | p-Value |
| H | 0.3 | 0.623 | 0.26 | 0.644 |
| L | 3.36 | 0.164 | 35.85 | 0.009 |
| θ | 2 | 0.252 | 7.92 | 0.067 |
| t | 20.92 | 0.02 | 6.31 | 0.087 |
| Yield Strength (σx) x Direction | Yield Strength (σy) y-Direction | |||
|---|---|---|---|---|
| Parameter | F-Value | p-Value | F-Value | p-Value |
| H | 9.7 | 0.053 | 0.1 | 0.779 |
| L | 115.88 | 0.002 | 31.23 | 0.031 |
| θ | 0.54 | 0.515 | 10.64 | 0.083 |
| t | 187.32 | 0.001 | 22.1 | 0.042 |
| Poisson’s Ratio (νxy) x Direction | Poisson’s Ratio (νyx) y Direction | |||
|---|---|---|---|---|
| Parameter | F-Value | p-Value | F-Value | p-Value |
| H | 2.15 | 0.239 | 0.02 | 0.895 |
| L | 32.39 | 0.011 | 0.02 | 0.895 |
| θ | 0.05 | 0.837 | 4.59 | 0.122 |
| t | 1.07 | 0.377 | 12.76 | 0.038 |
| Parameter | Effect | |||||
|---|---|---|---|---|---|---|
| Ex (GPa) | Ey (GPa) | σx (MPa) | σy (MPa) | νxy | νyx | |
| H | −0.064 | +0.195 | −6.44 | −1.65 | +0.408 | −0.003 |
| L | −0.215 | −2.274 | −22.27 | −28.71 | −1.583 | +0.003 |
| θ | +0.166 | −1.069 | −1.52 | −16.76 | −0.063 | +0.038 |
| t | +0.536 | +0.954 | +28.32 | +24.15 | −0.288 | +0.063 |
| ΔL1 (mm) | ΔL1 (mm) | ΔH (mm) | Δϴ (°) | |
|---|---|---|---|---|
| Dimension Change | −0.06 | −0.06 | +0.08 | 4.77 |
| A1 (mm) | A2 (mm) | B1 (mm) | B2 (mm) | |
| Dimension Change | −0.004 | −0.001 | +0.025 | +0.046 |
| ΔL1 (mm) | ΔL1 (mm) | ΔH (mm) | Δϴ (°) | |
|---|---|---|---|---|
| Dimension Change | −0.06 | −0.06 | +0.08 | 4.77 |
| A1 (mm) | A2 (mm) | B1 (mm) | B2 (mm) | |
| Dimension Change | −0.004 | −0.001 | +0.025 | +0.046 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maran, S.; Masters, I.G.; Gibbons, G.J. Additive Manufacture of 3D Auxetic Structures by Laser Powder Bed Fusion—Design Influence on Manufacturing Accuracy and Mechanical Properties. Appl. Sci. 2020, 10, 7738. https://doi.org/10.3390/app10217738
Maran S, Masters IG, Gibbons GJ. Additive Manufacture of 3D Auxetic Structures by Laser Powder Bed Fusion—Design Influence on Manufacturing Accuracy and Mechanical Properties. Applied Sciences. 2020; 10(21):7738. https://doi.org/10.3390/app10217738
Chicago/Turabian StyleMaran, Sibi, Iain G. Masters, and Gregory J. Gibbons. 2020. "Additive Manufacture of 3D Auxetic Structures by Laser Powder Bed Fusion—Design Influence on Manufacturing Accuracy and Mechanical Properties" Applied Sciences 10, no. 21: 7738. https://doi.org/10.3390/app10217738
APA StyleMaran, S., Masters, I. G., & Gibbons, G. J. (2020). Additive Manufacture of 3D Auxetic Structures by Laser Powder Bed Fusion—Design Influence on Manufacturing Accuracy and Mechanical Properties. Applied Sciences, 10(21), 7738. https://doi.org/10.3390/app10217738






