1. Introduction
Thin-walled beams are structural elements with three characteristic dimensions of different orders of magnitude: the thickness is small when compared to the dimensions of the cross-section, which in turn are small when compared to the beam length.
Starting from the second half of the 19th century, slender thin-walled members have found applications in civil and naval engineering as beams, columns, frame-works etc. Later they have been adopted to the needs of aeronautics and aerospace design, as well as, e.g., turbomachinery industry. They offer a number of advantages over the classical compact section beams. The most important ones are lightweight combined with strong rigidity and loads resistance, lower manufacturing costs due to reduced resource consumption and labor-saving design, lower transport and maintenance expenses etc.. Moreover, thanks to their specific layout they leave to the designer much more flexibility regarding the choice of the material and cross-section shape to meet any specific design requirements.
The slender thin-walled elements exhibit significantly different kinematic behavior when compared to solid section beams. In particular the profile warping occurs combined with elastic couplings involving bending and twisting; other local effects arise as well. Therefore, the recognized classical beam theories like Euler–Bernoulli and Timoshenko cannot be trustworthy to analyse thin-walled members.
The first successful attempt to model the kinematics of thin-walled beams was done by Vlasov [
1]. He developed the Theory of Sectorial Area postulating the non-uniform torsion along the beam axis contributing to out-of-plane warping of the cross-section. This hypothesis was accompanied by further assumptions regarding the cross-section being rigid in its own plane and no shear deformability along the profile mid-line. Vlasov’s analytical model was widely adopted by the research community and extended over the years to account for other effects like geometric non-linearities in longitudinal deformations caused by large cross sectional rotation [
2], shear deformability along the wall thickness [
3], variable cross section specimens (stepped or tapered) [
4,
5], curved axis beams [
6,
7] or nonlinear warping effects [
8].
A further generalization of Vlasov’s model was proposed by Capurso [
9]. He revisited the original assumptions to include shear deformation over the cross-section midline by generalizing the description of warping. Later, significant research was focused on modern materials with directional properties like composites and laminates. The works by Librescu and Song [
10] and Variational Asymptotic Beam Sectional (VABS) theory developed by Yu and Hodges [
11] extending the original Vlasov model are particularly worth noting. Research on the dynamics of composite thin-walled beams with closed sections was also carried out by Latalski et al. [
12,
13].
According to the original assumptions on beam profile kinematics the Vlasov theory fails to take into account the effects of cross-section distortion and any local in-plane deformations of the walls. In this respect, The Generalized Beam Theory (GBT) is an alternative modeling concept that adds to the Vlasov’s model the distortion of the cross-section.
The method was originally developed by Schardt [
14,
15] to deal with buckling stability of prismatic cross-section columns. In its original formulation the slender thin-walled element was considered as an assembly of plate segments which are free to bend in the plane of the cross-section. The consequence of this assumption were in-plane deformations of the profile. The latter were assumed to be expressed as the superposition of a series of cross-sectional natural modes whose magnitudes varied along the member span. As a result the two-dimensional (2D) analysis within the shell framework theory is condensed into one-dimensional (1D) beam theory.
Since the mid 1990s, Schardt’s original theory received significant attention from the research community and was extended to take into account other cases and effects. Renton [
16] proposed to use the Generalized Beam Theory to estimate the shear stiffnesses of various cross-sections as particular cases of a general analysis embracing torsion, bending, extension and shear of regular prismatic systems. Silvestre and Camotim [
17] developed a geometrically nonlinear Generalized Beam Theory to consider large structural deformations. The proposed formulation was used to study the post-buckling behavior of steel columns with cold-formed thin-walled profiles. The presented analysis showed, among other things, the need to include shear and transverse extension modes to properly capture system kinematics. The relevant shear-deformable GBT structural model was elaborated and presented in authors later research [
18,
19]. Taig and Ranzi [
20] adopted the GBT to study the response of prismatic thin-walled members stiffened at different cross-sections along their span.
Next, Ranzi and Luongo [
21] revisited the standard GBT algorithm for the determination of the conventional modes, in which bending, shear and local modes are evaluated separately. Authors proposed to use the dynamic modes of an unconstrained planar frame similar in shape to the member profile to calculate cross-section in-plane deformation modes. Next, based on the enforcement of shear conditions, the out-of-plane warping component was evaluated.
Piccardo et al. [
22,
23,
24] proposed the new method to evaluate a suitable basis of modes for the elastic analysis of thin-walled members. The suggested treatment relied on the solution of two distinct eigenvalue problems governing the in-plane and the out-of-plane free oscillations of a thin-walled beam cross-section. The first eigenvalue problem was solved posing an inextensibility condition for the planar frame beam having the shape of the TWB middle line. In the second eigenvalue analysis the transverse extension and membrane shear strain of the plate elements forming the cross-section were accounted for and modes orthogonal to the inextensional ones were calculated. The efficiency of the proposed method was confirmed by the outcomes of numerical examples.
The research was continued later by the authors to extend the theory to account for nonlinear effects exhibited by elastic thin-walled beams [
25]. To this aim, both linear and nonlinear functions were used to describe the displacement field of the member cross-section. The admissible set of trial functions was determined requiring that the classic Vlasov’s kinematic hypotheses of the linear theory (i.e., (a) transverse inextensibility and (b) unshearability) were satisfied also in the nonlinear sense. An illustrative example of C-lipped cross-section beam with uniform thickness subjected to a uniform vertical pressure load was presented. The accuracy of GBT analytical results was confirmed by the outcomes of FE simulations.
Studying the invoked above references and other GBT related literature one observes the vast majority of research deals with polygon-like cross sections while the cases of non-prismatic open or closed profiles are very scarce. This results from the fact that curved geometries make the problem to find the cross-section deformation modes quite complex. The exception might be tubular beam designs studied by Schardt in [
14], who presented solutions to the problem of uniform bending of a closed cylinder specimen. The analysis was enhanced by discussion of solution accuracy when approximating the cylinder profile by a regular polygon shape.
In recent years, Silvestre [
26] investigated the buckling behavior of circular hollow section (CHS) members. He postulated to extend the cross section analysis and include axisymmetric and torsional modes apart from the set of classical orthogonal shell-type deformations of the profile. The presented discussion concerned the influence of member length on the critical stress magnitude and corresponding buckling mode shape. Comparison of the analytical GBT results to FE simulations by shell elements revealed very good consistency with respect to both local and global structural behavior. Afterwards, the author extended his research to account for elliptical cylindrical shells and tubes under compression [
27]. The problem of variable curvature along the cross-section mid-line was solved by introducing parametric functions of tangential angle and their Fourier series expansions to approximate the local arch radius. The proposed formulation proved to be very effective since only three deformation modes (one local-shell, one distortional and one global) were required to accurately evaluate the buckling behavior of elliptical members for a wide range of specimen slenderness. The structural behavior of circular cross-section members was studied also by Nedelcu [
28]. The author considered conical shells under three different boundary conditions and subjected to buckling load. In the proposed approach the member deformed configuration was approximated by a combination of the predetermined shell-type deformation modes.
Thereafter, Luongo and Zulli [
29] adopted a GBT framework to analyse the ovalization of a tubular cross-section beam when subjected to bending. In the kinematic analysis of the member cross section, distortional and bi-distortional strains were introduced in addition to the regular strain measures of rigid cross-section beams. Several cases of static loadings applied at the free end were investigated followed by large-amplitude free vibrations analysis. This research was continued to account for tubular beams with a soft core, possibly made of foam materials [
30]. The findings showed the inclusion of a foam core could improve performance of the pipes due to the shifted structural instability limit load. In the subsequent paper [
31], Zulli adopted this model to capture the double-layered pipe designs. New terms representing longitudinal slipping of the two layers were added to the kinematic description of the structure profile. Next, a homogenization procedure was applied to obtain the nonlinear, coupled, elastic response function of the beam-like member.
An efficient method to model beams with arbitrary but open cross section shapes within Generalized Beam Theory was presented by Gonçalves and Camotim [
32]. The core of this approach was a modified two-stage cross sectional analysis procedure. Within the first step the curved mid-line of the cross-section was finely approximated by a series of straight segments constituting the polyline. The second stage consisted in selection just a few of natural nodes of this polyline to generate the independent DOFs for warping analysis while the intermediate nodes of the profile were treated like in classic procedure. By this approach it was possible to describe the cross-section geometry accurately, without generating an excessive number of deformation modes. The method was applied to several cross-sections with curved walls and it was shown it assured sufficiently accurate results even with a rough selection of cross-section DOFs. The method proved to be particularly efficient for polygonal sections with rounded corners.
The presented above discussion and review of thin-walled structures bibliography demonstrates that the problem of structural behavior of thin-walled beams with curvilinear open profiles has not been comprehensively studied within the GBT framework. The main purpose of present contribution is to fill this gap and to derive the analytical model of a generic thin-walled curvilinear cross-sections beam within the GBT modelling framework. Therefore the outline of the paper is as follows. In
Section 2.1 the analysis of the profile kinematics is presented and expressions for strains in curvilinear reference system are given. The constitutive law is introduced in
Section 2.2, and the procedure for setting trial in-plane and out-of-plane warping functions is explained in
Section 2.3. Next, in
Section 2.4, the governing equations are derived by means of the Hamilton’s method. In
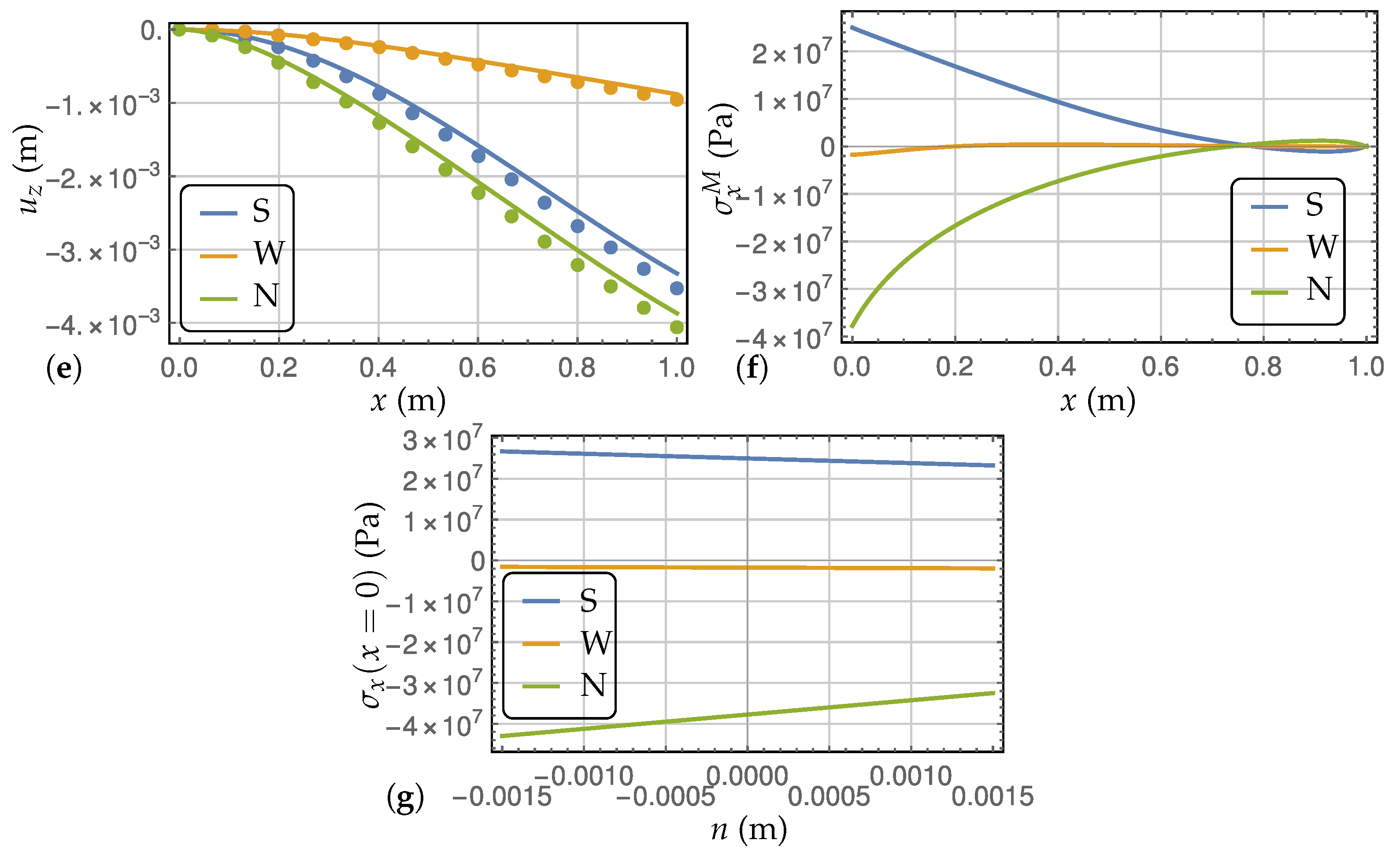
Section 3, the numerical examples of semi-annular specimen in two loading conditions are presented. The analytical results are compared to the outcomes of the FE simulations. Finally, the paper closes in
Section 4 with the concluding remarks.
2. The Beam Model
A thin-walled beam made of isotropic, homogeneous and linearly elastic material is considered. The specimen is initially straight and its cross-sections, which are constituted by curved webs and flanges, are assumed open, while the closed and multi-cell cases are left for future developments. Furthermore, it is assumed that the profile of the beam is constant spanwise with no taper nor pretwist.
First, linear strain-displacement relationship is written and then, following the hypothesis of plane stress in profile walls, the constitutive law for linear elastic material is used to calculate strain energy. Finally, Hamilton’s principle is used and the equilibrium equations in terms of kinematic descriptors are obtained, imposing that the total potential energy attains a minimum in the class of compatible displacements. According to GBT framework, the displacements are considered as linear combinations of pre-established trial functions and kinematic descriptors which change along the axis line of the beam. The adopted cross-section modal shapes describe both rigid displacements, as in classical beam models, and changes in the shape of the profile characteristic for thin-walled members.
2.1. Geometry and Kinematics
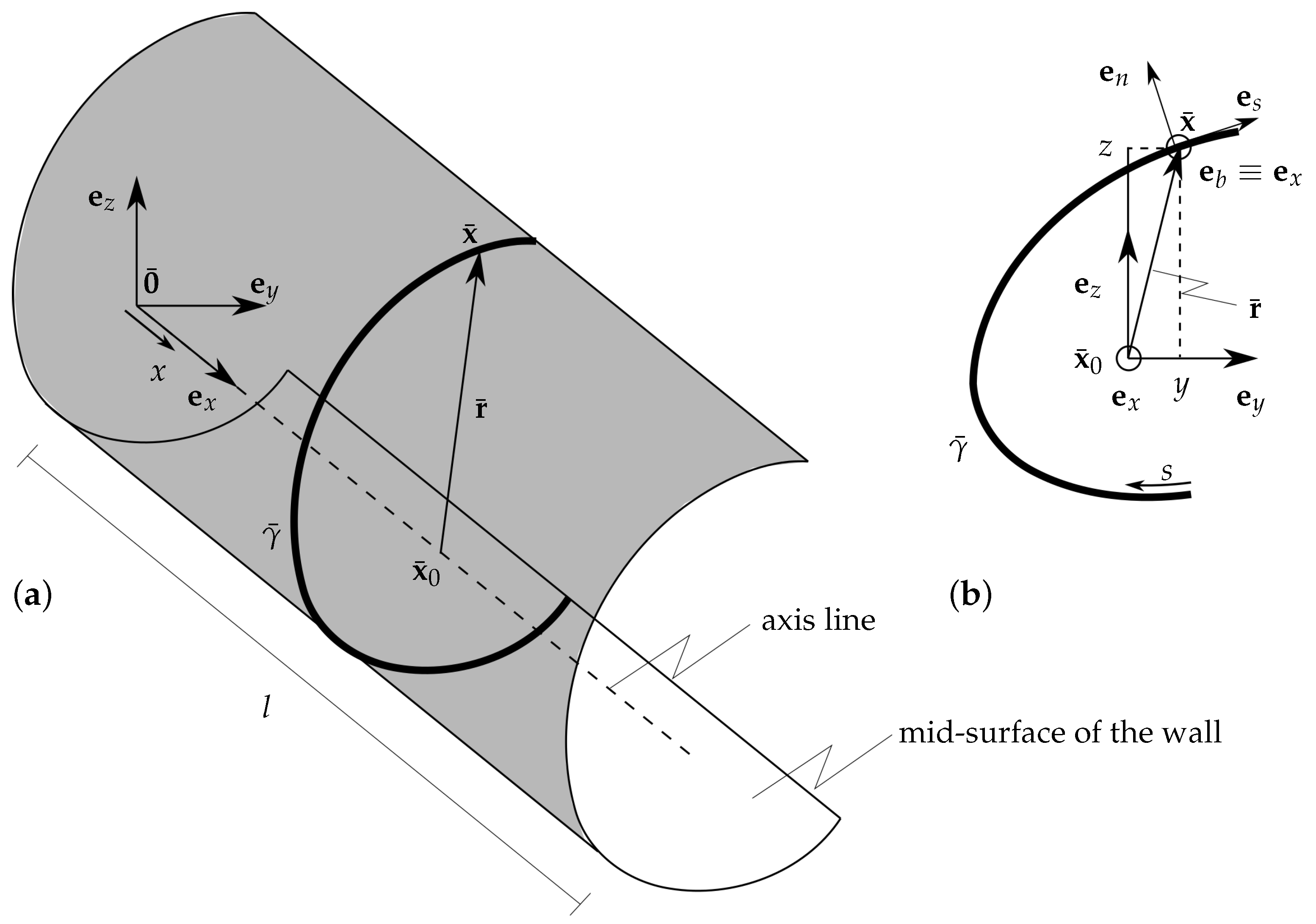
With reference to
Figure 1, the axis line of the beam is defined in correspondence of the cross-sections centroids. It is a straight line given as:
where
is the position of the origin, which is the centre of the left tip cross-section, and
x is an abscissa which runs in the interval
, where
l is the length of the beam; the unit vectors
are orthogonal to each other and define the canonical (global) basis. The initial position
of a generic point
located at the mid-surface of the wall is:
where
is the vector which defines the mid-curve
of the cross-section, having curvilinear coordinate
s as parameter. Specifically about the mid-curve
of the cross-section, the parameter
s is chosen so that
. Furthermore, it is convenient to set-up a local coordinate system along the curve and given by the tangent, normal and binormal unit vectors
where—with respect to global basis—the relations follow:
and the curvature around
is defined as:
Through the beam deformation, the point
undergoes a displacement
, which can be expressed in terms of components on both the global and local bases, namely
and
. According to Equation (
4) the two sets of displacements are related as:
In order to take into account the thickness
h of the walls, the webs and flanges are considered as singly curved thin shells, whose mid-surface coincides with
(
Figure 2). The displacements of any generic point located off the mid-surface (
) are obtained from the mid-surface counterpart ones using Kirchhoff’s thin plate assumption.
Thus, every line normal to the mid-surface at
before deformation remains normal after the deformation and relevant rotations about
and
directions are:
respectively. It is worth noting how the second term in the right hand side of Equation (
8) results from cross-section curvature about binormal axis [
33].
As a consequence, any point out of the mid-surface performs displacement
which has the following components on
:
respectively. Substituting Equations (
7) and (
8) into the above definitions, the local basis displacement components are as follows:
The infinitesimal strain components within the curved thin wall are defined as [
33]:
where
are longitudinal strain along
, respectively, and
is the shear strain. After substituting Equation (
10) in Equation (
11), the strain components attain the following expressions:
where the pure membrane strain components, i.e., relevant to the mid-surface (
) and indicated with superscript
M, and the flexural strain components, i.e., proportional to
n and indicated with superscript
F, are:
and
Following the idea of the Kantorovitch semi-variational method the individual components of the mid-curve
points displacement are expressed as a linear combination of
K triplets of trial functions
,
, and unknown amplitude parameters
:
where the prime indicates derivative with respect to
x. The functions
represent the three components of the assumed
deformation field, defined on the section profile.
The use of Equation (
15) in Equations (
13) and (
14) allows one to express the strain measures in terms of the kinematic descriptors
, for
:
and
2.2. Constitutive Law
It is assumed that the beam is made of an isotropic, homogeneous and linearly elastic material. Moreover, the plane stress state hypothesis is adopted to a thin shell representing any individual beam wall. For thin-walled structures this assumption is realistic and provides reliable results. According to this formulation, the two-dimensional stresses are functions of solely two coordinates
x and
s, while all the transverse stresses are negligible:
Thus, the corresponding 3D Hooke’s law is simplified to:
where
are the material Young’s and Kirchhoff’s moduli, and Poisson ratio, respectively. Equation (
19), when solved in terms of stresses, becomes:
Substituting Equation (
12) in Equation (
20), the expressions of the individual stress components can be decomposed to the sum of membrane and flexural related terms, as well:
Finally, the use of Equations (
16) and (
17) allows one to express the stress components in (
21) in terms of the trial functions
and kinematic descriptors
,
. The final expressions are omitted for the sake of brevity.
2.3. Trial Functions and Vlasov’s Constraints
The regular Vlasov’s internal constraints specific for any open cross-section require that the profile mid-curve
is inextensible and the middle surface of the thin-walled beam is shear indeformable. Thereby two relations follow:
As a consequence, regarding Equation (
16), every
j-th set of assumed trial functions must satisfy the following conditions:
In this study, the trial functions
,
are evaluated in two stages as proposed by Ranzi and Luongo in [
21]. At first, the in-plane deformation field components
are evaluated as the dynamical normal modes of the planar unconstrained inextensional (i.e., satisfying the first Vlasov’s condition) frame having the shape similar to profile mid-curve
. Thereby the considered frame is constituted by a monodimensional curved beam element or assembly of them in case of piece-wise regularity of
. Having found the in-plane deformation modes, at the next stage the third trial function
is determined. This represents the component relevant to the out-of-plane warping of the cross-section and it is consistently evaluated by integration of Equation (
24). The emerging unknown integration constant is obtained by imposing the orthogonality condition of
to the uniform axial extension, i.e.,
. Therefore, the triple of thus deduced deformation fields
satisfy both Vlasov’s conditions given by Equation (
22).
In the above analysis a uniform mass per unit length is assigned to the referenced frame in order to evaluate the in-plane deformation components; the latter must also be consistent with Equation (
23), i.e., the curved beam constituting
is axially indeformable. Furthermore, a suitable normalization condition on the normal modes is imposed.
It is worth noting that, due to the lack of external constraints, among the set of determined in-plane modes, three independent rigid motions of the cross-section in its plane are present as well. These are two translations in directions and , respectively, and rotation about . Moreover, consistently with the internal constraint in Equation (24), the out-of-plane components relevant to the two translations in directions and turn out to describe rotations of the cross-section about axes and , respectively, as in an Euler–Bernoulli beam bending. Thus, it should be pointed out that, with the present approach, it is precluded the possibility of introducing independent bending rotations as it would be done in Timoshenko beam models.
An additional trial function, which describes the uniform extension in direction is defined as well, and it is assigned to ordering . Therefore, the triplets for describe rigid motions of the profile and are given as follows: : ; : ; : ; : . The other triplets () describe in-plane deformation of the cross-section and its corresponding kinematically consistent out-of-plane warping.
It is worth mentioning that the Vlasov’s conditions (
22) can be removed in the framework of GBT, as well: This is the case, for instance, of structures where shear-lag might occur, as shown in [
22]; there, further trial functions are introduced, which account for both shear and extensional deformation.
2.4. Equilibrium Equations
Equilibrium equations in terms of generalized amplitudes
are obtained imposing the stationary condition to the sum of elastic and load potential energy (conservative external loads are assumed). In particular, the elastic potential energy has the following expression:
where
is the total volume of the beam and the differential volume element being
. In the above the membrane components of strain in tangential direction
s and shear mid-surface indeformability are omitted according to Vlasov’s conditions Equation (
22).
After expressing the stress and strain components in Equation (
25) in terms of the unknown amplitudes
, by means of the relevant equations from
Section 2.1 and
Section 2.2, the elastic potential energy becomes:
where
, the dot stands for scalar product, the prime indicates derivative with respect to
x and the expressions of the elements of the individual matrices are:
It is worth noting that are symmetric matrices.
The load potential energy is evaluated for a general case of a force per unit area acting in correspondence of the mid-surface. The generally oriented force is defined by the three components vector
that yields the energy:
where the displacement components can be expressed in terms of
as well, by means of Equations (
6) and (
15).
The minimum of the total potential energy is attained imposing that
,
,
, where
is the variation operator, which produces the following set of Euler-Lagrange equations:
and boundary conditions in
:
where the elements of
and
are:
Equations (
29) and (
30) represent a linear, ordinary differential boundary value problem with constant coefficients, governing the evolution of the functions
along the span of the beam. Even if it can be analytically solved using the well-known method of variation of constants, which provides the exact solution, numerical tools capable to solve BVP will be used to find the solution, for practical purposes. In spite of this, the outcomes will be referred to as analytical solution in the following part of the paper.
It is noteworthy that the case of branched cross-section can be addressed piecewise evaluating along
the integrals in Equations (
27) and (
31).