Multi-Steps Registration Protocol for Multimodal MR Images of Hip Skeletal Muscles in a Longitudinal Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. MRI Acquisitions
- A fast field echo (FFE) T1-weighted sequence, acquired with resolution 1 × 1 × 6 mm3, 30 slices, echo time (TE) = 2 ms, repetition time (TR) = 620 ms, SENSE factor 2, number of averages (NA) = 2, acquisition time 2 min 35 s;
- A Dixon FFE sequence for fat fraction (FF) quantification, acquired with resolution 1.6 × 1.6 × 6 mm3, 40 slices, 12 echoes, flip angle 3°, echo time (TE) = 1.2 ms, inter-echo time 2.7 ms, repetition time (TR) = 16.17 ms, SENSE factor 2, acquisition time 1 min 37 s;
- A multi-echo spin-echo T2 sequence (MESE) with 15 echoes for T2 quantification, acquired with resolution 2 × 2 × 6 mm3, 40 slices, TE = 9.3 ms, inter-echo time 12.5 ms, TR = 14 s, SENSE factor 2, NA = 1, acquisition time 15 min 30 s;
- A multi-shell dMRI echo-planar imaging (EPI) sequence including 14 volumes at b = 0 s/mm2, 6 directions each at b = 2, 5, 10, 20, 50, 100, and 200 s/mm2, 10 directions at b = 400 s/mm2, 15 directions at b = 700 s/mm2, 25 directions at b = 900 s/mm2, and 30 directions at b = 1100 s/mm2 Data were acquired with resolution 2.5 × 2.5 × 5 mm3, 20 slices, TE = 58 ms, TR = 4.5 s, SENSE factor 2, NA = 1, acquisition time 11 min 33 s. Fat suppression was performed using Spectral Presaturation with Inversion Recovery (SPIR) and Spoiled Gradient Recalled (SPGR) approaches.
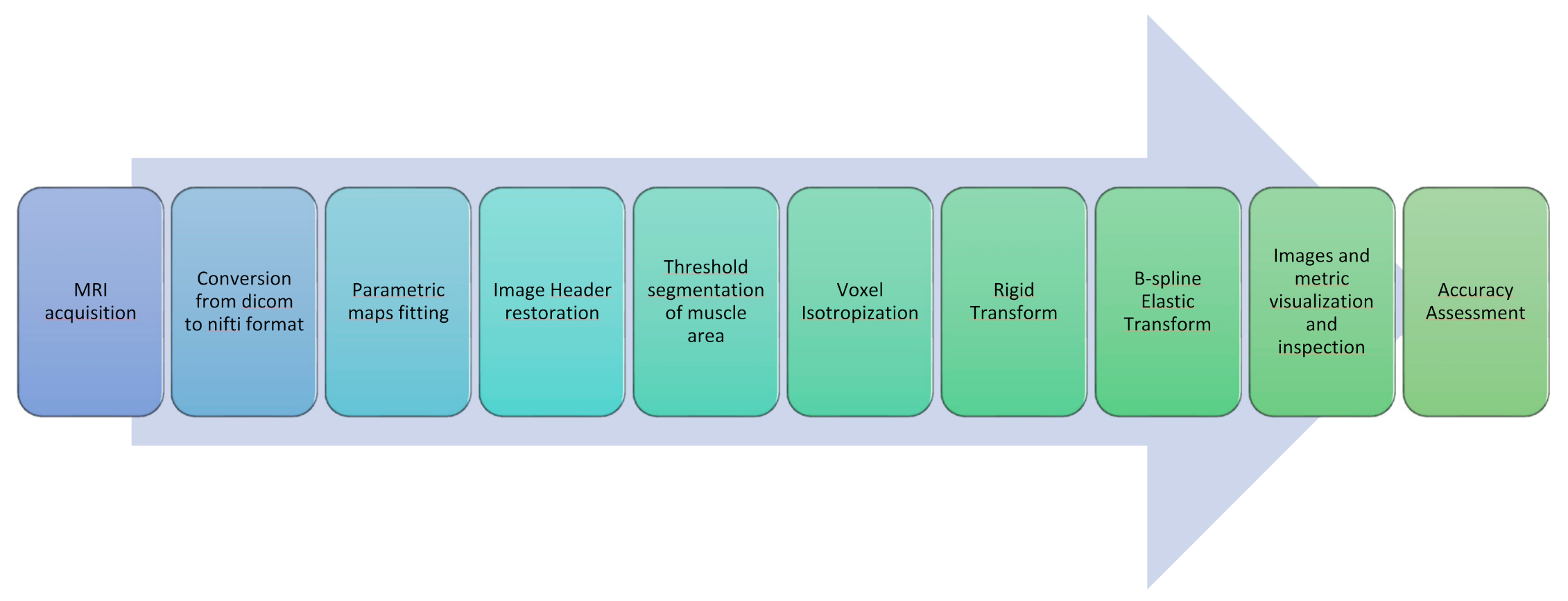
2.3. Registration and Image Processing Workflow
- As a very first step, all Dicom images obtained from the MRI scanner were converted to Nifti files with dcm2nii [30].
- A further step was devoted to the generation of quantitative parametric maps at t0 and t1. Fat Fraction and T2 relaxation maps were obtained with an in-house script from the Dixon and the MESE T2 sequences, respectively; T2 maps were calculated voxel-wise fitting a standard mono-exponential decay through a least-square minimization approach [31], whereas Fat Fraction maps were estimated using the regularized field map formulation and graph cut solution [32]. Finally, DTI maps, obtained from the EPI multi-shell sequence, were generated using the ExploreDTI software (v4.8.6, University Medical Center Utrecht, Utrecht, The Netherlands) [33]. All the quantitative maps generation process was carried out in the MATLAB environment.
- The headers of the estimated quantitative maps were systematically matched with the corresponding source image headers that were used as a reference. This step ensures the recovery of the correct geometrical orientation for the following registration steps.
- Finally, the voxels of the images were made isotropic to account for the sampling unevenness to improve the registration performance along the slice direction (final voxel resolution was 1×1×1 mm3).
- The initial rigid roto-translations was performed in three conditions:
- Native resolution without selecting a mask (NM)
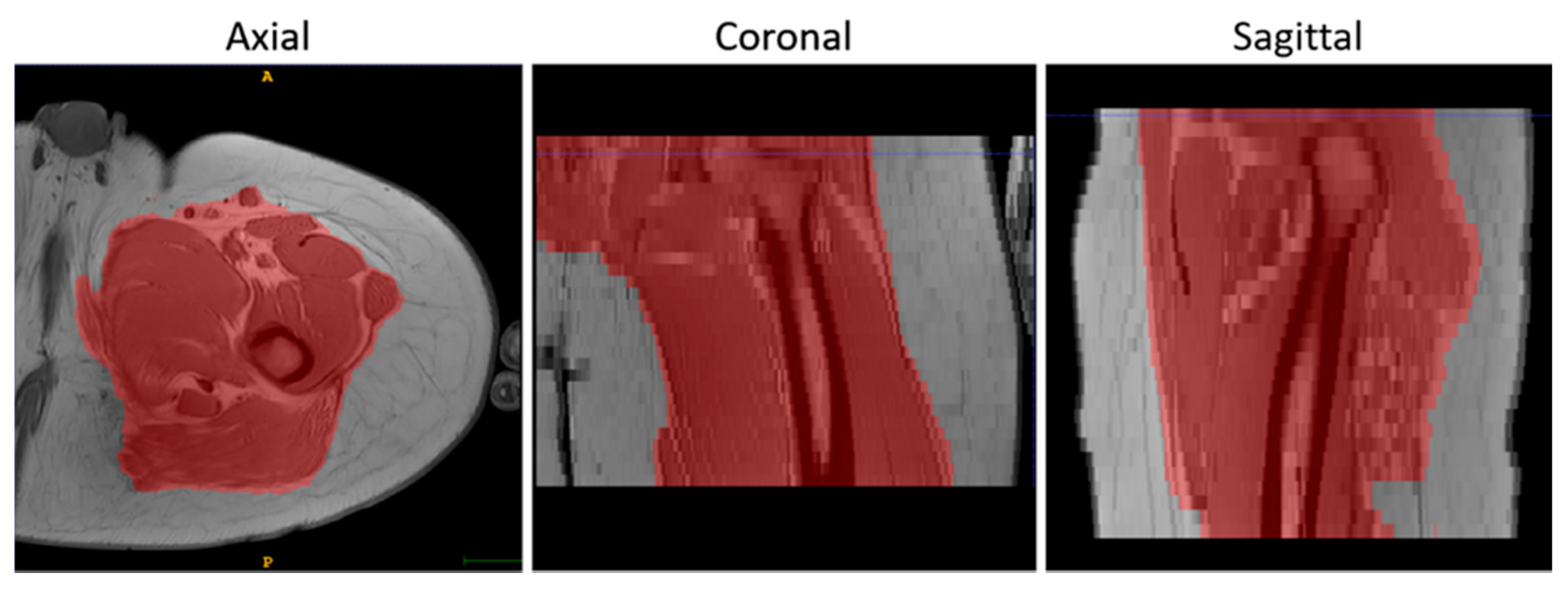
- Native resolution with mask (M)
- Isotropic voxels with mask (IM)
- In a second step, a nonrigid transformation was used, based on b-splines, with a polynomial warping of the third order. We evaluated two learning rates—2 and 4—and four—3×3×3, 5×5×5, 8×8×8, and 8×8×4—and three—3×3×3, 5×5×5, and 8×8×8—different mesh size for the native and isotropic resolution, respectively.
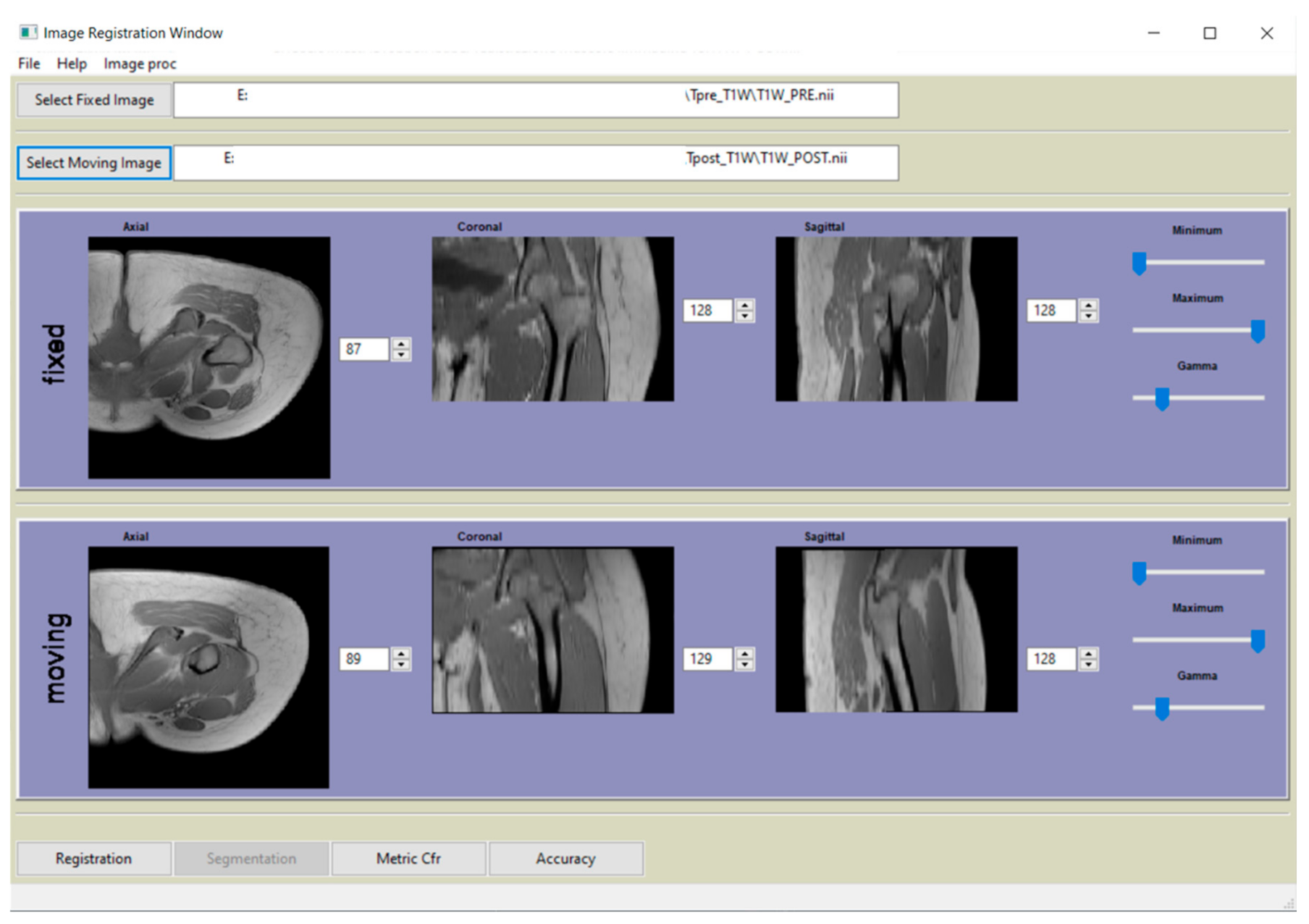
2.4. Registration Software Implementation
2.5. Registration Accuracy Assessment
- Dice similarity index (DSI) [40], quantifying the agreement between contours according to the degree of overlap of their volumes. It ranges between 0 and 1, where 1 indicates a perfect overlap:
- Mean surface distance (MSD), calculated in SimpleITK as the average symmetric distance between two contours A and B:
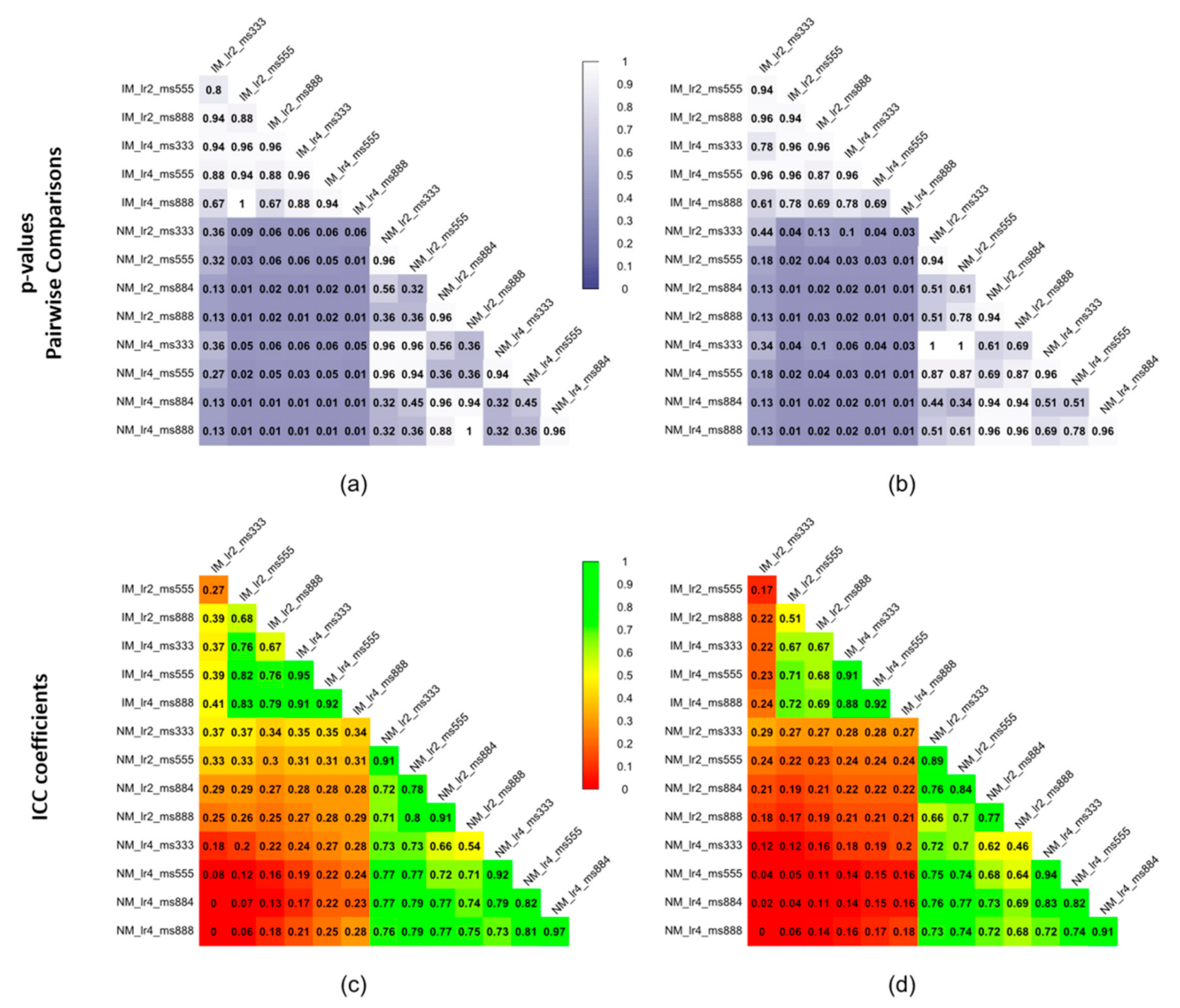
2.6. Statistical Methods
3. Results
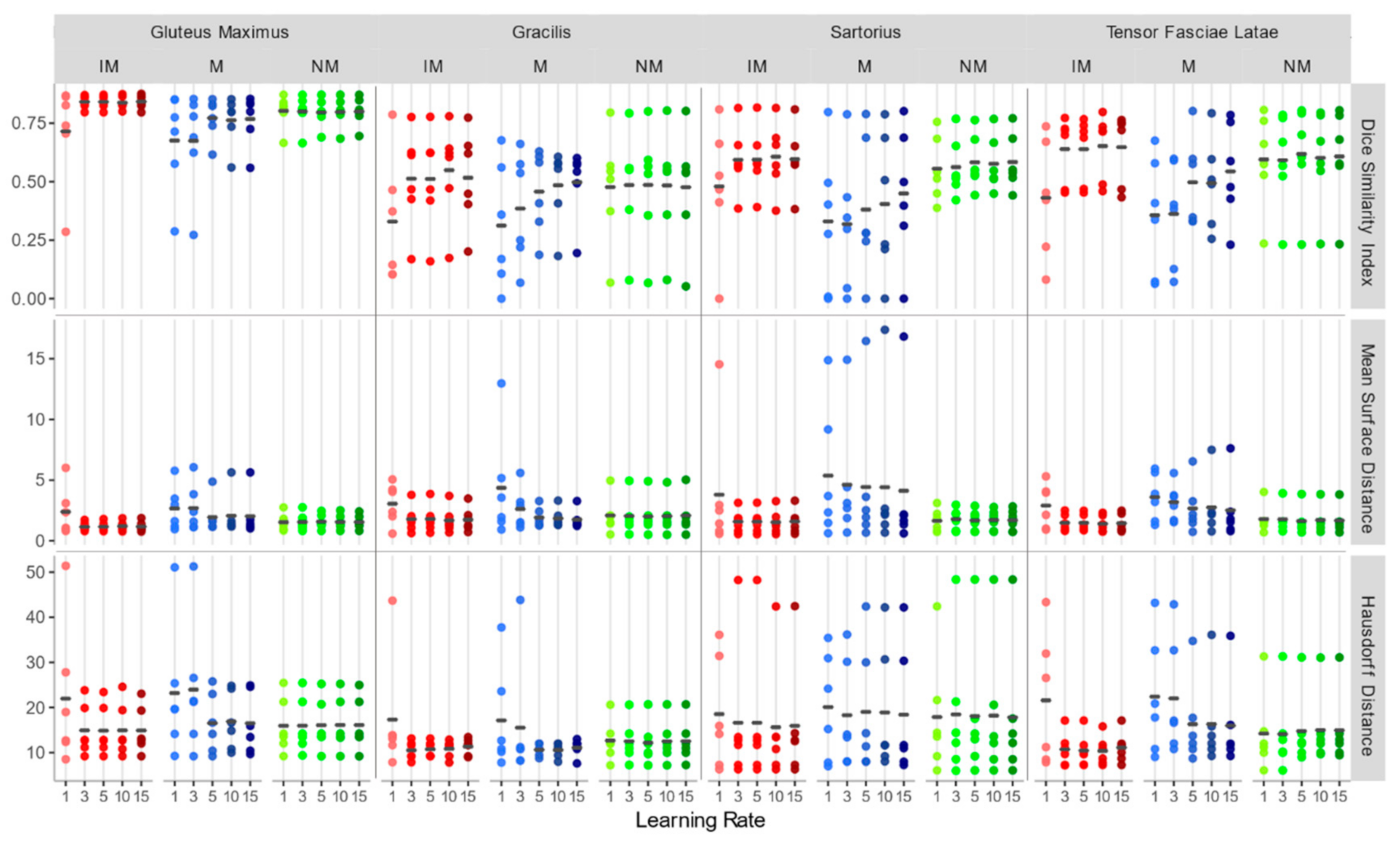
3.1. Accuracy Assessment for Rigid Registration
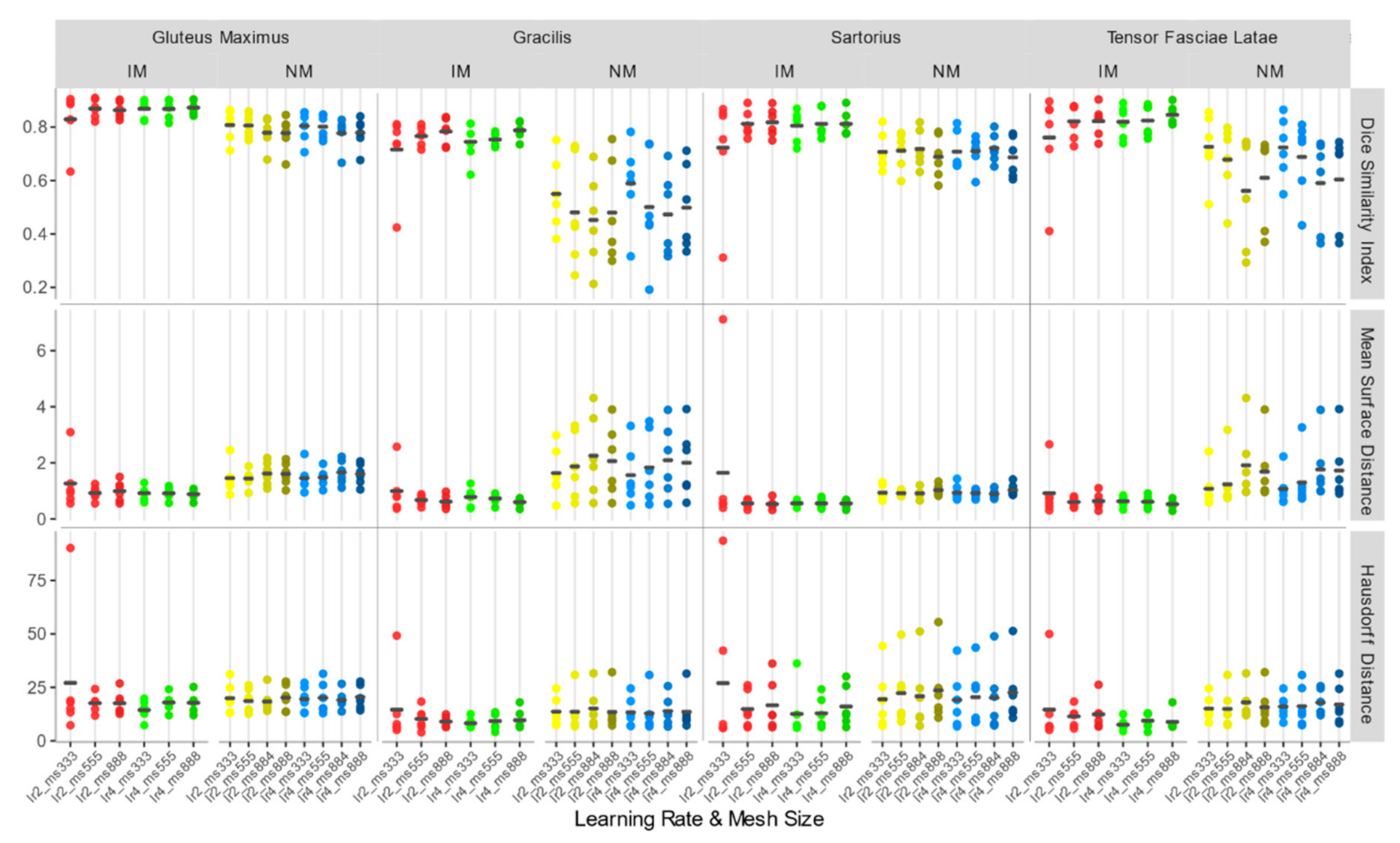
3.2. Accuracy Assessment for Rigid + Non-Rigid Registration
4. Discussion
- Rigid transformation is not sufficient to achieve a good registration performance in muscle MRI, and a second deformable step is needed.
- In the first rigid step, the use of a masking strategy alone is not sufficient to obtain good results. Furthermore, the performances are poorly depending on the learning rates of the gradient descent optimizer and a larger learning rate is preferable to speed up the process.
- Regarding the deformable transformation step, working with an isotropic voxel in combination with a masking strategy leads to better accuracy, and larger learning rates are preferable.
Author Contributions
Funding
Conflicts of Interest
References
- Erlandson, M.C.; Lorbergs, A.L.; Mathur, S.; Cheung, A.M. Muscle analysis using pQCT, DXA and MRI. Eur. J. Radiol. 2016, 85, 1505–1511. [Google Scholar] [CrossRef] [PubMed]
- Rivas, D.A.; Fielding, R.A. Skeletal Muscle. In Encyclopedia of Human Nutrition; Elsevier Inc.: Amsterdam, The Netherlands, 2012; Volume 4, pp. 193–199. ISBN 9780123848857. [Google Scholar]
- Engelke, K.; Museyko, O.; Wang, L.; Laredo, J.D. Quantitative analysis of skeletal muscle by computed tomography imaging—State of the art. J. Orthop. Transl. 2018, 15, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Pillen, S.; van Alfen, N. Skeletal muscle ultrasound. Neurol. Res. 2011, 33, 1016–1024. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Z.; Wang, Z.M.; Lohman, T.; Heymsfield, S.B.; Outwater, E.; Nicholas, J.S.; Bassford, T.; LaCroix, A.; Sherrill, D.; Punyanitya, M.; et al. Dual-energy X-ray absorptiometry is a valid tool for assessing skeletal muscle mass in older women. J. Nutr. 2007, 137, 2775–2780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dahlqvist, J.R.; Widholm, P.; Leinhard, O.D.; Vissing, J. MRI in Neuromuscular Diseases: An Emerging Diagnostic Tool and Biomarker for Prognosis and Efficacy. Ann. Neurol. 2020, 88, 669–681. [Google Scholar] [CrossRef] [PubMed]
- Smitaman, E.; Flores, D.V.; Mejía Gómez, C.; Pathria, M.N. MR imaging of atraumatic muscle disorders. Radiographics 2018, 38, 500–522. [Google Scholar] [CrossRef]
- Froeling, M.; Oudeman, J.; Strijkers, G.J.; Maas, M.; Drost, M.R.; Nicolay, K.; Nederveen, A.J. Muscle changes detected with diffusion-tensor imaging after long-distance running. Radiology 2015, 274, 548–562. [Google Scholar] [CrossRef] [PubMed]
- Farrow, M.; Biglands, J.; Tanner, S.F.; Clegg, A.; Brown, L.; Hensor, E.M.A.; O’Connor, P.; Emery, P.; Tan, A.L. The effect of ageing on skeletal muscle as assessed by quantitative MR imaging: An association with frailty and muscle strength. Aging Clin. Exp. Res. 2020, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Díaz-Manera, J.; Llauger, J.; Gallardo, E.; Illa, I. Muscle MRI in muscular dystrophies. Acta Myol. Myopathies Cardiomyopathies Off. J. Mediterr. Soc. Myol. 2015, 34, 95–108. [Google Scholar]
- Carlier, P.G.; Reyngoudt, H. The expanding role of MRI in neuromuscular disorders. Nat. Rev. Neurol. 2020, 16, 301–302. [Google Scholar] [CrossRef]
- Weber, M.A.; Wolf, M.; Wattjes, M.P. Imaging Patterns of Muscle Atrophy. Semin. Musculoskelet. Radiol. 2018, 22, 299–306. [Google Scholar] [CrossRef]
- Psatha, M.; Wu, Z.; Gammie, F.M.; Ratkevicius, A.; Wackerhage, H.; Lee, J.H.; Redpath, T.W.; Gilbert, F.J.; Ashcroft, G.P.; Meakin, J.R.; et al. A longitudinal study of muscle rehabilitation in the lower leg after cast removal using magnetic resonance imaging and strength assessment. Int. Biomech. 2015, 2, 101–112. [Google Scholar] [CrossRef] [Green Version]
- Pons, C.; Borotikar, B.; Garetier, M.; Burdin, V.; Ben Salem, D.; Lempereur, M.; Brochard, S. Quantifying skeletal muscle volume and shape in humans using MRI: A systematic review of validity and reliability. PLoS ONE 2018, 13, e207847. [Google Scholar] [CrossRef]
- Mercuri, E.; Talim, B.; Moghadaszadeh, B.; Petit, N.; Brockington, M.; Counsell, S.; Guicheney, P.; Muntoni, F.; Merlini, L. Clinical and imaging findings in six cases of congenital muscular dystrophy with rigid spine syndrome linked to chromosome 1p (RSMD1). Neuromuscul. Disord. 2002, 12, 631–638. [Google Scholar] [CrossRef]
- Kalia, V.; Leung, D.G.; Sneag, D.B.; Del Grande, F.; Carrino, J.A. Advanced MRI Techniques for Muscle Imaging. Semin. Musculoskelet. Radiol. 2017, 21, 459–469. [Google Scholar] [CrossRef]
- Oudeman, J.; Nederveen, A.J.; Strijkers, G.J.; Maas, M.; Luijten, P.R.; Froeling, M. Techniques and applications of skeletal muscle diffusion tensor imaging: A review. J. Magn. Reson. Imaging 2016, 43, 773–788. [Google Scholar] [CrossRef]
- Damon, B.M.; Buck, A.K.W.; Ding, Z. Diffusion-tensor MRI-based skeletal muscle fiber tracking. Imaging Med. 2011, 3, 675–687. [Google Scholar] [CrossRef] [Green Version]
- Mastropietro, A.; Porcelli, S.; Cadioli, M.; Rasica, L.; Scalco, E.; Gerevini, S.; Marzorati, M.; Rizzo, G. Triggered intravoxel incoherent motion MRI for the assessment of calf muscle perfusion during isometric intermittent exercise. NMR Biomed. 2018, 31, e3922. [Google Scholar] [CrossRef]
- Jenkinson, M.; Bannister, P.; Brady, M.; Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 2002, 17, 825–841. [Google Scholar] [CrossRef]
- Klein, A.; Andersson, J.; Ardekani, B.A.; Ashburner, J.; Chiang, M.-C.; Christensen, G.E.; Collins, D.L.; Gee, J.; Hellier, P.; Song, J.H.; et al. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage 2009, 46, 786–802. [Google Scholar] [CrossRef] [Green Version]
- Tavakoli, V.; Amini, A.A. A survey of shaped-based registration and segmentation techniques for cardiac images. Comput. Vis. Image Underst. 2013, 117, 966–989. [Google Scholar] [CrossRef]
- Tsadok, Y.; Friedman, Z.; Haluska, B.A.; Hoffmann, R.; Adam, D. Myocardial strain assessment by cine cardiac magnetic resonance imaging using non-rigid registration. Magn. Reson. Imaging 2016, 34, 381–390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Montin, E.; Belfatto, A.; Bologna, M.; Meroni, S.; Cavatorta, C.; Pecori, E.; Diletto, B.; Massimino, M.; Oprandi, M.C.; Poggi, G.; et al. A multi-metric registration strategy for the alignment of longitudinal brain images in pediatric oncology. Med. Biol. Eng. Comput. 2020, 58, 843–855. [Google Scholar] [CrossRef] [PubMed]
- Barnhill, E.; Kennedy, P.; Hammer, S.; Van Beek, E.J.R.; Brown, C.; Roberts, N. Statistical mapping of the effect of knee extension on thigh muscle viscoelastic properties using magnetic resonance elastography. Physiol. Meas. 2013, 34, 1675–1698. [Google Scholar] [CrossRef] [PubMed]
- Fouré, A.; Le Troter, A.; Guye, M.; Mattei, J.P.; Bendahan, D.; Gondin, J. Localization and quantification of intramuscular damage using statistical parametric mapping and skeletal muscle parcellation. Sci. Rep. 2015, 5, 18580. [Google Scholar] [CrossRef] [Green Version]
- Fatehi, F.; Salort-Campana, E.; Le Troter, A.; Lareau-Trudel, E.; Bydder, M.; Fouré, A.; Guye, M.; Bendahan, D.; Attarian, S. Long-term follow-up of MRI changes in thigh muscles of patients with Facioscapulohumeral dystrophy: A quantitative study. PLoS ONE 2017, 12, e0183825. [Google Scholar] [CrossRef] [Green Version]
- Arrigoni, F.; De Luca, A.; Velardo, D.; Magri, F.; Gandossini, S.; Russo, A.; Froeling, M.; Bertoldo, A.; Leemans, A.; Bresolin, N.; et al. Multiparametric quantitative MRI assessment of thigh muscles in limb-girdle muscular dystrophy 2A and 2B. Muscle Nerve 2018, 58, 550–558. [Google Scholar] [CrossRef]
- Le Troter, A.; Fouré, A.; Guye, M.; Confort-Gouny, S.; Mattei, J.P.; Gondin, J.; Salort-Campana, E.; Bendahan, D. Volume measurements of individual muscles in human quadriceps femoris using atlas-based segmentation approaches. Magn. Reson. Mater. Phys. Biol. Med. 2016, 29, 245–257. [Google Scholar] [CrossRef]
- Li, X.; Morgan, P.S.; Ashburner, J.; Smith, J.; Rorden, C. The first step for neuroimaging data analysis: DICOM to NIfTI conversion. J. Neurosci. Methods 2016, 264, 47–56. [Google Scholar] [CrossRef]
- Carneiro, A.A.O.; Vilela, G.R.; De Araujo, D.B.; Baffa, O. MRI Relaxometry: Methods and Applications. Braz. J. Phys. 2006, 36, 9–15. [Google Scholar] [CrossRef]
- Hernando, D.; Kellman, P.; Haldar, J.P.; Liang, Z.P. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magn. Reson. Med. 2010, 63, 79–90. [Google Scholar] [CrossRef] [Green Version]
- Leemans, A.; Jeurissen, B.; Sijbers, J.; Jones, D. ExploreDTI: A graphical toolbox for processing, analyzing, and visualizing diffusion MR data. Proc. 17th Sci. Meet. Int. Soc. Magn. Reson. Med. 2009, 17, 3537. [Google Scholar]
- Yushkevich, P.A.; Piven, J.; Hazlett, H.C.; Smith, R.G.; Ho, S.; Gee, J.C.; Gerig, G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage 2006, 31, 1116–1128. [Google Scholar] [CrossRef] [Green Version]
- Mattes, D.; Haynor, D.R.; Vesselle, H.; Lewellyn, T.K.; Eubank, W. Nonrigid multimodality image registration. In Medical Imaging 2001: Image Processing; International Society for Optics and Photonics: San Diego, CA, USA, 2009; Volume 4322, pp. 1609–1620. [Google Scholar]
- White, R.L.; Helfand, D.J.; Becker, R.H.; Glikman, E.; de Vries, W. Signals from the Noise Image Stacking for Quasars in the FIRST Survey. Astrophys. J. 2006, 208, 99. [Google Scholar] [CrossRef] [Green Version]
- Lowekamp, B.C.; Chen, D.T.; Ibáñez, L.; Blezek, D. The design of simpleITK. Front. Neuroinform. 2013, 7, 45. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R.J. Fast computation of the median by successive binning. arXiv 2008, arXiv:0806.3301. [Google Scholar]
- Welford, B.P. Note on a Method for Calculating Corrected Sums of Squares and Products. Technometrics 1962, 4, 419–420. [Google Scholar] [CrossRef]
- Dice, L.R. Measures of the Amount of Ecologic Association between Species; Ecological Society of America Stable: Washington, DC, USA, 1945; pp. 297–302. Available online: http://www.jstor.org/stable/1932409 (accessed on 2 November 2020).
- Huttenlocher, D.P.; Rucklidge, W.J.; Klanderman, G.A. Comparing images using the Hausdorff distance under translation. In Proceedings of the 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Champaign, IL, USA, 15–18 June 1992. [Google Scholar] [CrossRef]
- Rote, G. Computing the minimum Hausdorff distance between two point sets on a line under translation. Inf. Process. Lett. 1991, 38, 123–127. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Ou, Y.; Akbari, H.; Bilello, M.; Da, X.; Davatzikos, C. Comparative evaluation of registration algorithms in different brain databases with varying difficulty: Results and insights. IEEE Trans. Med. Imaging 2014, 33, 2039–2065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scheys, L.; Loeckx, D.; Spaepen, A.; Suetens, P.; Jonkers, I. Atlas-based non-rigid image registration to automatically define line-of-action muscle models: A validation study. J. Biomech. 2009, 42, 565–572. [Google Scholar] [CrossRef]
- Karlsson, A.; Rosander, J.; Romu, T.; Tallberg, J.; Grönqvist, A.; Borga, M.; Dahlqvist Leinhard, O. Automatic and quantitative assessment of regional muscle volume by multi-atlas segmentation using whole-body water-fat MRI. J. Magn. Reson. Imaging 2015, 41, 1558–1569. [Google Scholar] [CrossRef]
- Benito, P.J.; Cupeiro, R.; Ramos-Campo, D.J.; Alcaraz, P.E.; Rubio-Arias, J. A systematic review with meta-analysis of the effect of resistance training on whole-body muscle growth in healthy adult males. Int. J. Environ. Res. Public Health 2020, 17, 1285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Y.; Arfat, Y.; Wang, H.; Goswami, N. Muscle atrophy induced by mechanical unloading: Mechanisms and potential countermeasures. Front. Physiol. 2018, 9, 235. [Google Scholar] [CrossRef]
- Bouhrara, M.; Lehallier, B.; Clerjon, S.; Damez, J.L.; Bonny, J.M. Mapping of muscle deformation during heating: In situ dynamic MRI and nonlinear registration. Magn. Reson. Imaging 2012, 30, 422–430. [Google Scholar] [CrossRef] [PubMed]
- Vos, S.B.; Jones, D.K.; Viergever, M.A.; Leemans, A. Partial volume effect as a hidden covariate in DTI analyses. Neuroimage 2011, 55, 1566–1576. [Google Scholar] [CrossRef]
- Oouchi, H.; Yamada, K.; Sakai, K.; Kizu, O.; Kubota, T.; Ito, H.; Nishimura, T. Diffusion anisotropy measurement of brain white matter is affected by voxel size: Underestimation occurs in areas with crossing fibers. Am. J. Neuroradiol. 2007, 28, 1102–1106. [Google Scholar] [CrossRef] [Green Version]
- Hajnal, J.V.; Saeed, N.; Oatridge, A.; Williams, E.J.; Young, I.R.; Bydder, G.M. Detection of subtle brain changes using sub voxel registration and subtraction of serial mr images. J. Comput. Assist. Tomogr. 1995, 19, 677–691. [Google Scholar] [CrossRef]
- Blaffert, T.; Wiemker, R. Comparison of different follow-up lung registration methods with and without segmentation. In Proceedings of the Medical Imaging 2004: Image Processing, San Diego, CA, USA, 16–19 February 2004; Fitzpatrick, J.M., Sonka, M., Eds.; SPIE: St. Bellingham, WA, USA, 2004; p. 1701. [Google Scholar]



| Rigid Registration | Elastic Registration | |
|---|---|---|
| Transformation | Euler transform (6 parameters) | FFD based on cubic B-Splines |
| Similarity metric | Mattes Mutual Information | Mattes Mutual Information |
| Sampling strategy for metric evaluation | 50% of voxels randomly chosen | 50% of voxels randomly chosen |
| Optimizer | Gradient descent | Gradient descent |
| Number of iterations | 5000 | 2000 |
| Minimum convergence value | 10−7 | 10−7 |
| Number of multi-resolution steps | 3 | 2 |
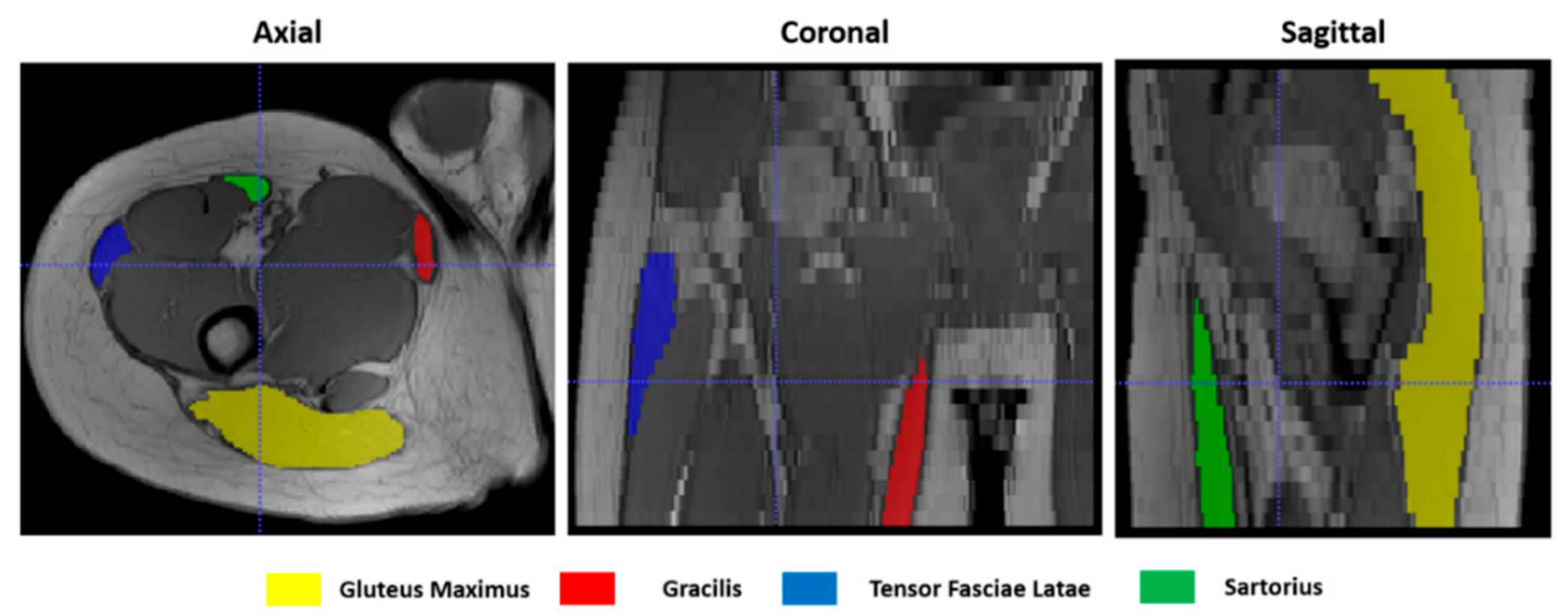
| Subject | Muscle Volume (cm3) | |||||||
|---|---|---|---|---|---|---|---|---|
| Sartorius | Gracilis | Gluteus Maximus | Tensor Fasciae Latae | |||||
| t0 | t1 | t0 | t1 | t0 | t1 | t0 | t1 | |
| 1 | 33.5 | 33.29 | 11.65 | 12.80 | 330.80 | 351.30 | 41.80 | 42.82 |
| 2 | 30.66 | 30.34 | 15.83 | 15.90 | 306.80 | 309.50 | 31.39 | 37.79 |
| 3 | 18.22 | 19.43 | 12.76 | 15.41 | 316.50 | 296.00 | 14.82 | 17.00 |
| 4 | 15.40 | 18.71 | 11.15 | 13.98 | 351.50 | 346.30 | 40.96 | 37.85 |
| 5 | 40.02 | 51.32 | 12.93 | 11.58 | 588.20 | 610.00 | 69.50 | 72.93 |
| 6 | 23.32 | 26.21 | 21.83 | 28.94 | 326.60 | 353.10 | 26.48 | 30.07 |
| mean | 26.85 | 30.42 | 14.36 | 16.79 | 370.07 | 380.87 | 37.46 | 39.74 |
| std. dev. | 9.49 | 12.24 | 4.00 | 6.14 | 107.92 | 115.65 | 18.58 | 18.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fontana, L.; Mastropietro, A.; Scalco, E.; Peruzzo, D.; Beretta, E.; Strazzer, S.; Arrigoni, F.; Rizzo, G. Multi-Steps Registration Protocol for Multimodal MR Images of Hip Skeletal Muscles in a Longitudinal Study. Appl. Sci. 2020, 10, 7823. https://doi.org/10.3390/app10217823
Fontana L, Mastropietro A, Scalco E, Peruzzo D, Beretta E, Strazzer S, Arrigoni F, Rizzo G. Multi-Steps Registration Protocol for Multimodal MR Images of Hip Skeletal Muscles in a Longitudinal Study. Applied Sciences. 2020; 10(21):7823. https://doi.org/10.3390/app10217823
Chicago/Turabian StyleFontana, Lucia, Alfonso Mastropietro, Elisa Scalco, Denis Peruzzo, Elena Beretta, Sandra Strazzer, Filippo Arrigoni, and Giovanna Rizzo. 2020. "Multi-Steps Registration Protocol for Multimodal MR Images of Hip Skeletal Muscles in a Longitudinal Study" Applied Sciences 10, no. 21: 7823. https://doi.org/10.3390/app10217823
APA StyleFontana, L., Mastropietro, A., Scalco, E., Peruzzo, D., Beretta, E., Strazzer, S., Arrigoni, F., & Rizzo, G. (2020). Multi-Steps Registration Protocol for Multimodal MR Images of Hip Skeletal Muscles in a Longitudinal Study. Applied Sciences, 10(21), 7823. https://doi.org/10.3390/app10217823








