Novel Application of Uncertainty Analysis Methods for Quantitative Precipitation Estimation Based on Weather Radars in the Korean Peninsula
Abstract
:1. Introduction
2. Uncertainty Quantification Methods in Radar-Based Precipitation Estimation
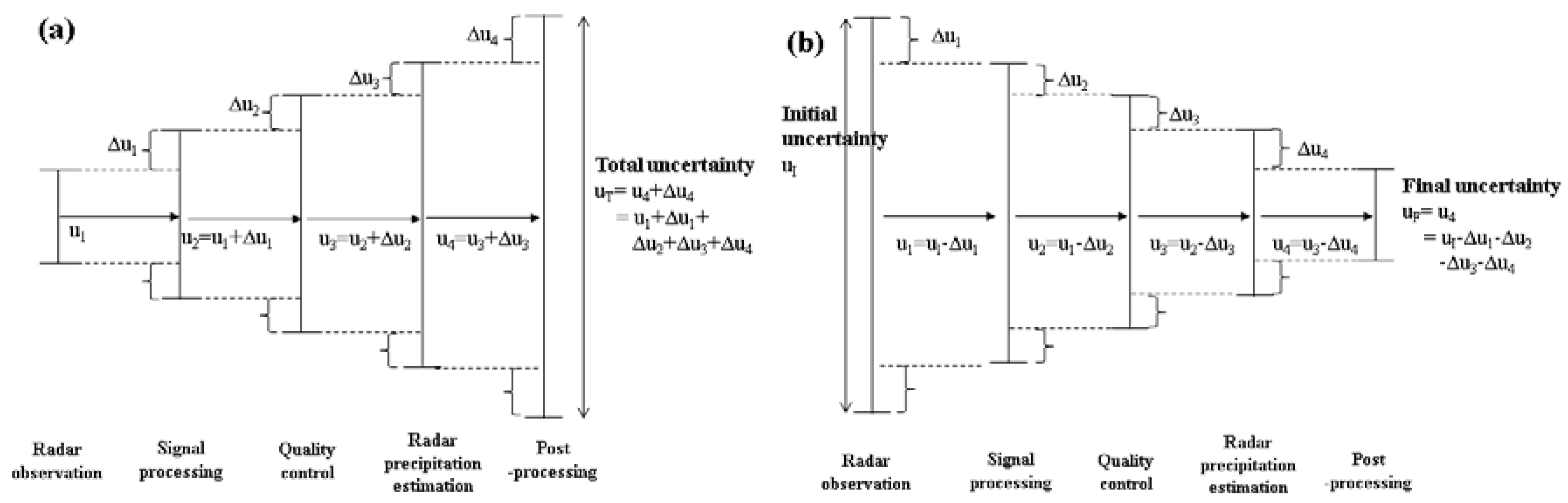
2.1. Identification of Uncertainty Propagation
2.2. How to Quantify Uncertainty
2.2.1. Maximum Entropy Method
2.2.2. Uncertainty Delta Method
2.2.3. Modified-Fractional Uncertainty Method
3. Application of Uncertainty Quantification Methods and Results
3.1. Application Outline
3.1.1. Data
3.1.2. Quality Control
3.1.3. Quantitative Precipitation Estimation
3.1.4. Post-Processing
3.2. Results of Quantitative Radar-Based Precipitation Estimation
3.3. Results and Discussion of Uncertainty Quantification
3.3.1. Analysis of Quantified Uncertainty
3.3.2. Discussion of the Uncertainty Quantification
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huff, F.A. Sampling errors in measurement of mean precipitation. J. Appl. Meteorol. 1970, 9, 35–44. [Google Scholar] [CrossRef]
- Woodley, W.; Olsen, A.; Herndon, A.; Wiggert, V. Comparison of gage and radar methods of convective rain measurement. J. Appl. Meteorol. 1975, 14, 909–928. [Google Scholar] [CrossRef] [Green Version]
- Wilson, J.W.; Brandes, E.A. Radar measurement of rainfall: A Summary. Bull. Am. Meteorol. Soc. 1979, 60, 1048–1058. [Google Scholar] [CrossRef] [Green Version]
- Austin, P.M. Relation between measured radar reflectivity and surface rainfall. Mon. Weather Rev. 1987, 115, 1053–1070. [Google Scholar] [CrossRef] [Green Version]
- Campos, E.; Zawadzki, I. Instrumental uncertainties in Z–R relations. J. Appl. Meteorol. 2000, 39, 1088–1102. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Smith, J. Radar hydrology: Rainfall estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Shakti, P.C.; Maki, M. Application of a modified digital elevation model method to correct radar reflectivity of X-band dual-polarization radars in mountainous regions. Hydrol. Res. Lett. 2014, 8, 77–83. [Google Scholar] [CrossRef] [Green Version]
- Park, S.G.; Bringi, V.N.; Chandrasekar, V.; Maki, M.; Iwanami, K. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band. Part I: Theoretical and empirical basis. J. Atmos. Ocean. Technol. 2005, 22, 1621–1632. [Google Scholar] [CrossRef] [Green Version]
- Park, S.G.; Maki, M.; Iwanami, K.; Bringi, V.N.; Chandrasekar, V. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band. Part II: Evaluation and application. J. Atmos. Ocean. Technol. 2005, 22, 1633–1655. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Empirically-based modeling of spatial sampling uncertainties associated with rainfall measurements by rain gauges. Adv. Water Resour. 2008, 31, 1015–1023. [Google Scholar] [CrossRef]
- Sebastianelli, S.; Fabio, R.; Napolitano, F.; Baldini, L. On precipitation measurements collected by a weather radar and a rain gauge network. Nat. Hazard Earth Syst. 2013, 13, 605–623. [Google Scholar] [CrossRef] [Green Version]
- Jordan, P.; Seed, A.; Austin, G. Sampling errors in radar estimates of rainfall. J. Geophys. Res. 2000, 105, 2247–2257. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Sensitivity studies of the models of radar-rainfall uncertainties. J. Appl. Meteorol. Clim. 2010, 49, 288–309. [Google Scholar] [CrossRef]
- Moulin, L.; Gaume, E.; Obled, C. Uncertainties in mean areal precipitation: Assessment and impact on streamflow simulations. Hydrol. Earth Syst. Sci. 2009, 13, 99–114. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-S.; Kang, M.-Y.; Lee, D.-I.; Kim, J.-H.; Choi, B.-C.; Kim, K.E. Reflectivity Z and differential reflectivity ZDR correction for polarimetric radar rainfall measurement. In Proceedings of the Spring Meeting of Korean Meteorological Society, Goyang-si Kintex, Korea, 12 October 2006; pp. 130–131. [Google Scholar]
- Germann, U.; Galli, G.; Boscacci, M.; Bolliger, M. Radar precipitation measurement in a mountainous region. Q. J. R. Meteor. Soc. 2006, 132, 1669–1692. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F. On the estimation of radar rainfall error variance. Adv. Water Resour. 1999, 22, 585–595. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F.; Villarini, G. Product-error-driven uncertainty model for probabilistic quantitative precipitation estimation with NEXRAD data. J. Hydrometeorol. 2007, 8, 1325–1347. [Google Scholar] [CrossRef]
- Zhang, Y.; Adams, T.; Bonta, J.V. Subpixelscale rainfall variability and the effects on the separation of radar and gauge rainfall errors. J. Hydrometeorol. 2007, 8, 1348–1363. [Google Scholar] [CrossRef]
- Oh, H.-M.; Ha, K.-J.; Kim, K.-E.; Bae, D.-H. Precipitation rate combined with the use of optimal weighting of radar and rain gauge data. Atmos. Korean Meteorol. Soc. 2003, 13, 316–317. [Google Scholar]
- Yoo, C.; Kim, J.; Yoon, J.; Park, C.; Park, C.; Jun, C. Use of the Kalman filter for the correction of mean-field bias of radar rainfall. In Proceedings of the 5th Korea-Japan-China Joint Conference on Meteorology, Busan, Korea, 24–26 October 2011. [Google Scholar]
- Krajewski, W.F.; Villarini, G.; Smith, J.A. Radar-rainfall uncertainties. Bull. Am. Meteorol. Soc. 2010, 91, 87–94. [Google Scholar] [CrossRef]
- McMillan, H.; Jackson, B.; Clark, M.; Kavetski, D.; Woods, R. Rainfall uncertainty in hydrological modeling: An evaluation of multiplicative error models. J. Hydrol. 2011, 400, 83–94. [Google Scholar] [CrossRef]
- Jones, R.N. Managing uncertainty in climate change projections—Issues for impact assessment: An editorial comment. Clim. Change 2000, 45, 403–419. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2001: Impacts, Adaptations, and Vulnerability; Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Gay, C.; Estrada, F. Objective probabilities about future climate are a matter of opinion. Clim. Chang. 2010, 99, 27–46. [Google Scholar] [CrossRef]
- Kottegoda, N.T.; Rosso, R. Statistics, Probability, and Reliability for Civil and Environmental Engineers; McGraw-Hill: New York, NY, USA, 1997; pp. 61–64. [Google Scholar]
- Hawkins, E.D.; Sutton, R. The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1107. [Google Scholar] [CrossRef] [Green Version]
- Weather Radar Center. Weather Radar Data Analysis Guidance; Weather Radar Center Technical Note; Weather Radar Center: Seoul, Korea, 2013.
- Rosenfeld, D.; Wolff, D.B.; Amitai, E. The window probability matching method for rainfall measurements with radar. J. Appl. Meteorol. 1994, 33, 682–693. [Google Scholar] [CrossRef] [Green Version]
- Marshall, J.S.; Langille, R.C.; Palmer, W.M.K. Measurement of rainfall by radar. J. Meteorol. 1947, 4, 186–192. [Google Scholar] [CrossRef]
- Morin, E.; Maddox, R.A.; Goodrich, S.; Sorooshin, S. Radar Z-R Relationship for summer monsoon storm in Arizona. Weather Forecast 2005, 20, 672–679. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Howard, K.; Langston, C.; Vasiloff, S.; Kaney, B.; Arthur, A.; Van Cooten, S.; Kelleher, K.; Kitzmiller, D.; Ding, F. National mosaic and multi-sensor QPE (NMW) system. Bull. Am. Meteorol. Soc. 2011, 92, 1321–1338. [Google Scholar] [CrossRef] [Green Version]



| (a) Weather radars. | |||||
| Item | Detail | ||||
| Radar | 11 single-polarization radars operated by the Korea Meteorological Administration: Baegnyeondo (BRI, S-band), Kwanaksan (KWK, S-band), Oseonsan (KSN, S-band), Jindo (JNI, S-band), Gosan (GSN, S-band), Seongsan (SSP, S-band), Gudeoksan (PSN, S-band), Myeonbongsan (MYN, C-band), Gangneung (GNG, S-band), Gwnagdeoksan (GDK, S-band), Incheon (IIA, C-band) | ||||
| Calibration data | 18 Precipitation cases from 1 June 2012 to 31 September 2016 | ||||
| (b) Precipitation cases (* represents the observed spatial-averaged precipitation intensity from automatic weather stations (AWSs)). LST: local standard time. | |||||
| Case | Period (LST) | Source | Case | Period (LST) | Source |
| Case1 | 18062012 00:00 –19062012 13:00 | Changma front (15.0 mm/h) * | Case10 | 22082012 22:00 –25082012 11:00 | Local torrential precipitation (22.9 mm/h) |
| Case2 | 23062012 13:00 –24062012 19:00 | Local torrential precipitation (8.6 mm/h) | Case11 | 27082012 13:00 –28082012 18:00 | Changma front and Typhoon (32.0 mm/h) |
| Case3 | 29062012 08:00 –01072012 01:00 | Changma front (11.0 mm/h) | Case12 | 29082012 15:00 –30082012 23:00 | Typhoon (18.1 mm/h) |
| Case4 | 05072012 04:00 –07072012 02:00 | Changma front (17.1 mm/h) | Case13 | 06082013 13:00 –06082013 16:00 | Local torrential precipitation (29.7 mm/h) |
| Case5 | 10072012 10:00 –11072012 19:00 | Changma front (20.8 mm/h) | Case14 | 29082013 13:00 –29082013 18:00 | Local torrential precipitation (34.9 mm/h) |
| Case6 | 12072012 23:30 –13072012 07:30 | Changma front (27.0 mm/h) | Case15 | 13092013 01:00 –13092013 14:00 | Local torrential precipitation (24.2 mm/h) |
| Case7 | 14072012 08:00 –15072012 15:00 | Changma front (29.2 mm/h) | Case16 | 31072014 12:00 –31072014 18:00 | Local torrential precipitation (23.5 mm/h) |
| Case8 | 18072012 14:00 –19072012 13:00 | Typhoon (45.0 mm/h) | Case17 | 27082016 15:00 ~28082016 18:50 | Changma front (29.5 mm/h) |
| Case9 | 10082012 03:00 –10082012 22:00 | Local torrential precipitation (24.9 mm/h) | Case18 | 29092016 17:00 ~3092016 01:50 | Local torrential precipitation (23.4 mm/h) |
| (a) Accuracy of the quality control algorithms (open radar product generator: ORPG and fuzzy algorithms). | ||
| Accuracy | ORPG | Fuzzy |
| RMSE (mm/h) | 8.56 | 8.32 |
| Correlation Coefficient | 0.79 | 0.81 |
| (b) Accuracy of bias correction methods (gauge-to-radar: G/R ratio; local gauge correction: LGC methods). | ||
| Accuracy | G/R ratio | LGC |
| RMSE (mm/h) | 7.29 | 6.06 |
| Correlation coefficient | 0.93 | 0.94 |
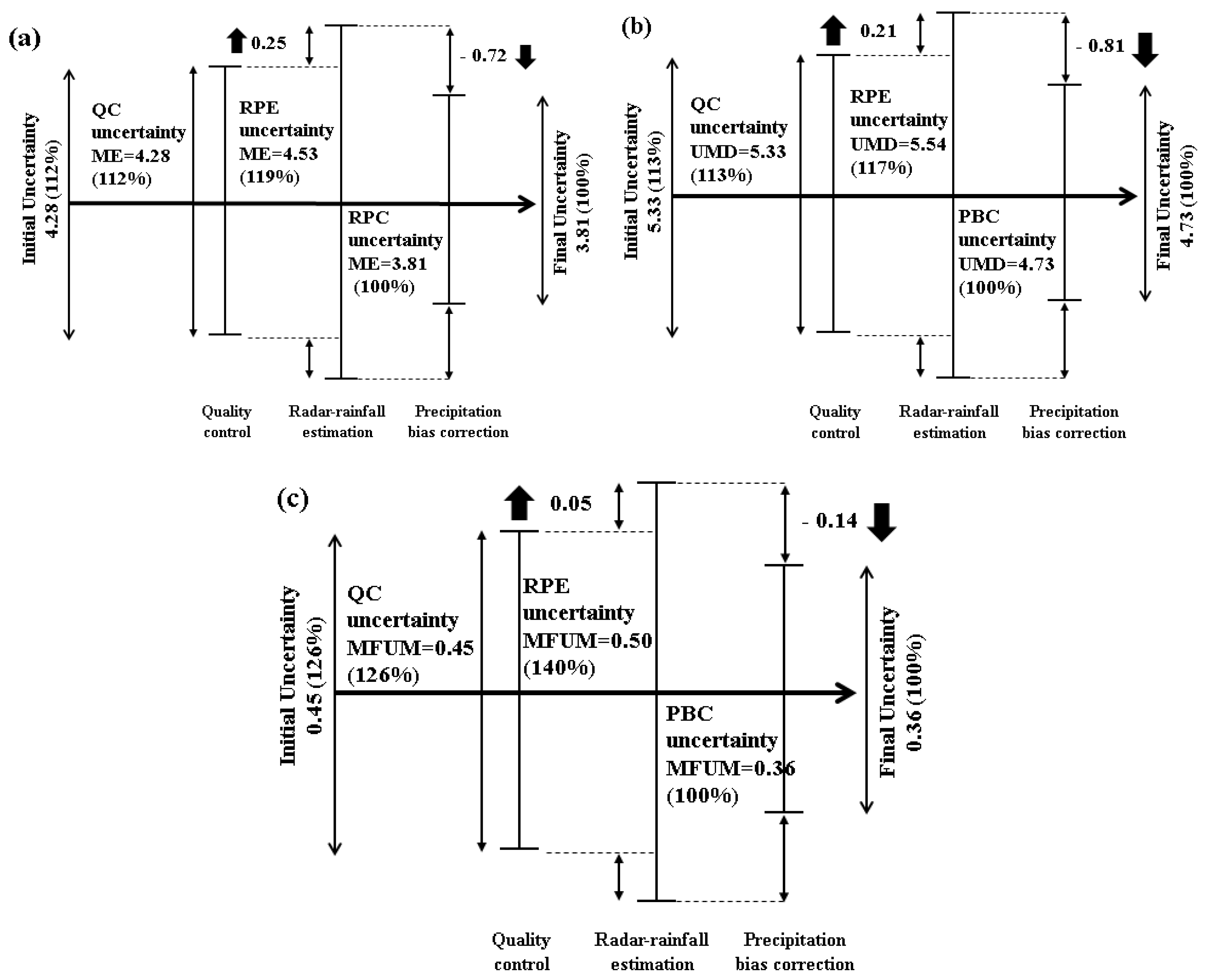
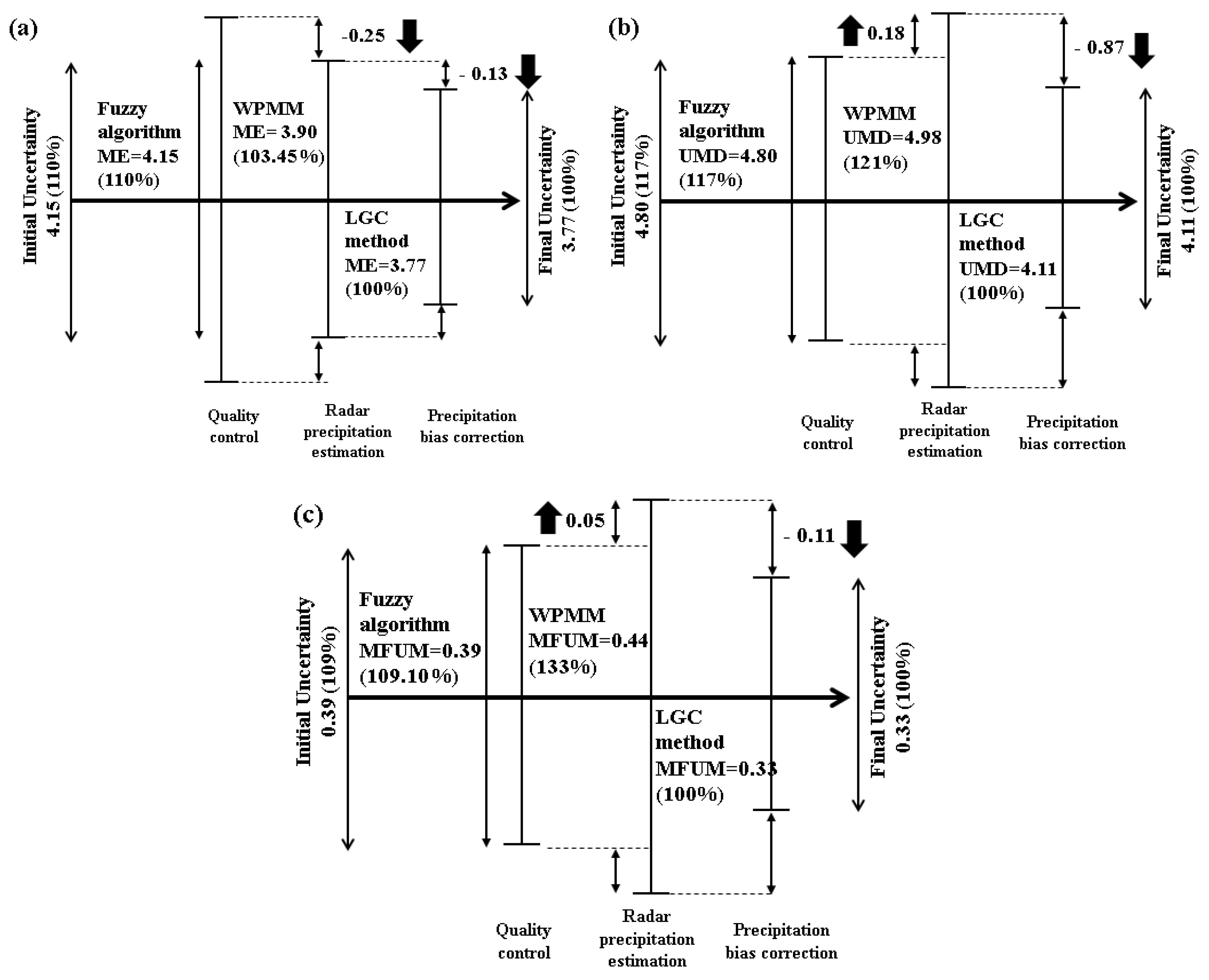
| (a) MEM. | |||||
| Procedure | MEV ** | Maximum of ME | Incremental | Ratio (%) to the Final Uncertainty | |
| Initial uncertainty | 4.28 | 4.28 | - | 112 | |
| QC * | ORPG | 4.28 | 4.28 | - | 112 |
| Fuzzy | 4.15 | ||||
| RPE * | WPMM | 3.90 | 4.53 | 0.25 | 119 (+7) |
| M–P | 4.53 | ||||
| PBC * | LGC | 3.77 | 3.81 | −0.72 | 100 (−19) |
| G/R ratio | 3.81 | ||||
| Final uncertainty | 3.81 | 3.81 | - | 100 | |
| (b) Uncertainty Delta method (UDM). | |||||
| Procedure | UMD | Maximum of UMD | Final UMD | Ratio (%) to the Final Uncertainty | |
| Initial uncertainty | 5.33 | 5.33 | - | 113 | |
| QC | ORPG | 5.33 | 5.33 | 5.33 | 113 |
| Fuzzy | 4.80 | ||||
| RPE | WPMM | 0.18 | 0.21 | 5.54 | 117 (+4) |
| M–P | 0.21 | ||||
| PBC | LGC | −0.79 | −0.81 | 4.73 | 100 (−17) |
| G/R ratio | −0.81 | ||||
| Final uncertainty | 4.73 | 4.73 | 4.73 | 100 | |
| (c) Modified-fractional uncertainty method (M-FUM). | |||||
| Procedure | M-FUM | Maximum of M-FUM | Incremental | Ratio (%) to the Final Uncertainty | |
| Initial uncertainty | 0.45 | 0.45 | - | 126 | |
| QC | ORPG | 0.45 | 0.45 | - | 126 |
| Fuzzy | 0.39 | ||||
| RPE | WPMM | 0.44 | 0.50 | 0.05 | 140 (+14) |
| M–P | 0.50 | ||||
| PBC | LGC | 0.33 | 0.36 | −0.14 | 100 (−40) |
| G/R ratio | 0.36 | ||||
| Final uncertainty | 0.36 | 0.36 | - | 100 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-K.; Song, C.G. Novel Application of Uncertainty Analysis Methods for Quantitative Precipitation Estimation Based on Weather Radars in the Korean Peninsula. Appl. Sci. 2020, 10, 7928. https://doi.org/10.3390/app10217928
Lee J-K, Song CG. Novel Application of Uncertainty Analysis Methods for Quantitative Precipitation Estimation Based on Weather Radars in the Korean Peninsula. Applied Sciences. 2020; 10(21):7928. https://doi.org/10.3390/app10217928
Chicago/Turabian StyleLee, Jae-Kyoung, and Chang Geun Song. 2020. "Novel Application of Uncertainty Analysis Methods for Quantitative Precipitation Estimation Based on Weather Radars in the Korean Peninsula" Applied Sciences 10, no. 21: 7928. https://doi.org/10.3390/app10217928
APA StyleLee, J.-K., & Song, C. G. (2020). Novel Application of Uncertainty Analysis Methods for Quantitative Precipitation Estimation Based on Weather Radars in the Korean Peninsula. Applied Sciences, 10(21), 7928. https://doi.org/10.3390/app10217928




