Novel Resistive Sensor Design Utilizing the Geometric Freedom of Additive Manufacturing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Design Methodology
2.2. The Additive Manufacturing Process and Design Variants
2.3. Experimental Set-Up
3. Results
3.1. Mechanical Behavior
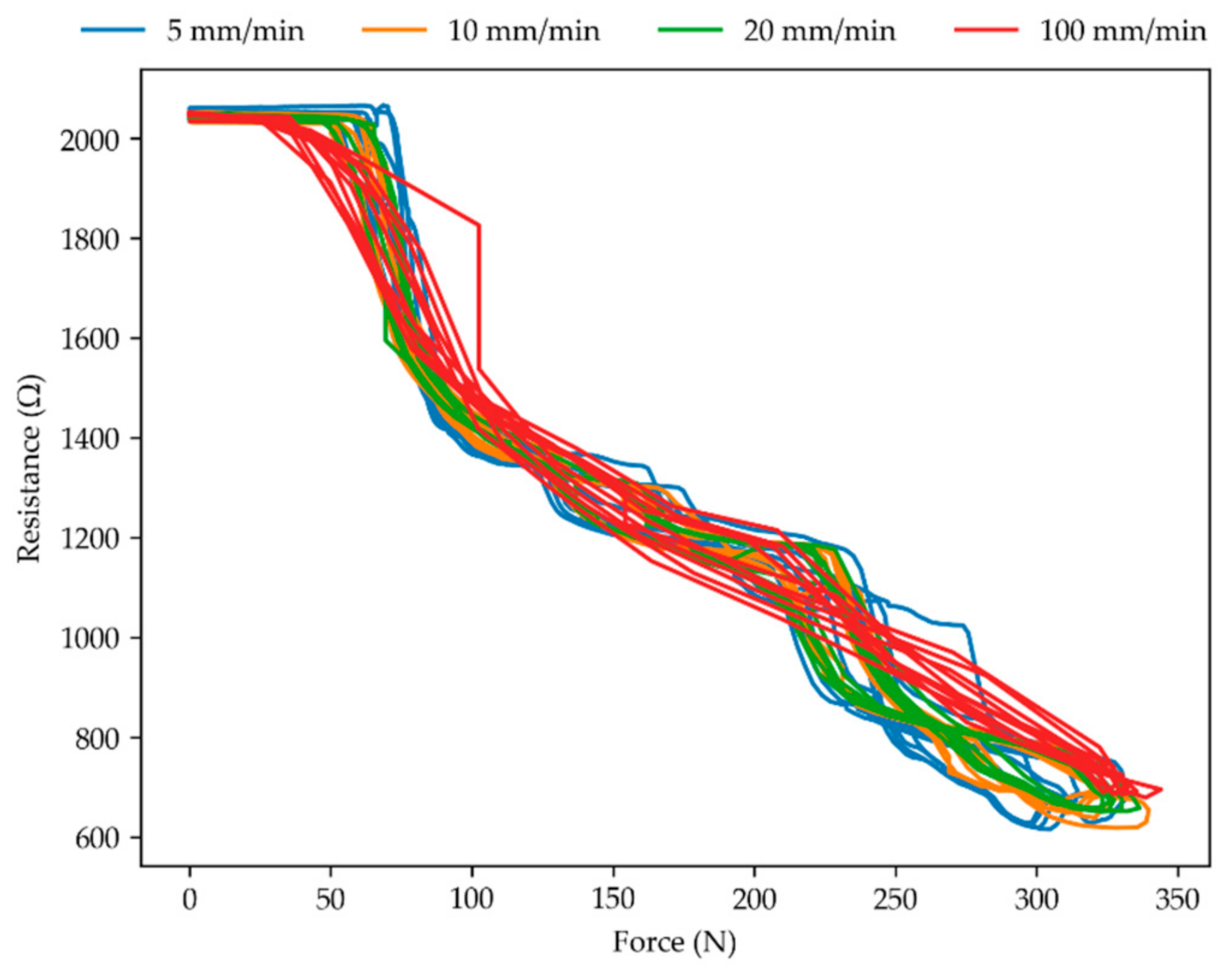
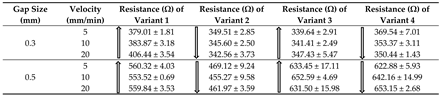
3.2. Resistive Behavior
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Postiglione, G.; Natale, G.; Griffini, G.; Levi, M.; Turri, S. Conductive 3D microstructures by direct 3D printing of polymer/carbon nanotube nanocomposites via liquid deposition modeling. Compos. Part A 2015, 76, 110–114. [Google Scholar] [CrossRef]
- CEN European Committee for Standardization. DIN EN ISO/ASTM 52900:2018: Additive Manufacturing-General Principles-Terminology; CEN European Committee for Standardization: Brussels, Belgium, 2018. [Google Scholar]
- Agarwala, S.; Goh, G.L.; Le, T.-S.D.; An, J.; Peh, Z.K.; Yeong, W.Y.; Kim, Y.-J. Wearable bandage-based strain sensor for home healthcare: Combining 3D aerosol jet printing and laser sintering. ACS Sensors 2018, 4, 218–226. [Google Scholar] [CrossRef] [PubMed]
- Lehmhus, D.; Aumund-Kopp, C.; Petzoldt, F.; Godlinski, D.; Haberkorn, A.; Zöllmer, V.; Busse, M. Customized smartness: A survey on links between additive manufacturing and sensor integration. Procedia Technol. 2016, 26, 284–301. [Google Scholar] [CrossRef]
- Vaezi, M.; Chianrabutra, S.; Mellor, B.; Yang, S. Multiple material additive manufacturing–Part 1: A review. Virtual Phys. Prototyp. 2013, 8, 19–50. [Google Scholar] [CrossRef]
- Watschke, H.; Hilbig, K.; Vietor, T. Design and characterization of electrically conductive structures additively manufactured by material extrusion. Appl. Sci. 2019, 9, 779. [Google Scholar] [CrossRef] [Green Version]
- Zapciu, A.; Constantin, G. Additive manufacturing integration of thermoplastic conductive materials in intelligent robotic end effector systems. Proc. Manuf. Syst. 2016, 11, 201–206. [Google Scholar]
- Hampel, B.; Monshausen, S.; Schilling, M. Properties and applications of electrically conductive thermoplastics for additive manufacturing of sensors. TM-Tech. Mess. 2017, 84, 593–599. [Google Scholar] [CrossRef]
- Brink, M.; Ohlendorf, J.-H.; Thoben, K.-D. Development of a handling system with integrated sensors for textile preforms using additive manufacturing. Procedia Manuf. 2018, 24, 114–119. [Google Scholar] [CrossRef]
- Stano, G.; Percoco, G. Design, 3D printing and characterization of a soft actuator with embedded strain sensor. In Proceedings of the 2020 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Bari, Italy, 1 June–1 July 2020; pp. 1–6. [Google Scholar]
- Shemelya, C.; Cedillos, F.; Aguilera, E.; Espalin, D.; Muse, D.; Wicker, R.; Macdonald, E. Encapsulated copper wire and copper mesh capacitive sensing for 3-D printing applications. IEEE Sensors J. 2014, 15, 1280–1286. [Google Scholar] [CrossRef]
- Jaksic, N.I.; Desai, P.D. Characterization of resistors created by fused filament fabrication using electrically-conductive filament. Procedia Manuf. 2018, 17, 37–44. [Google Scholar] [CrossRef]
- Flowers, P.F.; Reyes, C.; Ye, S.; Kim, M.J.; Wiley, B.J. 3D printing electronic components and circuits with conductive thermoplastic filament. Addit. Manuf. 2017, 18, 156–163. [Google Scholar] [CrossRef]
- Schouten, M.; Sanders, R.; Krijnen, G. 3D printed flexible capacitive force sensor with a simple micro-controller based readout. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Kim, W.S.; Kim, W.S. Toward a smart compliant robotic gripper equipped with 3D-designed cellular fingers. Adv. Intell. Syst. 2019, 1, 1900019. [Google Scholar] [CrossRef] [Green Version]
- Christ, J.F.; Aliheidari, N.; Ameli, A.; Pötschke, P. 3D printed highly elastic strain sensors of multiwalled carbon nanotube/thermoplastic polyurethane nanocomposites. Mater. Des. 2017, 131, 394–401. [Google Scholar] [CrossRef]
- Kwok, S.W.; Goh, K.H.H.; Tan, Z.D.; Tan, S.T.M.; Tjiu, W.W.; Soh, J.Y.; Ng, Z.J.G.; Chan, Y.Z.; Hui, H.K.; Goh, K.E.J. Electrically conductive filament for 3D-printed circuits and sensors. Appl. Mater. Today 2017, 9, 167–175. [Google Scholar] [CrossRef]
- Liu, C.; Huang, N.; Xu, F.; Tong, J.; Chen, Z.; Gui, X.; Fu, Y.; Lao, C. 3D printing technologies for flexible tactile sensors toward wearable electronics and electronic skin. Polymers (Basel) 2018, 10, 629. [Google Scholar] [CrossRef] [Green Version]
- Horst, D.J.; Junior, P.P.A. 3D-printed conductive filaments based on carbon nanostructures embedded in a polymer matrix. Int. J. Appl. Nanotechnol. Res. 2019, 4, 26–40. [Google Scholar] [CrossRef]
- Avilés, F.; Oliva-Avilés, A.I.; Cen-Puc, M. Piezoresistivity, strain, and damage self-sensing of polymer composites filled with carbon nanostructures. Adv. Eng. Mater. 2018, 20, 1701159. [Google Scholar] [CrossRef]
- Palmić, T.B.; Slavič, J.; Boltežar, M. Process parameters for FFF 3D-printed conductors for applications in sensors. Sensors 2020, 20, 4542. [Google Scholar] [CrossRef]
- Xiang, D.; Zhang, X.; Harkin-Jones, E.; Zhu, W.; Zhou, Z.; Shen, Y.; Li, Y.; Zhao, C.; Wang, P. Synergistic effects of hybrid conductive nanofillers on the performance of 3D printed highly elastic strain sensors. Compos. Part A 2020, 129, 105730. [Google Scholar] [CrossRef]
- Leigh, S.J.; Bradley, R.J.; Purssell, C.P.; Billson, D.R.; Hutchins, D.A. A simple, low-cost conductive composite material for 3D printing of electronic sensors. PLoS ONE 2012, 7, e49365. [Google Scholar] [CrossRef]
- Christ, J.F.; Aliheidari, N.; Pötschke, P.; Ameli, A. Bidirectional and stretchable piezoresistive sensors enabled by multimaterial 3D printing of carbon nanotube/thermoplastic polyurethane nanocomposites. Polymers (Basel) 2018, 11, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maurizi, M.; Slavič, J.; Cianetti, F.; Jerman, M.; Valentinčič, J.; Lebar, A.; Boltežar, M. Dynamic measurements using FDM 3D-printed embedded strain sensors. Sensors 2019, 19, 2661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dul, S.; Pegoretti, A.; Fambri, L. Fused filament fabrication of piezoresistive carbon nanotubes nanocomposites for strain monitoring. Front. Mater. 2020, 7, 7. [Google Scholar] [CrossRef] [Green Version]
- Dijkshoorn, A.; Werkman, P.; Welleweerd, M.; Wolterink, G.; Eijking, B.; Delamare, J.; Sanders, R.; Krijnen, G.J.M. Embedded sensing: Integrating sensors in 3-D printed structures. J. Sensors Sens. Syst. 2018, 7, 169–181. [Google Scholar] [CrossRef] [Green Version]
- Schouten, M.; Prakken, B.; Sanders, R.; Krijnen, G. Linearisation of a 3D printed flexible tactile sensor based on piezoresistive sensing. In Proceedings of the 2019 IEEE Sensors Applications Symposium (SAS), Montreal, QC, Canada, 27–30 October 2019; pp. 1–4. [Google Scholar]
- Kim, K.; Park, J.; Suh, J.-h.; Kim, M.; Jeong, Y.; Park, I. 3D printing of multiaxial force sensors using carbon nanotube (CNT)/thermoplastic polyurethane (TPU) filaments. Sens. Actuators A Phys. 2017, 263, 493–500. [Google Scholar] [CrossRef]
- Hohimer, C.J.; Petrossian, G.; Ameli, A.; Mo, C.; Potschke, P. 3D printed conductive thermoplastic polyurethane/carbon nanotube composites for capacitive and piezoresistive sensing in soft pneumatic actuators. Addit. Manuf. 2020, 34, 101281. [Google Scholar] [CrossRef]
- Mousavi, S.; Howard, D.; Zhang, F.; Leng, J.; Wang, C.H. Direct 3D printing of highly anisotropic, flexible, constriction-resistive sensors for multidirectional proprioception in soft robots. ACS Appl. Mater. Interfaces 2020, 12, 15631–15643. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Reinicke, T. 3D-printed sensors: Current progress and future challenges. Sens. Actuators A Phys. 2020, 305, 111916. [Google Scholar] [CrossRef]
- Pradel, P.; Zhu, Z.; Bibb, R.; Moultrie, J. Investigation of design for additive manufacturing in professional design practice. J. Eng. Des. 2018, 29, 165–200. [Google Scholar] [CrossRef] [Green Version]
- Kumke, M.; Watschke, H.; Hartogh, P.; Bavendiek, A.-K.; Vietor, T. Methods and tools for identifying and leveraging additive manufacturing design potentials. Int. J. Interact. Des. Manuf. 2017, 12, 481–493. [Google Scholar] [CrossRef]
- Bloesch-Paidosh, A.; Shea, K.; Blösch-paidosh, a. design heuristics for additive manufacturing validated through a user study1. J. Mech. Des. 2019, 141, 399. [Google Scholar] [CrossRef]
- Watschke, H.; Kuschmitz, S.; Heubach, J.; Lehne, G.; Vietor, T. A methodical approach to support conceptual design for multi-material additive manufacturing. Proc. Des. Soc. Int. Conf. Eng. Des. 2019, 1, 659–668. [Google Scholar] [CrossRef] [Green Version]
- Freund, R.; Watschke, H.; Heubach, J.; Vietor, T. Determination of influencing factors on interface strength of additively manufactured multi-material parts by material extrusion. Appl. Sci. 2019, 9, 1782. [Google Scholar] [CrossRef] [Green Version]
- Technical data sheet-NinjaFlex® 85A by NinjaTek. Available online: https://ninjatek.com/wp-content/uploads/2019/10/NinjaFlex-TDS.pdf (accessed on 3 November 2020).
- Technical Data Sheet-Conductive pla. Available online: https://www.proto-pasta.com/pages/technical-data-sheets (accessed on 3 November 2020).
- Tan, L.J.; Zhu, W.; Zhou, K. Recent progress on polymer materials for additive manufacturing. Adv. Funct. Mater. 2020, 30, 2003062. [Google Scholar] [CrossRef]
- Ntagios, M.; Escobedo, P.; Dahiya, R. 3D printed robotic hand with embedded touch sensors. In Proceedings of the 2020 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Manchester, UK, 16–19 August 2020; pp. 1–4. [Google Scholar]











| Working Principle | Tensile Load | Compressive Load | Flexural Load |
|---|---|---|---|
| Capacitive | [7,14,23] | ||
| Piezoresistive | [16,22,24,25,26,27] | [7,23,28,29,30] | |
| Resistive path adjustment | [31] | [31] |
| Parameter | Conductive PLA | TPU Variants 1,2, & 4 | TPU Variant 3 |
|---|---|---|---|
| Extrusion width (mm) | 0.4 | 0.4 | 0.4 |
| Nozzle temperature (°C) | 230 | 235 | 235 |
| Bed temperature (°C) | 40 | 40 | 40 |
| Layer height (mm) | 0.2 | 0.2 | 0.2 |
| Infill (%, pattern) | 100, only shells | 100, only shells | 20, honeycomb |
| Extrusion speed (mm/s) | 30 | 35 | 35 |
| Perimeter shells (-) | 3 | 3 | 2 |
| Gap Size (mm) | Velocity (mm/min) | Force (N) (Variant 1) | Force (N) (Variant 2) | Force (N) (Variant 3) | Force (N) (Variant 4) |
|---|---|---|---|---|---|
| 0.3 | 5 | 52.05 ± 0.35 | 110.89 ± 0.56 | 316.46 ± 3.51 | 350.99 ± 12.75 |
| 10 | 52.68 ± 0.35 | 112.93 ± 0.54 | 326.28 ± 7.98 | 435.64 ± 17.14 | |
| 20 | 51.58 ± 0.54 | 114.64 ± 0.61 | 332.75 ± 10.67 | 427.37 ± 7.69 | |
| 0.5 | 5 | 40.28 ± 0.25 | 92.05 ± 0.69 | 203.54 ± 2.27 | 317.16 ± 10.02 |
| 10 | 40.65 ± 0.30 | 99.87 ± 1.60 | 207.25 ± 2.76 | 328.47 ± 7.54 | |
| 20 | 39.24 ± 0.34 | 100.74 ± 0.66 | 206.29 ± 5.88 | 328.65 ± 4.99 |
| Gap Size (mm) | Velocity (mm/min) | Relative Peak Resistance (%) (Variant 1) | Relative Peak Resistance (%) (Variant 2) | Relative Peak Resistance (%) (Variant 3) | Relative Peak Resistance (%) (Variant 4) |
|---|---|---|---|---|---|
| 5 | 19.48 | 29.47 | 17.55 | 21.98 | |
| 0.3 | 10 | 19.72 | 28.56 | 17.43 | 18.68 |
| 20 | 23.79 | 27.23 | 27.08 | 18.14 | |
| 5 | 27.64 | 22.9 | 30.99 | 30.62 | |
| 0.5 | 10 | 27.24 | 22.37 | 31.81 | 31.57 |
| 20 | 27.41 | 22.73 | 30.68 | 32.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watschke, H.; Goutier, M.; Heubach, J.; Vietor, T.; Leichsenring, K.; Böl, M. Novel Resistive Sensor Design Utilizing the Geometric Freedom of Additive Manufacturing. Appl. Sci. 2021, 11, 113. https://doi.org/10.3390/app11010113
Watschke H, Goutier M, Heubach J, Vietor T, Leichsenring K, Böl M. Novel Resistive Sensor Design Utilizing the Geometric Freedom of Additive Manufacturing. Applied Sciences. 2021; 11(1):113. https://doi.org/10.3390/app11010113
Chicago/Turabian StyleWatschke, Hagen, Marijn Goutier, Julius Heubach, Thomas Vietor, Kay Leichsenring, and Markus Böl. 2021. "Novel Resistive Sensor Design Utilizing the Geometric Freedom of Additive Manufacturing" Applied Sciences 11, no. 1: 113. https://doi.org/10.3390/app11010113
APA StyleWatschke, H., Goutier, M., Heubach, J., Vietor, T., Leichsenring, K., & Böl, M. (2021). Novel Resistive Sensor Design Utilizing the Geometric Freedom of Additive Manufacturing. Applied Sciences, 11(1), 113. https://doi.org/10.3390/app11010113





